1 Introduction

With the continuous development of energy technology, electric vehicles have become an important part of the green road in the field of transportation with the advantages of energy-saving and emission reduction [1]. In EV drive systems, permanent magnet synchronous motors are widely used because of their high efficiency, high torque to inertia ratio, high power density, and wide range of operating speeds [2]- [3]. However, the driving system of PMSM is highly nonlinear, strongly coupled, and multivariable [4]. At the same time, the variation of electric vehicle parameters and external load interference make the precise speed regulation of permanent magnet synchronous motor complicated.

For electric vehicles, with the random change of road conditions and the long-term operation of the motor, the motor parameters such as stator resistance, inductance, and permanent magnet flux will change [5]. Due to the model-based backstepping control strategy, its control performance and effect greatly depend on the accuracy of the model [6]. In order to prevent the reduction of motor control performance caused by parameter perturbation, when the motor parameters change, the identified parameters are fed back to the controller and corrected to ensure the control accuracy of the controller. Considering the error of off-line parameter identification of permanent magnet synchronous motor, it is hoped to realize online parameter identification and feedback accurate motor parameters to the control system for motor speed regulation control. Traditional online parameter identification methods include: the least square method, extended Kalman filter method, model parameter adaptive method, and some other intelligent identification (neural network, genetic optimization algorithm). Based on the traditional least square method, the nonlinear least square method is introduced in [8], reducing the parameter identification error and improving the convergence speed. However, only two parameters of resistance and quadrature axis inductance can be identified. Other scholars use the Kalman filter algorithm [9] and neural network intelligent algorithm [10] for identification. However, most algorithms can only identify two parameters, and the amount of calculation is significant, especially the results generated by the intelligent algorithm are uncertain. In order to realize the simultaneous identification of multiple parameters of the motor, people use the model reference adaptive system to identify the stator resistance, inductance, and permanent magnet flux linkage of the permanent magnet synchronous motor. In [11]- [12], when the model refers to the identification parameters of the adaptive system, the adaptive convergence rate of each parameter to be identified is derived with the help of Popov hyperstability theory, which ensures the convergence of the identification algorithm. However, the accuracy of parameter identification depends on the adjustment of PI parameters in the adaptive convergence rate. In the identification parameters of the model reference adaptive system, its performance mainly depends on the design of the adaptive rate. Because it is challenging to select the corresponding Lyapunov function when designing the adaptive rate through Lyapunov, for this reason, there are few reports about the model reference adaptive system identification parameters based on Lyapunov selection of the adaptive rate at home and abroad.

In recent years, people have studied to solve the disturbance problem caused by torque change by introducing disturbance observer (DO) into the control system [13]- [14]. In addition, due to the unmodeled dynamics and time-varying parameters, PMSM cannot establish an accurate mathematical model. These factors are also considered to interfere with the PMSM driving system. Through the combination of DO and sliding mode control method [15], the problem of mismatched interference is solved. However, the disadvantage of sliding mode disturbance observer is that the interference estimation noise is severe, the filter will lead to estimation delay, and the initial estimation peak of the disturbance observer is not taken into account. In reference [16], a finite time disturbance observer is constructed for the PMSM system. The error of the disturbance observer can converge in finite time and reduce the influence of the chattering problem. However, the permanent magnet synchronous motor system may be damaged due to the initial estimated peak value entering the system. In [17], a nonlinear disturbance observer is designed, which has the advantages of simple design and high estimation accuracy. Generally speaking, the accuracy of the observer is improved by increasing the gain coefficient of the disturbance observer, but the estimation peak will be seriously increased due to the increase of the gain. When a larger estimated peak is compensated in the initial time of the system, the hardware will be damaged. Obviously, there are still some challenges in the current methods to suppress the interference of the driving system.

Motivated by these observations, in order to improve the speed, accurate tracking control, and anti-interference ability of the permanent magnet synchronous motor of an electric vehicle, a second-order nonlinear disturbance observer-based adaptive disturbance rejection controller is proposed in this paper. The main contributions of this paper are summarized as follows:

  1. 1

    Considering the time-varying parameters of permanent magnet synchronous motor, a step-by-step online identification method for an improved model reference adaptive system is designed. The adaptive law is set by Lyapunov stability theory to ensure the system’s stability during identification.

  2. 2

    The unmodeled disturbance of the PMSM motor system is estimated, and a time-varying second-order nonlinear disturbance observer is designed to compensate the PMSM controller of the electric vehicle, and the initial estimation peak of the disturbance observer is eliminated.

  3. 3

    Through the backstepping control algorithm combined with the command filter, the direct derivation of the virtual control quantity in the traditional backstepping controller is avoided, and the output signal of the command filter is the derivative of the virtual controller after all.

The rest of this paper is organized as follows. Section 2, the dynamic model of PMSM is established, and some common lemmas are given. In Sect.  3, a model reference adaptive system parameter identification controller based on a second-order disturbance observer (MRAS-SODO) is designed and the stability of the system is proved. Section 4 verifies the effectiveness of the designed synchronous controller through the hardware in the loop simulation platform of permanent magnet synchronous motor. Sect. 5 summarizes the conclusions.

2 Dynamic Model of PMSM

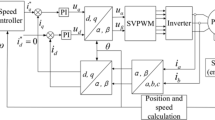
As shown in Fig. 1, the motor drive system of the electric vehicle is mainly composed of the following parts. The direct current (DC) power supply is provided by the electric vehicle battery, the DC bus capacitor can filter out the high-frequency voltage fluctuation, and the inverter is used as the actuator for electric energy conversion [19]- [20]. The dynamic model of PMSM in the dq-frame can be described as

$$\begin{aligned} \begin{aligned}&\frac{{d{i_{d}}}}{{dt}} = - \frac{{{R_s}}}{{{L_s}}}{i_{d}} + p{\omega _m}{i_{q}} + \frac{1}{{{L_s}}}{u_{d}}\\&\frac{{d{i_{q}}}}{{dt}} = - \frac{{{R_s}}}{{{L_s}}}{i_{q}} - p{\omega _m}{i_{d}} - p{\omega _m}\frac{{{\varphi _f}}}{{{L_s}}} + \frac{1}{{{L_s}}}{u_{q}}\\&\frac{{d{\omega _m}}}{{dt}} = \frac{1}{J}\left( {{T_{e}} - B{\omega _m} - {T_{L}} - {T_{d}}} \right) \\&{T_{e}} = \frac{3}{2}p{{\varphi _f}{i_{q}} } \end{aligned} \end{aligned}$$
(1)

where \(i_{d}\), \(i_{q}\), \(u_{d}\) and \(u_{q}\) denote the stator currents and voltages in the dq-frame; \(R_s\) is the stator resistance; \(L_s\) is the stator inductances in the dq-frame; p is the number of pole pairs; \(\varphi _f\) represents the permanent magnet flux; J is the moment of inertia; B is the viscous friction of the rotor; \(T_{e}\) denotes the electromagnetic torque; \(T_{L}\) is the load torque and disturbance torque, respectively, and \(T_{d}\) represents friction torque and some unknown torque.

Fig. 1
figure 1

The PMSM drive system in EVs

Full size image

Define \(\phi _{d} = - \Delta \frac{{3p{\varphi _f}}}{{2J}}{i_q} + \Delta \frac{B}{J}{\omega _m} + \Delta \frac{1}{J}{T_L}\) denotes the unknown lumped disturbance.The mechanical motion equation of dynamic model (1) can be rewritten as

$$\begin{aligned} \begin{aligned} \frac{{d{\omega _m}}}{{dt}} = \frac{{3p{\varphi _f}}}{{2J}}{i_q} - \frac{B}{J}{\omega _m} - \frac{1}{J}{T_L} - {\phi _{d}} \end{aligned} \end{aligned}$$
(2)

2.1 Related Lemmas

To design the proposed control method and stability analysis, the following Lemmas are introduced.

Lemma 1

The polynomial represented by the Hurwitz matrix is stable, and all roots of the polynomial have negative real parts. The coefficient matrix of linear ordinary differential equation is Hurwitz matrix, which is the asymptotic stability of the modified system.

Lemma 2

[21] : Young’s inequality: for any nonnegative real number x,y, the following inequality holds

$$\begin{aligned} \begin{aligned} xy \le \frac{{{x^p}}}{p} + \frac{{{y^q}}}{q} \end{aligned} \end{aligned}$$
(3)

where \({p > 1}\) and \({\frac{1}{p} + \frac{1}{q} = 1}\). The equality sign holds when and only when \({{x^p} = {y^q}}\).

3 Design of the Controller for PMSM of EVs

In this part, we propose an online parameter identification controller based on a second-order nonlinear disturbance observer for PMSM of electric vehicles to improve tracking accuracy and anti-interference efficiency.In this design process, \(\hat{*}\) is defined as the estimated value of variable \(*\), and \(\tilde{*}\) is the estimated error, which satisfies \(\tilde{*} \mathrm{{ = }}\hat{*} - *\).

3.1 Identification Parameter Online

Model reference adaptive system (MRAS) designs the model containing the parameters to be identified as the identification model and takes the existing system as the reference model. Under the same input-output conditions, the errors of the reference model and the identification model are taken as the input of the parameter adaptive convergence rate. The parameters of the identification model are adjusted according to the designed adaptive rate to make the error between it and the reference model converge to zero to complete the online parameter identification.

First, fix the rotor flux linkage \({\varphi _f}\), identify the \({R_s}\) and \({L_s}\) parameters.

Design reference model as

$$\begin{aligned} \begin{aligned} \left( {\begin{array}{*{20}{c}} {{{\dot{i}}_d}}\\ {{{\dot{i}}_q}} \end{array}} \right) =\,&\left( {\begin{array}{*{20}{c}} { - m}&{}{p{\omega _m}}\\ { - p{\omega _m}}&{}{ - m} \end{array}} \right) \left( {\begin{array}{*{20}{c}} {{i_d}}\\ {{i_q}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} n&{}0\\ 0&{}n \end{array}} \right) \left( {\begin{array}{*{20}{c}} {{U_d}}\\ {{U_q}} \end{array}} \right) \\&+ \left( {\begin{array}{*{20}{c}} 0\\ { - p{\omega _m}{\varphi _f}n} \end{array}} \right) \end{aligned} \end{aligned}$$
(4)

Design identification model as

$$\begin{aligned} \begin{aligned} \left( {\begin{array}{*{20}{c}} {\dot{i}_d^c}\\ {\dot{i}_q^c} \end{array}} \right) =\,&\left( {\begin{array}{*{20}{c}} { - {\hat{m}}}&{}{p{\omega _m}}\\ { - p{\omega _m}}&{}{ - {\hat{m}}} \end{array}} \right) \left( {\begin{array}{*{20}{c}} {i_d^c}\\ {i_q^c} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{\hat{n}}}&{}0\\ 0&{}{{\hat{n}}} \end{array}} \right) \left( {\begin{array}{*{20}{c}} {{U_d}}\\ {{U_q}} \end{array}} \right) \\&+ \left( {\begin{array}{*{20}{c}} 0\\ { - p{\omega _m}{\varphi _f}{\hat{n}}} \end{array}} \right) \end{aligned} \end{aligned}$$
(5)

where \({i_d^c}\) and \({i_q^c}\) are the reference values of stator current \({i_d}\) and \({i_q}\) respectively.

Based on the reference model and identification model, the error between them is

$$\begin{aligned} \begin{aligned}&\left( {\begin{array}{*{20}{c}} {{{\dot{i}}_d} - \dot{i}_d^c}\\ {{{\dot{i}}_d} - \dot{i}_q^c} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { - m}&{}{p{\omega _m}}\\ { - p{\omega _m}}&{}{ - m} \end{array}} \right) \left( {\begin{array}{*{20}{c}} {{i_d} - i_d^c}\\ {{i_q} - i_q^c} \end{array}} \right) \\&+ \left( {\begin{array}{*{20}{c}} {i_d^c}&{}{ - {U_d}}\\ {i_q^c}&{}{ - ({U_q} - p{\omega _m}{\varphi _f})} \end{array}} \right) \left( {\begin{array}{*{20}{c}} {{\hat{m}} - m}\\ {{\hat{n}} - n} \end{array}} \right) \end{aligned} \end{aligned}$$
(6)

Define \({e_1} = \left( {\begin{array}{*{20}{c}}{{i_d} - i_d^c}\\ {{i_q} - i_q^c} \end{array}} \right)\), \(A = \left( {\begin{array}{*{20}{c}}{ - m}&{}{p{\omega _m}}\\ { - p{\omega _m}}&{}{ - m} \end{array}} \right)\), \(B = \left( {\begin{array}{*{20}{c}} {i_d^c}&{}{ - {U_d}}\\ {i_q^c}&{}{ - ({U_q} - p{\omega _m}{\varphi _f})} \end{array}} \right)\), \(C = \left( {\begin{array}{*{20}{c}} {{\hat{m}} - m}\\ {{\hat{n}} - n} \end{array}} \right)\)

Transform model (6) to the following form

$$\begin{aligned} \begin{aligned} {\dot{e}_1} = A{e_1} + BC \end{aligned} \end{aligned}$$
(7)

The Lyapunov function is defined as

$$\begin{aligned} \begin{aligned} V\left( {{e_1}} \right) = \frac{1}{2}\left( {e_1^TQ{e_1} + {C^T}KC} \right) \end{aligned} \end{aligned}$$
(8)

where Q and K is a real symmetric positive definite matrix, And \(Q = K\mathrm{{ = }}\left( {\begin{array}{*{20}{c}}1&{}0\\ 0&{}1\end{array}} \right)\).

Combining (7), the derivative of \(V\left( {{e_1}} \right)\) is

$$\begin{aligned} \begin{aligned} \dot{V}\left( {{e_1}} \right) = \frac{1}{2}\left( {\dot{e}_1^TQ{e_1} + e_1^TQ{{\dot{e}}_1} + {{\dot{C}}^T}KC + {C^T}K\dot{C}} \right) \end{aligned} \end{aligned}$$
(9)

where \(\left\{ {\begin{array}{*{20}{c}} {{} {} {} {} \dot{e}_1^TQ{e_1} = {C^T}{B^T}Q{e_1} + e_1^T{A^T}Q{e_1}}\\ {e_1^TQ{{\dot{e}}_1} = e_1^TQA{e_1} + e_1^TQBC{} {} {} {} {} {} {} {} {} {} {} {} {} {} } \end{array}} \right.\), The dynamic model (9) can be rewritten as

$$\begin{aligned} \begin{aligned}&\dot{V}\left( {{e_1}} \right) = \frac{1}{2}\left[ e_1^T\left( {{A^T}Q + QA} \right) {e_1} + {C^T}{B^T}Q{e_1} + e_1^TQBC{} {} {} {} {} {} \right. \\&\left. \qquad+ {{\dot{C}}^T}KC + {C^T}K\dot{C} \right] \end{aligned} \end{aligned}$$
(10)

Because of

$$\begin{aligned} \begin{aligned}&{A^T}Q + QA \\&\quad = \left( {\begin{array}{*{20}{c}} { - m}&{}{ - p{\omega _m}}\\ {p{\omega _m}}&{}{ - m}\end{array}} \right) \left( {\begin{array}{*{20}{c}}1&{}0\\ 0&{}1\end{array}} \right) + \left( {\begin{array}{*{20}{c}}1&{}0\\ 0&{}1 \end{array}} \right) \left( {\begin{array}{*{20}{c}}{ - m}&{}{p{\omega _m}}\\ { - p{\omega _m}}&{}{ - m}\end{array}} \right) \\&\quad = \left( {\begin{array}{*{20}{c}}{ - 2m}&{}0\\ 0&{}{ - 2m} \end{array}} \right) \end{aligned} \end{aligned}$$
(11)

where \(- 2m = - 2 \times \frac{{{R_s}}}{{{L_s}}} < 0\), therefore \(e_1^T\left( {{A^T}Q + QA} \right) {e_1}\) is a negative definite function.

For the rest of formula (10), simplify it to get

$$\begin{aligned} \begin{aligned}&{C^T}{B^T}Q{e_1} + e_1^TQBC{} {} {} {} {} {} + {{\dot{C}}^T}KC + {C^T}K\dot{C}\\ {}&= 2\left( {{\hat{m}} - m} \right) \left[ {i_d^c\left( {{i_d} - i_d^c} \right) + i_q^c\left( {{i_q} - i_q^c} \right) + \left( {\dot{{\hat{m}}} - \dot{m}} \right) } \right] \\ {}&+ 2\left( {{\hat{n}} - n} \right) \left[ { - {U_d}\left( {{i_d} - i_d^c} \right) - \left( {{U_q} - p{\omega _m}{\varphi _f}} \right) \left( {{i_q} - i_q^c} \right) } \right. \\ {}&\left. { + \left( {\dot{{\hat{n}}} - \dot{n}} \right) } \right] \end{aligned} \end{aligned}$$
(12)

When \(\left( {{C^T}{B^T}Q{e_1} + e_1^TQBC{} {} {} {} {} {} + {{\dot{C}}^T}KC + {C^T}K\dot{C}} \right) = 0\), then \(\dot{V}\left( {{e_1}} \right) < 0\) can be satisfied.

Define\(\left\{ {\begin{array}{*{20}{l}} {i_d^c\left( {{i_d} - i_d^c} \right) + i_q^c\left( {{i_q} - i_q^c} \right) + \left( {\dot{{\hat{m}}} - \dot{m}} \right) = 0}\\ { - {U_d}\left( {{i_d} - i_d^c} \right) - \left( {{U_q} - p{\omega _m}{\varphi _f}} \right) \left( {{i_q} - i_q^c} \right) {} {} + \left( {\dot{{\hat{n}}} - \dot{n}} \right) = 0} \end{array}} \right.\)

The adaptive rate of m and n can be calculated as

$$\begin{aligned} \begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{\hat{m}} = \int _0^t { - \left[ {i_d^c\left( {{i_d} - i_d^c} \right) + i_q^c\left( {{i_q} - i_q^c} \right) } \right] dt} + {m_0}}\\ { {\hat{n}} {}{}= \int _0^t {\left[ {{U_d}\left( {{i_d} - i_d^c} \right) \mathrm{{ + }}\left( {{U_q} - p{\omega _m}{\varphi _f}} \right) \left( {{i_q} - i_q^c} \right) } \right] dt} + {n_0}} \end{array}} \right. \end{aligned} \end{aligned}$$
(13)

After obtaining the stator resistance \({R_s}\) and inductance numbers \({L_s}\), identify the rotor flux linkage \({\varphi _f}\) as follows

Design reference model

$$\begin{aligned} \begin{aligned} \frac{{d{i_q}}}{{dt}} = - \frac{{{R_s}}}{{{L_s}}}{i_q} - p{\omega _m}{i_d} - \frac{1}{{{L_s}}}p{\omega _m}{\varphi _f} + \frac{1}{{{L_s}}}{U_q} \end{aligned} \end{aligned}$$
(14)

Design identification model

$$\begin{aligned} \begin{aligned} \frac{{di_q^c}}{{dt}} = - \frac{{{R_s}}}{{{L_s}}}i_q^c - p{\omega _m}{i_d} - \frac{1}{{{L_s}}}p{\omega _m}{{\hat{\varphi }} _f} + \frac{1}{{{L_s}}}{U_q} \end{aligned} \end{aligned}$$
(15)

Similarly, according to Lyapunov stability, the adaptive rate of rotor flux linkage \({\varphi _f}\) can be calculated as

$$\begin{aligned} \begin{aligned} {{\hat{\varphi }} _f} = \int _0^t { - \left[ {p{\omega _m}\left( {{i_q} - i_q^c} \right) } \right] dt} + {\varphi _{f0}} \end{aligned} \end{aligned}$$
(16)

3.2 Disturbance Observer Design and Stability Proof

Assumption 1

Assuming that the unknown lumped disturbance \(\phi _{d}\) is of Eq. (2) continuous and bounded, and satisfying \(\left\| {\phi _{d}^{(i)}} \right\| \le {\mu _1}{} {} ,{} {} {} {} i = 0{} {} ,{} {} 1{} {} ,{} {} 2\).

Here \(\phi _{d}\) indicates that the perturbation and the gradient of the parameters (such as viscous friction B, the moment of inertia J, permanent maget flux \(\varphi _f\), etc.) are not only continuous but also have an upper bound.

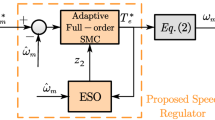
In order to estimate the mismatch disturbance in the permanent magnet synchronous motor system and eliminate the peak value of the initial time estimation, a time-varying second-order nonlinear disturbance observer is used for compensation, which can be designed as follows

$$\begin{aligned}&\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{\hat{\phi }} _{d} = {\rho _1} + {\lambda _1}{x_1}}\\ {{{{\dot{\rho }} }_1} = - {\lambda _1}\left( {{x_2} + {\hat{\phi }} _d} \right) + {\hat{\dot{\phi _d}}}}\\ {{\hat{\dot{\phi _{d}}}} = {\rho _2} + {\lambda _2}{x_1}}\\ { {{{\dot{\rho }} }_2} = - {\lambda _2}\left( {{x_2} + {\hat{\phi }} _{d}} \right) } \end{array}} \right. \end{aligned} \end{aligned}$$
(17)
$$\begin{aligned}&\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{\lambda _1} = {\mu _1}\left( {1 - {e^{ - {\mu _2}t}}} \right) }\\ {{{{\dot{\lambda }} }_1} = {\mu _1}{\mu _2}{e^{ - {\mu _2}t}}}\\ {{\lambda _2} = {\mu _3}\left( {1 - {e^{ - {\mu _4}t}}} \right) }\\ {{{{\dot{\lambda }} }_2} = {\mu _3}{\mu _4}{e^{ - {\mu _4}t}}} \end{array}} \right. \end{aligned} \end{aligned}$$
(18)

where \({x_1} = {\omega _{mref}} - {\omega _m}\), \({x_2} = {\dot{x}_1} + {\phi _{d}}\), \({\mu _1}, {\mu _2}, {\mu _3}, {\mu _4}\) is the positive constant, \({\rho _1},{\rho _2}\) is the auxiliary variable of the second-order observer, \({\lambda _1},{\lambda _2}\) is the gain coefficient of the observer.

Theorem 1

According to the time-varying second-order nonlinear disturbance observers (17) , the disturbances and their derivatives of the system (2) are uniformly ultimately bounded.

Proof

The error of disturbance observation \(\phi _{d},{\dot{\phi }} _{d}\) can be defined as \({\tilde{\phi }} _{d},\tilde{\dot{\phi _{d}}}\)

$$\begin{aligned}&\begin{aligned} \tilde{\dot{\phi _{d}}} = \dot{\phi _{d}} - \hat{\dot{\phi _{d}}} \end{aligned} \end{aligned}$$
(19)
$$\begin{aligned}&\begin{aligned} \dot{\tilde{\phi _{d}}} = \dot{\phi _{d}} - \left( { - {\lambda _1}\left( {{x_2} + \hat{\phi _{d}}} \right) + \hat{\dot{\phi _{d}}} + {\lambda _1}{{\dot{x}}_1}} \right) \end{aligned} \end{aligned}$$
(20)

Then take the \({x_2} = {\dot{x}_1} + {\phi _{d}}\) in (20)

$$\begin{aligned} \begin{aligned} \dot{ \tilde{\phi _{d}}}&= \dot{\phi _{d}} - \left( { - {\lambda _1}{x_2} - {\lambda _1}\hat{\phi _{d}} + \hat{\dot{\phi _{d}}}+ {\lambda _1}{x_2} + {\lambda _1}{\phi _{d}}} \right) \\ {} {} {} {} {} {} {} {} {}&= \hat{\dot{\phi _{d}}} - {\lambda _1}\tilde{\phi _{d}} \end{aligned} \end{aligned}$$
(21)

Similarly, the following expression can be obtained.

$$\begin{aligned} \begin{aligned} \dot{ \tilde{\dot{\phi _{d}}}} = \ddot{\phi _{d}} - {\lambda _2}\tilde{\phi _{d}} \end{aligned} \end{aligned}$$
(22)

Define error as

$$\begin{aligned}&\begin{aligned} {e_d} = {\left[ {\begin{array}{*{20}{c}} {\tilde{\phi _{d}}}&{\tilde{\dot{\phi _{d}}}} \end{array}} \right] ^T} \end{aligned} \end{aligned}$$
(23)
$$\begin{aligned}&\begin{aligned} {\dot{e}_d} = {A_d}{e_d} + {B_d}\ddot{\phi _{d}} \end{aligned} \end{aligned}$$
(24)

where \({A_d} = \left[ {\begin{array}{*{20}{c}} { - {\lambda _1}}&{}1\\ { - {\lambda _2}}&{}0 \end{array}} \right]\), \({B_d} = \left[ {\begin{array}{*{20}{c}} 0\\ 1 \end{array}} \right]\).

As a result,through design \({\lambda _1} = 2{k_0},{\lambda _2} = k_0^2\), Then can get \(\lambda \left( {{A_d}} \right) = {\lambda _{\max }}\left( {{A_d}} \right) = {\lambda _{\max }}\left( {A_d^T} \right) = - {k_0}\), Thus, it is constructed as Hurwitz matrix. In addition, the influence of the estimated peak is weakened by design \({\mu _2}> \frac{1}{{{k_0}}},{\mu _4} > \frac{1}{{{k_0}}}\) .

Design the Lyapunov function for \({\dot{e}_d} = {A_d}{e_d} + {B_d}\ddot{\phi _{d}}\) as

$$\begin{aligned} \begin{aligned} V\left( {{e_d}} \right) = e_d^TP{e_d} \end{aligned} \end{aligned}$$
(25)

where P and Q are real symmetric positive definite matrices, \(A_d^TP + P{A_d} = - Q\). Take the derivative of \(V\left( {{e_d}} \right)\) and get

$$\begin{aligned} \begin{aligned}&\dot{V}\left( {{e_d}} \right) \\&\quad = \dot{e}_d^TP{e_d}\mathrm{{ + }}e_d^TP{{\dot{e}}_d}\\&\quad ={\left( {{B_d}\ddot{\phi _{d}}} \right) ^T}P{e_d} + e_d^TA_d^TP{e_d} + e_d^TP{A_d}{e_d} + e_d^TP{B_d}\ddot{\phi _{d}}\\&\quad = e_d^T\left( {A_d^TP + P{A_d}} \right) {e_d} + {\left( {{B_d}\ddot{\phi _{d}}} \right) ^T}P{e_d} + e_d^TP{B_d}\ddot{\phi _{d}}\\&\quad = - e_d^TQ{e_d} + {\left( {{B_d}\ddot{\phi _{d}}} \right) ^T}P{e_d} + e_d^TP{B_d}\ddot{\phi _{d}} \end{aligned} \end{aligned}$$
(26)

Because P is a real symmetric matrix, so

$$\begin{aligned} \begin{aligned} \dot{V}\left( {{e_d}} \right)&= - e_d^TQ{e_d} + 2e_d^TP{B_d}\ddot{\phi _{d}}\\ {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {}&\le - e_d^TQ{e_d} + 2{\left\| {{e_d}} \right\| _2}{\lambda _{\max }}\left( P \right) {\left\| {{B_d}} \right\| _2}{\left\| {\ddot{\phi _{d}}} \right\| _2}\\ {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {}&\le - e_d^TQ{e_d} + 2{\left\| {{e_d}} \right\| _2}{\lambda _{\max }}\left( P \right) {\mu _1}\\ {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {}{} {} {} {}&\le - \left( {1 - \kappa } \right) e_d^TQ{e_d} - \kappa e_d^TQ{e_d}\\ {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {}&+ 2{\left\| {{e_d}} \right\| _2}{\lambda _{\max }}\left( P \right) {\mu _1} \end{aligned} \end{aligned}$$
(27)

where \(0< \kappa < 1\)

If let \(- \kappa e_d^TQ{e_d} + 2{\left\| {{e_d}} \right\| _2}{\lambda _{\max }}\left( P \right) {\mu _1} \le 0\), then can get the \({\left\| {{e_d}} \right\| _2} \le \frac{{\kappa e_d^TQ{e_d}}}{{2{{\left\| {{e_d}} \right\| }_2}{\lambda _{\max }}\left( P \right) {\mu _1}}}\).

Then \(\dot{V}\left( {{e_d}} \right) {} \le - \left( {1 - \kappa } \right) e_d^TQ{e_d}_1 \le 0\) holds, The proof is completed. \(\square\)

Remark 1

In our design of second-order nonlinear disturbance observer, if only the gain term exists as in a normal sliding mode observer, ensuring convergence or improving the accuracy of the observer by expanding the gain coefficient may seriously increase the problems of estimated peaks and chattering. To summarize, the estimated errors of the observers of a second-order nonlinear disturbance observer can be asymptotically stable.

3.3 Design of Controller and Stability Proof

Step 1: Construct the transformed error and Command Filter.

In order to realize the accurate speed tracking performance constraint of PMSM, based on dynamic model (1),the system tracking error is defined as

$$\begin{aligned} \begin{aligned} {z_1} = {\omega _m} - {\omega _{mref}}{} {} {} ,{} {} {} {} {} {} {z_2} = {i_q} - i_q^c{} {} ,{} {} {} {} {z_3} = {i_d} - i_d^c \end{aligned} \end{aligned}$$
(28)

where, \({\omega _{mref}}\) is the target reference speed, \(i_q^c\) is the reference value of q-axis current and \(i_q^d = 0\), \(i_q^c\) is the reference value of d-axis current.

In order to solve the differential expansion problem in the traditional backstepping control design, and considering the input saturation in practice, the instruction filter is introduced, so that the derivative of the virtual controller can be obtained from the integral link [18]. The Command Filter is difined as

$$\begin{aligned} \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{{\dot{q}}_1}}\\ {{{\dot{q}}_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&{}1\\ { - 2{\zeta _\mathrm{{i}}}{\sigma _{\mathrm{{ni}}}}{S_\mathrm{{R}}}\left( {\frac{{{\sigma _{\mathrm{{ni}}}}}}{{2{\zeta _\mathrm{{i}}}}}} \right) }&{}{ - 2{\zeta _\mathrm{{i}}}{\sigma _{\mathrm{{ni}}}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{q_1}}\\ {{q_2}} \end{array}} \right] \\ \qquad + {}{} \left[ {\begin{array}{*{20}{c}} 0\\ { - 2{\zeta _\mathrm{{i}}}{\sigma _{\mathrm{{ni}}}}{S_\mathrm{{R}}}\left( {\frac{{{\sigma _{\mathrm{{ni}}}}}}{{2{\zeta _\mathrm{{i}}}}}} \right) } \end{array}} \right] {S_\mathrm{{M}}}(u) \end{array} \end{aligned}$$
(29)

where, \({S_\mathrm{{M}}}(.)\) and \({S_\mathrm{{R}}}(.)\) are the amplitude limiting and rate limiting respectively; \({\zeta _\mathrm{{i}}}\) and \({{\sigma _{\mathrm{{ni}}}}}\) are the damping and bandwidth of the Command Filter respectively.

Considering the estimation error of Command Filter, the filter error compensation signal \(\varepsilon\) is designed as

$$\begin{aligned} \begin{aligned} {\dot{\varepsilon }} = - {k_1}\varepsilon + \frac{{3p{\varphi _f}}}{{2J}}\left( {i_q^c - i_q^d} \right) \end{aligned} \end{aligned}$$
(30)

where, \(i_q^c\) is the output of the virtual control law after passing through the command filter.

Step 2: Construct the virtual control law.

Redefine speed tracking error as

$$\begin{aligned} \begin{aligned} {{\bar{z}}_1} = {z_1} - {\varepsilon _1} \end{aligned} \end{aligned}$$
(31)

According to function (2) and (30), the derivative of \({{\bar{z}}_1}\) is calculated as

$$\begin{aligned} \begin{aligned} {{\dot{ {\bar{z}}}}_1}&= \frac{{3P{\varphi _f}}}{{2J}}{i_q} - \frac{1}{J}{B_m}{\omega _m} - \frac{1}{J}{T_L} - \phi _{d}\\ {} {} {} {} {} {} {} {} {}&\quad - {} {} {} {\dot{\omega }} mref\mathrm{{ + }}{K_1}\xi - \frac{{3P{\varphi _f}}}{{2J}}\left( {i_q^c - i_q^d} \right) \\ {} {} {} {} {} {} {} {} {} {}&= - {K_1}{{{\bar{z}}}_1} + \frac{{3P{\varphi _f}}}{{2J}}{z_z} + \tilde{\phi _{d}} - {\hat{\rho }} sign\left( {{{{\bar{z}}}_1}} \right) \end{aligned} \end{aligned}$$
(32)

where \(\rho\) is the observation error boundary of disturbance \({\phi _{d}}\),and satisfy \(\left\| {\tilde{\phi _{d}}} \right\| \le \rho\) , \({\hat{\rho }}\) is an estimate of \(\rho\). \({L_1}\) and \({w_1}\) are positive constant.

In order to stabilize the error \({{{\bar{z}}}_1}\), define the Lyapunov function of \({V_2} = \frac{1}{2}{{\bar{z}}_1}^2\) and the derivative of \({V_2}\) is obtained

$$\begin{aligned} \begin{aligned} {\dot{V}_2}\mathrm{{ = }} - {K_1}{{\bar{z}}_1}^2 + \frac{{3P{\varphi _f}}}{{2J}}{{\bar{z}}_1}{z_z} + {{\bar{z}}_1}\left( {\tilde{\phi _{d}} - {\hat{\rho }} sign\left( {{{{\bar{z}}}_1}} \right) } \right) \end{aligned} \end{aligned}$$
(33)

Step 3: Construct the real control law.

In order to improve the robustness of the system, the linear sliding mode surface is introduced into the inner loop control, and the sliding mode surfaces of d-axis and q-axis are defined as

$$\begin{aligned} \begin{aligned}&{S_q} = \sigma {z_2}\\&{S_d} = \sigma {z_3} \end{aligned} \end{aligned}$$
(34)

At the same time, the sliding mode reaching laws are chosen as

$$\begin{aligned} \begin{aligned}&{{\dot{S}}_q} = - {h_2}\mathrm{{sig}}\left( {{S_q}} \right) - {\rho _2}{S_q}\\&{{\dot{S}}_d} = - {h_3}\mathrm{{sig}}\left( {{S_d}} \right) - {\rho _3}{S_d} \end{aligned} \end{aligned}$$
(35)

where, \({h_2}\), \({h_3}\), \({\rho _2}\), \({\rho _3} > 0\) is the designed controller parameter.

Sign (x) is also commonly referred to as a sign function and is defined as follows

$$\begin{aligned} \begin{aligned} \mathrm{{sign}}\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {1,\quad {} {} {} {} {} {} {} {} x > 0}\\ {0,\quad{} {} {} {} {} {} {} {} x = 0}\\ { - 1,\quad {} {} {} {} x < 0} \end{array}} \right. \end{aligned} \end{aligned}$$
(36)

It can be seen that sign (x) is a discontinuous function, so the existence of symbolic function will further aggravate the chattering phenomenon. In this paper, sigmoid function is considered, that is, sig (.) in Eq. (35), Instead of the traditional symbolic function, the sliding mode chattering phenomenon is weakened.

$$\begin{aligned} \begin{aligned} \mathrm{{sig}}\left( x \right) = \frac{2}{{1 + \exp \left( { - \mathcal{Q}x} \right) }} - 1 \end{aligned} \end{aligned}$$
(37)

where \(\mathcal{Q} > 0\), it can be seen from the expression that the sigmoid function is smooth and continuous.

According to the mathematical model of IPMSM, the derivative of Eq. (34) can be obtained as

$$\begin{aligned} \begin{aligned} {{\dot{S}}_q}&= \sigma {{\dot{z}}_2} = \sigma \left( {{{\dot{i_q}}} - \dot{i_q^c}} \right) \\&= \sigma \left( { - m{i_q} - p{\omega _m}{i_d} - np{\omega _m}{\varphi _f} + n{U_q} - \dot{i_q^c}} \right) \\&= \sigma \left( { - \left( {{\hat{m}} - {\tilde{m}}} \right) {i_q} - p{\omega _m}{i_d} - \left( {{\hat{n}} - {\tilde{n}}} \right) p{\omega _m}{\varphi _f}} \right. \\&\qquad \left. { + \left( {{\hat{n}} - {\tilde{n}}} \right) {U_q} - \dot{ i_q^c}} \right) \\ {{\dot{S}}_d}&= \sigma {{\dot{z}}_3} = \sigma \left( {{{\dot{i_d}}} - \dot{i_d^c}} \right) \\&= \sigma \left( { - m{i_d} + p{\omega _m}{i_q} + n{U_d} - {\dot{i_d^c}}} \right) \\&= \sigma \left( { - \left( {{\hat{m}} - {\tilde{m}}} \right) {i_d} + p{\omega _m}{i_q} + \left( {{\hat{n}} - {\tilde{n}}} \right) {U_d} - \dot{i_d^c}} \right) \end{aligned} \end{aligned}$$
(38)

Define the Lyapunov function as

$$\begin{aligned} \begin{aligned} {V_3} = {V_2}\mathrm{{ + }}\frac{1}{2}{S_q}^2\mathrm{{ + }}\frac{1}{2}{S_d}^2 + \frac{1}{2}{\sigma ^2}{{\tilde{m}}^2} + \frac{1}{2}{\sigma ^2}{{\tilde{n}}^2} \end{aligned} \end{aligned}$$
(39)

The derivative of \({V_3}\) can be calculated as

$$\begin{aligned} \begin{aligned} {{\dot{V}}_3}&= {{{\bar{z}}}_1}{{\dot{\bar{z_1}}}} + {S_q}{{\dot{S}}_q} + {S_d}{{\dot{S}}_d} + {\delta ^2}{\tilde{m}}\dot{{\hat{m}}} + {\delta ^2}{\tilde{n}}\dot{{\hat{n}}}\\ {} {} {} {} {} {} {} {} {} {}&= - {k_1}{\bar{z}}_1^2 + \frac{{3p{\varphi _f}}}{{2J}}{{{\bar{z}}}_1}{z_2}{} + {{{\bar{z}}}_1}\left( {\tilde{\phi _{d}} - {\hat{\rho }} sign\left( {{{{\bar{z}}}_1}} \right) } \right) {} \\ {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {}{}&\quad+ \sigma {S_q}\left( { - {\hat{m}}{i_q} - p{\omega _m}{i_d} - {\hat{n}}p{\omega _m}{\varphi _f} + {\hat{n}}{U_q} - \dot{i_q^c}} \right) \\ {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {}&\quad+ \sigma {S_d}\left( { - {\hat{m}}{i_d} + p{\omega _m}{i_q} + {\hat{n}}{U_d} - \dot{i_d^c}\mathrm{{ + }}{h_3}\mathrm{{sig}}\left( {{S_d}} \right) } \right) \\ {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {}{}&\quad+ \sigma {\rho _2}S_q^2\mathrm{{ + }}\sigma {h_2}{S_q}\mathrm{{sig}}\left( {{S_q}} \right) + \sigma {\rho _3}S_d^2\mathrm{{ + }}\sigma {h_3}{S_d}\mathrm{{sig}}\left( {{S_d}} \right) \\ {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {}&\quad- {h_2}{S_q}\mathrm{{sig}}\left( {{S_q}} \right) - {h_3}{S_d}\mathrm{{sig}}\left( {{S_d}} \right) - {\rho _2}S_q^2 - {\rho _3}S_d^2\\ {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {}&\quad+ {\tilde{m}}\left( {{\delta ^2}\dot{{\hat{m}}} + \sigma {S_q}{i_q} + \sigma {S_d}{i_d}} \right) \\ {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {}{}&\quad+ {\tilde{n}}\left( {{\delta ^2}\dot{{\hat{n}}} + \sigma {S_q}\left( {p{\omega _m}{\varphi _f} - {U_q}} \right) - \sigma {S_d}{U_d}{} {} } \right) \end{aligned} \end{aligned}$$
(40)

According to Eq. (40) and Lyapunov stability theorem, the d-axis and q-axis controllers are designed as

$$\begin{aligned}&\begin{aligned}&{u_q} = \frac{1}{{{\hat{n}}}}\left( {{\hat{m}}{i_q} + p{\omega _m}{i_d} + p{\omega _n}{\varphi _\mathrm{{f}}}{\hat{n}} + \dot{i_q^c} - } \right. {h_2}\mathrm{{sig}}\left( {{S_q}} \right) - {\rho _2}{S_q}) \end{aligned} \end{aligned}$$
(41)
$$\begin{aligned}&\begin{aligned}&{u_d} = \frac{1}{{{\hat{n}}}}\left( {{\hat{m}}{i_d} - p{\omega _m}{i_q} + i_d^c - } \right. {h_3}\mathrm{{sig}}\left( {{S_d}} \right) - {\rho _3}{S_d}) \end{aligned} \end{aligned}$$
(42)

According to the adaptive rate designed by MRAS

$$\begin{aligned} \begin{aligned} \left\{ {\begin{array}{*{20}{l}} {\dot{{\hat{m}}} = - \left( {i_d^c{z_3} + i_q^c{z_2}} \right) }\\ { \dot{{\hat{n}}} = {U_d}{z_3} + \left( {{U_q} - p{\omega _m}{\varphi _f}} \right) {z_2}} \end{array}} \right. \end{aligned} \end{aligned}$$
(43)

Equations (41) and (42) are brought into the Eq. (40)

$$\begin{aligned} \begin{aligned} {{\dot{V}}_3} =&- {k_1}{\bar{z}}_1^2 + \frac{{3p{\varphi _f}}}{{2J}}{{{\bar{z}}}_1}{z_2} - {h_2}{S_q}\mathrm{{sig}}\left( {{S_q}} \right) - {h_3}{S_d}\mathrm{{sig}}\left( {{S_d}} \right) \\ {} {} {} {} {} {} {} {} {} {} {}{} {} {} {} {} {} {} {} {} {} {}&- {\rho _2}S_q^2 - {\rho _3}S_d^2 + {{{\bar{z}}}_1}\left( {\tilde{\phi _{d}} - {\hat{\rho }} sign\left( {{{{\bar{z}}}_1}} \right) } \right) \\ {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {}{} {} {} {}&+ {\tilde{m}}\left( {{\delta ^2}z_2^2 + {\delta ^2}z_3^2} \right) \end{aligned} \end{aligned}$$
(44)

In order to consider the stability of time-varying second-order non-linear disturbance observer, reselect Lyapunov candidate function as

$$\begin{aligned} \begin{aligned} {V_4}&= {V_3}\mathrm{{ + }}\frac{1}{2}\left( {{{{\tilde{d}}}^2} + {{{\tilde{\rho }} }^2}/{L_1}} \right) \\ {} {} {} {} {} {} {} {} {} {} {} {}&= \frac{1}{2}{{{\bar{z}}}_1}^2 + \frac{1}{2}{S_d}^2\mathrm{{ + }}\frac{1}{2}{S_q}^2 + \frac{1}{2}{\sigma ^2}{{{\tilde{m}}}^2} + \frac{1}{2}{\sigma ^2}{{{\tilde{n}}}^2}\\ {} {} {} {} {} {} {} {} {} {}&+ \frac{1}{2}\left( {{{\tilde{\phi _{d}}}^2} + {{{\tilde{\rho }} }^2}/{L_1}} \right) \end{aligned} \end{aligned}$$
(45)

Subsequently, the derivative of \({V_4}\) can be calculated as

$$\begin{aligned} \begin{aligned} {\dot{V}_4} = {\dot{V}_3}\mathrm{{ + }}\tilde{\phi _{d}}\dot{\hat{\phi _{d}}} + {\tilde{\rho }} \dot{ {\hat{\rho }}} /{L_1} \end{aligned} \end{aligned}$$
(46)

Furthermore, in order to eliminate the coupling term \(\frac{{3p{\varphi _f}}}{{2J}}{{\bar{z}}_1}{z_2}\) in Eq. (44), define \(0<\gamma <1\), then we can obtain

$$\begin{aligned} \begin{aligned} - {k_1}{\bar{z}}_1^2 + {{{\bar{z}}}_1}{z_2}\frac{{3p{\varphi _f}}}{{2J}} \le&- {k_1}\gamma {|{{{{\bar{z}}}_1}} |^2} - {k_1}\left( {1 - \gamma } \right) {\bar{z}}_1^2\\ {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {}&+ \frac{{3p{\varphi _f}}}{{2J}}|{{{{\bar{z}}}_1}} ||{{z_2}} | \end{aligned} \end{aligned}$$
(47)

Assuming the condition \(|{{{{\bar{z}}}_1}} |\ge \frac{{3p{\varphi _f}|{{z_2}} |}}{{2{k_1}\gamma J}}\) can be satisfied, then inequality Eq. (47) can be represented as

$$\begin{aligned} \begin{aligned} - {k_1}{\bar{z}}_1^2 + \frac{{3p{\varphi _f}{{{\bar{z}}}_1}{z_2}}}{{2J}} \le - {k_1}\left( {1 - \gamma } \right) {\bar{z}}_1^2 \end{aligned} \end{aligned}$$
(48)

Evidently, this condition can be achieved by adjusting the parameter \({k_1}\).

Note that the term \(- {} {{\bar{z}}_1}\left( {\hat{\phi _{d}} + {\hat{\rho }} sign\left( {{{{\bar{z}}}_1}} \right) } \right)\) in (44) has the following unequal relationship

$$\begin{aligned} \begin{aligned}&{{{\bar{z}}}_1}\left( {\hat{\phi _{d}} - {\hat{\rho }} sign\left( {{{{\bar{z}}}_1}} \right) } \right) \le |{{{{\bar{z}}}_1}} ||{\hat{\phi _{d}}} |- {{{\bar{z}}}_1}\rho sign\left( {{{{\bar{z}}}_1}} \right) \\&- {{{\bar{z}}}_1}{\tilde{\rho }} sign\left( {{{{\bar{z}}}_1}} \right) \le - {{{\bar{z}}}_1}{\tilde{\rho }} sign\left( {{{{\bar{z}}}_1}} \right) \le - {\tilde{\rho }} \dot{{\hat{\rho }} }/{L_1} - {w_1}{\tilde{\rho }} {\hat{\rho }} /{L_1} \end{aligned} \end{aligned}$$
(49)

According to Lemma 2 , the following inequality can be obtained for \(- {w_1}{\tilde{\rho }} {\hat{\rho }} /{L_1}{}\)

$$\begin{aligned} \begin{aligned} - {w_1}{\tilde{\rho }} {\hat{\rho }} /{L_1}{} \le - {w_1}{{\tilde{\rho }} ^2}/2{L_1}{} + {w_1}{\rho ^2}/2{L_1}{} \end{aligned} \end{aligned}$$
(50)

According to (48), (50), Then, Eq. (46) can be rewritten as

$$\begin{aligned} \begin{aligned} {{\dot{V}}_4}&\le - {k_1}\left( {1 - \gamma } \right) {\bar{z}}_1^2 - {\rho _2}S_q^2 - {\rho _3}S_d^2 - {w_1}{{{\tilde{\rho }} }^2}/2{L_1}{} \\ {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {}&\quad+ {w_1}{\rho ^2}/2{L_1}{} + {\tilde{m}}\left( {{\delta ^2}z_2^2 + {\delta ^2}z_3^2} \right) \\ {} {} {} {} {} {} {} {} {} {} {} {} {}&\le - \kappa {V_4} + \upsilon \end{aligned} \end{aligned}$$
(51)

where \(\kappa = \min \left\{ {2{K_1}\left( {1 - \ell } \right) } \right. ,2{\rho _3},2{\rho _2},\left. {{w_1}} \right\}\), \(\upsilon \mathrm{{ = }}{w_1}{\rho ^2}/2{L_1}{} + {\tilde{m}}\left( {{\delta ^2}z_2^2 + {\delta ^2}z_3^2} \right)\), for \(\forall t \ge {t_0}\), the (51) can be obtained.

Further, for \(\forall t \ge {t_0}\)

$$\begin{aligned} \begin{aligned} {V_4}\left( t \right) \le \left( {{V_4}\left( {{t_0}} \right) - \frac{\xi }{\kappa }} \right) {\mathrm{{e}}^{ - \kappa \left( {t - {t_0}} \right) }} + \frac{\xi }{\kappa } \le {V_4}\left( {{t_0}} \right) + \frac{\xi }{\kappa } \end{aligned} \end{aligned}$$
(52)

The proof is completed.

Remark 2

The filtering error of command filter is bounded in finite time. Thus, compensated tracking error is bounded, indicating that all the signals in the control system can be regarded as semi-globally uniformly ultimately bounded.

4 Results and Analysis

Built an electric vehicle PMSM hardware in the loop platform based on FPGA, and the effectiveness of the proposed parameter identification control method is clarified by the HIL test [23]- [24], which can be seen in Fig. 2. The real-time implementation platform adopts FPGA+dSPACE architecture. In this system, dSPACE is the controller, and FPGA is used to simulate the PMSM and inverter. The real-time control system is constructed using the DS1202 baseboard and DS1302 I/O board, which are included in the dSPACE.The FPGA board consists of Cyclone IV E: EP4CE115F23I7 device, a 48Mhz clock, and twelve 12-bit digital to analog converter (DAC) channels, which can realize powerful parallel real-time computing function [25]- [26].

Fig. 2
figure 2

HIL platform setup

Full size image

Using the Verilog language in the Quartus II software, the FPGA program is downloaded into the FPGA chip. In the FPGA program, the equivalent circuit of PMSM and the operation principle of DC power supply and inverter are described. A voltage signal is superimposed on a random noise to create a virtual DC voltage source, and a PWM signal is used to control the voltage at the input of the PMSM equivalent circuit. In the PMSM HIL platform, the dead-time, turn-on, and turn-off times of IGBT are also emulated in order to make it more realistic [27], which can be seen in Fig. 3.

Fig. 3
figure 3

Topology of the HIL platform

Full size image

Unlike simulation, the PMSM HIL platform is able to operate in real-time, which means that when designing the control method, the real-time computing power of the controller must be considered. Due to the transmission of signals through metal wires in the PMSM HIL platform, the signals may contain some noise and delays, which is consistent with the experimental platform. The PMSM HIL platform operates as follows: (1) The stator current and angular velocity of the PMSM calculated by the FPGA board are transmitted to the dSPACE via wires in real-time; (2) dSPACE calculates real-time the control signal; (3) To generate pulse signals, the control signal of the PMSM is modulated with space vector pulse width modulation (SVPWM) and sent to the FPGA board.

The above results prompted the development of a PMSM hardware-in-the-loop simulation platform, where the FPGA is responsible for describing the PMSM dynamic model, and dSPACE is used as the PMSM controller for electric vehicles to calculate the control signals for each permanent magnet synchronous motor in real-time. The parameters of PMSM and the proposed control method are set forth in Tables 1 and 2 .

Table 1 Parameters of the PMSM
Full size table
Table 2 Parameters of the control method
Full size table

An appropriate sampling time is chosen as \(100\mu \mathrm{{s}}\), the dead-time is set to \(3\mu \mathrm{{s}}\), the turn-on time of IGBT is set to \(0.35\mu \mathrm{{s}}\), and the turn-off time of IGBT is set to \(0.1\mu \mathrm{{s}}\). In FPGA boards, the turn-on voltage drop of the diode and the insulated gate bipolar transistor (IGBT) is simulated and set to 0.7V and 1.8V, respectively. In order to provide a fair and comprehensive comparison, the proposed control method in Fig. 4 is compared to the two other methods, one is the Backstepping nonlinear control method (BSC), and the other is traditional PI control. The two cases are then used to analyze the speed tracking performance as well as the anti-disturbance performance of EVs at variable speeds under three control strategies.

Fig. 4
figure 4

Composite control strategy

Full size image

As a measure of the effectiveness of the method and to simulate the fluctuation of the speed of electric vehicles on urban roads more realistically, the reference speed is used as the speed change signal. Furthermore, owing to the complexity of road conditions, the load torque is suddenly increased and decreased at t = 4s and t = 8s, respectively. The speed tracking control responses of three controllers are shown in Figs. 5, 6 and 7. During the startup phase of the electric vehicle, the PI control and BSC have a lag in speed tracking; however, the control strategy proposed in this paper does not have a lag and has an immediate response to speed tracking. It is noteworthy that when a load disturbance occurs, the PI control and backstep control have tracking speed errors, but the control strategy using the second-order disturbance observer has a smaller tracking speed error and no initial estimated peak value. Additionally, the MRAS-SODO speed tracking accuracy is relatively accurate.

Fig. 5
figure 5

Speed tracking control response of PI control

Full size image
Fig. 6
figure 6

Speed tracking control response of Backstepping control

Full size image
Fig. 7
figure 7

Speed tracking control response of MRAS-SODO control

Full size image

To compare the current control performance between different control methods, Figs. 8 and 9 shows the dq-frame currents of the outer front in-wheel PMSM under different control methods. The proposed control method reduces the chattering of the dq-frame currents significantly compared to the other two methods. Table 3 is the quantitative comparison of motor speed overshoot, response time, and peak current under different control methods during the starting phase of the vehicle. From the data in Table 3, it can be seen that MRAS-SODO has a faster tracking performance than PI and BSC. In addition, the chattering of motor speed, \(i_{d}\) and \(i_{q}\) under MRAS-SODO control is smaller than that of PI and BSC. In addition, MRAS-SODO effectively suppresses the transient current at the initial moment.

Fig. 8
figure 8

Response curves of \(i_{q}\) under different control methods

Full size image
Fig. 9
figure 9

Response curves of \(i_{d}\) under different control methods

Full size image
Table 3 Vehicle start-up phase performance
Full size table

When the load torque changes suddenly, it can be seen from the data comparing the performance in Table  4 that MRAS-SODO can restore the PMSM system to a steady state faster compared to PI and BSC. In addition, the \(i_{d}\) and \(i_{q}\) in MRAS-SODO have the smallest transient overshoot when the load changes abruptly compared to PI and BSC.

Table 4 Performance at the phase of a sudden load torque
Full size table

Figure 10 shows the curve of the input signal and output signal of the command filter. Selecting appropriate parameters \({\zeta _\mathrm{{i}}}\) and \({{\sigma _{\mathrm{{ni}}}}}\) can make the output signal accurately track the change of the input signal. When the speed changes step by step, the overshoot is reduced after passing through the command filter, so as to solve the problem of differential expansion.

Fig. 10
figure 10

Command filter input and output signal

Full size image

In order to verify the tracking performance of the online identification algorithm for parameter changes, the motor parameters are changed under constant speed and torque. After the parameter identification is stable, after the simulation time of 3s, stator resistance \(R_{s}\) and flux linkage \(\varphi _f\) should be increased, and stator inductance \(L_{s}\) should be decreased, respectively. As shown in Figs. 11, 12 and 13, after a short dynamic adjustment, the motor parameters can converge to the modified parameter values, among them, the speed waveforms of the three controllers when the parameters change are shown in Fig. 14. The identification error of stator resistance \(R_{s}\) is 2.5 \(\%\), the identification error of stator inductance \(L_{s}\) is 4.8 \(\%\), and the identification error of stator inductance \(L_{s}\) is 2 \(\%\). This paper shows that the parameter identification used in this paper is highly accurate.

Fig. 11
figure 11

Stator resistance \(R_{s}\) identification waveform

Full size image
Fig. 12
figure 12

Stator inductance \(L_{s}\) identification waveform

Full size image
Fig. 13
figure 13

permanent magnet flux \(\varphi _f\) identification waveform

Full size image
Fig. 14
figure 14

Speed tracking control response of different controls

Full size image

5 Conclusion

In this paper, we study the accuracy of speed tracking control of PMSM in electric vehicles through the use of MRAS and second-order disturbance observers and solve the problems related to parameter perturbation and anti-interference ability. First, a dynamic model for the PMSM drive system is established in the dq-frame, and we consider the unmodeled dynamics, time-varying parameters, and torque variations. Additionally, a step-by-step MRAS can also be implemented, and the speed of parameter adaptation is determined by Lyapunov stability theory, which can match the design parameters of the motor controller after the motor parameters have changed. Following this, a new second-order disturbance observer is designed in order to account for the mismatch disturbance caused by different road conditions and eliminate the initial peak value of the disturbance observer. On the basis of this data, the d-inner frame ring and q-frame controller are used to design a linear sliding surface, thus improving the robustness of the PMSM drive system. Further, the derivative of the virtual signal is approximated by an instruction filter, which solves the problem of complexity explosion. Finally, the stability of the controller is determined, as well as the performance of the proposed control strategy based on the simulation and real-time simulation results: electric vehicle variable speed and constant speed drive. In future work, the control scheme proposed in this paper will be validated using real-life PMSM experimental platforms.