An Efficient New Hybrid ICA-PSO Approach for Solving Large Scale Non-convex Multi Area Economic Dispatch Problems

Abstract

Multi-area economic dispatch (MAED) is one of the vital problems in economic operation of interconnected power systems. This paper proposes a novel hybrid approach based on combined imperialist competitive algorithm (ICA) and particle swarm optimization (PSO) methods in order to determine the feasible optimal solution of the non-convex economic dispatch (ED) problem considering valve loading effects. In the proposed algorithm we have defined new type of countries in ICA algorithm, namely independent countries. These types of countries improve their position using a PSO based search strategy. The proposed method benefits from the advantage of the both algorithms. The proposed hybrid approach based on ICA-PSO is applied on different test systems and compared with most of the recent methodologies. Also, a large scale multi-area economic dispatch (MAED) problem is solved using the proposed hybrid approach to minimize total fuel cost in all areas while satisfying power balance constraints, generating limits and tie-line capacity constraints. The results show the effectiveness of the proposed approach and prove that ICA-PSO is applicable for solving the power system economic load dispatch problem, especially in large scale power systems.

1 Introduction

One of the basic problems in operation of power systems is economic load dispatch (ELD) problem in which the goal is to minimize the cost of power generation so that the overall system constraints are met. Taking into account realistic equality and inequality constraints of ELD problem such as ramp-rate constraints, prohibited operating zones, valve-points effect, multi fuel option and multi area lead to a non-convex optimization problem with many local minima [1].

1.1 Literature Review of ELD

There are two main optimization methods (i.e. classical and intelligent) for solving ELD problem. Generally, it is not easy or possible to find global optima of the ELD problem using classical methods due to its high non-linearity and non-convexity nature. Hence, using meta-heuristic algorithms have been proposed recently in which there is no concern about non-linearity and non-convexity nature of ELD problem. An algorithm based on θ-particle swarm optimization is produced in [2] to solve constrained ELD problems of thermal plants. The constraints include transmission losses, ramp rate limits, prohibited operating zones, and valve point effects. A hybrid heuristic search method which combines the differential evolution (DE) and PSO algorithms is proposed in [3] to solve the practical ELD problem in which the PSO procedure is integrated as additional mutation operator to improve the global optimization property of DE. A differential harmony search algorithm is proposed in [4] in which the pitch adjustment is enhanced by different mutation operation and memory consideration. A hybrid method involving modified shuffled frog leaping algorithm with genetic algorithm crossover is introduced in [5] to solve the ELD problem of generating units considering the valve-point effects. A hybrid harmony search with arithmetic crossover operation for solving different types of ELD is proposed in [6]. Krill herd algorithm is utilized in [7] to solve both convex and non-convex ELD problems of thermal power units considering valve point loading, multiple fuel operation, transmission losses and constraints such as ramp rate limits and prohibited operating zones. A hybrid algorithm consisting of imperialist competitive algorithm (ICA) and sequential quadratic programming technique is presented in [8] to solve the ELD problem. In [9] a method based on the quantum particle swarm optimization is proposed and applied to ELD problem in order to solve this problem possessing non-smooth and smooth cost functions. To improve the effectiveness and quality of ELD problems' solutions, an algorithm based on real coded chemical reaction is proposed in [10] which involve different equality and inequality constraints. The simulated annealing algorithm is used to minimize the fuel cost and the gas emissions in [11]. The synergic predator–prey optimization (SPPO) algorithm is used to solve ELD problem for thermal units with practical aspects by using of collaborative decision for movement and direction of prey and maintains diversity in the swarm due to fear factor of predator, which acts as the baffled state of preys’ mind [12].

1.2 Literature Review of Non-convex Multi Area ELD

ED (economic dispatch) [13] is one of the important optimization problems in power system operation. ED allocates the load demand among the committed generators most economically while satisfying the physical and operational constraints in a single area. Generally, the generators are divided into several generation areas interconnected by tie-lines. Multi-area economic dispatch (MAED) is an extension of economic dispatch. MAED determines the generation level and interchange power between areas such that total fuel cost in all areas is minimized while satisfying power balance constraints, generating limits constraints and tie-line capacity constraints.

A complete formulation of multi-area generation scheduling, and a framework for multi-area studies is presented in [14]. Reference [15] presented the Dantzige–Wolfe decomposition principle to the constrained economic dispatch of multi-area systems. A multi-area economic dispatch problem by using spatial dynamic programming is solved in [16]. An application of linear programming to transmission constrained production cost analysis was proposed in [17]. Multi-area economic dispatch with area control error is solved in [18]. Reference [19] proposed heuristic multi-area unit commitment with economic dispatch. A decomposition approach for solving multi-area generation scheduling with tie-line constraints using expert systems is proposed in [20]. Network flow models for solving the multi-area economic dispatch problem with transmission constraints have been proposed in [21]. An algorithm for multi-area economic dispatch and calculation of short range margin cost based prices has been presented in [22], where the multi-area economic dispatch problem was solved via Newton Raphson’s method. Ref [23] solved multi-area economic dispatch problems by using Hopfield neural network approach. Multi-area economic dispatch problems with tie line constraints using evolutionary programming are solved in [24]. The direct search method for solving economic dispatch problem considering transmission capacity constraints was presented in [25]. Teaching learning-based optimization algorithm for solving MAED problem with tie line constraints considering transmission losses, multiple fuels, valve-point loading and prohibited operating zones is presented in [26]. The performance of the various evolutionary algorithms on multi-area economic dispatch (MAED) problems is explored in [27].

In recent years, more new meta-heuristic methods have also been adopted. The particle swarm optimization with damping factor and cooperation mechanism (PSO-DFCM) has been applied to search the global optima in a large scale and high-dimensional searching space [28]. The unified semi-definite programming (SDP) formulation of different ED problems through cost function decomposition was presented in [29] that presents a solution to economic dispatch (ED) problems with non-convex, non-smooth fuel cost functions. A deterministic approach has proposed to solve multi-objective, no-convex and non-differentiable environmental and economic dispatch problem with valve-point loading effect in [30]. The Lightning flash algorithm is proposed in order to increase the diversity of the solutions, accelerate the convergence speed with less calculation time and provide an applicable method for the non-convex combined emission economic dispatch problem with generator constraints [31]. Also, the problem of non-convex combined environmental economic dispatch has solved by a hybrid algorithm based on a novel combination of a modified genetic algorithm and an improved version of particle swarm optimization that balance the ratio process between the exploration and exploitation as well as avoiding any premature convergence efficiently during the optimization process [32].

1.3 Procedure and Contribution

The contribution of this study is the development of a new hybrid algorithm consisting of imperialist competitive algorithm and particle swarm optimization (ICA-PSO) for solving practical ELD problems including all mentioned realistic constraints. Since the proposed method is the first step to utilize a hybrid approach based on ICA and PSO algorithms in solving non-convex economic dispatch problem, to avoid overly computational complexity as well as a better and easier representation of the basic capabilities of the proposed method, this paper aims to achieve classical economic dispatch only in the presence of realistic constraints, and future researches are necessary so that the proposed approach can be applied for solving more general MAED problems that incorporate the enhanced modeling aspects and constraints. PSO is one of the well-known and powerful swarm intelligence algorithms which extensively used in wide variety of economic dispatch problems [e.g. 2, 3] due to its simplicity and high convergence rate. Imperialist competitive algorithm (ICA) is a newly developed evolutionary method which has recently been applied to solve some optimization problems and has shown great performance in both convergence rate and better global optimum achievement [33, 34]. The main features of the proposed ICA-PSO algorithm are use of strength of both ICA and PSO and better response in comparison with ordinary evolutionary methods. The proposed ICA-PSO algorithm is applied to four medium and large-scale power systems and five selected benchmark functions. Therefore, the comparison results has confirmed that the proposed hybrid approach is more effective and has higher capability in finding optimum solutions in comparison to ICA and PSO methods. Also, convergence of proposed hybrid approach is higher than ICA and PSO methods.

1.4 Paper Organization

The rest of the paper is organized as follows: Sect. 2 presents the problem formulation of the ELD problem taking into account prohibited operating zones constraint (POZs), multi fuel option, ramp-rate limits, valve-point effects, transmission losses and multi area. Section 3 describes the proposed hybrid approach based on ICA-PSO algorithm and its implementation procedure for solving non-convex ELD problem. The proposed method is applied on some benchmark test functions and several test power systems in Sect. 4 and the results are compared with most recently reported methods. Finally, Sect. 5 concludes this paper.

There are two main optimization methods (i.e. classical and intelligent) for solving ELD problem. Generally, it is not easy or possible to find global optima of the ELD problem using classical methods due to its high non-linearity and non-convexity nature. Hence, using meta-heuristic algorithms have been proposed recently in which there is no concern about non-linearity and non-convexity nature of ELD problem. An algorithm based on θ-particle swarm optimization is produced in [2] to solve constrained ELD problems of thermal plants. The constraints include transmission losses, ramp rate limits, prohibited operating zones, and valve point effects. A hybrid heuristic search method which combines the differential evolution (DE) and PSO algorithms is proposed in [3] to solve the practical ELD problem in which the PSO procedure is integrated as additional mutation operator to improve the global optimization property of DE. A differential harmony search algorithm is proposed in [4] in which the pitch adjustment is enhanced by different mutation operation and memory consideration. A hybrid method involving modified shuffled frog leaping algorithm with genetic algorithm crossover is introduced in [5] to solve the ELD problem of generating units considering the valve-point effects. A hybrid harmony search with arithmetic crossover operation for solving different types of ELD is proposed in [6]. Krill herd algorithm is utilized in [7] to solve both convex and non-convex ELD problems of thermal power units considering valve point loading, multiple fuel operation, transmission losses and constraints such as ramp rate limits and prohibited operating zones. A hybrid algorithm consisting of imperialist competitive algorithm (ICA) and sequential quadratic programming technique is presented in [8] to solve the ELD problem. In [9] a method based on the quantum particle swarm optimization is proposed and applied to ELD problem in order to solve this problem possessing non-smooth and smooth cost functions. To improve the effectiveness and quality of ELD problems' solutions, an algorithm based on real coded chemical reaction is proposed in [10] which involve different equality and inequality constraints. The simulated annealing algorithm is used to minimize the fuel cost and the gas emissions in [11]. The synergic predator–prey optimization (SPPO) algorithm is used to solve ELD problem for thermal units with practical aspects by using of collaborative decision for movement and direction of prey and maintains diversity in the swarm due to fear factor of predator, which acts as the baffled state of preys’ mind [12].

Table 1 Effect of the parameters of hybrid on optimization of f5

Table 2 Benchmark functions [42]

Table 3 Comparison of different algorithm mean and standard deviation for benchmark functions

Table 4 Comparison of simulation results for 6-unit test system (load = 1263 MW)

Table 5 Comparison of simulation results for 10-unit test system

Table 6 Comparison of simulation results for 15-unit test system

Table 7 Comparison of simulation results for 140-unit test system for different runs

Table 8 Optimal solution results for Korean power system with non-convex cost functions

2 Problem Formulation

The main objective of ELD problem is to minimize the operating costs of generating units so that the equality and inequality constraints of the power system are met.

2.1 Objective Function of ELD Problem

The cost function of generating units can be expressed as a quadratic function, so the objective function of ELD problem can be formulated as follows:

$$\min F_{C} = \sum\limits_{i = 1}^{ng} {F_{i} (P_{i} )} = \sum\limits_{i = 1}^{ng} {a_{i} P_{i}^{2} + b_{i} P_{i} + c_{i} }$$

(1)

where, F_c is the total fuel cost of generating units; F_i(P_i) is the fuel cost associated with the unit i; ng is the total number of generating units; and a_i, b_i, and c_i are fuel cost coefficients of unit i.

2.2 Objective Function of Non-Convex ELD Problem

If the valve-point effects are considered in the generators fuel cost functions, their cost functions exhibit non-convex characteristics. This effect is modeled with adding sinusoidal term to quadratic cost function as follows:

$$F_{i} (P_{i} ) = a_{i} P_{i}^{2} + b_{i} P_{i} + c_{i} \, + \,\left| {e_{i} \times \sin (f_{i} \times (P_{i}^{\min } - P_{i} ))} \right|\,$$

(2)

where, e_i and f_i are represented coefficients of cost function which indicate valve-point effect of unit i. $P_{i}^{\min }$ is the lower limit constraint for generator i [35].

2.3 Objective Function of Non-Convex ELD Problem Considering Multi-fuel Effect

When the generating units are operating with multiple fuel types, cost function of each unit is expressed with several equations, where each equation is corresponding to one type of fuel. This can be formulated as follows:

$$F_{i} (P_{i} ) = \left\{ \begin{gathered} a_{i1} P_{i}^{2} + b_{i1} P_{i} + c_{i1} + \,\left| {e_{i1} \times \sin (f_{i1} \times (P_{i}^{\min } - P_{i} ))} \right|\,\,\,\,\,\,\,\,\,\,\,\,fuel1,\,\,\,\,\,\,\,P_{i}^{\min } \le P_{i} \le P_{i1} \hfill \\ a_{i2} P_{i}^{2} + b_{i2} P_{i} + c_{i2} + \,\left| {e_{i2} \times \sin (f_{i2} \times (P_{i}^{\min } - P_{i} ))} \right|\,\,\,\,\,\,\,\,\,\,fuel2,\,\,\,\,\,\,\,P_{i1} \le P_{i} \le P_{i2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\begin{array}{*{20}c} : \\ : \\ \end{array} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\begin{array}{*{20}c} : \\ : \\ \end{array} \, \hfill \\ a_{ik} P_{i}^{2} + b_{ik} P_{i} + c_{ik} + \,\left| {e_{im} \times \sin (f_{im} \times (P_{i}^{\min } - P_{i} ))} \right|\,\,\,\,\,\,\,\,\,fuelk,\,\,\,\,\,\,\,P_{ik - 1} \le P_{i} \le P_{i}^{\max } \hfill \\ \end{gathered} \right.$$

(3)

where, a_ik, b_ik, and c_ik are cost function coefficients of unit i for fuel type k and $P_{i}^{\max }$ is the upper limit constraint for generator i. If the valve-point effects are considered in addition to multiple fuel types, the sinusoidal term in Eq. (1) is added to each of the above quadratic equations [36].

2.4 Non-Convex ELD Constraints

A non-convex ELD optimization problem has equality and inequality constraints such as ramp-rate constraints, prohibited operating zones, valve-points effect, and multi fuel option.

2.4.1 Power Balance Constraint

In order to maintain the balance between generation and consumption in the power system, the following equality constraint must be satisfied:

$$\sum\limits_{i = 1}^{ng} {P_{i} } = P_{load} + P_{loss}$$

(4)

where, P_load and P_loss are the system load and loss amount, respectively. P_loss can be achieved using B-matrix coefficients as a quadratic function of power outputs as follows:

$$P_{loss} = \,\sum\limits_{i = 1}^{ng} {\sum\limits_{j = 1}^{ng} {P_{i} .B_{ij} .P_{j} } } \, + \,\sum\limits_{i = 1}^{ng} {B_{0i} .P_{i} } + B_{00}$$

(5)

where, B_ij, B₀₀, B_0i are coefficients of loss function of transmission system.

2.4.2 Generators' Capacity Constraint

Production of each generator must be between its upper and lower capacity limits. This constraint is expressed by the following inequality:

$$P_{i}^{\min } \le P_{i} \le P_{i}^{\max } \,\,;\,\,\,i = 1,......,ng\,$$

(6)

2.4.3 Generators' Ramp Rate Constraints

The range of output power of a generator in a certain time is determined according to its ramp rate constraint. In fact, this constraint causes the lower and upper production limit of a generator to be dependent on its initial production at any particular time. Considering this constraint, the above formula (6) changes to:

$$\max \{ P_{i}^{\min } ,P_{i}^{0} - DR_{i} \} \le P_{i} \le \min \{ P_{i}^{\max } ,P_{i}^{0} + UR_{i} \} \,$$

(7)

where, $P_{i}^{0}$ is initial output power, DR_i, and UR_i are ramp up and ramp down limits of each unit respectively.

2.4.4 Prohibited Operating Zones Constraint

In some cases, a generating unit cannot produce energy in all the range between its upper and lower capacity limits due to machine components or instability concerns. The zone where power cannot be produced is called prohibited operating zones (POZs). The POZs constraint can be formulated mathematically as follows:

$$P_{i} \in \left\{ \begin{gathered} P_{i}^{\min } \le P_{i} \le P_{i,1}^{l} \hfill \\ P_{i,k - 1}^{u} \le P_{i} \le P_{i,k}^{l} \hfill \\ P_{{i,z_{i} - 1}}^{u} \le P_{i} \le P_{i}^{\max } \hfill \\ \end{gathered} \right.;\,\,\,k = 2,3,......,z_{i\,\,\,} \,\,,\,\,\,i = 1,2,....,nz$$

(8)

where, $P_{i,k}^{l}$ and $P_{i,k}^{u}$ are the lower and upper boundaries of the k'th prohibited zone of unit i, respectively. z_i is the number of POZs of unit i, and nz is the number of units with POZs.

2.5 Non-Convex Multi Area ELD Constraints

In non-convex multi area ELD, the real power balance constrain is different from non-convex ELD. Therefore, the real power balance constrain in non-convex multi area ELD as follow:

$$\sum\limits_{j = 1}^{{M_{i} }} {P_{ij} } = P_{load,i} + P_{Loss,i} \, + \sum\limits_{k,k \ne i} {T_{ik} } \,\,\,\,;\,\,\,\,\,\forall \,i$$

(9)

where T_ik is the tie line real power transfer from area i to area k. T_ik is positive when power flows from area i to area k and T_ik is negative when power flows from area k to area i.

Also, the tie line real power transfer T_ik from area i to area k should not exceed the tie line transfer capacity for security consideration.

$$- T_{ik}^{\max } \le T_{ik} \le T_{ik}^{\max } \,$$

(10)

where $T_{ik}^{\max }$ is the power flow limit from area i to area k and $- T_{ik}^{\max }$ is the power flow limit from area k to area i.

3 Proposed Hybrid ICA-PSO Algorithm

In this section, the background of PSO, ICA, and proposed hybrid approach based on ICA-PSO methods are presented.

3.1 PSO Background

PSO is a population based method that was introduced by Kennedy and Eberhart [37]. In PSO, each particle moves in the search space with a velocity according to its own previous best solution and its group’s previous best solution. Each particle updates its position and velocity with the following equations:

$${X}_{i}\left(t+1\right)={X}_{i}\left(t\right)+{V}_{i}(t+1)$$

(11)

where ${X}_{i}\left(t\right)$ and ${V}_{i}(t)$ are vectors representing the position and velocity of the $i$th particle, respectively and

$${V}_{ij}(t+1)=w{V}_{ij}(t)+{c}_{1}{r}_{1j}({pb}_{ij}-{X}_{ij}\left(t\right))+{c}_{2}{r}_{2j}({gb}_{j}-{X}_{ij}\left(t\right))$$

(12)

where j $\epsilon$ 1, 2, …, d represents the dimension of the particle; $0<w<1$ is an inertia weight determining how much of particle’s previous velocity is preserved; ${c}_{1}$ and ${c}_{2}$ are two positive acceleration constants;${r}_{1j}$, ${r}_{2j}$ are two uniform random sequences sampled from [0, 1]; ${pb}_{i}$ is the personal best position found by the $i$th particle; and $gb$ is the best position found by the entire swarm so far. The PSO has been proven to be very effective for static and dynamic optimization problems. But in some cases, it converges prematurely without finding even a local optimum.

3.2 ICA Background

Imperialist competitive algorithm (ICA) [33] is one of the recently proposed evolutionary algorithm, which is based on the human’s socio-political evolution.

In this algorithm, all individuals are grouped in several empires. The mechanisms in the algorithm are designed to bring out an empire, stronger than the others, that finds the best solutions. Imperialistic competition aims to suppress the weakest empire and strengthen the strongest empire. The main steps of the algorithm are summarized in Algorithm 1. More detailed information can be found in [33].

3.3 Proposed Hybrid ICA-PSO

This paper applied the hybrid approach of imperialist competitive algorithm (ICA) and particle swarm optimization (PSO) for obtaining better optimizer. In the standard ICA, there are only two types of countries: imperialists and colonies. In the proposed hybrid algorithm (ICA-PSO) we added another type of country, ‘Independent’. Independent countries do not fall into the category of empires, and are anti-imperialism. In addition, they are united and their shared goal is to get stronger in order to rescue colonies and help them join independent countries. These independent countries are aware of each other positions and make use of swarm intelligence in PSO for their own progress.

With these definitions, steps of the proposed algorithm can be summarized as presented in the following:

4 Step 1: initialization;

• Generate and initialize N_pop initial population countries and sort them in ascending order (country with lower cost in higher order);

• Select the first N_ind countries as independent countries;

• Select the next N_imp countries as imperialist countries;

• Select the rest of countries (N_colony = N_pop-N_ind-N_imp) as colonies;

• Form the empires from imperialists and colonies;

• Select the strongest independent country (independent country with the lowest cost) as the best collective experience of independent countries ($gbest_{ind}^{tot}$);

• Select the strongest imperialist country (imperialist country with the lowest cost) as the best collective experience of imperialist countries ($gbest_{imp}^{tot}$);

5 Step2: Assimilation of the independent countries:

• Attitude of independent countries toward the strongest independent country according to Fig. 1 (similar to assimilation process in ICA);

• Update best personal experience of independent countries (similar to ICA);

  $$\begin{gathered} \mathop X\nolimits_{ind}^{K + 1} = \mathop X\nolimits_{ind}^{K} + \beta_{1} *d\,*U( - \theta ,\theta ) \hfill \\ \beta_{1} > 1 \hfill \\ \theta \approx \frac{\pi }{4} \hfill \\ \end{gathered}$$

  (13)

Fig. 1

Independent Country movement toward global best of independent country in new hybrid

6 Step3: Movement of colonies of every emperor similar to PSO background;

• Choose imperialist of every empire as g_best of its colonies;

• Move every colony based on its g_best, best individual experience, and current position according to Fig. 2;

  $$\begin{aligned} V^{K + 1} &= w_{2} V^{K} + C_{1} rand(\,)(P_{colony}^{K} - X_{colony}^{K} ) \\ &\quad+ C_{2} rand(\,)(G_{colony}^{K} - X_{colony}^{K} ) \end{aligned}$$

  (14)
  $$X_{colony}^{K + 1} = X_{colony}^{K} + V^{K + 1}$$

  (15)

  Fig. 2

  

  Movement of colonies of every emperor

• Update best personal experience of every colony;

• Attitude of colonies toward their own imperialist according to Fig. 3 (similar to assimilation process in ICA);

  Fig. 3

  

  Colony movement toward Imperialist in new hybrid

• Update best personal experience of every colony;

  $$X_{colony}^{K + 1} = X_{colony}^{K} + \beta *d_{1} *U( - \theta ,\theta )$$

  (16)

7 Step4: Movement of imperialists of every emperor similar to PSO:

• Move every imperialist based on its best individual experience and current position, and $gbest_{imp}^{tot}$ according to Fig. 4;

  $$\begin{aligned} V^{K + 1} &= w_{3} \,V^{K} + C_{1} rand(\,)\,(P_{imp}^{K} - X_{imp}^{K} ) \\ &\quad+ C_{2} rand(\,)\,(gbest_{imp}^{tot} - X_{imp}^{K} )\, \end{aligned}$$

  (17)
  $$X_{imp}^{K + 1} = X_{imp}^{K} + V^{K + 1}$$

  (18)

  Fig. 4

  

  Movement of imperialists of every emperor

• Update best personal experience and $gbest_{imp}^{tot}$ of imperialists;

• Attitude of imperialists toward the strongest imperialist according to Fig. 5;

  Fig. 5

  

  Imperialist movement toward global best Imperialist in new hybrid

• Update best personal experience and $gbest_{imp}^{tot}$ of imperialists;

  $$\begin{gathered} X_{imp}^{K + 1} = X_{imp}^{K} + \beta *d_{2} *U( - \theta ,\theta ) \hfill \\ \beta > 1 \hfill \\ \end{gathered}$$

  (19)

8 Step5: Revolution:

• Update the best individual experience of colonies after the revolution;

9 Step6: Assimilation between imperialists and independent countries:

• If $gbest_{imp}^{tot} > gbest_{ind}^{tot}$(i.e. if the best collective experience of independent countries is better than the best collective experience of imperialists), then:

• Attitude the imperialists' gbest toward the independent countries' gbest according to Fig. 6;

  $$\begin{gathered} X_{gbest\,\,imp}^{K + 1} = X_{gbest\,\,imp}^{K} + \beta_{1} *d_{3} *U( - \theta ,\theta )\, \hfill \\ \beta_{1} > 1 \hfill \\ \end{gathered}$$

  (20)

  Fig. 6

  

  Global best of imperialist countries movement toward global best of independent countries in new hybrid

• If due to this attitude, the cost of imperialists (best collective experience of imperialists) becomes better than previous state, the new position is updated (as the new best collective experience of imperialists);

• But if $gbest_{imp}^{tot} > gbest_{ind}^{tot}$(i.e. if the best collective experience of imperialists is better than the best collective experience of independent countries), then:

• Attitude the independent countries' gbest toward the imperialists' gbest according to Fig. 7;

  $$\begin{gathered} X_{gbest\,\,inp}^{K + 1} = X_{gbest\,\,inp}^{K} + \beta_{1} *d_{3} *U( - \theta ,\theta ) \hfill \\ \beta_{1} > 1 \hfill \\ \end{gathered}$$

  (21)

  Fig. 7

  

  Global best of independent countries movement toward global best of imperialist countries in new hybrid

• If due to this attitude, the cost of independent countries (best collective experience of independent countries) becomes better than previous state, the new position is updated (as the new best collective experience of independent countries);

10 Step7: Comparison of imperialist with the best colony (similar to ICA);

• Exchange imperialist with best colony if is necessary;

11 Step8: Competition for independency:

• Independent countries have anti-imperialism behavior and are in competition with imperialists. Independent countries’ aim is to free the colonies from the empires and let them join independent countries to cause the collapse of all empires. Similar to [38], in this part of algorithm, we calculate the total cost of independent countries with the mean of each ones cost;

  $$TC_{I} = mean\{ Cost(Independent\,Country)\}$$

  (22)

• If emperor k be weaker than independent countries, we select the weakest colony of that emperor. Then, the selected colony is moved toward the independent countries according to following Eqs. (14) and (15);

• select the weakest colony of each empire that was weaker than independent countries. This was obtained by comparing the total cost of independent countries with the empires total cost. Then, we moved the selected colony toward the independent countries according to Eqs. (14) and (15). This normally happens due to the fact that the colonies are not interested to be a colony, and they try to separate themselves from their empires;

  $$\begin{aligned} V^{K + 1} &= w_{3} \,V^{K} + C_{ind1} rand(\,)\,(P_{colony}^{K} - X_{colony}^{K} )\\ &\quad + C_{ind2} rand(\,)\,(G_{indpendent\,country}^{K} - X_{colony}^{K} )\, \end{aligned}$$

  (23)
  $$X_{colocny}^{K} = X_{colony}^{K} + V^{K + 1}$$

  (24)

• If this weakest colony gets stronger than its imperialist country after the movement toward independent countries, then they will leave that empire and join independent countries;

12 Step9: Competition to colonize independent countries:

• If the power of independent countries is less than that of all empires, then one of the independent countries will be available for competition between all empires like the “imperialistic competition” stage in ICA [38];

Step10: Imperialistic competition:

• Eliminate the weakest colony of the weakest empire;

• Eliminate empires which have no any colonies;

• Check the stop criteria, otherwise go to Step 2;

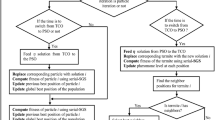
The proposed algorithm flowchart is dedicated in Fig. 8.

Fig. 8

Flowchart of the proposed hybrid methodology

13 Case Studies

In this section the proposed hybrid algorithm has been applied on some benchmark functions and ELD problems. Results of the proposed hybrid algorithm are compared with results of the latest reported algorithms in the literature. It should be mentioned that optimum values obtained using the proposed hybrid algorithm are presented in bold in Tables 3, 4, 5, 6, 7.

13.1 Parameter Selection

The maximum number of iterations is set to 250 for all benchmarks and 300 for all ELD test systems. It should be mentioned that, these values are selected in a way to insure that the further convergence is not possible. Similar to [39], the population size for benchmark functions is set to 100 and for ELD problems the population size of 200 is used. Using larger population size results in a better exploration of the search space with the cost of increasing computational time. In order to determine the parameters of the proposed ICA-PSO algorithm, a number of simulations are done using benchmark function $f_{5} (x) = \sum\nolimits_{{\text{i } = \text{ 1}}}^{{\text{n}}} {\left( {\left\lfloor {x_{i} + 5} \right\rfloor } \right)}^{2}$. Table 1 shows the average value of function over 50 trial runs. From this table it can be observed that the $\beta = 1$ and $\beta_{1} = 3$ result in better solution.

13.2 Benchmarks

Five benchmark functions are studied in this section in order to evaluate the performance of the proposed Hybrid PSO-ICA algorithm. Definitions of the benchmark functions [39] are presented in Table 2. Proposed hybrid PSO-ICA is applied to mentioned benchmark functions for 1000 times and minimum, mean, maximum, and standard deviation of the results is presented in Table 3. The obtained results are compared with GA, PSO, GSO, CQGSO, S-PSO, MFG-PSO, G-PSO, PSO-DTT and PSO-DFCM [28, 40] in Table 3. Default parameters are used for PSO and GA in [39]. The results of PSO and GA are directly quoted from [32]. It can be observed from this table that the proposed algorithm converges to better results in comparison with GA, PSO, GSO, CQGSO, S-PSO, MFG-PSO, G-PSO, PSO-DTT and PSO-DFCM algorithms. Finally, Fig. 9 shows the convergence of proposed hybrid approach is better than conventional ICA and PSO methods for 5th benchmark functions simulations.

Fig. 9

The comparison of convergence for proposed hybrid with conventional ICA and PSO methods in 5th benchmark functions

13.3 Test System I: 6-Unit

A six-thermal unit sample system with transmission losses, POZs and ramp rate is used to demonstrate the performance of the proposed method. Coefficients of the Kron’s loss formula (5) in per unit (with a 100 MVA base capacity) along with the generators’ characteristics can be found in [41]. Table 4 shows the obtained optimal power output, minimum cost for this test system over the 50 trial runs. These results are compared with particle swarm optimization (PSO) [42], genetic algorithm (GA) [42], multiple Tabu search (MTS) algorithm [41], new particle swarm optimization with local random search (NPSO-LRS) [43], bacterial foraging optimization (BFO) [44], new adaptive particle swarm optimization (NAPSO) algorithm [45], self-organizing hierarchical particle swarm optimization (SOH-PSO) method [46], biogeography-based optimization (BBO) [47], new modified particle swarm approach (New-MPSO) [48], string structure GA (SGA) [49], differential evolution (DE) [50,51,52], improved DE (IDE) [51], and Grey Wolf Optimizer (GWO) [53] in Table 4. Although the obtained solution is not guaranteed to be the global optimum, the results of the literature are better in comparison with existing methods.

13.4 Test System II: 10-Unit

This test system is a 10-generator system with valve-point loading effect and multi-fuel option. The coefficients are provided in [35] and fuel cost function is described in (4). The total load demand is 2700 MW. It should be noted that the transmission losses are not considered for the sake of comparison. Optimal power outputs and corresponding fuel types are presented in Table 6. 10-unit ELD problem is solved using proposed algorithm for 100 trial runs. The minimum cost of the proposed algorithm are compared with the results of PSO with local random search (PSO-LRS) algorithm [43], new PSO (NPSO) [43], new PSO with local random search (NPSO-LRS) [43], PSO [54], anti-predatory PSO (APSO) [54], advanced PSO (CPSO) [36], PSO with Gaussian mutation (PSO-GM) [35], Tabu search algorithm (TSA) [55], distributed Sobol PSO and TSA (DSPSO–TSA) [55], PSO with the constriction factor and inertia weight (CBPSO) [36], hybrid integer coded differential evolution–dynamic programming (ICDEDP) [56], DE [57], estimation of distribution and differential evolution cooperation (ED–DE) [57], auction algorithm (AA) [58], Colonial competitive differential evolution (CCDE) [59], Synergic predator–prey optimization (SPPO) [12], improved particle swarm optimization (IPSO) [60], modified shuffled frog leaping algorithm (MSFLA) [61], global-best harmony search algorithm (GHS) [61], shuffled frog leaping algorithm- global-best harmony search algorithm (SFLA-GHS) [61], and shuffled differential evolution (SDE) [61] in Table 5. It can be observed from Table 5 that the proposed algorithm results in a better solution in comparison with the most of the approaches reported in the literature.

13.5 Test System III: 15-Unit

A fifteen-thermal unit sample system with transmission losses, POZs and ramp rate is used to demonstrate the performance of the proposed method. Coefficients of the Kron’s loss formula (5) in per unit (with a 100 MVA base capacity) along with the generators’ characteristics can be found in [62]. Table 6 shows the obtained optimal power output, minimum cost for this test system over the 50 trial runs. These results are compared with particle swarm optimization (PSO) [42], genetic algorithm (GA) [42], improved dynamic programming [62], exchange market algorithm (EMA) [63], exchange market algorithm with smart searching (EMA-SS) [63], and particle swarm optimization with smart inertia factor (PSO-SIF) [63]. The obtained results outperform the existing methods, although the obtained solution is not guaranteed to be the global optimum.

13.6 Test System IV: Four Area 140-Unit Test System

This case is Korean power system. This is a large scale test case which consisted of 140 generating units with valve-points effect and POZs constraints. The generator data has been taken from [64]. The total demand is 49,342 MW. The 140 generators are divided into four areas. Area 1 includes first 35 units and 32% of the total load demand. Area 2 has second 35 units and 20% of the total load demand. Area 3 consists of 35 units and 33.5% of the total load demand. Area 4 includes last 35 generators and 14.5% of the total load demand. The power flow limit between different areas is limited to 100 MW. Transmission loss is neglected here. The problem is solved by using proposed hybrid ICA-PSO algorithm. For this test system, the population size (NP) and maximum number of iterations have been selected to be 100 and 250, respectively. To validate the proposed hybrid ICA-PSO, the same test system is solved using conventional ICA and PSO methods. Comparison of simulation results for 140-unit test system for different runs using the ICA, PSO, and proposed hybrid methods are shown in Table 7. Also, Table 8 shows the optimal solution results for Korean power system with non-convex cost functions. Finally, Fig. 10 shows the convergence of the proposed hybrid approach is higher than conventional ICA and PSO methods.

Fig. 10

The comparison of convergence for proposed hybrid with conventional ICA and PSO methods in 140-unit test system

14 Conclusion

In this paper, the non-convex multi area economic dispatch problem with valve-point effects was solved using the proposed ICA-PSO approach. The proposed hybrid approach combined ICA with PSO methods. To validate the proposed approach, some test systems with non-convex solution spaces were solved. Compared with previous approaches, the results showed the effectiveness of the proposed approach in terms of high-quality solution, convergence and good computation efficiency. According to the results, it can be concluded that the proposed approach is a successful method for solving non-convex economic dispatch problems, especially in large scale systems. Also, a large scale multi-area economic dispatch (MAED) problem is solved using the proposed hybrid approach. In MAED, the generation level and interchange power between areas such that total fuel cost in all areas is minimized while satisfying power balance constraints, generating limits constraints and tie-line capacity constraints. So, it can be concluded that the proposed hybrid approach has a good potential for solving the complex non-smooth problems in power system operation. Using optimized PSO in hybridization with ICA, taking into account AC network modeling, the impact of security constraints and considerations on environmental conditions and other influencing factors can be a good way to complete studies in this area.