Keywords

1 Introduction

Economic dispatch problem is of considerable importance in the area of power generation. Economic dispatch is the determination of electrical power outputs from all the thermal generators supplying power to the system at minimum total cost in a single area subject to the condition that total meets the load demand including losses while power capacity limit constraints of generators are satisfied. Multi-area economic dispatch (MAED) is formulated by extending ED model. The goal of MAED is to find out electric power outputs of committed generators in all the interconnected areas at minimum cost while satisfying load balance constraints, electric power capacity limits of generators and transmission line capacity constraints. An electrical power system consists of generation, transmission and distribution utilities to enhance electrical power to the consumers. ED problem for single area power system is addressed by most of the research papers, whereas only few papers address ED for multi-area power system but the optimization problem still solved in a sequential way. The objective is to find the solution MAED problem using a developed Lagrange’s decomposed method. Large networked systems are break down into areas or zones. MAED problem is a methodology in power network operation that allows measure of generation to committed units within the areas. Earlier ED problem is solved by lambda iteration method, gradient method, reduced gradient method, Newton method and other methods like participation factor method, binary weighted method. All these classical techniques have several disadvantages like: problem complexity, time computation factor, characteristics should be non-convex in nature. All these factors are removed by other classical methods like priority method, dynamic programming and Lagrange relaxation method. These methods have several advantages that these techniques are applied to complex characteristics problems of generator but there is problem in these techniques that they have take several stages to solve the problem and time taken is too large [1]. These things are overcome by meta-heuristics methodologies. Many methodologies are implemented on economic dispatch like GA, ABCO and PSO [2,3,4,5,6]. But proposed DPSO when varying all variants of PSO has not implemented yet.

2 Nomenclatures

a ij , b ij , c ij :

The cost coefficients of the jth generator in area i (Rs/h), (Rs/h MW−1), (Rs/h MW−2)

C1, C2:

Acceleration coefficients for best and social experience of PSO

C1b, C1p:

Acceleration coefficients for best and preceding experience

e ij and f ij :

The valve-point effect coefficients of the jth generator in area i (Rs/h, MW−1)

gbestt:

Best particle during tth iteration

grmst:

Root mean square experience of the swarm during tth iteration

itr:

Current iteration count

itrmax:

Maximum iteration count

itrmin:

Minimum iteration count

k :

Ratio of dynamic cognitive and social acceleration coefficients

k w :

Ratio of maximum and minimum bound of the inertia weight

M :

Number of areas

N Gi :

Number of generating units in the system in area i

N Gi :

Number of generating units in the ith area

Pbest n :

Best position of nth particle achieved based on its own experience

PD:

Total real power demand of the system (MW)

P Di :

Total real power demand of area i (MW)

P Gi :

Total real power generation in area i (MW)

P Gij :

Real power output of the jth generator in area i (MW)

P minGij /P maxGij :

Minimum/maximum generation limits of jth generator in area i (MW)

P min Tim /P max Tim :

Minimum/maximum tie-line power limit from area i to area m (MW)

ppreceding n :

Preceding position of nth particle achieved based on its just previous experience

P Tim :

Tie-line real power flow from area i to area m (MW) rand1 () and rand2 () random numbers in [0,1]

V t n :

Velocity of nth particle at tth iteration

W :

Inertia weight

Wmin/Wmax:

Minimum/maximum value of inertia weight

∆t :

Time step (s)

ζ1 and ζ2:

Exponential constriction functions

\(\eta\) :

Ratio of current and maximum iteration count

\(\eta_{t}\) :

The value of g at which cognitive and social behaviour equalizes

µ :

Constant

µ1, µ2:

Coefficients of exponent terms

2.1 Problem Formulation

Cost function of generator is generally quadratic when valve-point loading is not considered. Large turbine generator usually has no. of fuel admissions valve that are operated such that to meet the increased generation. Objective function of MAED is stated as:

$${\text{Minimize}}\;F\left( {P_{{{\text{G}}ij}} } \right) = \sum\limits_{i = 1}^{M} {\sum\limits_{j = 1}^{{N_{Gi} }} {\left( {a_{ij} + b_{ij} P_{{{\text{G}}ij}} + c_{ij} P_{{{\text{G}}ij}}^{2} } \right)} } + \left| {e_{ij} \sin \left( {f_{ij} \left( {P_{{{\text{G}}ij}}^{\hbox{min} } - P_{{{\text{G}}ij}} } \right)} \right)} \right|$$
(1)

Subject to following constraints,

Area power balance constraints:

Total power generation of all generators is equal to the demand PDi.

$$\sum\limits_{j = 1}^{{N_{Gi} }} {P_{{{\text{G}}ij}} = P_{{{\text{D}}i}} + \sum\limits_{m,i \ne m} {P_{Tim} } } \quad i \in \left\{ {1,2, \ldots M} \right\}$$
(2)

Generator constraints:

$$P_{{{\text{G}}ij}}^{\hbox{min} } \le P_{{{\text{G}}ij}} \le P_{{{\text{G}}ij}}^{\hbox{max} }$$
(3)

Tie-line constraints:

$$- P_{Tim}^{\hbox{min} } \le P_{Tim} \le P_{Tim}^{\hbox{max} }$$
(4)

3 Solutions Technique

3.1 Proposed DPSO

PSO mainly depends on three components, i.e. inertial weight, cognitive and social influence factors.

Each particle velocity and position is updated by the equations that are

$$\begin{aligned} \upsilon_{n}^{t + 1} & = W \times \upsilon_{n}^{t} + e_{1} \times c_{1b} \times r_{1} () \times (p{\text{best}}_{n} - x_{n}^{t} ) + (1 - e_{1} ) \\ & \quad \times c_{1p} \times r_{2} () \times (x_{n}^{t} - p{\text{preceding}}_{n} ) + e_{2} \times c_{2} \times r_{3} () \\ & \quad \times (g{\text{best}}^{t} - x_{n}^{t} ) + e_{2} \times c_{2} \times r_{4} () \times (g{\text{rms}}^{t} - x_{n}^{t} ) \\ \end{aligned}$$
$$S_{n}^{t + 1} = S_{n}^{t} + V_{n}^{t + 1} \times \Delta t$$
(5)

where ∆t is time generally taken as 1 s.

Inertia weight equation is:

$$W = W_{\hbox{min} } + \frac{{(W_{\hbox{max} } - W_{\hbox{min} } ) \times ({\text{itr}}_{\hbox{max} } - {\text{itr}})}}{{{\text{itr}}_{\hbox{max} } }}$$
(6)

In proposed DPSO, the inertial weight W is changed by proposing an exponentially decomposed function to check trade-off between overall explorations and ceil exploitation of swarm. The preceding expertise of particle ppreceding n is taken to enrich the cognitive part by studying just older experience, whereas total experience of group of swarms is embedded in grmst to enrich the social part of particles. Further, dynamic acceleration coefficients have been introduced using constriction functions e1 and e2 dynamically to regulate the cognitive and social nature of birds. These modifications are explained below:

  • Updating inertia weight: The trend of linear module of inertial weight is succeeded to solve ED problems using PSO by many researchers. In the suggested method, inertial weight is permitted to vary an exponential decomposed function and module suggested to modernize the inertial weight which is controlled by the following relation:

    $$W = {\text{e}}^{{( - \eta \ln k_{w} )}}$$
    $$k_{w} = \frac{{w_{\hbox{min} } }}{{w_{\hbox{max} } }}$$

    where \(\eta = {\text{itr}}/{\text{itr}}_{\hbox{max} }\) and k w is selected within minimum and maximum bounds of inertial weight. In this study, value of k w is proportion of max and min condition of inertial weight.

    Updating preceding experience: The cognitive behaviour was split in by considering also the bad experience in addition to good idea of particle and provides certain more diverseness, but it results in poor local exploitation unless supported by a local random search. Therefore in existing method, the plan of preceding experience is evoked where existing fitness of every particle is compared with its fitness value in that preceding iteration, and if it is found less, it will be treated as the preceding experience. The past experience of the random particle produces less variety in comparison with the worst experience resulting in better exploration and exploitation of entire quest space without the aid of any additional local random search or else.

  • Updating RMS experience: In PSO, only local and global best positions are transparent to other particles. This poor communication among particles may lead to lack of diversity and thus results in poor performance, especially while dealing with large dimensional problems. One way to improve communication of particles is to add RMS component of all particles’ velocities in the measured equation. These results in overall sharing of data and particles gained from the discoveries and older experience of each escort during their search.

  • Dynamic regulation of acceleration coefficients: Governance via aid of static acceleration coefficients of social and cognitive nature of particles is done in conventional PSO. It is suggested by many researchers that in order to regulate particle velocity dynamic control must be experienced. In the recent work, with the introduction of two exponential constrictions function e1 and e2 acceleration coefficients are made dynamic. The cognitive and social conduct of swarm is regulated by the aid of constriction functions while this regulation is taking place. Velocities of particles are limited during their flight and are as follows:

    $$\begin{aligned} e_{1} & = {\text{e}}^{{( - \mu_{1} \eta )}} \\ e_{2} & = k \cdot {\text{e}}^{{(\mu_{2} \eta )}} \\ k & = \frac{{e_{1} \cdot c_{1b} }}{{e_{2} \cdot c_{2} }} \\ \end{aligned}$$

    where k is proportion of conducted dynamic cognitive and social acceleration coefficients. For same values of these coefficients at \(\eta = \eta_{t}\).

    These variations control the conventional PSO that regulates particles velocity, within predefined limits without any extra formulation is bang in various enhanced performance of PSO, yet preserving variety because of stochastic nature of cognitive and social behaviours of swarm.

    The coefficients of the exponents \(\mu {}_{1}\) and \(\mu_{2}\) are selected as 5 and 3.9, as beyond that the term \({\text{e}}^{{ - \mu {}_{1}\eta }}\) is not perceptible in ending of search. Further, the most applicable value of \(\eta_{t}\) is obtained as 2/3 after experimentations.

Thereafter, performing 1000 independent trials of DPSO we get average fuel cost, and on the basis of this average cost, we obtain optimal solution.

3.2 Methodology of DPSO

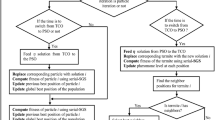
The solution of an MAED problem is the set of most optimal generations for the desired objective bounded by certain operational constraints. In the proposed PSO, the particles are encoded in real numbers as the set of current generations in MW, as shown in Figs. 1 and 2.

Fig. 1
figure 1

Flowchart of MAED using DPSO

Full size image
Fig. 2
figure 2

Constraint handling algorithm of DPSO

Full size image
  1. (a)

    Particle encoding and initialization: The initial population is randomly created with predefined number of particles to maintain diversity. Each of these particles satisfies the problem constraints already defined. Infeasible particle, whenever appeared, is corrected by employing a constrained handling algorithm as described later in the section. The fitness of each particle is evaluated using Eq. (1), and then pbest, ppreceding, gbest and grms are initialized. The initial velocity of particles is assumed to be zero.

  2. (b)

    Constrained handling: The velocity and position update may create infeasible solutions. In profound research, constrained handling algorithm is used to correct the infeasible individuals by the help of feasible ones. Using this process, power is adjusted within its limits and tie-line variables as given in Eqs. (2) and (3), respectively. If the generated power is within its min or max generation level, then set it as its lower or higher bound limits as in Eq. (4). Similarly, if the transfer of real tie-line powers from area i to area k exceeds its limit then the tie-line power is fixed at tie-line limits as mentioned in Eq. (4) for security consideration. The power balance error is calculated by Eq. (2). The error is equally divided among all generators, and the procedure is iterated till it disrates to a predefined mismatch value e. In this work, e is taken as 0.001.

  3. (c)

    Solution preservation and termination criterion: In stochastic-based algorithms like PSO, the solution with the good fitness in the present iteration may be lost in the next iteration. Particle with best fitness is k hold preserved for upcoming iteration. The algorithm stops when we reached to maximum iteration or all particles converges to a single position.

PG11

PG12

…

PG1j

…

PG1N

PG21

PG22

…

PG2j

…

PG2N

…

…

…

….

…

…

PGi1

PGi2

…

PGij

…

PGiN

  1. Particle encoding

3.3 Particle Encoding and Initialization Methodology Algorithm

  • Step 1: Initialize the control parameters and enter the system data.

  • Step 2: Initialize new particle randomly.

  • Step 3: If the current particle is not feasible, run constraint handling algorithm for it.

  • Step 4: Else go to Step 5.

  • Step 5: Increase population count by 1. If population count is less than its maximum, go to Step 2.

  • Step 6: Else go to Step 7.

  • Step 7: Evaluate fitness by (Eq. 1), pbest, ppreceding, grms, inertia weight, constriction function by Eqs. (5) and (6).

  • Step 8: Initialize iteration count.

  • Step 9: Repeat Step 2 and Step 3. Update ppreceding for the current particle. Then repeat Step 5.

  • Step 10: Update gbest and grms.

  • Step 11: Increase iteration count by 1. If iteration count is less than its maximum repeat Step 9.

  • Step 12: Print final results.

4 Test Systems and Results

4.1 Test System 1: Single Area Problem

Test system 1 simply has one area having no tie line. Table 1 shows coefficients of three generators with maximum and minimum limits of power, whereas Table 2 shows cost when demand is varying of test system 1, and its results are compared with classical methods, i.e. lambda iteration method (Fig. 3).

Table 1 Cost coefficients of three generators [1]
Full size table
Table 2 Cost of three generator units according to demand
Full size table
Fig. 3
figure 3

Test system 2: two areas, four generator units and a tie line

Full size image

Test system 2 simply has one area having a tie line. Table 3 shows coefficients of four generators with maximum and minimum limits of power, whereas Table 4 shows cost when demand is varying of test system 2, and its results are compared with base paper (Fig. 4; Tables 5, 6, 7 and 8).

Table 3 Cost coefficients of four generators
Full size table
Table 4 Cost of four generator units and its tie-line value
Full size table
Fig. 4
figure 4

Test system 3: 4 areas, 40 generation units, 6 tie-lines limit. Each area consists of ten generators with valve-point loading and is connected with three tie lines [7]

Full size image
Table 5 Results of four generator units and two areas
Full size table
Table 6 PSO-TVAC parameters [7]
Full size table
Table 7 Statistical analysis for 25 runs of the system
Full size table
Table 8 Parameters taken into account to deal with test system 3 [8]
Full size table

Test system 3 simply has four areas having six tie lines. Table 9 shows power of each generator, whereas Table 11 shows tie-line limit of each area of test system 3, and its results are compared with base paper (Table 10).

Table 9 Results of power of 40 generators by DPSO
Full size table
Table 10 Statistical analysis for 25 runs of the system
Full size table
Table 11 Tie-line results of test system 3 in both DCPSO
Full size table

4.2 Convergence Curve of Test System 3

5 Conclusion

The conditions of today’s market require the complex network to be considered as a set of separated, but interconnected areas and case are also very complex as it is characterized with huge number of networks, constraints, tie lines and loads. The research is successful in establishing a reliable, an efficient and fast heuristic search technique, DPSO and OPF to unravel MAED problems. The results obtained are substantially better both in the terms of cost and CPU time. MAED problem if high dimensional (as in the present case) also suffers with the case of local trappings when solved using any population-based algorithm. But as DPSO has improved the results significantly from the previous best results of powers, hence the problem is of high dimensionality and local trappings are assumed to be mitigated. The presented work can be extended to a larger problem of MAED which can further establish the validity of the present work and the DPSO technique. In future, the DPSO technique can be further modified within itself or it can be merged with another optimization technique, classical or meta-heuristic or otherwise, so that it further reduces the gap of obtained results and global best results which are not established as of now.