Asymptotic Properties of Least Squares Estimators and Sequential Least Squares Estimators of a Chirp-like Signal Model Parameters

Abstract

Sinusoidal model and chirp model are the two fundamental models in digital signal processing. Recently, a chirp-like model was introduced by Grover et al. (International conference on computing, power and communication technologies, IEEE, pp. 1095–1100, 2018). A chirp-like model is a generalization of a sinusoidal model and provides an alternative to a chirp model. We derive, in this paper, the asymptotic properties of least squares estimators and sequential least squares estimators of the parameters of a chirp-like signal model. It is observed theoretically as well as through extensive numerical computations that the sequential least squares estimators perform at par with the usual least squares estimators. The computational complexity involved in the sequential algorithm is significantly lower than that involved in calculating the least squares estimators. This is achieved by exploiting the orthogonality structure of the different components of the underlying model. The performances of both the estimators for finite sample sizes are illustrated by simulation results. In the specific real-life data analyses of signals, we show that a chirp-like signal model is capable of modeling phenomena that can be otherwise modeled by a chirp signal model, in a computationally more efficient manner.

1 Introduction

Underlying a great deal of signal processing applications such as speech and music processing [28], electrocardiography [30], seismology [32], astronomy [40] and economics [13] are sinusoidal signals embedded in noise. In a general form, a sinusoidal signal can be written as:

$$\begin{aligned} y(t) = \sum _{j=1}^{p} \left\{ A_j^0 \cos \left( \alpha _j^0 t\right) + B_j^0 \sin \left( \alpha _j^0 t\right) \right\} + X(t),\ t = 1, \ldots , n. \end{aligned}$$

(1)

Here, $A_j^0$s, $B_j^0$s are the amplitudes, $\alpha _j^0$s are the frequencies and X(t) is the random error component of the observed signal y(t). Due to the widespread applicability of this model, many methods have been proposed for its parameter estimation. In this respect, one may look into the monograph of Kundu and Nandi [19]. We also invoke readers to the interesting articles by Kay and Marple [16], Prasad et al. [34] and Stoica [39] for more contributions in this area.

Another important model in digital signal processing is a chirp signal model, encountered in many natural as well as man-made phenomena such as navigational chirps emitted by bats [7, 8], bird sounds [15], human voice [5], radar and sonar systems [25, 41] and communications [11]. Mathematically, a chirp signal is expressed as follows:

$$\begin{aligned} y(t) = \sum _{j=1}^{p} \left\{ A_j^0 \cos (\alpha _j^0 t + \beta _j^0 t^2) + B_j^0 \sin (\alpha _j^0 t + \beta _j^0 t^2)\right\} + X(t),\ t = 1, \ldots , n. \end{aligned}$$

(2)

Here, $\beta _j^0$s are the frequency rates and again, $A_j^0$s, $B_j^0$s are the amplitudes, $\alpha _j^0$s are the frequencies and X(t) is the random error component of the observed signal y(t). In the last few decades, numerous algorithms have been developed for estimating the unknown parameters of this model. For some of the earliest references on the joint estimation of frequency and frequency rate, see Bello [2], Kelly [17] and Abatzoglou [1]. Thereafter, several other estimation methods have been proposed as well, such as methods based on phase unwrapping [6], suboptimal FFT [33], quadratic phase transform [14], maximum likelihood [37], nonlinear least squares [31], least absolute deviation [21], MCMC-based Bayesian sampling [26], linear prediction approach [10], sigmoid transform [23], modified discrete chirp Fourier transform [38] and many more.

Of particular interest to us here is the method of least squares principle. It is the most commonly used method and is one of the first methods in classical estimation theory [24]. For the chirp model in the presence of stationary noise, the least squares estimators (LSEs) are strongly consistent and asymptotically normally distributed. In fact, if the errors are assumed to be Gaussian, LSEs achieve the Cramer Rao lower bound [18]. However, despite these optimal statistical properties, finding them in practice is computationally challenging. The reason behind this is the highly nonlinear nature of the least squares surface. Recently, Lahiri et al. [22] proposed the sequential LSEs which have the same statistical properties as the usual LSEs but they reduce the complexity involved in finding the LSEs to a great extent. This is obtained by breaking the multi-dimensional search into multiple two-dimensional searches, using the orthogonality structure of different chirp components present in the model. Nevertheless, there is still a huge computational cost involved in finding the sequential LSEs, and there is a need to develop computationally more efficient algorithms for practical implementation.

The subject of the present paper is a novel model, a chirp-like model first introduced in [12], mathematically expressed as follows:

$$\begin{aligned} y(t)= & {} \sum _{j=1}^p \left\{ A_j^0 \cos \left( \alpha _j^0 t\right) + B_j^0 \sin \left( \alpha _j^0 t\right) \right\} \nonumber \\&+ \sum _{k=1}^q \left\{ C_k^0 \cos \left( \beta _k^0 t^2\right) + D_k^0 \sin \left( \beta _k^0 t^2\right) \right\} + X(t), \ t = 1, \ldots , n, \end{aligned}$$

(3)

where $A_j^0$s, $B_j^0$s, $C_k^0$s and $D_k^0$s are the amplitudes, $\alpha _j^0$s are the frequencies and $\beta _k^0$s are the frequency rates. X(t) accounts for the noise present in the signal. This new model is a linear combination of a sinusoidal model (1) and an elementary chirp model¹. This choice is made mainly because of the following three reasons:

• First, it is observed that this model exhibits same type of behavior as the chirp model (2) and is capable of modeling similar physical phenomena. To demonstrate, we analyze a speech signal data set “UUU” using both a chirp model and a chirp-like model. The corresponding “best” fittings are plotted together in the following figure:

  It is evident from the above figure that the two signals are well-matched.

• Second, this model not only provides an alternative to a chirp model but can be seen as a generalization of a sinusoidal model also. For the special case of $C_k^0 = D_k^0 = 0$ for all $k = 1, \ldots , q$, the proposed model (3) reduces to the sinusoidal model (1).

• Lastly, parameter estimation of this model using a sequential algorithm is computationally simpler and faster compared to the sequential LSEs of a chirp model.

Parameter estimation of a chirp-like model is first formulated as a multidimensional nonlinear least squares estimation problem in this paper. We theoretically develop the statistical properties of the LSEs such as strong consistency and asymptotic normality. For a practical solution with computational simplicity, we propose a sequential algorithm. The proposed method turns the multidimensional optimization search into a string of one-dimensional optimization problems. We derive the large-sample properties of the sequential LSEs as well and observe that they have the same properties as the usual LSEs. The theoretical results are then corroborated through extensive simulation studies and a few data analyses (Fig. 1).

Fig. 1

Fitted chirp signal (red solid line) and fitted chirp-like signal (pink dashed line) to the “UUU” sound data (Color figure online)

The rest of the paper is organized as follows. In the next section, we define a one-component chirp-like model and study the asymptotic properties of the LSEs and the sequential LSEs of the parameters of this model. In Sect. 3, we study the asymptotic properties of a more generalized model, a multiple-component chirp-like model (3). In Sect. 4, we perform simulations to validate the asymptotic results and in Sect. 5, we analyze four speech signal data sets and a simulated dataset to see how the proposed model performs in practice. We conclude the paper in Sect. 6.

2 One Component Chirp-like Model

In this section, we consider a one-component chirp-like model, expressed mathematically as follows:

$$\begin{aligned} \begin{aligned} y(t)&= A^0 \cos \left( \alpha ^0 t\right) + B^0 \sin \left( \alpha ^0 t\right) + C^0 \cos \left( \beta ^0 t^2\right) + D^0 \sin \left( \beta ^0 t^2\right) + X(t). \end{aligned} \end{aligned}$$

(5)

Our problem is to estimate the unknown parameters of the model, namely $A^0$, $B^0$, $C^0$, $D^0$, $\alpha ^0$ and $\beta ^0$ under the following assumption on the noise component:

Assumption 1

Let Z be the set of integers. $\{X(t)\}$ is a stationary linear process of the form:

$$\begin{aligned} X(t) = \sum _{j = -\infty }^{\infty } a(j)e(t-j), \end{aligned}$$

(6)

where $\{e(t); t \in Z\}$ is a sequence of independently and identically distributed (i.i.d.) random variables with $E(e(t)) = 0$, $V(e(t)) = \sigma ^2$, and a(j)s are real constants such that

$$\begin{aligned} \sum \limits _{j= - \infty }^{\infty }|a(j)| < \infty . \end{aligned}$$

(7)

For a stationary linear process, this is a standard assumption. This assumption covers a large class of stationary processes. For instance, any finite-dimensional stationary MA, AR, or ARMA process can be formulated in the above-stated representation.

We will use the following notations for further development: $\varvec{\theta }$ = $(A, B, \alpha , C, D, \beta )$, the parameter vector, $\varvec{\theta }^0$ = $(A^0, B^0, \alpha ^0, C^0, D^0, \beta ^0)$, the true parameter vector, $\widehat{\varvec{\theta }}$ = $({\widehat{A}}, {\widehat{B}}, {\widehat{\alpha }}, {\widehat{C}}, {\widehat{D}}, {\widehat{\beta }})$, the LSE of $\varvec{\theta }^0$ and $\varvec{\varTheta }$ = $[-M, M] \times [-M, M] \times [0,\pi ] \times [-M, M] \times [-M, M] \times [0,\pi ]$, where M is a positive real number. Also we make the following assumption on the unknown parameters:

Assumption 2

The true parameter vector $\varvec{\theta }^0$ is an interior point of the parametric space $\varvec{\varTheta }$, and ${A^0}^2 + {B^0}^2 + {C^0}^2 + {D^0}^2 > 0$.

Under these assumptions, we discuss two estimation procedures: the least squares estimation method and the sequential least squares estimation method. We then study the asymptotic properties of the estimators obtained using these methods.

2.1 Least Squares Estimators

The usual LSEs of the unknown parameters of model (5) can be obtained by minimizing the error sum of squares:

$$\begin{aligned} \begin{aligned} Q(\varvec{\theta })&= \sum _{t=1}^{n}\left( y(t) - A\cos (\alpha t)\right. \\&\left. - B \sin (\alpha t) - C\cos (\beta t^2) - D\sin \left( \beta t^2\right) \right) ^2, \end{aligned}\end{aligned}$$

with respect to A, B, $\alpha$, C, D and $\beta$ simultaneously. In matrix notation,

$$\begin{aligned} Q(\varvec{\theta }) = ({{\varvec{{Y}}}} - {{\varvec{{Z}}}}(\alpha , \beta )\varvec{\mu })^{\top }({{\varvec{{Y}}}} - {{\varvec{{Z}}}}(\alpha , \beta )\varvec{\mu }). \end{aligned}$$

(8)

Here, ${{\varvec{{Y}}}}_{n \times 1} = \begin{pmatrix} y(1)&\cdots&y(n)\end{pmatrix}^{\top },$ $\varvec{\mu }_{4 \times 1} = \begin{pmatrix} A&B&C&D \end{pmatrix}^{\top }$ and

$$\begin{aligned} {{\varvec{{Z}}}}(\alpha , \beta )_{n \times 4} = \begin{pmatrix} \cos (\alpha ) &{} \sin (\alpha ) &{} \cos (\beta ) &{} \sin (\beta ) \\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ \cos (n \alpha ) &{} \sin (n \alpha ) &{} \cos (n^2 \beta ) &{} \sin (n^2 \beta ) \end{pmatrix}. \end{aligned}$$

Since $\varvec{\mu }$ is a vector of conditionally linear parameters, by separable linear regression technique of Richards [36], we have:

$$\begin{aligned} \widehat{\varvec{\mu }}(\alpha , \beta ) = \left[ {{\varvec{{Z}}}}(\alpha , \beta )^{\top }{{\varvec{{Z}}}}(\alpha , \beta )\right] ^{-1}{{\varvec{{Z}}}}(\alpha , \beta )^{\top } {{\varvec{{Y}}}}. \end{aligned}$$

(9)

Using (9) in (8), we obtain:

$$\begin{aligned} R(\alpha , \beta )&= Q({\widehat{A}}(\alpha , \beta ), {\widehat{B}}(\alpha , \beta ), \alpha , {\widehat{C}}(\alpha , \beta ), {\widehat{D}}(\alpha , \beta ), \beta )\\&= {{\varvec{{Y}}}}^{\top }({{\varvec{{I}}}} - {{\varvec{{Z}}}}(\alpha , \beta )[{{\varvec{{Z}}}}(\alpha , \beta )^{\top }{{\varvec{{Z}}}}(\alpha , \beta )]^{-1}{{\varvec{{Z}}}}(\alpha , \beta )^{\top }){{\varvec{{Y}}}}. \end{aligned}$$

To obtain ${\widehat{\alpha }}$ and ${\widehat{\beta }}$, the LSEs of $\alpha ^0$ and $\beta ^0$ respectively, we minimize $R(\alpha , \beta )$ with respect to $\alpha$ and $\beta$ simultaneously. Once we obtain ${\widehat{\alpha }}$ and ${\widehat{\beta }}$, by substituting them in (9), we obtain the LSEs of the linear parameters.

The following results provide the consistency and asymptotic normality properties of the LSEs.

Theorem 1

Under Assumptions 1 and 2, $\widehat{\varvec{\theta }}$ is a strongly consistent estimator of $\varvec{\theta }^0$, that is,

$$\begin{aligned} \widehat{\varvec{\theta }} \xrightarrow {a.s.} \varvec{\theta }^0 as n \rightarrow \infty . \end{aligned}$$

Proof

See Sect. B.1. $\square$

Theorem 2

Under Assumptions 1 and 2,

$$\begin{aligned} \left( \widehat{\varvec{\theta }} - \varvec{\theta }^0\right) \mathbf{D }^{-1} \xrightarrow {d} {\mathcal {N}}\left( 0, c \sigma ^2 \varvec{\varSigma }^{-1}\left( \varvec{\theta }^0\right) \right) as n \rightarrow \infty , \end{aligned}$$

where $\mathbf{D } = \hbox {diag}(\frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}}, \frac{1}{n\sqrt{n}}, \frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}}, \frac{1}{n^2\sqrt{n}})$, $c = \sum \limits _{j=-\infty }^{\infty } a(j)^2$ and

$$\begin{aligned} \varvec{\varSigma }^{-1}\left( \varvec{\theta }^0\right) = \begin{pmatrix}\begin{array}{c|c} {\varvec{\varSigma }^{(1)}}^{-1}\left( \varvec{\theta }^0\right) &{} \quad {\mathbf {0}}\\ \hline {\mathbf {0}} &{} \quad {\varvec{\varSigma }^{(2)}}^{-1}\left( \varvec{\theta }^0\right) \\ \end{array} \end{pmatrix}, \end{aligned}$$

with

$$\begin{aligned} {\varvec{\varSigma }^{(1)}}^{-1}\left( \varvec{\theta }^0\right) = \begin{pmatrix} \frac{2\left( {A^0}^2 + 4 {B^0}^2\right) }{{A^0}^2 + {B^0}^2} &{} \frac{-6A^0B^0}{{A^0}^2 + {B^0}^2} &{} \frac{-12B^0}{{A^0}^2 + {B^0}^2}\\ \frac{-6A^0B^0}{{A^0}^2 + {B^0}^2} &{} \frac{2\left( 4 {A^0}^2 + {B^0}^2\right) }{{A^0}^2 + {B^0}^2} &{} \frac{12A^0}{{A^0}^2 + {B^0}^2} \\ \frac{-12B^0}{{A^0}^2 + {B^0}^2} &{} \frac{12A^0}{{A^0}^2 + {B^0}^2} &{} \frac{24}{{A^0}^2 + {B^0}^2} \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} {\varvec{\varSigma }^{(2)}}^{-1}\left( \varvec{\theta }^0\right) = \begin{pmatrix} \frac{4 {C^0}^2 + 9{D^0}^2}{2\left( {C^0}^2 + {D^0}^2\right) } &{} \frac{-5 C^0 D^0}{2\left( {C^0}^2 + {D^0}^2\right) } &{} \frac{-15 D^0}{2\left( {C^0}^2 +{D^0}^2\right) }\\ \frac{-5 C^0 D^0}{2\left( {C^0}^2 + {D^0}^2\right) } &{} \frac{9 {C^0}^2 + 4 {D^0}^2}{2\left( {C^0}^2 + {D^0}^2\right) } &{} \frac{15 C^0}{2\left( {C^0}^2 + {D^0}^2\right) }\\ \frac{-15D^0}{2\left( {C^0}^2 + {D^0}^2\right) } &{} \frac{15 C^0}{2\left( {C^0}^2 + {D^0}^2\right) } &{} \frac{45}{2\left( {C^0}^2 + {D^0}^2\right) } \end{pmatrix}. \end{aligned}$$

Proof

See Sect. B.1. $\square$

Note that to estimate the frequency and frequency rate parameters, we need to solve a 2D nonlinear optimization problem. Even for a special case of this model, when $C^0 = D^0 = 0$, it has been observed that the least squares surface is highly nonlinear and has several local minima near the true parameter value (for details, see Rice and Rosenblatt [35]). Therefore, it is evident that computation of the LSEs is a numerically challenging problem for the proposed model as well.

It is important to note that under stronger assumptions of i.i.d. Gaussian distribution on the error random variables X(t), the asymptotic variances of the LSEs coincide with the corresponding CRLBs.

2.2 Sequential Least Squares Estimators

To overcome the computational difficulty of finding the LSEs without compromising on the efficiency of the estimates, we propose a sequential procedure to find the estimates of the unknown parameters of model (5). In this section, we present the algorithm to obtain the sequential estimators and study the asymptotic properties of these estimators.

Note that the matrix ${{\varvec{{Z}}}}(\alpha , \beta )$ can be partitioned into two $n \times 2$ blocks as follows:

$$\begin{aligned} {{\varvec{{Z}}}}(\alpha , \beta ) = \begin{pmatrix}\begin{array}{c|c} {{\varvec{{Z}}}}^{(1)}(\alpha )\ \&\quad {{\varvec{{Z}}}}^{(2)}(\beta ) \end{array} \end{pmatrix}. \end{aligned}$$

Here,

$$\begin{aligned} {{\varvec{{Z}}}}^{(1)}(\alpha )_{n \times 2} = \begin{pmatrix}\begin{array}{cc} \cos (\alpha ) &{} \quad \sin (\alpha ) \\ \vdots &{} \quad \vdots \\ \cos (n \alpha ) &{} \quad \sin (n \alpha ) \end{array} \end{pmatrix} \text { and } {{\varvec{{Z}}}}^{(2)}(\beta )_{n \times 2} = \begin{pmatrix} \cos (\beta ) &{} \quad \sin (\beta ) \\ \vdots &{} \quad \vdots \\ \cos (n^2 \beta ) &{} \quad \sin (n^2 \beta ) \end{pmatrix}. \end{aligned}$$

Similarly, the linear parameter vector can be written as:

$$\begin{aligned} \varvec{\mu } = \begin{pmatrix} \begin{array}{c|c} {\varvec{\mu }^{(1)}}^{\top } \ \&\quad {\varvec{\mu }^{(2)}}^{\top } \end{array} \end{pmatrix}^{\top }, \end{aligned}$$

where $\varvec{\mu }^{(1)}_{2 \times 1} = \begin{pmatrix} A,&\quad B \end{pmatrix}^{\top }$ and $\varvec{\mu }^{(2)}_{2 \times 1} = \begin{pmatrix} C,&D \end{pmatrix}^{\top }.$ Also, the parameter vector,

$$\begin{aligned} \varvec{\theta } = \begin{pmatrix} \begin{array}{c|c} \varvec{\theta }^{(1)}\ \&\quad \varvec{\theta }^{(2)} \end{array} \end{pmatrix}, \end{aligned}$$

with $\varvec{\theta }^{(1)} = \begin{pmatrix} A,&\quad B,&\quad \alpha \end{pmatrix}$ and $\varvec{\theta }^{(2)} = \begin{pmatrix} C,&\quad D,&\quad \beta \end{pmatrix}.$ The parameter space can be written as $\varvec{\varTheta }^{(1)} \times \varvec{\varTheta }^{(2)}$ so that $\varvec{\theta }^{(1)} \in \varvec{\varTheta }^{(1)}$ and $\varvec{\theta }^{(2)} \in \varvec{\varTheta }^{(2)},$ with $\varvec{\varTheta }^{(1)} = \varvec{\varTheta }^{(2)} = [-M, M] \times [-M, M] \times [0, \pi ]$.

Following is the algorithm to find the sequential estimators:

Step 1::

First minimize the following error sum of squares:

$$\begin{aligned} Q_1\left( \varvec{\theta }^{(1)}\right) = \left( {\varvec{Y}} - {\varvec{Z}}^{(1)}(\alpha )\varvec{\mu }^{(1)}\right) ^{\top }\left( {\varvec{Y}} - {\varvec{Z}}^{(1)}(\alpha )\varvec{\mu }^{(1)}\right) \end{aligned}$$

(10)

with respect to A, B and $\alpha$. Using separable linear regression technique, for fixed $\alpha$, we have:

$$\begin{aligned} \widetilde{\varvec{\mu }}^{(1)}(\alpha ) = [{\varvec{Z}}^{(1)}(\alpha )^{\top }{\varvec{Z}}^{(1)}(\alpha )]^{-1}{\varvec{Z}}^{(1)}(\alpha )^{\top }{\varvec{Y}}. \end{aligned}$$

(11)

Now, replacing $\varvec{\mu }^{(1)}$ by $\widetilde{\varvec{\mu }}^{(1)}(\alpha )$ in (10), we have:

$$\begin{aligned} \begin{aligned}&R_1(\alpha ) = {\varvec{Y}}^{\top }\left( {\varvec{I}} - {\varvec{Z}}^{(1)}(\alpha )\left[ {\varvec{Z}}^{(1)}(\alpha )^{\top }{\varvec{Z}}^{(1)}(\alpha )\right] ^{-1}{\varvec{Z}}^{(1)}(\alpha )^{\top }\right) {\varvec{Y}}. \end{aligned} \end{aligned}$$

Minimizing $R_1(\alpha )$, we obtain ${\widetilde{\alpha }}$ and replacing $\alpha$ by ${\widetilde{\alpha }}$ in (11), we get the linear parameter estimates ${\widetilde{A}}$ and ${\widetilde{B}}$.

Step 2::

At this step, we eliminate the effect of the sinusoidal component from the original data, and obtain a new data vector:

$$\begin{aligned} {\varvec{Y}}_1 = {\varvec{Y}} - {\varvec{Z}}^{(1)}({\widetilde{\alpha }})\widetilde{\varvec{\mu }}^{(1)}. \end{aligned}$$

Now we minimize the error sum of squares:

$$\begin{aligned} Q_2\left( \varvec{\theta }^{(2)}\right) =\left( {\varvec{Y}}_1 - {\varvec{Z}}^{(2)}(\beta )\varvec{\mu }^{(2)}\right) ^{\top }\left( {\varvec{Y}}_1 - {\varvec{Z}}^{(2)}(\beta )\varvec{\mu }^{(2)}\right) , \end{aligned}$$

(12)

with respect to C, D and $\beta$. Again by separable linear regression technique, we have:

$$\begin{aligned} \widetilde{\varvec{\mu }}^{(2)}(\beta ) = [{\varvec{Z}}^{(2)}(\beta )^{\top }{\varvec{Z}}^{(2)}(\beta )]^{-1}{\varvec{Z}}^{(2)}(\beta )^{\top }{\varvec{Y}}_{1} \end{aligned}$$

(13)

for a fixed $\beta$. Now replacing $\varvec{\mu }^{(2)}$ by $\widetilde{\varvec{\mu }}^{(2)}$ in (12), we obtain:

$$\begin{aligned}\begin{aligned}&R_2(\beta ) = {\varvec{Y}}_1^{\top }\left( {\varvec{I}} - {\varvec{Z}}^{(2)}(\beta )\left[ {\varvec{Z}}^{(2)}(\beta )^{\top }{\varvec{Z}}^{(2)}(\beta )\right] ^{-1}{\varvec{Z}}^{(2)}(\beta )^{\top }\right) {\varvec{Y}}_1. \end{aligned} \end{aligned}$$

Minimizing $R_2(\beta )$, with respect to $\beta$, we obtain ${\widetilde{\beta }}$, and using ${\widetilde{\beta }}$ in (13), we obtain ${\widetilde{C}}$ and ${\widetilde{D}}$, the linear parameter estimates.

We use the following notations: ${\varvec{\theta }^{(1)}}^0= (A^0,\ B^0,\ \alpha ^0)$ and ${\varvec{\theta }^{(2)}}^0= (C^0,\ D^0,\ \beta ^0)$ are the true parameter vectors, $\widetilde{\varvec{\theta }}^{(1)} = ({\widetilde{A}},\ {\widetilde{B}},\ {\widetilde{\alpha }})$ is the sequential LSE of ${\varvec{\theta }^{(1)}}^{0}$ and $\widetilde{\varvec{\theta }}^{(2)} = ({\widetilde{C}},\ {\widetilde{D}},\ {\widetilde{\beta }})$ that of ${\varvec{\theta }^{(2)}}^{0}$.

In the following theorems, we prove that the proposed sequential LSEs are strongly consistent as the usual LSEs. Moreover, if Conjecture 1 (see Sect. A) holds true, the sequential LSEs have the same asymptotic distribution as the corresponding LSEs.

Theorem 3

Under Assumptions 1 and 2, $\widetilde{\varvec{\theta }}^{(1)}$ and $\widetilde{\varvec{\theta }}^{(2)}$ are strongly consistent estimators of ${\varvec{\theta }^{(1)}}^{0}$ and ${\varvec{\theta }^{(2)}}^{0}$, respectively, that is,

• (a)
  $$\begin{aligned} \widetilde{\varvec{\theta }}^{(1)} \xrightarrow {a.s.} {\varvec{\theta }^{(1)}}^{0} as n \rightarrow \infty , \end{aligned}$$
• (b)
  $$\begin{aligned} \widetilde{\varvec{\theta }}^{(2)} \xrightarrow {a.s.} {\varvec{\theta }^{(2)}}^{0} as n \rightarrow \infty . \end{aligned}$$

Proof

See Sect. B.2. $\square$

Theorem 4

Under Assumptions 1 and 2 and presuming Conjecture 1 (see Sect. A) holds true,

• (a)
  $$\begin{aligned} \left( \widetilde{\varvec{\theta }}^{(1)} - {\varvec{\theta }^{(1)}}^{0}\right) \mathbf{D }_1^{-1} \xrightarrow {d} {\mathcal {N}}_3\left( 0, c\sigma ^2{\varvec{\varSigma }^{(1)}}^{-1}\right) as n \rightarrow \infty , \end{aligned}$$
• (b)
  $$\begin{aligned} \left( \widetilde{\varvec{\theta }}^{(2)} - {\varvec{\theta }^{(2)}}^{0}\right) \mathbf{D }_2^{-1} \xrightarrow {d} {\mathcal {N}}_3\left( 0, c\sigma ^2{\varvec{\varSigma }^{(2)}}^{-1}\right) as n \rightarrow \infty , \end{aligned}$$

where $\mathbf{D }_1$ and $\mathbf{D }_2$, are sub-matrices of order $3 \times 3$, of the diagonal matrix $\mathbf{D }$ such that $\mathbf{D } = \begin{pmatrix}\begin{array}{c|c} \mathbf{D }_1 &{} \quad {\mathbf {0}}\\ \hline {\mathbf {0}} &{} \quad \mathbf{D }_2\\ \end{array} \end{pmatrix}.$ Note that, $\mathbf{D }$, c and $\varvec{\varSigma }_1^{-1}(\varvec{\theta }^0)$ and $\varvec{\varSigma }_2^{-1}(\varvec{\theta }^0)$ are as defined in Theorem 2.

Proof

See Sect. B.2. $\square$

3 Multiple Component Chirp-like Model

To model real-life data, we require a more adaptable model. In this section, we consider a multiple-component chirp-like model (3), a natural generalization of the one-component model.

Under certain assumptions in addition to Assumption 1 on the noise component, that we state below, we study the asymptotic properties of the LSEs and provide the results in the following subsection.

Let us denote by $\varvec{\vartheta }$ the parameter vector for model (3),

$$\begin{aligned} \varvec{\vartheta } = \left( A_1, B_1, \alpha _1, \ldots , A_p, B_p, \alpha _p, C_1, D_1, \beta _1, \ldots , C_q, D_q, \beta _q\right) . \end{aligned}$$

Also, let $\varvec{\vartheta }^0$ denote the true parameter vector and $\widehat{\varvec{\vartheta }}$, the LSE of $\varvec{\vartheta }^0.$

Assumption 3

$\varvec{\vartheta }^0$ is an interior point of ${\varvec{{{\mathcal {V}}}}} = {\varvec{\varTheta }_{1}}^{(p+q)}$, the parameter space and the frequencies $\alpha _{j}^0s$ are distinct for $j = 1, \ldots p$ and so are the frequency rates $\beta _{k}^0s$ for $k = 1, \ldots q$. Note that $\varvec{\varTheta }_{1} = [-M, M] \times [-M, M] \times [0,\pi ].$

Assumption 4

The amplitudes, $A_j^0$s and $B_j^0$s, satisfy the following relationship:

$$\begin{aligned} 2M^2> {A_{1}^{0}}^2 + {B_{1}^{0}}^2> {A_{2}^{0}}^2 + {B_{2}^{0}}^2> \cdots> {A_{p}^{0}}^2 + {B_{p}^{0}}^2 > 0. \end{aligned}$$

Similarly, $C_k^0$s and $D_k^0$s satisfy the following relationship:

$$\begin{aligned} 2M^2> {C_{1}^{0}}^2 + {D_{1}^{0}}^2> {C_{2}^{0}}^2 + {D_{2}^{0}}^2> \cdots> {C_{q}^{0}}^2 + {D_{q}^{0}}^2 > 0. \end{aligned}$$

3.1 Least Squares Estimators

The LSEs of the unknown parameters of the proposed model, see (3), can be obtained by minimizing the error sum of squares:

$$\begin{aligned} \begin{aligned} Q\left( \varvec{\vartheta }\right)&= \sum _{t=1}^{n}\left( y(t) - \sum _{j=1}^{p} \left\{ A_j cos\left( \alpha _j t\right) + B_j sin\left( \alpha _j t\right) \right\} \right. \\&\left. - \sum _{k=1}^{q}\left\{ C_k cos\left( \beta _k t^2\right) + D_k sin\left( \beta _k t^2\right) \right\} \right) ^2 \end{aligned} \end{aligned}$$

(14)

with respect to $A_1$, $B_1$, $\alpha _1$, $\ldots$, $A_p$, $B_p$ $\alpha _p$, $C_1$, $D_1$, $\beta _1$, $\ldots$, $C_q$, $D_q$ and $\beta _q$ simultaneously. Similar to the one-component model, $Q(\varvec{\vartheta })$ can be expressed in matrix notation and then the LSE, $\widehat{\varvec{\vartheta }}$ of $\varvec{\vartheta }^0$, can be obtained along the similar lines.

Next, we examine the consistency property of the LSE $\widehat{\varvec{\vartheta }}$ along with its asymptotic distribution.

Theorem 5

If Assumptions 1, 3 and 4, hold true, then:

$$\begin{aligned} \widehat{\varvec{\vartheta }} \xrightarrow {a.s.} \varvec{\vartheta }^0 as n \rightarrow \infty . \end{aligned}$$

Proof

The consistency of the LSE $\widehat{\varvec{\vartheta }}$ can be proved along the similar lines as the consistency of the LSE $\widehat{\varvec{\theta }}$, for the one-component model. $\square$

Theorem 6

If the above Assumptions 1, 3 and 4 , then:

$$\begin{aligned} \left( \widehat{\varvec{\vartheta }} - \varvec{\vartheta }^0\right) {\mathfrak {D}}^{-1} \xrightarrow {d} {\mathcal {N}}_{3(p+q)}\left( 0, c \sigma ^2 {\mathcal {E}}^{-1}\left( \varvec{\vartheta }^0\right) \right) as n \rightarrow \infty . \end{aligned}$$

$Here, {\mathfrak {D}} = \hbox {diag}(\underbrace{\mathbf{D }_1, \cdots \mathbf{D }_1}_{p\ times}, \underbrace{\mathbf{D }_2, \ldots , \mathbf{D }_2}_{q\ times}) , where \mathbf{D }_1 = \hbox {diag}(\frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}}, \frac{1}{n\sqrt{n}}) and \mathbf{D }_2 = \hbox {diag}(\frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}}, \frac{1}{n^2\sqrt{n}})$.

$$\begin{aligned} {\mathcal {E}}(\varvec{\vartheta }^0) = \begin{pmatrix} \varvec{\varSigma }^{(1)}_1 &{} \quad 0 &{} \quad \cdots &{} \quad &{} \cdots &{} \quad 0 &{} \\ 0 &{} \quad \ddots &{} \quad 0 &{} \quad &{} \cdots \quad &{} \quad 0 &{} \\ \vdots &{} \quad \vdots &{} \quad \varvec{\varSigma }^{(1)}_{p} &{} \quad 0 &{} \quad \cdots &{} \quad 0 \\ 0 &{} \quad \cdots &{} \quad 0 &{} \quad \varvec{\varSigma }^{(2)}_1 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad \cdots &{} \quad \cdots &{} \quad 0 &{} \quad \ddots &{} \quad 0 \\ 0 &{} \quad \cdots &{} \quad &{} \cdots \quad &{} \quad 0 &{} \quad \varvec{\varSigma }^{(2)}_{q} \\ \end{pmatrix}{,} \end{aligned}$$

with $\varvec{\varSigma }^{(1)}_j = \begin{pmatrix} \frac{1}{2} &{} 0 &{} \frac{B_j^0}{4} \\ 0 &{} \frac{1}{2} &{} \frac{-A_j^0}{4} \\ \frac{B_j^0}{4} &{} \frac{-A_j^0}{4} &{} \frac{{A_j^0}^2 + {B_j^0}^2}{6} \end{pmatrix},\ j = 1, \cdots , p$ and

$\varvec{\varSigma }^{(2)}_k = \begin{pmatrix} \frac{1}{2} &{} \quad 0 &{} \quad \frac{D_k^0}{6} \\ 0 &{} \quad \frac{1}{2} &{} \quad \frac{-C_k^0}{6} \\ \frac{D_k^0}{6} &{} \quad \frac{-C_k^0}{6} &{} \quad \frac{{C_k^0}^2 + {D_k^0}^2}{10} \end{pmatrix},\ k = 1, \ldots , q.$

Proof

See Sect. C.1. $\square$

3.2 Sequential Least Squares Estimators

For the multiple-component chirp-like model, if the number of components, p and q are very large, finding the LSEs becomes computationally challenging. To resolve this issue, we propose a sequential procedure to estimate the unknown parameters similar to the one-component model. Using the sequential procedure, the $(p+q)$-dimensional optimization problem can be reduced to $p+q$, 1D optimization problems. The algorithm for the sequential estimation is as follows:

Step 1::

Perform Step 1 of the sequential algorithm for the one-component chirp-like model as explained in Sect. 2.2 and obtain the estimate, $\widetilde{\varvec{\theta }}^{(1)}_1 = ({\widetilde{A}}_1$, ${\widetilde{B}}_1$, ${\widetilde{\alpha }}_1$).

Step 2::

Eliminate the effect of the estimated sinusoidal component and obtain new data vector:

$$\begin{aligned} y_1(t) = y(t) - {\widetilde{A}}_1 \cos \left( {\widetilde{\alpha }}_1 t\right) - {\widetilde{B}}_1 \sin \left( {\widetilde{\alpha }}_1 t\right) . \end{aligned}$$

Step 3::

Minimize the following error sum of squares to obtain the estimates of the next sinusoid, $\widetilde{\varvec{\theta }}^{(1)}_2 = ({\widetilde{A}}_2$, ${\widetilde{B}}_2$, ${\widetilde{\alpha }}_2$):

$$\begin{aligned} Q_2(A,B,\alpha ) = \sum _{t=1}^{n}\left( y_1(t) - A \cos (\alpha t) - B \sin (\alpha t)\right) ^2. \end{aligned}$$

Repeat these steps until all the p sinusoids are estimated.

Step $\mathbf {p+1}$::

At $(p+1)$-th step, we obtain the data:

$$\begin{aligned} y_p(t) = y_{p-1}(t) - {\widetilde{A}}_p \cos \left( {\widetilde{\alpha }}_p t\right) - {\widetilde{B}}_p \sin \left( {\widetilde{\alpha }}_p t\right) . \end{aligned}$$

Step $\mathbf {p+2}$::

Using this data, we estimate the first chirp component parameters, and obtain $\widetilde{\varvec{\theta }}^{(2)}_1$ = $({\widetilde{C}}_1$, ${\widetilde{D}}_1$, ${\widetilde{\beta }}_1$): by minimizing:

$$\begin{aligned} Q_{p+1}(C,D,\beta ) = \sum _{t=1}^{n}\left( y_{p}(t) - C\cos \left( \beta t^2\right) - D \sin \left( \beta t^2\right) \right) ^2. \end{aligned}$$

Step ${\mathbf {p}}+{\mathbf {3}}$::

Now, eliminate the effect of this estimated chirp component and obtain: $y_{p+1}(t) = y_{p}(t) - {\widetilde{C}}_1 \cos ({\widetilde{\beta }}_1 t^2) - {\widetilde{D}}_1 \sin ({\widetilde{\beta }}_1 t^2)$ and minimize $Q_{p+2}(C, D, \beta )$ to obtain $\widetilde{\varvec{\theta }}^{(2)}_2 = ({\widetilde{C}}_2$, ${\widetilde{D}}_2$, ${\widetilde{\beta }}_2$).

Continue to do so and estimate all the q chirp components.

We now investigate the consistency property of the proposed sequential estimators, when p and q are unknown. Thus, we consider the following two cases: (a) when the number of components of the fitted model is less than the actual number of components, and (b) when the number of components of the fitted model is more than the actual number of components.

Theorem 7

If Assumptions 1, 3 and 4 are satisfied, then the following are true:

• (a)
  $$\begin{aligned} \widetilde{\varvec{\theta }}_1^{(1)} \xrightarrow {a.s.} {\varvec{\theta }_1^{(1)}}^{0} as n \rightarrow \infty , \end{aligned}$$
• (b)
  $$\begin{aligned} \widetilde{\varvec{\theta }}_1^{(2)} \xrightarrow {a.s.} {\varvec{\theta }_1^{(2)}}^{0} as n \rightarrow \infty . \end{aligned}$$

Proof

See Sect. C.2. $\square$

Theorem 8

If Assumptions 1, 3 and 4 are satisfied, the following are true:

• (a)
  $$\begin{aligned} \widetilde{\varvec{\theta }}_j^{(1)} \xrightarrow {a.s.} {\varvec{\theta }_j^{(1)}}^{0} as n \rightarrow \infty , for all j = 2, \ldots , p, \end{aligned}$$
• (b)
  $$\begin{aligned} \widetilde{\varvec{\theta }}_k^{(2)} \xrightarrow {a.s.} {\varvec{\theta }_k^{(2)}}^{0} as n \rightarrow \infty , for all k = 2, \ldots , q. \end{aligned}$$

Proof

See Sect. C.2. $\square$

Theorem 9

If Assumptions 1, 3 and 4 are true, then the following are true:

• (a)
  $$\begin{aligned} {\widetilde{A}}_{p+k} \xrightarrow {a.s.} 0, \quad {\widetilde{B}}_{p+k} \xrightarrow {a.s.} 0 \text { for } k = 1,2, \ldots , \text { as } n \rightarrow \infty , \end{aligned}$$
• (b)
  $$\begin{aligned} {\widetilde{C}}_{q+k} \xrightarrow {a.s.} 0, \quad {\widetilde{D}}_{q+k} \xrightarrow {a.s.} 0 \text { for } k = 1,2, \ldots , \text { as } n \rightarrow \infty . \end{aligned}$$

Proof

See Sect. C.2. $\square$

Next, we determine the asymptotic distribution of the proposed estimators at each step through the following theorems:

Theorem 10

If Assumptions 1, 3 and 4 are satisfied and presuming Conjecture 1 (see Sect. A) hold true, then:

• (a)
  $$\begin{aligned} \left( \widetilde{\varvec{\theta }}_1^{(1)} - {\varvec{\theta }^0_1}^{(1)}\right) \mathbf{D }_1^{-1} \xrightarrow {d} {\mathcal {N}}_3(0, c \sigma ^2{\varvec{\varSigma }^{(1)}_1}^{-1}) as n \rightarrow \infty , \end{aligned}$$
• (b)
  $$\begin{aligned} \left( \widetilde{\varvec{\theta }}_1^{(2)} - {\varvec{\theta }^0_1}^{(2)}\right) \mathbf{D }_2^{-1} \xrightarrow {d} {\mathcal {N}}_3(0, c \sigma ^2{\varvec{\varSigma }^{(2)}_1}^{-1}) as n \rightarrow \infty . \end{aligned}$$

Here, c, the diagonal matrices $\mathbf{D }_1$ and $\mathbf{D }_2$ and the matrices ${\varvec{\varSigma }^{(2)}_1}^{-1}$ and ${\varvec{\varSigma }^{(2)}_1}^{-1}$ are as defined in Theorem 6.

Proof

See Sect. C.2. $\square$

This result can be extended for $2 \leqslant j \leqslant p$ and $2 \leqslant k \leqslant q$ as follows:

Theorem 11

If Assumptions 1, 3 and 4 are satisfied and presuming Conjecture 1 (see Sect. A) hold true,, then for all $j = 2, \ldots , p$ and $k = 2, \ldots , q$:

• (a)
  $$\begin{aligned} \left( \widetilde{\varvec{\theta }}_j^{(1)} - {\varvec{\theta }^0_j}^{(1)}\right) \mathbf{D }_1^{-1} \xrightarrow {d} {\mathcal {N}}_3\left( 0, c \sigma ^2 {\varvec{\varSigma }^{(1)}_j}^{-1}\right) as n \rightarrow \infty , \end{aligned}$$
• (b)
  $$\begin{aligned} \left( \widetilde{\varvec{\theta }}_k^{(2)} - {\varvec{\theta }^0_k}^{(2)}\right) \mathbf{D }_2^{-1} \xrightarrow {d} {\mathcal {N}}_3\left( 0, c \sigma ^2 {\varvec{\varSigma }^{(2)}_k}^{-1}\right) as n \rightarrow \infty . \end{aligned}$$

$\varvec{\varSigma }^{(1)}_j$ and $\varvec{\varSigma }^{(2)}_k$ are as defined in Theorem 6.

Proof

This can be obtained along the same lines as the proof of Theorem 10. $\square$

From the above results, it is evident that the sequential LSEs are strongly consistent and have the same asymptotic distribution as the LSEs and at the same time can be computed more efficiently. Thus for the simulation studies and to analyze the real datasets as well, we compute the sequential LSEs instead of the LSEs.

4 Simulation Studies

In this section, we present the results obtained from some numerical experiments, performed both for a one-component and a multiple-component model. These results demonstrate the applicability of our model and the performance of the LSEs and the sequential LSEs. Since we are primarily interested in the estimation of the nonlinear parameters, here we report only these estimates. The linear parameter estimates can be obtained by simple linear regression.

4.1 Results for a One-Component Chirp-like Model

In the first set of experiments, we consider a one-component chirp-like model (5) with the following true parameter values:

$$\begin{aligned} A^0 = 10, B^0 = 10, \alpha ^0 = 1.5, C^0 = 10, D^0 = 10 and \beta ^0 = 0.1{.} \end{aligned}$$

The error structure used to generate the data is as follows:

$$\begin{aligned} X(t) = \epsilon (t) + 0.5 \epsilon (t-1). \end{aligned}$$

Here, $\epsilon (t)$s are i.i.d. normal random variables with mean zero and variance $\sigma ^2$. We consider different sample sizes: $n = 100, 200, 300, 400$ and 500 and different error variances: $\sigma ^2$: 0.1, 0.25, 0.5, 0.75 and 1. For each n and $\sigma ^2$, we generate the data and obtain the LSEs. Based on 1000 iterations, we compute the biases and MSEs of the LSEs. We also compute the theoretical asymptotic variances of the proposed estimators to compare with the corresponding computed MSEs. Figures 2 and 3 represent the biases and MSEs of the LSEs of $\alpha$ and $\beta$ compared to the asymptotic variances versus different sample sizes. Similarly in Figs. 4 and 5, the biases and MSEs versus signal-to-noise ratio (SNR) are shown.

Fig. 2

In each sub-plot, the solid line represents the absolute value of the biases of the estimators of parameters of the underlying simulated one-component model versus the sample size

Fig. 3

In each sub-plot, the dashed line represents the MSEs of the estimates and the solid line represents the corresponding theoretical asymptotic variances of the estimators of parameters of the underlying simulated one-component model versus the sample size

Fig. 4

In each sub-plot, the solid line represents the absolute value of the biases of the estimators of parameters of the underlying simulated one-component model versus SNR

Fig. 5

In each sub-plot, the dashed line represents the MSEs of the estimates and the solid line represents the corresponding theoretical asymptotic variances of the estimators of parameters of the underlying simulated one-component model versus SNR

Figures 2 and 4 show that the biases of the estimates are quite small, and therefore the average estimates are close to the true values. Figure 3 depicts the consistent behaviour of the LSEs. It can be seen that as n increases, the MSEs decrease. Similarly, Fig. 5 represents the performance of the LSEs for different SNRs compared with the asymptotic variances. The figure shows that MSEs decrease as the SNR increases, and they match the corresponding asymptotic variances quite well.

4.2 Results for a Multiple-component Chirp-like Model

Here, we present the simulation results for the multiple-component chirp-like model (3) with $p = q = 2$. Following are the true parameter values used for data generation:

$$\begin{aligned} A_1^0= & {} 10, B_1^0 = 10, \alpha _1^0 = 1.5, C_1^0 = 10, D_1^0 = 10 and \beta _1^0 = 0.1,\\ A_2^0= & {} 8, B_2^0 = 8, \alpha _2^0 = 2.5, C_2^0 = 8, D_2^0 = 8 and \beta _2^0 = 0.2. \end{aligned}$$

The error structure used for data generation is again a moving average process, the same as used for the one-component model simulations. We compute the sequential LSEs of the parameters and report their biases, MSEs, and asymptotic variances. Again, the different sample sizes and error variances used for the simulations are the same as those for the one-component model. Figures 6 and 7 display the biases and the MSEs of the obtained estimates versus the varying sample size. It is observed that the estimates obtained have significantly small biases and thereby are close to the true values. We also observe that as n increases the biases and the MSEs decrease, thus depicting the desired consistency of the estimators. Moreover, the MSEs are on an equal footing with the corresponding asymptotic variances. The observations, therefore, validate the derived theoretical properties of the sequential estimators.

Fig. 6

In each sub-plot, the solid line represents the absolute value of the biases of the estimators of parameters of the underlying simulated two component model versus sample size

Fig. 7

In each sub-plot, the dashed line represents the MSEs of the estimates and the solid line represents the corresponding theoretical asymptotic variances of the estimators of parameters of the underlying simulated two component model versus sample size

In Figs. 8 and 9, the biases and the MSEs of the sequential estimates of the first component parameters versus the SNR are shown, and in Figs. 10 and 11, the biases and the MSEs of the sequential estimates of the second component parameters versus SNR are displayed. The lines representing the MSEs and the asymptotic variances in Figs. 9 and 11 are visually indistinguishable, indicating high accuracy of the estimators.

Fig. 8

In each sub-plot, the solid line represents the absolute value of the biases of the estimators of parameters of the first component of the simulated two component model versus SNR

Fig. 9

In each sub-plot, the dashed line represents the MSEs of the estimates and the solid line represents the corresponding theoretical asymptotic variances of the estimators of parameters of the first component of the simulated two component model versus SNR

Fig. 10

In each sub-plot, the solid line represents the absolute value of the biases of the estimators of parameters of the second component of the simulated two component model versus SNR

Fig. 11

In each sub-plot, the dashed line represents the MSEs of the estimates and the solid line represents the corresponding theoretical asymptotic variances of the estimators of parameters of the second component of the simulated two-component model versus SNR

4.3 Fitting a Chirp Model Versus a Chirp-like Model to a Given Data

In this section, we make a comparison of computational complexities involved in fitting a chirp-like model to a data set and that involved in modeling a data set using a chirp model. The method of estimation that we will use to fit either of these models is sequential LSEs as it significantly reduces the computational burden involved in finding the traditional LSEs. This is discussed in more detail in the next section.

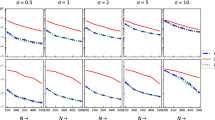
It must be noted that for fitting a nonlinear model finding the initial values is of prime importance. Once we have found the initial values, we can employ any iterative algorithm to find the sequential LSEs of the parameters. To find precise initial values, we have to resort to a fine grid search throughout the parameter space, but performing a grid search entails high computational load. We demonstrate in the following figures how replacing a chirp model with a chirp-like model reduces this computational load significantly. In Fig. 12, we plot the size of the grid required to find accurate initial values of the parameters of one component of a chirp model and a chirp-like model. It is visually evident that the difference in the computational complexity involved in fitting a chirp model and a chirp-like model is huge. In Fig. 13, time taken to fit a component of a chirp model and a chirp-like model is shown and the picture gives more insight into the computational difference.

Fig. 12

Comparison of computational complexity involved in fitting a component of chirp model and of a chirp-like model

Fig. 13

Comparison of time consumption of fitting a component of chirp model and of a chirp-like model

4.4 Fitting a Chirp-like Model using LSEs Versus Sequential LSEs

In this section, we see how it is more expensive from a computational point of view to find the LSEs. As discussed before, finding the initial values accounts for most of the time consumption of finding the estimators of the nonlinear parameters. Therefore, the computational complexity of finding the LSEs and the sequential LSEs heavily depends on the grid search for initial values. In Fig. 14, we bring out this comparison between the LSEs and the sequential LSEs. The number of grid points in the parameter space required for precise initial values of the parameter estimates of a chirp-like model with two sinusoids and two chirp components is reported. The figure reveals that the sequential method reduces the computational burden involved in finding the LSEs significantly.

Fig. 14

Comparison of computational complexity involved in finding the LSEs and sequential LSEs of a chirp-like model with two sinusoids and two chirp components

5 Data Analysis

5.1 Real Data Analysis

In this section, we analyze four different speech signal data sets: “AAA”, “AHH”, “UUU” and “EEE” using the chirp model as well as the proposed chirp-like model. These data sets have been obtained from a sound instrument at the Speech Signal Processing laboratory of the Indian Institute of Technology Kanpur. The dataset “AAA” has 477 data points, the set “AHH” has 469 data points and the rest of them have 512 points each.

We fit the chirp-like model to these data sets using the sequential LSEs following the algorithm described in Sect. 3.2. As is evident from the description, we need to solve a 1D optimization problem to find these estimators and since the problem is nonlinear, we need to employ some iterative method to do so. Here we use Brent’s method [3] to solve 1D optimization problems, using an inbuilt function in R, known as ‘optim’. For this method to work, we require very good initial values in the sense that they need to be close to the true values. Now one of the well-received methods for finding initial values for the frequencies of the sinusoidal model is to maximize the periodogram function:

$$\begin{aligned} I_1(\alpha ) = \frac{1}{n} \bigg |\sum _{t=1}^{n} y(t)e^{-i\alpha t}\bigg |^2 \end{aligned}$$

at the points: $\displaystyle {\frac{\pi j}{n}}$; $j = 1, \ldots , n-1,$ called the Fourier frequencies. The estimators obtained by this method, are called the Periodogram Estimators. After all the p sinusoidal components are fitted, we need to fit the q chirp components. Again, we need to solve 1D optimization problem at each stage and for that we need good initial values. Analogous to the periodogram function $I_1(\alpha )$, we define a periodogram-type function as follows:

$$\begin{aligned} I_2(\beta ) = \frac{1}{n} \bigg |\sum _{t=1}^{n} y(t)e^{-i\beta t^2}\bigg |^2. \end{aligned}$$

To obtain the starting points for the frequency rate parameter $\beta$, we maximize this function at the points: $\displaystyle {\frac{\pi k}{n^2}}$; $k = 1, \ldots , n^2-1$, similar to the Fourier frequencies.

Since in practice, the number of components of a model are unknown, we need to estimate them. We use the following Bayesian information criterion (BIC), as a tool to estimate p and q:

$$\begin{aligned} \begin{aligned} BIC (j,k) = n \ ln(SS _{res}(j,k)) + 2\ (3j + 3k)\ ln(n); j = 1, \ldots , J;\ k = 1, \ldots , K, \end{aligned} \end{aligned}$$

(15)

for the present analysis of the datasets. For reference on the form of this criterion function, one may refer to the monograph by Kundu and Nandi [19]. Here, $SS _{res}$ is the residual sum of squares when j sinusoidal components and k chirp components are fitted to the data. This is based on the assumption that the maximum number of sinusoidal components is J and chirp components is K and in practice, we choose a large values of J and K. We select the pair (j, k) as an estimate of the pair (p, q) corresponding to the minimum BIC.

For comparison of the chirp-like model with the chirp model, we re-analyze these data sets by fitting a chirp model to each of them (for methodology, see Lahiri, Kundu and Mitra [22]). In Table 1, we report the number of components required to fit the chirp model and the chirp-like model to each of the data sets and in Figs. 15 and 16, we plot the original data along with the estimated signals obtained by fitting a chirp model and a chirp-like model to these data. In both scenarios, the model is fitted using the sequential LSEs.

To validate the error assumption of stationarity, we test the residuals, for all the cases, using the augmented Dickey-Fuller test (for more details see Fuller [9]). This tests the following null hypothesis:

$H_0$: There is a unit root present in the series,

against the following alternative:

$H_1$ : No unit root present in the series, that is, the series is stationary.

We use an inbuilt function ‘adftest’ in MATLAB for this purpose. The test statistic values result in rejection of the null hypothesis of the presence of a unit root indicating that residuals, in all the cases, are stationary (Table 1).

It is evident from the figures above that visually both the models provide a good fit for all the speech datasets. However, to fit a chirp-like model using the sequential LSEs, we solve a 1D optimization problem at each step, while for the fitting of a chirp model, at each step, we need to deal with a 2D optimization problem. Moreover, to find the initial values, in both cases, a grid search is performed and for the chirp-like model, this means evaluation of the periodogram functions $I_1(\alpha )$ and $I_2(\beta )$ at n and $n^2$ grid points, respectively, as opposed to the $n^3$ grid points for the chirp model. Note that this is done at each step for the sequential estimators and hence becomes more complex as the number of components increases. Thus, fitting a chirp-like model is computationally much more efficient than fitting a chirp model (Fig. 15).

Table 1 Number of components used to fit chirp and chirp-like model to the speech data sets

Fig. 15

Speech Signal data sets: “AAA” and “AHH”; Observed data (red solid line) and fitted signal (blue dashed line). The sub-plots on the left represent chirp model fitting and those on the right represent chirp-like model fitting (Color figure online)

5.2 Simulated Data Analysis

We generate the data from a multiple-component chirp model. The number of components is set to 5 and the parameters, amplitudes, frequencies, and frequency rates are assigned prefixed values provided in Table 2.

Table 2 True parameters values of the synthetic data

The data here are generated with the following error structure:

$$\begin{aligned} X(t) = 0.8897 X(t-1) - 0.4858X(t-2) + e(t) - 0.2279e(t-1) + 0.2488 e(t-2) \end{aligned}$$

Here, e(t) are i.i.d. Gaussian random variables with mean 0 and variance 2. The simulated signal consists of 512 sample points and is shown in Fig. 16.

Fig. 16

Speech Signal data sets: “EEE” and “UUU”; Observed data (red solid line) and fitted signal (blue dashed line). The sub-plots on the left represent chirp model fitting and those on the right represent chirp-like model fitting

The objective is to evaluate and compare the performance of the chirp model and the chirp-like model to fit the simulated data. First, we fit a chirp model to the data using the sequential least squares estimation method. For estimating the number of chirp components, we use the following form of BIC:

$$\begin{aligned} \begin{aligned} BIC (j) = n \ ln\left( SS _{res}(j)\right) + 2\ * 4j\ * ln(n); j = 1, \ldots , J. \end{aligned} \end{aligned}$$

(16)

Corresponding to the minimum value of BIC, ${\widetilde{p}} = 5.$ Using these five chirp components and sequential LSEs of the parameters, we compute the estimated signal. The fitted chirp signal overlapping the synthesized signal is shown in Fig. 17.

Fig. 17

Simulated data

Next, to illustrate the effectiveness of a chirp-like model to clone a chirp signal, we fit a chirp-like model to the above synthesized data. We fit this model using the proposed sequential LSEs. Since the number of sinusoids and chirp components needed to fit this model to the simulated data is unknown, we again use BIC for the model selection as defined in (15). Corresponding to the minimum value of BIC, we choose ${\widetilde{p}} = 9$ and ${\widetilde{q}} = 1$, the estimates of the model order. In Fig. 18, the model fitting corresponding to the selected model is shown along with the simulated data.

Fig. 18

Simulated data signal along with estimated signal using chirp model

It can be seen that the estimated signals using the chirp model as well as the chirp-like model envelop the simulated chirp data quite accurately. We also measure the accuracy of these fittings by calculating the residual root-mean-square errors (RMSEs) for the two model fittings. The residual RMSE for the chirp model fitting is 0.8750, while for the chirp-like model fitting, it is 4.0727. The difference in the RMSEs is also reflected in Fig. 19 as a small gap can be observed at some time points. However, this gap can be reduced with an increase in the number of components fitted to the model. It is important to note that fitting five components of a chirp model to a dataset of size 512, needs $512^3 * 5 = 67,10,88,640$ function evaluations. On the other hand, fitting nine sinusoid components and 1 chirp component of a chirp-like model to this dataset requires $(512 * 9) + (512 * 512 * 1) = 2,66,752$ function evaluations. Therefore, a trade-off must be made between the computational complexity and accuracy of the estimated fitting.

Fig. 19

Simulated data signal along with estimated signal using chirp-like model

Another important point is that by increasing the number of components, we can improve the performance of the chirp-like model and reduce the residual RMSE to get at par with that in the case of the chirp model fitting. For example, if we use 48 sinusoids and 41 chirp components of a chirp-like model to explain this simulated data, the residual RMSE of the new fitting turns out to be 0.8720, which is less than that obtained by chirp model fitting. Moreover the computational expense ($(512 * 48) + (512 * 512 * 41) = 1,07,47,904$ function evaluations which is approximately 63 times less expensive than the chirp model fitting) will still be lower than that involved in fitting a five-component chirp model. Therefore, a chirp-like model can provide a better fit at a lower expense. From here, we can also conclude that the BIC method for model selection can under-estimate the model order and may not give the best estimation performance. We believe that there is a need to develop more efficient methods of model selection for better results. However, this is not explored here and is an open problem.

6 Conclusion

Chirp signals are ubiquitous in many areas of science and engineering and hence their parameter estimation is of great significance in signal processing. But it has been observed that parameter estimation of this model, particularly using the method of least squares is computationally complex. In this paper, we put forward an alternate model, named the chirp-like model. We observe that the data that have been analyzed using chirp models can also be analyzed using the chirp-like model and estimating its parameters using sequential LSEs is simpler than that for the chirp model. We show that the LSEs and the sequential LSEs of the parameters of this model are strongly consistent and asymptotically normally distributed. The rates of convergence of the parameter estimates of this model are the same as those for the chirp model. We analyze four speech datasets, and it is observed that the proposed model can be used quite effectively to analyze these data sets.

Appendices

Some Preliminary Results

To provide the proofs of the asymptotic properties established in this manuscript, we will require the following results:

Lemma 1

If $\phi \in (0, \pi )$, then the following hold true:

• (a) $\lim \limits _{n \rightarrow \infty } \frac{1}{n} \sum \limits _{t=1}^{n}\cos (\phi t) = \lim \limits _{n \rightarrow \infty } \frac{1}{n} \sum \limits _{t=1}^{n}\sin (\phi t) = 0.$

• (b) $\lim \limits _{n \rightarrow \infty } \frac{1}{n^{k+1}} \sum \limits _{t=1}^{n}t^{k} \cos ^2(\phi t) = \lim \limits _{n \rightarrow \infty } \frac{1}{n^{k+1}} \sum \limits _{t=1}^{n}t^{k} \sin ^2(\phi t) = \frac{1}{2(k+1)};\ k = 0, 1, 2, \ldots .$

• (c) $\lim \limits _{n \rightarrow \infty } \frac{1}{n^{k+1}} \sum \limits _{t=1}^{n}t^{k} \sin (\phi t) \cos (\phi t) = 0;\ k = 0, 1, 2, \ldots .$

Proof

Refer to Kundu and Nandi [19]. $\square$

Lemma 2

If $\phi \in (0, \pi )$, then except for a countable number of points, the following hold true:

• (a) $\lim \limits _{n \rightarrow \infty } \frac{1}{n} \sum \limits _{t=1}^{n}\cos (\phi t^2) = \lim \limits _{n \rightarrow \infty } \frac{1}{n} \sum \limits _{t=1}^{n}\sin (\phi t^2) = 0.$

• (b) $\lim \limits _{n \rightarrow \infty } \frac{1}{n^{k+1}} \sum \limits _{t=1}^{n}t^{k} \cos ^2(\phi t^2) = \lim \limits _{n \rightarrow \infty } \frac{1}{n^{k+1}} \sum \limits _{t=1}^{n}t^{k} \sin ^2(\phi t^2) = \frac{1}{2(k+1)};\ k = 0, 1, 2, \ldots .$

• (c) $\lim \limits _{n \rightarrow \infty } \frac{1}{n^{k+1}} \sum \limits _{t=1}^{n}t^{k} \sin (\phi t^2) \cos (\phi t^2) = 0;\ k = 0, 1, 2, \ldots .$

Proof

Refer to Lahiri [20]. $\square$

Lemma 3

If $(\phi _1, \phi _2) \in (0, \pi ) \times (0, \pi )$, then except for a countable number of points, the following holds true:

• (a) $\lim \limits _{n \rightarrow \infty } \frac{1}{n^{k+1}} \sum \limits _{t=1}^{n} t^k \cos (\phi _1 t)\cos (\phi _2 t^2) = 0$

• (b) $\lim \limits _{n \rightarrow \infty } \frac{1}{n^{k+1}} \sum \limits _{t=1}^{n} t^k \cos (\phi _1 t)\sin (\phi _2 t^2) = 0$

• (c) $\lim \limits _{n \rightarrow \infty } \frac{1}{n^{k+1}} \sum \limits _{t=1}^{n} t^k \sin (\phi _1 t)\cos (\phi _2 t^2) = 0$

• (d) $\lim \limits _{n \rightarrow \infty } \frac{1}{n^{k+1}} \sum \limits _{t=1}^{n} t^k \sin (\phi _1 t)\sin (\phi _2 t^2) = 0$

$k = 0, 1, 2, \ldots$

Proof

This proof follows from the number theoretic result proved by Lahiri [20] (see Lemma 2.2.1 of the reference). $\square$

Lemma 4

If X(t) satisfies Assumptions 1, 3 and 4 , then for $k \geqslant 0$:

• (a) $\sup \limits _{\phi } \bigg |\frac{1}{n^{k+1}} \sum \limits _{t=1}^{n} t^k X(t)e^{i(\phi t)}\bigg | \xrightarrow {a.s.} 0$

• (b) $\sup \limits _{\phi } \bigg |\frac{1}{n^{k+1}} \sum \limits _{t=1}^{n} t^k X(t)e^{i(\phi t^2)}\bigg | \xrightarrow {a.s.} 0$

Here, $i = \sqrt{-i}.$

Proof

These can be obtained as particular cases of Lemma 2.2.2 of Lahiri [20]. $\square$

Following is the famous number theoretic conjecture of Montgomery [29].

Conjecture 1

If $\theta _1$, $\theta _2$, $\theta '_1$, $\theta '_2$ $\in$ $(0, \pi )$, then except for a countable number of points:

• (a)
  $$\begin{aligned}\begin{aligned} \lim _{n \rightarrow \infty } \frac{1}{n^k \sqrt{n}}\sum _{t=1}^{n} t^k \cos \left( \theta _1 t + \theta _2 t^2\right) \sin \left( \theta '_1 t + \theta '_2 t^2\right) = 0;\ k = 0,1,2, \ldots , \end{aligned}\end{aligned}$$
• (b)
  $$\begin{aligned}\begin{aligned} \lim _{n \rightarrow \infty } \frac{1}{n^k \sqrt{n}}\sum _{t=1}^{n} t^k \cos \left( \theta _1 t + \theta _2 t^2\right) \cos \left( \theta '_1 t + \theta '_2 t^2\right) = 0;\ k = 0,1,2, \ldots ;\ if \theta _2 \ne \theta '_2, \\ \lim _{n \rightarrow \infty } \frac{1}{n^k \sqrt{n}}\sum _{t=1}^{n} t^k \sin \left( \theta _1 t + \theta _2 t^2\right) \sin \left( \theta '_1 t + \theta '_2 t^2\right) = 0;\ k = 0,1,2, \ldots ;\ if \theta _2 \ne \theta '_2. \end{aligned} \end{aligned}$$

The following conjecture follows from Montgomery’s conjecture:

Conjecture 2

If $(\phi _1, \phi _2) \in (0, \pi ) \times (0, \pi )$, then except for a countable number of points, the following holds true:

• (a) $\lim \limits _{n \rightarrow \infty } \frac{1}{n^k\sqrt{n}} \sum \limits _{t=1}^{n} t^k \cos (\phi _1 t^2) = 0$

• (b) $\lim \limits _{n \rightarrow \infty } \frac{1}{n^k\sqrt{n}} \sum \limits _{t=1}^{n} t^k \sin (\phi _1 t^2) = 0$

• (c) $\lim \limits _{n \rightarrow \infty } \frac{1}{n^k\sqrt{n}} \sum \limits _{t=1}^{n} t^k \cos (\phi _1 t)\cos (\phi _2 t) = 0$

• (d) $\lim \limits _{n \rightarrow \infty } \frac{1}{n^k\sqrt{n}} \sum \limits _{t=1}^{n} t^k \cos (\phi _1 t)\sin (\phi _2 t) = 0$

• (e) $\lim \limits _{n \rightarrow \infty } \frac{1}{n^k\sqrt{n}} \sum \limits _{t=1}^{n} t^k \sin (\phi _1 t)\sin (\phi _2 t) = 0$

• (f) $\lim \limits _{n \rightarrow \infty } \frac{1}{n^k\sqrt{n}} \sum \limits _{t=1}^{n} t^k \cos (\phi _1 t)\cos (\phi _2 t^2) = 0$

• (g) $\lim \limits _{n \rightarrow \infty } \frac{1}{n^k\sqrt{n}} \sum \limits _{t=1}^{n} t^k \cos (\phi _1 t)\sin (\phi _2 t^2) = 0$

• (h) $\lim \limits _{n \rightarrow \infty } \frac{1}{n^k \sqrt{n}} \sum \limits _{t=1}^{n} t^k \sin (\phi _1 t)\cos (\phi _2 t^2) = 0$

• (i) $\lim \limits _{n \rightarrow \infty } \frac{1}{n^k \sqrt{n}} \sum \limits _{t=1}^{n} t^k \sin (\phi _1 t)\sin (\phi _2 t^2) = 0$

$k = 0, 1, 2, \ldots$.

In the subsequent appendices, we show that if the above conjecture holds, then the asymptotic distribution of the sequential LSEs coincides with that of the usual LSEs.

One Component Chirp-like Model

1.1 Proofs of the Asymptotic Properties of the LSEs

We need the following lemmas to prove the consistency of the LSEs:

Lemma 5

Consider the set $S_c = \{\varvec{\theta }: |\varvec{\theta } - \varvec{\theta }^0| > c; \varvec{\theta } \in \varvec{\varTheta }\}$. If the following holds true,

$$\begin{aligned} \liminf \inf \limits _{S_c} \frac{1}{n} \left( Q\left( \varvec{\theta }\right) - Q(\varvec{\theta }^0)\right) > 0 a.s., \end{aligned}$$

(17)

then $\hat{\varvec{\theta }} \xrightarrow {a.s.} \varvec{\theta }^0$ as $n \rightarrow \infty$

Proof

Let us denote $\hat{\varvec{\theta }}$ by $\hat{\varvec{\theta }}_{n}$, to highlight the fact that the estimates depend on the sample size n. Now suppose, $\hat{\varvec{\theta }}_{n} \nrightarrow \varvec{\theta }^0$, then there exists a subsequence $\{n_k\}$ of $\{n\}$, such that $\hat{\varvec{\theta }}_{n_k} \nrightarrow \varvec{\theta }^0$. In such a situation, one of two cases may arise:

• 1. $|{\hat{A}}_{n_k}| + |{\hat{B}}_{n_k}| + |{\hat{C}}_{n_k}| + |{\hat{D}}_{n_k}|$ is not bounded, that is, at least one of the $|{\hat{A}}_{n_k}|$ or $|{\hat{B}}_{n_k}|$ or $|{\hat{C}}_{n_k}|$ or $|{\hat{D}}_{n_k}|$ $\rightarrow \infty$ $\Rightarrow \frac{1}{n_k}Q_{n_k}(\hat{\varvec{\theta }}_{n_k}) \rightarrow \infty$

  But, $\lim \limits _{n_k \rightarrow \infty } \frac{1}{n_k} Q_{n_k}(\varvec{\theta }^0) < \infty$ which implies, $\frac{1}{n_k} (Q_{n_k}(\hat{\varvec{\theta }}_{n_k}) - Q_{n_k}(\varvec{\theta }^0)) \rightarrow \infty .$ This contradicts the fact that:

  $$\begin{aligned} Q_{n_k}\left( \hat{\varvec{\theta }}_{n_k}\right) \leqslant Q_{n_k}(\varvec{\theta }^0), \end{aligned}$$

  (18)

  which holds true as $\hat{\varvec{\theta }}_{n_k}$ is the LSE of $\varvec{\theta }^0$.

• 2. $|{\hat{A}}_{n_k}| + |{\hat{B}}_{n_k}| + |{\hat{C}}_{n_k}| + |{\hat{D}}_{n_k}|$ is bounded, then there exists a $c > 0$ such that $\hat{\varvec{\theta }}_{n_k} \in S_c$, for all $k = 1, 2, \ldots$. Now, since (17) is true, this contradicts (18).

Hence, the result. $\square$

Proof of Theorem 1:

Consider the difference:

$$\begin{aligned}&\frac{1}{n}\left( Q(\varvec{\theta }) - Q\left( \varvec{\theta }^0\right) \right) \\&\quad = \frac{1}{n}\sum _{t=1}^{n}\left( y(t) - A\cos (\alpha t) - B \sin (\alpha t) - C \cos \left( \beta t^2\right) - D \sin \left( \beta t^2\right) \right) ^2 \\&\qquad - \frac{1}{n}\sum _{t=1}^{n}\left( y(t) - A^0\cos \left( \alpha ^0 t\right) - B^0 \sin \left( \alpha ^0 t\right) - C^0 \cos \left( \beta ^0 t^2\right) - D^0 \sin \left( \beta ^0 t^2\right) \right) ^2 \\&\quad = \frac{1}{n} \sum _{t=1}^{n}\left( A^0 \cos \left( \alpha ^0 t\right) - A \cos (\alpha t) + B^0 \sin \left( \alpha ^0 t\right) \right. \\&\qquad \left. - B \sin (\alpha t) + C^0 \cos \left( \beta ^0 t^2\right) - C \cos (\beta t^2) + D^0 \sin \left( \beta ^0 t^2\right) - D \sin \left( \beta t^2\right) \right) ^2 \\&\qquad + \frac{1}{n} \sum _{t=1}^{n} X(t) \left( A^0 \cos (\alpha ^0 t) - A \cos (\alpha t) + B^0 \sin \left( \alpha ^0 t\right) - B \sin (\alpha t) + C^0 \cos \left( \beta ^0 t^2\right) \right. \\&\quad \left. - C \cos \left( \beta t^2\right) + D^0 \sin \left( \beta ^0 t^2\right) - D \sin \left( \beta t^2\right) \right) \\&\quad = f(\varvec{\theta }) + g(\varvec{\theta }). \end{aligned}$$

Now using Lemma 4, it can be easily seen that:

$$\begin{aligned} \lim _{n \rightarrow \infty } \sup _{\varvec{\theta } \in S_c} g(\varvec{\theta }) = 0 a.s. \end{aligned}$$

(19)

Thus, we have:

$$\begin{aligned} \liminf \inf _{\varvec{\theta } \in S_c} \frac{1}{n}\left( Q(\varvec{\theta }) - Q(\varvec{\theta }^0)\right) = \liminf \inf _{\varvec{\theta } \in S_c} f(\varvec{\theta }). \end{aligned}$$

Note that the proof will follow if we show that $\liminf \inf _{\varvec{\theta } \in S_c} f(\varvec{\theta }) > 0$. Consider the set $S_c = \{\varvec{\theta }: |\varvec{\theta } - \varvec{\theta }^0| \geqslant 6c; \varvec{\theta } \in \varvec{\varTheta }\} \subset S_c^{(1)} \cup S_c^{(2)} \cup S_c^{(3)} \cup S_c^{(4)} \cup S_c^{(5)} \cup S_c^{(6)}$, where

$$\begin{aligned} S_c^{(1)}&= \left\{ \varvec{\theta }: |A - A^0| \geqslant c; \varvec{\theta } \in \varvec{\varTheta }\right\} \qquad S_c^{(2)} = \left\{ \varvec{\theta }: |B - B^0| \geqslant c; \varvec{\theta } \in \varvec{\varTheta }\right\} \\ S_c^{(3)}&= \left\{ \varvec{\theta }: |\alpha - \alpha ^0| \geqslant c; \varvec{\theta } \in \varvec{\varTheta }\right\} \qquad S_c^{(4)} = \left\{ \varvec{\theta }: |C - C^0| \geqslant c; \varvec{\theta } \in \varvec{\varTheta }\right\} \\ S_c^{(5)}&= \left\{ \varvec{\theta }: |D - D^0| \geqslant c; \varvec{\theta } \in \varvec{\varTheta }\right\} \qquad S_c^{(6)} = \left\{ \varvec{\theta }: |\beta - \beta ^0| \geqslant c; \varvec{\theta } \in \varvec{\varTheta }\right\} \end{aligned}$$

Now, we split the set $S_c^{(1)}$ as follows:

$$\begin{aligned} S_c^{(1)}&= \left\{ \varvec{\theta }: |A - A^0| \geqslant c; \varvec{\theta } \in \varvec{\varTheta }\right\} \\&\qquad \subset \left\{ \varvec{\theta }: |A - A^0| \geqslant c; \varvec{\theta } \in \varvec{\varTheta }; \alpha = \alpha ^0; \beta = \beta ^0 \right\} \\&\qquad \cup \left\{ \varvec{\theta }: |A - A^0| \geqslant c; \varvec{\theta } \in \varvec{\varTheta }; \alpha \ne \alpha ^0; \beta = \beta ^0 \right\} \\&\qquad \cup \left\{ \varvec{\theta }: |A - A^0| \geqslant c; \varvec{\theta } \in \varvec{\varTheta }; \alpha = \alpha ^0; \beta \ne \beta ^0 \right\} \\&\qquad \cup \left\{ \varvec{\theta }: |A - A^0| \geqslant c; \varvec{\theta } \in \varvec{\varTheta }; \alpha \ne \alpha ^0; \beta \ne \beta ^0 \right\} \\&= S_c^{(1)_{1}} \cup S_c^{(1)_{2}} \cup S_c^{(1)_{3}} \cup S_c^{(1)_{4}} \end{aligned}$$

Now let us consider:

$$\begin{aligned}&\liminf \inf _{\varvec{\theta } \in S_c^{(1)_{1}}} f(\varvec{\theta }) \\&\quad = \liminf \inf _{\varvec{\theta } \in S_c^{(1)_{1}}} \frac{1}{n} \sum _{t=1}^{n} \left( A^0 \cos \left( \alpha ^0 t\right) - A \cos (\alpha t) + B^0 \sin \left( \alpha ^0 t\right) - B \sin (\alpha t)\right. \\&\qquad + C^0 \cos \left( \beta ^0 t^2\right) - C \cos \left( \beta t^2\right) \\&\qquad \left. + D^0 \sin (\beta ^0 t^2) - D \sin \left( \beta t^2\right) \right) ^2 \\&\quad = \liminf \inf _{\varvec{\theta } \in S_c^{(1)_{1}}} \frac{1}{n} \sum _{t=1}^{n} \left( \left( A^0 - A\right) \cos \left( \alpha ^0 t\right) \right. \\&\qquad \left. + \left( B^0 - B\right) \sin \left( \alpha ^0 t\right) + \left( C^0 - C\right) \cos \left( \beta ^0 t^2\right) + \left( D^0 - D\right) \sin \left( \beta ^0 t^2\right) \right) ^2 \\&\quad = \frac{\left( A^0 - A\right) ^2}{2} + \frac{\left( B^0 - B\right) ^2}{2}\\&\qquad + \frac{\left( C^0 - C\right) ^2}{2} + \frac{\left( D^0 - D\right) ^2}{2}> 0\\&\liminf \inf _{\varvec{\theta } \in S_c^{(1)_{2}}} f(\varvec{\theta }) \\&\quad = \liminf \inf _{\varvec{\theta } \in S_c^{(1)_{1}}} \frac{1}{n} \sum _{t=1}^{n} \left( A^0 \cos \left( \alpha ^0 t\right) \right. \\&\qquad - A \cos (\alpha t) + B^0 \sin \left( \alpha ^0 t\right) - B \sin (\alpha t) + \left( C^0 - C\right) \cos \left( \beta ^0 t^2\right) \\&\qquad \left. + \left( D^0 - D\right) \sin (\beta ^0 t^2)\right) ^2 = \frac{{A^0}^2}{2} + \frac{{A}^2}{2} + \frac{{B^0}^2}{2} + \frac{{B}^2}{2} + \frac{\left( C^0 - C\right) ^2}{2}\\&\qquad + \frac{\left( D^0 - D\right) ^2}{2}> 0\\&\liminf \inf _{\varvec{\theta } \in S_c^{(1)_{3}}} f(\varvec{\theta }) \\&\quad = \liminf \inf _{\varvec{\theta } \in S_c^{(1)_{3}}} \frac{1}{n} \sum _{t=1}^{n} \left( \left( A^0 - A\right) \cos \left( \alpha ^0 t\right) \right. \\&\qquad + \left( B^0 - B\right) \sin \left( \alpha ^0 t\right) + C^0 \cos \left( \beta ^0 t^2\right) - C \cos \left( \beta t^2\right) \\&\qquad \left. + D^0 \sin \left( \beta ^0 t^2\right) - D \sin \left( \beta t^2\right) \right) ^2 = \frac{\left( A^0 - A\right) ^2}{2}\\&\qquad + \frac{\left( B^0 - B\right) ^2}{2} + \frac{{C^0}^2}{2} + \frac{C^2}{2}+ \frac{{D^0}^2}{2} + \frac{{D}^2}{2} > 0\\ \end{aligned}$$

Finally,

$$\begin{aligned}&\liminf \inf _{\varvec{\theta } \in S_c^{(1)_{4}}} f(\varvec{\theta }) \\&\quad = \liminf \inf _{\varvec{\theta } \in S_c^{(1)_{1}}} \frac{1}{n} \sum _{t=1}^{n} \left( A^0 \cos \left( \alpha ^0 t\right) - A \cos \left( \alpha t\right) \right. \\&\qquad + B^0 \sin (\alpha ^0 t) - B \sin (\alpha t) + C^0 \cos \left( \beta ^0 t^2\right) - C \cos \left( \beta t^2\right) \\&\qquad \left. + D^0 \sin \left( \beta ^0 t^2\right) - D \sin \left( \beta t^2\right) \right) ^2 = \frac{{A^0}^2}{2} + \frac{{A}^2}{2} + \frac{{B^0}^2}{2}\\&\qquad + \frac{{B}^2}{2} + \frac{{C^0}^2}{2} + \frac{C^2}{2} + \frac{{D^0}^2}{2} + \frac{{D}^2}{2} > 0 \end{aligned}$$

Note that we used Lemmas 1 and 2 in all the above computations of the limits. On combining all the above, we have $\liminf \inf \limits _{\varvec{\theta } \in S_c^{(1)}} f(\varvec{\theta }) > 0.$ Similarly, it can be shown that the result holds for the rest of the sets. Therefore, by Lemma 5, $\hat{\varvec{\theta }}$ is a strongly consistent estimator of $\varvec{\theta }^0$. $\square$

Proof of Theorem 2:

To obtain the asymptotic distribution of the LSEs, we express $\mathbf{Q }'(\hat{\varvec{\theta }})$ using multivariate Taylor series expansion arount the point $\varvec{\theta }^0$, as follows:

$$\begin{aligned} \mathbf{Q }'\left( \hat{\varvec{\theta }}\right) - \mathbf{Q }'\left( \varvec{\theta }^0\right) = \left( \hat{\varvec{\theta }} - \varvec{\theta }^0\right) \mathbf{Q }''\left( \bar{\varvec{\theta }}\right) . \end{aligned}$$

(20)

Here, $\bar{\varvec{\theta }}$ is a point between $\hat{\varvec{\theta }}$ and $\varvec{\theta }^0$. Since, $\hat{\varvec{\theta }}$ is the LSE of $\varvec{\theta }^0$, $\mathbf{Q }'(\hat{\varvec{\theta }}) = 0$. Thus, we have:

$$\begin{aligned} \left( \hat{\varvec{\theta }} - \varvec{\theta }^0\right) = - \mathbf{Q }'\left( \varvec{\theta }^0\right) \left[ \mathbf{Q }''\left( \bar{\varvec{\theta }}\right) \right] ^{-1}. \end{aligned}$$

(21)

Multiplying both sides of (21)) by the $6 \times 6$ diagonal matrix $\mathbf{D } = \hbox {diag}(\frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}}, \frac{1}{n\sqrt{n}}, \frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}}, \frac{1}{n^2\sqrt{n}})$, we get:

$$\begin{aligned} \left( \hat{\varvec{\theta }} - \varvec{\theta }^0\right) \mathbf{D }^{-1} = - \mathbf{Q }'\left( \varvec{\theta }^0\right) \mathbf{D }\left[ \mathbf{D }\mathbf{Q }''\left( \bar{\varvec{\theta }}\right) \mathbf{D }\right] ^{-1}. \end{aligned}$$

(22)

First, we will show that:

$$\begin{aligned} \lim _{n \rightarrow \infty } \mathbf{Q }'\left( \varvec{\theta }^0\right) \mathbf{D } \xrightarrow {d} N\left( 0, 4c \sigma ^2 \varvec{\varSigma }\right) . \end{aligned}$$

(23)

Here,

$$\begin{aligned} \varvec{\varSigma } = \begin{pmatrix} \frac{1}{2} &{} \quad 0 &{} \quad \frac{B^0}{4} &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad \frac{1}{2} &{} \quad \frac{-A^0}{4} &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ \frac{B^0}{4} &{} \quad \frac{-A^0}{4} &{} \quad \frac{{A^0}^2 + {B^0}^2}{6} &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad \frac{1}{2} &{} \quad 0 &{} \quad \frac{D^0}{6} \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad \frac{1}{2} &{} \quad \frac{-C^0}{6} \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad \frac{D^0}{6} &{} \quad \frac{-C^0}{6} &{} \quad \frac{{C^0}^2 +{D^0}^2}{10} \end{pmatrix} \end{aligned}$$

(24)

To prove (23)), we compute the elements of the $6 \times 1$ vector

$\mathbf{Q }'(\varvec{\theta }^0)\mathbf{D } = \begin{pmatrix} \frac{1}{\sqrt{n}}\frac{\partial Q(\varvec{\theta })}{\partial A}&\frac{1}{\sqrt{n}}\frac{\partial Q(\varvec{\theta })}{\partial B}&\frac{1}{n\sqrt{n}}\frac{\partial Q(\varvec{\theta })}{\partial \alpha }&\frac{1}{\sqrt{n}}\frac{\partial Q(\varvec{\theta })}{\partial C}&\frac{1}{\sqrt{n}}\frac{\partial Q(\varvec{\theta })}{\partial D}&\frac{1}{n^2\sqrt{n}}\frac{\partial Q(\varvec{\theta })}{\partial \beta } \end{pmatrix}$ as follows:

$$\begin{aligned}&\frac{1}{\sqrt{n}}\frac{\partial Q\left( \varvec{\theta }\right) }{\partial A} = \frac{-2}{\sqrt{n}} \sum _{t=1}^{n} \left( y(t) - A \cos (\alpha t)\right. \\&\left. - B \sin (\alpha t) - C \cos (\beta t^2) - D \sin (\beta t^2)\right) \cos (\alpha t)\\&\quad \Rightarrow \frac{1}{\sqrt{n}}\frac{\partial Q(\varvec{\theta }^0)}{\partial A} = \frac{-2}{\sqrt{n}} \sum _{t=1}^{n} X(t)\cos \left( \alpha ^0 t\right) . \end{aligned}$$

Similarly, the rest of the elements can be computed and we get:

$$\begin{aligned} \mathbf{Q }'(\varvec{\theta }^0)\mathbf{D } = \begin{pmatrix} \frac{-2}{\sqrt{n}} \sum \limits _{t=1}^{n} X(t)\cos \left( \alpha ^0 t\right) \\ \frac{-2}{\sqrt{n}} \sum \limits _{t=1}^{n} X(t)\sin \left( \alpha ^0 t\right) \\ \frac{-2}{n\sqrt{n}} \sum \limits _{t=1}^{n} t X(t)\left( -A^0\sin \left( \alpha ^0 t\right) + B^0 \cos \left( \alpha ^0 t\right) \right) \\ \frac{-2}{\sqrt{n}}\sum \limits _{t=1}^{n} X(t)\cos \left( \beta ^0 t^2\right) \\ \frac{-2}{\sqrt{n}}\sum \limits _{t=1}^{n} X(t)\sin \left( \beta ^0 t^2\right) \\ \frac{-2}{n^2\sqrt{n}} \sum \limits _{t=1}^{n} t^2 X(t)\left( -C^0\sin \left( \beta ^0 t^2\right) + D^0 \cos \left( \beta ^0 t^2\right) \right) \end{pmatrix}. \end{aligned}$$

Now using the central limit theorem (CLT) of stochastic processes (see Fuller [9]), the above vector tends to a six-variate Gaussian distribution with mean 0 and variance $4 c \sigma ^2 \varvec{\varSigma }$ and hence (23) holds true. Now, we consider the second-derivative matrix $\mathbf{D }\mathbf{Q }''(\bar{\varvec{\theta }})\mathbf{D }$. Note that since $\hat{\varvec{\theta }} \xrightarrow {a.s.} \varvec{\theta }^0$ as $n \rightarrow \infty$ and $\bar{\varvec{\theta }}$ is a point between $\hat{\varvec{\theta }}$ and $\varvec{\theta }^0$,

$$\begin{aligned} \lim \limits _{n \rightarrow \infty } \mathbf{D }\mathbf{Q }''\left( \bar{\varvec{\theta }}\right) \mathbf{D } = \lim \limits _{n \rightarrow \infty } \mathbf{D }\mathbf{Q }''\left( \varvec{\theta }^0\right) \mathbf{D }. \end{aligned}$$

Using Lemmas 1, 2, 3 and 4 and after some calculations, it can be shown that:

$$\begin{aligned} \mathbf{D }\mathbf{Q }''\left( \varvec{\theta }^0\right) \mathbf{D } = 2\varvec{\varSigma }, \end{aligned}$$

(25)

where $\varvec{\varSigma }$ is as defined in (24). On combining, (22),(23) and (25), the desired result follows. $\square$

1.2 Proofs of the Asymptotic Properties of the Sequential LSEs

Following lemmas are required to prove the consistency of the sequential LSEs:

Lemma 6

Let us define the set $M_c = \{\varvec{\theta }^{(1)}: |\varvec{\theta }^{(1)} - {\varvec{\theta }^0}^{(1)}| \geqslant 3 c; \varvec{\theta }^{(1)} \in \varvec{\varTheta }^{(1)}\}$. If the following holds true,

$$\begin{aligned} \liminf \inf \limits _{M_c} \frac{1}{n} \left( Q_1\left( \varvec{\theta }^{(1)}\right) - Q_1\left( {\varvec{\theta }^0}^{(1)}\right) \right) > 0 a.s. \end{aligned}$$

(26)

then $\tilde{\varvec{\theta }}^{(1)} \xrightarrow {a.s.} {\varvec{\theta }^0}^{(1)}$ as $n \rightarrow \infty$

Proof

This can be proved by contradiction along the same lines as Lemma 5. $\square$

Lemma 7

Let us define the set $N_c = \{\varvec{\theta }^{(2)} : \varvec{\theta }^{(2)} \in \varvec{\varTheta }^{(2)} ;\ |\varvec{\theta }^{(2)} - {\varvec{\theta }^0}^{(2)}| \geqslant 3c\}.$ If for any $c>0$,

$$\begin{aligned} \liminf \inf \limits _{\varvec{\theta }^{(2)} \in N_c} \frac{1}{n} \left( Q_2\left( \varvec{\theta }^{(2)}\right) - Q_2\left( {\varvec{\theta }^0}^{(2)}\right) \right) > 0 a.s. \end{aligned}$$

(27)

then $\tilde{\varvec{\theta }}^{(2)} \xrightarrow {a.s.} {\varvec{\theta }^0}^{(2)}$ as $n \rightarrow \infty .$

Proof

This can be proved by contradiction along the same lines as Lemma 5. $\square$

Proof of Theorem 3:

First we prove the consistency of the parameter estimates of the sinusoidal component, $\tilde{\varvec{\theta }}^{(1)}$. For this, consider the difference:

$$\begin{aligned}&\frac{1}{n}\left( Q_1\left( \varvec{\theta }^{(1)}\right) - Q_1\left( {\varvec{\theta }^0}^{(1)}\right) \right) \\&\quad = \frac{1}{n}\left[ \sum _{t=1}^{n}\left( y(t) - A\cos (\alpha t) - B\sin (\alpha t)\right) ^2\right. \\&\qquad \left. - \left( y(t) - A^0 \cos \left( \alpha ^0 t\right) - B^0 \sin \left( \alpha ^0 t\right) \right) ^2 \right] \\&\quad = \frac{1}{n} \sum _{t=1}^n\left( A^0 \cos \left( \alpha ^0 t\right) - A\cos (\alpha t) + B^0 \sin \left( \alpha ^0 t\right) \right. \\&\qquad \left. - B \sin (\alpha t) + C^0 \cos \left( \beta ^0 t^2\right) + D^0 \sin \left( \beta ^0 t^2\right) + X(t)\right) ^2\\&\qquad - \frac{1}{n}\sum _{t=1}^{n}\left( C^0 \cos \left( \beta ^0 t^2\right) + D^0 \sin \left( \beta ^0 t^2\right) + X(t)\right) ^2 \\&\quad = \frac{1}{n} \sum _{t=1}^n\left( A^0 \cos \left( \alpha ^0 t\right) + B^0 \sin \left( \alpha ^0 t\right) - A\cos (\alpha t) - B \sin (\alpha t) \right) ^2\\&\qquad + \frac{2}{n}\sum _{t=1}^n\left( C^0 \cos \left( \beta ^0 t^2\right) + D^0 \sin \left( \beta ^0 t^2\right) + X(t) \right) \left( A^0 \cos \left( \alpha ^0 t\right) \right. \\&\qquad \left. + B^0 \sin \left( \alpha ^0 t\right) - A\cos (\alpha t) - B\sin (\alpha t)\right) \\&\quad = f_1\left( \varvec{\theta }^{(1)}\right) + g_1\left( \varvec{\theta }^{(1)}\right) . \end{aligned}$$

Here,

$$\begin{aligned} f_1\left( \varvec{\theta }^{(1)}\right)= & {} \frac{1}{n} \sum _{t=1}^n\left( A^0 \cos \left( \alpha ^0 t\right) + B^0 \sin \left( \alpha ^0 t\right) - A\cos (\alpha t) - B \sin (\alpha t) \right) ^2 and, \\ g_1\left( \varvec{\theta }^{(1)}\right)= & {} \frac{2}{n} \sum _{t=1}^{n}\left( C^0 \cos \left( \beta ^0 t^2\right) + D^0 \sin \left( \beta ^0 t^2\right) + X(t) \right) \left( A^0 \cos \left( \alpha ^0 t\right) \right. \\&\left. + B^0 \sin \left( \alpha ^0 t\right) - A\cos (\alpha t) - B \sin (\alpha t)\right) \end{aligned}$$

Now using Lemmas 3 and 4 , it is easy to see that:

$$\begin{aligned} \sup \limits _{\varvec{\theta } \in M_c} |g_1\left( \varvec{\theta }^{(1)}\right) | \xrightarrow {a.s.} 0. \end{aligned}$$

Thus, if we prove that $\liminf \inf \limits _{M_c}f_1(\varvec{\theta }^{(1)}) > 0$ a.s., it will follow that $\liminf \inf \limits _{M_c} \frac{1}{n} (Q_1(\varvec{\theta }^{(1)}) - Q_1({\varvec{\theta }^0}^{(1)})) > 0 a.s.$. First consider the set $M_c = \{\varvec{\theta }^{(1)}: |\varvec{\theta }^{(1)} - {\varvec{\theta }^0}^{(1)}| \geqslant 3c; \varvec{\theta }^{(1)} \in \varvec{\varTheta }^{(1)}\}$. It is evident that:

$$\begin{aligned} M_c \subset M_c^{(1)} \cup M_c^{(2)} \cup M_c^{(3)}, \end{aligned}$$

where $M_c^{(1)} = \{\varvec{\theta }^{(1)}: |A - A^0| \geqslant c; \varvec{\theta }^{(1)} \in \varvec{\varTheta }^{(1)}\}$, $M_c^{(2)} = \{\varvec{\theta }^{(1)}: |B - B^0| \geqslant c; \varvec{\theta }^{(1)} \in \varvec{\varTheta }^{(1)}\}$ and $M_c^{(3)} = \{\varvec{\theta }^{(1)}: |\alpha - \alpha ^0| \geqslant c; \varvec{\theta }^{(1)} \in \varvec{\varTheta }^{(1)}\}.$ Now, we further split the set $M_c^{(1)}$ which can be written as: $M_c^{(1)_{1}} \cup M_c^{(1)_{2}}$, where

$$\begin{aligned} M_c^{(1)_{1}}&= \left\{ \varvec{\theta }^{(1)}: |A - A^0| \geqslant c; \varvec{\theta }^{(1)} \in \varvec{\varTheta }^{(1)}; \alpha = \alpha ^0\right\} and M_c^{(1)_{2}}\\&= \left\{ \varvec{\theta }^{(1)}: |A - A^0| \geqslant c; \varvec{\theta }^{(1)} \in \varvec{\varTheta }^{(1)}; \alpha \ne \alpha ^0\right\} \end{aligned}$$

Consider,

$$\begin{aligned} \liminf \inf \limits _{M_c^{(1)_{1}}}f_1\left( \varvec{\theta }^{(1)}\right)&= \liminf \inf \limits _{M_c^{(1)_{1}}} \frac{1}{n} \sum _{t=1}^n\left( A^0 \cos \left( \alpha ^0 t\right) \right. \\&\quad \left. + B^0 \sin \left( \alpha ^0 t\right) - A\cos (\alpha t) - B \sin (\alpha t)\right) ^2 \\&= \frac{\left( A^0 - A\right) ^2}{2} + \frac{(B^0 - B)^2}{2} > 0 a.s. \text { (using Lemma}~1{\text{) }.} \end{aligned}$$

Again, using Lemma 1,

$$\begin{aligned}&\liminf \inf \limits _{M_c^{(1)_{2}}} \frac{1}{n} \sum _{t=1}^n\left( A^0 \cos \left( \alpha ^0 t\right) + B^0 \sin \left( \alpha ^0 t\right) - A\cos (\alpha t) - B \sin (\alpha t) \right) ^2 \\&\quad = \frac{{A^0}^2}{2} + \frac{{B^0}^2}{2} + \frac{A^2}{2} + \frac{B^2}{2} > 0 a.s. . \end{aligned}$$

Similarly, it can be shown that $\liminf \inf \limits _{M_c^{(2)}}f_1(\varvec{\theta }^{(1)}) > 0$ a.s. and $\liminf \inf \limits _{M_c^{(3)}}f_1(\varvec{\theta }^{(1)}) > 0$ a.s. Now using Lemma 6, ${\tilde{A}}$, ${\tilde{B}}$ and ${\tilde{\alpha }}$ are strongly consistent estimators of $A^0$, $B^0$ and $\alpha ^0$, respectively. To prove the consistency of the chirp parameter sequential estimates, ${\tilde{C}}$, ${\tilde{D}}$ and ${\tilde{\beta }}$, we need the following lemma:

Lemma 8

If Assumptions 1, 2 and 3 are satisfied, then:

$$\begin{aligned} \left( \tilde{\varvec{\theta }}^{(1)} - {\varvec{\theta }^0}^{(1)}\right) \left( \sqrt{n}\mathbf{D }_1\right) ^{-1} \xrightarrow {a.s.} 0. \end{aligned}$$

Here, $\mathbf{D }_1 = \hbox {diag}(\frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}}, \frac{1}{n\sqrt{n}})$.

Proof

Consider the error sum of squares: $Q_1(\varvec{\theta }) = \frac{1}{n}\sum \limits _{t=1}^n(y(t) - A \cos (\alpha t) - B \sin (\alpha t))^2.$

By Taylor series expansion of $\mathbf{Q }_1'(\tilde{\varvec{\theta }}^{(1)})$ around the point ${\varvec{\theta }^0}^{(1)}$, we get:

$$\begin{aligned} \mathbf{Q }_1'\left( \tilde{\varvec{\theta }}^{(1)}\right) - \mathbf{Q }_1'\left( {\varvec{\theta }^0}^{(1)}\right) = \left( \tilde{\varvec{\theta }}^{(1)} - {\varvec{\theta }^0}^{(1)}\right) \mathbf{Q }_1''\left( \bar{\varvec{\theta }}^{(1)}\right) \end{aligned}$$

(28)

where $\bar{\varvec{\theta }}^{(1)}$ is a point lying between $\tilde{\varvec{\theta }}^{(1)}$ and ${\varvec{\theta }^0}^{(1)}$. Since $\tilde{\varvec{\theta }}^{(1)}$ minimizes $Q_1(\varvec{\theta })$, it implies that $\mathbf{Q }_1'(\tilde{\varvec{\theta }}^{(1)}) = 0$, and therefore, (28) can be written as:

$$\begin{aligned}&\left( \tilde{\varvec{\theta }}^{(1)} - {\varvec{\theta }^0}^{(1)}\right) = - \mathbf{Q }_1'\left( {\varvec{\theta }^0}^{(1)}\right) \left[ \mathbf{Q }_1''\left( \bar{\varvec{\theta }}^{(1)}\right) \right] ^{-1} \end{aligned}$$

(29)

$$\begin{aligned}&\Rightarrow \left( \tilde{\varvec{\theta }}^{(1)} -{\varvec{\theta }^0}^{(1)}\right) (\sqrt{n}\mathbf{D }_1)^{-1} = \left[ - \frac{1}{\sqrt{n}}\mathbf{Q }_1'\left( {\varvec{\theta }^0}^{(1)}\right) \mathbf{D }_1\right] \left[ \mathbf{D }_1 \mathbf{Q }_1''\left( \bar{\varvec{\theta }}^{(1)}\right) \mathbf{D }_1\right] ^{-1} \end{aligned}$$

(30)

Now let us calculate the right-hand side explicitly. First consider the first-derivative vector $\frac{1}{\sqrt{n}}\mathbf{Q }_1'({\varvec{\theta }^0}^{(1)})\mathbf{D }_1$.

$$\begin{aligned} \frac{1}{\sqrt{n}}\mathbf{Q }_1'\left( {\varvec{\theta }^0}^{(1)}\right) \mathbf{D }_1 = \begin{pmatrix} \frac{1}{n}\frac{\partial Q_1\left( {\varvec{\theta }^0}^{(1)}\right) }{\partial A}&\frac{1}{n}\frac{\partial Q_1\left( {\varvec{\theta }^0}^{(1)}\right) }{\partial B}&\frac{1}{n^2}\frac{\partial Q_1\left( {\varvec{\theta }^0}^{(1)}\right) }{\partial \alpha } \end{pmatrix} \end{aligned}$$

By straightforward calculations and using Lemmas 3 and 4(a), one can easily see that:

$$\begin{aligned} \frac{1}{\sqrt{n}}\mathbf{Q }_1'\left( {\varvec{\theta }^0}^{(1)}\right) \mathbf{D }_1 \rightarrow 0 a.s. \end{aligned}$$

(31)

Now let us consider the second-derivative matrix $\mathbf{D }_1 \mathbf{Q }_1''(\bar{\varvec{\theta }}^{(1)})\mathbf{D }_1$. Since $\tilde{\varvec{\theta }}^{(1)} \xrightarrow {a.s.} {\varvec{\theta }^0}^{(1)}$ and $\bar{\varvec{\theta }}^{(1)}$ is a point between them, we have:

$$\begin{aligned} \mathbf{D }_1 \mathbf{Q }_1''\left( \bar{\varvec{\theta }}^{(1)}\right) \mathbf{D }_1 = \lim _{n \rightarrow \infty } \mathbf{D }_1 \mathbf{Q }_1''\left( {\varvec{\theta }^0}^{(1)}\right) \mathbf{D }_1 \end{aligned}$$

Again by routine calculations and using Lemmas 1, 3 and 4(a) , one can evaluate each element of this $3 \times 3$ matrix, and get:

$$\begin{aligned} \lim _{n \rightarrow \infty } \mathbf{D }_1 \mathbf{Q }_1''\left( {\varvec{\theta }^0}^{(1)}\right) \mathbf{D }_1 = 2 \varvec{\varSigma }_1, \end{aligned}$$

(32)

where $\varvec{\varSigma }_1 = \begin{pmatrix} \frac{1}{2} &{} 0 &{} \frac{B^0}{4} \\ 0 &{} \frac{1}{2} &{} \frac{-A^0}{4} \\ \frac{B^0}{4} &{} \frac{-A^0}{4} &{} \frac{{A^0}^2 + {B^0}^2}{6} \\ \end{pmatrix} > 0,$ a positive definite matrix. Hence, combining (31) and (32), we get the desired result. $\square$

Using the above lemma, we get the following relationship between the sinusoidal component of the model and its estimate:

$$\begin{aligned} {\tilde{A}} \cos ({\tilde{\alpha }} t) + {\tilde{B}} \sin ({\tilde{\alpha }} t) = A^0 \cos (\alpha ^0 t) + B^0 \sin (\alpha ^0 t) + o(1) \end{aligned}$$

(33)

Now to prove the consistency of $\tilde{\varvec{\theta }}^{(1)} = ({\tilde{C}}, {\tilde{D}}, {\tilde{\beta }})$, we consider the following difference:

$$\begin{aligned}&\frac{1}{n}\left( Q_2\left( {\varvec{\theta }}^{(2)}\right) - Q_2\left( {\varvec{\theta }^0}^{(2)}\right) \right) \\&\quad = \frac{1}{n}\left[ \sum _{t=1}^{n}\left( y_1(t) - C\cos \left( \beta t^2\right) - D\sin (\beta t^2)\right) ^2\right. \\&\qquad \left. - \left( y_1(t) - C^0 \cos \left( \beta ^0 t^2\right) - D^0 \sin \left( \beta ^0 t^2\right) \right) ^2 \right] \\&\quad = \frac{1}{n} \sum _{t=1}^n\left( C^0 \cos \left( \beta ^0 t^2\right) \right. \\&\qquad \left. + D^0 \sin \left( \beta ^0 t^2\right) - C\cos \left( \beta t^2\right) - D \sin \left( \beta t^2\right) \right) ^2\\&\qquad + \frac{2}{n}\sum _{t=1}^n\left( A^0 \cos \left( \alpha ^0 t\right) + B^0 \sin \left( \alpha ^0 t^2\right) + X(t) \right) \left( C^0 \cos \left( \beta ^0 t^2\right) \right. \\&\qquad \left. + D^0 \sin \left( \beta ^0 t^2\right) - C\cos \left( \beta t^2\right) - D \sin \left( \beta t^2\right) \right) \\&\quad = f_2\left( {\varvec{\theta }}^{(2)}\right) + g_2\left( {\varvec{\theta }}^{(2)}\right) . \end{aligned}$$

Using Lemmas 3 and 4 , we have

$$\begin{aligned} \sup \limits _{{\varvec{\theta }} \in N_c} |g_2\left( {\varvec{\theta }}^{(2)}\right) | \xrightarrow {a.s.} 0, \end{aligned}$$

and using straightforward, but lengthy calculations and splitting the set $N_c$, similar to the splitting of set $M_c$, before, it can be shown that $\liminf \inf \limits _{\varvec{\xi } \in N_c} f_2({\varvec{\theta }}^{(2)}) > 0$.

$\text {Thus, }\tilde{\varvec{\theta }}^{(2)} \xrightarrow {a.s.} {\varvec{\theta }^0}^{(2)} as n \rightarrow \infty$   by Lemma 7. Hence, the result. $\square$

Proof of Theorem 4:

We first examine the asymptotic distribution of the sequential estimates of the sinusoidal component, that is, $\tilde{\varvec{\theta }}^{(1)}$ from 29, we have:

$$\begin{aligned} \left( \tilde{\varvec{\theta }}^{(1)} - {\varvec{\theta }^0}^{(1)}\right) \mathbf{D }_1^{-1} = - \mathbf{Q }_1'\left( {\varvec{\theta }^0}^{(1)}\right) \mathbf{D }_1\left[ \mathbf{D }_1\mathbf{Q }_1''\left( \bar{\varvec{\theta }}^{(1)}\right) \mathbf{D }_1\right] ^{-1}. \end{aligned}$$

First, we show that $\mathbf{Q }_1'({\varvec{\theta }^0}^{(1)})\mathbf{D }_1 \rightarrow N_3(0, 4 \sigma ^2 c \varvec{\varSigma }_1).$ We compute the elements of the derivative vector $\mathbf{Q }_1'({\varvec{\theta }^0}^{(1)})$ and using Conjecture 2(e), (f), (g) and (h) (see Sect. A), we obtain:

$$\begin{aligned} \mathbf{Q }_1'\left( {\varvec{\theta }^0}^{(1)}\right) \mathbf{D }_1 \overset{a.eq.}{=} -2 \begin{pmatrix} \frac{1}{\sqrt{n}}\sum \limits _{t=1}^{n} X(t) \cos \left( \alpha ^0 t\right) \\ \frac{1}{\sqrt{n}}\sum \limits _{t=1}^{n} X(t) \sin \left( \alpha ^0 t\right) \\ \frac{1}{n\sqrt{n}}\sum \limits _{t=1}^{n} t X(t)\left( -A_1^0\sin \left( \alpha ^0 t\right) + B^0 \cos \left( \alpha ^0 t\right) \right) \end{pmatrix}. \end{aligned}$$

(34)

Here, $\overset{a.eq.}{=}$ means asymptotically equivalent. Now again using CLT, the right-hand side of (34) tends to three-variate Gaussian distribution with mean 0 and variance–covariance matrix, $4 \sigma ^2 c \varvec{\varSigma }_1.$ Using this and (32), we have the desired result.

Next, we determine the asymptotic distribution of $\tilde{\varvec{\theta }}^{(2)}.$ For this, we consider the error sum of squares, $Q_2(\varvec{\theta }^{(2)})$ as defined in (12). Let ${\varvec{Q}}'_2({\varvec{\theta }}^{(2)})$ be the first-derivative vector and ${\varvec{Q}}''_2(\varvec{\theta }^{(2)})$, the second-derivative matrix of $Q_2(\varvec{\theta }^{(2)})$. Using multivariate Taylor series expansion, we expand ${\varvec{Q}}'_2(\tilde{\varvec{\theta }}^{(2)})$ around the point ${\varvec{\theta }^0}^{(2)}$, and get:

$$\begin{aligned} \left( \tilde{\varvec{\theta }}^{(2)} - {\varvec{\theta }^0}^{(2)}\right) = -{\varvec{Q}}'_2\left( {\varvec{\theta }^0}^{(2)}\right) [{\varvec{Q}}''_2(\bar{\varvec{\theta }}^{(2)})]^{-1}. \end{aligned}$$

Multiplying both sides by the matrix ${\varvec{D}}_2^{-1}$, where ${\varvec{D}}_2 = \hbox {diag}(\frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}},\frac{1}{n^2\sqrt{n}})$, we get:

$$\begin{aligned} \left( \tilde{\varvec{\theta }}^{(2)} - {\varvec{\theta }^0}^{(2)}\right) \mathbf{D }_2^{-1} = -{\varvec{Q}}'_2\left( {\varvec{\theta }^0}^{(2)}\right) \mathbf{D }_2 \left[ \mathbf{D }_2{\varvec{Q}}''_2\left( \bar{\varvec{\theta }}^{(2)}\right) \mathbf{D }_2\right] ^{-1}. \end{aligned}$$

Now, when we evaluate the first-derivative vector ${\varvec{Q}}'_2({\varvec{\theta }^0}^{(2)})\mathbf{D }_2$, using Conjecture 2(a) (see Sect. A), we obtain:

$$\begin{aligned} {\varvec{Q}}'_2\left( {\varvec{\theta }^0}^{(2)}\right) \mathbf{D }_2 \overset{a.eq.}{=} -2 \begin{pmatrix} \frac{1}{\sqrt{n}}\sum \limits _{t=1}^{n} X(t) \cos \left( \beta ^0 t^2\right) \\ \frac{1}{\sqrt{n}}\sum \limits _{t=1}^{n} X(t) \sin \left( \beta ^0 t^2\right) \\ \frac{1}{n^2\sqrt{n}}\sum \limits _{t=1}^{n} t X(t)\left( -C^0\sin \left( \beta ^0 t^2\right) + D^0 \cos \left( \beta ^0 t^2\right) \right) \end{pmatrix}. \end{aligned}$$

(35)

Again using the CLT, the vector on the right-hand side of (35) tends to $N_3(0, 4\sigma ^2 c \varvec{\varSigma }_2),$ where $\varvec{\varSigma }_2 = \begin{pmatrix} \frac{1}{2} &{} \quad 0 &{} \quad \frac{D^0}{6} \\ 0 &{} \quad \frac{1}{2} &{} \quad \frac{-C^0}{6} \\ \frac{D^0}{6} &{} \quad \frac{-C^0}{6} &{} \quad \frac{{C^0}^2 + {D^0}^2}{10} \\ \end{pmatrix} > 0.$

Note that:

$$\begin{aligned} \lim _{n \rightarrow \infty }\mathbf{D }_2{\varvec{Q}}''_2\left( \bar{\varvec{\theta }}^{(2)}\right) \mathbf{D }_2 = \lim _{n \rightarrow \infty }\mathbf{D }_2{\varvec{Q}}''_2\left( {\varvec{\theta }^0}^{(2)}\right) \mathbf{D }_2. \end{aligned}$$

On computing the second derivative $3 \times 3$ matrix $\mathbf{D }_2{\varvec{Q}}''_2({\varvec{\theta }^0}^{(2)})\mathbf{D }_2$ and using Lemmas 2, 3 and 4(b), we get:

$$\begin{aligned} \lim _{n \rightarrow \infty }\mathbf{D }_2{\varvec{Q}}''_2\left( {\varvec{\theta }^0}^{(2)}\right) \mathbf{D }_2 = 2\varvec{\varSigma }_2. \end{aligned}$$

(36)

Combining results (35) and (36), we get the stated asymptotic distribution of $\tilde{\varvec{\theta }}^{(2)}.$ Hence, the result. $\square$

Multiple Component Chirp-like Model

1.1 Proofs of the Asymptotic Properties of the LSEs

Proof of Theorm 6:

Consider the error sum of squares, defined in (14). Let us denote $\mathbf{Q }'(\varvec{\vartheta })$ as the $3(p+q) \times 1$ first-derivative vector and $\mathbf{Q }''(\varvec{\vartheta })$ as the $3(p+q) \times 3(p+q)$ second-derivative matrix. Using multivariate Taylor series expansion, we have:

$$\begin{aligned} \mathbf{Q }'\left( \hat{\varvec{\vartheta }}\right) - \mathbf{Q }'\left( \varvec{\vartheta }^0\right) = \left( \hat{\varvec{\vartheta }} - \varvec{\vartheta }^0\right) \mathbf{Q }''\left( \bar{\varvec{\vartheta }}\right) . \end{aligned}$$

Here, $\bar{\varvec{\vartheta }}$ is a point between $\hat{\varvec{\vartheta }}$ and $\varvec{\vartheta }^0.$ Now, using the fact that $\mathbf{Q }'(\hat{\varvec{\vartheta }}) = 0$ and multiplying both sides of the above equation by ${\mathfrak {D}}^{-1}$, we have:

$$\begin{aligned} \left( \hat{\varvec{\vartheta }} - \varvec{\vartheta }^0\right) {\mathfrak {D}}^{-1} = - \mathbf{Q }'\left( \hat{\varvec{\vartheta }}\right) {\mathfrak {D}}\left[ {\mathfrak {D}}\mathbf{Q }''\left( \bar{\varvec{\vartheta }}\right) {\mathfrak {D}}\right] ^{-1}. \end{aligned}$$

Also note that $(\hat{\varvec{\vartheta }} - \varvec{\vartheta }^0){\mathfrak {D}}^{-1} = \bigg (({\hat{\varvec{\theta }}_1}^{(1)} - {\varvec{\theta }_1^0}^{(1)}), \ldots , ({\hat{\varvec{\theta }}_p}^{(1)} - {\varvec{\theta }_p^0}^{(1)}), ({\hat{\varvec{\theta }}_{1}}^{(2)} - {\varvec{\theta }_{1}^0}^{(2)}), \ldots , ({\hat{\varvec{\theta }}_q}^{(2)} - {\varvec{\theta }_q^0}^{(2)}) \bigg ){\mathfrak {D}}^{-1}.$

Now, we evaluate the elements of the vector $\mathbf{Q }'(\varvec{\vartheta }^0)$ and the matrix $\mathbf{Q }''(\bar{\varvec{\vartheta }})$:

$$\begin{aligned} \frac{\partial Q(\varvec{\vartheta })}{\partial A_j}\bigg |_{\varvec{\vartheta }^0}&= -2 \sum _{t=1}^{n} X(t)\cos \left( \alpha _j^0 t\right) , \quad \frac{\partial Q(\varvec{\vartheta })}{\partial B_j}\bigg |_{\varvec{\vartheta }^0} = -2 \sum _{t=1}^{n} X(t)\sin \left( \alpha _j^0 t\right) , and \\ \frac{\partial Q(\varvec{\vartheta })}{\partial \alpha _j}\bigg |_{\varvec{\vartheta }^0}&= -2 \sum _{t=1}^{n} t X(t)\left( -A_j^0 \sin \left( \alpha _j^0 t\right) + B_j^0 \cos \left( \alpha _j^0 t\right) \right) , for j = 1, \ldots , p. \end{aligned}$$

Similarly, for

$$\begin{aligned} k&= 1, \ldots , q,\ \frac{\partial Q(\varvec{\vartheta })}{\partial C_k}\bigg |_{\varvec{\vartheta }^0} = -2 \sum _{t=1}^{n} X(t)\cos \left( \beta _k^0 t^2\right) , \quad \frac{\partial Q(\varvec{\vartheta })}{\partial D_k}\bigg |_{\varvec{\vartheta }^0}\\&= -2 \sum _{t=1}^{n} X(t)\sin \left( \beta _k^0 t^2\right) and \\&\quad \frac{\partial Q(\varvec{\vartheta })}{\partial \beta _k}\bigg |_{\varvec{\vartheta }^0} = -2 \sum _{t=1}^{n} t^2 X(t)\left( -C_k^0 \sin \left( \beta _k^0 t^2\right) + D_k^0 \cos \left( \beta _k^0 t\right) \right) .\\&\quad \frac{\partial ^2 Q(\varvec{\vartheta })}{\partial A_j^2}\bigg |_{\varvec{\vartheta }^0} = 2\sum _{t=1}^{n}\cos ^2\left( \alpha _j^0 t\right) , \ \frac{\partial ^2 Q(\varvec{\vartheta })}{\partial B_j^2}\bigg |_{\varvec{\vartheta }^0} = 2\sum _{t=1}^{n}\sin ^2\left( \alpha _j^0 t\right) ,\ j = 1, \ldots , p, \\&\quad \frac{\partial ^2 Q(\varvec{\vartheta })}{\partial C_k^2}\bigg |_{\varvec{\vartheta }^0} = 2\sum _{t=1}^{n}\cos ^2\left( \beta _k^0 t^2\right) and \frac{\partial ^2 Q(\varvec{\vartheta })}{\partial D_k^2}\bigg |_{\varvec{\vartheta }^0} = 2\sum _{t=1}^{n}\sin ^2\left( \beta _k^0 t^2\right) ,\ k = 1, \ldots , q. \\&\quad \frac{\partial ^2 Q(\varvec{\vartheta })}{\partial A_j \partial B_j}\bigg |_{\varvec{\vartheta }^0} = 2 \sum _{t=1}^{n} \sin \left( \alpha _j^0 t\right) \cos \left( \alpha _j^0 t\right) ,\\&\quad \frac{\partial ^2 Q(\varvec{\vartheta })}{\partial A_j \partial \alpha _j}\bigg |_{\varvec{\vartheta }^0} = 2 \sum _{t=1}^{n}t X(t) \sin \left( \alpha _j^0 t\right) \\&\qquad - 2 A_j^0 \sum _{t=1}^{n} t \cos \left( \alpha _j^0 t\right) \sin \left( \alpha _j^0 t\right) + 2 B_j^0 \sum _{t=1}^{n} t\cos ^2\left( \alpha _j^0 t\right) ,\\&\quad \frac{\partial ^2 Q(\varvec{\vartheta })}{\partial A_j \partial C_k}\bigg |_{\varvec{\vartheta }^0} = 2 \sum _{t=1}^{n} \cos \left( \beta _k^0 t^2\right) \cos \left( \alpha _j^0 t\right) ,\ \frac{\partial ^2 Q(\varvec{\vartheta })}{\partial A_j \partial D_k}\bigg |_{\varvec{\vartheta }^0} = 2 \sum _{t=1}^{n} \sin \left( \beta _k^0 t^2\right) \cos \left( \alpha _j^0 t\right) , \\&\quad \frac{\partial ^2 Q(\varvec{\vartheta })}{\partial A_j \partial \beta _k}\bigg |_{\varvec{\vartheta }^0} = - 2 C_k^0 \sum _{t=1}^{n} t^2 \cos \left( \alpha _j^0 t\right) \sin \left( \beta _k^0 t^2\right) + 2 D_k^0 \sum _{t=1}^{n} t^2\cos \left( \alpha _j^0 t\right) \cos \left( \beta _k^0 t^2\right) . \end{aligned}$$

Similarly the rest of the partial derivatives can be computed and using Lemmas 1, 2, 3 and 4 , it can be shown that:

$$\begin{aligned} {\mathfrak {D}}\mathbf{Q }''\left( \bar{\varvec{\vartheta }}\right) {\mathfrak {D}} \rightarrow 2 {\mathcal {E}}\left( \varvec{\vartheta }^0\right) . \end{aligned}$$

Now, using CLT on the first-derivative vector, $\mathbf{Q }'(\varvec{\vartheta }^0){\mathfrak {D}}$, it can be shown that it converges to a multivariate Gaussian distribution. Using routine calculations, and again using Lemmas 1, 2, 3 and 4, we compute the asymptotic variances for each of the elements and their covariances and we get:

$$\begin{aligned} \mathbf{Q }'\left( \varvec{\vartheta }^0\right) {\mathfrak {D}} \xrightarrow {d} N_{3(p+q)}\left( 0, 4c \sigma ^2 {\mathcal {E}}\left( \varvec{\vartheta }^0\right) \right) . \end{aligned}$$

Hence, the result. $\square$

1.2 Proofs of the Asymptotic Properties of the LSEs

To prove Theorems 7 and 8 , we need the following lemmas:

Lemma 9

• (a) Consider the set $M_c^{(j)} = \{\varvec{\theta }^{(1)}_j: |\varvec{\theta }^{(1)}_j - {\varvec{\theta }_j^0}^{(1)}| \geqslant 3 c; \varvec{\theta }_j^{(1)} \in \varvec{\varTheta }^{(1)}\},\ j = 1, \ldots , p$. If the following holds true:

  $$\begin{aligned} \liminf \inf \limits _{M_c^{(j)}} \frac{1}{n} \left( Q_{2j-1}\left( \varvec{\theta }^{(1)}_j\right) - Q_{2j-1}\left( {\varvec{\theta }_j^0}^{(1)}\right) \right) > 0 a.s. \end{aligned}$$

  (37)

  then $\tilde{\varvec{\theta }}_j^{(1)} \xrightarrow {a.s.} {\varvec{\theta }_j^0}^{(1)}$ as $n \rightarrow \infty$

• (b) Let us define the set $N_c^{(k)} = \{\varvec{\theta }_k^{(2)} : \varvec{\theta }_k^{(2)} \in \varvec{\varTheta }^{(2)} ;\ |\varvec{\theta }_k^{(2)} - {\varvec{\theta }_k^0}^{(2)}| \geqslant 3c\},\ k = 1, \ldots , q.$ If for any $c>0$,

  $$\begin{aligned} \liminf \inf \limits _{\varvec{\theta }_k^{(2)} \in N_c^{(k)}} \frac{1}{n} \left( Q_{2k}\left( \varvec{\theta }_k^{(2)}\right) - Q_{2k}\left( {\varvec{\theta }_k^0}^{(2)}\right) \right) > 0 a.s. \end{aligned}$$

  (38)

  then $\tilde{\varvec{\theta }}_k^{(2)} \xrightarrow {a.s.} {\varvec{\theta }_k^0}^{(2)}$ as $n \rightarrow \infty .$

Proof

This can be proved by contradiction along the same lines as Lemma 5. $\square$

Lemma 10

If the Assumptions 1, 3 and 4 are satisfied, then for $j \leqslant p$ and $k \leqslant q$:

• (a) $(\tilde{\varvec{\theta }_j} - \varvec{\theta }_j^0)(\sqrt{n}{\varvec{D}}_1)^{-1} \xrightarrow {a.s.} 0.$

• (b) $(\tilde{\varvec{\xi }_k} - \varvec{\xi }_k^0)(\sqrt{n}{\varvec{D}}_2)^{-1} \xrightarrow {a.s.} 0.$

Here, ${\varvec{D}}_1 = \hbox {diag}(\frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}}, \frac{1}{n\sqrt{n}})$ and ${\varvec{D}}_2 = \hbox {diag}(\frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}}, \frac{1}{n^2\sqrt{n}})$.

Proof

This proof can be obtained along the same lines as Lemma 8. $\square$

Now the proofs of Theorems  7 and 8 can be obtained by using the above lemmas and following the same argument as in Theorem 3.

Next, we examine the situation when the number of components is overestimated (see Theorem 9). The proof of Theorem 9 will follow consequently from the below-stated lemmas:

Lemma 11

If X(t), is the error component as defined before, and if ${\tilde{A}}$, ${\tilde{B}}$ and ${\tilde{\alpha }}$ are obtained by minimizing the following function:

$$\begin{aligned} Q_{p+q+1}\left( \varvec{\theta }^{(1)}\right) = \frac{1}{n}\sum _{t=1}^{N}\left( X(t) - A \cos (\alpha t) - B \sin (\alpha t)\right) ^2, \end{aligned}$$

then ${\tilde{A}} \xrightarrow {a.s.} 0$ and ${\tilde{B}} \xrightarrow {a.s.} 0.$

Proof

The sum of squares function $Q_{p+q+1}(\varvec{\theta }^{(1)})$ can be written as:

$$\begin{aligned}&\frac{1}{n} \sum _{t=1}^{n}X^2(t) - \frac{2}{n} \sum _{t=1}^{n} X(t)\left( A \cos (\alpha t) + B \sin (\alpha t)\right) + \frac{A^2 + B^2}{2} + o(1)\\&\quad = R\left( \varvec{\theta }^{(1)}\right) + o(1). \end{aligned}$$

Since the difference between $Q_{p+q+1}(\varvec{\theta }^{(1)})$ and $R(\varvec{\theta }^{(1)})$ is o(1), replacing former with latter will have negligible effect on the estimators. Thus, we have

$$\begin{aligned} {\tilde{A}} = \frac{2}{n}\sum \limits _{t=1}^{n} X(t)\cos (\alpha t) + o(1) and {\tilde{B}} = \frac{2}{n}\sum _{t=1}^{n} X(t)\sin (\alpha t) + o(1). \end{aligned}$$

Now using Lemma 4(a), the result follows. $\square$

Lemma 12

If X(t), is the error component as defined before, and if ${\tilde{C}}$, ${\tilde{D}}$ and ${\tilde{\beta }}$ are obtained by minimizing the following function:

$$\begin{aligned} \frac{1}{n}\sum _{t=1}^{N}\left( X(t) - C \cos \left( \beta t^2\right) - D \sin \left( \beta t^2\right) \right) ^2, \end{aligned}$$

then ${\tilde{C}} \xrightarrow {a.s.} 0$ and ${\tilde{D}} \xrightarrow {a.s.} 0.$

Proof

The proof of this lemma follows along the same lines as Lemma 11. $\square$

Now, we provide the proof of the fact that the sequential LSEs have the same asymptotic distribution as the LSEs.

Proof of Theorem 10:

(a) By Taylor series expansion of ${\varvec{Q}}'_1(\tilde{\varvec{\theta }}_1^{(1)})$ around the point ${\varvec{\theta }_1^0}^{(1)}$, we have:

$$\begin{aligned} \left( \tilde{\varvec{\theta }}_1^{(1)} - {\varvec{\theta }_1^0}^{(1)}\right) = -{\varvec{Q}}'_1\left( {\varvec{\theta }_1^0}^{(1)}\right) \left[ {\varvec{Q}}''_1\left( \bar{\varvec{\theta }}_1^{(1)}\right) \right] ^{-1} \end{aligned}$$

Multiplying both sides by the matrix ${\varvec{D}}_1^{-1}$, where ${\varvec{D}}_1 = \hbox {diag}(\frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}},\frac{1}{n\sqrt{n}})$, we get:

$$\begin{aligned} \left( \tilde{\varvec{\theta }}_1^{(1)} - {\varvec{\theta }_1^0}^{(1)}\right) {\varvec{D}}_1^{-1} = -{\varvec{Q}}'_1\left( {\varvec{\theta }_1^0}^{(1)}\right) {\varvec{D}}_1 \left[ {\varvec{D}}_1{\varvec{Q}}''_1\left( \bar{\varvec{\theta }}_1^{(1)}\right) {\varvec{D}}_1\right] ^{-1} \end{aligned}$$

First, we show that ${\varvec{Q}}'_1({\varvec{\theta }_1^0}^{(1)}){\varvec{D}}_1 \rightarrow N_3(0, 4 \sigma ^2 c \varvec{\varSigma }_1^{(1)}).$

To prove this, we compute the elements of the derivative vector ${\varvec{Q}}'_1({\varvec{\theta }_1^0}^{(1)})$:

$$\begin{aligned}&\frac{\partial Q_1\left( {\varvec{\theta }_1^0}^{(1)}\right) }{\partial A_1}\\&\quad = -2 \sum _{t=1}^n \left( \sum _{j=2}^p\left( A_j^0 \cos \left( \alpha _j^0 t\right) + B_j^0 \sin \left( \alpha _j^0 t\right) \right) + \sum _{k=1}^q \left( C_k^0 \cos \left( \beta _k^0 t^2\right) + D_k^0 \sin \left( \beta _k^0 t^2\right) \right) \right. \\&\qquad \left. +X(t)\right) \cos \left( \alpha _1^0 t\right) ,\\&\quad \frac{\partial Q_1\left( {\varvec{\theta }_1^0}^{(1)}\right) }{\partial B_1} = -2 \sum _{t=1}^n \left( \sum _{j=2}^p\left( A_j^0 \cos \left( \alpha _j^0 t\right) + B_j^0 \sin \left( \alpha _j^0 t\right) \right) + \sum _{k=1}^q \left( C_k^0 \cos \left( \beta _k^0 t^2\right) \right. \right. \\&\qquad \left. \left. + D_k^0 \sin \left( \beta _k^0 t^2\right) \right) + X(t)\right) \sin \left( \alpha _1^0 t\right) ,\\&\quad \frac{\partial Q_1\left( {\varvec{\theta }_1^0}^{(1)}\right) }{\partial \alpha _1}\\&\quad = -2 \sum _{t=1}^n t \left( \sum _{j=2}^p\left( A_j^0 \cos \left( \alpha _j^0 t\right) + B_j^0 \sin \left( \alpha _j^0 t\right) \right) \right. \\&\qquad \left. + \sum _{k=1}^q \left( C_k^0 \cos \left( \beta _k^0 t^2\right) + D_k^0 \sin \left( \beta _k^0 t^2\right) \right) + X(t)\right) \\&\qquad \times \left( -A_1^0 \sin \left( \alpha _1^0 t\right) + B_1^0 \cos \left( \alpha _1^0 t\right) \right) . \end{aligned}$$

Using Conjecture 2 (see Sect. A), it can be shown that:

$$\begin{aligned} {\varvec{Q}}'_1({\varvec{\theta }_1^0}^{(1)}){\varvec{D}}_1 \overset{a.eq.}{=} -2 \begin{pmatrix} \frac{1}{\sqrt{n}}\sum \limits _{t=1}^{n} X(t) \cos (\alpha _1^0 t) \\ \frac{1}{\sqrt{n}}\sum \limits _{t=1}^{n} X(t) \sin (\alpha _1^0 t) \\ \frac{1}{n\sqrt{n}}\sum \limits _{t=1}^{n} t X(t)(-A_1^0\sin (\alpha _1^0 t) + B_1^0 \cos (\alpha _1^0 t)) \end{pmatrix}. \end{aligned}$$

Now using CLT, we have:

$$\begin{aligned} {\varvec{Q}}'_1\left( {\varvec{\theta }_1^0}^{(1)}\right) {\varvec{D}}_1 \rightarrow N_3\left( 0, 4 \sigma ^2 c \varvec{\varSigma }_1^{(1)}\right) \end{aligned}$$

Next, we compute the elements of the second-derivative matrix, ${\varvec{D}}_1 {\varvec{Q}}''_1({\varvec{\theta }_1^0}^{(1)}){\varvec{D}}_1$. By straightforward calculations and using Lemmas 1, 2, 3 and 4 , it is easy to show that:

$$\begin{aligned} {\varvec{D}}_1 {\varvec{Q}}''_1\left( {\varvec{\theta }_1^0}^{(1)}\right) {\varvec{D}}_1 = 2\varvec{\varSigma }_1^{(1)}. \end{aligned}$$

Thus, we have the desired result.

(b) Consider the error sum of squares $Q_2(\varvec{\theta }^{(2)}) = \sum \limits _{t=1}^{n}\bigg (y_1(t) - C\cos (\beta t^2) - D\sin (\beta t^2)\bigg )^2$. Here $y_1(t) = y(t) - {\tilde{A}} \cos ({\tilde{\alpha }} t) - {\tilde{B}} \sin ({\tilde{\alpha }} t)$, $t = 1, \ldots , n$. Let ${\varvec{Q}}'_2(\varvec{\theta }^{(2)})$ be the first-derivative vector and ${\varvec{Q}}''_2(\varvec{\theta }^{(2)})$, the second-derivative matrix of $Q_2(\varvec{\theta }^{(2)})$. By Taylor series expansion of ${\varvec{Q}}'_2(\tilde{\varvec{\theta }}_1^{(2)})$ around the point ${\varvec{\theta }_1^0}^{(2)}$, we have:

$$\begin{aligned} \left( \tilde{\varvec{\theta }}_1^{(2)} - {\varvec{\theta }_1^0}^{(2)}\right) = -{\varvec{Q}}'_2\left( {\varvec{\theta }_1^0}^{(2)}\right) \left[ {\varvec{Q}}''_2\left( \bar{\varvec{\theta }}_1^{(2)}\right) \right] ^{-1} \end{aligned}$$

Multiplying both sides by the matrix ${\varvec{D}}_2^{-1}$, where ${\varvec{D}}_2 = \hbox {diag}(\frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}}, \frac{1}{n^2\sqrt{n}})$, we get:

$$\begin{aligned} \left( \tilde{\varvec{\theta }}_1^{(2)} - {\varvec{\theta }_1^0}^{(2)}\right) {\varvec{D}}_2^{-1} = -{\varvec{Q}}'_2\left( {\varvec{\theta }_1^0}^{(2)}\right) {\varvec{D}}_2 \left[ {\varvec{D}}_2{\varvec{Q}}''_2\left( \bar{\varvec{\theta }}_1^{(2)}\right) {\varvec{D}}_2\right] ^{-1} \end{aligned}$$

Now using (33), and proceeding exactly as in part (a), we get:

$$\begin{aligned} \left( \tilde{\varvec{\theta }}_1^{(2)} -{\varvec{\theta }_1^0}^{(2)}\right) {\varvec{D}}_2^{-1} \xrightarrow {d} N_3\left( 0, \sigma ^2 c {\varvec{\varSigma }_1^{(2)}}^{-1}\right) . \end{aligned}$$

Hence, the result. $\square$