1 Introduction

Decision making is a significant branch of management science, which includes the selection problem, outranking problem and sorting problem. Information fusion plays a vitally important role in the process of decision making, among which information aggregation operators are an effective and widely concerned research direction (Beliakov 2003; Eriz 2007; Calvo and Beliakov 2010; Mardani et al. 2018). It involves the fields including recommender system (Qin 2017), investment management (Ma et al. 2016) and supplier selection (Zhang 2018; Qin and Liu 2014). In order to handle the high complex uncertain problem, the type-2 fuzzy sets (T2FSs) was developed as an extension of type-1 fuzzy sets (T1FSs) (Zadeh 1975a; Zadeh 1975b; Zadeh 1975c). The notable difference between T2FSs and T1FSs lies in the two membership functions in T2FSs, i.e. the primary membership function (PMF) and the secondary membership function (SMF). In addition, since an interval type-2 fuzzy sets (IT2FSs) have the apparent merit in information representation and comprehensibility, many scholars paid more attention to the theory and application of IT2FSs. The former mainly includes the type reduction method (Karnik and Mendel 2001; Liu and Mendel 2011), ranking method (Wu and Mendel 2007a; Chen 2012; Sang and Liu 2016), aggregation operators and other knowledge (Mendel and John 2002; Mendel et al. 2006; Wu and Mendel 2007b), and the later mainly involves the multiple criteria decision making (MCDM) problems (Wu and Liu 2016; Kundu et al. 2017; Qin et al. 2017). Type-2 fuzzy aggregation operators, as a key technique, have been investigated by many scholars.

In the literature, we collect 61 references about this topic, the relationship between numbers of papers and year can be shown in Fig. 1. Several different families of type-2 fuzzy aggregation operators have been presented in Table 1 and the distribution of papers is displayed in Fig. 2. However, there is a lack in the previous studies concerning the systematic review of type-2 fuzzy aggregation operators. In this paper, we will handle this problem and further present the future research directions. Considering the situation, the weights and attributes represented by IT2FSs, the linguistic weighted average (LWA) operator was developed and have better application in hierarchical decision making (Wu and Mendel 2007b; John et al. 2018). Zhou et al. (Zhou et al. 2008; Zhou et al. 2010) proposed the T2FS ordered weighted averaging (OWA) operator, which can aggregate directly the linguistic preferences provided by decision makers (DMs). Based on triangle norm operations, triangle interval type-2 fuzzy Frank weighted averaging (TIT2FFWA) operator and triangle interval type-2 fuzzy Frank geometric average (TIT2FFWG) operator were developed (Qin and Liu 2014). Based on the non-negative trapezoidal IT2FNs, Wang et al. (Wang et al. 2015) put forward a family of information aggregation operators, i.e. trapezoidal interval type-2 fuzzy arithmetic averaging aggregation operator (TIT2AA), trapezoidal interval type-2 fuzzy ordered weighted averaging aggregation operator (TIT2OWA) and trapezoidal interval type-2 fuzzy hybrid weighted averaging aggregation operator (TIT2HWA). In order to describe the interaction between any two aggregated information, the Bonferroni mean was extended into different environments as a result of the characteristic of combining averaging and “anding” operator (Liu et al. 2017; Gou et al. 2017). Gong et al. (Gong et al. 2015) extended Bonferroni mean operator into the interval type-2 fuzzy environment and named them as trapezoidal interval type-2 fuzzy geometric Bonferroni mean (TIT2FGBM) operator and trapezoidal interval type-2 fuzzy weighted geometric Bonferroni mean (TIT2FWGBM) operator. Other type-2 fuzzy aggregation operators were presented such as interval type-2-dependent ordered weighted averaging (IT2DOWA) operator and interval type-2 power averaging (IT2PA) operator (Ma et al. 2016). Wu and Liu proposed interval type-2 fuzzy weighted geometric averaging (WGA) operator and interval type-2 fuzzy combined weighted geometric averaging (CWGA) operator (Wu and Liu 2016). Based on multi-granular linguistic environment, 2-dimension interval type-2 trapezoidal fuzzy ordered weighted average (2DIT2TFOWA) operator and quasi-2-dimension interval type-2 trapezoidal fuzzy ordered weighted average (quasi-2DIT2TFOWA) operator were developed (Wu et al. 2017). To consider the interaction among all the aggregated information, Qin presented the interval type-2 fuzzy Hamy mean (HM) operators, i.e. symmetric triangular interval type-2 fuzzy Hamy mean (STIT2FHM) operator and weighted symmetric triangular interval type-2 fuzzy Hamy mean (WSTIT2FHM) operator, which was applied to the tourism recommender system (Qin 2017). Zhang presented some trapezoidal interval type-2 fuzzy aggregation operators, such as trapezoidal interval type-2 fuzzy weighted averaging (TIT2FWA) operator, generalized trapezoidal interval type-2 fuzzy weighted averaging (GTIT2FWA) operator, trapezoidal interval type-2 fuzzy ordered weighted averaging (TIT2FOWA) operator, generalized trapezoidal interval type-2 fuzzy ordered weighted averaging (GTIT2FOWA) operator, trapezoidal interval type-2 fuzzy hybrid averaging (TIT2FHA) operator, and generalized trapezoidal interval type-2 fuzzy hybrid averaging (GTIT2FHA) operator (Zhang 2018). Except from these type-2 fuzzy operators, some operators were developed based on the fuzzy measures and fuzzy integrals, such as type-2 fuzzy Choquet integral and Sugeno integral (Havens et al. 2010; Bustince et al. 2013). More relevant type-2 fuzzy operators can refer to other literatures (Lee and Chen 2008; Andelkovic and Saletic 2012; Chen and Lee 2010; Wang et al. 2012; Li et al. 2018).

Fig. 1
figure 1

Papers related to type-2 fuzzy sets

Full size image
Table 1 Type-2 fuzzy aggregation operators and corresponding references
Full size table
Fig. 2
figure 2

The distribution of papers of type-2 fuzzy aggregation operators across journals

Full size image

This paper is organized as follows: in Section 2, we introduce some basic knowledge on I2FSs, which are comprised of the definitions, operations, type reduction method and ranking method. Section 3 summarizes type-2 fuzzy aggregation operators and their advantages and disadvantages. Furthermore, some application fields with regard to type-2 fuzzy aggregation operations are reviewed in Section 4. Finally, Section 5 discusses the current challenges and outlines future research directions on type-2 fuzzy aggregation operations.

2 Type-2 fuzzy sets and basic knowledge

In this section, we first introduce some basic knowledge about information aggregation function. Then type-2 fuzzy sets, operations, type reduction approaches and ranking methods are reviewed. The basic theories are shown in Fig. 3.

Fig. 3
figure 3

The graphical representation of type-2 fuzzy basic theories

Full size image

2.1 Information aggregation function

Definition 1

(Eriz 2007) The information aggregation function f : [0, 1]n → [0, 1] (n > 1) should satisfy the following properties:

  1. (1)

    f(0, 0, ⋯, 0) = 0 and f(1, 1, ⋯, 1) = 1;

  2. (2)

    If x ≤ y, then f(x) ≤ f(y) for ∀x, y ∈ [0, 1]n

wherex, yare two inputs vectors. The above aggregation function can deal with the problem of the same input components. In order to handle any number of arguments, the extended aggregation function is defined as follows:

Definition 2

(Eriz 2007) The extended aggregation function, as a mapping, is defined as follows:

$$ F:\underset{n\in \left\{1,2,\cdots \right\}}{\cup }{\left[0,1\right]}^n\to \left[0,1\right] $$

The aggregation functions are divided into four categories: averaging, conjunctive, disjunctive, and mixed ones. Let us introduce the corresponding definitions.

Definition 3

(Eriz 2007) An averaging aggregation function f should satisfy the following relationship for any x:

$$ \min \left(\mathbf{x}\right)\le f\left(\mathbf{x}\right)\le \max \left(\mathbf{x}\right) $$

Definition 4

(Eriz 2007) A conjunctive aggregation function f should satisfy the following relationship for any x:

$$ f\left(\mathbf{x}\right)\le \min \left(\mathbf{x}\right)=\min \left({x}_1,{x}_2,\cdots, {x}_n\right) $$

Definition 5

(Eriz 2007) A disjunctive aggregation function f should satisfy the following relationship for any x:

$$ f\left(\mathbf{x}\right)\ge \max \left(\mathbf{x}\right)=\max \left({x}_1,{x}_2,\cdots, {x}_n\right) $$

The mixed aggregation function is not the above any one, which includes the different behavior types for different parts of the domain.

In general, some aggregation operators could satisfy the following properties (Eriz 2007):

Property 1

(Idempotency) If the input information is the same, viz. x = (t, t, ⋯, t), t ∈ [0, 1], then the aggregated result is the same as the input information f(t, t, ⋯, t) = t. We call this aggregation function f idempotent.

Property 2

(Symmetry) There is a collection of input information. If we exchange the position of input information in a permutation, then the aggregated result is left unchanged. The aggregation function f is symmetric if it satisfies the following relationship:

$$ f\left({x}_1,{x}_2,\cdots, {x}_n\right)=f\left({x}_{P(1)},{x}_{P(2)},\cdots, {x}_{P(n)}\right) $$

Where the P(1), P(2), ⋯, P(n) is some other permutation of 1, 2, ⋯, n.

Property 3

(Monotonicity) If the input information is monotonically increasing (decreasing), then the aggregated result is also monotonically increasing (decreasing).. The aggregation function f is monotonicity if it satisfies the following relationship:

$$ \mathbf{x}\le \mathbf{y}\to f\left(\mathbf{x}\right)\le f\left(\mathbf{y}\right), for\forall \mathbf{x},\mathbf{y}\in {\left[0,1\right]}^n $$

Property 4

(Boundness) The aggregated result is bigger than the minimum of all the input information and smaller than the maximum all the input information. The aggregation function f is bounded if it satisfies the following relationship:

$$ f\left(\min (x)\right)\le f\left(\mathbf{x}\right)\le f\left(\max (x)\right) $$

2.2 Definitions of Type-2 fuzzy sets

For the definitions of type-2 fuzzy sets, some scholars presented their individual opinions, see Table 2. Next, we introduce a representative one.

Table 2 The definitions of type-2 fuzzy sets available in research studies
Full size table

Definition 6

(Mendel and John 2002) For a given type-2 fuzzy set A associated with universe of discourse X and Jx ⊆ [0, 1], A is defined as follows:

$$ A=\left\{\left(x,u\right),{\mu}_A\left(x,u\right)|\forall x\in X,u\in {J}_x,0\le {\mu}_A\left(x,u\right)\le 1\right\} $$
(1)

The other representation is shown as follows:

$$ A={\int}_{x\in X}{\int}_{u\in {J}_x}{\mu}_A\left(x,u\right)/\left(x,u\right)={\int}_{x\in X}\left({\int}_{u\in {J}_x}{\mu}_A\left(x,u\right)/\left(x,u\right)\right)/x $$
(2)

where Jx is denoted as the primary membership at x, and \( {\int}_{u\in {J}_x}{\mu}_A\left(x,u\right)/\left(x,u\right) \) means the secondary membership at x. ∬represents the union over all admissible xand u. ∫can be replaced by ∑when dealing with discrete spaces. The graphical representation is shown in Fig. 4.

Fig. 4
figure 4

A general type-2 fuzzy sets

Full size image

Based on the idea of set theory, Mo and Wang proposed discrete T2FS, as a special representation (Mo and Wang 2017). The definition on discrete T2FS is given as follows:

Definition 7

(Mo and Wang 2017) Assuming ω is a discrete T2FS, for X = {x1, x2, ⋯, xK}, then ω and associated with its primary membership function Lx and secondary membership function are represented by

$$ \omega =\sum \limits_{k=1}^K\sum \limits_{n=1}^{N_k}\frac{a_{kn}}{\left({x}_k,{u}_{kn}\right)} $$

and

$$ {\mu}_{\omega}^1(x)={L}_x=\Big\{{\displaystyle \begin{array}{l}\left\{{u}_{11},{u}_{12},\cdots, {u}_{1{N}_1}\right\}, if\ x={x}_1\\ {}\left\{{u}_{21},{u}_{22},\cdots, {u}_{2{N}_1}\right\}, if\ x={x}_2\\ {}\cdots \\ {}\left\{{u}_{K1},{u}_{K2},\cdots, {u}_{K{N}_1}\right\}, if\ x={x}_K\end{array}} $$

and

$$ {\mu}_{\omega}^2\left(x,u\right)=\Big\{{\displaystyle \begin{array}{l}{a}_{11}, if\;x={x}_1,u={u}_{11}\\ {}\cdots \\ {}{a}_{1{N}_1}, if\;x={x}_1,u={u}_{1{N}_1}\\ {}{a}_{21}, if\;x={x}_2,u={u}_{21}\\ {}\cdots \\ {}{a}_{2{N}_2}, if\;x={x}_2,u={u}_{2{N}_2}\\ {}\cdots \\ {}{a}_{K1}, if\;x={x}_K,u={u}_{K1}\\ {}\cdots \\ {}{a}_{K{N}_K}, if\;x={x}_K,u={u}_{K{N}_K}\end{array}} $$

The graphical representation is shown in Fig. 5.

Fig. 5
figure 5

The discrete T2FS

Full size image

Definition 8

(Mendel and John 2002) Let \( \tilde{A} \) be a type-2 fuzzy set in the universe of discourse X represented by a type-2 membership function μA(x, u). If all μA(x, u) = 1 holds, then it is denoted as an interval type-2 fuzzy set (IT2FS) in Fig. 6. It is a special case of type-2 fuzzy set, which can be described as follows:

$$ \tilde{A}={\int}_{x\in X}{\int}_{u\in {J}_x}1/\left(x,u\right)={\int}_{x\in X}\left({\int}_{u\in {J}_x}1/\left(x,u\right)\right)/x $$
(3)

where Jx is denoted as the primary membership at x, and \( {\int}_{u\in {J}_x}1/\left(x,u\right) \) means the secondary membership at x.

Fig. 6
figure 6

The FOU of an IT2FS \( \tilde{A} \)

Full size image

Definition 8

(Mendel and John 2002) For given an IT2FS \( \tilde{A} \) with a universe of discourse X shown in Fig. 5, the footprint of uncertainty (FOU) is defined as follows:

$$ \mathrm{FOU}\left(\tilde{A}\right)=\underset{x\in X}{\cup }{J}_x $$
(4)

where Jx is denoted as the primary membership at x.

2.3 Operations of type-2 fuzzy sets

In this section, we introduce some operations of T2FSs.

Definition 9

(Karnik and Mendel 2001) Let \( \tilde{A} \) and \( \tilde{B} \) be two T2FSs defined on the universe of discourse X, their primary membership functions are defined as:

$$ {\displaystyle \begin{array}{l}{\mu}_{\tilde{A}}(x)={\int}_u{f}_x(u)/u\\ {}{\mu}_{\tilde{B}}(x)={\int}_w{g}_x(w)/w\end{array}} $$
(5)

where u, w ∈ Jx, then the union and intersection operations are defined as:

$$ \mathbf{Union}\kern0.5em {\mu}_{\tilde{A}\cup \tilde{B}}(x)={\int}_{u\in {J}_x}{\int}_w\left[{f}_x(u)\wedge {g}_x(w)\right]/\left(u\vee w\right) $$
(6)
$$ \mathbf{Intersection}\kern0.5em {\mu}_{\tilde{A}\cap \tilde{B}}(x)={\int}_{u\in {J}_x}{\int}_w\left[{f}_x(u)\wedge {g}_x(w)\right]/\left(u\wedge w\right) $$
(7)

when \( \tilde{A} \) and \( \tilde{B} \) are two IT2FSs, the above two operations can be simplified as follows:

$$ {\mu}_{\tilde{A}\cup \tilde{B}}(x)=\left[{\underline{\mu}}_{\tilde{A}}(x)\vee {\underline{\mu}}_{\tilde{B}}(x),{\overline{\mu}}_{\tilde{A}}(x)\vee {\overline{\mu}}_{\tilde{B}}(x)\right] $$
(8)
$$ {\mu}_{\tilde{A}\cap \tilde{B}}(x)=\left[{\underline{\mu}}_{\tilde{A}}(x)\wedge {\underline{\mu}}_{\tilde{B}}(x),{\overline{\mu}}_{\tilde{A}}(x)\wedge {\overline{\mu}}_{\tilde{B}}(x)\right] $$
(9)

Obviously, the results shown above can be easy extended to the case of multiple T2FSs.

Regarding to complementary operation, it is defined as:

$$ {\mu}_{{\tilde{A}}^c}(x)={\int}_{u\in {J}_x}\frac{f_x(u)}{1-u} $$
(10)

Definition 10

(Karnik and Mendel 2001) The operations of T2FSs satisfy the following properties:

$$ A\cap B=B\cap A,A\cup B=B\cup A $$
$$ \left(A\cap B\right)\cap C=A\cap \left(B\cap C\right),\left(A\cup B\right)\cup C=A\cup \left(B\cup C\right) $$
$$ A\cup A=A,A\cap A=A $$
$$ {\left(A\cup B\right)}^C={A}^C\cap {B}^C,{\left(A\cap B\right)}^C={A}^C\cup {B}^C $$

It is noted that the operations of T2FSs do not satisfy absorption, distribution and identity.

Definition 11

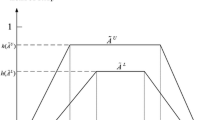
Let \( \tilde{\tilde{A}}=\left({\tilde{A}}^{+},{\tilde{A}}^{-}\right) \) and \( \tilde{\tilde{B}}=\left({\tilde{B}}^{+},{\tilde{B}}^{-}\right) \) be two TraIT2FSs, the graphic representation of a TraIT2FS \( \tilde{\tilde{A}} \) is contained in Fig. 7. The arithmetic operations are defined as follows:

  1. 1.

    Addition operation (Chen 2012)

Fig. 7
figure 7

The graphic representation of a TraIT2FS \( \tilde{\tilde{A}} \)

Full size image
$$ \tilde{\tilde{A}}\oplus \tilde{\tilde{B}}=\left({\tilde{A}}^{+},{\tilde{A}}^{-}\right)\oplus \left({\tilde{B}}^{+},{\tilde{B}}^{-}\right)=\left(\begin{array}{l}\left({a}_{11}^{+}+{b}_{11}^{+},{a}_{12}^{+}+{b}_{12}^{+},{a}_{13}^{+}+{b}_{13}^{+},{a}_{14}^{+}+{b}_{14}^{+};\min \left({h}_{\tilde{\tilde{A}}}^{+},{h}_{\tilde{\tilde{B}}}^{+}\right)\right),\\ {}\left({a}_{11}^{-}+{b}_{11}^{-},{a}_{12}^{-}+{b}_{12}^{-},{a}_{13}^{-}+{b}_{13}^{-},{a}_{14}^{-}+{b}_{14}^{-};\min \left({h}_{\tilde{\tilde{A}}}^{-},{h}_{\tilde{\tilde{B}}}^{-}\right)\right)\end{array}\right) $$
(11)
  1. 2.

    Subtraction operation (Lee and Chen 2008)

$$ \tilde{\tilde{A}}\varTheta \tilde{\tilde{B}}=\left({\tilde{A}}^{+},{\tilde{A}}^{-}\right)\varTheta \left({\tilde{B}}^{+},{\tilde{B}}^{-}\right)=\left(\begin{array}{c}\left({a}_{11}^{+}-{b}_{14}^{+},{a}_{12}^{+}-{b}_{13}^{+},{a}_{13}^{+}-{b}_{12}^{+},{a}_{14}^{+}-{b}_{11}^{+};\min \left(h\begin{array}{c}+\\ {}\approx \\ {}A\end{array},h\begin{array}{c}+\\ {}\approx \\ {}B\end{array}\right)\right),\\ {}\left({a}_{11}^{-}-{b}_{14}^{-},{a}_{12}^{-}-{b}_{13}^{-},{a}_{13}^{-}-{b}_{12}^{-},{a}_{14}^{-}-{b}_{11}^{-};\min \left(h\begin{array}{c}-\\ {}\approx \\ {}A\end{array},h\begin{array}{c}-\\ {}\approx \\ {}B\end{array}\right)\right)\end{array}\right) $$
(12)
  1. 3.

    Multiplication operation (Lee and Chen 2008)

$$ \tilde{\tilde{A}}\otimes \tilde{\tilde{B}}=\left({\tilde{A}}^{+},{\tilde{A}}^{-}\right)\otimes \left({\tilde{B}}^{+},{\tilde{B}}^{-}\right)=\left(\begin{array}{l}\left({a}_{11}^{+}\times {b}_{11}^{+},{a}_{12}^{+}\times {b}_{12}^{+},{a}_{13}^{+}\times {b}_{13}^{+},{a}_{14}^{+}\times {b}_{14}^{+};\min \left({h}_{\tilde{\tilde{A}}}^{+},{h}_{\tilde{\tilde{B}}}^{+}\right)\right),\\ {}\left({a}_{11}^{-}\times {b}_{11}^{-},{a}_{12}^{-}\times {b}_{12}^{-},{a}_{13}^{-}\times {b}_{13}^{-},{a}_{14}^{-}\times {b}_{14}^{-};\min \left({h}_{\tilde{\tilde{A}}}^{-},{h}_{\tilde{\tilde{B}}}^{-}\right)\right)\end{array}\right) $$
(13)
  1. 4.

    Multiplication by real number operation (Chen 2012)

$$ k\tilde{\tilde{A}}=\left(\begin{array}{l}\left(k{a}_{11}^{+},k{a}_{12}^{+},k{a}_{13}^{+},k{a}_{14}^{+};{h}_{\tilde{\tilde{A}}}^{+}\right),\\ {}\left(k{a}_{11}^{-},k{a}_{12}^{-},k{a}_{13}^{-},k{a}_{14}^{-};{h}_{\tilde{\tilde{A}}}^{-}\right)\end{array}\right) $$
(14)
  1. 5.

    Power operation (Chen 2012)

$$ {\tilde{\tilde{A}}}^{\lambda }=\left(\begin{array}{l}\left({\left({a}_{11}^{+}\right)}^{\lambda },{\left({a}_{12}^{+}\right)}^{\lambda },{\left({a}_{13}^{+}\right)}^{\lambda },{\left({a}_{14}^{+}\right)}^{\lambda };{h}_{\tilde{\tilde{A}}}^{+}\right),\\ {}\left({\left({a}_{11}^{-}\right)}^{\lambda },{\left({a}_{12}^{-}\right)}^{\lambda },{\left({a}_{13}^{-}\right)}^{\lambda },{\left({a}_{14}^{-}\right)}^{\lambda };{h}_{\tilde{\tilde{A}}}^{-}\right)\end{array}\right) $$
(15)
  1. 6.

    Radical operation (Kahraman et al. 2014)

$$ \sqrt[n]{\tilde{\tilde{A}}}=\left(\begin{array}{c}\left(\sqrt[n]{a_{11}^{+}},\sqrt[n]{a_{12}^{+}},\sqrt[n]{a_{13}^{+}},\sqrt[n]{a_{14}^{+}};h\begin{array}{c}+\\ {}\approx \\ {}A\end{array}\right),\\ {}\left(\sqrt[n]{a_{11}^{-}},\sqrt[n]{a_{12}^{-}},\sqrt[n]{a_{13}^{-}},\sqrt[n]{a_{14}^{-}};h\begin{array}{c}-\\ {}\approx \\ {}A\end{array}\right)\end{array}\right) $$
(16)

2.4 Type reduction of type-2 fuzzy sets

Calculating the centroid of a type-2 fuzzy sets and reducing a type-2 fuzzy sets to a type-1 fuzzy sets are operations that must be taken into consideration. From the representation theorem for IT2FSs, we introduce the Karnik–Mendel (KM) algorithms for type reduction of type-2 fuzzy sets.

Definition 12

(Karnik and Mendel 2001) The centroid of IT2FSs \( \tilde{A} \) is the union of the centroids of all its embedded T1FSs c(Ae), which is defined as:

$$ C\left(\tilde{A}\right)=\underset{\forall {A}_e}{\cup }{c}_{\tilde{A}}\left({A}_e\right)=\left\{{c}_l\left(\tilde{A}\right),\cdots, {c}_r\left(\tilde{A}\right)\right\} $$
(17)

where

$$ {c}_l\left(\tilde{A}\right)=\underset{\forall {A}_e}{\min }{c}_{\tilde{A}}\left({A}_e\right)=\underset{\forall {\theta}_i\in \left[{\underset{\_}{\mu}}_{\tilde{A}}\left({x}_i\right),{\overline{\mu}}_{\tilde{A}}\left({x}_i\right)\right]}{\min}\left(\frac{\sum_{i=1}^N{x}_i{\theta}_i}{\sum_{i=1}^N{\theta}_i}\right) $$
(18)
$$ {c}_r\left(\tilde{A}\right)=\underset{\forall {A}_e}{\max }{c}_{\tilde{A}}\left({A}_e\right)=\underset{\forall {\theta}_i\in \left[{\underset{\_}{\mu}}_{\tilde{A}}\left({x}_i\right),{\overline{\mu}}_{\tilde{A}}\left({x}_i\right)\right]}{\max}\left(\frac{\sum_{i=1}^N{x}_i{\theta}_i}{\sum_{i=1}^N{\theta}_i}\right) $$
(19)

\( {c}_l\left(\tilde{A}\right) \) and \( {c}_r\left(\tilde{A}\right) \)can be computed by the iterative KM algorithm presented in Table 3.

Table 3 KM algorithm for IT2FSs
Full size table

Liu and Mendel (Liu and Mendel 2011) proposed a continuous KM for the direct centroid computation of IT2FSs, which can transform the centroid computation into the Root-Finding problems shown in Fig. 8.

Fig. 8
figure 8

KM algorithm and Newton–Raphson method. (a) and (b) Computation of cl = ξ4. (c) and (d) Computation of cr = ξ4

Full size image

Assume that all the xi are different, and they are bounded in [a, b], where\( a=\underset{1\le i\le N}{\min}\left\{{x}_i\right\},b=\underset{1\le i\le N}{\max}\left\{{x}_i\right\} \), which denote the smallest and the largest sampled values of x, respectively. Then, the continuous versions of (20) and (21) are:

$$ {c}_l=\underset{\xi \in \left[a,b\right]}{\min }{c}_l\left(\xi \right)=\underset{\xi \in \left[a,b\right]}{\min}\left(\frac{\int_a^{\xi }x{\overline{\mu}}_{\tilde{A}}(x) dx+{\int}_{\xi}^bx{\underset{\_}{\mu}}_{\tilde{A}}(x) dx}{\int_a^{\xi }{\overline{\mu}}_{\tilde{A}}(x) dx+{\int}_{\xi}^b{\underset{\_}{\mu}}_{\tilde{A}}(x) dx}\right) $$
(20)
$$ {c}_r=\underset{\xi \in \left[a,b\right]}{\max }{c}_r\left(\xi \right)=\underset{\xi \in \left[a,b\right]}{\max}\left(\frac{\int_a^{\xi }x{\underset{\_}{\mu}}_{\tilde{A}}(x) dx+{\int}_{\xi}^bx{\overline{\mu}}_{\tilde{A}}(x) dx}{\int_a^{\xi }{\underset{\_}{\mu}}_{\tilde{A}}(x) dx+{\int}_{\xi}^b{\overline{\mu}}_{\tilde{A}}(x) dx}\right) $$
(21)

Theorem 1

(Liu and Mendel 2011) (a) Let cl = cl(ξ∗) be the unique minimum value of (22), and ξ∗ is the unique simple root of the monotonic increasing convex function:

$$ \varphi \left(\xi \right)={\int}_a^{\xi}\left(\xi -x\right){\overline{\mu}}_{\tilde{A}}(x) dx+{\int}_{\xi}^b\left(\xi -x\right){\underset{\_}{\mu}}_{\tilde{A}}(x) dx $$
(22)

Furthermore, ξ∗ is the fixed point of cl(ξ) with ξ∗ = cl(ξ∗), so that

$$ {c}_l={c}_l\left({\xi}^{\ast}\right)={\xi}^{\ast } $$
(23)

(b) Let cr = cr(ξ∗) be the unique maximum value of (23), and ξ∗ is the unique simple root of the monotonic decreasing convex function:

$$ \psi \left(\xi \right)=-{\int}_a^{\xi}\left(\xi -x\right){\underset{\_}{\mu}}_{\tilde{A}}(x) dx-{\int}_{\xi}^b\left(\xi -x\right){\overline{\mu}}_{\tilde{A}}(x) dx $$
(24)

Furthermore, ξ∗ is the fixed point of cr(ξ) with ξ∗ = cr(ξ∗), so that

$$ {c}_r={c}_r\left({\xi}^{\ast}\right)={\xi}^{\ast } $$
(25)

2.5 Ranking methods for type-2 fuzzy sets

The ranking of type-2 fuzzy sets is another basic topic on the agenda of computing with type-2 fuzzy sets. Not surprising, there have been a number of different ranking methods. Wu and Mendel proposed the KM centroid ranking method, which is the common ranking method associated with low computation complexity (Wu and Mendel 2007a). Chen presented the signed-based distance ranking method in virtue of directed distance, i.e. signed distance (Chen 2012). Sang and Liu developed a new ranking method based on the possibilistic mean and variation coefficient, which is more effective in terms of comparing symmetric IT2FSs (Sang and Liu 2016). In what follows, we present the KM centroid ranking method and signed-based distance ranking method.

Definition 13

(Wu and Mendel 2007a) For given an IT2FS \( \tilde{A} \), we obtain the ranking value \( C\left(\tilde{A}\right) \) using the following expression:

$$ c\left(\tilde{A}\right)=\frac{c_l\left(\tilde{A}\right)+{c}_r\left(\tilde{A}\right)}{2} $$
(26)

For any two IT2FSs \( \tilde{A} \) and \( \tilde{B} \), we can employ the ranking value to compare them:

  1. 1)

    If \( c\left(\tilde{A}\right)>c\left(\tilde{B}\right) \), then\( \tilde{A}\succ \tilde{B} \);

  2. 2)

    If \( c\left(\tilde{A}\right)=c\left(\tilde{B}\right) \), then\( \tilde{A}\sim \tilde{B} \);

  3. 3)

    If \( c\left(\tilde{A}\right)<c\left(\tilde{B}\right) \), then\( \tilde{A}\prec \tilde{B} \).

Definition 14

(Chen 2012) Let \( \tilde{A} \) be a non-negative IT2FS defined on the universe of discourseXand \( \tilde{A}=\left[{A}^L,{A}^U\right]=\left[\left({a}_1^L,{a}_2^L,{a}_3^L,{a}_4^L;{h}_A^L\right),\left({a}_1^U,{a}_2^U,{a}_3^U,{a}_4^U;{h}_A^U\right)\right] \)(\( {h}_A^U\ne 0 \)), the signed distance from \( \tilde{A} \) to 0˜ is expressed as follows:

$$ d\left(\tilde{A},\tilde{0}\right)=\frac{1}{8}\left[{a}_1^L+{a}_2^L+{a}_3^L+{a}_4^L+\frac{2{h}_A^U+3{h}_A^L}{h_A^U}\left({a}_2^U+{a}_3^U\right)+\frac{4{h}_A^U-3{h}_A^L}{h_A^U}\left({a}_1^U+{a}_4^U\right)\right] $$
(27)

where 0˜ is a reference point map onto the y-axis at x = 0.

For any two IT2FSs \( \tilde{A} \) and \( \tilde{B} \), we have the following order relationship:

  1. 1)

    If \( d\left(A,\tilde{0}\right)>d\left(B,\tilde{0}\right) \), then \( \tilde{A} \) is better than or preferred to \( \tilde{B} \), denoted by\( \tilde{A}\succ \tilde{B} \);

  2. 2)

    If \( d\left(A,\tilde{0}\right)=d\left(B,\tilde{0}\right) \), then the preference relation between \( \tilde{A} \) and \( \tilde{B} \) is indifferent, denoted by\( \tilde{A}\sim \tilde{B} \);

  3. 3)

    \( d\left(A,\tilde{0}\right)<d\left(B,\tilde{0}\right) \), then \( \tilde{A} \) is worse than or less preferred to \( \tilde{B} \), denoted by\( \tilde{A}\prec \tilde{B} \).

Furthermore, the concept of ranking values of trapezoidal interval type-2 fuzzy sets is proposed by Lee and Chen as follows (Lee and Chen 2008):

Definition 15

(Lee and Chen 2008) Let \( {\tilde{\tilde{A}}}_i \) be an IT2FS, where \( {\tilde{\tilde{A}}}_i=\left[{\tilde{A}}_i^U,{\tilde{A}}_i^L\right]= \)\( \left[\left({a}_{i1}^U,{a}_{i2}^U,{a}_{i3}^U,{a}_{i4}^U;{H}_1\left({\tilde{A}}_i^U\right),{H}_2\left({\tilde{A}}_i^U\right)\right),\left({a}_{i1}^L,{a}_{i2}^L,{a}_{i3}^L,{a}_{i4}^L;{H}_1\left({\tilde{A}}_i^L\right),{H}_2\left({\tilde{A}}_i^L\right)\right)\right] \). The ranking value \( Rank\left({\tilde{\tilde{A}}}_i\right) \) of the TrIT2FS \( {\tilde{\tilde{A}}}_i \) is defined as follows:

$$ {\displaystyle \begin{array}{l} Rank\left({\tilde{\tilde{A}}}_i\right)={M}_1\left({\tilde{A}}_i^U\right)+{M}_1\left({\tilde{A}}_i^L\right)+{M}_2\left({\tilde{A}}_i^U\right)+{M}_2\left({\tilde{A}}_i^L\right)+{M}_3\left({\tilde{A}}_i^U\right)+{M}_3\left({\tilde{A}}_i^L\right)\\ {}\kern4.25em -\frac{1}{4}\Big({S}_1\left({\tilde{A}}_i^U\right)+{S}_1\left({\tilde{A}}_i^L\right)+{S}_2\left({\tilde{A}}_i^U\right)+{S}_2\left({\tilde{A}}_i^L\right)+{S}_3\left({\tilde{A}}_i^U\right)+{S}_3\left({\tilde{A}}_i^L\right)\\ {}\kern4.25em +{S}_4\left({\tilde{A}}_i^U\right)+{S}_4\left({\tilde{A}}_i^L\right)+{H}_1\left({\tilde{A}}_i^U\right)+{H}_1\left({\tilde{A}}_i^L\right)+{H}_2\left({\tilde{A}}_i^U\right)+{H}_2\left({\tilde{A}}_i^L\right)\Big)\end{array}} $$
(28)

where \( {M}_p\left({\tilde{A}}_i^j\right)=\left({a}_{ip}^j+{a}_{i\left(p+1\right)}^j\right)/2 \), 1 ≤ p ≤ 3; \( {S}_4\left({\tilde{A}}_i^j\right)=\sqrt{\frac{1}{4}{\sum}_{k=1}^4{\left({a}_{ik}^j-\frac{1}{4}{\sum}_{k=1}^4{a}_{ik}^j\right)}^2} \), \( {H}_p\left({\tilde{A}}_i^j\right) \) denotes the membership value of \( {a}_{i\left(p+1\right)}^j \) in the trapezoidal membership function \( {\tilde{A}}_i^j \), 1 ≤ p ≤ 2, j ∈ {U, L}, and 1 ≤ i ≤ n.

In Eq. (28), the sum of \( {M}_1\left({\tilde{A}}_i^U\right),{M}_1\left({\tilde{A}}_i^L\right),{M}_2\left({\tilde{A}}_i^U\right),{M}_2\left({\tilde{A}}_i^L\right),{M}_3\left({\tilde{A}}_i^U\right),{M}_3\left({\tilde{A}}_i^L\right), \)\( {H}_1\left({\tilde{A}}_i^U\right),{H}_1\left({\tilde{A}}_i^L\right),{H}_2\left({\tilde{A}}_i^U\right),{H}_2\left({\tilde{A}}_i^L\right) \)represent the basic ranking score, where we deduct the average of \( {S}_1\left({\tilde{A}}_i^U\right),{S}_1\left({\tilde{A}}_i^L\right),{S}_2\left({\tilde{A}}_i^U\right),{S}_2\left({\tilde{A}}_i^L\right),{S}_3\left({\tilde{A}}_i^U\right),{S}_3\left({\tilde{A}}_i^L\right),{S}_4\left({\tilde{A}}_i^U\right), \)\( {S}_4\left({\tilde{A}}_i^L\right) \) from the basic ranking score to give the dispersive IT2FS a penalty, where 1 ≤ i ≤ n.

3 Type-2 fuzzy information aggregation

In this section, we review some basic type-2 fuzzy information aggregation operators, such as interval type-2 FWA, interval type-2 fuzzy OWA, interval type-2 fuzzy BM, interval type-2 fuzzy MSM and interval type-2 fuzzy HM, respectively.

3.1 Interval type-2 fuzzy FWA

The fuzzy weighted average (FWA) has great influence on the type-2 fuzzy logic theory and multi-criteria decision making (Wu and Mendel 2007a; Liu et al. 2012; Liu and Wang 2013). Therefore, it is significant to have a grasp of the FWA.

Definition 16

(Dong and Wong 1987) For given fuzzy numbers Xi and Wi, the FWA is expressed as follows:

$$ {Y}_{LWA}=\frac{\sum_{i=1}^n{X}_i{W}_i}{\sum_{i=1}^n{W}_i} $$
(29)

The computation methods for obtaining FWA were investigated by many scholars, which mainly include Dong and Wong’s algorithm based on α-cuts and an α-cut decomposition theorem (Dong and Wong 1987). In order to reduce the computational complexity, Liou and Wang proposed the improved FWA (IFWA) algorithm (Liou and Wang 1992). Lee and Park presented the efficient FWA (EFWA) algorithm to decrease the numbers of iterations (Lee and Park 1997). In addition, some literature focuses on Karnik Mendel (KM) algorithm and its extension, such as (Liu and Mendel 2008; Wu and Mendel 2009). In terms of analytical solution for the FWA, Kao and Liu (Kao and Liu 2001), Liu et al. (Liu et al. 2012) and Liu and Wang (Liu and Wang 2013) express their individual opinions, which have good structure and simple computation. In order to exploit the advantages of computing with words, Wu and Mendel proposed the LWA based on IT2FSs, which is an extension of the FWA (Wu and Mendel 2007b).

Definition 17

(Wu and Mendel 2007b) For given two IT2FSs \( {\tilde{X}}_i \) and \( {\tilde{W}}_i \), the LWA is defined as follows:

$$ {\tilde{Y}}_{LWA}=\frac{\sum_{i=1}^n{\tilde{X}}_i{\tilde{W}}_i}{\sum_{i=1}^n{\tilde{W}}_i} $$
(30)

It is noteworthy that the aggregation result \( {\tilde{Y}}_{LWA} \) is an IT2FS, which can be computed using the LMF \( {\underset{\_}{Y}}_{LWA} \) and UMF \( {\overline{Y}}_{LWA} \).

$$ {\underset{\_}{Y}}_{LWA}=\underset{\forall {W}_i\in \left[{\underset{\_}{W}}_i,{\overline{W}}_i\right]}{\min}\frac{\sum_{i=1}^n{\underset{\_}{X}}_i{W}_i}{\sum_{i=1}^n{W}_i} $$
(31)
$$ {\overline{Y}}_{LWA}=\underset{\forall {W}_i\in \left[{\underset{\_}{W}}_i,{\overline{W}}_i\right]}{\max}\frac{\sum_{i=1}^n{\overline{X}}_i{W}_i}{\sum_{i=1}^n{W}_i} $$
(32)

In order to obtain the \( {\underset{\_}{Y}}_{LWA} \) and \( {\overline{Y}}_{LWA} \), we can adopt the α-cut based approach. The detail can refer to (Wu and Mendel 2007b; John et al. 2018).

3.2 Interval type-2 fuzzy OWA

Type-2 fuzzy sets provide an effective way to model uncertain information and experts’ preferences in soft decision making. And OWA operator is a kind of effective and applicable operator (Yager et al. 2011). The motivation for the type-2 OWA operator is suggested to aggregate linguistic variables modeled as type-2 fuzzy sets by the OWA mechanism.

Definition 18

(Zhou et al. 2008) Given IT2FSs \( {\left\{{\tilde{W}}_i\right\}}_{i=1}^n \) and \( {\left\{{\tilde{X}}_i\right\}}_{i=1}^n \), the membership function of an interval type-2 fuzzy ordered weighted averaging (IT2FOWA) is computed by:

$$ {\mu}_{{\tilde{Y}}_{IT2 FOWA}}(y)=\underset{\forall {W}_i^e,{X}_i^e}{\cup}\left[\underset{y=\frac{\sum_{i=1}^n{w}_i{x}_{\sigma (i)}}{\sum_{i=1}^n{w}_i}}{\sup}\min \left({\mu}_{W_1^e}\left({w}_1\right),\cdots, {\mu}_{W_n^e}\left({w}_n\right),{\mu}_{X_1^e}\left({w}_1\right),\cdots, {\mu}_{X_n^e}\left({w}_n\right)\right)\right] $$
(33)

where \( {W}_i^e \) and \( {X}_i^e \) are embedded T1FSs of \( {\tilde{W}}_i \) and \( {\tilde{X}}_i \), respectively, and σ: {1,…, n} → {1,…, n} is a permutation function such that {xσ(1), xσ(2), ⋯, xσ(n)}are in descending order.

Observe that the bracketed term is a T1FOWA, and the IT2FOWA is the union of all possible T1FOWAs calculated from the embedded T1FSs of \( {\tilde{X}}_i \) and \( {\tilde{W}}_i \). The Wavy Slice Representation Theorem (Mendel 2008) for IT2FSs is implicitly used in this definition.

3.3 Interval type-2 fuzzy Bonferroni mean

When the decision information is relevant, the BM can deal with this problem and has the good flexibility. Therefore, Gong et al. (Gong et al. 2015). proposed the TIT2FGBM operator and the TIT2FWGBM operator.

Definition 19

(Gong et al. 2015) For given a collection of trapezoidal interval type-2 fuzzy numbers (IT2FNs) \( {\tilde{A}}_i=\left({\tilde{A}}_i^U,{\tilde{A}}_i^L\right)=\left(\left({a}_{i1}^U,{a}_{i2}^U,{a}_{i3}^U,{a}_{i4}^U\right),\left({a}_{i1}^L,{a}_{i2}^L,{a}_{i3}^L,{a}_{i4}^L\right)\right)\left(i=1,2,\cdots, n\right) \) and the parameter p, q ≥ 0, the TIT2FGBM is defined as follows:

$$ TIT2 FGB{M}^{p,q}\left({\tilde{A}}_1,{\tilde{A}}_2,\cdots, {\tilde{A}}_n\right)=\frac{1}{p+q}{\left(\underset{\begin{array}{l}i,j=1\\ {}\;i\ne j\end{array}}{\overset{n}{\otimes }}\left(p{\tilde{A}}_i\oplus q{\tilde{A}}_j\right)\right)}^{1/n\left(n-1\right)} $$
(34)

The TIT2FGBM can be employed to aggregate the IT2FNs the result is also an IT2FN. This operator maintains the properties of idempotency, boundedness, monotonicity and commutativity. When p and q are equal to 1, the TIT2FGBM can be reduced to trapezoidal interval type-2 fuzzy interrelated square geometric mean operator. In consideration of different weight of aggregated information, the TIT2FWGBM is presented.

Based on the above definition, we have:

$$ TIT2 FGB{M}^{p,q}\left({\tilde{A}}_1,{\tilde{A}}_2,\cdots, {\tilde{A}}_n\right)=\tilde{A}=\left({\tilde{A}}^U,{\tilde{A}}^L\right) $$

where

$$ {\displaystyle \begin{array}{l}{\tilde{A}}^U=\Big(\frac{1}{p+q}{\left(\prod \limits_{\begin{array}{l}i,j=1\\ {}i\ne j\end{array}}^n\left(p{a}_{i1}^U+q{a}_{j1}^U\right)\right)}^{\frac{1}{n\left(n-1\right)}},\frac{1}{p+q}{\left(\prod \limits_{\begin{array}{l}i,j=1\\ {}i\ne j\end{array}}^n\left(p{a}_{i2}^U+q{a}_{j2}^U\right)\right)}^{\frac{1}{n\left(n-1\right)}},\\ {}\kern2.25em \frac{1}{p+q}{\left(\prod \limits_{\begin{array}{l}i,j=1\\ {}i\ne j\end{array}}^n\left(p{a}_{i3}^U+q{a}_{j3}^U\right)\right)}^{\frac{1}{n\left(n-1\right)}},\frac{1}{p+q}{\left(\prod \limits_{\begin{array}{l}i,j=1\\ {}i\ne j\end{array}}^n\left(p{a}_{i4}^U+q{a}_{j4}^U\right)\right)}^{\frac{1}{n\left(n-1\right)}};\underset{i=1,\cdots, n}{\min}\left\{{h}_i^U\right\}\Big)\end{array}} $$
(35)

and

$$ {\displaystyle \begin{array}{l}{\tilde{A}}^L=\Big(\frac{1}{p+q}{\left(\prod \limits_{\begin{array}{l}i,j=1\\ {}i\ne j\end{array}}^n\left(p{a}_{i1}^L+q{a}_{j1}^L\right)\right)}^{\frac{1}{n\left(n-1\right)}},\frac{1}{p+q}{\left(\prod \limits_{\begin{array}{l}i,j=1\\ {}i\ne j\end{array}}^n\left(p{a}_{i2}^L+q{a}_{j2}^L\right)\right)}^{\frac{1}{n\left(n-1\right)}},\\ {}\kern2.25em \frac{1}{p+q}{\left(\prod \limits_{\begin{array}{l}i,j=1\\ {}i\ne j\end{array}}^n\left(p{a}_{i3}^L+q{a}_{j3}^L\right)\right)}^{\frac{1}{n\left(n-1\right)}},\frac{1}{p+q}{\left(\prod \limits_{\begin{array}{l}i,j=1\\ {}i\ne j\end{array}}^n\left(p{a}_{i4}^L+q{a}_{j4}^L\right)\right)}^{\frac{1}{n\left(n-1\right)}};\underset{i=1,\cdots, n}{\min}\left\{{h}_i^L\right\}\Big)\end{array}} $$
(36)

Definition 20

(Gong et al. 2015) For given a collection of IT2FNs \( {\tilde{A}}_i=\left({\tilde{A}}_i^U,{\tilde{A}}_i^L\right)=\left(\left({a}_{i1}^U,{a}_{i2}^U,{a}_{i3}^U,{a}_{i4}^U\right),\left({a}_{i1}^L,{a}_{i2}^L,{a}_{i3}^L,{a}_{i4}^L\right)\right)\left(i=1,2,\cdots, n\right) \) with corresponding weight vector w = (w1, w2, ⋯, wn)T, where wi ∈ [0, 1] and \( {\sum}_{i=1}^n{w}_i=1 \) should be satisfied, andp, q ≥ 0, the TIT2FWGBM can be described as follows:

$$ TIT2 FWGB{M}^{p,q}\left({\tilde{A}}_1,{\tilde{A}}_2,\cdots, {\tilde{A}}_n\right)=\frac{1}{p+q}{\left(\underset{\begin{array}{l}i,j=1\\ {}\;i\ne j\end{array}}{\overset{n}{\otimes }}\left(p{\left({\tilde{A}}_i\right)}^{w_i}\oplus q{\left({\tilde{A}}_j\right)}^{w_j}\right)\right)}^{1/n\left(n-1\right)} $$
(37)

Similarly, we can obtain the same properties as TIT2FGBM, for the detail referring to (Gong et al. 2015).

3.4 Interval type-2 fuzzy Maclaurin symmetric mean

The Maclaurin symmetric mean (MSM) is a classical generalized symmetric mean that is an extended Bonferroni mean. It can aggregate multiple related elements and overcome the shortcomings of the relationship between each two elements in Bonferroni mean (Xu and Yager 2011; Zhu and Xu 2013; Zhu et al. 2012), which can solve the problem of related information aggregation to some extent.

The definition of the interval type-2 fuzzy Maclaurin symmetric mean (IT2FMSM) is as follows:

Definition 21

Let \( {A}_i=\left({A}_i^U,{A}_i^L\right)=\left(\left({a}_{i1}^U,{a}_{i2}^U,{a}_{i3}^U,{a}_{i4}^U;{h}_i^U\right),\left({a}_{i1}^L,{a}_{i2}^L,{a}_{i3}^L,{a}_{i4}^L;{h}_i^L\right)\right)\left(i=1,2,\cdots, n\right) \) be a collection of interval type-2 fuzzy set, and k = 1, 2, ⋯, n, then the IT2FMSM can be defined as

$$ \mathrm{IT}2{\mathrm{FMSM}}^{(k)}\left({A}_1,{A}_2,\cdots, {A}_n\right)={\left(\frac{1}{C_n^k}\underset{1\le {i}_1<\cdots <{i}_k\le n}{\oplus}\underset{j=1}{\overset{k}{\otimes }}{A}_{i_j}\right)}^{\frac{1}{k}} $$
(38)

Based on the above definition, we have

$$ \mathrm{IT}2{\mathrm{FMSM}}^{(k)}\left({A}_1,{A}_2,\cdots, {A}_n\right)=A=\left({A}^U,{A}^L\right) $$
(39)

where

$$ {\displaystyle \begin{array}{l}{A}^U=\Big({\left(\frac{1}{C_n^k}\sum \limits_{1\le {i}_1<\cdots <{i}_k\le n}\prod \limits_{j=1}^k{a}_{i{1}_j}^U\right)}^{\frac{1}{k}},{\left(\frac{1}{C_n^k}\sum \limits_{1\le {i}_1<\cdots <{i}_k\le n}\prod \limits_{j=1}^k{a}_{i{2}_j}^U\right)}^{\frac{1}{k}},\\ {}{\left(\frac{1}{C_n^k}\sum \limits_{1\le {i}_1<\cdots <{i}_k\le n}\prod \limits_{j=1}^k{a}_{i{3}_j}^U\right)}^{\frac{1}{k}},{\left(\frac{1}{C_n^k}\sum \limits_{1\le {i}_1<\cdots <{i}_k\le n}\prod \limits_{j=1}^k{a}_{i{4}_j}^U\right)}^{\frac{1}{k}};\underset{i=1,2,\cdots, n}{\min}\left\{{h}_i^U\right\}\Big)\end{array}} $$
(40)

and

$$ {\displaystyle \begin{array}{l}{A}^L=\Big({\left(\frac{1}{C_n^k}\sum \limits_{1\le {i}_1<\cdots <{i}_k\le n}\prod \limits_{j=1}^k{a}_{i{1}_j}^L\right)}^{\frac{1}{k}},{\left(\frac{1}{C_n^k}\sum \limits_{1\le {i}_1<\cdots <{i}_k\le n}\prod \limits_{j=1}^k{a}_{i{2}_j}^L\right)}^{\frac{1}{k}},\\ {}{\left(\frac{1}{C_n^k}\sum \limits_{1\le {i}_1<\cdots <{i}_k\le n}\prod \limits_{j=1}^k{a}_{i{3}_j}^L\right)}^{\frac{1}{k}},{\left(\frac{1}{C_n^k}\sum \limits_{1\le {i}_1<\cdots <{i}_k\le n}\prod \limits_{j=1}^k{a}_{i{4}_j}^L\right)}^{\frac{1}{k}};\underset{i=1,2,\cdots, n}{\min}\left\{{h}_i^L\right\}\Big)\end{array}} $$
(41)

In the process of information aggregation, we usually need to consider the importance of every element, i.e. weight information. Therefore, we give the definition of weighted interval type-2 fuzzy Maclaurin symmetric mean (WIT2FMSM).

Definition 22

Let Ai(i = 1, 2, ⋯, n) be a collection of type-2 fuzzy number, w = (w1, w2, ⋯, wn)T represents the weight vector, where wi is the importance of Ai satisfying wi ∈ [0, 1] and \( {\sum}_{i=1}^n{w}_i=1 \). If

$$ \mathrm{WIT}2{\mathrm{FMSM}}_w^{(k)}\left({A}_1,{A}_2,\cdots, {A}_n\right)=\Big\{{\displaystyle \begin{array}{l}\frac{\underset{1\le {i}_1<\cdots <{i}_k\le n}{\oplus}\left(1-{\sum}_{j=1}^k{w}_{i_j}\right)\underset{j=1}{\overset{k}{\otimes }}{A}_{i_j}}{C_{n-1}^k}\kern0.24em \left(1\le k<n\right)\\ {}\underset{i=1}{\overset{k}{\otimes }}{A}_i^{\frac{1-{w}_i}{n-1}}\kern4.079998em k=n\end{array}} $$
(42)

\( \mathrm{WIT}2{\mathrm{FMSM}}_w^{(k)} \) is an interval weighted type-2 fuzzy Maclaurin symmetric mean. Obviously, when w = (1/n, 1/n, ⋯, 1/n)T, WIT2FMSM is reduced to the IT2FMSM.

It should be noted that the WIT2FMSM satisfies the idempotency property when the function of WIT2FMSM is represented by using piecewise function, which is remarkable feature difference between WIT2FMSM and other operators.

3.5 Type-2 fuzzy fuzzy Hamy mean

In order to represent the interrelationship among integrated information, Qin proposed the interval type-2 fuzzy HM, which is comprised of STIT2FHM operator and WSTIT2FHM operator (Qin 2017). Compared with interval type-2 FWA and interval type-2 fuzzy BM, the computing complexity of interval type-2 fuzzy HM is lower than the complexity of these two operators.

Definition 23

(Qin 2017) For given a collection of symmetric triangular interval type-2 fuzzy numbers (STIT2FNs) \( {\tilde{A}}_i=\left({c}_{{\tilde{A}}_i},{\delta}_{{\tilde{A}}_i},{\underset{\_}{h}}_{{\tilde{A}}_i},{\overline{h}}_{{\tilde{A}}_i}\right)\left(i=1,2,\cdots, n\right) \) and parameter k = 1, 2, ⋯, n, the STIT2FHM can be represented as follows:

$$ \mathrm{STIT}2{\mathrm{HM}}^{(k)}\left({\tilde{A}}_1,{\tilde{A}}_2,\cdots, {\tilde{A}}_n\right)=\frac{\oplus_{1\le {i}_1<\cdots <{i}_k\le n}{\left({\otimes}_j^k{\tilde{A}}_{i_j}\right)}^{\frac{1}{k}}}{\left(\begin{array}{l}n\\ {}k\end{array}\right)} $$
(43)

The aggregation result is still a STIT2FN by using STIT2FHM, and the STIT2FHM satisfies the properties of idempotency, commutativity and monotonicity. For the details, the reader can refer to (Qin 2017). With regard to different values of the parameter k, the STIT2FHM is called as different operators, such as k = 1 named symmetric triangular interval type-2 fuzzy averaging (STIT2FA) operator and k = n named symmetric triangular interval type-2 fuzzy geometric (STIT2FG) operator. Considering that the weight of information has a significant influence for aggregation, Qin defined the WSTIT2FHM operator (Qin 2017).

Definition 24

(Qin 2017) For given a collection of STIT2FNs \( {\tilde{A}}_i\left(i=1,2,\cdots, n\right) \) associated with the corresponding weight vector w = (w1, w2, ⋯, wn)T, where the relationships wi ∈ [0, 1] and \( {\sum}_{i=1}^n{w}_i=1 \) hold, the WSTIT2FHM is defined as follows:

$$ {\displaystyle \begin{array}{l}\mathrm{WSTIT}2{\mathrm{FHM}}_w^{(k)}\left({\tilde{A}}_1,{\tilde{A}}_2,\cdots, {\tilde{A}}_n\right)=\Big\{\begin{array}{l}\frac{\oplus_{1\le {i}_1<\cdots <{i}_k\le n}\left(1-{\sum}_{j=1}^k{w}_{i_j}\right){\left({\otimes}_{j=1}^k{\tilde{A}}_{i_j}\right)}^{\frac{1}{k}}}{\left(\begin{array}{l}n-1\\ {}k\end{array}\right)}\;\left(1\le k<n\right)\\ {}\underset{j=1}{\overset{k}{\otimes }}{\tilde{A}}_j^{\frac{1-{w}_j}{n-1}}\kern0.24em \left(k=n\right)\end{array}\\ {}\end{array}} $$
(44)

Similarly, the aggregation consequence is still a STIT2FN by using WSTIT2FHM operator. The relationship between STIT2FHM and WSTIT2FHM is that the WSTIT2FHM is a special case of STIT2FHM.

It is noteworthy that the most significant difference between type-2 MSM operator and type-2 HM operator lies in the emphasized element. The former stresses the importance of the whole element, but the later pays attention to the importance of each element.

3.6 Type-2 fuzzy Choquet integral and Sugeno integral

As another research direction in aggregation operators, fuzzy measures and fuzzy integrals have been extended into different environments, which can capture the interaction among provided information and uncertainty present in the information sources. The fuzzy integrals of interest are Choquet integral and Sugeno integral. Next, we introduce type-2 fuzzy Choquet integral and Sugeno integral aggregation operators.

Definition 25

(Havens et al. 2010). Based on the idea, i.e. Choquet integral with an IT2FN-valued integrand \( \tilde{H} \) producing an IT2FN, the FOU of \( {C}_g\left(\tilde{H}\right) \) as the union of all \( {C}_g\left({H}_e^j\right) \) can be defined as follows:

$$ FOU\left({C}_g\left(\tilde{H}\right)\right)=\underset{j}{\cup }{C}_g\left({H}_e^j\right) $$
(45)

where \( {H}_e^j\in FOU\left(\tilde{H}\left({x}_i\right)\right), for\forall i,j \) is embedded T1FN-valued functions. Then we obtain

$$ {C}_g\left(\tilde{H}\right)=1/ FOU\left({C}_g\left(\tilde{H}\right)\right) $$
(46)

The type-2 fuzzy Choquet integral satisfies the proposition that the UMF and LMF of \( FOU\left({C}_g\left(\tilde{H}\right)\right) \) can be derived by the Choquet integral on the individual functions on UMFs and LMFs of the set \( \tilde{H} \). The other proposition is that level-cut \( {}^{\alpha}\left({\cup}_j{C}_g\left({H}_e^j\right)\right) \) consists of two closed intervals between theUMF and LMF of \( FOU\left({C}_g\left(\tilde{H}\right)\right) \).

Definition 26

(Bustince et al. 2013). For given information source set X associated with its fuzzy measure μc, a IT2FS [μL, μR] defined on X, the interval type-2 Sugeno integral for μc is defined as follows:

$$ {\displaystyle \begin{array}{l}\tilde{h}\left({\sigma}_1,{\sigma}_2,\cdots, {\sigma}_n\right)\\ {}=\left[{h}_L,{h}_R\right]\\ {}={\cup}_{i=1}^n\left(\cap \left(\left[{\sigma}_L\left({x}_i\right),{\sigma}_R\left({x}_i\right)\right],\left[{\mu}_L\left({A}_i\right),{\mu}_R\left({A}_i\right)\right]\right)\right)\end{array}} $$
(47)

where 0 ≤ σL(xi) ≤ σL(xi + 1) ≤ ⋯ ≤ σL(xn) ≤ 1 and 0 ≤ σR(xi) ≤ σR(xi + 1) ≤ ⋯ ≤ σR(xn) ≤ 1.

4 Applications of type-2 fuzzy aggregation operations

As a flexible tool in representing human qualitative and subjective cognitive aspects, the aggregation operations have gained success in practical applications. Table 4 lists the recent applications of these operations.

Table 4 Applications of type-2 fuzzy aggregation operations
Full size table

From Table 4, we can see that many type-2 fuzzy aggregation operations have been implemented addressing various aspects of management in our daily life. Especially, this concerns supplier selection and investment management. For example, the TIT2FHA, TIT2FGBM, TIT2FWGBM, TIT2FFWA, TIT2FFWG and IT2FWA operators have been applied to supplier selection problem. The IT2PA, IT2DOWA, TIT2OWA, TITHWA WIFMSM operators are widely used in investment management. The OWA, CWGA, STIT2FHM, 2DIT2TFOWA, LWA operators were applied to employment and hiring management, tourism recommender system and others. It seems that numerous evaluation problems with qualitative assessment information can be solved by the fuzzy decision-making approaches. With the promotion and development of the research in type-2 fuzzy aggregation operations, more and more practical problems could be solved by this comprehensively qualitative tool.

Compared with application of type-2 fuzzy multiple criteria decision making, the application range of type-2 fuzzy aggregation operations is somewhat narrow. Considering the application of type-2 fuzzy multiple criteria decision making, we should extend type-2 fuzzy aggregation operations into these MCDM fields, such as green supplier selection (Qin et al. 2015), human resource management (Abdullah and Zulkifli 2015), clustering (Yang and Lin 2009) and medical diagnosis (Own 2009). In general, these type-2 fuzzy aggregation operations are directly applied to group decision making, which do not pay attention to combining with other multiple criteria decision making methods or ranking methods. Therefore, we can exploit the advantages of type-2 fuzzy aggregation operations and multiple criteria decision making methods or ranking methods to make decision.

5 Summary and future research directions

Type-2 fuzzy sets exhibit merits in terms of describing higher degree of ambiguity and uncertainty. In this paper, we review type-2 fuzzy information aggregation operators and some applications to multiple criteria decision making. We have summarized some essential fundamentals of type-2 fuzzy sets and information aggregation function. The former is comprised of the definitions, operations, type reduction and ranking methods, and the later includes the characteristics, categories and properties of information aggregation function. Next, some representative type-2 fuzzy information aggregation operators have been reviewed, such as interval type-2 fuzzy FWA, interval type-2 fuzzy OWA, interval type-2 fuzzy BM, interval type-2 fuzzy MSM, interval type-2 fuzzy HM along with its extensions and properties.

The existing research have developed some different type-2 fuzzy operators, which have been applied to many fields such as supplier selection, investment management and recommender systems. The existing challenges and future research directions are summarized as follows:

  1. (1)

    The existing research focus on the aggregation operations of IT2FSs, but the general T2FSs has been paid little attention. The zSlices method is adopted to deal with the general T2FSs (Wagner and Hagras 2008; Wagner and Hagras 2010; Bilgin et al. 2013; Kumbasar and Hagras 2015). However, the research on information aggregation operators of general T2FSs still constitutes a big challenge. In addition, one can develop and propose some interaction information aggregations which can integrate the Choquet integral into the process of information aggregation. It will be a better information fusion in multiple criteria decision making.

  2. (2)

    Owing to the accuracy and lower computation complexity, Liu et al. presented the analytical method to compute the FWA (Liu et al. 2012). But there are no the analytical solutions of IT2FSs aggregation. Therefore, this is a noteworthy direction for the information aggregation in the context of IT2FSs. If the interaction information were proposed, we could present analytical solutions of these operators.

  3. (3)

    The existing aggregation operators on T2FSs do not consider the problem of data driven. In order to aggregate objectively information, some IT2FSs aggregation operators based on data driven should be developed. For instance, we should pay attention the integration the information aggregation and granular computing (Pedrycz and Song 2012; Yao et al. 2013; Cabrerizo et al. 2013). We can establish the optimization model to maximize the product of coverage and specificity to obtain the consequence of information aggregation.

  4. (4)

    Type-2 fuzzy information aggregation involves complex uncertain information, as a powerful tool for dealing with uncertain optimization, robust optimization should be paid more attention (Ben 1998). In the future, the theory about linear, non-linear, distributionally robust optimization, and robust optimal regression should be applied to type-2 fuzzy information aggregation to obtain the analytical solution associated with good analytical properties, which can further enrich and improve the type-2 fuzzy information aggregation theory. Other open questions and potential research directions in type-2 fuzzy aggregation area are worthy to be discussed in future research.