Keywords

1 Introduction

Multi-attribute decision-making (MADM) based on fuzzy information is an interesting and promising research topic, which has received much attention in the past decades. When considering fuzzy information based MADM methods, some researchers have focused on the issue of how decision makers’ complicated and uncertain decision-making information can be effectively depicted. As an extension of intuitionistic fuzzy set [1], Pythagorean fuzzy set (PFSs) [2], originated by Dr. Yager, has been proved to be effective in depicting decision makers’ fuzzy information [3]. Later on, Dr. Garg [4] extended PFSs and proposed the linguistic Pythagorean fuzzy sets (LPFSs), which use linguistic term to denote the membership and non-membership degrees. Compared to the linguistic intuitionistic fuzzy sets [5], LPFs can denote more complicated fuzzy decision-making information. Soon after its appearance, MADM based on LPFSs has been a hot research topic. Liu et al. [6] investigated aggregation operators (AOs) and decision-making methods under LPFSs based on t-norm and t-conorm. Lin et al. [7] introduced interaction operations for LPFSs and based on which a novel partitioned Bonferroni mean was developed for LPFSs. Xu et al. [8] generalized LPFSs into cubic LPFSs and under which a power Hamy mean based decision-making method was presented. Sarkar and Biswas [9] investigated novel MADM method in LPFSs under Einstein t-norm and t-conorm.

LPFS is a powerful tool in MADM, however, its disadvantage is still obvious. The constraint of LPFS is that the square sum of the scripts of linguistic membership and non-membership degrees should not exceeds the pre-defined linguistic term set. As a matter of fact, this constraint cannot be always satisfied in actual decision-making situations, which motivates us to investigate novel fuzzy information representation tool. The Fermatean fuzzy set (FFS) [10], originated by Yager, is with the constraint that the cubic sum of membership and non-membership degrees is less than or equal to one. Obviously, compared with PFSs, FFSs have larger information space and can depict more complicated decision-making information. Hence, FFSs have been widely applied in solving realistic MADM problems [11,12,13]. The powerfulness of FFS motivates us to investigate its extension to accommodate more complicated decision-making environment. Just like extending PFSs to LPFs, this paper extends FFSs to linguistic Fermatean fuzzy sets (LFFSs), which satisfy the condition that the cubic sum of script of linguistic membership and non-membership degrees should be less than or equal to the pre-predefined linguistic term set. Hence, LFFS is more powerful and flexible than LPF. In the paper, we further study properties and AOs of LFFSs. Afterward, we use LFFS to propose a new MADM method.

The rest of this paper is organized as follows. Section 2 reviews some basic concepts that will be used in the following sections. Section 3 proposes the concept of LFFSs and investigate their desirable properties. Section 4 presents some AOs for linguistic Fermatean fuzzy information and discuss their properties. A novel MADM method is presented in Sect. 5. An illustrative example is provided in Sect. 6.

2 Basic Notions

2.1 Fermetean Fuzzy Sets

Definition 1 [10]. Let X be a given fixed set, then a Fermatean fuzzy set (FFS) defined on X is expressed as.

$$F=\left\{\langle x,{\alpha }_{F}\left(x\right),{\beta }_{F}\left(x\right)\rangle |x\in X\right\},$$
(1)

where \({\alpha }_{F}\left(x\right)\) and \({\beta }_{F}\left(x\right)\) denote the membership and non-membership degrees of element \(x\in X\) to the set F, such that \(0\le {\alpha }_{F}\left(x\right),{\beta }_{F}\left(x\right)\le 1\) and \(0{\le \left({\alpha }_{F}\left(x\right)\right)}^{3}+{\left({\beta }_{F}\left(x\right)\right)}^{3}\le 1\). For convenience, the ordered pair \(f=\left(\alpha ,\beta \right)\) is called a Fermatean fuzzy number (FFN).

Basic operational rules for FFNs are presented as follows.

Definition 2 [10].

Let \(f=\left(\alpha ,\beta \right)\), \({f}_{1}=\left({\alpha }_{1},{\beta }_{1}\right)\), and \({f}_{2}=\left({\alpha }_{2},{\beta }_{2}\right)\) be any three FFNs, and \(\lambda\) be a positive real number, then.

  1. (1)

    \({f}_{1}\oplus {f}_{2}=\left({\left({\alpha }_{1}^{3}+{\alpha }_{2}^{3}-{\alpha }_{1}^{3}{\alpha }_{2}^{3}\right)}^{1/3},{\beta }_{1}{\beta }_{2}\right)\);

  2. (2)

    \({f}_{1}\otimes {f}_{2}=\left({\alpha }_{1}{\alpha }_{2},{\left({\beta }_{1}^{3}+{\beta }_{2}^{3}-{\beta }_{1}^{3}{\beta }_{2}^{3}\right)}^{1/3}\right)\);

  3. (3)

    \(\lambda f=\left({\left(1-{\left(1-{\alpha }^{3}\right)}^{\lambda }\right)}^{1/3},{\beta }^{\lambda }\right)\);

  4. (4)

    \({f}^{\lambda }=\left({\alpha }^{\lambda },{\left(1-{\left(1-{\beta }^{3}\right)}^{\lambda }\right)}^{1/3}\right);\)

2.2 Power Average Operator

Definition 3 [14]. Let \({x}_{i}\left(i=\mathrm{1,2},\dots ,n\right)\) be a collection of positive real numbers, then the power average operator is defined as.

$$PA\left({x}_{1},{x}_{2},\dots ,{x}_{n}\right)=\frac{{\sum }_{i=1}^{n}\left(1+T\left({x}_{i}\right)\right){x}_{i}}{{\sum }_{i=1}^{n}\left(1+T\left({x}_{i}\right)\right)},$$
(2)

where \(T\left({x}_{i}\right)={\sum }_{j=1;j\ne i}^{n}Sup\left({x}_{i},{x}_{j}\right)\) and \(Sup\left({x}_{i},{x}_{j}\right)\) denotes the support degree for \({x}_{i}\) from \({x}_{j}\), satisfying the following properties:

  1. (1)

    \(Sup\left({x}_{i},{x}_{j}\right)\in \left[\mathrm{0,1}\right]\);

  2. (2)

    \(Sup\left({x}_{i},{x}_{j}\right)=Sup\left({x}_{j},{x}_{i}\right)\);

  3. (3)

    \(Sup\left({x}_{i},{x}_{j}\right)\ge Sup\left({x}_{m},{x}_{n}\right)\) if and only if \(\left|{x}_{i}-{x}_{j}\right|\le \left|{x}_{m}-{x}_{n}\right|\)

3 Linghuistic Fermatean Fuzzy Sets and Their Properties

In this section, the definition of LFSs and their properties. First of all, the definition of LFS are presented. Then, some other notions, such as operational rules, distance measure, comparison method, etc.

3.1 Definition of Linghuistic Fermatean Fuzzy Sets

Definition 4. Let X be a given fixed set and \(\tilde{S }=\left\{{s}_{\alpha }|0\le \alpha \le l\right\}\) be a continuous linguistic term set with odd cardinality. A LFFS A definition on X is expressed as.

$$A=\left\{\left(x,{s}_{a}\left(x\right),{s}_{b}\left(x\right)\right)|x\in X\right\},$$
(3)

where \({s}_{a}\left(x\right),{s}_{b}\left(x\right)\in \tilde{S }\) denote the linguistic membership and non-membership degree of the element x to the set A, respectively, such that \({a}^{3}+{b}^{3}\le {l}^{3}\). The linguistic hesitant degree of x to A is expressed as \(\pi ={s}_{\sqrt[3]{{l}^{3}-{a}^{3}-{b}^{3}}}\). The ordered pair \(\gamma =\left({s}_{a},{s}_{b}\right)\) is called a LFFN.

Remark 1.

It is noted from Definition 4 that all LIFSs and LPFSs are LFFSs. In other words, LIFSs and LPFSs are two special cases of LFFSs.

3.2 Operational Rules of Linguistic Fermatean Fuzzy Numbers

Based on the operational of FFNs and considering the basic operations of LIFNs and LPVs, the operational rules for LFFNs are proposed as follows.

Definition 5.

Let \({\gamma }_{1}=\left({s}_{{a}_{1}},{s}_{{b}_{1}}\right)\), \({\gamma }_{2}=\left({s}_{{a}_{2}},{s}_{{b}_{2}}\right)\) and \(\gamma =\left({s}_{a},{s}_{b}\right)\) be any three LFFNs defined on a continuous linguistic term set \(\tilde{S }=\left\{{s}_{\alpha }|0\le \alpha \le l\right\}\), and \(\xi\) be a positive real number, then.

  1. (1)

    \({\gamma }_{1}\oplus {\gamma }_{2}=\left({s}_{{\left({a}_{1}^{3}+{a}_{2}^{3}-{a}_{1}^{3}{a}_{2}^{3}/{l}^{3}\right)}^{1/3}},{s}_{{b}_{1}{b}_{2}/l}\right);\)

  2. (2)

    \({\gamma }_{1}\otimes {\gamma }_{2}=\left({s}_{{a}_{1}{a}_{2}/l},{s}_{{\left({b}_{1}^{3}+{b}_{2}^{3}-{b}_{1}^{3}{b}_{2}^{3}/{l}^{3}\right)}^{1/3}}\right);\)

  3. (3)

    \(\xi \gamma =\left({s}_{l{\left(1-{\left(1-{a}^{3}/{l}^{3}\right)}^{\xi }\right)}^{1/3}},{s}_{l{\left(b/l\right)}^{\xi }}\right);\)

  4. (4)

    \({\gamma }^{\xi }=\left({s}_{l{\left(a/l\right)}^{\xi }},{s}_{l{\left(1-{\left(1-{b}^{3}/{l}^{3}\right)}^{\xi }\right)}^{1/3}}\right).\)

Theorem 1.

Let \({\gamma }_{1}=\left({s}_{{a}_{1}},{s}_{{b}_{1}}\right)\), \({\gamma }_{2}=\left({s}_{{a}_{2}},{s}_{{b}_{2}}\right)\) and \(\gamma =\left({s}_{a},{s}_{b}\right)\) be any three LFFNs defined on a continuous linguistic term set \(\tilde{S }=\left\{{s}_{\alpha }|0\le \alpha \le l\right\}\), then.

  1. (1)

    \({\gamma }_{1}\oplus {\gamma }_{2}={\gamma }_{2}\oplus {\gamma }_{1}\);

  2. (2)

    \({\gamma }_{1}\otimes {\gamma }_{2}={\gamma }_{2}\otimes {\gamma }_{1}\);

  3. (3)

    \(\upxi \left({\gamma }_{1}\oplus {\gamma }_{2}\right)={\upxi \gamma }_{1}\oplus\upxi {\gamma }_{2}\),\(\upxi >0\);

  4. (4)

    \(\gamma \left({\upxi }_{1}+{\upxi }_{2}\right)={\gamma\upxi }_{1}\oplus {\gamma\upxi }_{2}, {\upxi }_{1},{\upxi }_{2}>0\);

  5. (5)

    \({\left({\gamma }_{1}\otimes {\gamma }_{2}\right)}^{\xi }\)=\({\left({\gamma }_{1}\right)}^{\xi }\otimes {\left({\gamma }_{2}\right)}^{\xi }\),\(\upxi >0\);

  6. (6)

    \({\left(\gamma \right)}^{{\xi }_{1}}\otimes {\left(\gamma \right)}^{{\xi }_{2}}\)=\({\left(\gamma \right)}^{{\xi }_{1}+{\xi }_{2}}, {\upxi }_{1},{\upxi }_{2}>0\)

3.3 Distance Measure Between Any Two Linguistic Fermatean Fuzzy Numbers

Definition 6. Let \({\gamma }_{1}=\left({s}_{{a}_{1}},{s}_{{b}_{1}}\right)\) and \({\gamma }_{2}=\left({s}_{{a}_{2}},{s}_{{b}_{2}}\right)\) be any two LFFNs defined on a continuous linguistic term set \(\tilde{S }=\left\{{s}_{\alpha }|0\le \alpha \le l\right\}\), then the normalized Hamming distance between \({\gamma }_{1}\) and \({\gamma }_{2}\) is defined by.

$$dis\left({\gamma }_{1},{\gamma }_{2}\right)=\frac{\left|{a}_{1}^{3}-{a}_{2}^{3}\right|+\left|{b}_{1}^{3}-{b}_{2}^{3}\right|+\left|{\pi }_{1}^{3}-{\pi }_{2}^{3}\right|}{2{l}^{3}}.$$
(4)

3.4 Comparison Method of Linguistic Fermatean Fuzzy Numbers

Definition 7. Let \(\gamma =\left({s}_{a},{s}_{b}\right)\) be a LFFN defined on a continuous linguistic term set \(\tilde{S }=\left\{{s}_{\alpha }|0\le \alpha \le l\right\}\), then the score function of \(\gamma\) is defined as.

$$S\left(\gamma \right)={\left(\frac{{l}^{3}+{a}^{3}-{b}^{3}}{2}\right)}^{1/3},$$
(5)

and the accuracy function of \(\gamma\) is defined as.

$$H\left(\gamma \right)={\left({a}^{3}+{b}^{3}\right)}^{1/3}.$$
(6)

For any two LFFNs \({\gamma }_{1}=\left({s}_{{a}_{1}},{s}_{{b}_{1}}\right)\) and \({\gamma }_{2}=\left({s}_{{a}_{2}},{s}_{{b}_{2}}\right)\) defined on a continuous linguistic term set \(\tilde{S }=\left\{{s}_{\alpha }|0\le \alpha \le l\right\}\), then.

  1. (1)

    If \(S\left({\gamma }_{1}\right)>S\left({\gamma }_{2}\right)\), then \({\gamma }_{1}>{\gamma }_{2}\);

  2. (2)

    If \(S\left({\gamma }_{1}\right)=S\left({\gamma }_{2}\right)\), then

    • If \(H\left({\gamma }_{1}\right)>H\left({\gamma }_{2}\right)\), then \({\gamma }_{1}>{\gamma }_{2}\);

    • If \(H\left({\gamma }_{1}\right)=H\left({\gamma }_{2}\right)\), then \({\gamma }_{1}={\gamma }_{2}\).

4 Power Average Operators for Linguistic Fermatean Fuzzy Numbers

In this section, the classical PA operators is extended into the LFSs and some new AOs for LFNs are proposed. In addition, significant properties of these AOs are also investigated.

4.1 The Linguistic Fermatean Fuzzy Power Average Operator

Definition 8. Let \({\gamma }_{i}=\left({s}_{{a}_{i}},{s}_{{b}_{i}}\right)\left(i=\mathrm{1,2},\dots ,n\right)\) be a collection of LFFNs defined on a continuous linguistic term set \(\tilde{S }=\left\{{s}_{\alpha }|0\le \alpha \le l\right\}\), then the linguistic Fermatean fuzzy power average (LFFPA) operator is expressed as

$$LFFPA(\gamma_{1} ,\gamma_{2} , \ldots \gamma_{n} ) = \frac{{ \oplus_{i = 1}^{n} (1 + TT(\gamma_{i} )\gamma_{i} )}}{{\sum\nolimits_{i = 1}^{n} {(1 + T(\gamma_{i} ))} }},$$
(7)

where \(T\left({\gamma }_{i}\right)={\sum }_{j=1;j\ne i}^{n}Sup\left({\gamma }_{i},{\gamma }_{j}\right)\) and \(Sup\left({\gamma }_{i},{\gamma }_{j}\right)\) denotes the support degree for \({\gamma }_{i}\) from \({\gamma }_{j}\), satisfying the following properties:

  1. (4)

    \(Sup\left({\gamma }_{i},{\gamma }_{j}\right)\in \left[\mathrm{0,1}\right]\);

  2. (5)

    \(Sup\left({\gamma }_{i},{\gamma }_{j}\right)=Sup\left({\gamma }_{j},{\gamma }_{i}\right)\);

  3. (6)

    \(Sup\left({\gamma }_{i},{\gamma }_{j}\right)\ge Sup\left({\gamma }_{m},{\gamma }_{n}\right)\) if and only if \(\left|{\gamma }_{i}-{\gamma }_{j}\right|\le \left|{\gamma }_{m}-{\gamma }_{n}\right|\)

;

If we assume

$${\varphi }_{i}=\frac{\left(1+T\left({\gamma }_{i}\right)\right)}{{\sum }_{i=1}^{n}\left(1+T\left({\gamma }_{i}\right)\right)},$$
(8)

then Eq. (7) can be

$$LFFPA(\gamma_{1} ,\gamma_{2} , \ldots \gamma_{n} ) = \oplus_{i = 1}^{n} \varphi_{i} \gamma_{i},$$
(9)

where \(\varphi ={\left({\varphi }_{1},{\varphi }_{2},\dots ,{\varphi }_{n}\right)}^{T}\) is called the power vector weight, such that \(0\le {\varphi }_{i}\le 1\) and \({\sum }_{i=1}^{n}{\varphi }_{i}=1\).

Based on the operational rules that presented in Definition 5, the following theorem is derived.

Theorem 2.

Let \({\gamma }_{i}=\left({s}_{{a}_{i}},{s}_{{b}_{i}}\right)\left(i=\mathrm{1,2},\dots ,n\right)\) be a collection of LFFNs defined on a continuous linguistic term set \(\tilde{S }=\left\{{s}_{\alpha }|0\le \alpha \le l\right\}\), the aggregated value by the LFFPA operator is still a LFFNs and

$$LFFPA\left({\gamma }_{1},{\gamma }_{2},\dots ,{\gamma }_{n}\right)=\left({s}_{l{\left(1-{\prod_{i=1}^{n}\left(1-{a}_{i}^{3}/{l}^{3}\right)}^{{\varphi }_{i}}\right)}^{1/3}},{s}_{l{\prod }_{i=1}^{n}{\left({b}_{i}/l\right)}^{{\varphi }_{i}}}\right),$$
(10)

Proof.

When \(n=1\), the LFFPA operator is

$$LFFPA\left({\gamma }_{1}\right)={\varphi }_{1}{\gamma }_{1}=\left({s}_{l{\left(1-{\left(1-{a}_{1}^{3}/{l}^{3}\right)}^{{\varphi }_{1}}\right)}^{1/3}},{s}_{l{\left({b}_{1}/l\right)}^{{\varphi }_{1}}}\right)$$

Suppose that when \(n=k\), then the LFFPA operator is

$$LFFPA\left({\gamma }_{1},{\gamma }_{2},\dots ,{\gamma }_{k}\right)=$$
$$\left({s}_{l{\left(1-{\prod_{i=1}^{k}\left(1-{a}_{i}^{3}/{l}^{3}\right)}^{{\varphi }_{i}}\right)}^{1/3}},{s}_{l{\prod }_{i=1}^{k}{\left({b}_{i}/l\right)}^{{\varphi }_{i}}}\right)$$

When \(n=k\)+1, the LFFPA operator is

$$\begin{aligned} LFFPA(\gamma_{1} ,\gamma_{2} , \ldots \gamma_{k + 1} ) & = \oplus_{i = 1}^{k} \varphi_{i} \gamma_{i} \\ & \oplus \varphi_{k + 1} \gamma_{k + 1} \\ \end{aligned}$$
$$=\left({s}_{l{\left(1-{\prod_{i=1}^{k}\left(1-{a}_{i}^{3}/{l}^{3}\right)}^{{\varphi }_{i}}\right)}^{1/3}},{s}_{l{\prod }_{i=1}^{k}{\left({b}_{i}/l\right)}^{{\varphi }_{i}}}\right)\oplus \left({s}_{l{\left(1-{\left(1-{a}_{k+1}^{3}/{l}^{3}\right)}^{{\varphi }_{k+1}}\right)}^{1/3}},{s}_{l{\left({b}_{k+1}/l\right)}^{{\varphi }_{k+1}}}\right)$$
$$=\left({s}_{l{\left(1-{\prod_{i=1}^{k}\left(1-{a}_{i}^{3}/{l}^{3}\right)}^{{\varphi }_{i}}*{\left(1-{a}_{k+1}^{3}/{l}^{3}\right)}^{{\varphi }_{k+1}}\right)}^{1/3}}\right.,$$
$$\left.{s}_{\left(l{\prod }_{i=1}^{k}{\left({b}_{i}/l\right)}^{{\varphi }_{i}}\right)*l{\left({b}_{k+1}/l\right)}^{{\varphi }_{k+1}}}\right)$$
$$=\left({s}_{l{\left(1-{\prod_{i=1}^{k+1}\left(1-{a}_{i}^{3}/{l}^{3}\right)}^{{\varphi }_{i}}\right)}^{1/3}},{s}_{l{\prod }_{i=1}^{k+1}{\left({b}_{i}/l\right)}^{{\varphi }_{i}}}\right)$$

Therefore, the proof of the Theorem 2 is complete.

Theorem 3

(Idempotency). Let \({\gamma }_{i}=\left({s}_{{a}_{i}},{s}_{{b}_{i}}\right)\left(i=\mathrm{1,2},\dots ,.n\right)\) be a collection of LFFNs defined on a continuous linguistic term set \(\tilde{S }=\left\{{s}_{\alpha }|0\le \alpha \le l\right\}\), if \({\gamma }_{i}=\gamma =\left({s}_{a},{s}_{b}\right)\) for all i, then.

$$LFFPA\left({\gamma }_{1},{\gamma }_{2},\dots ,{\gamma }_{n}\right)=\gamma$$
(11)

Proof:

According to the aggregations of According to \({\gamma }_{i}=\gamma =\left({s}_{a},{s}_{b}\right)\), we can have \(Sup\left({\gamma }_{i},{\gamma }_{j}\right)=1\) for all \(i,j=\left(\mathrm{1,2},3,\dots ,n\right),\left(i\ne j\right)\), then \({\varphi }_{i}=\frac{1}{n}\) hold for all i. Then, we can get.

$$LFFPA\left({\gamma }_{1},{\gamma }_{2},\dots ,{\gamma }_{n}\right)$$
$$=\left({s}_{l{\left(1-{\prod_{i=1}^{n}\left(1-{a}_{i}^{3}/{l}^{3}\right)}^{{\varphi }_{i}}\right)}^{1/3}},{s}_{l{\prod }_{i=1}^{n}{\left({b}_{i}/l\right)}^{{\varphi }_{i}}}\right)$$
$$=\left({s}_{l{\left(1-{\prod_{i=1}^{n}\left(1-{a}^{3}/{l}^{3}\right)}^\frac{1}{n}\right)}^{1/3}},{s}_{l{\prod }_{i=1}^{n}{\left(b/l\right)}^\frac{1}{n}}\right)$$
$$=\left({s}_{l{\left(1-{\left(1-{a}^{3}/{l}^{3}\right)}^{\frac{1}{n}*n}\right)}^{1/3}},{s}_{{l\left(b/l\right)}^{\frac{1}{n}*n}}\right)$$
$$=\left({s}_{l{\left({a}^{3}/{l}^{3}\right)}^{1/3}},{s}_{l{\left(b/l\right)}^{\frac{1}{n}*n}}\right)$$
$$=\left({s}_{a},{s}_{b}\right)=\gamma$$

Theorem 4

(Boundedness). Let \({\gamma }_{i}=\left({s}_{{a}_{i}},{s}_{{b}_{i}}\right)\left(i=\mathrm{1,2},\dots ,n\right)\) be a collection of LFFNs defined on a continuous linguistic term set \(\tilde{S }=\left\{{s}_{\alpha }|0\le \alpha \le l\right\}\), and \({\gamma }^{-}=\mathrm{min}\left({\gamma }_{1},{\gamma }_{2},\dots ,{\gamma }_{n}\right)\) and \({\gamma }^{+}=\mathrm{max}\left({\gamma }_{1},{\gamma }_{2},\dots ,{\gamma }_{n}\right)\), then.

$${\gamma }^{-}\le LFFPA\left({\gamma }_{1},{\gamma }_{2},\dots ,{\gamma }_{n}\right)\le {\gamma }^{+}.$$
(12)

Proof. According to the Definition 5, we can obtain

$${\varphi }_{i}{\gamma }_{i}\le {\varphi }_{i}{\gamma }^{+}$$

and

\({\sum }_{i=1}^{n}{\varphi }_{i}{\gamma }_{i}\le {\sum }_{i=1}^{n}{\varphi }_{i}{\gamma }^{+}\).

which means that \(LFFPA\left({\gamma }_{1},{\gamma }_{2},\dots ,{\gamma }_{n}\right)\le {\gamma }^{+}\).

Similarly, we can also prove that \({\gamma }^{-}\le LFFPA\left({\gamma }_{1},{\gamma }_{2},\dots ,{\gamma }_{n}\right)\). Thus the proof of Theorem 4 is completed.

4.2 The Linguistic Fermatean Fuzzy Power Weighted Average Operator

Definition 9. \({\gamma }_{i}=\left({s}_{{a}_{i}},{s}_{{b}_{i}}\right)\left(i=\mathrm{1,2},\dots ,n\right)\) be a collection of LFFNs defined on a continuous linguistic term set \(\tilde{S }=\left\{{s}_{\alpha }|0\le \alpha \le l\right\}\) and the corresponding weight vector be \(\varpi ={\left({\varpi }_{1},{\varpi }_{2},\dots {\varpi }_{n}\right)}^{T}\), such that \({\sum }_{i=1}^{n}{\varpi }_{i}=1\) and \({0\le \varpi }_{i}\le 1\). Then the linguistic Fermatean fuzzy power weighted average (LFFPWA) operator is expressed as.

$$LFFPWA\left({\gamma }_{1},{\gamma }_{2},\dots ,{\gamma }_{n}\right)=\frac{{\sum }_{i=1}^{n}{\varpi }_{i}\left(1+T\left({\gamma }_{i}\right)\right){\gamma }_{i}}{{\sum }_{i=1}^{n}{\varpi }_{i}\left(1+T\left({\gamma }_{i}\right)\right)},$$
(13)

where \(T\left({\gamma }_{i}\right)={\sum }_{j=1;j\ne i}^{n}Sup\left({\gamma }_{i},{\gamma }_{j}\right)\) and \(Sup\left({\gamma }_{i},{\gamma }_{j}\right)\) denotes the support degree for \({\gamma }_{i}\) from \({\gamma }_{j}\), satisfying the following properties presented in Definition 8.

If we assume

$${\psi }_{i}=\frac{{\varpi }_{i}\left(1+T\left({\gamma }_{i}\right)\right)}{{\sum }_{i=1}^{n}{\varpi }_{i}\left(1+T\left({\gamma }_{i}\right)\right)},$$
(14)

then Eq. (10) can be.

$$LFFPWA\left({\gamma }_{1},{\gamma }_{2},\dots ,{\gamma }_{n}\right)={\sum }_{i=1}^{n}{\psi }_{i}{\gamma }_{i},$$
(15)

where \(\psi ={\left({\psi }_{1},{\psi }_{2},\dots ,{\psi }_{n}\right)}^{T}\) is called the power weight vector, such that \({\sum }_{i=1}^{n}{\psi }_{i}=1\) and \(0\le {\psi }_{i}\le 1\).

Theorem 5. Let \({\gamma }_{i}=\left({s}_{{a}_{i}},{s}_{{b}_{i}}\right)\) be a collection of LFFNs defined on a continuous linguistic term set \(\tilde{S }=\left\{{s}_{\alpha }|0\le \alpha \le l\right\}\), the aggregated value by the LFFPWA operator is still a LFFNs and

$$LFFPA\left({\gamma }_{1},{\gamma }_{2},\dots ,{\gamma }_{n}\right)=\left({s}_{l{\left(1-{\prod_{i=1}^{n}\left(1-{a}_{i}^{3}/{l}^{3}\right)}^{{\psi }_{i}}\right)}^{1/3}},{s}_{l{\prod }_{i=1}^{n}{\left({b}_{i}/l\right)}^{{\psi }_{i}}}\right),$$
(16)

The specific proof process of Theorem 5 is omitted here because it is similar to the proof of Theorem 2. In addition, it is easy to prove that the LFFPWA operator has the property of boundedness.

5 The Procedure of A novel Multi-Attribute Decision-Making Method

In this part, based on LFFSs and their AOs, a novel MADM method is presented. Assume that, there are m alternative, which can be denoted by \(A=\left\{{A}_{1},{A}_{2},\dots ,{A}_{m}\right\}\). The m alternatives are evaluated under n attributes, which can be denoted by \(C=\left\{{C}_{1},{C}_{2},\dots ,{C}_{n}\right\}\). The weight of the attributes is \(\varpi ={\left({\varpi }_{1},{\varpi }_{2},\dots ,{\varpi }_{n}\right)}^{T}\), such that \(0\le {\varpi }_{i}\le 1\) and \({\sum }_{i=1}^{n}{\varpi }_{i}=1\). Suppose \(\tilde{S }=\left\{{s}_{\alpha }|0\le \alpha \le l\right\}\) be a continuous linguistic term set with odd cardinality, and decision makers use LFFNs defined on \(\tilde{S }\) to express their evaluation opinion over alternatives. In the following, we present the main steps of our proposed MADM method.

Step 1: Collect decision makers’ evaluation opinion. Based on the pre-defined linguistic term set \(\tilde{S }\), decision makers use a LFFN \({\gamma }_{ij}=\left({s}_{{a}_{ij}},{s}_{{b}_{ij}}\right)\) express their evaluation value for attribute \({C}_{j}\left(j=\mathrm{1,2},\dots ,n\right)\) of alternative \({A}_{i}\left(i=\mathrm{1,2},\dots ,m\right)\). Hence, a linguistic Fermatean fuzzy decision matrix is \(\mathrm{D}={\left({\gamma }_{ij}\right)}_{m\times n}\) is constructed.

Step 2: Normalize the original decision matrix according to the following formula.

$${\gamma }_{ij}=\left\{\begin{array}{c}\left({s}_{{a}_{ij}},{s}_{{b}_{ij}}\right),{C}_{i}\in {I}_{1}\\ \left({s}_{{b}_{ij}},{s}_{{a}_{ij}}\right),{C}_{i}\in {I}_{2}\end{array}\right.$$
(17)

where \({I}_{1}\) and \({I}_{2}\) denote benefit type attributes and cost type attributes, respectively.

Step 3: Calculate the \(Sup\left({\gamma }_{ip},{\gamma }_{iq}\right)\) as follows.

$$Sup\left({\gamma }_{ip},{\gamma }_{iq}\right)=1-dis\left({\gamma }_{ip},{\gamma }_{iq}\right),$$
(18)

where \(dis\left({d}_{ip},{d}_{iq}\right)\) denotes the Hamming distance between \({\gamma }_{ip}\) and \({\gamma }_{iq}\), and \(p,q=\mathrm{1,2},3,\dots ,n\left(p\ne q\right)\),

Step 4: Compute the \(T\left({\gamma }_{ij}\right)\) according to

$$T\left({\gamma }_{ij}\right)={\sum }_{p=q=1,p\ne q}^{n}Sup\left({\gamma }_{ip},{\gamma }_{iq}\right),$$
(19)

Step 5: Compute the power weight \(\psi \left({d}_{ij}\right)\) associating with the LFFN \({\gamma }_{ij}\) according to

$$\psi \left({\gamma }_{ij}\right)=\frac{{\varpi }_{i}\left(1+T\left({\gamma }_{ij}\right)\right)}{{\sum }_{i=1}^{n}{\varpi }_{i}\left(1+T\left({\gamma }_{ij}\right)\right)},$$
(20)

Step 6: Obtain the overall values of the alternatives \(\left\{{A}_{1},{A}_{2},\dots ,{A}_{m}\right\}\) by using the LFFPWA operator, i.e.,

$${\gamma }_{i}=LFFPWA\left({\gamma }_{i1},{\gamma }_{i2},\dots ,{\gamma }_{in}\right).$$
(21)

Step 7: Calculate the score values \({\gamma }_{i}\left(i=\mathrm{1,2},\dots ,n\right)\) according to Eq. (5).

Step 8: Determine the optimal alternative according to the score values of each alternatives.

We provide the following flowchart to between demonstrate the calculation steps of our proposed MADM method (Fig. 1).

Fig. 1.
figure 1

The schedule of the proposed method

Full size image

6 An Illustrative Example

This section applies our proposed method in a real MADM method to show its effectiveness.

Example: Let’ consider a software systems selection problems. An enterprise is now considering to select a suitable software system, and there are four alternatives (\({A}_{1}\), \({A}_{2}\), \({A}_{3}\), and \({A}_{4}\)). The four software systems are evaluated by a group of experts under for attributes, i.e., contribution about organization performance (\({C}_{1}\)), effort to transform from current system (\({C}_{2}\)), benefit of the software system (\({C}_{3}\)), and outsourcing software developer reliability (\({C}_{4}\)). The weight vector of attributes is\(\varpi ={\left(\mathrm{0.2,0.3,0.25,0.25}\right)}^{T}\). Let S = {\({s}_{0}=\) “Extremely poor”, \({s}_{1}=\) “Very poor”, \({s}_{2}=\) “Poor”, \({s}_{3}=\) “Slightly poor”, \({s}_{4}=\) “Fair”, \({s}_{5}=\) “Slightly good”, \({s}_{6}=\) “Good”, \({s}_{7}=\) “Very good”, \({s}_{8}=\) “Extremely good”} be a linguistic term. Decision makers use LFFNs defined on S to express their evaluation values. In the following, we use our propose method to help the enterprise to determine the best software system.

Step 1: Decision makes use a LFFN \({\gamma }_{ij}=\left({s}_{{a}_{ij}},{s}_{{b}_{ij}}\right)\) to denote the evaluation value of the attribute \({C}_{j}\left(j=\mathrm{1,2},\mathrm{3,4}\right)\) of alternative \({A}_{i}\left(i=\mathrm{1,2},\mathrm{3,4}\right)\), and the original decision matrix is constructed, which is listed in Table 1.

Table 1. The original decision matrix denoted by LFFNS.
Full size table

Step 2: Normalize the original decision matrix. It is obviously that all the attributes are benefit and hence the original decision matrix does not need to be normalized.

Step 3: Calculate the \(Sup\left({\gamma }_{ip},{\gamma }_{iq}\right)\) according to the Eq. (18). For convenience, we use \({S}^{pq}\) to denoted the \(Sup\left({\gamma }_{ip},{\gamma }_{iq}\right).\) Then, we can obtain

$${S}^{12}={S}^{12}=(0.5520, \mathrm{0.6480,0.8480}, 0.6960)$$
$${S}^{13}={S}^{31}=(0.9440, 0.9440, 0.4960, 0.4960)$$
$${S}^{14}={S}^{41}=(0.7040, 0.7920, 0.4960, 0.9440)$$
$${S}^{23}={S}^{32}=(0.4960, \mathrm{0.7040,0}.3440, 0.7920)$$
$${S}^{24}={S}^{42}=(0.7920, 0.5520, 0.3440, 0.6400)$$
$${S}^{34}={S}^{43}=(0.7040, 0.8480, 0.9440, 0.4960)$$

Step 4: Compute the \(T\left({\gamma }_{ij}\right)\) according to the Eq. (19) and have

$$T=\left[\begin{array}{c}2.2000, 1.8400, 2.1440, 2.2000\\ 2.3840, 1.9040, \mathrm{2.4960,2.1920}\\ 1.8400, 1.5360, 1.7840, 1.7840\\ 2.1360, 2.1280, 1.7840, 2.0800\end{array}\right]$$

Step 5: Compute the power weight \(\psi \left({\gamma }_{ij}\right)\) by Eq. (20)

$$\psi =\left[\begin{array}{c}0.2079, 0.2768, 0.2554, 0.2599\\ 0.2102, \mathrm{0.2706,0.2714}, 0.2478\\ 0.2088, 0.2796, 0.2558, 0.2558\\ 0.2069, 0.3095, 0.2296, 0.2540\end{array}\right]$$

Step 6: Aggregate the evaluation values and obtain the overall evaluation values \({\gamma }_{i}\left(i=\mathrm{1,2},\dots ,n\right)\) of alternatives

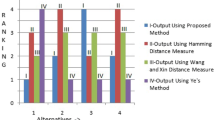
$${\gamma }_{1}=\left({s}_{1.8339}, {s}_{4.1326}\right); {\gamma }_{2}=\left({s}_{0.5952}, {s}_{4.4910}\right);$$
$${\gamma }_{3}=\left({s}_{1.1968}, {s}_{4.7724}\right); {\gamma }_{4}=\left({s}_{0.5921}, {s}_{4.7744}\right)$$

Step 7: Calculate the score values of alternatives and we have

$$S\left({\gamma }_{1}\right)=3.1173;S\left({\gamma }_{2}\right)=2.5871; $$

\(S\left({\gamma }_{3}\right)=2.0808;S\left({\gamma }_{4}\right)=2.0155\).

Step 8. According to the score values shown in Step 7, we can get the ranking orders of alternatives, i.e., \({A}_{1}\succ {A}_{2}\succ {A}_{3}\succ {A}_{4}\) and \({A}_{1}\) is the optimal alternative.

7 Conclusions

This paper introduced a novel MADM method for decision makers to determine the ranking order of alternatives. In order to this, we first proposed the concept of LFFS, which is a powerful tool to depict decision makers’ complicated evaluation values. LFFS absorbs the advantages of FFS and linguistic term set and hence it has obvious superiorities over LPFS and LIFS. Afterwards, some new AOs for LFFSs based on PA were presented and their important properties are investigated in detail. Furthermore, based on LFFSs and their AOs, a novel MADM method was originated and its calculation steps were clearly presented. Finally, our method was applied in solving a real case to demonstrate its effectiveness. Our future research directions include the following two aspects. First, shall consider MADM methods under LFFSs based on consensus to make the final decision-making results more acceptable and reliable. Second, we will consider large-scale group decision-making problems based on LFFSs.