1 Introduction

Investors are increasingly concerned with risks associated with investment decisions. Many mining projects are economically marginal and components of the mining project must be optimized with an understanding of the relevant risks. In an open pit mining project, the life-of-mine plan incorporates a geologic model, mining limits, and economic parameters to determine the mining limits of the final pit, which are then used in a production plan to estimate the project value [12]. Geological uncertainty can have a major effect on mine plan optimization [1, 19, 22]. However, the geological uncertainty is often not used properly in the decision-making process.

The classic method for modeling geological properties, such as the mineral grade of a deposit, is with estimation techniques like ordinary Kriging. Silva, and Boisvert [24] surveyed NI 43-101 reports published in Canada and found that estimation modeling techniques were used for the determination of resources and reserves in 90% of the reports. Estimation-based grade models produce a 3D block model with a single locally accurate estimate of the mineral grade for each block [14]. The local best estimate is not sufficient to quantify joint uncertainty in mineral grade. An alternative approach is to model the geological uncertainty, including the uncertainty from the ore body model, the rock type model, the grade model, and parameter uncertainty [23]. Stochastic modeling is one approach to model the geological uncertainty where simulation is used to create multiple equally probable realizations of the geological variables. Often at least 100 realizations are constructed to represent model uncertainty [4, 23]. Each realization is conditionally unbiased, honors the local data, and honors the spatial variability [14, 23].

Fig. 1
figure 1

Schematic comparing the traditional pit optimizer approach with a single model restrictions (left), to optimizing for all realizations with HPO (right)

Full size image
Fig. 2
figure 2

Schematic of the efficient frontier that Markowitz [20] used for comparing risk versus expected return. Generalized here for pit optimization

Full size image

Equally probable realizations provide many benefits for quantifying resources but utilizing all realizations is non-trivial for planning and downstream processes, such as pit optimization. Few tools have been developed to use all realizations from stochastic models in the pit optimization stage of mine planning. In a mine plan, optimization is key to maximizing the forecasted value of pit designs.

Incorporating the uncertainty from stages of a business plan into the decision-making process is not a new concept. The risk tolerance for the project should be understood [26, 27], and risk management practices can be implemented to choose between many solutions. The mean-variance criterion, proposed by [20] and commonly known as the “Efficient Frontier,” is one risk management tool commonly used to rank solutions that maximize the expected return for a given measurement of risk. Additionally, stochastic dominance rules can be used to help choose between solutions that have an associated probability distribution for a response value [13].

This paper presents an approach for optimizing final pit limits in the presence of geological uncertainty using a previously developed heuristic pit optimization algorithm [2]. The models used in this study are created using real data from a complex folded gold vein deposit in Africa. The data consists of exploration drill holes and economic data from multiple years of mining. The benefit of the heuristic pit optimizer (HPO) is its ability to optimize a final pit shell over many realizations concurrently. This study highlights some differences between classical solutions to the final pit limit problem and solutions optimized over all realizations of a stochastic model.

2 Pit Optimization

Classical approaches to pit optimization focus on a single economic block model derived from an estimation modeling workflow. An optimal final pit is found and then production scheduling algorithms are used to sequence nested shells within the final pit by maximizing a time-weighted value such as net present value (NPV) or rate of return. Classical algorithms for final pit optimization include the Lerchs–Grossman algorithm [16], floating cone methods [3, 6], and the maximum-flow or pseudo-flow algorithms [9, 11]. These algorithms operate on geological models with a single value at each location and cannot minimize the uncertainty from stochastic geological models which have multiple “possible” values for each block. It is common to have up to 100 realizations, or 100 possible values for each block in a stochastic model.

Deutsch et al. [5] present an approach to optimize with stochastic models within this single model restriction by using a scripting approach that optimizes a pit shell for each realization. The pit shell for each realization is then analyzed and individual blocks are ranked based on the probability to be within all of the pit shells. With this approach each optimization only considers one realization independently of the other realizations, the joint uncertainty is not considered and the full uncertainty is not shown [2].

Some algorithms have been developed for optimizing pit shells from a stochastic modeling workflow [2, 10, 15]. Goodfellow and Dimitrakopoulos [10] and Koushavand [15] utilize information from the stochastic models by summarizing the realizations on a block by block basis. Their approaches focus on optimizing the production schedule. Acorn and Deutsch [2] manage the uncertainty in the total pit reserves and focus on optimizing the final pit with the ability to find risk rated pit shells.

Goodfellow and Dimitrakopoulos [10] demonstrate an approach for optimizing production schedules. The realizations are summarized on a block by block basis with summary variables, such as probability to be ore, upper and lower deficient amounts, and the expected value of the block. Uncertainty is penalized on a block-by-block basis and the blocks with higher uncertainty are pushed to later periods of the production schedule with a time-weighted factor. Koushavand [15] optimizes the production schedule within a final pit shell determined from an estimation type model using traditional optimizers. Similarly, Koushavand [15] summarizes the stochastic model at the block level and applies constraints to the blocks to optimize the production schedule.

Acorn and Deutsch [2] present a heuristic pit optimization algorithm (HPO), for optimizing a pit shell over all realizations from a stochastic workflow. The HPO maximizes the expected net value and uses a penalization factor to manage the uncertainty in the total reserves within the pit. Changing the penalization factor results in different uncertainty rated pit shells. The objective function for HPO, Eq. 1, optimizes the expected net value of the pit shell, (Vp), defined in Eq. 2. Uncertainty in the pit shell is managed with a user defined penalization factor, ωpv, applied to the risk, (Rpv). Rpv is the standard deviation of the net value as calculated across all realizations (Eq. 3). In these equations, L is the total number of realizations in the stochastic model, often 100. By increasing ωpv, a more stringent constraint is applied to the optimization problem which decreases the uncertainty in the pit value and causes the pit shell to shrink.

$$ \text{Maximize}: V_{p} - \omega_{\text{pv}}*R_{\text{pv}} $$
(1)
$$ V_{p} = \frac{1}{L} \sum\limits_{l=1}^{L}{V_{p}(l)} $$
(2)
$$ R_{\text{pv}} = \sqrt{\frac{1}{L} \sum\limits_{l=1}^{L}{\left( V_{p}(l) - V_{p} \right)^{2}}} $$
(3)

It should be noted that the penalization factor, ωpv, used by HPO to target levels of uncertainty is not directly correlated to a specific measure of uncertainty. Instead, ωpv is a user defined value used to add a constraint to the objective function. Different ωpv values find different solutions that maximize the expected net value for different levels of uncertainty in the pit shell resources. The specific uncertainty managed is the uncertainty in the final pit resources. HPO manages this uncertainty with an objective function that evaluates the value of a single pit shell over all of the input model realizations; therefore, the uncertainty managed is determined by the input models used. Grade uncertainty can be included with a stochastic grade model. Economic uncertainty can be included with a distribution of grade to economic transfer functions. Geotechnical uncertainty is not currently incorporated in HPO. HPO is still being further developed and currently uses a simple block precedence rule set in order to test this heuristic optimization concept. A more complex geotechnical rule set would need to be developed for the algorithm to incorporate geotechnical uncertainty into the workflow.

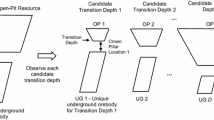
HPO differs from the traditional final pit limit optimizers with the ability to optimize one pit shell for all realizations (Fig. 1) and manage uncertainty by applying an uncertainty constraint, ωpv, to the optimizer. One way of analyzing the results from HPO is with the risk versus expected return (Fig. 2) popularized by Markowitz [20]. Once the HPO algorithm and its heuristic settings are tuned, as explained in Acorn and Deutsch [2], ωpv can be changed to find different pit shells along the efficient frontier. HPO differs from other stochastic model optimizers that penalize the uncertainty locally on a block-by-block basis by addressing the uncertainty in the total pit reserves.

3 Decision-making with Uncertainty

Gallardo and Deutsch [7, 8] present one approach to incorporate geological uncertainty into a decision-making workflow when choosing between a set of feasible actions. For this study, the set of feasible actions refers to the set of final pit limits from which a choice is made to mitigate risk. The final pit limits represent the life-of-mine plan, which incorporates a geological model, mining limits, and economic parameters. The full set of feasible actions is extremely high dimensional and an exhaustive global search for optimization purposes is impractical. To choose from the set of all feasible actions, different uncertainty rated solutions are found along the efficient frontier using the HPO. Stochastic dominance decision rules can then be used to rank and help choose between uncertain projects based on the distributions of a response variable. Each stochastic dominance rule makes certain assumptions about the risk aversion preferences of the decision-maker [17] and specific rules can be chosen to tailor the process to the decision-maker’s risk profile.

In this work, the mean-variance criterion is used to find pit shells along the efficient frontier with the uncertainty represented by the standard deviation of the pit values over all realizations. The efficient frontier can be approximated empirically [2], with each point on the frontier representing a final pit shell with the maximum expected net value for a given level of uncertainty (Fig. 2), and conjointly each point also represents the minimum level of uncertainty for a given expected net value.

Different regions of the frontier are more applicable for risk management than others and some generalities can be assumed about the shape of the frontier (Fig. 2). The efficient frontier starts with the option that maximizes the expected net value, regardless of the uncertainty in the pit shell (point A on Fig. 2). Any point with a greater uncertainty is not applicable for the decision-making process. The frontier represents solutions with maximum value for a given level of risk. With decreasing risk, solutions have decreased value. The slope of the frontier represents changes in value over a range of uncertainty.

This study incorporates two stochastic dominance decision rules, first- and second-degree stochastic dominance. These decision rules are chosen based on the assumptions for each rule as discussed by Levy and Sarnat [18] and Levy [17]. The two rules match a risk management profile where the decision-maker prefers projects that return more money rather than less and are risk averse.

First-degree stochastic dominance assumes that investors always prefer projects that return more money rather than less. As shown in Eq. 4, first-degree stochastic dominance states that, given the cumulative distributions of the response variable for two projects F(x) and G(x), if F(x) is always greater than G(x) (Fig. 3), then project F is said to dominate project G [17]

$$ F(x) \geq G(x), \forall x $$
(4)
Fig. 3
figure 3

Schematic highlighting the first stochastic dominance rule that assumes the decision-maker prefers a project that returns more money rather then less. In this case F(x) dominates G(x)

Full size image

Second-degree stochastic dominance assumes that the decision-maker is risk averse. When comparing the cumulative distribution function for two different project distributions, a risk averse decision-maker will choose the project with a higher overall return. In this case, if the project distributions F and G consist of real numbers between the limits a and b, then as shown in Eq. 5, second-degree stochastic dominance states that project F dominates project G if for every point, x, along the cumulative density function, the area between the two distributions is non-negative [17]. An example of this is shown in Fig. 4. If there is a negative area between the two distributions (A2 in Fig. 4 between x1 and x2), F(x) still dominates G(x) as long the sum of the areas to the left are larger and positive, in this case A1 (between x0 and x1).

$$ {{\int}_{a}^{x}}[G(t) - F(t)]\text{dt}\geq 0, \forall x \in [a,b] $$
(5)
Fig. 4
figure 4

Schematic highlighting the second stochastic dominance rule that assumes the decision-maker is risk averse. When F(x) is below G(x), the area between the two distributions is positive. In this case, F(x) dominates G(x) because for every point. x, the area to the sum of the areas to the left is positive

Full size image

This study incorporates the first- and second-degree dominance rules; however, Levy [17] continues to describe other stochastic dominance rules that could be used to eliminate options from the set of efficient solutions. Each stochastic dominance rule is based on an assumption about the decision-maker and could be used to model more complex risk management profiles. For instance, the third-degree stochastic dominance assumes a preference for positive skewness in the response distribution. Stochastic dominance is a larger area of study that although useful for this paper, is too large to fully summarize here. A deeper look at the stochastic dominance rules available would be required to customize the approach to the specific uncertainty concerns for a project.

4 Site Characteristics

The gold deposit in Africa that is modeled in this study exhibits complex geology with a large mine-scale fold pattern and nested small-scale fold patterns on the limbs (Fig. 5). Since the domain contains complex structural relationships, ordinary Kriging with locally varying anisotropy is used to generate locally accurate grade estimates with the correct structural relationships [21]. The complex geological relationships combined with low short-range continuity present a unique and challenging geological environment.

Fig. 5
figure 5

Plan view of the domains, colored by reference number, for the folded gold deposit

Full size image

4.1 Geostatistical Models

Exploration drill data is used to create the geostatistical models for this study. The complex-folded vein deposit contains multi-phase folding at the mine scale that host mineralized vein sets. The deposit also exhibits a high nugget effect in the variograms which increases the expected local uncertainty in the models.

The deposit is split into four domains that represent the predominant structural zones. The domains are numbered 8850, 8870, 8880, and 8890. Grade values are simulated at locations within the mineralization wire frames. The domains are shown in plan view (Fig. 5) and in an east-west cross-section (Fig. 6), which highlight the complexity and orientation of the deposit. Two of the domains are considered low grade only regions, while two domains consist of both high-grade and low-grade regions.

Fig. 6
figure 6

East-west cross-section of the folded gold deposit domains colored by reference number

Full size image

4.2 Operational Parameters

The deposit modeled for this study is from an active mine with historic mining data. Historic mining and economic data are used to calculate the economic block value from the geostatistical grade models for use in the pit optimizer (Table 1). The block size of the selective mining unit is determined for this study to be 10 m × 10 m horizontally and 6 m vertically resulting in 7.9 million cells in the model. A block precedence rule set is used to set the geotechnical slope angles of the final pit shells to 30∘.

Table 1 Surface mining cost data used for economic block value calculations. Cost data comes from a feasibility study for the deposit [25]
Full size table

5 Optimizing Pit Shells with a Heuristic Optimizer

To manage the uncertainty in the modeled deposit, a heuristic algorithms, HPO, is used to find uncertainty rated pit shells. The first step in managing the uncertainty in the pit shell resources is the creation of the input models. Stochastic realizations of the geological grade model are created using sequential Gaussian simulation and standard geostatistical practices to model the uncertainty in the grade variables. The geological realizations are converted to economic block models using an economic transfer function created from historic mining data of the deposit [25] and the subsequent economic models are the input for HPO. For this study, not enough economic data was available to create a distribution of grade to economic transfer functions so the same transfer function is used for all realizations; therefore, economic uncertainty is not specifically targeted in this study.

HPO is tuned by comparing the results to a known optimal solution, such as the results from the Lerchs–Grossman algorithm [2]. Since the Lerchs–Grossman algorithm can only optimize over a single estimation type model, HPO is first tuned with an averaged response model to find the gap in optimality of the tuned optimization settings. The average response model is determined by averaging the block values across all realization to create a single estimation type model. Once HPO is tuned, multiple uncertainty rated final pit limits are found with HPO by changing the penalization factor, ωpv, and the solutions are analyzed from a risk management perspective. The mean-variance criterion of the efficient frontier shows the value versus uncertainty trade-off between the solutions. Stochastic dominance rules are applied to eliminate some pits.

5.1 Simulation Models Versus Estimation Models in Pit Optimization

The optimization of a final pit limit is required for production scheduling and sets the boundary for the life-of-mine production [12]. Uncertainty can be managed during the pit limits optimization by considering all realizations simultaneously. A pit optimized for the stochastic model still has a single set of mining limits; however, it differs from the classical approach in that there is a value associated with each realization of the model. Figure 7 shows the net values with an empirical cumulative distribution function. Statistics from the distribution of the net values can be used either in the optimization process or in making decisions between solutions. HPO allows the practitioner to decide how the uncertainty is penalized during the optimization process. In certain cases, there might be seemingly minor difference between the pit shells, as seen later. However, by optimizing over all realizations, you can penalize the standard deviation of this distribution to target different uncertainty rated solutions.

Fig. 7
figure 7

Cumulative distribution function of the net value of a pit shell for all realizations

Full size image

5.2 Tuning the Pit Optimization

HPO is a heuristic algorithm that uses a random restart tuning parameter to escape local optima traps [2]. To tune the parameter, the results from HPO are compared to a known optimal solution, in this case, the Lerchs–Grossman algorithm. The Lerchs–Grossman algorithm can only optimize over estimation style models (i.e., with single locally accurate block grade estimates); therefore, HPO is first tuned on the estimation style model or with an averaged stochastic model [2]. The gap in optimality is compared and the optimization settings for HPO are tuned to decrease the gap if needed [2]. HPO uses a greedy optimizer and can get caught in local optima. If the gap between HPO and Lerchs–Grossman is large, the number of random restarts can be increased until the results are sufficiently close to the Lerchs–Grossman solutions.

For the current domain, Lerchs–Grossman found a final pit shell with a net value of $1.5Bn. HPO found a solution with a net value within 1% of the Lerchs–Grossman pit shell. Although HPO can find nearly optimal solutions in a single model test case, targeting specific levels of uncertainty while optimizing over all realizations is a more complex problem due to the incorporation of many realizations. After tuning the HPO algorithm, the efficient frontier for final pit limits can be found by changing ωpv.

6 Managing the Risk in the Resources Within Pit Shells

6.1 The Efficient Frontier for Final Pit Limits

The proposed iterative uncertainty penalization workflow generates a set of final pits that consider the suite of geostatistical realizations for this deposit. The profit/costs data (Table 1) are applied to the full suite of realizations. For this study, ωpv is then iteratively increased from 0 (which finds a similar result as Lerchs–Grossman) to 11 to find pit shells with decreasing variance in the distribution of pit values.

The efficient frontier is constructed and the results are plotted in the value-risk space (Fig. 8). Since ωpv does not directly correlate to a specific measure of uncertainty, the range of values to use for a specific study will change. A multi-scale step approach is therefore useful. First, the overall shape of the frontier is found using large step increases in ωpv. This study started with a step size of 3. Then, specific regions of the frontier are filled in with smaller incremental changes of ωpv.

Fig. 8
figure 8

A mean-variance plot showing the efficient frontier of final pit limits found by optimized over all realizations

Full size image

Utilizing the results from HPO requires a project specific understanding of the acceptable level of risk in future mine plans; however, the probability distributions for the pit values provides insight into the level of uncertainty and potential risk of different pits on the efficient frontier and can be used to narrow the efficient options. In addition, regional changes in the pit limits between solutions can provide insight into local effects of the geological uncertainty on the final pit limits.

The efficient frontier consists of efficient solutions based on the mean-variance criterion. Stochastic dominance rules can be used to analyze the pit value distributions and find smaller subsets of efficient solutions. Certain assumptions, such as an aversion to risk, are used to find a compromise between maximizing the expected value and minimizing the uncertainty in that value. The smaller subset of efficient pits can then be further optimized and evaluated for production scheduling. Regardless of the final choices made, reviewing the solutions provide insight into the potential risks of the project and gain insight into regions of the deposit that could warrant further exploration drilling to decrease the uncertainty.

6.2 Eliminating Solutions on the Frontier

The effect of grade variability on future mine plans can be seen in the risk-value space (Fig. 8). It is tempting to choose the option that maximizes the expected return, however, that choice does not account for any associated risk. In this study, each solution shows a significant coefficient of variation (6.3–6.0%) in the expected pit value. The distributions in Fig. 9 provide a better visual representation of the variability in the net value of the final pit limits with a slight skew towards the lower values. At the lower end, the fifth percentile values range from $1.3Bn to $1.1Bn (Table 2), which provides an idea of the risk of a lower than expected return. The upper end, the 95th percentile values, ranges from $1.6Bn to $1.3Bn (Table 2), which provides insight into the potential upsides of each solution.

Fig. 9
figure 9

The ECDF for each pit shell along the efficient frontier is labeled A through G, with the ECDFs for pits A through D nearly overlapping. The empirical cumulative distribution functions of the value distributions for all of the pit shells are presented together

Full size image
Table 2 Summary statistics for the pit value distributions of the pits found along the efficient frontier
Full size table

Pit A is the start of the efficient frontier for this study. As seen in Table 2, there is a corresponding decrease in the expected value with a decreasing uncertainty. Stochastic dominance can be used to find the trade-off between expected value and the uncertainty to account for certain risk averse preferences.

Stochastic dominance rules are an objective approach for narrowing solutions along the efficient frontier. For the current study, the first-degree stochastic dominance and second-degree stochastic dominance rules are applied and the efficient set is narrowed down to pits A, B, and C. Pits E, F, and G are dominated by both first- and second-degree stochastic dominance and are therefore inefficient solutions. Pit D is only dominated by pit B with both first- and second-degree stochastic dominance, but is dominated by pits A and C with second-degree stochastic dominance.

The remaining efficient set of pits (A, B, and C) are found at the start of the efficient frontier where the slope is shallowest (Fig. 10). Although the other solutions significantly decrease the uncertainty in the resources within the pit, the cost in the loss of value is too great, as shown by stochastic dominance. These three pit shells can now be advanced to the next stage of the mine planning process for further analysis. Productions schedules would be optimized for each final pit limit and for all realizations.

Fig. 10
figure 10

Expected value versus risk of final pit limits optimized over all realizations to maximize the expected net value for targeted levels of risk. The efficient set (A-B-C) are labeled at the upper end of the efficient frontier

Full size image

6.3 Local Effects of Geological Uncertainty on the Pit Limits

Local changes in the pit limits can be used to target regions of the pits for further study. Figure 11 illustrates three potential ways the pit might change when the geological uncertainty is penalized. Figure 11 a illustrates the side wall of a pit being incrementally shaved away, thus decreasing the overall width of the pit, while in Fig. 11b the depth of the pit is incrementally decreased. Figure 11 c differs from the first two, in that instead of an incremental change, sometimes sudden losses of a sub-region of a pit are seen with a decrease in the uncertainty.

Fig. 11
figure 11

Ways the pit can change as the uncertainty is decreased. a Decreasing the width of the pit; b decreasing the depth of the pit; c removing a large sub-region of the pit

Full size image

A combination of all three of these effects are seen in this study. Plan views of two selected solutions, pit D in Fig. 12 and pit E in Fig. 13, illustrate the third effect where a large region is removed when the uncertainty is decreased. The probability distributions for pits A through D are very similar (Fig. 9) and pit E shows where a slight increase in ωpv caused a significant change in the cumulative distribution function. The change from pit D to pit E also corresponds to the southern tail of the pit being removed from the mining limits, as seen by comparing Figs. 12 and 13. Two cross-sections are taken through the averaged grade model to further show how the pit shells change as the uncertainty is penalized (Figs. 14 and 15).

Fig. 12
figure 12

Plan view of pit D on the efficient frontier. Dotted orange lines show the location of cross-sections A and B

Full size image
Fig. 13
figure 13

Plan view of pit E on the frontier where the decrease in uncertainty causes the southern tail of the pit shell to be dropped. Dotted orange lines show the location of cross-sections A and B

Full size image
Fig. 14
figure 14

East to west cross-section of the averaged grade model showing the outlines of each pit shell along the efficient frontier

Full size image
Fig. 15
figure 15

North to south cross-section of the averaged grade model showing the outlines of each pit shell along the efficient frontier. Pits A through D nearly overlap each other

Full size image

The east-west cross-section (A-A’), shown in Fig. 14 shows minimal changes between the different uncertainty rated solutions, with the majority of the changes occurring on the western slope of the pit shell. Here, the primary effect of the decrease in uncertainty is that the pit walls are moved inwards, thus decreasing the overall width of the pit. This decrease in width also corresponds to a decrease in pit depth. The north-south cross-section (B-B’), shown in Fig. 15, shows major differences in the lowest uncertainty rated solutions. The first four solutions along the efficient frontier, pits A through D, show minimal variation through this cross-section. However, the three lowest uncertainty rated solutions, pits E through G, drop the southern portion of the pit. In addition, from the southern section of the pit to the center, the depth of the pit is further decreased. This shows two regions of the pit shell that are affected when the uncertainty is penalized with a large enough factor. The seemingly high grade ore zone in the bottom of Fig. 15 is deceiving in this 2D slice. The actual size of the ore pocket is smaller than it appears in the 2D slice and does not offset the additional waste above it.

7 Discussion

Traditional pit optimizers are constrained by their ability to optimize over a single economic block model derived from an estimation type grade model. This limitation hampers the ability of the practitioner to manage the risk in the pit shell designs that are derived from the uncertainty in the underlying models. A heuristic algorithm such as HPO can instead optimize concurrently over all of the realizations in a stochastic model. By optimizing over all realizations, uncertainty in such parameters as the rock type and grade values can be managed by the optimization algorithm. By applying a penalization factor, a constraint on the desired pit value uncertainty, an uncertainty rated pit shell solution is found. Iteratively changing the penalization factor provides multiple uncertainty rated solutions that are useful when applying risk management principals to a project.

The uncertainty in the pits can be analyzed through multiple uncertainty rated solutions and risk management principals can be applied during the optimization of final pit limits. In this study, HPO is used to estimate the efficient frontier for the final pit limits. The chosen stochastic dominance rules eliminated all but three of the uncertainty rated solutions. The three remaining solutions showed minimal differences in the pit limits. The expected pit values also showed minimal difference and ranged from $1.510Bn to $1.507Bn (a max difference of 0.23%). Although the standard deviation showed a larger max difference of 1.5% while ranging from $95.3Mn to $93.9Mn, the coefficient of variance for the pits stayed fairly constant at 6.31% to 6.23%.

Reviewing the changes in the mining limits for the pits along the efficient frontier can be used to inform future studies, such as targeting regions for future laybacks or regions where correctly setting the starting mining limits are important. If the local changes are large enough, i.e., larger than the minimum mining width required for a layback, then the region could be evaluated as a potential location for future laybacks. If the local changes are smaller then the minimum mining width, then correctly setting the initial cut is of higher importance.

The three remaining solutions, after applying stochastic dominance rules, are oriented roughly north to south with a shallow pit sitting in a southern tail of the final limits. In contrast, the solutions with the lowest variance do not show the pit taking the shallow region to the south (Fig. 13). The western slopes of the pit shells also show significant but incremental decreases in the pit width. All other slopes show a consistent but minimal decrease in the limits.

The changes in the mining limits highlights two large regions where the uncertainty from the geological models greatly affect the final mine plans in a way that could be of interest for a future layback study in the production scheduling phase of the project. Additionally, the eastern slopes of the pits show minimal changes highlighting a region where setting the initial mining limits correctly are of importance; errors in setting the location would cause either a loss of ore, or a needless increase in waste mined. A further study in this region could be of interest to decrease the uncertainty of the location of the optimal highwall.

8 Conclusion

HPO represents a fundamental shift in the practice of pit limit optimization in the presence of uncertainty. Using a heuristic algorithm like HPO allows the practitioner to simultaneously consider value and uncertainty captured with a suite of geostatistical realizations when optimizing a pit shell for a given deposit. The uncertainty captured is determined by the input models therefore multiple types of uncertainty, such as geological and economic uncertainty, can be managed. The additional information generated by optimizing over all realizations can be used to improve decision-making with risk management principals, or to target different zones that affect uncertainty in the pit shells.

The approach presented in this study relies on an algorithm that can find pit shells on the efficient frontier, the mean-variance criterion. The algorithm used in this study, HPO, is still in its infancy and there are limitations in the mining parameters used to determine the pit shells. Currently, only simple block precedence rules are used to determine the pit slopes. More complex mining parameter rules would need to be developed for the algorithm in order to incorporate mining parameter uncertainty into the analysis.

The study presented herein demonstrates the utility of pit optimization over all realizations for understanding the risk-value outcomes of the different possible decisions. The complexly folded gold deposit has short-range continuity and complex mineralization envelopes that increase the variability in the grade models and present a challenging environment for decision-making. Without considering the stochastic variability in the grade distribution traditional methods can only optimize for a single model at a time, such as an estimated model, and therefore cannot account for the underlying uncertainty. Alternatively, a suite of uncertainty rated pit shells are generated by targeting varying levels of uncertainty using the HPO algorithm. In the presented study, the uncertainty rated pit shells range in expected value between $1.5Bn and $1.2Bn and range in standard deviation between $95.3Mn and $72.6Mn. In this case, the coefficient of variation decreased from 6.3 to 6.0%. This directly contrasts with a traditional approach that can only provide one estimated pit shell value and no measure of the variance of that value for one set of geostatistical, economic, and mining parameters.

Incorporating the full suite of stochastic realizations into the pit optimization process is key to managing the geologic uncertainty. However, using the suite of realizations is a complex problem and has not yet been fully or consistently embraced by the mining industry. Embracing the present uncertainty is the first step of staying relevant in a competitive industry with marginal mining deposits. The second step is to manage that uncertainty to meet business objectives. The results from this study show the potential for further developing a pit optimization algorithm that can optimize over all realizations concurrently. This provides a new tool that can be used to apply risk management principals to the pit optimization process of a open pit mining project.