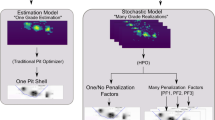
Abstract
Traditional implementations of open pit optimisation algorithms are designed simply to find a set of nested open pit limits that maximise the undiscounted financial pay-off for a series of commodity prices using a single ‘estimated’ orebody model. Then, the maximum Net Present Value (NPV) open pit limit is derived by considering alternate (usually only best and worst-case) mining schedules for each open pit limit. Divorcing the open pit limit delineation from the NPV calculation in this two-step approach does not guarantee that an optimal NPV open pit solution will be found. A new open pit optimisation algorithm that considers the mining schedule is proposed. As a consequence, it can also account explicitly for commodity price cycles and uncertainty that can be modelled by stochastic simulation techniques. This state-of-the-art algorithm integrates Monte Carlo-based simulation and heuristic optimisation techniques into a global system that directly provides NPV optimal pit outlines. This new approach to open pit optimisation is demonstrated for a large copper deposit using multiple orebody models.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
Introduction
Several open pit optimisation techniques such the Lerchs–Grossman algorithm (Lerchs and Grossman 1965; Whittle 1999), network flow (Johnson 1968), pseudoflow network models (Hochbaum and Chan 2000) and others, involve a 3D grid of regular blocks that is converted a priori into a pay-off matrix by considering a 3D block model of mineral grades and economic and mining parameters. These algorithms rely on the block pay-offs averaging linearly, as is the case when undiscounted block pay-offs are considered. However, the Net Present Value (NPV) of the block pay-offs is a non-linear function of the undiscounted block pay-offs that depends explicitly on the discount to be applied to the individual blocks, which in turn depends on the block mining schedule. To overcome the issue of discounting block pay-offs, traditional implementations of open pit optimisation algorithms are designed simply to find a set of nested open pit limits that maximise the undiscounted financial pay-off for a series of constant commodity prices using a single ‘estimated’ orebody model. Then, the maximum NPV open pit limit is derived by considering alternate (usually only best and worst-case) mining schedules for each open pit limit. This two-step approach to finding the maximum NPV open pit limit raises three significant issues:
-
1.
Divorcing the open pit limit delineation from the NPV calculation does not guarantee that an optimal (maximum) NPV open pit solution will be found;
-
2.
NPV calculations are based on a constant commodity price that fails to consider its time-dependant and uncertain nature; and
-
3.
The single ‘estimated’ orebody model is invariably smoothed, thus it fails to consider short-scale grade variations.
Consequently, the block model does not accurately reflect the grade and tonnage of ore that will be extracted and processed during mining.
To overcome the inadequacy of undiscounted pay-offs in commonly used algorithms for open pit optimisation, it is proposed to embed a scheduling heuristic within an open pit optimisation algorithm. This may be seen as an alternative avenue to that taken by mixed integer programming approaches (eg. Caccetta and Hill 2003; Ramazan 2007; Stone et al. 2018; Menabde et al. 2007) that may become numerically demanding in the case of large deposits. As a consequence, uncertain and time-dependent variables such as commodity prices can also be incorporated stochastically into the optimisation process. This permits strategic options for project timing and staging to be assessed as discrete optimisation problems and compared quantitatively and is more advanced than other recent approaches (Monkhouse and Yeates 2018 in this volume; Dimitrakopoulos and Abdel Sabour 2007). It is also proposed to consider multiple conditional simulations in the optimisation process such that the mining and financial implications related to small-scale grade variations are honoured (Menabde et al. 2018 in this volume; Ramazan and Dimitrakopoulos 2013, 2017 in this volume; Leite and Dimitrakopoulos 2007; Godoy and Dimitrakopoulos 2004; Ravenscroft 1992). By considering discounted block pay-offs, stochastic models of commodity prices and short-scale grade variations a more accurate discounted pay-off matrix (revenue block model) is generated, which in turn will yield an open pit limit that will be closer to the true optimum.
NPV Calculations with Uncertain Variables
Calculation of the NPV for a given open pit limit relies on estimates of numerous parameters, including (but not restricted to) the mineral grades, extraction sequence and timing, mineral recovery, prevailing commodity price and capital and operating costs. All of these parameters are uncertain and should be modelled stochastically. For example, mineral grade values by geostatistical simulations, operating costs with growth functions and commodity prices using long-term mean reverting models that account for periodicity. Consequently, the cumulative distribution of total financial pay-offs for an open pit limit can be derived from the combination of a series of stochastic models of mineral grades, costs, prices, recoveries, etc.
Given L potential NPV outcomes for a block (related to L realisations of grade values, commodity prices, etc), we can calculate the NPV for any realisation l:
and the expected NPV for L realisations:
where:
- B :
-
is the number of blocks under consideration
- d l(b j ):
-
is the discounted value for block b j for the lth realisation
- i j = 1:
-
if b j falls within the open pit limit and 0 otherwise
The idea being to find the open pit limit that maximises NPV L . Additional financial goals, for example minimising downside risk (Richmond 2004a) could also be considered, but are outside the scope of this paper.
Accounting for Multiple Orebody Models
Pit optimisation algorithms found in the literature invariably consider an orebody block model with a single grade value for each block (or parcel). In such an approach, a simple decision rule is used where block b j is processed using option k if g k ≤ z*(b j ) < g k+1, where:
g k is the cut-off grade for processing option k (by convention g 1 = 0 and k = 1 indicates waste)
z* is the estimated grade value
To account for grade uncertainty in open pit optimisation, Richmond (2004a) proposed incorporating L grade values for each block. In this approach, multiple grade values z l(b j ), l=1,…,L were generated by conditional simulation and a processing option k l(b j ) was determined for each realisation. Alternatively, conditional simulation provides short-scale grade variations that permit local ore loss and mining dilution to be readily accounted for in open pit optimisation by (Richmond 2004a):
-
Generating geometrically irregular dig-lines (that separate ore and waste) based on small-scale grade simulations with a floating circle algorithm, and
-
Assimilating the dig-lines into large-scale geometrically regular blocks by a novel re-blocking method.
This two-step approach accounts for short-scale grade variation, but also provides ‘recoverable’ grade and tonnage information for large regular blocks suitable for open pit optimisation. In other words, the simulated grade models are compressed without loss of accuracy so that optimisation is computationally tractable.
An NPV Open Pit Optimisation Algorithm
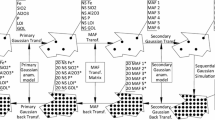
For the vast majority of open pit optimisation techniques a directed graph is superimposed onto the pay-off matrix to identify the blocks that constitute an optimal open pit limit. To paraphrase Dowd and Onur (1993)—each block in the grid, represented by a vertex, is assigned a mass equal to its net expected revenue. The vertices are connected by arcs in such a way that the connections leading from a particular vertex to the surface define the set of vertices (blocks) that must be removed if that vertex (block) is to be mined. A simple 2D example is shown in Fig. 1. Blocks connected by an arc pointing away from the vertex of a block are termed successors of that block, ie. b i is a successor of b i if there exists an arc directed from b i to b i . In this paper, the set of all successors of b j will be denoted as Γ j . For example, in Fig. 1, Γ8 = {2, 3, 4}. A closure of a directed graph, which consists of a set of blocks B, is a set of blocks B p ⊂B such that if b j ∈B p then Γ j ∈B p . For example, in Fig. 1, B p = {1–5, 7–9, 13} is a closure of the directed graph. The value of a closure is the sum of the pay-offs of the vertices in the closure. As each closure defines a possible open pit limit, the closure with the maximum value defines the optimal open pit limit.
For simplicity of notation, the algorithm proposed in this paper is described for a single orebody model. The undiscounted pay-off matrix {w(b), b∈B} typically used for open pit optimisation is calculated as:
where:
- ton b :
-
represents the tonnage of block b
- v :
-
is the commodity (attribute z) value per concentration unit
- r k :
-
is the proportion of the mineral recovered using processing option k
- c k :
-
is the mining and processing cost for k ($/ton)
In practice, r k and c k commonly vary spatially and v and c k temporally. The discounted pay-off matrix {d(b|S), b∈B}, conditional to a mining schedule S, that is required for NPV open pit optimisation is calculated as:
where:
- t :
-
is the time period in which block b is scheduled for extraction and processing
- v t c k, t :
-
are the prevailing commodity price and operating cost at time t
- DR:
-
is the discount rate
In Eq. 4, discounted pay-offs are conditional to the mining schedule as alternate schedules can be derived for the same open pit closure. It is also important to note that, cut-off grades and consequently the processing option k, may change in response to commodity price and operating cost fluctuations over time. Does not imply that the discounted value for is positive.
The traditional floating cone algorithm decomposes the full directed graph problem into a series of independent evaluations of individual Γj and if the sum of the pay-offs associated with Γj is positive, then bj is added to Bp. However, a positive undiscounted value for Γj. does not imply that the discounted value for Γj is positive. In other words, negatively-valued successors bj or block bj that may be mined significantly earlier in the mining schedule and receive substantially less discounting may not be carried by a more heavily discounted positively-valued bj. Furthermore, the modified schedule may have shifted more profitable bj into later periods and additional wasted blocks into earlier periods, reducing the discounted value of the pit. As traditional independent evaluation of locally decomposed Γj.
To allow for discounting, it is proposed that a Direct NPV Floating Cone algorithm (DFC) proceeds as follows:
-
1.
Select the time for initial investment (start of construction) t I;
-
2.
Define a cone that satisfies the physical constraints of the desired open pit slope angles;
-
3.
Define an ordered sequence of visiting blocks [1,2,…#<B] with positive w(b), by ordering the blocks b i firstly on decreasing elevation, and then for blocks with identical elevations on decreasing value in w(b i );
-
4.
Set the open pit closure counter n = 0, the initial open pit closure \( B_{p}^{n} \) to a null set of blocks, and the Net Present Value of initial open pit closure NPV n = 0;
-
5.
Set j = 0;
-
6.
Set j = j + 1;
-
7.
Float the cone to bj to create a new closure \( B_{p}^{n + 1} \) = \( B_{p}^{n} \) + Γj (excluding from Γ j any block that currently belongs to \( B_{p}^{n} \));
-
8.
Determine the schedule S for the new closure \( B_{p}^{n + 1} \);
-
9.
Calculate the discounted pay-off matrix {d(b|S), b∈\( B_{p}^{n + 1} \)} using Eq. 4 and the Net Present Value of the new closure using Eq. 1;
-
10.
Accept the new closure if NPV n + 1−NPV n > 0, whereupon the current closure is updated into a new optimal closure, ie. n = n + 1 and go to step 5; and
-
11.
if j < #, the number of blocks with positive pay-offs w(b), then go to step 6.
The deterministic floating cone algorithm presented above is heuristic in nature and not be optimal. Alternate B p can be generated by varying the initial investment timing (step 1), the ordered path (step 3) and/or the mining schedule (step 8).
Investment timing to satisfy corporate constraints or to take advantage of cyclical commodity prices can be investigated as mutually exclusive opportunities by varying t I, which modifies implicitly the mining schedule in step 8 above. For example, given a schedule S commencing at t = 0, the modified schedule t′ = t + t I. For delayed investment, the NPV for many potential production assets will typically be reduced unless maximum production/grade happens to coincide with the peak in cyclical commodity prices. However, for a risk averse and capital constrained company, the shift of the capital cost into future years may be strategically advantageous when considered in conjunction with other mining assets. Re-initiating the test sequence from the top of the mineral deposit each time a positively-valued cone is found and added to the closure is generally regarded to estimate the heuristic maximum undiscounted pay-off solution (Lemieux 1979). Computational experimentation on the ordering of blocks in step 3 above suggested that this also holds true for the discounted case when t I is fixed. Note that, due to re-initiation of the test sequence it is p common for \( B_{p}^{n + 1} \) = \( B_{p}^{n} \) in step 7 above. For such instances, steps 8–10 above are ignored.
It is well known that the floating cone algorithm may not return the maximum undiscounted pay-off solution. However, it is used in the algorithm presented above to generate physically feasible solutions. The author has not investigated whether the Lerchs–Grossman and network flow algorithms could be substituted for the floating cone algorithm, but the non-linearity of the proposed objective function may present some difficulty. The computational efficiency of the proposed algorithm is enhanced significantly when a simple scheduling algorithm in step 8 above is employed. However, more complex risk-based scheduling algorithms to account for multiple orebody models and production goals (eg. Godoy 2002; Richmond and Beasley 2004) could be considered.
Application to a Copper Deposit
This section demonstrates the proposed concepts for a large subvertical copper deposit. The geometry and contained copper per level are variable, but there is no strong trend. The options considered in this study were:
-
Two processing options (ore and waste), ie. K = 2;
-
60 Mt/year mill constraint;
-
25 realisations of copper grades by Sequential Gaussian Simulation (SGS);
-
25 stochastic simulations of future copper prices with a two factor Pilipovic model that was modified to account for periodicity and cap and collar aversion (Fig. 2);
-
25 stochastic simulations of operating costs with a growth model (Fig. 3);
-
Monthly copper recoveries randomly drawn from normal distribution with mean of 80% and a standard deviation of 1%;
-
A fixed annual discount rate of 10%; and
-
Initial investment timings at discrete yearly intervals for five years.
Figure 2 shows 25 stochastic simulations of future copper prices. The assumptions in this study were:
-
A long-term copper price of $1.30/lb,
-
The present time ($2.50/lb) was near the peak of the price cycle,
-
An average eight year copper price cycle, and
-
$0.50/lb and $3.00/lb lower and upper aversion values.
Note that, as time increases uncertainty in the simulated copper price increases and the deviation of the average simulated value to the long-term price decreases. The average copper price does not fluctuate symmetrically around the long-term copper price due to the asymmetrical aversion limits. Figure 3 shows 25 stochastic simulations of waste and ore processing costs.
To assess the potential improvement in NPV against the traditional two-stage pit optimisation approach a base case scenario ($1.30/lb—80% recovery, $1.90/t waste cost and $8.50/t milling cost) was run to generate a series of nested pits using a FCA. The E-type (or average) of the 25 SGS realisations was adopted as the single grade model as it is known to be smoothed. The NPV for this series of pits using the base case assumptions are shown in Fig. 4 as crosses. The maximum NPV under the base case scenario is associated with a pit closure of 26,402 blocks. Note that, the capital cost, which could also be modelled stochastically, was not included in this study.
The NPV for the FCA nested pits were also calculated using the simulated grades, metal prices, costs and recoveries for the six annual investment timings, shown in Fig. 4. Note that:
-
These curves vary substantially from the base case.
-
In all instances the maximum NPV pit is significantly larger (49,239–85,093 blocks) than the base case and the maximum NPV is higher than for the base case.
-
Delaying the investment from Year 3 to Year 5 results in a higher NPV ($3.02 billion versus $2.88 billion). At first this relationship appears counter-intuitive as costs are greater and discounting greater. However it is related to higher Cu prices in key production periods.
The NPV of the proposed DFC approach for the six annual investment timings are also shown in Fig. 4. Note that, considering the mining schedule explicitly in the optimisation process was successful in finding the maximum NPV pit in a single run. Whilst the improvement over the maximum NPV pit from the two-step approach that considered the stochastic inputs was limited (usually <0.5% in NPV), there was often some difference in the pit dimension. It is likely that these differences would be reduced further if additional pit closures had been generated for evaluation in the two-step approach. Computationally, it was more efficient to post process a finite series of pit closures than embed the scheduler in the pit optimisation process. In the example shown, the DFC approach that generated a single pit required around the same computational time as that required in generating 36 nested pits by a simple FC approach.
Figure 5 shows the distribution of potential NPVs for the set of nested FCA pits without any investment delay. As expected, the uncertainty increases with pit size with some possibility of negative NPVs for large pit closures. If minimising downside financial risk is of greater importance than maximising the NPV then the financially efficient set (frontier) of open pit limits could be determined under a stochastic framework (Richmond 2004a).
Conclusions
A novel method for working with discounted pay-off matrices during open pit optimisation was proposed. The approach used in this study embedded a simple ore scheduler in a floating cone-based heuritic algorithm. It was a trivial exercise to further consider multiple orebody models, local ore loss and mining dilution, time-dependent commodity prices and costs and variable metal recoveries during optimisation. As a consequence, alternate project development timings could be strategically assessed. Traditional evaluation of a set of nested pit shells with constant metal prices and operating costs failed to determine the maximum NPV pit under uncertain conditions. However, provided that sufficient pit shells were generated and evaluated with the same stochastic price and cost input as for the proposed algorithm there was little difference in the maximum NPV shell derived. Further experimentation should be undertaken to determine whether this observation holds for more complex mining schedule algorithms and geometrically irregular orebodies, as well as when a smoothed block model other than the E-type of the stochastic grade model is used to generate a series of nested closures.
This study demonstrated that uncertainty in future metal prices and operating costs cannot be adequately captured in open pit optimisation by simply post-processing a series of nested pit closures with constant values. Stochastic modelling of mineral grades, mineral recovery, commodity prices and capital and operating costs provide an ideal platform to:
-
Generate an optimal pit to maximise the overall project NPV considering geological and market uncertainty,
-
Determine the optimum investment and project start up timing, and
-
Quantify the multiple aspects of uncertainty in a mine plan.
The example studied in this paper indicates periods of potential financial weakness that could benefit from management focus (eg. forward selling strategies and placing the mine on care and maintenance) prior to difficulties arising.
References
Caccetta L, Hill SP (2003) An application of branch and cut to open pit mine scheduling. J Glob Optimisation 27:349–365
Dimitrakopoulos R, Abdel Sabour SA (2007) Evaluating mine plans under uncertainty: can the real options make a difference? Resour Policy 32:116–125
Dowd PA, Onur AH (1993) Open pit optimisation—part 1: optimal open-pit design. Trans Inst Min Metall Min Technol 102:A95–A104
Godoy M (2002) The effective management of geological risk in long-term production scheduling of open pit mines. Ph.D. thesis, University of Queensland, Brisbane
Godoy MC, Dimitrakopoulos R (2004) Managing risk and waste mining in long-term production scheduling. SME Trans 316:43–50
Hochbaum DS, Chan A (2000) Performance analysis and best implementations of old and new algorithms for the open-pit mining problem. Oper Res 48:894–914
Johnson TB (1968) Optimum open pit mine production scheduling. Ph.D. thesis, University of California, Berkeley, p 120
Korobov S (1974) Method for determining ultimate open pit limits, department of mineral engineering. Ecole Polytechnique, Montreal
Leite A, Dimitrakopoulos R (2007) A stochastic optimisation model for open pit mine planning: application and risk analysis at a copper deposit. Trans Inst Min Metall Min Technol 116:A109–A118
Lemieux M (1979) Moving cone optimising algorithm. In: Computer methods for the 80s, SME of AIMMPE, New York, pp 329–345
Lerchs H, Grossman IF (1965) Optimum design of open pit mines. Bull Can Inst Min 58:47–54
Menabde M, Froyland G, Stone P, Yeates, GA (2018) Mining schedule optimisation for conditionally simulated orebodies, in this volume
Menabde M, Stone P, Law B, Baird B, (2007) Blasor—a generalised strategic mine planning optimisation tool, 2007 SME Annual Meeting and Exhibit
Monkhouse PHL, Yeates G (2018) Beyond naive optimisation, in this volume
Ramazan S (2007) The new fundamental tree algorithm for production scheduling of open pit mines. Eur J Oper Res 177:1153–1166
Ramazan S, Dimitrakopoulos R (2013) Production scheduling with uncertain supply: a new solution to the open pit mining problem. Optim Eng 14:361–380
Ramazan S, Dimitrakopoulos R (2017) Stochastic optimisation of long-term production scheduling for open pit mines with a new integer programming formulation, in this volume
Ravenscroft PJ (1992) Risk analysis for mine scheduling by conditional simulation. Trans Inst Min Metall Min Tech, 101:A101–108
Richmond AJ (2004a) Integrating multiple simulations and mining dilution in open pit optimisation algorithms. In: Dimitrakopoulos R (ed) Orebody modelling and strategic mine planning, spectrum series, vol 14. The Australasian Institute of Mining and Metallurgy, Melbourne, pp 317–322
Richmond AJ (2004b) Financially efficient mining decisions incorporating grade uncertainty. Ph.D. thesis, Imperial College, London, p 208
Richmond AJ, Beasley JE (2004) An iterative construction heuristic for the ore selection problem. J Heuristics 10(2):153–167
Stone P, Froyland G, Menabde M, Law B, Pasyar R, Monkhouse P (2018) Blended iron-ore mine planning optimisation at Yandi Western Australia, in this volume
Whittle J (1999) A decade of open pit mine planning and optimisation—the craft of turning algorithms into packages. In: Proceedings APCOM’ 99 computer applications in the minerals industries 28th international symposium, Colorado School of Mines, Golden, pp 15–24
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 The Australasian Institute of Mining and Metallurgy
About this chapter
Cite this chapter
Richmond, A. (2018). Direct Net Present Value Open Pit Optimisation with Probabilistic Models. In: Dimitrakopoulos, R. (eds) Advances in Applied Strategic Mine Planning. Springer, Cham. https://doi.org/10.1007/978-3-319-69320-0_15
Download citation
DOI: https://doi.org/10.1007/978-3-319-69320-0_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-69319-4
Online ISBN: 978-3-319-69320-0
eBook Packages: Earth and Environmental ScienceEarth and Environmental Science (R0)