1 Introduction

In many industries, structural metals are designed to withstand repeated uni-or-multi-axial loading conditions. In many cases, current designs for these structures based on elastic (yield-limited) analysis fail to capitalize on the material load-bearing reserve and lead to inefficient designs. In contrast, designs to shakedown (a safe cyclic elastoplastic behavior relevant for applications not limited by high cycle fatigue) may exploit enhanced design space enabled by the arrest of plastic accumulation. While shakedown concepts, limit theorems, and numerical methods have been developed since the 1920s and 1930s [1,2,3,4], their widespread acceptance and application in engineering design communities remains limited [1, 5,6,7]. One reason for this is the lack of full-field cyclic displacement and strain information that will convince designers to adopt shakedown criteria as a safe-state beyond first-yield, which is the focus of this article. Notable exceptions where shakedown designs are utilized include: vessels for demilitarization of munitions [8, 9], tribology [10,11,12], multilayer semiconductor devices [13], pavement design [14, 15], shape memory alloy components [16, 17], and nuclear pressure vessels [1,2,3,4, 18,19,20,21,22].

To promote the use of shakedown for design purposes across more industrial sectors, experimental programs need to leverage the advances in non-contact strain kinematic measurements provided by digital image correlation (DIC). Full-field DIC measurements are extensively used in solid mechanics [23,24,25,26,27,28,29,30,31,32,33,34], from very small scales [35] to structures [36,37,38]. Using full-field kinematic measurements from DIC will provide ample evidence for the stability, reliability, and tolerances associated with designing to shakedown. DIC will also enable the study of macroscopic shakedown for more complex structures and loadings than have previously been experimentally investigated [9, 39,40,41,42] and can aid in validating designs. Recently, at the mesoscale, Charkaluk et al. have pioneered the quantification of plastic dissipation through combined thermal and kinematic measurements of polycrystal grains via DIC [43,44,45,46,47,48] which provides prospects for understanding and designing microstructures for shakedown response.

This article presents a first demonstration of the utility of DIC in identifying the macroscopic shakedown behavior of simple structures under multiaxial loadings. In particular, a strategy is proposed to extract inelastic strains from DIC measurements to specifically identify cyclic behavior (i.e. limited or unbounded strain accumulation) under axial torsional loadings. A similar experimental approach to Heitzer et al. [18] is followed with the addition of full-field measurements. The authors Heitzer et al. used an INSTRON 1343 test rig to subject hollow cylindrical ferritic steel samples (commonly used in the nuclear industry) to cyclic tension with nonzero mean stress and constant torque under ambient conditions. In Heitzer et al. [18], the thickness of the cylinder was choosen in order to induce a shear stress distribution through the hollow tube wall and create structural effects. In this paper, to increase the structural effect, solid specimens are used. In Heitzer et al. [18], an INSTRON extensometer was used to monitor strains and the torsional angle was recorded. Several tests with various combinations of axial and torsional loads were used to distinguish shakedown behavior (manifested by the stabilization of torsional angle with cyclic axial force) from undesirable accumulation of inelastic strain (manifested by the torsional angle increasing in an unbounded manner despite the constant moment applied). The interpretation of the accumulation of inelastic strain was discussed as being the result of ratchetting or transient ratchetting in Heitzer et al. [18]. However, typically ratchetting is only considered possible (assuming isotropic material with symmetric yield in tension/compression) when applied cyclic loads produce equivalent stresses that exceed twice the yield stress limit [49]. From the reported conditions in Heitzer et al. [18] it is unclear whether this particular ratchetting condition condition was applicable and met. In any case, in Heitzer et al. [18], ambient creep was not considered as a possible interpretation of the reported evolution of inelastic strain (expressed through the evolution of the angle of twist) during the cyclic loadings with multiaxial mean stresses. In the present work, it is shown that most of the inelastic strain accumulated during cyclic loading is due to ambient creep. It should also be emphasized that, in the present work, the utility utility of the full-field surface DIC measurements will be demonstrated for one of the simplest of structures. In particular, the measurements can rule out surface heterogeneous response and confirm shakedown states. Certainly the benefits of the proposed DIC-based approach (compared to point-based extensometry) only increases with the geometric complexity of the structures considered.

In the following, the test methods, equipment, and material are described in Sect. 2. The nature of the cyclic mechanical tests and the post-processing strategy are given in Sects. 3 and 4 respectively. Results from these tests are presented in Sect. 5, along with discussion and followed by conclusions.

2 Materials and equipment

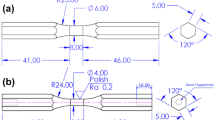
All multiaxial test specimens were made from a common high strength AISI 1144 medium carbon steel (ASTM A29, A311, A510 or SAE J1397, J403, J412) with a typical composition of 97.5–98.01% Iron, 0.4–0.48% Carbon, 1.35–1.65% Manganese, 0.24–0.33% Sulfur, and a maximum of 0.04% Phosphorus. Solid cylindrical bar samples were machined to the dimensions shown in Fig. 1 from 25.4 mm diameter and 304.8 mm long rods. Solid samples were chosen in order to introduce non-homogeneous stress-states and structural aspects to the tests. The geometry is in compliance with ASTM Standards E8, A370, E466 [50]. A high-contrast speckle pattern was applied to each sample to facilitate DIC measurements. The samples were first sprayed with a background coating of white VHT ESP101000 FlameProof paint, followed by a speckle coating of VHT SP102 black paint. Segments of the samples that were to be placed inside the testing machine grips were not painted.

Fig. 1
figure 1

Sample geometry with dimensions in mm

Full size image

All tests were performed on a servo-hydraulic Axial/Torsional 319.25 MTS machine capable of \(\pm 250\) kN axially and \(\pm 200\) \(\hbox {N}\cdot \hbox {m}\) in torque. The experimental rig is shown in Fig. 2, highlighting a sample and the instrumentation. The top grip of the load frame is attached to an axial-torsional load cell that is in turn attached to the cross-head that is fixed during a test. The bottom grip is attached to an actuator capable of independent rotational and vertical translational motions. The use of a MTS FlexTest 40 Controller and Multipurpose Software enables user-defined independent control of the torque and force cells. Specimens were held by hydraulically actuated cylindrical collet grips.

Fig. 2
figure 2

A speckled sample is gripped by the MTS axial/torsional machine while the stereo camera rig is positioned for DIC measurements

Full size image

Monotonic tensile tests were performed in order to provide material characterization for room temperature mechanical properties. Figure 3 shows a representative true stress–strain curve based on tests with an applied strain rate of \(1 \cdot 10^{-5}\) \(s^{-1}\). The measured values for the Young’s Modulus (E) and yield stress (\(\sigma _0\)) are reported in Table 1.

Fig. 3
figure 3

Representative axial true stress–strain response

Full size image

The monotonic tensile test shows the elastoplastic behavior of the material as the test is performed up to 6% strain. The yield limit is determined as the first point of loading at which the material behavior deviates from linear elasticity (no offset). Also included in Table 1 is a cut-off stress corresponding to 6% strain. This represents a state approaching ultimate collapse.

Table 1 Mechanical properties of as-received carbon steel AISI 1144
Full size table

2.1 Stereo DIC setup

A stereo DIC system was used to analyze the 3D surface displacement and 2D strain fields on the viewable portion of the cylindrical samples during all of the tests performed. The DIC system consisted of two Proscilica GX3300 GigE cameras which have definitions of \(3296 \times 2472\) pixels at a pixel size of 5.5 \(\upmu \hbox {m}\). A CCD progressive sensor allowed for a maximum frame rate of 17.1 fps at full definition. C-Mount Schneider–Kreuznach 2.8/50 lenses were used on both cameras to reach a resolution of 25 \(\upmu \hbox {m/pixel}\). Best practices reported in [51] to overcome gray level variations due to the change in lighting conditions upon torque application were applied. In particular, gray level corrections, with a set of polynomial functions up to order 2 were used to alleviate the non-conservation of the gray levels due to the angle of twist. The number of knots describing the NURBS surface was set at 36 [37, 38]. A custom GUI interface was developed, via Matlab, to synchronize both cameras and trigger the acquisition with the MTS machine. The acquisition frequency was set such that 10 images per loading cycle were recorded. After each experiment, the DIC images were analyzed using the CAD-based stereo DIC software described in references [37, 52], across a region of interest (ROI) centered on the tube axis (roughly 510 pixels across 12.7 mm, see Fig. 4a,b). Representative images, captured by the left and right cameras, of the gray levels for the speckled surface are shown in 4c–e. The residual map (which corresponds to the difference between the left and right images after determination of their respective projection matrices, Fig. 4f,g) shows a good calibration stage for the stereo DIC system [51]. In order to verify the quality of the DIC calibration, rigid body motions were applied using the MTS cells in displacement and angle control. The sample was gripped only on the bottom part and the top part was free (see Fig. 2). First a 0.080 mm axial displacement was applied while the DIC measurement detected a translation of 0.083 mm. A rotation of 1.0 degree was applied and a measurement of 0.94 degree was obtained [51]. This gives an indication of measurement uncertainty, approximately 4% in axial displacement and 6% in rotation. The error in the displacement/rotation value can be assumed to be identical from one cycle to another. Therefore the determination of incremental accumulation of inelastic strain with time can be supposed to be affected in a negligible manner by such uncertainties.

Fig. 4
figure 4

The ROI represented on the (a) left (red) and (b) right (blue) camera images in the sensor pixel space (2D). The stereovision calibration step allows the reconstruction of the speckled surface of the sample in 3D space (c,d) from the left and right camera images. The images in are encoded in 256 gray levels where the limits 255 and 0 correspond to the pure white and black colors (e), respectively. f The gray level residuals (consisting in the difference between the left and right images (c,d) presented indicates a good DIC calibration quality [as indicated by the color bar in (g)]

Full size image

3 Experimental methods: cyclic multiaxial force-controlled tests

In this study, we perform a series of tests to determine stable inelastic shakedown behavior and the effects of multiaxial loading at room temperature. Cyclic axial-torsional tests consisted of three phases and were based on similar shakedown tests performed by Heitzer et al. [18]. However, the authors Heitzer et al. used hollow tubes that are well suited for material characterization. Here, solid samples are used to elicit structural effects. First, an initial ramp in force, \(F_R\), was made, where the axial load was applied with a rate of 350 N/s or 2.75 MPa/s. Next, a ramp in torque, T, was applied in order to reach a target equivalent mean stress, \(\sigma _{eq}\). The torque was applied at a rate of 210 \(N\cdot\) mm/s or 1.30 MPa/s. Once the ramp in torque was completed, it was held constant for the remainder of the tests. A short dwell period of 1 min was used to ensure instrumentation stability while both force and torque were held constant before the cyclic phase of the test was initiated. Finally, the axial force was cycled around the target equivalent mean stress. The cyclic axial loading, \(\varDelta F\), was applied with a frequency, f (Eq. 1), that was at the same rate as that applied in the initial ramp phase (the same stress rate is applied in order to avoid any time-dependent effects on the interpretation of the results. The frequency of the cyclic triangle waves is calculated based on the amplitude of the force applied during the cyclic portion of the test and the rate of force applied during the initial ramp, which is: \(\dot{F}_{R}\) = 350 N/s or 2.75 MPa/s):

$$\begin{aligned} f = \dfrac{\dot{F}_{R}}{4 \varDelta F}. \end{aligned}$$
(1)

An example of the applied loading phases is presented in Fig. 5, which displays the axial stress, \(\sigma _{yy}\) (vertical axis on the left) and shear stress, \(\tau _{xy}\) (vertical axis on the right), over the test time in seconds. The initial phase for the ramp in force \(F_R\) lasts 4.5 min and creates an axial stress of 740 MPa. Next, the ramp in torque \(T_R\) lasts 7 min; during this phase, shear stresses reaching 220 MPa are introduced at the surface of the sample (the shear stress is not homogeneous through the thickness). A short 1 min dwell is used before the cyclic axial force is applied; 150 load cycles are performed over 77.6 min. Note that during the cyclic force loading \(\varDelta F\), the torque remains constant.

Fig. 5
figure 5

An example of Sample 2 Case # 1’s applied load history, where the mean force \(F_R\) is 90 kN and the torque \(T_R\) is 89 \(\hbox {N}\cdot \hbox {m}\) and the cyclic axial load is \(\varDelta F = 2\) kN. This test corresponds to the red circled point in the Bree-like load interaction diagram in Fig. 7

Full size image

A list of all of the 14 loading cases investigated is given in Table 2, where the mean force, maximum torque, and cyclic force amplitude are given as well as two non-dimensional loading metrics. These metrics are the normalized maximum axial stress, \(\sigma ^{max}_{yy}/\sigma _0\) (where \(\sigma _0 = 750\) MPa), and normalized nominal shear stress, \(\tau _{xy}/\tau _0\) (where \(\tau _0 = 434\) MPa, Table 1). The shear stress value corresponds to that applied at the sample surface. The largest value is at the outer surface; the shear stress amplitude decreases through the sample thickness. These two non-dimensional quantities give an indication of the extremity of the loading cases with respect to simple yielding. Following the cyclic testing method from Lemaitre and Chaboche (Chapter V) [49], each HS1144 sample was tested at several equivalent stress levels, increasing in severity. In these tests, all samples were subjected to N = 150 cycles at each stress level. Using one sample under subsequent increasing stress levels was shown to have a negligible effect on the measured cyclic behavior for stainless steel 316 at room temperature [49]. This was demonstrated by first testing a single sample at different cyclic strain levels between 0–4%. Then separate samples were used to test each strain level. The results from both types of tests were compared and shown to have negligible difference [49].

Table 2 Multiaxial cyclic shakedown test matrix for the HS1144 samples
Full size table

A schematic of the applied load history is illustrated in Fig. 6. The equivalent stress corresponds to the Mises equivalent stress \(\sigma _{eq}^2 = \sigma _{yy}^2 + 3 \sigma _{xy}^2\). The axial stress \(\sigma _{yy}\) is the quotient of the axial force \(F_R\) and the cross-sectional area of the gage section, \(S = \pi R^2\) (R is the radius of the specimen). The shear stress evolves through the thickness. Let r be the position through the cylindrical sample thickness, from \(r = R\) at the outer surface to \(r = 0\) at the centerline.The shear stress is \(\sigma _{xy} (r) = \dfrac{rT_R}{J}\) where J is the moment of inertia (\(J = \dfrac{\pi }{2} R^4\)). The maximum shear stress is then at \(r=R\) and equals \(\sigma _{xy} = \dfrac{RT_R}{J}\). In the following, shear stress will only be used to refer to the maximum value at the outer surface.

Fig. 6
figure 6

Schematic of a single sample with multiple load cases from Table 2

Full size image

3.1 Bree interaction diagram: loading case amplitudes

In order to visualize the range of the testing program, the load cases (Table 2) are also plotted on a typical Bree-like load interaction diagram, Fig. 7. The ordinate is the normalized axial stress, \(\sigma _{yy}/\sigma _0\), and the abscissa is the normalized shear stress, \(\tau _{xy}/\tau _0\) . In the diagram, the von Mises equivalent yield stress function is used to outline the region of expected elastic response between axes values of \(\sigma _{yy}/\sigma _0 = \tau _{xy}/\tau _0= 1\) (solid black line). The same function, substituting the cut-off stress (\(\sigma ^{6\%}_{cutoff}\)) for yield, is used to give a conservative estimate of the collapse limit as the region above the dashed red line. Each data point (black cross) in the diagram corresponds to an experimental test load case in Table 2. In this way, a broad set of loading conditions is explored, ranging from purely axial mean stresses (along the ordinate) to approaching pure shear (along the abscissa), with a majority of cases well above the nominal elastic limit and approaching ultimate stress levels (approximated by the cut-off stress at 6% strain). It should be noted that in the case where only an axial load is applied, homogeneous stress states are expected and the test no longer mimics structural behavior, but instead aids in understanding the material-level response to cyclic loading.

Fig. 7
figure 7

Bree-like load interaction diagram illustrating the different load cases that are evaluated experimentally

Full size image

4 Analysis: post-processing approach for shakedown determination

While there are many theoretical and numerical approaches to identify cyclic elastoplastic shakedown behavior that are based on monitoring stress states [53,54,55,56,57,58,59,60,61], the most straightforward and convenient experimental metric is strain-based. From the full-field measurements provided by the DIC described in Sect. 2, here a method to extract the inelastic strain field and a metric to determine if the structure shakes down or not during cyclic loading is proposed. The inelastic strain is assumed to be resulting from two contributions: the plastic strain accumulated during hardening of the material, and creep strain.

It is possible to determine, at the surface of the sample, the inelastic strain by subtracting the analytical elastic strain fields from the total strain derived from the DIC full field measurements:

$$\begin{aligned} \pmb {\epsilon ^{in}}(\pmb {x}) = \pmb {\epsilon ^{tot}_{DIC}}(\pmb {x}) - \pmb {\epsilon ^{e}}(\pmb {x}) \end{aligned}$$
(2)

\(\pmb {\epsilon ^{in}}(\pmb {x})\), \(\pmb {\epsilon ^{tot}_{DIC}}(\pmb {x})\) and \(\pmb {\epsilon ^{e}}(\pmb {x})\) are the inelastic, total and elastic strain tensors respectively. The total strain tensor is derived from the DIC displacement measurements along the x,y, and z components. The elastic strain tensor components can be found from the displacement fields \(U_{x}^e\), \(U_{y}^e\) and \(U_{z}^e\) which are calculated as follows:

$$\begin{aligned} U_{x}^{e} =\dfrac{R\sigma _{xy}}{GL^2} z y - \nu \dfrac{\sigma _{yy}}{E} \dfrac{x^2}{R}, \quad U_{y}^e = \dfrac{\sigma _{yy}}{E} y, \quad U_{z}^{e} = - \dfrac{R\sigma _{xy}}{GL^2} x y - \nu \dfrac{\sigma _{yy}}{E} \dfrac{z^2}{R}, \end{aligned}$$
(3)

where \(R =\) 6.35 mm and \(G = \frac{E}{2(1+ \nu )}\). With the surface DIC displacements, the elastic components, \(\epsilon _{xy}^{e}\) and \(\epsilon _{yy}^{e}\), can be calculated as:

$$\begin{aligned} \epsilon _{yy}^{e}=\dfrac{\sigma _{yy}}{E} , \quad \epsilon _{xy}^{e} = \dfrac{R\sigma _{xy}}{GL^2} z \end{aligned}$$
(4)

Subtracting these elastic components from the total strain fields obtained with DIC provides the inelastic strain components. In this way, only the shear \(\epsilon ^{in}_{xy}\) and axial \(\epsilon ^{in}_{yy}\) components can be derived from the DIC measurements. The elastic shear strain component depends on the z coordinate. This indicates that the strain distribution is varying through the depth of the specimen. As the comparison is performed on the outer surface with DIC measurements, the elastic shear strain is calculated for \(z = R\). Figure 8 displays the plastic strain field components \(\epsilon ^{in}_{xy}\) and \(\epsilon ^{in}_{yy}\) for Load Case #2 on Sample 1 at the maximum load of the last cycle.

Fig. 8
figure 8

Plastic strain fields obtained from (Eq. 2) for Sample 2 Load Case #1 at the maximum loading level of the last cycle: (a) \(\epsilon ^{in}_{xy}\) and (b)\(\epsilon ^{in}_{yy}\)

Full size image

The shear \(\epsilon ^{in}_{xy}\) and \(\epsilon ^{in}_{yy}\) components, at the surface of the sample, have homogeneous strain distributions (Fig. 8a and b, respectively). With these components, the (reduced) equivalent inelastic strain, \(\epsilon ^{in}_{eq}\) as a function of time, t, (which is needed to determine if shakedown occurs) can be calculated as follows:

$$\begin{aligned} {\epsilon }^{in}_{eq}(t)={\epsilon }^{p}_{eq}(t) + {\epsilon }^{cr}_{eq}(t), \end{aligned}$$
(5)

with

$$\begin{aligned} {\epsilon }^{p}_{eq}(t)= \dfrac{1}{\mid \varOmega \mid }\int _{\varOmega }^{} \begin{pmatrix}\dfrac{2}{3}{\pmb {\epsilon }}^p(\pmb {x},t):{\pmb {\epsilon }}^p(\pmb {x},t) \end{pmatrix}^{\frac{1}{2}} d\varOmega , \end{aligned}$$
(6)

and

$$\begin{aligned} {\epsilon }^{cr}_{eq}(t)= \dfrac{1}{\mid \varOmega \mid }\int _{\varOmega }^{} \begin{pmatrix}\dfrac{2}{3}{\pmb {\epsilon }}^{cr}(\pmb {x},t):{\pmb {\epsilon }}^{cr}(\pmb {x},t) \end{pmatrix}^{\frac{1}{2}} d\varOmega , \end{aligned}$$
(7)

where \({\pmb {\epsilon }}^p\) is the plastic strain tensor, \({\pmb {\epsilon }}^{cr}\) is the creep strain tensor and \(\varOmega\) is the spatial domain of the structure (which in the present work is the ROI for the DIC measurements, that are surface measurements). A structure will shakedown when the equivalent inelastic strain (\({\epsilon }^{in}_{eq} (t)\)) stabilizes to an asymptotic value upon cycling. In equivalent stress–strain space, this could correspond to any stress-strain hysteresis loops present collapsing to recover linear elastic behavior (with zero inelastic work per cycle). The variation of the inelastic strain (\({\varDelta \epsilon }^{in}_{eq} (t)\)) from cycle to cycle can be determined by:

$$\begin{aligned} {\varDelta \epsilon }^{in}_{eq}(t)= {\varDelta \epsilon }^{p}_{eq}(t) + {\varDelta \epsilon }^{cr}_{eq}(t). \end{aligned}$$
(8)

with the evolution, cycle to cycle, of the equivalent plastic strain reads:

$$\begin{aligned} {\varDelta \epsilon }^{p}_{eq}(t)= \int _{T}^{}{\epsilon }^{p}_{eq}(t+T)- {\epsilon }^{p}_{eq}(t)dt. \end{aligned}$$
(9)

and with the evolution, cycle to cycle, of the equivalent creep strain reads:

$$\begin{aligned} {\varDelta \epsilon }^{cr}_{eq}(t)= \int _{T}^{}{\epsilon }^{cr}_{eq}(t+T)- {\epsilon }^{cr}_{eq}(t)dt. \end{aligned}$$
(10)

A cycle is defined from time t to \(t+T\) (T is the period of the cycle and t is the current time). If \({\varDelta \epsilon }^{in}_{eq} (t)\) is approaching “zero” (in most cases it is necessary to define a threshold, which in this paper is \(1.0\cdot 10^{-8} /s\)), the behavior of the structure can be defined as shakedown [62,63,64].

If no creep is exhibited by the material, the evolution of the inelatic equivalent strain will be driven by the plastic response (due to ratchetting for instance) and Eq. 8 simplifies to Eq. 9. If only creep is exhibited, and no cyclic plasticity is introduced, Eq. 8 simplifies to Eq. 10. If both phenomenon are exhibited simulateneously, the separation of each effect based on simple experimental data is a difficult task. It is necessary to use a numerical model, where an elastoviscoplastic model allows one to reproduce the material response. However, the equivalent inelastic strain is sufficient to define if the structure stabilizes (in the sense of shakedown) with cycles.

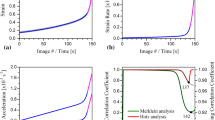
An example of the evolution of the equivalent inelastic strain with cycles (or time) based on the post-processed DIC results is shown in Fig. 9a. This result corresponds to Sample 1 Load Case #2 ( see also Fig. 5, Table 2)—with \(\sigma ^{max}_{yy}/\sigma _0 = 1.04\) and \(\tau _{xy}/\tau _0 = 0.51\). The grey line is the equivalent stress (von Mises, this corresponds to the maximum equivalent stress which is located at the outer surface) and the dashed grey line indicates the onset of yielding. The black line is the equivalent plastic strain (Eq. 6) based on all of the strain components from the averaged DIC results. The two main components, axial plastic strain (\(\epsilon ^{in}_{yy}\)) and shear inelastic strain (\(\epsilon ^{in}_{xy}\)), are shown in red crosses and blue circles, respectively. The shear component (blue) reaches a value of 0.39% during the initial loading test phase and remains steady with cycles, while the axial component (red) reaches 0.21% inelastic strain and accumulates gradually with cycles. The equivalent inelastic strain (black) reaches 0.49% during the initial loading test phase and evolves to 0.52% inelastic strain after 150 cycles. In this way the evolution of the accumulation of inelastic strain after the first cycle is mainly due to the axial component.

The evolution of the variation of the inelastic strain from cycle to cycle (Eq. 9) is illustrated in Fig. 9b for the same test (Sample 1 Load Case #2), Table 2). The natural logarithmic change in axial inelastic strain ((\(ln \begin{pmatrix}\varDelta \epsilon ^{in}_{yy} \end{pmatrix}\)) extracted from the averaged DIC results from cycle to cycle is shown as a red line with crosses. The corresponding change in inelastic shear strain (\(ln \begin{pmatrix} \varDelta \epsilon ^{in}_{xy}\end{pmatrix}\)) is indicated in blue (circles) and the calculated change in equivalent inelastic strain (\(ln \begin{pmatrix}\varDelta \epsilon ^{in}_{eq} \end{pmatrix}\) is shown as a black line over the 150 test cycles. In this example, the asymptotic behavior of the variation of the equivalent inelastic strain stabilizes to a rate of \(4.5 \cdot 10^{-5} /cycle\) (or \(7.5 \cdot 10^{-7} /s\)).

Fig. 9
figure 9

Example of using the post-processed averaged DIC results for Sample 2 Load Case #1 (see also Fig. 5) to find the evolution of the (a) inelastic strain with cycles (or time) and the (b) natural logarithmic variation of inelastic strain from cycle to cycle

Full size image

For larger loading levels—corresponding to Sample 2 Load Case #3 in Table 2—with \(\sigma ^{max}_{yy}/\sigma _0 = 1.12\) and \(\tau _{xy}/\tau _0 = 0.52\), similar plots to Fig. 9a and b are presented. The only difference between the load cases is the larger cyclic axial force applied (\(\varDelta F = 12\) kN for Sample 2 Load Case #3 instead of 2 kN for Sample 2 Load Case #1). Figure 10a gives the evolution of inelastic strain with cycles (or time) and Fig. 10b the variation of equivalent inelastic strain from cycle to cycle. In Fig. 10a, the shear strain component (in solid blue line with circle markers) reaches a value of 0.8% during the initial test loading phase and remains steady with cycles, while the axial component (red line with crosses) reaches 1.15% inelastic strain initially and accumulates to 1.3% inelastic strain at the end of cycling. The equivalent inelastic strain (black line) reaches 1.2% before the onset of the cyclic test phase and evolves to 1.4% inelastic strain after 150 cycles. Based on Fig. 10b, the natural logarithmic variation of equivalent inelastic strain from cycle to cycle (black line) converges to \(8.3 \cdot 10^{-7} /s^{-1}\) after the twentieth cycle.

Fig. 10
figure 10

Example of using the post-processed averaged DIC results for Sample 2 Load Case #3 (Table 2) to find the evolution of the (a) inelastic strain with cycles (or time) and the (b) natural logarithmic variation of inelastic strain from cycle to cycle

Full size image

The influence of creep on the accumulation of inelastic strain complicates the straightforward determination of shakedown using the criteria presented in Eqs. 5 and 8. Indeed, the variation of the creep strain may not reach an asymptotic value. In such cases, it is proposed to use strain/time based design criteria. By determining the creep strain rate at the prescribed or expected loading conditions and by defining a target service lifetime and an allowable amount of strain (\({\epsilon }_{SD-C}\)) one can determine whether the inelastic response would be acceptable or not. By considering a secondary ambient creep regime one can define:

$$\begin{aligned} {\epsilon }^{in}_{eq}(t)={\epsilon }^{p}_{eq}(t) + {\epsilon }^{cr}_{eq}(t)\le {\epsilon }_{SD-C}, \end{aligned}$$
(11)

The inelastic strain, \({\epsilon }_{eq}(t)\), can be limited by a threshold for safety. The time of service \(T_{life}\) combined with the creep rate \(\dot{{\epsilon }}^{cr}_{eq}\) could provide an estimation of the accumulation of inelastic strain induced by creep \({\epsilon }^{cr}_{eq}(t)\). If the predicted inelastic strain, due to creep, is below the design criteria for the target service lifetime, the structural response is accepted as part of the feasible design space.

5 Results and discussion

The 14 load cases that lie above the nominal elastic limit (Fig. 7) were chosen with the expectation that they would all exhibit shakedown behaviors upon cycling. There are several undesirable cyclic time-independent plastic behaviors: alternating plasticity which leads to low-cycle fatigue (LCF) and ratchetting, which leads to incremental collapse. Neither alternating plasticity nor ratcheting should be present in the tests performed. As all of the tests involve tension-tension loadings with an additional mean torque, there is no opportunity for alternating plasticity behavior to occur. This is because alternating plasticity is defined by the plastic strain increment obtained during the first half of each loading cycle being balanced by a plastic strain increment of equal magnitude but opposite sign during the second half of the loading cycle—no net strain accrues during each cycle but the structure ultimately fails by LCF. Under the applied loading conditions, for ratchetting to occur, the following condition for the equivalent stress would have to be exceeded [49]:

$$\begin{aligned} \varDelta \sigma _{eq} \ge 2\sigma _{0}. \end{aligned}$$
(12)

During ratchetting, a net increment of plastic strain accumulates during each cycle, eventually causing rupture (incremental collapse). The accumulation of plastic strain in ratchetting cases for this sample geometry and material, is related to the back and forth motion of the von Mises yield loci during the mechanical solicitation. In our experiments, the stress amplitudes applied are significantly smaller than twice the limit to induce ratchetting: none of the tests performed obey the condition in Eq. 12 so that ratchetting is not expected.

The results in Figs. 9 and 10 for Sample 2 Load Cases #1 and #3 indicate that the rate of plastic strain accumulation with cycles is non-zero. By examining only the variation of plastic strain with cycles, it appears that shakedown behavior and the arrest of the accumulation of plastic strain is not exhibited for these load cases.

However, in order to better understand the cyclic behaviors, one must also examine the equivalent stress–strain response. This is demonstrated for Sample 3 Load Case #1 in Fig. 11 for the entire loading program. An inset is shown to highlight the first few cycles of load. It is seen that there is significant rounding of the curves during unloading, which indicates the presence of ambient creep during the test [65,66,67]. Although unexpected here, cyclic loading induced creep at ambient temperatures and general room temperature creep are well-established behaviors that have been reported for different steels including some carbon steels [67,68,69,70,71,72]. In fact this indication of ambient creep is exhibited in all of the 14 load cases investigated. In all 14 cases, the total amount of inelastic strain continues to increase with cycles (recall for example Figs. 9 and 10 for Sample 2 Load Cases #1 and #3).

Fig. 11
figure 11

The equivalent stress–strain response of Sample 3 Load Case #1, highlighting rounding of the curves during unloading (a signature of creep) [65,66,67]

Full size image

The implication is that in all of the loading cases examined, the accumulation of inelastic strain is due to creep. In work by Taleb and Cailletaud [67] on SS304L, tests were proposed and utilized to distinguish between contributions from time-dependent cyclic creep and time-independent accumulation of cyclic plastic strain: namely, by repeating a load-case but introducing a creep testing phase before the cyclic tests are performed (adapted and shown schematically for our test program in Fig. 12). By comparing the stress–strain response between pairs of tests—the classic cyclic plasticity test and the creep-cyclic plasticity test, Taleb et al. were able to identify creep-cyclic plasticity interactions. If creep was not significant, both tests should lead to similar cyclic plastic strain accumulation. If creep was dominant, then after the creep phase of the test, no significant cyclic accumulation of inelastic strain should be observed.

Fig. 12
figure 12

A schematic of the original (a) shakedown and the (b) adapted creep-shakedown tests based on Taleb and Cailletaud [67]

Full size image

A similar approach is adopted here in order to distinguish between contributions from cyclic creep and shakedown. A new Sample 6 was used with several test phases (see schematic in Fig. 12). First the force was ramped to 100 kN at a rate of 350 N/s, such that the target stress of 790 MPa was reached and would be similar to the test performed on Sample 4 Load Case #1. This load was maintained for 120 min (the original duration of the cyclic portion of the test for Sample 4 Load Case #1). After 120 min, the force was unloaded and reloaded by 2 kN to begin the cyclic portion of the test for an additional 100 cycles at the original frequency of 0.032 \(s^{-1}\) (reproducing the original cyclic test frequency in this phase). With another Sample 7, an additional creep-shakedown test at a higher loading level was performed. For Sample 7, the force was ramped to 12  kN to achieve a target stress of 950 MPa (equivalent to that achieved by the combination of force and torque in Sample 1 Case#4) and maintained for two hours. After the two hours, the force was unloaded and reloaded by 2 kN to begin the cyclic portion of the test for an additional 20 cycles at the original frequency of 0.032 \(s^{-1}\) (also reproducing the original cyclic test frequency in this phase). The number of cycles is reduced to 20 instead of 100 as after reaching the secondary creep regime the accumulation of inelastic strain remains constant with time (or cycles). For both samples 6 and 7, there is only an axial loading applied and no torque. The results for both creep-shakedown tests are presented in Fig. 13.

Fig. 13
figure 13

Creep-Shakedown interaction test results (a) axial stress response and (b) total axial strain (no torque has been applied in these two cases). The dashed vertical black line shows the beginning of the cyclic phase of the test after the creep dwell of 2 h at the maximum forces indicated

Full size image

Figure 13 a and b present, respectively, the axial stress and total axial strain as a function of time for the two loading cases. The creep-shakedown test results (Sample 6 with a ramp to 100 kN force) corresponding to the original shakedown test on Sample 4 Load Case #1 are shown in black. Similarly, the creep-shakedown test results (Sample 7 with a ramp to 120 kN force) similar to the original shakedown test on Sample 1 Load Case#4 are shown in red. In Fig. 14, the black and red lines show the axial creep strain evolution during the creep dwell (before the vertical black dashed line) and during the cyclic testing phase.

Fig. 14
figure 14

Evolution of the axial creep strain during the creep-Shakedown interaction test. The dashed vertical black line shows the beginning of the cyclic phase of the test after the creep dwell of 2 h at the maximum forces indicated

Full size image

It is observed that for both load cases on Samples 6 and 7, after the creep phase of the test, no further significant cyclic accumulation of inelastic strain is present during the cyclic portion of the test (Fig. 14). This observation suggests that all of the cyclic accumulation of inelastic strain exhibited in the results for Sample 1 Load Case #4 and Sample 4 Load Case #1, are due to creep. The further implication is that the cyclic accumulation of inelastic strain detected for all of the 14 load cases (in Table 2) is due to creep. That is, the inelastic strain rate measured at all of the sample surfaces stabilizes but does not converge to zero during the tests. In these particular cases, the Eq. 8 reduces to 10. The plastic contribution is only due to the hardening of the material to reach the maximum equivalent stress value. In Eq. 11 the plastic strain contribution acts as an offset value due to the hardening. After reaching for the first time (here at the first cycle) the maximum multiaxial stress level, the accumulation of plastic strain stabilizes and the structure shakes down. Indeed, the cyclic loading does not induce the motion of the von Mises yield surface. However, the structure cannot be considered as globally shaking down in terms of the global inelastic strain because of the creep effects 8.

For the following, a target service lifetime of \(T_{life} = 60\) hours and an allowable total strain of \({\epsilon }_{SD-C} = 2\)% are chosen to illustrate the modified design approach for shakedown in the presence of creep (Eqs. 11 and 13). For simplicity assume that the strain accumulation is only due to creep and that the rate does not change for the length of service life, \(T_{life}\) , the total strain should respect :

$$\begin{aligned} {\epsilon }_{SD-C} \ge \dot{{\epsilon }}^{cr}_{eq} \cdot T_{life} . \end{aligned}$$
(13)

Then the strain rate, \(\dot{{\epsilon }}^{cr}_{eq}\) from Eq 13, could be found from the slope of the curves in Fig. 14 . In this example, the creep rate should not exceed \(0.925 \cdot 10^{-7} s^{-1}\). The Bree-like load interaction diagram from Fig. 7 is now repeated as Fig. 15 but this time with markers to indicate the structural response at all investigated load cases. In particular, load cases that reach the “cut-off” stress (Table 1) are marked with red triangles, cases that result in acceptable limited inelastic behavior (Eqs. 11) are marked as “shakedown” with grey circle markers and those with undesirable cyclic inelastic responses are marked as “creep” with blue squares. Note that the analytical “collapse” limit (using the cut-off stress corresponding to 6% strain as the critical stress in the von Mises criterion) is drawn with the dashed red line. The black line shows the analytical limit for the elastic response and the blue dotted line represents an estimate for the “shakedown” limit based on the experimental shakedown load cases in grey circles. This approximate limit line is drawn using extrapolation considering a von Mises equivalent stress. The approximation is conservative as it assumes a homogeneous stress state throughout the sample radius in the gage section.

Fig. 15
figure 15

Bree-like load interaction diagram showing the response domains for elastic, shakedown and undesirable cyclic inelasticity (accumulation of inelastic strain)

Full size image

In this way, the results in Fig. 15 can be interpreted as a measure of the loading regimes where shakedown (bounded inelastic response) occurs despite the presence of ambient cyclic creep (for the values of target service lifetime of \(T_{life} = 60\) hours and allowable total strain of \({\epsilon }_{SD-C} = 2 \%\) chosen for this illustration). The experimentally determined shakedown-safe domain is highlighted below the dotted blue line in Fig. 15. This represents a 1.25 times increase in feasible design space compared to traditional yield-limited design (below black line). Above this preliminary shakedown limit line is the expected loading domain where cyclic creep interactions with multiaxial shakedown may dominate and undesirable cyclic inelastic behaviors result (the continued accumulation of inelastic strain).

Although this determination of the shakedown limit in the presence of creep considers only the strain measurement at the surface of the simple structures, it remains conservative. This is because the stress at the outer surface of the sample is at a maximum and the strain rate due to creep is also expected to be the highest at the surface. As the stress distribution is non-homogeneous in the radial direction, the structure as a whole may creep at lower rates. One way to determine the creep strain of the sample is to consider information provided by the MTS cell readings (displacement and angles). As an example, Fig. 16 shows the evolution of the inelastic strain for Sample 1 Load Case #1 (Fig. 16a) and Sample 2 Load Case #3 (Fig. 16b) calculated using both surface DIC and volumetric MTS displacement cell measurements. The volumetric MTS cell based calculations of inelastic strain considers the measured angle and displacement. The shear strain is calculated using \(\epsilon _{xy} = \dfrac{R*\theta }{L_{Cell}}\) (with R the sample radius, \(\theta\) the measured angle and \(L_{Cell}\) the length between the two load cells). The axial strain is estimated by dividing the measured variation of displacement \(\varDelta u\) by the length between load cells as \(\epsilon _{yy} = \dfrac{ \varDelta u}{L_{Cell}}\).

Fig. 16
figure 16

Surface and volumetric strain response for (a) Sample 1 Case # 1 and (b) Sample 2 Case #3 showing the structural effect on the creep strain accumulation with time

Full size image

From Fig. 16 one can notice structural effects in the difference between surface (DIC in black) and the approximate volumetric (MTS in red) responses for the two load cases. The strain rates for the volumetric response are lower than the surface measurements. As a result, considering shakedown limits based on the maximum surface strain rates (from surface DIC measurements) provide more conservative results than those derived from the structural volume response. Certainly, it would be further beneficial to identify 3D stress–strain fields. One could use a Finite Element Model Updating (FEMU) approach [27,28,29]. Strategies to identify the appropriate model parameters to capture the cyclic plasticity and interactions with creep would need to be found and are the subject of future work. These validated simulations could then be used to identify shakedown states with information throughout the structure and beyond the surface level. Nevertheless, the utility of the full-field surface DIC measurements has been demonstrated for these simple structures with inhomogeneous stress-states. In particular, the measurements rule out heterogeneous response at the surface and confirm shakedown states. Certainly the necessity and utility of this DIC-based approach (compared to point-based extensometry) only increases with the geometric complexity of the structures considered.

6 Conclusions

A study of the shakedown behavior of AISI 1144 high strength steel under multiaxial loading is presented. A range of loading cases were investigated for which the cyclic strain behavior was monitored using a Stereo-DIC system. The equivalent plastic strain fields using an analytical solution and the total strain fields obtained with the help of the DIC results was exploited to distinguish bounded cyclic shakedown responses from undesirable or unbounded cyclic inelasticity. As the measured cyclic equivalent stress–strain responses also showed significant rounding during unloading (a signature of creep), interactions between cyclic induced ambient creep and shakedown were also investigated. While all of the load cases investigated included creep effects, more robust shakedown designs (compared to yield-limited designs) may still be viable. A demonstration was provided based on considerations of when the rate of accumulation of the equivalent plastic strain reaches an allowable value within the service life of the structure, with acceptable total strain levels. Within the context of this demonstration, the experimentally determined multiaxial load interaction diagram was presented and showed that the feasible design space considering shakedown was 1.25 times larger than traditional elastic yield-limited approaches.