Introduction

Stereo-DIC is a powerful method to measure 3D shapes, 3D displacement and 2D strain fields [1, 2]. This technique has been used at different scales, from the smallest ones with SEM images [3–6] to large structures [7, 8]. It is mostly used as a medium scale measurement method [1, 9–11] in place of standard 2D-DIC methods to avoid artifacts associated with out-of-plane motions [12] or to measure 3D displacements of a 3D geometry.

The stereo-DIC algorithms usually consist of the local registration of sub-images between at least two pairs of pictures from different points of view [1]. Using projection matrices, formerly determined through a calibration procedure with a (planar) target [13–15], the positions of the sub-images in the 3D space are reconstructed as a cloud of 3D points to measure the shape of the observed surface. By performing DIC during an experiment the displacements of the cloud of 3D points is obtained. By post-processing them, a cloud of 2D strain is obtained in the tangent plane of the surface [1].

Although most stereo-DIC techniques lead to a cloud of 3D points containing a large number of data, these descriptions still consist of local measurements. Recent works on dense multiview systems focus on performing the 3D reconstruction by describing observed surfaces as continuous and mathematically defined objects such as facets [8, 16] or freeform surfaces (e.g., non uniform rational B-splines or NURBS [17]). This last description will be used in the sequel.

The present work is dedicated to the measurement of continuous 3D displacement fields. It follows up on a previous work [17] focusing on calibration and 3D shape measurements. Unlike other stereovision techniques [1, 11, 18], the present method provides a dense description of the measured fields (i.e., 3D shape, 3D displacements) based upon freeform surfaces using NURBS descriptions of the observed surface. Moreover, the number of degrees of freedom is reduced and this description provides a direct link with CAD softwares [19].

The outline of the paper is as follows. First, the formulation of the displacement measurement procedure using a continuous description of the observed surface is presented. Then, the particular case of NURBS surface representation will be detailed. Finally two different applications will be presented. They were also studied in Ref. [17] to determine the 3D shape, which will not be discussed hereafter. The first one aims to estimate displacement and rotation resolutions. The second is related to an industrial application devoted to the welding of a roof top.

Global formulation of displacement measurements

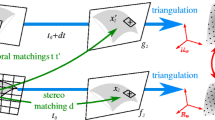
In this section, the formulation of the 3D displacement field measurement via stereo-DIC is introduced. Let us make the assumption that the calibration of the stereovision setup has already been performed and that the geometrical model of the surface is known in an appropriate frame (see e.g., Ref. [17]). For the sake of simplicity, the stereovision setup consists of two cameras. Let (u,v) denote the 2D parameterization of the considered 3D surface. The position of the surface points in the 3D space is related to both right and left pictures (of coordinates (x l,y l) and (x r,y r), respectively) by two projection matrices [M l] and [M r] evaluated thanks to the calibration algorithm [1, 14, 18]

$$ \left\{ \begin{array}{c} s^{l} x^{l} \\ s^{l} y^{l} \\ s^{l} \end{array} \right\} = \left[\mathbf{M}^{l}\right] \{\overline{\mathbf{X}}\} \quad \text{and}\quad \left\{ \begin{array}{c} s^{r} x^{r} \\ s^{r} y^{r} \\ s^{r} \end{array} \right\} = \left[\mathbf{M}^{r}\right] \{\overline{\mathbf{X}}\}~, $$
(1)

where s l and s r are scale factors, and \(\{\overline {\mathbf {X}}\} = (X, Y, Z, 1)^{t}\) the corresponding homogeneous coordinates of any 3D point [14]. During the motion, the coordinates of a 3D point are expressed as x=X+u. It follows that \(\mathbf {x}^{l,r} = \mathbf {x}_{0}^{l,r} + \mathbf {u}^{l,r}(\mathbf {u},[\mathbf {M}^{l,r}],\mathbf {x}_{0}^{l,r})\) where u l,r denotes the apparent motion in the left and right pictures of the pixels initially located at positions \(\mathbf {x}_{0}^{l,r}\).

Let us denote by f l (resp. f r) the reference picture and g l (resp. g r) the picture in the deformed configuration shot with the left resp. right camera as indicated by the superscript l or r. A global approach to stereo-DIC consists of minimizing the functional

$$\begin{array}{@{}rcl@{}} \eta^{2}(\mathbf{u}) && ={\int}_{\text{ROI}} \left[g^{l}(\mathbf{x}^{l}_{0}+\mathbf{u}^{l}(\mathbf{u}))-f^{l}(\mathbf{x}_{0}^{l})\right]^{2}\mathrm{d}u\mathrm{d}v\\ &&+ {\int}_{\text{ROI}} \left[g^{r}(\mathbf{x}^{r}_{0}+\mathbf{u}^{r}(\mathbf{u}))- f^{r}(\mathbf{x}_{0}^{r})\right]^{2}~\mathrm{d}u\mathrm{d}v \end{array} $$
(2)

with respect to the parameters defining the displacement field u.

Using a first order Taylor expansion, the linearized functional reads

$$\begin{array}{@{}rcl@{}} \eta^{2}_{\text{lin}}(\delta\mathbf{u}) &&={\int}_{\text{ROI}}\left[\tilde{g}^{l}+\boldsymbol{\nabla} f^{l}\cdot \frac{\partial\mathbf{u}^{l}}{\partial \mathbf{u}}\delta\mathbf{u}-f^{l}\right]^{2}~\mathrm{d}u\mathrm{d}v\\ &&+ {\int}_{\text{ROI}}\left[\tilde{g}^{r}+\boldsymbol{\nabla} f^{r}\cdot \frac{\partial\mathbf{u}^{r}}{\partial \mathbf{u}}\delta\mathbf{u}-f^{r}\right]^{2}~\mathrm{d}u\mathrm{d}v \end{array} $$
(3)

where δ u denotes the displacement increment, \(\tilde {\mathbf {u}}\) the current estimate of the 3D displacement u so that \(\tilde {\mathbf {x}}^{l,r} = \mathbf {x}_{0}^{l,r} +\mathbf {u}^{l,r}(\tilde {\mathbf {u}})\) and \(\tilde {g}^{l,r} = g(\tilde {\mathbf {x}}^{l,r})\). It is worth noting that the dependencies to the parameters (u,v) of the various quantities in the integrands of equation (3) have been omitted for the sake of readability.

Let us decompose u over an arbitrary basis of fields ϕ i

$$ \mathbf{u}(\overline{\mathbf{X}})= \sum\limits_{i} a_{i}\boldsymbol{\phi}_{i}(\overline{\mathbf{X}}) $$
(4)

where a i are the unknown amplitudes gathered in the column vector {a}.

Since x l,r depend on the parameterization of u, the linearized functional equation (3) becomes

$$\begin{array}{@{}rcl@{}} \eta^{2}_{\text{lin}}(\{\delta\mathbf{a}\}) & = & {\int}_{\text{ROI}}\left[\tilde{g}^{l}-f^{l}+\boldsymbol{\nabla} f^{l}\cdot \sum\limits_{i} \frac{\partial \mathbf{u}^{l}}{\partial a_{i}}\delta a_{i}\right]^{2}~\mathrm{d}u\mathrm{d}v \\ &+ & {\int}_{\text{ROI}}\left[\tilde{g}^{r}-f^{r}+\boldsymbol{\nabla} f^{r}\cdot \sum\limits_{i} \frac{\partial \mathbf{u}^{r}}{\partial a_{i}}\delta a_{i}\right]^{2}~\mathrm{d}u\mathrm{d}v\qquad \end{array} $$
(5)

where \(\{\tilde {\mathbf {a}}\}\) is the current estimate of the sought amplitudes so that \(\tilde {\mathbf {x}}^{l,r} = \mathbf {x}_{0}^{l,r} + \mathbf {u}^{l,r}(\{\tilde {\mathbf {a}}\})\). This procedure corresponds to an a priori regularized DIC scheme as the output of the registration is directly the unknown set of parameters a i , which correspond to the a priori parameterization of the displacement field equation (4). It is worth noting that the results of the registration are expressed as 3D displacement fields (depending on the chosen parameterization). Therefore, it is a global approach to stereo-DIC to estimate 3D displacements.

This problem is solved by iterating the following linear system written in terms of the displacement correction vector {δ a}

$$ \left( \left[\vphantom{C^{r}}\right.\!\!\hspace*{.5pt}\mathbf{C}^{l}\hspace*{.3pt}\!\!\left.\vphantom{C^{r}}\right]+\left[\mathbf{C}^{r}\right]\right)\{\delta\mathbf{a}\} = \left( \{\mathbf{b}^{l}\}+\{\mathbf{b}^{r}\}\right), $$
(6)

with

$$ C^{l,r}_{ij} = {\int}_{\text{ROI}} \left( \boldsymbol{\nabla} f^{l,r}\cdot \frac{\partial \mathbf{u}^{l,r}}{\partial a_{i}}\right) \left( \boldsymbol{\nabla} f^{l,r}\cdot \frac{\partial \mathbf{u}^{l,r}}{\partial a_{j}}\right)~\mathrm{d}u\mathrm{d}v $$
(7)

and

$$ b^{l,r}_{i} = {\int}_{\text{ROI}} \left( \boldsymbol{\nabla} f^{l,r}\cdot \frac{\partial \mathbf{u}^{l,r}}{\partial a_{i}}\right) \left( \tilde{g}^{l,r}-f^{l,r}\right)~\mathrm{d}u\mathrm{d}v. $$
(8)

Using the sensitivity displacement fields \(\frac {\partial \mathbf {u}^{l,r}}{\partial a_{i}}\) as the trial basis, the amplitude vector {a} of the displacement field of the observed surface is obtained (Fig. 1).

Fig. 1
figure 1

Determination of the displacement field in each point thanks to a global approach to stereo-DIC. In the present case N ij corresponds to the parameterization of the 3D shape (e.g., with control points or facet nodes)

Full size image

Unlike most of the stereocorrelation techniques where two 2D displacement fields are projected back onto the 3D space using the projection matrices [1, 18], this formulation provides results directly expressed with 3D kinematic bases without any additional transformation or interpolation. This formulation is not equivalent to first determining the two 2D displacement vectors u l and u r, and then using these four scalar components to reconstruct a 3D vector u, since the above proposed procedure directly uses the 3D u vector as the unknown. A strict equivalence would be recovered if (and only if) the 4D to 3D triangulation were weighted according to the uncertainty attached to each elementary information. Generally, the full covariance matrices of the individual measurement of u l and u r are not computed and hence the standard triangulation is not optimal. Working with the final unknown 3D vector provides the optimal solution without having to make explicit the covariance matrices of each projection and a priori uses the redundancy associated with the explicit dependence of u l,r with the 3D displacement u.

CAD-based Displacement Measurement

In this study, which is the next step of the CAD-based shape measurement technique [17], the description is chosen to be a freeform surface (using NURBS patches [20]). Most studied parts have a CAD representation based on this type of model [19], which provides a generic representation of complex shapes with fewer degrees of freedom than standard meshes, and thus limits the amount of calculation needed to perform the measurement of 3D shapes [17]. Similarly, the displacements will be parameterized in the same space since the deformed configuration will be obtained by moving the control points of the NURBS surface.

NURBS-based Displacement Measurement

A NURBS patch is defined by its order, a network of control points with associated weights, and its knot vector (Fig. 2). The surface X(u,v)=(X,Y,Z) is defined in the parametric space (u,v) as

$$ \mathbf{X}(u,v)=\frac{{\sum}_{i=0}^{m}{\sum}_{j=0}^{n}N_{i,p}(u)N_{j,q}(v)\omega_{ij}\mathbf{P}_{\mathbf{ij}}} {{\sum}_{i=0}^{m}{\sum}_{j=0}^{n}N_{i,p}(u)N_{j,q}(v)\omega_{ij}} $$
(9)

with

$$ \forall u \in [0,1], N_{i,0}(u)= \left\{\begin{array}{l} 1 \text{ when } u_{i} \leq u \leq u_{i+1} \\ 0 \text{ otherwise} \end{array}\right. $$
(10)

and

$$ N_{i,p}(u)=\frac{u-u_{i}}{u_{i+p}-u_{i}}N_{i,p-1}(u)+ \frac{u_{i+p+1}-u}{u_{i+p+1}-u_{i+1}}N_{i+1,p-1}(u)\;, $$
(11)

where N i,p are mixing functions, P i j are the coordinates of control points of the surface, ω i j corresponding weights, (m×n) the number of control points and (p,q) the degrees of the surface.

Fig. 2
figure 2

Theoretical NURBS patch. The blue dots define the control points and the red surface is the 3D shape of interest. Dimensions are in millimeters [17]

Full size image

The calibration of the stereosystem is achieved using a global approach to DIC [21] described in Ref. [17]. First, the projection matrices [M l] and [M r] are estimated by resorting to integrated DIC [22] in which the sensitivity fields with respect to each of their component \(\partial \mathbf {u}^{l}/\partial M_{ij}^{l}\) and \(\partial \mathbf {u}^{r}/\partial M_{ij}^{r}\) are assessed to minimize the correlation residuals. Then, an a priori regularized approach using the sensitivity fields with respect to the control points of the geometry are used to measure the shape of the observed surface. This second step consists of moving the control points to get the best possible match (in the sense of the correlation residuals) between the observed surface and its virtual (i.e., nominal) definition. The second step allows one to account for deviations from the CAD reference. These two steps can be repeated several times to reach a stationary solution, and our experience so far is that convergence is achieved in a few iterations.

Using a NURBS description of the analyzed surface, equation (5) is rewritten as

$$\begin{array}{@{}rcl@{}} \eta^{2}_{\text{lin}}(\delta\mathbf{P}_{ij}) & = & {\int}_{\text{ROI}}\left[\tilde{g}^{l}-f^{l}-\boldsymbol{\nabla} f^{l}\cdot \sum\limits_{i}\sum\limits_{j}\frac{\partial \mathbf{x}^{l}}{\partial \mathbf{P}_{ij}}\delta\mathbf{P}_{ij}\right]^{2}\mathrm{d}u\mathrm{d}v \\ & + & {\int}_{\text{ROI}}\left[\tilde{g}^{r}-f^{r}-\boldsymbol{\nabla} f^{r}\cdot \sum\limits_{i}\sum\limits_{j}\frac{\partial \mathbf{x}^{r}}{\partial \mathbf{P}_{ij}}\delta\mathbf{P}_{ij}\right]^{2}~\mathrm{d}u\mathrm{d}v\qquad \end{array} $$
(12)

where \(\tilde {\mathbf {x}}^{r,l}\) are the current estimates of x r,l(P i j ). The solution to the minimization problem is thus the motion δ P i j of control points P i j parameterizing the surface. The deformation of the observed surface represents the 3D displacement field between the reference and deformed configurations. The freeform surface is composed of the same parametric space as the original part. For any point belonging to the surface, the 3D displacement is known (Fig. 3). In the present case, the displacement field is a NURBS surface whose shape functions are those of the 3D shape in the reference configuration, and the control points are the motions ΔP i j between their positions in the deformed configuration with respect to the reference configuration.

Fig. 3
figure 3

Isogeometric approach for the measurement of 3D displacement fields of a series of deformed configurations with respect to the reference configuration

Full size image

Coarsening or Enrichment of the Kinematic Basis

The fact that the kinematics is described using the same basis as the object shape may appear as un-natural and possibly limiting. It is worth noting that the NURBS description allows for an easy enrichment through the inclusion of additional control points where needed [20, 23], so that even the regularity (or continuity of a specific order of derivatives) can be controlled through multiple control points at the same location. Therefore, the number of degrees of freedom can be increased at will. However, as for any DIC method, such enrichments may lead to ill-conditioning or even ill-posedness [21]. One possible solution is to resort to a regularization à-la-Tikhonov [24] that is consistent with the expected solution. In this spirit, a mechanical regularization such as the one used in DIC [25, 26] could be considered. It thus couples the present setting with recent developments of mechanical modeling based on isogeometric description [23].

On the other hand, one may seek to reduce the number of degrees of freedom. A projection onto a smaller space can be implemented through Lagrange multipliers or penalization. Following a remark formulated above, a projection can be performed in a post-processing step. However, the optimal projection should be made using a least squares regression with a metric that is the inverse of the covariance matrix [27, 28]. If the kinematic constraints are implemented directly in the formulation, the optimal (i.e., the least noise-sensitive) determination is obtained without having to compute the full covariance matrices. It should be noted that uncertainties are partially driven by the degree and the number of control points. The more numerous the kinematic unknowns, the less accurate their determination. A theoretical analysis and quantitative assessment of this effect in this particular framework is currently under investigation [29].

Remarks About Continuity Issues

Even if the part of interest is described by NURBSs, as soon as less continuous reliefs are included in the geometric model, they can be taken into account in the shape or the displacement measurement. To address issues with C0-continuous shapes in the geometric model (e.g., scallop heights, shoulders), the same framework can be used with Finite Element based model, which is a continuous discretization of the surface with facets [30, 31].

Results and Application

The present method has been tested on two different cases as in Ref. [17]. First, a simple Bézier surface machined as an aluminium alloy part has been moved in front of the two cameras. Only rigid body motions have been applied. This experimental test is a validation of the measurement algorithm and a way to estimate displacement and rotation uncertainties. Then, the algorithm has been used to measure 3D displacement fields of a 2- m2 automotive roof during welding. As the calibration procedure did not take into account optical distortions, they have been evaluated and removed a priori using integrated digital image correlation [32].

Validation on a Test Part

The test part is a machined Bézier patch (Fig. 4(a)). It is a 100×100 mm2 aluminium alloy part and it was designed as a 3×3 order NURBS patch whose NURBS description is shown in Fig. 2. There are 4×4×3 unknowns describing the shape. Black and white paint has been sprayed onto the surface of interest to create a speckle pattern compatible with DIC registration (Fig. 4(b)).

Fig. 4
figure 4

Test part consisting of a single 3×3 degree Bézier patch. The picture definition is 1528×1528 pixels with a resolution of ≈0.13 mm/pixel

Full size image

The validation test consists of applying rigid body motions to the part and evaluate them with the CAD-based stereo-DIC system. The latter ones have been prescribed thanks to three perpendicular translation stages coupled with a rotation stage about the Z-axis. Table 1 gives the prescribed displacement amplitudes. The highest amplitude corresponds to about 40-pixel motions in the images. The resolutions provided by the manufacturer of the stages are 1 μm along each axis, and 0.15 mrad for the rotation stage. It is worth noting that 9 pictures are acquired at the end of the procedure to evaluate the measurement resolutions independently of any motions. Two Canon EOS 60D cameras with Sigma 100-mm lenses have been used.

Table 1 Rigid body motions applied to the test part along each of its axis (see Fig. 2) for each image sequence
Full size table

The six sets of images have been processed using CAD-based Stereo-DIC. Displacements and rotations have been calculated using an iterative closest point registration algorithm [33] to obtain the global rotation matrix R and translation vector t. It is worth noting that instead of evaluating the 4×4×3=48 kinematic degrees of freedom and then post-processing them, an integrated approach could have been implemented whereby the motion of the control points is assumed to be that of a rigid body (i.e., six degrees of freedom). However this path is not followed herein because the goal is to estimate the performance of the method with the a priori chosen kinematic parameterization (i.e., with the 48 degrees of freedom) and not to measure at best rigid body motions. As the 3D space of the NURBS representation does not coincide with the 3D space of the actuators, the comparison of the displacement is only performed in terms of norm (i.e., distance) and not for each axis independently. The comparison between the theoretical and the measured displacements is shown in Fig. 5.

Fig. 5
figure 5

Comparison between prescribed (cross) and measured (solid line) displacements. The results correspond to the displacement norm (in mm) between the current position and the reference configuration. Since rotations about an unknown axis (in the CAD frame) are prescribed from image number 27 on, the prescribed displacement is no longer reported in this plot

Full size image

Figure 5 shows that the difference between prescribed and measured displacements is lower along the X-axis (images 4 to 17) than along the Z-axis (images 18 to 27). This effect can be caused by an imperfect calibration along the Z-axis. Moreover, in order to check that the displacement field is kinematically compatible with the prescribed motions (i.e., rigid body motions), Fig. 6 shows the standard deviation of the displacement field, which should vanish for a perfect rigid body motion. The values are found to be very high (i.e., only 10 times less than the displacement amplitude), which is not acceptable.

Fig. 6
figure 6

Standard deviation of the measured displacement fields (along each axis) expressed in mm

Full size image

It is proposed to correct for these imperfections by resorting to the prescribed displacements. First, the calibration is performed using for instance the procedure introduced in Ref. [17]. Then known displacement u p r e are prescribed to the object of interest (or to the stereosystem as this leads to equivalent motions) and the apparent displacement u m e a is measured. Each row of the projection matrices can subsequently be corrected by a factor u p r e /u m e a , which is proportional to the scale factors s l,r. This procedure was used herein to correct the calibration matrices after the first measurement. It can be noted that if such procedure were used on a systematic way to make the initial calibration more robust, it is advised to use a reduced kinematic basis consisting in rigid body motions (i.e., only 6 degrees of freedom).

Figure 7 shows the comparison between prescribed and measured displacements after the correction step. The motions along the X-direction have a root mean square (RMS) difference less than 10μm. The measurements along the Z-axis yield accurate results but the RMS difference between prescribed and measured displacement is about 25μm, which is three times higher than along the X-axis. This difference can be understood by resorting to a resolution analysis to evaluate the covariance matrix associated with each measured degree of freedom (see hereafter). This result is in line with standard stereo-DIC approaches for which it was reported that the measurement uncertainties along the out-of-plane direction is of the order of three to five times that along in-plane directions [1, 21].

Fig. 7
figure 7

Comparison between prescribed (in cross) and measured (solid line) displacements after correcting the projection matrices. The displacement along the Z-axis is also correctly captured

Full size image

Once this correction is performed, the standard deviation of the measured displacement fields is computed again. Figure 8 shows the change of this standard uncertainty along each direction for all the considered steps. It has been significantly reduced (i.e., by a factor of 50). The levels along X- and Y-axes become higher than along the Z-axis, and all of them remain very low.

Fig. 8
figure 8

Standard deviation of the measured displacement field (along each axis) expressed in μm after correcting the projection matrices

Full size image

The L2-norm of the differences between the prescribed and the measured displacement field for the final step is shown in Fig. 9. The differences are higher on the corners, thereby indicating that the distortions may not have been fully corrected.

Fig. 9
figure 9

Map of the L2-norm (expressed in μm) of the raw differences between the measured and prescribed displacement fields (without any rotation or translation correction)

Full size image

Twice the noise variance times the inverse of the stereo-DIC matrix ([C l]+[C r]) can be used to evaluate the sensitivity to noise for each measured degree of freedom [22]. By resorting to this method enables theoretical values of this sensitivity to be obtained without running the complete registration procedure [34]. Figure 10 shows the covariance matrix obtained for the considered case. This matrix shows that the system is more sensitive to noise for Z displacements (bottom/right block). The ratio between the variances along X and Z-directions is of the order of 5. This result is in line with what was reported above (i.e., the standard displacement uncertainty ratio was found to be of the order of \(\sqrt {5}\)).

Fig. 10
figure 10

Covariance matrix of the measured degrees of freedom to acquisition noise expressed in mm2. The ratio between X (top/left 16 ×16 block) and Z (bottom/right 16 ×16 block) variances is about 5

Full size image

By using the trace of the rotation matrix R the angular value of the rotation is determined (i.e., C= cos−1((t r(R)−1)/2)). The eigenvector associated with the eigenvalue 1 gives the orientation of the actual axis of rotation in the 3D space. Figure 11 shows the comparison between the prescribed and the measured angles. The RMS difference between prescribed and measured angles is 60 μrad when the prescribed angle varies between 0 and 5 degrees. This level shows that the angular measurement is very accurate, even when a translation is prescribed during the rotation. Moreover, the axis of rotation is very close to the Z-axis as expected from the experimental configuration.

Fig. 11
figure 11

Comparison between prescribed (cross) and measured (solid line) rotation angles

Full size image

All these results validate the proposed implementation. The next step consists of applying the procedure to an industrial situation.

Application to an Industrial Part

The geometry considered in this section is a 2−m2 automotive roof (Fig. 12(a)). The present study focuses on determining the deformation (i.e., 3D displacement fields) of the surface induced by the welding brazing process of this part onto the car body. Two 12-Mpixel Teli CleverDragon® cameras equipped with NIKKOR® 24 mm lenses are used in this application. The configuration of the experiment is shown in Fig. 13. The acquisition frequency is 10 Hz. The physical size of one pixel is ≈0.3 mm.

Fig. 12
figure 12

(a) Picture of the analyzed roof (2 m2 surface) shot by the left camera [17]. (b) Corresponding NURBS surface after the calibration process

Full size image
Fig. 13
figure 13

Stereovision configuration used during the welding operation

Full size image

The stereo-rig was first calibrated by resorting to CAD-based stereo-DIC [17]. Figure 12(b) shows the measured initial 3D shape at the end of the calibration process. It is composed of one patch of 12×7=84 control points with unitary weight. Thus it corresponds to an eleventh times sixth order Bézier patch.

The reference configuration is chosen to be that at the end of the welding process since the shape of the welded roof is closer to the CAD model (i.e., the car is designed assembled). Moreover, the welding head is visible on the first image and not on the last one. Thus, starting from the end avoids an important part of each images to be masked because of the presence of the head. Each pair of images is processed using the algorithm described earlier. This led to 800 NURBS displacement fields. The calculation time for this application is more than 14 hours with a Matlab implementation. This can be improved by using highly parallelized implementations of the algorithm (e.g., by resorting to graphics processing units [35, 36]).

Figure 14 shows an example of the displacement along the three axes during the welding process. The measured displacement is about 6 mm along the Z-axis, which is consistent with the experimental setup (i.e., the roof is pushed against the automotive body during the welding operation) and previous estimates [17]. The number of iterations needed to achieve convergence of the algorithm is less than 5 in most cases.

Fig. 14
figure 14

Displacement fields of the roof during welding (picture 601 over 840). The color bar represents displacements along the three directions expressed in mm

Full size image

Figure 15 shows two residual maps that correspond to the absolute gray level differences \(\tilde {g}^{l,r}-f^{l,r}\) at convergence for a given set of images. Except for a small zone due to the presence of the welding head in the pictures, the residuals are very small in comparison with the dynamic range of the picture (i.e., 1024 gray levels). These maps validate the overall registration and therefore the correlation results are deemed trustworthy.

Fig. 15
figure 15

Gray level residual fields at step 350 for the left (a) end right (b) camera. The bright spot is caused by the welding head

Full size image

Figure 16 shows the change of the RMS gray level residuals during the welding process. A first set of results (red symbols) is shown when the residuals are computed over the whole ROI. The increase of the value can be explained by the presence of the welding head, which is moving during the welding operation (this part of the image is masked during the registration but the residuals are calculated using the whole surface) leading to a systematic gray level gap between the current and the reference configuration. The highest level is reached when the welding head is in the middle of the surface (see Fig. 15). The second set of results (blue symbols) corresponds to the RMS gray level residual when the masked part is not taken into account. The residuals are reaching low values in the middle of the process. At the beginning and the end of the experiment, the residuals are higher, which is due to reflections coming from the welding head. In order to remove this systematic error, an additional gray level correction should be implemented.

Fig. 16
figure 16

Change of the RMS correlation residuals normalized by the dynamic range of the pictures in the reference configuration during the welding process

Full size image

Conclusion and Outlook

By using an a priori regularized approach to stereo-DIC 3D fully continuous and dense displacement fields are measured in a NURBS formalism, which is totally consistent with the geometrical model used herein (i.e., based on the CAD description of the surface of interest). The standard uncertainty of the implemented method for displacement measurements has been investigated and evaluated to be about 10μm for in-plane displacements, 25μm in the out-of-plane direction, and 60 μrad for the rotations for a 1 dm2 Bézier patch of order 3×3. A method to improve the calibration of the stereo-system has been proposed, which is based upon the correction of the projection matrices by updating the scale factor from the comparison of the prescribed and measured out-of-plane displacements. Moreover, a complex experiment has been analyzed using this method in-situ during the welding process of an automotive roof.

With the increasing interest for the isogeometric analyses for mechanical analyses [23], this method will allow straightforward comparisons between computed and experimental kinematic fields. This type of comparison can be very useful for, say, identification and validation purposes [37]. Further, it can be noted that the 2D strain fields, which were not assessed herein, will be continuous as the displacement field is dense and the surface normals can be easily computed within an isogeometric framework.

Last, it is worth noting that the description used herein (i.e., with NURBS) can be extended to any parametric formulation of shapes such as continuous facets or mechanics-related displacement fields (e.g., provided by finite element or boundary element methods) [30]. For instance, 4-noded quadrangles (Q4) or 3-noded triangles (T3) can be used to mesh the external surface in a consistent way with standard finite element computations. Moreover, the developed global framework allows different formulations for the shape and displacement measurements to be used (e.g., NURBS surfaces for the 3D shape and 3D-Q4 elements for the displacement field discretization). However, the parametric space for the two discretization spaces have to be consistent with each other.