1 Introduction

Microfluidic and nanofluidic devices have large applications in the field of engineering. During the early stage of microfluidics, most of the attention was given to uncover physics of fluid flow through microchannel with uniform cross-section [1,2,3,4,5,6]. These studies have shown that new flow physics such as rarefaction, velocity and temperature jump at the solid–liquid interface, and compressibility effect at low Mach number are present at microscale flows with gas as the working fluid [2, 3]. In addition, other studies have shown that surface tension effects become significant at microscale in two-phase flows [7] and respiratory fluid mechanics [8]. Although flow through uniform microchannels has been largely understood, flow through non-uniform microchannels has not received sufficient attention. The fundamental flow phenomenon in non-uniform microchannel differs substantially from its uniform cross-section counterpart [9, 10]. Diverging–converging microchannels (diamond) are characteristic non-uniform channels and flow in diamond microchannels have numerous applications in medicine, engineering and biology, such as in heat transfer enhancement [11], flow rectification [12], DNA stretching [13], micromixer [14,15,16], particle separation [17], etc. These applications require a thorough, fundamental understanding of the flow physics in diamond microchannels especially from the viewpoint of design optimization.

Several attempts have been made to investigate flow in diverging–converging channels at the conventional and microscales, for which flow physics and different flow scenarios have been studied [18,19,20,21,22,23,24,25,26,27]. It is observed that the flow through mild converging–diverging tube is laminar for Reynolds number, Re < 900 [18], while flow through converging–diverging tube with relatively large convergence/divergence angle shows flow instability and turbulence when Re > 400 [28]. In other converging–diverging channels, flow remains laminar for Reynolds number ranging from 100-1000 [19]. The above observations show that the flow in diverging–converging channels is substantially different from straight channels. Therefore, studying the effect of geometrical configuration on the nature of the flow is relevant. Compared to other varying cross-section microchannels, diverging–converging microchannels have received less attention [11, 29,30,31]. Further, it is interesting to see whether the flow properties in microchannel with diverging–converging configuration are dependent on aspect ratios, diverging–converging angles and Reynolds numbers. Most of the available studies have not presented the underlying physics and no clear understanding of the effect of various geometric and flow parameters on the flow in a diamond microchannel is available in the literature. These issues provided the motivation for undertaking the present work.

Of particular interest is in defining the length scale (hydraulic diameter) required in the calculation of various non-dimensional numbers. Since the microchannel cross-section varies along the length, it is difficult to fix the appropriate value of the characteristic length scale [32,33,34]. Duryodhan et al. [35] provided a methodology to obtain the characteristic length scale for microchannel having a diverging or a converging cross-section. Based on a comprehensive study, they recommended that the value of hydraulic diameter be calculated at 33% and 28% of the total length of the microchannel from the narrow end for the diverging and converging configurations respectively. The above-mentioned length scale is not applicable to diamond microchannel with both diverging and converging sections; however, it interesting to see if the procedure for obtaining the length scale suggested by them is applicable to this more complex geometric configuration.

The specific objectives of this work are to study the local and global behavior of single-phase laminar liquid flow passing through diamond microchannel and obtain the critical parameters to characterize the flow. Towards this, a three-dimensional numerical study on laminar single-phase flow through diamond microchannel has been carried out. The effects of hydraulic diameter, total length, inlet diamond angle, width ratio on flow behavior have been studied in detail. The results are discussed with the help of pressure and velocity profiles, and wall shear stress. An appropriate length scale is also identified based on the methodology proposed in the literature.

2 Physical description of the problem

2.1 Geometric configuration of different non-uniform microchannels

Microchannels with variable cross-section along the axial direction are called non-uniform microchannels. There are flow passages with both converging and diverging sections of certain lengths. To generalize this, a parameter length ratio (δ) (Eq. 1), which is the ratio of length of the diverging section to the total length of the microchannel

$$\delta = \frac{{L_{d} }}{L}$$
(1)

is defined here. Table 1 shows the different non-uniform cross-section microchannels using the parameter \(\delta\). The present study is focused on diamond microchannels with equal length ratio i.e. δ = 0.5 (symmetric diamond microchannels). That is, in this study we are not considering asymmetric diamond channel to avoid the asymmetric transfer characteristic of a flow passage, or fluidic diodicity [12].

Table 1 Geometric configuration of different types of non-uniform cross-section microchannels based on length ratio (δ)
Full size table

2.2 Diamond microchannel

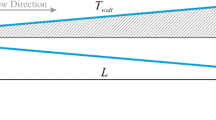
Diamond microchannel is a non-uniform cross-section microchannel with diverging and converging sections of certain lengths. Figure 1 shows the geometric configuration of diamond microchannel.

Fig. 1
figure 1

Geometric configuration of diamond microchannel used in the numerical simulation a top view and b isometric view

Full size image

In Fig. 1, Wi and Wo are the inlet and outlet width of the microchannel (taken to be equal here) to avoid complexity as described before, α is the inlet diamond angle, β is the outlet diamond angle, Wb is the larger width (interface width) of the microchannel, Ld and Lc are lengths of the diverging and converging section of the microchannel, L is the total length of the microchannel (which is the sum of the lengths of diverging and converging sections), δ is the length ratio (Eq. 1), and

$$\varepsilon = \frac{{W_{b} }}{{W_{i} }}$$
(2)

is the width ratio. Table 2 shows the range of parameters for the present numerical simulations.

Table 2 Geometrical and flow parameters considered for numerical analysis
Full size table

3 Mathematical formulation

Three-dimensional numerical simulations are performed on diamond microchannels using a commercially available software (ANSYS Fluent V16) to comprehend the liquid flow through diamond microchannel. Steady, three dimensional governing equations for mass and momentum conservation are solved using direct numerical simulation (DNS) along with appropriate boundary conditions. The minimum dimension of the model is greater than 10 µm and Reynolds number considered for numerical simulation are in the range of 0–400. Hence, steady and continuum flow assumptions are valid for the present model [18, 19, 28, 31, 36]. The governing equations for isothermal and incompressible Newtonian fluids can be expressed asConservation of mass

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0$$
(3)

X-momentum

$$\rho \left( {u\frac{\partial u}{dx} + v\frac{\partial u}{\partial y} + w\frac{\partial u}{dz}} \right) = - \frac{\partial P}{\partial x} + \mu \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{{\partial^{2} u}}{{\partial z^{2} }}} \right)$$
(4)

Y-momentum

$$\rho \left( {u\frac{\partial v}{dx} + v\frac{\partial v}{\partial y} + w\frac{\partial v}{dz}} \right) = - \frac{\partial P}{\partial y} + \mu \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }} + \frac{{\partial^{2} v}}{{\partial z^{2} }}} \right)$$
(5)

Z-momentum

$$\rho \left( {u\frac{\partial w}{dx} + v\frac{\partial w}{\partial y} + w\frac{\partial w}{dz}} \right) = - \frac{\partial P}{\partial z} + \mu \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{{\partial^{2} w}}{{\partial z^{2} }}} \right)$$
(6)

where x, y, z are coordinates along the length (mm), depth (µm) and width (µm), u, v, w are the corresponding flow velocities (m/s), ρ and µ are density (kg/m3) and dynamic viscosity (N-s/m2) of the fluid.

Boundary conditions are taken as constant mass flow rate at the inlet, constant pressure at the outlet, and no slip at the inner walls. Pressure based solver is used with semi implicit method for pressure linked equations (SIMPLE) scheme for pressure–velocity coupling. Second order discretization scheme is employed for pressure equation whereas momentum equation is discretized using quadratic upstream interpolation for convective kinetics (QUICK). Absolute convergence criterion is set as 10−5 for the residuals of all the equations.

A three-dimensional computational grid of the geometric model generated by using GAMBIT 2.4.6 (Fluent Inc.) is shown in Fig. 2. The computational domain is discretized into several number of hexahedral elements. To eliminate the influence of gird size on the accuracy of the numerical simulation, a grid independence study was carried out for a representative case of microchannel of inlet angle 16° with total length of 20 mm as shown in Table 3. The grid of 5,00,000 hexahedral elements is finally employed in the computations as the deviation in pressure drop between grid numbers of 5,00,000 and 9,00,000 is very small (0.38%).

Fig. 2
figure 2

Computational grid of the microchannel used in numerical simulations

Full size image
Table 3 Grid independent study for numerical simulations
Full size table

3.1 Validation

For the purpose of validation, detailed CFD computations were first undertaken for simple geometries for which there is a known solution. To validate the numerical model, the 4° diverging microchannel is simulated and compared with the experimental pressure drop of Duryodhan et al. [34]. It is observed that the results are in good agreement with the experimental data; the maximum deviation is obtained to be 12.1% from the results of Duryodhan et al. [34]. In addition, numerical pressure drop is directly compared with experimental pressure drop for a diamond microchannels of α = 8°, H = 200 µm, L = 20 mm and α = 4°, H = 240 µm, L = 20 mm. It is observed from Fig. 3 that the numerical results are in good agreement for microchannels with α = 4° (9% average and 12% maximum deviation) and α = 8° (12% average and 18% maximum deviation) with respect to the experimental data. The deviation can be attributed to some difference in the inlet and exit conditions; for example, there are inlet and exit reservoirs that have not been modelled in the simulations.

Fig. 3
figure 3

Validation of numerically obtained pressure drop with that of experimental pressure drop for a diamond microchannel

Full size image

4 Variation in pressure drop

4.1 Theory

For laminar flows, the total pressure drop in microchannel is expressed through the following equation

$$\Delta P = \mathop \smallint \limits_{0}^{L} \left( {2\rho V\left( x \right)^{2} f\left( x \right)\frac{1}{{D_{h} \left( x \right)}}} \right)dx$$
(7)

where L is the total length of channel, ρ is the density of liquid, V is the average velocity, f is the friction factor, Dh is the hydraulic diameter, and x is the flow direction. Since the cross-section changes along the flow direction, the hydraulic diameter at each location can be expressed as:

$$D_{h} \left( x \right) = \frac{2W\left( x \right)H}{W\left( x \right) + H}$$
(8)

where W(x) is the variable width of the microchannel along the flow direction and H is constant depth of the microchannel. The average velocity can be expressed as:

$$V\left( x \right) = \frac{{\dot{m}}}{\rho A\left( x \right)}$$
(9)

where \(\dot{m}\) is the mass flow rate, A(x) is the area of cross-section at x location. Reynolds number Re(x) along the flow direction can be written as:

$${\text{Re}}\left( x \right) = \frac{{\rho V\left( x \right)D_{h} \left( x \right)}}{\mu }$$
(10)

As per the theory of straight rectangular microchannel, the friction factor for fully developed, incompressible and laminar flow in a rectangular microchannel can be evaluated using the correlation [37]:

$$f \cdot {\text{Re}} = 24\left( {1 - 1.3553\gamma + 1.9467\gamma^{2} - 1.7012\gamma^{3} + 0.9564\gamma^{4} - 0.2537\gamma^{5} } \right)$$
(11)

where γ is the aspect ratio at the specified location

$$\gamma = \frac{H}{W\left( x \right)}$$
(12)
$$f\left( x \right) = \frac{{f \cdot {\text{Re}}}}{{{\text{Re}}\left( x \right)}}$$
(13)

Using the above equations, the theoretical pressure drop is calculated for different geometrical and flow parameters and compared with numerical pressure drop as discussed in the next section. The pressure drop is calculated over the flow rate range of 0.5–5 ml/min (8.33 × 10−6 to 8.33 × 10−5 kg/s).

4.2 Effect of inlet angle

Figure 4 shows that the pressure drop varies linearly with flow rate, which is qualitatively similar to that of uniform microchannel with the exception of microchannel with 16° inlet angle. The pressure drop is decreasing with increasing inlet angle for a given flow rate. In addition, it is observed that the theoretical and numerical pressure drops for different microchannels are in good agreement with each other (with an average discrepancy being 4%) which suggests that at an appropriate length scale using existing correlations for uniform microchannels can be applied to present configuration within specified range. For 16° inlet angle, variation of pressure drop with increasing flow rate is observed to be non-linear. The reason for the presence of non-linearity will be explained in Sect. 6.

Fig. 4
figure 4

Numerical and theoretical pressure drop variation with volume flow rate for different inlet angles with H = 100 µm and L = 20 mm

Full size image

4.3 Effect of width ratio

Figure 5 shows the variation of pressure drop with flow rate for different width ratios ranging from 3.33 to 15. Study has been done on microchannel with inlet angle of 8°, L = 20 mm, and H = 100 µm. The width ratio has been changed while keeping all other parameters constant.

Fig. 5
figure 5

Numerical and theoretical pressure drop variation with volume flow rate for different width ratios for a given microchannel with inlet angle of 8°, H = 100 µm and L = 20 mm

Full size image

It is observed from Fig. 5 that for a given flow rate, pressured drop increases with increase in width ratio. In addition, it can be seen that at larger width ratio, i.e. ɛ = 15, the pressure drop is a non-linear function with flow rate and it shows a large deviation from the theoretical pressure drop, whereas other cases are in good agreement with the theoretical pressure drop. The reason for this non-linearity is due to the appearance of flow reversal and separation zones, as explained in detail in Sect. 6.

4.4 Effect of depth and length

Figure 6 shows the variation of pressure drop with flow rate for three different depths (60–150 µm) considered for analysis. It is observed that depth has a notable effect on the pressure drop across the microchannel. The percentage difference between pressure drop for a given flow rate decreases with increase in hydraulic diameter. This is because the pressure drop is an inverse function of the hydraulic diameter for rectangular microchannels and depth has a significant influence on the hydraulic diameter.

Fig. 6
figure 6

Numerical and theoretical pressure drop variation with volume flow rate for different depth with α = 8°, L = 20 mm and ɛ = 8

Full size image

Along with the effect of inlet angle, depth and width ratio, the effect of total length of microchannel on pressure drop has also been studied. Three models of lengths 10, 20 and 30 mm with constant inlet angle of 8° and depth of 100 µm are considered for analysis. Figure 7 shows that the pressure drop is directly proportional to the length of microchannel. This trend is similar to that of straight microchannel.

Fig. 7
figure 7

Numerical and theoretical pressure drop variation with volume flow rate for different length with α = 8° and H = 100 µm

Full size image

5 Characteristic length scale for diamond microchannel

For flow through microchannels, the value of hydraulic diameter is a measure of the characteristic length scale. For microchannel with circular cross-section, hydraulic diameter is the diameter of the circular cross-section; but for microchannels with non-circular cross-section, the hydraulic diameter is the ratio of four times the cross-sectional area to the perimeter of the microchannel. The hydraulic diameter is usually defined for the purpose of pressure drop calculations. Hydraulic diameter is a function of cross-sectional area and it remains invariant if the area of the cross-section of the microchannel is constant. However, for microchannel with variable cross-section (diamond) encountered here, the hydraulic diameter is a non-linear function of position as plotted in Fig. 8. Previously, Stemme et al. [32] and Gerlach et al. [33] had defined the characteristic length scale of their non-uniform cross-sectional microchannel at the inlet of the microchannel:

$$D_{h} = \left. {D_{h} } \right|_{inlet}$$
(14)
Fig. 8
figure 8

Variation of hydraulic diameter along the streamwise direction for symmetric diamond microchannel with inlet diamond angle of 8° and total length of 20 mm

Full size image

Besides Eq. 14, the hydraulic diameter is defined by taking average of larger width and inlet width of the microchannel [11, 38, 39]. As per this definition, the hydraulic diameter is located at 1/4th part of the total length i.e. at about 25% of the total length. By comparing the pressure drop in microchannel with uniform cross-section using hydraulic diameter given by [11, 38, 39] against the pressure drop for diamond microchannel with α = 8°, L = 20 mm and H = 100 µm for a flow rate of 3 ml/min. The theoretical pressure drop is found to be 34% lesser than the actual pressure drop. Table 4 shows the hydraulic diameters calculated theoretically based on different methods and made a comparison of pressure drop between uniform and diamond microchannels for the above- mentioned case. The pressure drop for uniform microchannel is predicted by using Eq. 11 by employing the theoretically calculated hydraulic diameter by the above-mentioned methods. From Table 4, it is observed that the hydraulic diameters obtained by different theoretical methods are not the appropriate length scales for this problem and hence we need to look for better location to predict the theoretical pressure drop.

Table 4 Theoretically calculated hydraulic diameters using different methods and pressure drop comparison between diamond and uniform microchannel
Full size table

5.1 Equivalent hydraulic diameter

As discussed in Duryodhan et al. [35], the aforementioned parameters are not satisfactory. For example, Eq. 14 does not carry any information about the divergence angle. Duryodhan et al. showed that the microchannel with uniform cross-section having the hydraulic diameter calculated at the inlet of a diverging microchannel yielded about 550% higher pressure drop as compared to the actual pressure drop. In view of this, Duryodhan et al. suggested an algorithm to obtain the characteristic length scale. The idea is to define the characteristic length scale as an equivalent hydraulic diameter such that it establishes a frictional equivalence between non-uniform and corresponding uniform microchannels.

$$\left. {D_{h} } \right|_{uniform} = \left. {D_{h,equivalent} } \right|_{diamond}$$
(15)
$$\left. {\Delta P} \right|_{uniform} = \left. {\Delta P} \right|_{diamond}$$
(16)

The algorithm followed for estimating the equivalent hydraulic diameter is as follows:

Step 1

Calculate the value of Poiseuille number (f∙Re) at different locations in the microchannel and compare the calculated value of f∙Re with theoretical f∙Re obtained by using Eq. 11.

Step 2

Locate the width at which the numerically obtained Poiseuille number coincides with the theoretical value, which is called characteristic width.

Step 3

Identify the location at which the characteristic width is located from the inlet of the channel and obtain the characteristic length.

The Poiseuille number (Po) written as Po = f∙Re is given by

$$f \cdot {\text{Re}} = \left( {\frac{\rho }{2\mu L}} \right)\left( {\frac{\Delta P}{{\dot{m}}}} \right)\left( {D_{h}^{2} A} \right)$$
(17)

where ΔP and \(\dot{m}\) are the pressure drop and mass flow rate, f and Re are Fanning friction factor and Reynolds number, Dh, A are, respectively, hydraulic diameter, area of cross-section, which are calculated at characteristic location. The theoretical f∙Re values are calculated using Eq. 11. From Fig. 9,

$$W_{c} = W_{i} + \frac{2L}{n}{ \tan }\left( {\frac{\alpha }{2}} \right)$$
(18)

where Wc is the characteristic width which is located at L/n distance from the inlet of the microchannel width Wi and L’c (= L/n) refers to the characteristic length at which the equivalent hydraulic diameter is calculated.

Fig. 9
figure 9

Representation of characteristic location in a diamond microchannel

Full size image

Figure 10 shows the estimation of characteristic location for symmetric diamond microchannel with total length of 20 mm, inlet and outlet angle of 8°, and depth of the microchannel is 100 µm. It is observed that for the given case, the characteristic location is obtained at 1/7th of the total length of the microchannel from inlet. This can be explained by diodicity (D) [12] of the microchannel.

$$D = \frac{{\Delta P_{forward} }}{{\Delta P_{backward} }}$$
(19)

From Eq. 19, it can be understood that it has the same resistance for both the flow directions because of the symmetric nature of the microchannel. Similarly, we have obtained the characteristic location for the given range of geometric and flow parameters in Table 2 as a function of Reynolds number is shown in Fig. 11. Observe that the location of the equivalent hydraulic diameter lies between 1/6.4th and 1/7.9th of the total length of microchannel for all the cases under study, with the mean value of 1/7. It is also noted that the location is invariant of Reynolds number.

Fig. 10
figure 10

Estimation of characteristic location for the symmetric diamond microchannel with total length of 20 mm, inlet and outlet angle of 8°, and depth of 100 µm for the volume flow rate of 3 ml/min

Full size image
Fig. 11
figure 11

Variation of equivalent hydraulic diameter as a function of Reynolds number for all the geometric and flow parameters

Full size image

The location of hydraulic diameter, which is the mean value of all the obtained locations, therefore lies at 1/7th of the length of the microchannel. The characteristic width of the microchannel at the modified location, which is expressed in terms of known geometric parameters, is given as,

$$W_{c} = W_{i} + \frac{2L}{7}{ \tan }\left( {\frac{\alpha }{2}} \right)$$
(20)

5.2 Variation in Poiseuille number

The pressure drop and mass flow rate are converted to non-dimensional number (Fanning friction factor and Reynolds number) for the purpose of better comparison among various cases. The Poiseuille number (Po= f∙Re) is calculated using Eq. 17 and it is compared with the theoretical f∙Re obtained using Eq. 11. Figure 12 shows the Poiseuille number variation with Reynolds number for different cases for which hydraulic diameter is taken at the modified characteristic location. It is observed that f∙Re is almost invariant with Reynolds number and in good agreement with the Shah and London [37] correlation. In addition, f∙Re value lies within an absolute average error of 7% compared to theoretical f∙Re values (maximum deviation is 28%). The equivalent hydraulic diameter at the characteristic location provides frictional characteristics equivalence between diamond microchannel and uniform microchannel.

Fig. 12
figure 12

f∙Re values for cases with modified hydraulic diameter a different inlet angle, b different depth, c different length

Full size image

6 Flow characterization and critical parameters

In previous studies for microchannels with non-uniform cross-section, the averaged channel size is employed for flow characterization [40, 41]. For the geometric configuration considered in this work, hydraulic diameter Dh= 4A/P′ appears to be a proper parameter, where A and P′ are the cross-sectional area and the perimeter at the characteristic location (at L/7th location from inlet) obtained in Sect. 5 and the corresponding value of Re can be calculated using this value of hydraulic diameter.

From Sect. 4, it is clear that a large inlet angle α or large width ratio ɛ leads to anomalous behavior in pressure drop variation because of the strong flow velocity variation in the channel which enhances flow instability. For better understanding of this behavior, we are considering flow resistance Rf which is defined as the ratio of overall pressure drop across the microchannel to the given flow rate [23, 42]:

$$R_{f} = \frac{\Delta P}{Q}$$
(21)

Using Eq. 21, Fig. 13 shows the flow resistance, Rf as a function of Re for different inlet angles and width ratios. It is also known from the theory that for laminar flows, the flow resistance is independent of Reynolds number. From the figure, there exists a critical Re, Rec, which depends on the geometry of the microchannel. This is consistent with the previous findings in the literature for microchannels with non-uniform cross-sections [18,19,20,21].

Fig. 13
figure 13

Flow resistance Rf as a function of Re for a different inlet angle, b different width ratio

Full size image

For the four different cases presented in Fig. 13a, Rec is about 185 for inlet angle of 12° and 135 for 16° respectively. At this value, Rf deviates from its mean value by 5.5% for both angles. From Fig. 13b, it is about 139 for highest width ratio i.e. for ɛ =15 which is obtained at the flow rate of 2.5 ml/min and Rf shows 10% deviation from its mean value whereas for all other cases flow remains in laminar region as flow resistance shown to be independent of Reynolds number. This flow transition explains the anomalous behavior of pressure drop in Figs. 3 and 4 for higher inlet angle (α) and higher width ratio (ɛ). It also shows that the effect of width ratio is more significant than inlet angle on flow resistance, as confirmed further by velocity streamline plots shown in Fig. 14.

Fig. 14
figure 14

Velocity streamline plots showing recirculation and separation zones for a α = 8°, ɛ = 15, Re = 111, b α = 8°, ɛ = 15, Re = 139, c α = 8°, ɛ = 15, Re = 167, d α = 8°, ɛ = 15, Re = 278, e α = 12°, ɛ = 11.5, Re = 167, f α = 12°, ɛ = 11.5, Re = 185, g α = 16°, ɛ = 15, Re = 121, h α = 16°, ɛ = 15, Re = 136, i α = 16°, ɛ = 15, Re = 151 (Not to scale)

Full size image

From Fig. 14, the presence of recirculation zones and flow separation is evident for Re > Rec. Because of this, flow deviates from laminar behavior and hence uniform microchannel theory for laminar flows cannot be applied beyond this limit. This is consistent with Fig. 13 where f∙Re values for higher angle shows large deviation from its corresponding theoretical value. Furthermore, previous studies [23] mentioned that Rec> 100 for the converging–diverging cross-section microchannel employed in their study.

Although the presence of recirculation zones causes the change in the flow behavior, they are restricted to the entry region of the microchannel. These vortices, however may arise at the junction of the inflection region (region at which channel curvature changes from diverging to converging section) and becomes important for further increase in inlet angle and width ratio [43, 44].

6.1 Discussion

The disturbances in the flow pattern usually create flow instabilities [45]. Flow separation has a high tendency to destabilize the flow. The present geometry displays a flow separation zone at the entry region of the microchannels for the higher inlet angle and the higher width ratio (Fig. 14). However, the accelerating flow through converging microchannel causes the separated streamlines to reattach to the wall along the flow direction resulting in restricting the recirculation zones to the entry region of the microchannel. The flow reversal region is not strong enough to create the flow disturbance, however, the flow starts deviating from the laminar behaviour as evident from Fig. 13. This indicates a flow transition but this does not imply that the flow is turbulent. In other words, a new complex but still laminar flow evolves; however, for further increase in the values of α, ɛ and Re, the flow pattern tends to become unstable and may even transit to turbulent flow regime.

7 Flow physics

To understand the internal flow physics, it is necessary to understand the local distribution of pressure, velocity and shear stress for flow through diamond microchannels.

7.1 Local pressure distribution

Figure 15 shows a non-dimensional distribution of pressure along the stream wise direction for different angles (0° [straight], 4°, 8°, 12°, 16°). The centerline pressure has been taken for analysis and it has been non-dimensionalized based on following equation:

$$P^{*} = \frac{{P - P_{out} }}{{P_{in} - P_{out} }}$$
(22)

P is local centerline pressure along the flow direction and Pin and Pout are centerline pressures at inlet and outlet respectively. The length of the microchannel is 20 mm and the flow rate considered for this simulation is 5 ml/min.

Fig. 15
figure 15

Variation of non-dimensional local pressure along the streamline in symmetric diamond microchannel for different inlet angles of L = 20 mm and volume flow rate of 5 ml/min

Full size image

From Fig. 15, for straight microchannel, the pressure decreases along the flow direction with constant negative slope that indicates the fully developed flow. For microchannels with inlet angles of 4°–12°, the static pressure decreases along the flow direction, however, the dynamic pressure decreases and increases in diverging and converging sections. This is because the flow decelerates and accelerates in diverging and converging sections (Fig. 17). Consequently, the steep pressure drop is observed in the region 0 < x/L < 0.2 and this steepness increases as inlet angle increases. For the microchannel with α = 16°, the adverse pressure gradient occurs because of an increase in static pressure in the region 0 < x/L < 0.2. The increase in the static pressure is large enough to cause the excessive momentum loss inside the boundary layer, which leads to the occurrence of flow separation near the wall. In addition, the presence of steep pressure gradients has significant implications for the bubble dynamics in diamond microchannel. A bubble in a diamond microchannel moves easily especially near the entrance because of the presence of steep pressure gradient.

7.2 Velocity distribution

Figure 16 shows velocity contours taken at mid-plane for microchannel with different inlet angles (4°, 8°, 12°, 16°). The total length of the microchannel is 20 mm. Flow rate considered for this analysis is 5 ml/min. It is noted that velocity decreases along the streamwise direction in the diverging section and increases in the converging section. It shows non-linear variation from inlet to outlet. Velocity decreases with increase in inlet angle while maintain the same trend which indicates larger pressure recovery for larger angle. This is consistent with the decrease in pressure drop as inlet angle increases that is shown in Fig. 4.

Fig. 16
figure 16

Velocity contours for microchannel with different inlet angles of L = 20 mm and volume flow rate of 5 ml/min

Full size image

It is also observed that the flow profile remains in developing condition throughout the channel. Velocity remains constant at the inflection zone with increase in the inlet angle. In other words, the velocity gradient is minimum or non-existent in the inflection zone for larger angles in this region. This is further demonstrated by Fig. 17.

Fig. 17
figure 17

a Variation of \(u.\frac{du}{dx}\) along the flow direction for inlet angles of 4° and 16°, b enlarged view in the inflection zone (0.4 < x/L < 0.6)

Full size image

Figures 17a, b illustrate the effect of inlet angle on \(u.\frac{du}{dx}\) (convective deceleration and acceleration). The centerline velocity was considered for this purpose and the flow rate is 5 ml/min. From Fig. 17a, it is observed that the microchannel with inlet angle of 4° has larger deceleration rate (by 4%) and larger acceleration rate (by 32%) when compared to the microchannel with inlet angle of 16° although there is a sharp increase in acceleration rate for larger angle after x/L = 0.95. Figure 17b shows the enlarged view of the nature of \(u.\frac{du}{dx}\) in the inflection zone (0.4 < x/L < 0.6). It is noted that acceleration and deceleration for larger angle remains almost zero, which indicates that both the local and material acceleration are zero and nearly constant velocity is maintained in this region.

For further verification of nature of flow, non-dimensional velocity profiles taken along the width and depth at different streamwise locations for diamond microchannel with different inlet angles. Figure 18 shows the non-dimensionalized velocity profile considered along the width at different streamwise locations for diamond microchannel of different inlet angles with L = 20 mm and flow rate of 5 ml/min. Velocity profile taken at mid-plane of the microchannel is non-dimensionalized using the maximum velocity, which is at the midpoint of each plane. The velocity profile is parabolic at x/L = 0 as flow enters in fully developed condition (Fig. 18a). Figure 18b shows an underdeveloped parabolic profile at x/L = 0.2. The velocity profile remains flat throughout the channel, which indicates that the flow is in developing condition (Figs. 18c, d, e). This is because of the variation of Reynolds number (Rex) in the microchannel and its relation with the hydro-dynamically developing/entrance length (xh). It is known that the entrance length (xh) of the channel flow is directly proportional to Rex [46]

$$x_{h} = 0.05{\text{Re}}D_{h}$$
(23)
Fig. 18
figure 18

Non-dimensional velocity profile along the width at different location along flow direction at flow rate of 5 ml/min for diamond microchannel with different inlet angles

Full size image

In the converging section, because of flow acceleration, the Reynolds number increases rapidly towards the outlet of the microchannel. Hence, it is difficult to obtain developed flow and form a parabolic velocity profile along the width near the exit of the microchannel. Therefore, the velocity profile remains flat towards the exit of the microchannel. In addition, there is a difference in velocity profiles at x/L = 0.2 and x/L = 0.8 even though they are at the same location from the narrow ends of both diverging and converging section. This shows the difference in rate at which flow decelerates and accelerates in diverging and converging sections.

Figure 19 shows the non-dimensionalized velocity profiles taken along the depth at different streamwise locations with different inlet angles, L = 20 mm, and flow rate of 5 ml/min. The velocity profile along the depth of the microchannel is observed to be parabolic at all locations along the streamwise direction for all the microchannels. This implies that the flow remains in the fully developed condition along the depth of the microchannel irrespective of the location in microchannel.

Fig. 19
figure 19

Non-dimensional velocity profile along the depth at different location along flow direction at flow rate of 5 ml/min for diamond microchannel with different inlet angles

Full size image

7.3 Wall shear stress variation

Figure 20 shows the wall shear stress variation on the bottom and sidewalls along the flow direction for inlet angles of 4° and l6° and L = 20 mm. The flow rate is 5 ml/min for this analysis.

Fig. 20
figure 20

Variation of a bottom wall shear stress distribution, b sidewall shear stress along the flow direction for inlet angles of 4° and 16°

Full size image

From Fig. 20, it is observed that both bottom wall shear stress and sidewall shear stress decreases with increase in inlet angle even though there is a sharp increase in the wall shear stress for larger angle. This is because velocity along the flow direction decreases with increase in inlet angle (Fig. 16). In addition, the variation of shear stress along the flow direction justifies the continuous variation of velocity gradient at the wall along the flow direction. For the case of 4°, the bottom wall shear stress decreases in the diverging section and increases in the converging section, whereas on the sidewall, the shear stress drops suddenly at the entry and then maintains almost constant throughout the diverging region and increases in the converging region. The variation of bottom wall shear stress and sidewall shear stress in case of 16° is similar to that of smaller inlet angle with sharp increase in the shear stress towards the outlet of the microchannel. This is because of flow acceleration towards the outlet of the microchannel, which leads to a sharp increase in the velocity gradient towards the exit of the microchannel.

8 Conclusions

A three dimensional numerical study is conducted to understand the flow physics in diamond microchannel. A parameter length ratio (δ) is proposed to generalise the different cases of non-uniform microchannels. For the geometric and flow parameters considered in this study, the following observations have been made:

  1. 1.

    The pressure drop varies inversely with inlet angle, width ratio and hydraulic diameter has significant influence. It is also observed that the numerically obtained pressure drop is in good agreement with the theoretically calculated pressure drop, which implies that the existing theory for uniform microchannels can also be applied to present geometrical configuration by using an appropriate characteristic length scale.

  2. 2.

    The equivalent hydraulic diameter is calculated at 1/7th of the length of the microchannel from its inlet is proposed as the length scale for diamond microchannel. This can be used to design and fabricate corresponding equivalent uniform microchannel that has same pressure drop as diamond microchannel. The Hagen-Poiseuille equation can be applied to diamond microchannel using this length scale, its location is shown to be independent of geometric, and flow parameters considered in this study.

  3. 3.

    Inlet angle (α) and width ratio (ɛ) are parameters that characterize the flow through diamond microchannel. It is observed that effect of width ratio has more significance than inlet angle on flow resistance.

  4. 4.

    For 0° < α < 12° and 3.3 < ɛ < 11.5, the pressured drop can be predicted for the diamond microchannel using the straight microchannel theory in laminar flow regime for Re in the range of 0–400 whereas for 12° < α < 16° and 11.5 < ɛ < 15, it can be applied for Re < Rec.

  5. 5.

    Flow physics in diamond microchannel is explained with the help of local pressure, velocity, and the wall shear stress distribution. The presence of steep pressure gradients at the entry region of microchannel provides an easy movement of bubble through microchannel that may have significant implications in the study of bubble dynamics in multiphase flows. The present configuration may also have significant implications in the study of particle dynamics. The appearance of recirculation zones may contribute in entrapment of particles [47,48,49,50].

  6. 6.

    Flow remains in developing condition along the width throughout the microchannel even though flow enters the channel in fully developed condition. It is confirmed with the help of velocity profiles along the width at different locations along the flow direction. Flow however remains in fully developed condition along the depth throughout the microchannel.

  7. 7.

    Velocity varies along the flow direction because of the variable cross-section; however, the flow decelerates and accelerates in both diverging and converging flow passages at different rate even though both diverging and converging passages of same size. This continuous variation of velocity gradient along the flow direction is explained further with the help of wall shear stress distribution.