1 Introduction

Precipitation and mass transfer of nanoparticles in fluids are common phenomena in scientific and industrial applications, such as the monitoring and controlling of product manufacturing processes and their quality. In medical and biological fields, homogeneous PLA/insulin solutions containing different amounts of Da PEG (0–75 wt% PEG) were processed by semi-continuous, compressed CO2 antisolvent precipitation to fabricate protein-loaded polymeric nanoparticles (Caliceti et al. 2004). Polymeric scaffolds were fabricated with micro- and nanoscale porosity by developing a new technique that couples two conventional scaffold production methods: solvent casting-salt leaching and gas antisolvent precipitation to avoid the mass transport through biocompatible and biodegradable polymeric 3D porous scaffolds depleted by nonporous impermeable internal walls (Flaibani and Elvassore 2012). Engineers also investigated nanoparticle precipitation in a confined impinging jet reactor (CIJR) (Gavi et al. 2007). With the aim of obtaining controlled size and particle size distributions of these superconductor precursors, semi-continuous supercritical antisolvent (SAS) precipitation has been used to produce europium (EuAc) and gadolinium (GdAc) acetate nano- and microparticles (Reverchon et al. 2002). Most of the base fluids of nanosolutions in industrial and scientific fields are non-Newtonian fluids (i.e., fluids that do not satisfy the linear relationship between the shear stress and the shear rate of deformation). Non-Newtonian fluids cover a wide range of fluids including, but not limited to: colloidal emulsoid, cosmetics, UV protection gel, lubricants, corrosion resistant coatings, pigments, oils, paints, milk, toothpaste, mud, vivo blood, intra-articular synovial fluid, lymph fluid, cells fluid, cerebrospinal fluid and bronchial endocrine liquid (Bird et al. 1960). Shear thinning, stress relaxation, creep, hysteresis, residual stress, viscoelastic, turbulent drag reduction and slip in non-Newtonian fluids have important impacts on nanoparticles in flow fields (Tropea et al. 2007; Rao 2007). Thus, many researchers have focused on the characteristics of nanofluids of which the base fluids are non-Newtonian fluids. For instance, Moraveji et al. (2012) investigated the convective heat transfer effect on non-Newtonian nanofluids flow in the horizontal tube with constant heat flux. The forced convective heat transfer of these nanofluids in carboxymethyl cellulose (CMC) through a uniformly heated circular tube under turbulent flow conditions has been studied experimentally (Hojjat et al. 2011). Hady et al. (2011) focused on the study of the natural convection boundary-layer flow over a downward-pointing vertical cone in a porous medium saturated with a non-Newtonian nanofluid in the presence of heat generation or absorption. In paper (Mariano et al. 2013), the thermal conductivity, rheological behavior and the high-pressure density of several non-Newtonian ethylene glycol-based SnO2 nanofluids were analyzed.

Pascal (1996) proposed a one-dimensional convection–diffusion model with nonlinear molecular diffusion for mass transfer in a two-phase system. Niu et al. (2012) also adopted the power-law rheology to describe the characteristics of a non-Newtonian nanofluid flow in a microtube theoretically. Our own research work in this area initially was based on these pioneering works by modeling the volume fraction of nanoparticles and verified the experimental conclusion through the numerical simulation of particle distribution in nanofluid in a Petri dish under the influence of movement using the model (Zheng et al. 2012):

$$ \varphi_{t} + u \cdot \nabla \varphi = {\text{div}}(D_{B}^{0} \nabla C(x,y)), $$

where

$$ C(x,y) = (\varphi_{x}^{2} + \varphi_{y}^{2} )^{{\frac{n - 1}{2}}} . $$

In this paper, we will further this investigation by considering the vertical precipitation in nanofluid-based power-law fluids over a free-rotating disk. On a similar assumption that the mass diffusivity follows a power-law type, the coupled governing equations are transformed into ODEs in the boundary layer. The accuracy of the solutions is pursued by employing a homotopy analysis method rather than a pure numerical simulation. However, the power-law terms in the momentum and mass transfer equations are difficult to handle, and so special attention needs to be paid to the mathematical technique involved in the process of the mth-order deformation. Finally, we will qualitatively validate the numerical simulation by comparison with experiments of particle distribution in nanofluid in a Petri dish under the influence of movement.

2 Physical model and similarity transformation

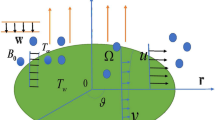
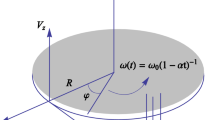
Consider a laminar non-Newtonian power-law flow in a rotating infinite disk with angular velocity Ω about the z-axis. No-slid and impermeability exist on the disk. Assume the flow is steady and axisymmetric. The cylindrical polar coordinate system and physical model are shown in Fig. 1.

Fig. 1
figure 1

The cylindrical polar coordinate system and physical model

Full size image

The pressure is considered to be constant in the boundary layer. Thus, the governing equations are:

$$ \frac{\partial u}{\partial r} + \frac{u}{r} + \frac{\partial w}{\partial z} = 0 $$
(1)
$$ \rho \left( {u\frac{\partial u}{\partial r} - \frac{{v^{2} }}{r} + w\frac{\partial u}{\partial z}} \right) = \frac{\partial }{\partial z}\left( {\mu \frac{\partial u}{\partial z}} \right) $$
(2)
$$ \rho \left( {u\frac{\partial v}{\partial r} + \frac{uv}{r} + w\frac{\partial v}{\partial z}} \right) = \frac{\partial }{\partial z}\left( {\mu \frac{\partial v}{\partial z}} \right) $$
(3)
$$ u\frac{\partial \phi }{\partial r} + w\frac{\partial \phi }{\partial z} = \frac{\partial }{\partial z}\left( {D_{B}^{0} \frac{\partial \phi }{\partial z}} \right) $$
(4)

where u, v and w are velocity components in the directions of r, φ and z, respectively. ϕ is the concentration while ρ is the density of the fluid. The viscosity μ obeys the power-law model \( \mu = \mu_{0} \left\{ {\left( {\frac{\partial u}{\partial z}} \right)^{2} + \left( {\frac{\partial v}{\partial z}} \right)^{2} } \right\}^{{{{(n - 1)} \mathord{\left/ {\vphantom {{(n - 1)} 2}} \right. \kern-0pt} 2}}} \), where μ 0 is the consistency coefficient of the fluid and n is the power-law index. For a Newtonian fluid, n = 1 and μ = μ 0. This so-called power-law model has been proposed by Ostwald–de Waele in 1920s and proved by some convincing experiments, such as Wu and Thompson (1996) demonstrated that an accurate (and useful) power-law model worked well for the flow of shear-thinning fluids even when the Reynolds number is not large.

Pascal (1996) generalized a convection–diffusion model where the diffusion term depends nonlinearly on both the concentration and the concentration gradient and is of the form:

$$ J = \upsilon C - BC^{m} \frac{\partial C}{\partial x}\left| {\frac{\partial C}{\partial x}} \right|^{n - 1} . $$

This model has been examined by a few experiments. One is about the case when the axial mixing generated by the buoyancy effect due to the injection of a fluid into a less dense one when the parameters in the model were m = 0 and n = 2/3 (Baird et al. 1992). Here, we adopt this proved model where the concentration diffusivity D 0 B follows the same power-law rule as \( D_{B}^{0} = D_{B}^{{}} \left| {\frac{\partial \phi }{\partial z}} \right|^{n - 1} \), where D B is the diffusion coefficient and n is the power-law index.

The boundary conditions are:

$$ \left. u \right|_{z = 0} = 0,\left. v \right|_{z = 0} = \varOmega r,\left. w \right|_{z = 0} = 0,\left. \phi \right|_{z = 0} = \phi_{w} , $$
(5)
$$ \left. u \right|_{z \to \infty } = 0, \, \left. v \right|_{z \to \infty } = 0, \, \left. \phi \right|_{z \to \infty } = \phi_{\infty } . $$
(6)

A generalized dimensionless similarity variable is defined as \( \xi = z\left( {\frac{{\varOmega^{2 - n} }}{{{{\mu_{0} } \mathord{\left/ {\vphantom {{\mu_{0} } \rho }} \right. \kern-0pt} \rho }}}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {(n + 1)}}} \right. \kern-0pt} {(n + 1)}}}} r^{{{{(1 - n)} \mathord{\left/ {\vphantom {{(1 - n)} {(1 + n)}}} \right. \kern-0pt} {(1 + n)}}}} \)

Let \( u = \varOmega r \cdot F(\xi ), \, v = \varOmega r \cdot G(\xi ), \, w = \left( {\frac{{\varOmega^{1 - 2n} }}{{{{\mu_{0} } \mathord{\left/ {\vphantom {{\mu_{0} } \rho }} \right. \kern-0pt} \rho }}}} \right)^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} {(n + 1)}}} \right. \kern-0pt} {(n + 1)}}}} r^{{{{(n - 1)} \mathord{\left/ {\vphantom {{(n - 1)} {(n + 1)}}} \right. \kern-0pt} {(n + 1)}}}} H(\xi ), \, \varPhi (\xi ) = \frac{{\phi - \phi_{\infty } }}{{\phi_{w} - \phi_{\infty } }}. \)

Equations (1)–(4) are then transformed to the following ordinary differential equations:

$$ H^{\prime} = - 2F - \frac{1 - n}{1 + n}\xi F^{\prime}, $$
(7)
$$ F^{2} - G^{2} + \left( {H + \frac{1 - n}{1 + n}\xi F} \right)F^{\prime} = \left\{ {\left[ {\left( {F^{\prime}} \right)^{2} + \left( {G^{\prime}} \right)^{2} } \right]^{{{{(n - 1)} \mathord{\left/ {\vphantom {{(n - 1)} 2}} \right. \kern-0pt} 2}}} F^{\prime}} \right\}^{\prime } , $$
(8)
$$ 2FG + \left( {H + \frac{1 - n}{1 + n}\xi F} \right)G^{\prime} = \left\{ {\left[ {\left( {F^{\prime}} \right)^{2} + \left( {G^{\prime}} \right)^{2} } \right]^{{{{(n - 1)} \mathord{\left/ {\vphantom {{(n - 1)} 2}} \right. \kern-0pt} 2}}} G^{\prime}} \right\}^{\prime } , $$
(9)
$$ \left( {\frac{1 - n}{1 + n}\xi F + H} \right)\varPhi^{\prime} = \frac{1}{{P_{DB} }}\left( {\left| {\varPhi^{\prime}} \right|^{n - 1} \varPhi^{\prime}} \right)^{\prime } , $$
(10)

where \( P_{DB} = \frac{1}{{D_{B}^{0} \left| {\phi_{w} - \phi_{\infty } } \right|^{n - 1} r^{(1 - n)} }}\frac{{{{\mu_{0} } \mathord{\left/ {\vphantom {{\mu_{0} } \rho }} \right. \kern-0pt} \rho }}}{{\varOmega^{(1 - n)} }}. \) With the corresponding boundary conditions:

$$ \left. F \right|_{\xi = 0} = 0, \, \left. G \right|_{\xi = 0} = 1, \, \left. H \right|_{\xi = 0} = 0, \, \left. \varPhi \right|_{\xi = 0} = 1, $$
(11)
$$ \left. F \right|_{\xi \to \infty } = 0, \, \left. G \right|_{\xi \to \infty } = 0, \, \left. \varPhi \right|_{\xi \to \infty } = 0. $$
(12)

We now use HAM (homotopy analysis method) to solve the two-parameter two-point boundary value problem to be given in the next section.

3 Application of HAM

Following the method presented by Liao and his collaborates (Liao 1995, 1997, 2003; Liao and Cheung 2003) , our nonlinear problem can be approximated efficiently by choosing a set of base functions to express \( H\left( \xi \right), \, F\left( \xi \right), \, G\left( \xi \right), \, \varPhi \left( \xi \right):\left\{ {e^{ - \xi } , \, \xi } \right\} \). The initial approximations and auxiliary linear operators can be chosen to be of the following form:

$$ H_{0} (\xi ) = \xi , \, F_{0} (\xi ) = 0, \, G_{0} (\xi ) = e^{ - \xi } , \, \varPhi_{0} (\xi ) = e^{ - \xi } , $$
(13)
$$ L_{H} (\phi ) = \frac{\partial \phi }{\partial \xi }, \, L_{F} (\varPsi ) = \frac{{\partial^{2} \varPsi }}{{\partial \xi^{2} }} + \frac{\partial \varPsi }{\partial \xi }, \, L_{G} (\varOmega ) = \frac{{\partial^{2} \varOmega }}{{\partial \xi^{2} }} + \frac{\partial \varOmega }{\partial \xi }, \, L_{\varPhi } (\varXi ) = \frac{{\partial^{2} \varXi }}{{\partial \xi^{2} }} + \frac{\partial \varXi }{\partial \xi }, $$
(14)
$$ \begin{gathered} L_{H} (C_{1} + C_{2} \xi ) = 0, \, L_{F} \left( {C_{1} + C_{2} e^{ - \xi } + C_{3} \xi } \right) = 0, \hfill \\ L_{G} (C_{1} + C_{2} e^{ - \xi } ) = 0, \, L_{\varPhi } (C_{1} + C_{2} e^{ - \xi } ) = 0, \hfill \\ \end{gathered} $$
(15)

where C 1, C 2 and C 3 are constants.Furthermore, the nonlinear operators are defined by the following forms:

$$ N_{H} [\phi (\xi ;q),\varPsi \left( {\xi ;q} \right)] = \frac{\partial \phi }{\partial \xi } + 2\varPsi + \frac{1 - n}{1 + n}\xi \frac{\partial \varPsi }{\partial \xi }, $$
(16)
$$ \begin{aligned} N_{F} [\varPsi \left( {\xi ;q} \right),\varOmega \left( {\xi ;q} \right),\phi \left( {\xi ;q} \right)] & = \varPsi^{2} - \varOmega^{2} + \left( {\phi + \frac{1 - n}{1 + n}\xi \varPsi } \right)\frac{\partial \varPsi }{\partial \xi } - \left[ {\left( {\frac{\partial \varPsi }{\partial \xi }} \right)^{2} + \left( {\frac{\partial \varOmega }{\partial \xi }} \right)^{2} } \right]^{{{{(n - 1)} \mathord{\left/ {\vphantom {{(n - 1)} 2}} \right. \kern-0pt} 2}}} \frac{{\partial^{2} \varPsi }}{{\partial \xi^{2} }} \\ & {\kern 1pt} \quad - \frac{n - 1}{2}\left[ {\left( {\frac{\partial \varPsi }{\partial \xi }} \right)^{2} + \left( {\frac{\partial \varOmega }{\partial \xi }} \right)^{2} } \right]^{{{{(n - 3)} \mathord{\left/ {\vphantom {{(n - 3)} 2}} \right. \kern-0pt} 2}}} \left( {2\frac{\partial \varPsi }{\partial \xi }\frac{{\partial^{2} \varPsi }}{{\partial \xi^{2} }} + 2\frac{\partial \varOmega }{\partial \xi }\frac{{\partial^{2} \varOmega }}{{\partial \xi^{2} }}} \right)\frac{\partial \varPsi }{\partial \xi }, \\ \end{aligned} $$
(17)
$$ \begin{aligned} N_{G} [\varOmega \left( {\xi ;q} \right),\varPsi \left( {\xi ;q} \right),\phi \left( {\xi ;q} \right)] & = 2\varPsi \varOmega + \left( {\phi + \frac{1 - n}{1 + n}\xi \varPsi } \right)\frac{\partial \varOmega }{\partial \xi } - \left[ {\left( {\frac{\partial \varPsi }{\partial \xi }} \right)^{2} + \left( {\frac{\partial \varOmega }{\partial \xi }} \right)^{2} } \right]^{{{{(n - 1)} \mathord{\left/ {\vphantom {{(n - 1)} 2}} \right. \kern-0pt} 2}}} \frac{{\partial^{2} \varOmega }}{{\partial \xi^{2} }} \\ & \quad - \frac{n - 1}{2}\left[ {\left( {\frac{\partial \varPsi }{\partial \xi }} \right)^{2} + \left( {\frac{\partial \varOmega }{\partial \xi }} \right)^{2} } \right]^{{{{(n - 3)} \mathord{\left/ {\vphantom {{(n - 3)} 2}} \right. \kern-0pt} 2}}} \left( {2\frac{\partial \varPsi }{\partial \xi }\frac{{\partial^{2} \varPsi }}{{\partial \xi^{2} }} + 2\frac{\partial \varOmega }{\partial \xi }\frac{{\partial^{2} \varOmega }}{{\partial \xi^{2} }}} \right)\frac{\partial \varOmega }{\partial \xi }, \\ \end{aligned} $$
(18)
$$ \begin{aligned} N_{\varPhi } [\varXi \left( {\xi ;q} \right),\varPsi \left( {\xi ;q} \right),\phi \left( {\xi ;q} \right)] = & \left( {\frac{1 - n}{1 + n}\xi \varPsi + \phi } \right)\frac{\partial \varXi }{\partial \xi } \\ & \quad - \frac{1}{{P_{DB} }}\left( {\left| {\frac{\partial \varXi }{\partial \xi }} \right|^{n - 1} \frac{{\partial^{2} \varXi }}{{\partial \xi^{2} }} + (n - 1)\left| {\frac{\partial \varXi }{\partial \xi }} \right|^{n - 2} \frac{\partial \varXi }{\partial \xi }\frac{{\partial^{2} \varXi }}{{\partial \xi^{2} }}} \right). \\ \end{aligned} $$
(19)

We then construct the following zeroth-order deformation equations:

$$ \left( {1 - q} \right)L_{H} [\phi (\xi ;q) - H_{0} (\xi )] = qh_{H} S_{H} \left( \xi \right)N_{H} [\phi \left( {\xi ;q} \right),\varPsi \left( {\xi ;q} \right)], $$
(20)
$$ \left( {1 - q} \right)L_{F} [\varPsi (\xi ;q) - F_{0} (\xi )] = qh_{F} S_{F} \left( \xi \right)N_{F} [\varPsi \left( {\xi ;q} \right),\varOmega \left( {\xi ;q} \right),\phi \left( {\xi ;q} \right)], $$
(21)
$$ \left( {1 - q} \right)L_{G} [\varOmega (\xi ;q) - G_{0} (\xi )] = qh_{G} S_{G} \left( \xi \right)N_{G} [\varOmega \left( {\xi ;q} \right),\varPsi \left( {\xi ;q} \right),\phi \left( {\xi ;q} \right)], $$
(22)
$$ \left( {1 - q} \right)L_{\varPhi } [\varXi (\xi ;q) - \varPhi_{0} (\xi )] = qh_{\varPhi } S_{\varPhi } \left( \xi \right)N_{\varPhi } [\varXi \left( {\xi ;q} \right),\varPsi \left( {\xi ;q} \right),\phi \left( {\xi ;q} \right)], $$
(23)

subject to the boundary conditions:

$$ \begin{aligned} \phi (0,q) = & 0, \, \varPsi (0,q) = 0, \, \varPsi (\infty ,q) = 0, \\ \varOmega (0,q) = & 1, \, \varOmega (\infty ,q) = 0, \, \varXi (0,q) = 1, \, \varXi (\infty ,q) = 0. \\ \end{aligned} $$
(24)

When q = 0 and q = 1, we have

$$ \begin{aligned} \phi (\xi ,0)& = H_{0} (\xi ),\phi (\xi ,1) = H(\xi ),\varPsi (\xi ,0) = F_{0} (\xi ),\varPsi (\xi ,1) = F(\xi ), \\ \varOmega (\xi ,0)& = G_{0} (\xi ),\varOmega (\xi ,1) = G(\xi ), \, \varXi (\xi ,0) = \varPhi_{0} (\xi ), \, \varXi (\xi ,1) = \varPhi (\xi ). \\ \end{aligned} $$
(25)

When q increases from 0 to 1, the functions \( H(\xi ),F(\xi ),G(\xi ) ,\varPhi (\xi ) \) vary from \( H_{0} (\xi ),F_{0} (\xi ) ,G_{0} (\xi ),\varPhi_{0} (\xi ) \) to\( H(\xi ),F(\xi ),G(\xi ),\varPhi (\xi ) \). According to Taylor’s theorem, \( \phi (\xi ,q),\varPsi (\xi ,q),\varOmega (\xi ,q),\begin{array}{*{20}c} {\varXi (\xi ,q)} \\ \end{array} \) can be expanded in a series of q as the follows:

$$ \phi (\xi ,q) = H_{0} + \sum\limits_{m = 1}^{\infty } {H_{m} (\xi )} q^{m} ,H_{m} (\xi ) = \frac{1}{m!}\left. {\frac{{\partial^{m} \phi (\xi ,q)}}{{\partial q^{m} }}} \right|_{q = 0} , $$
(26)
$$ \varPsi (\xi ,q) = F_{0} + \sum\limits_{m = 1}^{\infty } {F_{m} (\xi )} q^{m} ,F_{m} (\xi ) = \frac{1}{m!}\left. {\frac{{\partial^{m} \varPsi (\xi ,q)}}{{\partial q^{m} }}} \right|_{q = 0} , $$
(27)
$$ \varOmega (\xi ,q) = G_{0} + \sum\limits_{m = 1}^{\infty } {G_{m} (\xi )} q^{m} ,G_{m} (\xi ) = \frac{1}{m!}\left. {\frac{{\partial^{m} G(\xi ,q)}}{{\partial q^{m} }}} \right|_{q = 0} , $$
(28)
$$ \varXi (\xi ,q) = \varPhi_{0} + \sum\limits_{m = 1}^{\infty } {\varPhi_{m} (\xi )} q^{m} ,\varPhi_{m} (\xi ) = \frac{1}{m!}\left. {\frac{{\partial^{m} \varXi (\xi ,q)}}{{\partial q^{m} }}} \right|_{q = 0} . $$
(29)

If \( h_{H} ,h_{F} ,h_{G} ,h_{\varPhi } \) are properly chosen, the series (26)–(29) are convergent at q = 1. We have the solution series:

$$ \begin{aligned} H(\xi ) = & H_{0} (\xi ) + \sum\limits_{m = 1}^{\infty } {H_{m} (\xi )} , \, F(\xi ) = F_{0} (\xi ) + \sum\limits_{m = 1}^{\infty } {F_{m} (\xi )} , \\ G(\xi ) = & G_{0} (\xi ) + \sum\limits_{m = 1}^{\infty } {G_{m} (\xi )} , \, \varPhi (\xi ) = \varPhi_{0} (\xi ) + \sum\limits_{m = 1}^{\infty } {\varPhi_{m} (\xi )} . \\ \end{aligned} $$
(30)

Next, we define the vectors:

$$ \begin{gathered} F_{m} (\xi ) = \left\{ {F_{1} (\xi ),F_{2} (\xi ), \ldots ,F_{m} (\xi )} \right\}, \, H_{m} (\xi ) = \left\{ {H_{1} (\xi ),H_{2} (\xi ), \ldots ,H_{m} (\xi )} \right\}, \hfill \\ G_{m} (\xi ) = \left\{ {G_{1} (\xi ),G_{2} (\xi ), \ldots ,G_{m} (\xi )} \right\}, \, \varPhi_{m} (\xi ) = \left\{ {\varPhi_{1} (\xi ),\varPhi_{2} (\xi ), \ldots ,\varPhi_{m} (\xi )} \right\}. \hfill \\ \end{gathered} $$
(31)

We define \( \frac{n - 1}{2} = \mu + \varepsilon \) and n − 1 = υ + δ, where μ ≥ 0 and υ ≥ 0 are integers and |ɛ| < 1 and |δ| < 1 are real numbers. Notice that |Φ ′| = −Φ ′. The mth-order deformation equations become:

$$ L_{H} [H_{m} \left( \xi \right) - \chi_{m} H_{m - 1} \left( \xi \right)] = h_{H} S_{H} (\xi )R_{m}^{H} \left( \xi \right), $$
(32)
$$ L_{F} \left[ {F_{m} \left( \xi \right) - \chi_{m} F_{m - 1} \left( \xi \right)} \right] = h_{F} S_{F} \left( \xi \right)R_{m}^{F} \left( \xi \right), $$
(33)
$$ L_{G} \left[ {G_{m} \left( \xi \right) - \chi_{m} G_{m - 1} \left( \xi \right)} \right] = h_{G} S_{G} \left( \xi \right)R_{m}^{G} \left( \xi \right), $$
(34)
$$ L_{\varPhi } [\varPhi_{m} (\xi ) - \chi_{m} \varPhi_{m - 1} (\xi )] = h_{\varPhi } S_{\varPhi } (\xi )R_{m}^{\varPhi } (\xi ), $$
(35)

where

$$ \chi_{m} = \left\{ \begin{gathered} 0, \quad m \le 1, \hfill \\ 1, \quad m > 1. \hfill \\ \end{gathered} \right. $$

subject to the following boundary conditions:

$$ H_{m} (0) = 0,F_{m} (0) = 0,F_{m} (\infty ) = 0,G_{m} (0) = 1,G_{m} (\infty ) = 0,\varPhi_{m} (0) = 1,\varPhi_{m} (\infty ) = 0, $$
(36)

under the following conditions:

$$ R_{m}^{H} (\xi ) = H_{m - 1}^{{\prime }} (\xi ) + 2F_{m - 1}^{{\prime }} (\xi ) + \frac{1 - n}{1 + n}\xi F^{\prime}_{m - 1} (\xi ), $$
(37)
$$ \begin{aligned} R_{m}^{F} = & \sum\limits_{k = 0}^{m - 1} {F_{k} (\xi )F_{m - 1 - k} } (\xi ) - \sum\limits_{k = 0}^{m - 1} {G_{k} (\xi )G_{m - 1 - k} } (\xi ) \\ & \quad + \sum\limits_{k = 0}^{m - 1} {\left[ {H_{m - 1 - k} (\xi ) + \frac{1 - n}{1 + n}\xi F_{m - 1 - k} (\xi )} \right]F^{\prime}_{k} (\xi )} \\ & \quad - \sum\limits_{k = 0}^{m - 1} {H_{\mu ,m - 1 - k} (\xi )} W_{k} (\xi ) - \frac{n - 1}{2}\sum\limits_{k = 0}^{m - 1} {E_{\mu ,m - 1 - k} (\xi )} W_{k} (\xi ), \\ \end{aligned} $$
(38)

where

$$ H_{\mu ,k} (\xi ) = \frac{1}{k!}\left. {\left\{ {\frac{{\partial^{k} }}{{\partial q^{k} }}[F^{\prime\prime}(\xi ,q)((F^{\prime}(\xi ,q))^{2} + (G^{\prime}(\xi ,q))^{2} )^{\mu } ]} \right\}} \right|_{q = 0} , $$
(39)
$$ W_{k} (\xi ) = \frac{1}{k!}\left. {\left\{ {\frac{{\partial^{k} }}{{\partial q^{k} }}[(F^{\prime}(\xi ,q))^{2} + (G^{\prime}(\xi ,q))^{2} ]^{\varepsilon } } \right\}} \right|_{q = 0} , $$
(40)
$$ E_{\mu ,m - 1 - k} (\xi ) = \frac{1}{k!}\left. {\left\{ {\frac{{\partial^{k} }}{{\partial q^{k} }}[(F{\prime }(\xi ,q))^{2} + (G^{\prime}(\xi ,q))^{2} ]^{\mu + 1} (2F{\prime }(\xi ,q)F{\prime \prime }(\xi ,q) + 2G{\prime }(\xi ,q)G{\prime \prime }(\xi ,q))F{\prime }(\xi ,q)} \right\}} \right|_{q = 0} , $$
(41)
$$ \begin{aligned} R_{m}^{G} = & 2\sum\limits_{k = 0}^{m - 1} {F_{k} (\xi )} G_{m - 1 - k}^{{}} (\xi ) + \sum\limits_{k = 0}^{m - 1} {[H_{m - 1 - k} (\xi ) + \frac{1 - n}{1 + n}\xi F_{m - 1 - k} (\xi )]G^{\prime}_{k} (\xi )} \\ & \quad - \sum\limits_{k = 0}^{m - 1} {I_{\mu ,m - 1 - k} (\xi )} W_{k} (\xi ) - \frac{n - 1}{2}\sum\limits_{k = 0}^{m - 1} {J_{\mu ,m - 1 - k} (\xi )} W_{k} (\xi ). \\ \end{aligned} $$
(42)

Note that in the above, the subscript-indexed I and J are defined by:

$$ I_{\mu .k} (\xi ) = \frac{1}{k!}\left. {\left\{ {\frac{{\partial^{k} }}{{\partial q^{k} }}[G^{\prime\prime}(\xi ,q)((F^{\prime}(\xi ,q))^{2} + (G^{\prime}(\xi ,q))^{2} )^{\mu } ]} \right\}} \right|_{q = 0} , $$
(43)
$$ J_{\mu ,m - 1 - k} (\xi ) = \frac{1}{k!}\left. {\left\{ {\frac{{\partial^{k} }}{{\partial q^{k} }}[(F^{\prime}(\xi ,q))^{2} + (G^{\prime}(\xi ,q))^{2} ]^{\mu + 1} (2F^{\prime}(\xi ,q)F^{\prime \prime }(\xi ,q) + 2G^{\prime }(\xi ,q)G^{\prime \prime }(\xi ,q))G^{\prime }(\xi ,q)} \right\}} \right|_{q = 0} , $$
(44)
$$ R_{m}^{\varPhi } = \sum\limits_{k = 0}^{m - 1} {\left[ {\frac{1 - n}{1 + n}\xi F_{m - 1 - k} (\xi ) + H_{m - 1 - k} (\xi )} \right]\varPhi {\prime }_{k} (\xi )} - \frac{1}{{P_{DB} }}\left( {( - 1)^{\upsilon } n\sum\limits_{k = 0}^{m = 1} {K_{\upsilon ,m - 1 - k} (\xi )N_{k} (\xi )} } \right), $$
(45)

where:

$$ K_{\upsilon .k} (\xi ) = \frac{1}{k!}\left. {\left\{ {\frac{{\partial^{k} }}{{\partial q^{k} }}[\varPhi^{\prime\prime}(\xi ,q)(\varPhi^{\prime}(\xi ,q))^{\upsilon } ]} \right\}} \right|_{q = 0} , $$
(46)
$$ N_{k} (\xi ) = \frac{1}{k!}\left. {\left\{ {\frac{{\partial^{k} }}{{\partial q^{k} }}(\varPhi^{\prime}(\xi ,q))^{\delta } } \right\}} \right|_{q = 0} . $$
(47)

From the definition (39), (41), (43), (44) and (46), we have the recursive formulas:

$$ H_{\mu ,k} (\xi ) = \sum\limits_{i = 0}^{k} {H_{\mu - 1,i} (\xi )} [(F^{\prime}_{k - i} (\xi ))^{2} + (G^{\prime}_{k - i} (\xi ))^{2} ], \, \mu \ge 1 , $$
$$ E_{\mu ,k} (\xi ) = \sum\limits_{i = 0}^{k} {E_{\mu - 1,i} (\xi )} [(F^{\prime}_{k - i} (\xi ))^{2} + (G^{\prime}_{k - i} (\xi ))^{2} ], \, \mu \ge 1 , $$
$$ I_{\mu .k} (\xi ) = \sum\limits_{i = 0}^{k} {I_{\mu - 1,i} (\xi )} [(F^{\prime}_{k - i} (\xi ))^{2} + (G^{\prime}_{k - i} (\xi ))^{2} ], \, \mu \ge 1 , $$
$$ J_{\mu ,k} (\xi ) = \sum\limits_{i = 0}^{k} {J_{\mu - 1,i} (\xi )} [(F^{\prime}_{k - i} (\xi ))^{2} + (G^{\prime}_{k - i} (\xi ))^{2} ], \, \mu \ge 1 , $$
$$ K_{\upsilon .k} (\xi ) = \sum\limits_{i = 0}^{k} {K_{\upsilon - 1,i} (\xi )} \varPhi^{\prime}_{k - i} (\xi ), \, \upsilon \ge 1 , $$

From definitions (40) and (47), we have

$$ W_{k} (\xi ) = \sum\limits_{i = 0}^{k - 1} {\frac{i + 1}{k}[(F^{\prime}_{i + 1} (\xi ))^{2} + (G^{\prime}_{i + 1} (\xi ))^{2} ]} \frac{1}{k!}\left. {\left\{ {\frac{{\partial^{k} }}{{\partial q^{k} }}[\varepsilon ((F^{\prime}(\xi ,q))^{2} + (G^{\prime}(\xi ,q))^{2} )^{\varepsilon - 1} ]} \right\}} \right|_{q = 0} , $$
$$ N_{k} (\xi ) = \sum\limits_{i = 0}^{k - 1} {\frac{i + 1}{k}} \varPhi^{\prime}_{i + 1} (\xi )\frac{1}{k!}\left. {\left\{ {\frac{{\partial^{k} }}{{\partial q^{k} }}[\sigma (\varPhi^{\prime}(\xi ,q))^{\delta - 1} ]} \right\}} \right|_{q = 0} . $$

According to the Rule of Solution Expression and Rule of Solution Existence described by Liao (2003), we set \( S_{H} (\xi ) = S_{F} (\xi ) = S_{G} (\xi ) = S_{\varPhi } (\xi ) = e^{ - \xi } \).

In this paper, we choose \( h_{H} = h_{F} = h_{G} = h_{\varPhi } = m \) and pick a proper value of \( m = - \frac{1}{2} \), which ensures that the solution is convergent.

According to the above equations and boundary conditions, we now define the first-order solutions when n = 0.5 as:

$$ H_{1} (\xi ) = \frac{1}{4} - \frac{{e^{ - 2\xi } }}{4}, $$
$$ F_{1} (\xi ) = - \frac{1}{12}e^{ - 3 \, x} ( - 1 + e^{2 \, x} ), $$
$$ G_{1} (\xi ) = \frac{1}{12}e^{ - 3 \, x} (1 - 3e^{x} - 2e^{2 \, x} + 4e^{3 \, x} (e^{ - 2 \, x} )^{3/4} ), $$
$$ \varPhi_{1} (\xi ) = \frac{{e^{ - 3 \, x} (P_{DB} - 3e^{x} P_{DB} + 2e^{2 \, x} ( - 2 + 2\sqrt {e^{ - x} } + P_{DB} ))}}{{12P_{DB} }}. $$

We only list the first-order solutions in details as above in this paper as an example and omit others. While solutions pertaining to numerous cases can be obtained from the model presented in this paper, we restrict ourselves to just one case for brevity and proof of concept. We plot concentration profiles with certain characteristics. Figure 2 shows the effects of different P DB on the mass transfer of a pseudoplastic fluid for n = 0.5.

Fig. 2
figure 2

Concentration profiles when n = 0.5 with different P DB by the fifth-order approximation

Full size image

4 Experimental device and results

We devise the following experiment to investigate the sedimentation and precipitation of nanoparticles in power-law fluids. This innovative self-design experiment consists of: a laser light source, a group of beam expanding lenses, optical quartz glass Petri dishes, a CCD fast imaging system and a rotating platform. The laser and the lens are fixed by a customized mechanical optical frame on a shock-proof bed. The rotating platform system is composed of a ZK100 single-axis motion controller and a rotating circular platform, on which the Petri dish is placed (see Fig. 3).

Fig. 3
figure 3

Experimental setup

Full size image

The green laser emitted by LED semiconductor laser is transformed into planar light after going through the lens cascade. It is cast into the Petri dish vertically, beneath which the high-speed image recording system records the speckled pictures. Rayleigh scattering (Yang et al. 2009) is observed where the light with a short wavelength scatters easily. We chose a green laser in this experiment since the wavelength of green light (510 nm) is shorter than that of red light (650 nm).

According to the classic Rayleigh scattering model, nanoparticles are closely related to the speckles. The distribution and motion of nanoparticles can be deduced by the corresponding speckles in different moments. When the volume percentage of nanoparticles in fluids is appropriate and suspended, the requirements of spatial coherence are satisfied. Through the complex amplitude superposition, the light intensity is redistributed when the scattering light of particles is interfered with. At the same time, high-speed imaging system records clear speckle images with dark and small bright spots. Speckle images are observed by the high-speed imaging system below.

The base fluid of nanofluids adopted in this experiment was power-law fluids (i.e., carboxymethyl cellulose aqueous solution). This experiment first investigates systematically on the motion-diffusion-precipitation characteristics of nanofluids based on power-law fluid.

Figure 4 shows the laser speckle images of nanoparticles in different power-law base fluid of different height. The images found in Fig. 4a, b are of 0.1 M Cu nanoparticles suspended in 0.1 % CMC aqueous solution while those of Fig. 4c, d are of 0.01 M Cu nanoparticles suspended in 0.01 % CMC aqueous solution. The solution height in Fig. 4a, c is 0.01 cm while in Fig. 4b, d it is 0.1 cm. From these two sets of contrasting images, it can be clearly seen that the lighter and more well-balanced speckles exist in the higher solution, while the opposite is true for the solution of lower height. Due to the fact that brightness of speckles is proportional to the number of the suspended nanoparticles, a preliminary judgment about the number of nanoparticles can be deduced from the images. By the laser speckle method, these pictures depict the deposition of nanoparticles in power-law fluids vividly. These images are qualitatively consistent with the analytical solutions of the concentration equation of nanofluids.

Fig. 4
figure 4

Laser speckle images of nanofluids of different height

Full size image

Furthermore, we put one figure here to compare the experimental results and the predicted modeling data. To deal with the image, we adopt the basic fact that the numbers of bright speckles are proportional to the number of the suspended nanoparticles and compare the number of speckles of images of nanofluids of different height.

The comparison between the modeling results and the designed experimental data is shown in Fig. 5. To calculate P DB and \( D_{B}^{0} = kT/(6\pi \mu_{0} R) \), we use the following experimental data and parameters: \( \mu_{0} { = 0} . 0 1 7 5 4N \cdot s^{n} /m^{2} \), \( \phi_{w} = 0.2\,\% \) (concentration of mass), n = 0.85, r = 0.05 m, R = 5 × 10−8 m, Ω = π/35 rad/s, T = 300 K (room temperature), k is the Boltzmann constant, and ρ can be treated as the density of water.

Fig. 5
figure 5

Comparison between the modeling results and the designed experimental data

Full size image

Note in Fig. 5, dimensionless variable \( \xi = 0, \, \xi = 0.5, \, \xi = 5 \) corresponds to the experimental heights of nanofluids \( h = 0, \, h = 0.01\,{\text{cm}}, \, h = 0.1\,{\text{cm}} \), respectively. And the dimensionless variable Φ corresponds to the concentration of fluid (Φ = 1.0 means the concentration ϕ = ϕ w ). The continuous curve in the Fig. 5 is the calculated results, while the triangle marks are the experimental data obtained from images of nanofluids of 0.01 and 0.1 cm height. It is noticed that the experimental data are smaller than the predicable analytical result.

5 Conclusions

The objective of this paper is to find analytic solutions for flow and mass transfer within nanofluids whose motion is greatly affected by the base fluid of a power-law type. Comparisons with experimental results as well as discriminations with previously published works were performed and noted. In addition, unlike previous studies, analytic solutions of equations describing nanofluids in a rotating disk with a mass diffusivity model depending on a power-law function of concentration gradient are determined. We found that the homotopy analysis method works well for a class of fluid problems with strong nonlinear characteristics in both momentum and mass transfer equations, as described in (Dandapat et al. 2003; Chen 2003; Wang and Pop 2006). These analytic solutions obtained by HAM could prove useful in the understanding of transport behaviors of the nanofluid-based power-law fluids arising in manufacturing practices, such as polymer, coating and material processes. In the end of the paper, we compared the experimental data and the calculated results only in one case, and the experimental data are smaller than the predicable analytical one. In a sequel to this paper, we will perform a detailed quantitative assessment of the quality of the physical model and approximate analytic solutions by comparing them with experimental data. We will pay close attention on the varying parameters involved, the modified technique dealing with the images and the method to obtain more sophisticated data in the experiments.