Free Vibration Response of Porous FGM Plates Using Finite Element Analysis in Thermal Environment

Abstract

Background

The functionally graded materials (FGM) have excellent properties that make them suited for mechanical, automobile and aerospace applications. However, the presence of insidious porosity inside the bulk of the FGMs significantly alters their vibration response especially when working under thermal environment as in aero-engines, turbine blades and nuclear power plants.

Purpose

The paper presents a detailed investigation of the thermomechanical response of porous FGM blades that is crucial in order to ensure the safe service life of the structural components. The randomly varying porosity distribution is modelled mathematically using a cosine law whilst the material properties of the FGM constituents (metal and ceramic) are assumed to vary with the absolute temperature.

Methods

A finite element method (FEM)-based model is developed to predict the influence of porosity distribution and thermal gradient on the free vibration response of rotating functionally graded porous FGM fan blades idealised as cantilever pre-twisted rotating plates and shells with varying metal and ceramic FGM constituent combinations. The present formulation is based on first-order shear deformation theory wherein the internal non-linear rotational and thermal strains are taken into account based on suitably derived geometric stiffness matrices.

Results

The non-dimensional frequencies are studied based on variations in crucial parameters like power index, pre-twist angle, plate aspect ratio, porosity distribution pattern, rotational speed, blade taper ratio and thermal gradient across the FGM plate. The natural frequencies for a tapered cylindrical fan blade composed of SUS304/Si₃N₄ FGM constituents are studied for different temperature and porosity type.

Conclusions

For all the FGM constituent combinations considered, the highest fundamental frequency is observed for Porosity Type 1 followed by no porosity, Porosity Type 3 and Porosity Type 2. For a certain value of the power index, the fundamental frequencies are found to increase with an increase in the rotational speed. On the other hand, there is a reduction in the frequency values with an increase in the thermal gradient for all porosity types owing to internal stresses and material property degradation. The tapering of the fan blades and the porosity gradient are found to have significant influence on their natural frequency in thermal environment.

Introduction

The functionally graded materials (FGM) have gained prominence in the last few decades owing to their excellent graded properties and wide suitability for aerospace, automobile and naval applications. The material properties like Young’s modulus, density, Poisson’s ratio and thermal coefficients in FGM structures may be tailored across preferred directions. Since their inception, the beneficial properties of FGM materials and their excellent performance during service conditions have opened a huge opportunity for research in this area. The FGM materials are manufactured mostly using the powder metallurgy (PM) techniques whereby defects like cracks, holes and porosities are the most common maladies in the FGM structures. The blade profiles of thermal or nuclear reactors and aircraft fuselages may be mathematically idealised as pre-twisted plates made up of FGM. Using this idealisation, many researchers in the recent years have predicted the vibration behaviour of the FGM plates using numerical, mathematical and finite element methods. In conjunction, many research works have also tried to mathematically model the porosity distribution across the thickness of the FGM structures. However, it is quite cumbersome to visualise the random distribution of the inherent porosities and their interactions and coalescence at varying temperature and other operating conditions. Porosities and discontinuities may also develop in such structures owing to thermal gradients as in aerospace, nuclear, automotive and naval applications. The turbine or windmill blades may be fairly idealised as plates from structural analysis point of view, and the finite element method (FEM) provides a powerful tool to analyse their performance under varied service conditions. The free vibration response of the FGM plates taking the influence of the porosity effects is a highly complex phenomenon, and many researchers have tried to mathematically predict the influence of porosities based on many mathematical models.

Olson and Lindberg [1] performed dynamic analysis of shallow shell structures with a doubly curved triangular finite element considering thickness variations. Lee et al. [2] developed a procedure for analysing the vibrations of rotating turbomachinery blades based upon shallow shell theory utilising the Ritz method. The application of finite element methods to accurately predict the structural response of functionally graded materials has been well established by many prominent researcher works. Reddy [3] presented a linear third-order and a non-linear first-order theory to study the deflections and stresses in functionally graded plates. Reddy and Chin [4] also presented the dynamic thermoelastic response of functionally graded cylinders and plates using first-order shear deformation theory coupled with a three-dimensional heat conduction equation. Vel and Batra [5] developed an exact solution for the three-dimensional deformations of a simply supported functionally graded rectangular plate subjected to mechanical and thermal load. They compared the classical plate theory, the first-order shear deformation theory, and a third-order shear deformation theory to assess accurately the deformation and stresses in functionally graded plates. Vel and Batra [6] also presented a three-dimensional exact solution for free and forced vibrations of simply supported functionally graded rectangular plates. Ferreira et al. [7] analysed the static deformations of a simply supported functionally graded plate modelled using a third-order shear deformation theory. Huang and Shen [8] analysed the nonlinear vibration and dynamic response of functionally graded plates in thermal environment. Matsunaga [9] studied the natural frequencies and buckling stresses of FGM plates taking into account the effects of transverse shear and normal deformations and the rotatory inertia. Zhao et al. [10] used an element-free kp-Ritz method to study the free vibration of functionally graded plates based on first-order shear deformation plate theory wherein the displacement fields were approximated using mesh-free kernel particle functions. Neves et al. [11] presented a sinusoidal shear deformation theory accounting for through thickness deformations for vibration analysis of functionally graded plates. Taj et al. [12] performed the static analysis of FGM plates using a higher-order shear deformation theory by employing an efficient C° iso-parametric Lagrangian finite element with seven degrees of freedom for each node. Kim and Reddy [13] identified the effects of power law distribution and microstructure-dependent size parameter on the bending, buckling and vibration behaviour of FGM plates. Mantari and Soares [14] worked on a new trigonometric higher-order theory considering the stretching effects and found the results comparable to the 3D exact solution and with other higher-order shear deformation theories. Bandyopadhyay and Karmakar [15] studied the influence of temperature and moisture concentration on the bending characteristics of delaminated rotating composite conical shells for initial twist and moderate rotational speeds. Bandyopadhyay et al. [16] also presented a finite element-based method to investigate the hygrothermal effects on the transient dynamic response of delaminated composite pre-twisted conical shells with initial twist. Bich et al. [17] investigated the non-linear buckling analysis and post-buckling behaviour of FGM toroidal shell segments filled inside by an elastic medium under external pressure loads including temperature effects. The structural behaviour of porous FGM plates was analysed by some researchers using mathematical models to account for the porosity distribution inside the plates. Thang et al. [18] presented the elastic buckling and free vibration analyses of porous cellular plates based on the first-order shear deformation theory (FSDT) considering the porosities to be dispersed in both uniform and non-uniform (symmetric and asymmetric) patterns. Gao et al. [19] analysed the free vibration of functionally graded (FG) porous nanocomposite plates reinforced with graphene platelets (GPLs) resting on two-parameter elastic foundations. Cong et al. [20] investigated the buckling and post-buckling behaviour of FGM plate containing porosities based on the Reddy's higher-order shear deformation plate theory considering Von Karman nonlinearity, initial geometrical imperfections and Pasternak type of elastic foundations. Zenkour [21] analysed the bending responses of porous functionally graded (FG) single-layered and sandwich thick rectangular plates using a quasi-3D shear deformation theory. Wu et al. [22] introduced a finite element method (FEM) analysis framework for the free and forced vibration analyses of functionally graded porous (FGP) beam type structures. Kiran and Kattimani [23] analysed the free vibration characteristics and the static behaviour of porous functionally graded magneto-electro-elastic (FGMEE) plates using finite element method. The porosities or micro-voids arising due to the maladies in the fabrication processes are accounted for using modified power law in the work. Kim et al. [24] modelled the porosity distributions using cosine function forms and obtained analytical solutions for bending, free vibration and buckling response using the Navier solution technique. Coskun et al. [25] worked on a third-order plate theory to analyse the static bending, free vibration and buckling of functionally graded porous micro-plates. Bansal et al. [26] presented a vibrational study of the porous functionally graded plate with geometric discontinuities wherein the geometric discontinuities are incorporated in terms of a circular cut-out of different sizes at the centre of the plate. Li et al. [27] investigated the static bending, free vibration and buckling analysis of porous bi-directional functionally graded (BDFG) plates based on first-order shear deformation theory (FSDT) as well as iso-geometric analysis (IGA). Dastjerdi et al. [28] proposed a three‐dimensional approach for bending analysis of moderately thick porous plates with a nano-functionally graded material in hygrothermal surroundings. Genao et al. [29] developed a displacement-based nonlinear finite element model for functionally graded porous micro-plates based on the general third-order shear deformation plate theory and the modified couple stress theory. Tran et al. [30] presented numerical results for static bending and free vibration of functionally graded porous (FGP) variable-thickness plates using an edge-based smoothed finite element method (ES-FEM). Kumar et al. [31] analysed the vibration characteristics of porous FGM plate with variable thickness resting on Pasternak's foundation. Yin et al. [32] performed bending and free vibration analysis of functionally graded plates made of porous materials according to a novel the semi-analytical method. Ninh et al. [33] carried out vibration analyses of FGM convex–concave shells subjected to electro-thermal–mechanical loads surrounded by Pasternak foundation. Kumar and Kattimani [34] presented nonlinear vibration analysis of tapered porous functionally graded skew (TPFGS) plate considering the effects of geometrical non-uniformities to optimise the thickness in the structural design. Vinh et al. [35] investigated the static bending and buckling behaviours of bi-directional functionally graded (BFG) plates with porosity. Karakoti et al. [36] developed a finite element formulation based on C° continuity of transverse displacement for obtaining and comparing nonlinear transient response of porous functionally graded material (FGM) sandwich plates and shell panels. Ramteke et al. [37] estimated the nonlinear eigen-frequency responses of a functionally graded material (FGM) panel in a thermal environment using the finite element method (FEM). Ramteke et al. [38] also studied the eigen-frequency characteristics of the doubly curved FG panel considering multi-directional grading influence and geometrical large deformation utilising HSDT mid-plane kinematics along with Green Lagrange kind of nonlinear strain terms. Fang et al. [39] studied the size-dependent vibrations of porous functionally graded rotating microplates under thermal environment based on first-order shear deformation theory (FSDT) and modified couple stress theory (MCST). Thai et al. [40] investigated the nonlinear bending behaviour of multi-directional functionally graded plates with variable thickness. Xiong et al. [41] studied the thermal buckling behaviour of non-Lévy-type functionally graded (FG) rectangular plates using symplectic superposition method (SSM) whilst Xiong et al. [42] presented new analytic thermal buckling solutions of temperature-dependent moderately thick functionally graded plates with non-Lévy-type constraints within the symplectic solution framework. Ninh et al. [43] analysed the effect of cracks on non-linear dynamical response of double-variable-edge plates made of graphene nano-platelets-reinforced porous matrix and sur-bonded by piezoelectric layers when subjected to thermo-mechanical loads. Hu et al. [44] presented new symplectic analytic solutions for buckling of non-Lévy-type carbon nanotube (CNT) reinforced composite rectangular plates. Hu et al. [45] developed the new analytic free vibration solutions of non-Lévy-type functionally graded (FG) doubly curved shallow shells whilst Hu et al. [46] extended the study to analyse the free vibration solutions of non-Lévy-type porous functionally graded material (FGM) rectangular plates by the symplectic superposition method (SSM). Long et al. [47] studied the dynamical response of variable generatrix profile and thickness ceramic-matrix composite shells under electro-thermo-mechanical effects.

From the literature review, it is apparent that the free vibration behaviour of porous functionally graded plates was studied by some researchers though they mostly considered stationary and uniform-width plates. However, the study of the dynamic response of rotating functionally graded plates and shells in thermal environment considering the effects of pre-twist, porosity distribution pattern and blade taper ratio is found to be very limited. As such, the present work is focussed on the effects of porosity distribution on the thermomechanical response of pre-twisted functionally graded porous plates and cylindrical fan blades considering the effects of rotation and tapering of the blades. The present work intends to develop a mathematical model for predicting the vibration response of porous FGM plates based on a finite element formulation (FEM) considering the influence of some critical parameters like pre-twist angle, rotational speed, aspect ratio, blade taper ratio and thermal gradients across the ceramic and metallic interfaces. The FEM formulation is based on minimization of potential energy and employs an eight-node iso-parametric plate bending element comprising five degrees of freedom at each node wherein the effects of shear deformation are taken into account. The material properties of the FGM plate are assumed to vary along the thickness direction only. The FGM plate is assumed to be made of a finite number of isotropic layers smoothly bonded at the interfaces. The material properties at each of the assumed isotropic layers are computed based on the assumed property distribution laws. A study of the vibration response of tapered fan blades for typical twisted cylindrical fan blade geometry is also presented considering both span-wise and chord-wise tapers. The interaction between the porosities at elevated temperatures inside the bulk of the FGM structure is kept outside the scope of the present work.

Theoretical Formulation

Basic Equation

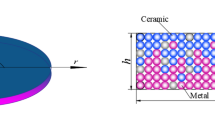
A pre-twisted FGM plate (Fig. 1) of length ‘a’, breadth ‘b’ and thickness ‘h’ is considered. The mid-plane of the FGM plate may be expressed mathematically as

$$z = - \frac{xy}{{R_{xy} }}$$

(1)

Fig. 1

An FGM blade (plate) showing the metal and ceramic interface and tapered blade

The radius of curvature $\left( {R_{xy} } \right)$ is related to the pre-twist angle $\left( \psi \right)$ and the span length ‘a’ of the FGM plate by

$$R_{xy} = - \frac{a}{\tan \psi }$$

(2)

Based on the first-order shear deformation theory, the spatial displacement of any point P (x, y, z) on the FGM plate (Fig. 1) is related to the mid-plane displacements and rotations as

$$\begin{aligned} u\left( {x,y,z} \right) & = u_{0} \left( {x,y} \right) + z\phi_{x} (x,y) \\ v\left( {x,y,z} \right) & = v_{0} \left( {x,y} \right) + z\phi_{y} (x,y) \\ w\left( {x,y,z} \right) & = w_{0} (x,y) \\ \end{aligned}$$

(3)

The linear strains corresponding to a lamina at a distance ‘z’ from the mid-surface of the FGM plate

$$\begin{aligned} \varepsilon_{x} & = u_{,x} = u_{,x}^{0} + z\theta_{y,x} \\ \varepsilon_{y} & = v_{,y} = v_{,y}^{0} + z\theta_{x,y} \\ \gamma_{xy} & = u_{,y} + v_{,x} + \frac{2w}{{R_{xy} }} = u_{,y}^{0} + v_{,x}^{0} + z\left( {\theta_{y,y} + \theta_{x,x} } \right) + \frac{2w}{{R_{xy} }} \\ \end{aligned}$$

(4)

where $u, v,$ and $w$ are the displacement variables along $x, y$, and $z$ axes, whilst $u^{0} , v^{0}$, and $w^{0}$ represent corresponding mid-plane displacement variables at a point within the plate, respectively. The symbols $\theta_{y}$ and $\theta_{x}$ signify the rotations of plate cross section about $y$- and $x$-axes, respectively. The in-plane strain vector may be represented as a sum of the mid-surface strain vector and vector of the change in curvature of the plate surface due to applied external loads

$$\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{xy} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } \\ {\varepsilon_{y}^{0} } \\ {\gamma_{xy}^{0} } \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} {\kappa_{x} } \\ {\kappa_{y} } \\ {\kappa_{xy} } \\ \end{array} } \right\}$$

(5)

where $\kappa_{x}$, $\kappa_{y}$, and $\kappa_{xy}$ denote the curvature vectors of the FGM plate.

The transverse strains $\gamma_{xz}$ and $\gamma_{yz}$ are given by

$$\gamma_{xz} = w_{,x}^{0} - \theta_{x}$$

(6)

$$\gamma_{yz} = w_{,y}^{0} - \theta_{y}$$

(7)

The constitutive equations considering the thermal effects can be expressed as

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\tau_{xy} } \\ {\tau_{xz} } \\ {\tau_{yz} } \\ \end{array} } \right\} & = \left[ {\begin{array}{*{20}c} {\overline{Q}_{11} } & {\overline{Q}_{12} } & 0 & 0 & 0 \\ {\overline{Q}_{12} } & {\overline{Q}_{22} } & 0 & 0 & 0 \\ 0 & 0 & {\overline{Q}_{66} } & 0 & 0 \\ 0 & 0 & 0 & {\overline{Q}_{44} } & 0 \\ 0 & 0 & 0 & 0 & {\overline{Q}_{55} } \\ \end{array} } \right]\left( {\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {\alpha_{x} } \\ {\alpha_{y} } \\ 0 \\ 0 \\ 0 \\ \end{array} } \right\}\Delta T} \right) \\ {\text{or}}\quad \left\{ \sigma \right\}_{k} & = \left[ {\overline{Q}_{ij} } \right]_{k} \left( {\left\{ \varepsilon \right\}_{k} - \alpha \Delta T} \right) \\ \end{aligned}$$

(8)

where $\alpha_{x}$ and $\alpha_{y}$ are the thermal expansion coefficients whilst $\left[ {\overline{Q}_{ij} } \right]_{k}$ are the transformed reduced stiffnesses of the kth layer of the FGM plate.

The on-axis stiffness matrix $\left( {\left[ {Q_{ij} } \right]_{k} } \right)$ of the kth layer is given by

$$\left[ {Q_{ij} } \right]_{k} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 \\ {Q_{12} } & {Q_{22} } & 0 \\ 0 & 0 & {Q_{66} } \\ \end{array} } \right],\quad i,j = 1,2,6,\quad \left[ {Q_{ij} } \right]_{k} = \left[ {\begin{array}{*{20}c} {Q_{44} } & 0 \\ 0 & {Q_{55} } \\ \end{array} } \right],\quad i,j = 4,5$$

$$Q_{11} = \frac{{E_{1} }}{{1 - \nu_{12} \nu_{21} }},\quad Q_{12} = \frac{{E_{1} }}{{1 - \nu_{12} \nu_{21} }}, \quad Q_{22} = \frac{{E_{2} }}{{1 - \nu_{12} \nu_{21} }}, \quad Q_{44} = G_{13} ,\quad Q_{55} = G_{23}$$

(9)

The transformation matrices are given by

$$\left[ {T_{1} } \right] = \left[ {\begin{array}{*{20}c} {m^{2} } & {n^{2} } & {2mn} \\ {n^{2} } & {m^{2} } & { - 2mn} \\ { - mn} & {mn} & {m^{2} - n^{2} } \\ \end{array} } \right],\quad \left[ {T_{2} } \right] = \left[ {\begin{array}{*{20}c} m & { - n} \\ n & m \\ \end{array} } \right]$$

(10)

The off-axis stiffness values for the kth lamina are given by

$$\begin{aligned} \left[ {\overline{Q}_{ij} } \right]_{k} & = \left[ {T_{1} } \right]^{ - 1} \left[ {Q_{ij} } \right]_{k} \left[ {T_{1} } \right]^{T} , \, \quad i,j = 1,2,6 \\ \left[ {\overline{Q}_{ij} } \right]_{k} & = \left[ {T_{2} } \right]^{ - 1} \left[ {Q_{ij} } \right]_{k} \left[ {T_{2} } \right], \quad i,j = 4,5 \\ \end{aligned}$$

(11)

An eight-node iso-parametric plate bending element in the non-dimensional (ξ − η) coordinates is considered (Fig. 2) having five degrees of freedom at each node for which the shape functions are assumed as

$$\begin{aligned} N_{i} & = \left( {1 + \xi \xi_{i} } \right)\left( {1 + \eta \eta_{i} } \right)\left( {\xi \xi_{i} + \eta \eta_{i} - 1} \right)/4, \quad i = 1,2,3,4 \\ N_{i} & = \left( {1 - \xi^{2} } \right)\left( {1 + \eta \eta_{i} } \right)/2, \quad i = 5,7 \\ N_{i} & = \left( {1 - \eta^{2} } \right)\left( {1 + \xi \xi_{i} } \right)/2,\quad i = 6,8 \\ \end{aligned}$$

(12)

Fig. 2

Iso-parametric plate bending element in the ξ − η space

The Lagrangian or the energy function is defined as

$$L = U_{{\text{e}}} - T$$

(13)

The potential energy $\left( {U_{{\text{e}}} } \right)$ is expressed as

$$U_{{\text{e}}} = \frac{1}{2}\iint\limits_{A} {\left\{ {\varepsilon^{T} } \right\}\left[ D \right]\left\{ \varepsilon \right\}{\text{d}}A}$$

(14)

where the strain vector $\left( {\left\{ \varepsilon \right\}} \right)$ is related to the displacement vector for an element $\left\{ {\delta_{{\text{e}}} } \right\}$ based on the strain–displacement matrix $\left( {\left[ B \right]} \right)$ written as

$$\left\{ \varepsilon \right\} = \left[ B \right]\left\{ {\delta_{{\text{e}}} } \right\}$$

(15)

The potential energy $\left( {U_{{\text{e}}} } \right)$ may then be reduced as

$$\begin{aligned} U_{{\text{e}}} & = \frac{1}{2}\mathop \smallint \limits_{{ - {\raise0.7ex\hbox{$a$} \!\mathord{\left/ {\vphantom {a 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}^{{{\raise0.7ex\hbox{$a$} \!\mathord{\left/ {\vphantom {a 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \mathop \smallint \limits_{{ - {\raise0.7ex\hbox{$b$} \!\mathord{\left/ {\vphantom {b 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}^{{{\raise0.7ex\hbox{$b$} \!\mathord{\left/ {\vphantom {b 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \left\{ {\delta_{{\text{e}}} } \right\}^{{\text{T}}} \left[ B \right]^{{\text{T}}} \left[ D \right]\left[ B \right]\left\{ {\delta_{{\text{e}}} } \right\} {\text{d}}x{\text{d}}y \\ & = \left[ {\delta_{{\text{e}}} } \right]^{{\text{T}}} \left[ {K_{{\text{e}}} } \right]\left\{ {\delta_{{\text{e}}} } \right\} \\ \end{aligned}$$

(16)

The element stiffness matrix $\left( {\left[ {K_{{\text{e}}} } \right]} \right)$ is given by,

$$\left[ {K_{{\text{e}}} } \right] = \mathop \smallint \limits_{ - 1}^{1} \mathop \smallint \limits_{ - 1}^{1} \left[ B \right]^{{\text{T}}} \left[ D \right]\left[ B \right] \left| J \right| {\text{d}}\xi {\text{d}}\eta$$

(17)

where [B] is the strain–displacement matrix, [D], the elasticity matrix and $\left| J \right|$ is the determinant of the Jacobian matrix. A (2 × 2) integration scheme is adopted to avoid shear locking.

The expression for the strain–displacement matrix is defined as

$$\left[ B \right] = \left[ {\begin{array}{*{20}c} {N_{i,x} } & 0 & 0 & 0 & 0 \\ 0 & {N_{i,y} } & 0 & 0 & 0 \\ {N_{i,y} } & {N_{i,x} } & {\frac{{2N_{i} }}{{R_{xy} }}} & 0 & 0 \\ 0 & 0 & 0 & 0 & {N_{i,x} } \\ 0 & 0 & 0 & { - N_{i,y} } & 0 \\ 0 & 0 & 0 & { - N_{i,x} } & { - N_{i,y} } \\ 0 & 0 & { - N_{i,x} } & {N_{i} } & 0 \\ 0 & 0 & { - N_{i,y} } & 0 & { - N_{i} } \\ \end{array} } \right]_{{\begin{array}{*{20}c} { i = 1\,{\text{to}}\,8 } \\ {\left( {40 \times 40 } \right)} \\ \end{array} }}$$

(18)

The Kinetic energy expression in Eq. (13) is defined as

$$T = \frac{1}{2}\left\{ {\dot{\delta }_{{\text{e}}} } \right\}^{{\text{T}}} \left[ {M_{{\text{e}}} } \right]\left\{ {\dot{\delta }_{{\text{e}}} } \right\} + \frac{1}{2}\left\{ {\delta_{{\text{e}}} } \right\}^{{\text{T}}} \left[ {K_{{{\text{Rot}}}} } \right]\left\{ {\delta_{{\text{e}}} } \right\} + \frac{1}{2}\left\{ {\delta_{{\text{e}}} } \right\}^{{\text{T}}} \left[ {K_{{{\text{Th}}}} } \right]\left\{ {\delta_{{\text{e}}} } \right\}$$

(19)

The element level mass matrix $\left[ {M_{{\text{e}}} } \right]$ is arrived at from the first term in Eq. (19) as

$$\left[ {M_{{\text{e}}} } \right] = \rho \int\limits_{{{\text{vol}}}} {\left[ N \right]^{{\text{T}}} \left[ N \right]{\text{d}}\left( {{\text{vol}}} \right)}$$

(20)

where $\rho$ denotes the density of the FGM plate material while [N] is the shape function matrix.

The element geometric stiffness matrix arising out of rotation is

$$\left[ {K_{{\sigma {\text{e}}}} } \right]_{{{\text{Rot}}}} = \int\limits_{{{\text{vol}}}} {\left[ {G_{{{\text{Rot}}}} } \right]^{{\text{T}}} \left[ {S_{{{\text{Rot}}}} } \right]\left[ {G_{{{\text{Rot}}}} } \right]{\text{d}}\left( {{\text{vol}}} \right)}$$

(21)

The element level in-plane stress and moment resultants $\left\{ {N^{{\text{e}}} } \right\}$ on the FGM plate due to thermal stresses $\left\{ {F_{{\text{e}}}^{{{\text{Th}}}} } \right\}$ at the element level is given by

$$\left\{ {N^{{\text{e}}} } \right\} = \left[ D \right]\left\{ \varepsilon \right\} - \left\{ {F_{{\text{e}}}^{{{\text{Th}}}} } \right\}$$

(22)

The element geometric stiffness matrix due to the induced thermal strains is

$$\left[ {K_{{\sigma {\text{e}}}} } \right]_{{{\text{Th}}}} = \int\limits_{{{\text{vol}}}} {\left[ {G_{{{\text{Th}}}} } \right]^{{\text{T}}} \left[ {S_{{{\text{Th}}}} } \right]\left[ {G_{{{\text{Th}}}} } \right]{\text{d}}\left( {{\text{vol}}} \right)}$$

(23)

The dynamic equilibrium equation for moderate rotational speeds due to the thermal gradient is given by

$$\left[ M \right]\left\{ {\ddot{\delta }} \right\} + \left\{ {\left[ K \right]_{L} + \left[ {K_{\sigma } } \right]_{{{\text{Rot}}}} + \left[ {K_{\sigma } } \right]_{{{\text{Th}}}} } \right\}\left\{ \delta \right\} = \{ F\}_{{{\text{Rot}}}} + \{ F\}_{{{\text{Th}}}}$$

(24)

where $\left\{ \delta \right\}$ and $\left\{ {\ddot{\delta }} \right\}$ are the global displacement and acceleration vectors, $\left[ K \right]_{L}$ is the linear global stiffness matrix, $\left[ {K_{\sigma } } \right]_{{{\text{Rot}}}}$ is the geometric stiffness matrix due to rotation and $\left[ {K_{\sigma } } \right]_{{{\text{Th}}}}$ is the geometric stiffness matrix resulting from the thermal gradient across the FGM plate.

The natural frequencies $\left( {\omega_{n} } \right)$ are determined from the standard eigenvalue problem which is represented below

$$\begin{aligned} \left[ A \right]\left\{ \delta \right\} & = \lambda \{ \delta \} \\ {\text{where}}\quad \left[ A \right] & = \left( {\left[ K \right] + \left[ {K_{\sigma } } \right]_{{{\text{Rot}}}} + \left[ {K_{\sigma } } \right]_{{{\text{Th}}}} } \right)^{ - 1} \left[ M \right], \\ & \quad {\text{and}}\quad \lambda = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\omega_{n}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\omega_{n}^{2} }$}} \\ \end{aligned}$$

(25)

A porosity distribution function $\varphi \left( z \right)$ is defined which is assumed to follow a cosine distribution law across the thickness of the FGM plate and is mathematically identified as of three types (Porosity Type 0 refers to No porosity/Intact FGM plate) as below:

• (a) Porosity Type 1: The porosity is maximum near the centre of the FGM plate and gradually reduces to zero on either of the metal or the ceramic sides.

  $$\varphi \left( z \right) = \varphi_{\max } \cos \left( {\frac{\pi z}{h}} \right)$$

  (26a)

• (b) Porosity Type 2: The porosity is maximum on the metallic side and is negligible on the ceramic side of the FGM plate.

  $$\varphi \left( z \right) = \varphi_{\max } \cos \left[ {\frac{\pi }{2}\left( {\frac{z}{h} + \frac{1}{2}} \right)} \right]$$

  (26b)

• (c) Porosity Type 3: The porosity is maximum on the ceramic side and is negligible on the metallic side of the FGM plate.

  $$\varphi \left( z \right) = \varphi_{\max } \cos \left[ {\frac{\pi }{2}\left( {\frac{z}{h} - \frac{1}{2}} \right)} \right]$$

  (26c)

  where $\varphi_{\max }$ is the maximum porosity and is expressed as a percentage. In the present study, the maximum porosity is considered to be $\varphi_{\max }$ = 0.50 for all the cases considered. A plot of the porosity distribution function $(\varphi )$ for different porosity distribution functions considered in Eq. (26a-c) is given in Fig. 3 for $\varphi_{\max }$ = 0.50 across the normalised FGM thickness (z/h) direction.

Fig. 3

The distribution of the porosity across the thickness of the FGM plate for the three porosity Types considered (Porosity Types 1, 2 and 3, φ_max = 0.50)

The temperature-dependent materials’ properties of either the metallic (bottom) of the ceramic (top) fibres are represented as a third-order non-linear polynomial of the absolute temperature (T) and expressed as:

$$P = P_{0} \left( {P_{ - 1} T^{ - 1} + 1 + P_{1} T^{1} + P_{2} T^{2} + P_{3} T^{3} } \right)$$

(27)

where the constant thermal coefficients $P_{0}$, $P_{ - 1} , P_{1} , P_{2} \,{\text{and}}\,P_{3}$ are considered for the different FGM combinations [10] in the current work and summarised in Table 1.

Table 1 The temperature coefficients for evaluation of the material properties like Elastic Modulus (E), Poisson’s ratio (ν), density (ρ) and thermal coefficient (α) for different metallic and ceramic constituents comprising the FGM plate [10] $P = P_{0} \left( {P_{ - 1} T^{ - 1} + 1 + P_{1} T^{1} + P_{2} T^{2} + P_{3} T^{3} } \right)$

The graded material properties of a FGM plate are assumed to be based on the power law and account for the porosity distribution $\varphi \left( z \right)$, expressed as

$$E\left( z \right) = \left\{ {\left( {E_{C} - E_{M} } \right)*\left[ {\frac{1}{2} + \left( \frac{z}{h} \right)} \right]^{k} + E_{M} } \right\} \times \left( {1 - \varphi \left( z \right)} \right)$$

(28a)

$$\rho \left( z \right) = \left\{ {\left( {\rho_{C} - \rho_{M} } \right)*\left[ {\frac{1}{2} + \left( \frac{z}{h} \right)} \right]^{k} + \rho_{M} } \right\} \times \left( {1 - \varphi \left( z \right)} \right)$$

(28b)

$$\nu \left( z \right) = \left\{ {\left( {\nu_{C} - \nu_{M} } \right)*\left[ {\frac{1}{2} + \left( \frac{z}{h} \right)} \right]^{k} + \nu_{M} } \right\} \times \left( {1 - \varphi \left( z \right)} \right)$$

(28c)

$$\alpha \left( z \right) = \left\{ {\left( {\alpha_{C} - \alpha_{M} } \right)*\left[ {\frac{1}{2} + \left( \frac{z}{h} \right)} \right]^{k} + \alpha_{M} } \right\} \times \left( {1 - \varphi \left( z \right)} \right)$$

(28d)

The variations of the effective material properties (P_eff) with the power index (k) are illustrated in the plots shown in Fig. 4a–d, for no porosity and Porosity Types 1, 2 and 3 respectively. In general, the variations of the properties like Young’s Modulus, Poisson’s ratio, density and Thermal expansion coefficients with the porosity types are similar in nature as evident from Eq. 28a-d. As such, only the variations in the effective Young’s modulus (E_eff) are presented in Fig. 4a–d and the observations apply to all other porosity dependent material properties. It is evident from Fig. 4a that in case of non-porous plates, there is a smooth transition of the effective material properties from metallic phase to the ceramic phase across the thickness of the FGM plate following a parabolic distribution (except at k = 1 which follow a linear variation). The effective material properties (E_eff) for Porosity Type 1 as in Fig. 4b are found to be minimum near the mid-surface of the FGM plate where the porosity distribution function (porosity density) happens to be a maximum as evident from Fig. 3. Similarly, comparing Figs. 3 and 4c, it may again be inferred that for Porosity Type 2, the effective material properties are a maximum near the ceramic part (top surface) where the porosity density happens to be minimum. For Porosity Type 3 also, the effective material properties are again a maximum near the metallic phase (bottom surface) where the porosity density is a minimum (Figs. 3 and 4d). It may thus be concluded from Fig. 4a–d that the effective material properties are a maximum near the zones where the porosity density happens to be a maximum and vice versa.

Fig. 4

a Thickness-wise variation of Effective Young’s Modulus (E_eff) for SUS304/Si₃N₄ FGM square plates for different power index and No Porosity [a = b = 0.1, h = 0.01, ψ = 0°, Non-Porous plate]. b Thickness-wise variation of Effective Young’s Modulus (E_eff) for SUS304/Si₃N₄ FGM square plates for different power index and Porosity Type = 1 [a = b = 0.1, h = 0.01, ψ = 0°, Porosity Type 1, φ_max = 0.50]. c Thickness-wise variation of Effective Young’s Modulus (E_eff) for SUS304/Si₃N₄ FGM square plates for different power index and Porosity Type = 2 [a = b = 0.1, h = 0.01, ψ = 0°, Porosity Type 2, φ_max = 0.50]. d Thickness-wise variation of Effective Young’s Modulus (E_eff) for SUS304/Si₃N₄ FGM square plates for different power index and Porosity Type = 3 [a = b = 0.1, h = 0.01, ψ = 0°, Porosity Type 3, φ_max = 0.50]

The properties of the FGM material are assumed to vary across the thickness direction (z) of the plate and derived by defining the volume fraction $\left( {V_{{\text{c}}} } \right)$ of the ceramic constituent,

$$V_{{\text{c}}} = \left( {\frac{1}{2} + \frac{z}{h}} \right)^{k}$$

(29)

The span-wise and the chord-wise taper in the FGM plate may be accounted for by defining the taper ratios $\beta_{x} \,{\text{and}}\,\beta_{y}$, respectively. For span-wise taper in the FGM plate wherein $\left( {h_{\min } } \right)_{{{\text{span}}}}$ and $\left( {h_{\min } } \right)_{{{\text{span}}}}$ are the minimum and the maximum thicknesses at x = 0 and x = L respectively, along the span. The uniform taper ratio along span-wise direction can then be denoted by $\beta_{x} = \left[ {\left( {h_{\min } } \right)_{{{\text{span}}}} /\left( {h_{\max } } \right)_{{{\text{span}}}} } \right]$. The thickness $h_{x}$ along the span-wise direction (x–) is then given by

$$\begin{aligned} \frac{{h_{x} }}{{\left( {h_{\max } } \right)_{{{\text{span}}}} }} & = 1 - \left[ {1 - \frac{{\left( {h_{\min } } \right)_{{{\text{span}}}} }}{{\left( {h_{\max } } \right)_{{{\text{span}}}} }}} \right]\left( \frac{x}{L} \right) \\ h_{x} & = \left[ {1 - \left( {1 - \beta_{x} } \right)\left( \frac{x}{L} \right)} \right] \cdot \left( {h_{\max } } \right)_{{{\text{span}}}} \\ \end{aligned}$$

(30)

Similarly, assuming the uniform taper ratio $\left( {\beta_{y} } \right)$ in the chord-wise direction $\beta_{y} = \left[ {\left( {h_{\min } } \right)_{{{\text{chord}}}} /\left( {h_{\max } } \right)_{{{\text{chord}}}} } \right]$, the thickness $h_{y}$ along the chord-wise direction (y–) is given by

$$\begin{aligned} \frac{{h_{y} }}{{\left( {h_{\max } } \right)_{{{\text{chord}}}} }} & = 1 - \left[ {1 - \frac{{\left( {h_{\min } } \right)_{{{\text{chord}}}} }}{{\left( {h_{\max } } \right)_{{{\text{chord}}}} }}} \right]\left( {\frac{y}{{b_{0} }} + 0.5} \right) \\ h_{y} & = \left[ {1 - \left( {1 - \beta_{y} } \right)\left( {\frac{y}{{b_{0} }} + 0.5} \right)} \right] \cdot \left( {h_{\max } } \right)_{{{\text{chord}}}} \\ \end{aligned}$$

(31)

where

$$\begin{array}{*{20}l} {\left( {\text{a}} \right)\quad h_{x} = \left( {h_{\max } } \right)_{{{\text{span}}}} \quad {\text{at}}\quad x = 0} \hfill & {\left( {\text{b}} \right)\quad h_{x} = \left( {h_{\min } } \right)_{{{\text{span}}}} \quad {\text{at}}\quad x = L} \hfill \\ {\left( {\text{c}} \right)\quad h_{y} = \left( {h_{\max } } \right)_{{{\text{chord}}}} \quad {\text{at}}\quad y = - {\raise0.7ex\hbox{${b }$} \!\mathord{\left/ {\vphantom {{b } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}} \hfill & {\left( {\text{d}} \right)\quad h_{y} = \left( {h_{\min } } \right)_{{{\text{chord}}}} \quad {\text{at}}\quad y = {\raise0.7ex\hbox{${b }$} \!\mathord{\left/ {\vphantom {{b } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}} \hfill \\ \end{array} .$$

(32)

Results and Discussion

Validation of FEM Formulation

Based on the formulation presented above, finite element codes are developed to study the effects of triggering parameters like FGM constituent combination, power index, plate aspect ratio, twist angle, rotational speed, porosity distribution pattern, blade taper ratio and thermal gradient on the non-dimensional frequencies of pre-twisted rotating porous FGM plates. A mesh size of (8 × 8) consisting of 64 elements and 225 nodes is considered for the analysis. Each node of the iso-parametric element is considered as having five degrees of freedom (three translations and two rotations). The natural frequencies $\left( {\omega^{*} = \omega h\sqrt {\frac{{\rho_{{\text{c}}} }}{{E_{{\text{c}}} }}} } \right)$ of simply supported square Al/Al₂O₃ FG plates are validated in Table 2 with Matsunaga [9] for different aspect ratio (a/h) and power index (k). The non-dimensional natural frequencies $\left( {\omega^{*} = \omega \left( {\frac{{a^{2} }}{h}} \right)\sqrt {\frac{{\rho_{{\text{c}}} }}{{E_{{\text{c}}} }}} } \right)$ corresponding the first four modes of vibration of the simply supported square (a = b, a/h = 10) FGM plates with constituent combinations of SUS304/Si₃N₄ and Ti–6Al–4V/Aluminium Oxide are compared with the available results [10] for a range of the FGM power index values (k = 0, 0.5, 1, 2, 5, 8 and 10) and the validation results are presented in Tables 3 and 4, respectively. The experimental vibration results for a typical cylindrical tapered fan blade with a taper in the chordwise direction $\left( {\beta_{x} = 1.0,\beta_{y} = 0.291} \right)$ are presented alongside the results of Olson and Lindberg [1] in Table 5. Similarly, the non-dimensional fundamental frequencies $\omega^{*} = \omega \left( {\frac{{a^{2} }}{h}} \right)\sqrt {\left( {\frac{{\rho_{m} \left( {1 - \nu_{m}^{2} } \right)}}{{E_{m} }}} \right)}$ of simply supported SUS304/Si₃N₄ and Ti–6Al–4V/ZrO₂ FGM plates are plotted for different thermal gradients (ΔT) between the ceramic and metallic layers and are compared in Table 6 with Huang and Shen [8]. Regarding validation of the porosity distribution models considered, the non-dimensional natural frequencies $\left( {\overline{\omega } = \omega \sqrt {\frac{{\rho_{b} a^{4} }}{{E_{b} h^{2} }}} } \right)$ of porous FGM plates are plotted alongside the results obtained by Kim et al. [24] for different porosity distribution patterns (Porosity Types 1, 2 and 3) in Fig. 5. The dimensions and the elastic properties of the functionally graded porous plate constituents considered by Kim et al. [24] are, a = 20 h, b = 20 h, and h = 17.6 × 10⁻⁶ m, E_t = 14.4 GPa, E_b = 1.44 GPa, ρ_t = 12.2 × 10³ kg/m, ρ_b = 1.22 × 10³ kg/m. The close agreement of the present FEM results with the benchmark values confirms the accuracy of the codes developed and their suitability in carrying out further analyses to predict the vibration response of porous twisted and rotating FGM plates with taper whilst operating in thermal environments. The minor variations in the results obtained using the present method may be attributed to the different methodologies adopted by different authors to predict the response from the present work.

Table 2 Non-dimensional frequencies $\left( {\omega^{*} = \omega h\sqrt {\frac{{\rho_{{\text{c}}} }}{{E_{{\text{c}}} }}} } \right)$ of simply supported square Al/Al₂O₃ FG plates for different aspect ratio (a/h) and power index (k) [9]

Table 3 Non-dimensional frequencies $\left( {\omega^{*} = \omega \left( {\frac{{a^{2} }}{h}} \right)\sqrt {\frac{{\rho_{{\text{c}}} }}{{E_{{\text{c}}} }}} } \right)$ of simple-supported square SUS304/Si₃N₄ FG plates for different power index values (a/b = 1, a/h = 10)

Table 4 Non-dimensional frequencies $\left( {\omega^{*} = \omega \left( {\frac{{a^{2} }}{h}} \right)\sqrt {\frac{{\rho_{{\text{c}}} }}{{E_{{\text{c}}} }}} } \right)$ of simply supported square Ti–6Al–4V/Aluminium oxide FG plates for different power index values

Table 5 Comparison of the first eight natural frequencies (Hz) of CFFF tapered fan blade with chord-wise taper with experimental results [E = 200 GPa, ρ = 7860 kg/m³, ν = 0.30, R_y = 30.0in, a = b = 12.0in, h_max = 0.165in h_min = 0.048in, $\beta_{x} = 1.0$, $\beta_{y} = 0.291$]

Table 6 Non-Dimensional frequencies $\omega^{*} = \omega \left( {\frac{{a^{2} }}{h}} \right)\sqrt {\left( {\frac{{\rho_{m} \left( {1 - \nu^{2} } \right)}}{{E_{m} }}} \right)}$ of simply supported square SUS304/Si₃N₄ and ZrO₂/Ti–6Al–4V FG plates for different power index values at different thermal gradients [a = b = 0.2 m, h = 0.025 m]

Fig. 5

Non-dimensional Fundamental frequencies $\left( {\overline{\omega } = \omega \sqrt {\frac{{\rho_{b} a^{4} }}{{E_{b} h^{2} }}} } \right)$ of porous FGM plates for three different cosine porosity distribution patterns [24] [a = 20 h, b = 20 h, h = 17.6 × 10⁻⁶ m, E_t = 14.4 GPa, E_b = 1.44 GPa, ρ_t = 12.2 × 10³ kg/m, ρ_b = 1.22 × 10.³ kg/m, ν_b = ν_t = 0.38]

Numerical Results Based on Current FEM Model

In the current study, a cantilevered square FGM plate of span length (a), chord or breadth (b) and thickness (h) is considered comprising of 4 different constituent combinations Al/Al₂O₃, Al/ZrO₂, SUS304/Si₃N₄ and Ti–6Al–4V/Aluminium oxide. For each of these FGM combinations, free vibration characteristics for different power index (k), aspect ratios (a/b), porosity types (No Porosity, 1, 2 and 3), twist angle (ψ), non-dimensional rotational speed (Δ_r) and thermal gradient (ΔT) are presented and analysed. The temperature coefficients of the FGM constituents considered are presented in Table 1 from which the properties P_c (E_c, ρ_c, ν_c, α_c) and P_m (E_m, ρ_m, ν_m, α_m) of the ceramic and the metal constituents can be evaluated using the non-linear thermal variation law given in Eq. (28).

Influence of Varying Twist Angle (ψ) for Different Porosity Types

The first natural frequencies $\left( {\omega^{*} = \omega \left( {\frac{{a^{2} }}{h}} \right)\sqrt {\frac{{\rho_{{\text{c}}} }}{{E_{{\text{c}}} }}} } \right)$ of square Al/Al₂O₃ FGM plates are presented in Table 7 for different twist angles (ψ = 0° and 30°), power index values (k) and porosity types (No Porosity, 1, 2 and 3). Similar data for FGM combinations of SUS304/Si₃N₄ and Ti–6Al–4V/Aluminium oxide, respectively, are also presented in Tables 8 and 9, respectively. For each of the FGM plates considered, it is observed that at a certain value of the power index k, the maximum value of the first natural frequencies is observed for the untwisted plate (ψ = 0°) and decreases with an increase in the twist angle (ψ). This clear trend of decrease in the natural frequency values is due to the fact that the stiffness of the plate decreases with an increase in the twist angle. In case of both twisted and untwisted plates, the first natural frequencies are found to decrease with an increase in the power index value for the range of the values considered (k = 1–10). As evident, the contribution of the metallic constituents predominates with an increase in the power index value (k). An increase in the power index results in a decrease in the natural frequency values owing to the structural weakness incurred due to transition from ceramic rich interface to the metal rich interfaces. In general, the highest values of the first natural frequencies are observed for Porosity Type 1 whilst the lowest value is observed for Porosity Type 2 at a particular twist angle and porosity type. This can be explained from Fig. 4b, c wherein the average material properties are the highest for Porosity Type 2 and are the lowest for Porosity Type 1 considering their variation across the thickness of the FGM plate.

Table 7 The non-dimensional fundamental frequencies $\left( {\omega^{*} = \omega \left( {\frac{{a^{2} }}{h}} \right)\sqrt {\frac{{\rho_{{\text{c}}} }}{{E_{{\text{c}}} }}} } \right)$ of square Al/Al₂O₃ cantilever FGM plates for different twist angles (ψ), power index values (k) and porosity types (0, 1, 2 and 3) [a = b = 0.1, h = 0.01, $\varphi_{\max }$ = 0.50]

Table 8 The non-dimensional fundamental frequencies $\left( {\omega^{*} = \omega \left( {\frac{{a^{2} }}{h}} \right)\sqrt {\frac{{\rho_{{\text{c}}} }}{{E_{{\text{c}}} }}} } \right)$ of square SUS304/Si₃N₄ cantilever FGM plates for different twist angles (ψ), power index values (k) and porosity types (0, 1, 2 and 3 [a = b = 0.1, h = 0.01, $\varphi_{\max }$ = 0.50]

Table 9 The non-dimensional fundamental frequencies $\left( {\omega^{*} = \omega \left( {\frac{{a^{2} }}{h}} \right)\sqrt {\frac{{\rho_{{\text{c}}} }}{{E_{{\text{c}}} }}} } \right)$ of square Ti–6Al–4V/Aluminium oxide cantilever FGM plates for different twist angles (ψ), power index values (k) and porosity types (0, 1, 2 and 3) [a = b = 0.1, h = 0.01, $\varphi_{\max }$ = 0.50]

Effects of Aspect Ratio (a/h)

The non-dimensional fundamental frequencies $\left( {\omega^{*} = \omega \left( {\frac{{a^{2} }}{h}} \right)\sqrt {\frac{{\rho_{{\text{c}}} }}{{E_{{\text{c}}} }}} } \right)$ of both intact and porous Al/Al₂O₃ and SUS304/Si₃N₄ FGM square untwisted (ψ = 0°) plates are plotted in Fig. 6a, b respectively for different aspect ratios (a/h) and porosity variations. It is noted that with an increase in the plate aspect ratio, there is a decrease in the non-dimensional fundamental frequency values for all the porosity distribution types considered along with the non-porous plates. This can be explained from the fact that an increase in the aspect ratio of the plate results in a decrease in the structural stiffness of the FGM plate resulting in a reduction in the natural frequency values. For a particular aspect ratio, the maximum value of the fundamental frequency is observed for Type 1 porosity variation followed by Type 3, Type 0 and Type 2 porosity variations. A convergence is observed in the frequency values after the aspect ratio of the plate (a/h) approaches a value of 10.

Fig. 6

a Non-dimensional fundamental frequencies $\left( {\omega^{*} = \omega \left( {\frac{{a^{2} }}{h}} \right)\sqrt {\frac{{\rho_{{\text{c}}} }}{{E_{{\text{c}}} }}} } \right)$ of perfect and porous Al/Al₂O₃ FGM square untwisted (ψ = 0°) plates (maximum porosity = 0.50) for different aspect ratios (a/b) and power factors of flat plates and different porosity types (Types 1, 2 and 3). b Non-dimensional fundamental frequencies $\left( {\omega^{*} = \omega \left( {\frac{{a^{2} }}{h}} \right)\sqrt {\frac{{\rho_{{\text{c}}} }}{{E_{{\text{c}}} }}} } \right)$ of perfect and porous SUS304/Si₃N₄ FGM square untwisted (ψ = 0°) plates (maximum porosity = 0.50) for different aspect ratios (a/b) and power factors of flat plates and different porosity types (Types 1, 2 and 3)

Influence of Non-dimensional Rotational Speed $\left( {\Delta_{r} = \frac{\omega }{{\omega_{0} }}} \right)$ for Different Porosity Types

The FGMs are mostly employed as rotating components, such as turbine or fan blades and windmill propellers. Such structures are made to operate at high rotational speeds well within their resonance limits and the porosity of the blades play a pivotal role in the dynamic and vibration characteristics of the rotating porous FGM blades. In this study, the non-dimensional rotational speed $\Delta_{{\text{r}}} = \frac{\omega }{{\omega_{0} }}$ is considered wherein ω is the actual speed of rotation in rad/s, whilst ω₀ is the circular frequency at resonance (rad/s) which is obtained at the non-rotating conditions of the FGM plate. The Δ_r is varied from Δ_r = 0 (no rotation) to 100% of the circular frequency at resonance $\left( {\Delta_{{\text{r}}} = 1.0} \right)$. The non-dimensional natural frequencies $\left( {\omega^{*} = \omega \left( {\frac{{a^{2} }}{h}} \right)\sqrt {\frac{{\rho_{{\text{c}}} }}{{E_{{\text{c}}} }}} } \right)$ of square FGM plates for different combinations of non-dimensional rotational speeds (Δ_r) with varying power index values (k) and porosity types are presented in Figs. 7, 8 and 9 for FGM combinations of Al/Al₂O₃, SUS304/Si₃N₄ and Ti–6Al–4V/Aluminium Oxide, respectively. The non-dimensional rotational speeds are varied from 0 to 1.0 at a step of 0.25 whilst the power index values are varied from 1 to 10. For a certain value of the power index k, the first natural frequencies are found to increase with an increase in the non-dimensional rotational speeds $\left( {\Delta_{r} } \right)$ at all the porosity types considered. This increase in the natural frequencies may be attributed to the fact that there is a gradual increase in the structural stiffness of the FGM plate owing to centrifugal stiffening effect with increase in rotation. This increase in the stiffness results in higher values of the natural frequencies obtained. Since the increase in stiffness is independent of the presence of porosity in the rotating structure, as such the rise in the natural frequency values is observed for all the porosity types considered. The increase in the first natural frequency values is found to be higher at higher power index values (k = 10) compared to the lower ones (k = 0). Again for a particular rotational speed, the highest value of the fundamental frequency is observed for Porosity Type 1 whilst the lowest value is observed for Porosity Type 2.

Fig. 7

The first natural frequency values $\left( {\omega^{*} = \omega \left( {\frac{{a^{2} }}{h}} \right)\sqrt {\frac{{\rho_{{\text{c}}} }}{{E_{{\text{c}}} }}} } \right)$ of untwisted (ψ = 0°) Al/Al₂O₃ FGM plates for different rotational speeds (Δ_r) with varying power index values (k) and porosity type [a = b = 1.0, h = a/10, ψ = 0°]

Fig. 8

The first natural frequency values $\left( {\omega^{*} = \omega \left( {\frac{{a^{2} }}{h}} \right)\sqrt {\frac{{\rho_{{\text{c}}} }}{{E_{{\text{c}}} }}} } \right)$ of untwisted (ψ = 0°) SUS304/Si₃N₄ FGM plates for different rotational speeds (Δ_r) with varying power index values (k) and porosity type

Fig. 9

The first natural frequency values $\left( {\omega^{*} = \omega \left( {\frac{{a^{2} }}{h}} \right)\sqrt {\frac{{\rho_{{\text{c}}} }}{{E_{{\text{c}}} }}} } \right)$ of untwisted (ψ = 0°) Ti–6Al–4V/Aluminium Oxide FGM plates for different rotational speeds (Δ_r) with varying power index values (k) and porosity type

Influence of Thickness Taper Ratio $\left( {\beta_{x} , \beta_{x} } \right)$ Along the Span and Chordal Direction

The fundamental and the second natural frequencies (Hz) of tapered cylindrical fan blades of SUS304/Si₃N₄ are presented in Tables 10 and 11 respectively for different taper ratios considering different power index values and porosity distribution patterns. The taper ratios along the span-wise and the chord-wise directions are denoted by $\beta_{x}$ and $\beta_{y}$, respectively. It is observed that for span-wise taper $\left( {\beta_{y} = 1.0} \right)$, both the first and the second natural frequencies are highest for the triangular blade $\left( {\beta_{x} = 0.0} \right)$. The values are found to decrease as $\beta_{x}$ reaches 0.50 and then again increases for uniform thickness blades $\left( {\beta_{x} = 1.0} \right)$. However, in case of chord-wise $\left( {\beta_{x} = 1.0} \right)$ taper blades, the first and the second natural frequency values are found to increase with an increase in the chord taper ratio $\left( {\beta_{y} } \right)$ from 0.0 to 1.0. As such, for chord-wise tapered blades, the lowest values of the natural frequencies are observed triangular blades $\left( {\beta_{y} = 0.0} \right)$ and the highest value is observed for $\beta_{y} = 1.0$ (uniform thickness blades). In case of both taper and uniform-width blades, both the first and second natural frequencies are found to be the highest for Porosity Type 1 and the lowest for Porosity Type 3.

Table 10 The first natural frequencies (in Hz) of cantilevered untwisted tapered SUS304/Si₃N₄ FGM cylindrical fan blades for different taper ratios and Porosity distribution patterns and power index [E = 200 GPa, ρ = 7860 kg/m³, ν = 0.30, ψ = 0°, R_y = 30.0in, a = b = 12.0in, h_max = 0.165in h_min = 0.048in, $\beta_{x} = 0.0, 0.50\,{\text{and}}\,1.0$, $\beta_{y} = 1.0$]

Table 11 The second natural frequencies (in Hz) of cantilevered untwisted tapered SUS304/Si₃N₄ FGM cylindrical fan blades for different taper ratios and Porosity distribution patterns and power index [E = 200 GPa, ρ = 7860 kg/m³, ν = 0.30, ψ = 0°, R_y = 30.0in, a = b = 12.0in, h_max = 0.165in h_min = 0.048in, $\delta_{x} = 0.0, 0.50\,{\text{and}}\,1.0$, $\delta_{y} = 1.0$]

Influence of Temperature Variations for Different Porosity Types

The non-dimensional fundamental frequencies $\omega^{*} = \omega \left( {\frac{{a^{2} }}{h}} \right)\sqrt {\frac{{\rho_{m0} \left( {1 - \nu_{m0}^{2} } \right)}}{{E_{m0} }}}$ of cantilever untwisted (ψ = 0°) square SUS304/Si₃N₄ and Ti–6Al–4V/Aluminium Oxide FGM plates are presented in Tables 12 and 13 for different thermal gradients and porosity distribution types. The temperatures of the top and the bottom layers of the FGM plate are denoted by T_c and T_m respectively. The temperature of the bottom (metallic) fibre is assumed to be constant at T_m = 300 K, whilst the temperature of the ceramic surface is assumed to be at an elevated temperature of T_m + ΔT, where ΔT refers to the thermal gradient prevalent across the thickness of the FGM plate (ΔT = T_c—T_m). The material properties $\left( {E_{m0} , \rho_{m0} , \nu_{m0} } \right)$ at the base temperature (T = 300 K) are selected for calculation of the non-dimensional frequencies. The thickness-wise distribution of the effective Young’s modulus (E_eff) of the FGM plates at different temperatures of the metal and the ceramic layers for no porosity and Porosity Types 1, 2 and 3 is plotted in Fig. 10a–d for SUS304/Si₃N₄ FGM plates. The nature of variations in the other properties like Poisson’s ratio (ν), density (ρ) and thermal expansion coefficient (α) is same with thermal gradient as adopted in Eq. (28). For all the porosity types, a reduction in the effective Young’s Modulus is observed with increase in the thermal gradient (ΔT) leading to strength degradation. As a consequence, a gradual reduction in the non-dimensional frequencies in both the porous and non-porous plates is observed in both Tables 12 and 13 with increase in the temperature difference (ΔT) between the ceramic and the metal layers of the FGM plates. In addition to the material property degradation, internal thermal strains are also induced in the bulk of the FGM plates with rise in temperature (ΔT) that causes a reduction in the structural stiffness of the FGM plate. This stiffness reduction is attributed to the introduction of the geometric stiffness matrix $\left( {\left[ {K_{\sigma } } \right]_{{{\text{Th}}}} } \right)$ in the FEM formulation resulting from thermal effects which gets subtracted from the structural stiffness of the FGM plate owing to the thermal strains being compressive in nature. For a certain thermal gradient (ΔT) and porosity type, there is a reduction in the non-dimensional fundamental frequencies $\left( {\omega^{*} } \right)$ with an increase in the power index value (k). Also, for a certain power index value, the highest value of $\omega^{*}$ is observed for Porosity Type 1 whilst the lowest value is observed for Porosity Type 3. This may be explained from Fig. 10 where the highest average value of the effective Young’s modulus (E) is observed for Porosity Type 1 whilst the lowest value occurs for Porosity Type 3. The values of the non-dimensional frequencies are also dependent on the choice of the FGM constituent combination. For the FGM’s considered, the $\omega^{*}$ values are higher for the SUS304/Si3N4 FG plates compared to the Ti–6Al–4V/Aluminium Oxide FG plates at a particular thermal gradient and porosity type. In addition, the percentage decrease in the frequency values with an increase in the thermal gradient is higher in SUS304/Si3N4 FG plates owing to their higher effective thermal expansion coefficient values compared to the Ti–6Al–4V/Aluminium Oxide FG plates.

Table 12 Non-Dimensional frequencies $\left( {\omega^{*} = \omega \left( {\frac{{a^{2} }}{h}} \right)\sqrt {\frac{{\rho_{m0} \left( {1 - \nu_{m0}^{2} } \right)}}{{E_{m0} }}} } \right)$ of cantilevered untwisted square SUS304/Si₃N₄ FG plates at different thermal gradients and Porosity distribution patterns [a = b = 0.1, h = 0.01, φ_max = 0.50, ψ = 0°, E_m0 = 207.78E9, ν_m0 = 0.3177, ρ_m0 = 8166 kg/m³]

Table 13 Non-Dimensional fundamental frequencies $\left( {\omega^{*} = \omega \left( {\frac{{a^{2} }}{h}} \right)\sqrt {\frac{{\rho_{m0} \left( {1 - \nu_{m0}^{2} } \right)}}{{E_{m0} }}} } \right)$ of square Ti–6Al–4V/Aluminium Oxide FG plates at different thermal gradients and Porosity distribution patterns [a = b = 0.1, h = 0.01, ψ = 0°, E_m0 = 105.7E9, ν_m0 = 0.298, ρ_m0 = 4429 kg/m³]

Fig. 10

Thickness variation of the Young’s modulus (E) for SUS304/Si₃N₄ FGM square plates at different temperatures (ΔT) of the ceramic (T_c) and the metallic (T_m) layers for different Porosity types and power index, k = 1.0 [a = b = 0.1, h = 0.01, k = 1.0 ψ = 0°]

The frequency response of tapered untwisted cylindrical fan blade made of a FGM constituent combination of SUS304/Si₃N₄ is predicted using the present FEM formulation and are presented in Table 14 for different chord-wise taper ratios of $\beta_{y}$ = 0.291, 0.50 and 0.75 $\left( {\beta_{x} = 1.0} \right)$. The fan blade is assumed to have only chord-wise taper where $\beta_{x}$ and $\beta_{y}$ denotes the span-wise and the chord-wise tapers, respectively. It is observed that for a certain thermal gradient (ΔT), there is an increase in the fundamental frequency values with an increase in the chord-wise taper ratio $\beta_{y}$ for all the power index and porosity types considered. This may be explained from the fact that an increase in the chord-wise taper results in additional flexibility of the fan blade, which increases both the bending and the torsional modes of vibration of the cantilever FGM plate. It is also noted that with an increase in the thermal gradient (ΔT) between the ceramic and the metallic layers, there is a reduction in the frequency values for the tapered fan blade configuration considered. This may again be attributed to the reduction of the structural stiffness of the fan blades and the degradation of the effective material properties (P_eff) with a rise in the temperature across the ceramic and metallic interfaces of the FGM plate.

Table 14 The first natural frequencies (in Hz) of cantilevered both untwisted and twisted tapered SUS304/Si₃N₄ FGM cylindrical fan blade for chordwise taper ratios of (I) $\beta_{y}$ = 0.291 (h_max = 0.165 in, h_min = 0.048in), (II) $\beta_{y}$ = 0.50 (h_max = 0.165in, h_min = 0.0825in) and (III) $\beta_{y}$ = 0.75 (h_max = 0.165in, h_min = 0.12375in) with Porosity distribution patterns and power index, k [E = 200 GPa, ρ = 7860 kg/m³, ν = 0.30, ψ = 0°; R_y = 30.0 in, a = b = 12.0 in, h_max = 0.165 in]

Conclusions

A finite element-based formulation is developed to study the influence of porosity distribution on the free vibration response of FGM twisted plates considering some triggering parameters like rotational speed, blade taper ratio and thermal gradient across ceramic and the metallic interfaces of the FGM plate. This may be inferred that the porosity distribution pattern inside the FGM structures plays a crucial role in the vibration behaviour of plates and shells. For a certain value of the power index (k), the maximum value of the first natural frequencies is observed for the untwisted plate (ψ = 0°) and decreases with an increase in the twist angle (ψ). This is due to the fact that the stiffness of the plate decreases with an increase in the pre-twist angle. In case of both twisted and untwisted plates, the first natural frequencies are found to decrease with an increase in the power index value (k) for all the porosity types considered. This is due to the fact that the contribution of the metallic constituents predominates with an increase in the power index value (k) which has lower strength compared to their ceramic counterparts. For all the FGM combinations considered in the present work, the highest values of the fundamental frequencies of the FGM plates are observed for Porosity Type 1 whilst the lowest value is observed for Porosity Type 2. This is because the average material properties are highest for Porosity Type 2 and lowest for Porosity Type 1 considering the plots of their variation presented across the thickness of the FGM plate. For a certain value of the power index k, the maximum value of the first natural frequencies is observed for the square plate (a/b = 1) and decreases with an increase in the aspect ratio for all the porosity types. This clear trend of decrease in the natural frequency values is due to the fact that the stiffness of the plate decreases with an increase in the aspect ratio (a/b). Also, for a certain value of the power index (k), the first natural frequencies are found to increase with an increase in the non-dimensional rotational speeds (Δ_r) at all the porosity types considered. This increase is due to the gradual increase in the structural stiffness of the FGM plate owing to the inclusion of the spinning matrix with rise in rotation in addition to the structural stiffness. The first natural frequency values are however found to decrease with an increase in the temperature gradient (ΔT) from 0 to 300 K for all values of the power index (k) and porosity types. This is due to the fact that internal thermal strains (negative in nature) tend to develop inside the FGM plates with temperature rise which results in a decrease in the overall stiffness of the plates. In addition, there is a reduction in the effective material properties with rise in the temperature gradient (ΔT) resulting in strength reduction of the FGM structures. The study of the fundamental frequency response for a typical curved cylindrical fan blade geometry with FGM constituent combinations of SUS304/Si₃N₄ having a chord-wise taper (β_y = 0.291, 0.50 and 0.75, β_x = 1.0) suggests a gradual increase in the frequency values with an increase in the chord-wise taper ratio (β_y).