Free Vibration Investigation of Single-Phase Porous FG Sandwich Cylindrical Shells: Analytical, Numerical and Experimental Study

Abstract

This paper offers new analytical, numerical, and experimental methods for nonlinear free vibration analysis of single-phase functionally graded (FG) porous sandwich panels that are simply supported with cylindrical shell panels using the first-order shear deflection theory. This innovative sandwich shell comprises a single porous polymer core and two uniform skins that have not been previously considered into the vibration analysis, making it highly applicable in diverse fields, such as aircraft structures, biomedical engineering, and defense technology. The properties of the core metal are assumed to depend on the porosity and grade in the direction of thickness, with a power-law distribution concerning the volume fractions of the constituents. This study involved performing free vibration experiments on three-dimensional (3D printed) FGM shells. To validate the analytical solution, a numerical study was carried out employing modal analysis and finite element analysis with the help of ANSYS-2021-R1 software. The objective of this research is to study the impact of various critical factors, including power-law index, porous ratio, FG core thickness, skin thickness, different boundary conditions, and radius of curvature on the natural frequencies and transient deflection response. The findings manifested that the frequency parameter of sandwich shell is positively correlated with both the number of constraints in the boundary conditions and the porosity factor. It is observed that there is an acceptable level of agreement between the suggested analytical procedure and the numerical findings, with a maximum error difference of only 6.7%.

1 Introduction

Numerous applications, including those in the fields of power generation, automotive, bioengineering, aircraft, structural, and microelectronics, demand characteristics that are not possible to achieve in traditional engineering materials (Gupta 2017; Edwin et al. 2017). These applications need mutually incompatible qualities, such as the resistance to chemical stability and thermomechanical stresses. Daily, things need to fulfill various functions; for example, gears require inner strength to resist the breakage and surface hardness to prevent the wearing out (Gupta and Talha 2015). The concept of structural gradients was introduced in 1972 (Bohidar et al. 2014). Initially, functionally graded materials (FGMs) were developed for polymeric materials and composites to replicate the structure and behavior of natural materials. FGM was initially considered in Japan in 1984 (Kokanee 2017) when a space shuttle was designed. The goal was to create a body from a material that could tolerate a significant temperature differential of 1000 °C while also having superior mechanical and thermal capabilities.

Polylactic acid (PLA) is a biodegradable thermoplastic material that has gained popularity in recent years due to its eco-friendliness and sustainability (Singhvi et al. 2019). Although PLA is commonly used in consumer products, such as 3D printing, food packaging, and textiles, it also has several applications in engineering structures; Fig. 1 explains the application of PLA in engineering structures (Reichert et al. 2020). In general, PLA has several applications in engineering structures where the lightweight, low-load-bearing components are required. Its biodegradability and sustainability make it an attractive alternative to traditional materials in various industries (Reichert et al. 2020).

Fig. 1

Applications of PLA

Several shell theories exist based on the effects of static and dynamic studies of shell structures on the shell's transverse shear deformation. The vibration of the shells composed of FGM was analyzed by Loy et al. (1999). An analytical method was presented by Bich et al. (2012) to study the nonlinear dynamical response of eccentrically stiffened functionally graded material (ES-FGM) cylindrical panels. Huy Bich et al. (2014) demonstrated an analytical method to study the vibration and nonlinear dynamic response of the ES-FGM thick doubly curved shallow shells imperfectly resting on the elastic foundation using both the stress function and the first-order shear deformation theory (FSDT) with full equations of motion. Duc and Thang (2015) used the first-order shear deformation theory and stress function to analyze the vibration and nonlinear dynamic response of an imperfect (ES-FGM) thick circular cylindrical shell envelope of elastic foundations. Arefi et al. (2016) evinced an analytical approach to examine three-dimensional vibration for cylindrical sandwich shells consisting of three layers; the middle layer consists of FGM, while the other two layers comprise functionally graded piezoelectric (FGP). Deniz et al. (2016) employed the first-order shear deformation theory to study the vibration behavior of (FGM) truncated conical shells surrounded by Winkler and Pasternak foundations. Karamanlı (2018) used the third-order shear deformation theory to analyze the free vibration of a (2D-FGM) beam under different boundary conditions. Duc et al. (2016) utilized the third-order shear deformation plate theory to study the response of the nonlinear vibration of FGM thick plates resting on the elastic foundation under the influence of thermal stresses. Al-Waily et al. (2020a) studied the thermal buckling activity employing analytical and numerical processes for a composite plate with a range of nanofractions according to the finite element procedure and the Ansys package. Kumar and Kumar (2020) offered a mathematical technique based on first-order shear deformation theory to analyze the free vibration of doubly curved shallow ES-FGM shells under thermomechanical loading. Baghlani et al. (2020) used the higher-order shear deformation theory with power series in the radial direction to study partially fluid-filled circular cylinder shells made of ES-FGM and surrounded by a Pasternak elastic foundation in a thermal environment. Foroutan and Ahmadi (2020) analyzed the nonlinear free vibration properties of spiral stiffened multilayer FG circular shells with a viscoelastic Kelvin-Voigt foundation under a thermal condition. Zghal et al. (2021) offered the free vibration characteristics of thermally preloaded FGM plates and cylindrical panels employing an improved FSDT. Mirjavadi et al. (2022) investigated the nonlinear free vibration properties of annular stiffened spherical shell segments constructed of porous FGM, enveloped by an elastic medium, and supported by circumferential stiffeners. Fu et al. (2020) studied the response of porous FGM for cylindrical shells in nonlinear thermal conditions through thermoacoustic vibrations placed on elastic foundations. Chan et al. (2020) adopted the FSDT and Hamilton’s principal method to examine the nonlinear dynamic response of a truncated conical shell of porous FG with piezoelectric actuators that rest on the elastic foundation in thermal environments. Foroutan et al. (2020) demonstrated the analytical and semi-analytical techniques to scrutinize the nonlinear dynamics and static hygrothermal buckling for imperfect FG porous cylindrical shells under hygrothermal loading. Njim et al. (2021b, d, c, 2022a, b and Kadum Njim et al. (2021a) employed analytical, numerical, and experimental studies to examine the free vibrations and buckling stability characterizations of porous FG for the sandwich plate. On the other hand, the optimization design of the buckling and vibration characterizations for the FG porous metal core sandwich plate was studied by Kadum Njim et al. (2021b) and Njim et al. (2021e). Quan et al. (2022) described the nonlinear vibration responses of a porous FG sandwich plate resting on elastic foundations under blast loading. Pham et al. (2022b) developed a computational model utilizing the strain gradient theory and refined the higher-order shear deformation beam theory to investigate the dynamic instability of magnetically embedded functionally graded porous nanobeams. Doan et al. (2021) introduced a finite element method based on a nonlocal theory to examine the free vibration behavior of FG porous nanoplates with different shapes placed on an elastic foundation. Nguyen et al. (2022) extended the ES-MITC3 element, which is based on the FSDT, to analyze the free vibration behavior of FG porous plates resting on a partially supported elastic foundation. Pham et al. (2022a) conducted a study with the main objective of investigating the dynamic response of sandwich nanoplates containing a porous FG core utilizing isogeometric analysis based on the HSDT and examined the effects of different continuous functions f(z) on the nanoplate's behavior. Malekzadeh et al. (2012) investigated how the small size of finite-length nanotubes embedded in an elastic medium influenced their free vibration characteristics. Heydarpour et al. (2014b) conducted a study to investigate how the free vibration behavior of FG truncated conical shells is affected by internal pressure. The analysis was performed using the first-order shear deformation theory of shells. Heydarpour et al. (2014a) examined the effects of centrifugal and Coriolis forces on the free vibration characteristics of rotating functionally graded carbon nanotube-reinforced composite truncated conical shells according to FSDT. Malekzadeh and Heydarpour (2013) examined how the centrifugal and Coriolis forces, as well as other geometric and material factors, affected the free vibration behavior of rotating functionally graded truncated conical shells under different boundary conditions. Heydarpour and Aghdam (2016a) investigated the transient response of rotating multi-layered FG truncated conical shells under the influence of thermal shock, considering the properties that depend on temperature. Heydarpour and Aghdam (2016b) utilized the Lord–Shulman (L–S) theory of generalized coupled thermoelectricity to analyze the transient thermoelastic behavior of rotating functionally graded truncated conical shells under different boundary conditions when subjected to thermal shock. Heydarpour et al. (2020a) conducted a study to examine the impact of thermal shock loading on the rotating multilayer FG graphene platelets reinforced composite truncated conical shells by using the differential quadrature technique with a non-uniform rational B-spline (NURBS). Heydarpour et al. (2012, 2020b, 2021) carried out a study to explore the response of glass fiber-reinforced epoxy laminated composite cylindrical shells under an impulse load using the FSDT of shells. They developed a novel solution approach that involved employing the differential quadrature method with the direct projection of the Heaviside function and a multi-step time integration scheme based on non-uniform rational B-splines (NURBS).

Previous analysis investigated the buckling analysis and vibration problems of porous FGM structures, but most of these examinations concentrated on the cores constructed of two-phase materials (like ceramics and metals). Nevertheless, there have been few studies in this area, and this paper adds to this by assuming a single-phase metal as the core material for the entire thickness of shell, which forms its own FG property. This is the major originality of this study. This paper's significant contribution is to evaluate the effectiveness of FG porous materials, especially in tissue engineering, as they are frequently used for numerous biomedical applications. In the analysis of present paper, a novel analytical solution was introduced to investigate the nonlinear free vibration behavior of porous FG structures. The equations of motion were solved using the fourth-order Runge–Kutta and Galerkin approaches. This paper investigates the influences of various characteristics, such as porosity coefficients, FG core thickness, skin thickness, and various boundary conditions, on the natural frequency and time-deflection curve. To confirm the precision of analytical results, a numerical investigation was conducted using finite element analysis through the ANSYS 2021 R1 software. The results of this article can serve as a useful resource for researchers interested in conducting further research on sandwich structures in this field.

The article is structured into five main parts. The first part deals with the characteristics of FG porous structures, the constitutive equations, the theoretical framework and formulation of the study, and the analytical nonlinear free vibration of cylindrical porous sandwich panels employing the FSDT. The second part discusses the numerical investigation and finite element simulation. The third part explains the experimental technique for cylindrical shell panels of an FG sandwich. The fourth part offers the results and their corresponding discussions. Finally, the last part summarizes the research conclusions and provides a summary of the overall study.

2 Modeling of Porous FGM Sandwich Cylindrical Panel

2.1 Geometrical Configuration

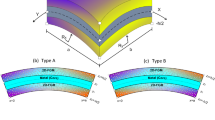
Consider a cylindrical sandwich FG panel with a porous FG core and two homogeneous faces as illustrated in Fig. 2, where a, b, R, and h display the dimensions of the sandwich panel. The sandwich cylindrical panel is composed of three layers; two homogeneous skins and an FG porous core. In Fig. 2b, ${h}_{L}$ and ${h}_{U}$ are the same thickness (${h}_{s}$) and made of the same homogeneous components. Additionally, z₀, z₁, z₂, and z₃ are thickness values.

Fig. 2

The geometry of the sandwich cylindrical panel with a porous FG core

2.2 Mathematical Formulation of FGM

Although there are numerous analyses of the FGM structure that have studied the vibrational characteristics of FG cylindrical shell, these studies assumed two phases such as metal-ceramic FGM because of its high mechanical strength, and the metallic polymers are less discussed. Consequently, if the volume fraction of the lower and upper surfaces is V_L and V_U, respectively, then by presenting a power-law distribution of the components toward the thickness of shell, the volume fraction of the upper component may be assumed to be as follows (Mouthanna et al. 2019):

$$ V_{{\text{U}}} \left( z \right) = \left( {\frac{2z + h}{{2h}}} \right)^{k} , $$

(1)

where k indicates the power-law index, which explains the variance in material characteristic thickness, and h represents the shell thickness. The mixture of volume fractions can be offered by the following:

$$ V_{{\text{U}}} \left( z \right) + V_{{\text{L}}} \left( z \right) = 1, $$

(2)

The effective material characteristics with even porosity distribution of the FGM cylindrical shell can be developed as (Liu et al. 2021):

$$ P\left( z \right) = P_{{\text{U}}} + \left( {P_{{\text{L}}} - P_{{\text{U}}} } \right)\left( {\frac{z}{h} + \frac{1}{2}} \right)^{k} - \frac{\beta }{2}\left( {P_{{\text{L}}} + P_{{\text{U}}} } \right), $$

(3)

In Eq. (3), P_U and P_L are the equivalent material characteristics of the upper and lower components of the porous FG cylindrical shell, respectively. The originality of the present study lies in creating a novel mathematical expression utilizing the FG core of a sandwich structure composed of a single-phase metal with varying porosity in the through-thickness direction. As a result, the mechanical characteristics of the FG structure are determined by the following (Njim et al. 2021e; Mouthanna et al. 2023):

$$ V_{{\text{P}}} \left( z \right) = V_{{\text{m}}} - \beta .V_{{\text{m}}} \left( {\frac{z}{h} + \frac{1}{2}} \right)^{k} , $$

(4)

For k = 0, ${V}_{\mathrm{P}}$(z) = ${V}_{m}-\beta {V}_{m},$, while for $k= \propto$, ${V}_{P}$= ${V}_{m}$=1, where $\beta$ is the porosity factor, ${V}_{m}$ is the volume of core metal, and ${V}_{\mathrm{P}}$ is the total volume of porous metal. Therefore, the suggested mechanical characteristics of the porous FGM metal can be expressed as:

$$ P\left( z \right) = P_{{\text{m}}} - \beta .P_{{\text{m}}} \left( {\frac{z}{h} + \frac{1}{2}} \right)^{k} , $$

(5)

Here, ${P}_{\mathrm{m}}$ refers to the metal's structural characteristics of the metal related to the FG shell. Consequently, for the homogeneous cylindrical panel, $\beta = 0,$, while for the imperfect cylindrical panel, $\beta < 1.$ Young's modulus $(E)$ and mass density $\left(\rho \right)$ can be illustrated, respectively, as:

$$ E\left( z \right) = E_{{\text{m}}} - \beta .E_{{\text{m}}} \left( {\frac{z}{h} + \frac{1}{2}} \right)^{k} , $$

(6a)

$$ \rho \left( z \right) = \rho_{{\text{m}}} - \beta .\rho_{{\text{m}}} \left( {\frac{z}{h} + \frac{1}{2}} \right)^{k} , $$

(6b)

To verify the mathematical equations suggested that (Eq. 6) calculates the material properties of porous FGM shells, a comparison can be made between the results obtained from the volume fraction analysis and the proposed models. For instance, if an FGM shell made of aluminum (Al) with porous metal is considered, with the material properties of $\mathrm{Em} = 70 \mathrm{GPa}, \rho =2702$Kg/m³ and $\upsilon =0.3$ as (Wattanasakulpong and Chaikittiratana 2015; Mouthanna et al. 2022a), Table 1 provides the values of the FGM shell's mass per unit length. The comparison offered in Table 1 presents a close match between the results forecasted by the suggested models and those obtained from the volume fraction analysis. Furthermore, Fig. 3 exhibits the material properties profile of imperfect FGM shells, which is obtained using Eq. 6 and is used to predict Young's modulus (E) and mass density ($\rho )$ across the thickness of the shell.

Table 1 The two different methods utilized to determine the mass density of both ideal and imperfect cores

Fig. 3

The material gradient at porosity ratio 10% of a mass densities and b Young’s modulus of the FG shell

3 Theoretical Formulation

3.1 Kinematics

In this section, the equations of motion will be derived according to the first-order shear deformation theory, which assumes that the transverse normal does not remain perpendicular to the mid-surface after deformation (Zhang et al. 2020). A displacement field $\left({u}^{\sim }{,v}^{\sim },{w}^{\sim }\right)$ that represents the displacements in the x, y, and z directions, respectively, at any point within the panel is considered as:

$$ \tilde{u}(x,y,z,t) = u(x,y,t) + z\phi_{x} \left( {x,y,t} \right), $$

(7a)

$$ \tilde{v}(x,y,z,t) = v(x,y,t) + z\phi_{y} \left( {x,y,t} \right), $$

(7b)

$$ \tilde{w}(x,y,z,t) = w(x,y,t), $$

(7c)

where $\left(u, v, w\right)$ are defined as the displacement of a material point in the middle plane concerning the coordinates $(x, y, z)$; $\left({\phi }_{x}\ \mathrm{and\ }{\phi }_{y}\right)$ explain the slopes of the transverse normal around $\left(x\right)$ and $\left(y\right)$ axes at $\left(z = 0\right)$. The parameter (t) is the time factor. The strain–displacement relationships with the Von Karman nonlinear terms are (Harsha and Kumar 2022):

$$ \left( {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{xy} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\varepsilon_{x}^{ \circ } } \\ {\varepsilon_{y}^{ \circ } } \\ {\gamma_{xy}^{ \circ } } \\ \end{array} } \right) + z\left( {\begin{array}{*{20}c} {\lambda_{x} } \\ {\lambda_{y} } \\ {\lambda_{xy} } \\ \end{array} } \right),\left( {\begin{array}{*{20}c} {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\frac{\partial w}{{\partial x}} + \phi_{x} } \\ {\frac{\partial w}{{\partial y}} + \phi_{y} } \\ \end{array} } \right), $$

(8)

with

$$ \left( {\begin{array}{*{20}c} {\varepsilon_{x}^{ \circ } } \\ {\varepsilon_{y}^{ \circ } } \\ {\gamma_{xy}^{ \circ } } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} } \\ {\frac{\partial v}{{\partial y}} - \frac{w}{R} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} } \\ {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}} + \frac{\partial w}{{\partial x}}\frac{\partial w}{{\partial y}}} \\ \end{array} } \right),\left( {\begin{array}{*{20}c} {\lambda_{x} } \\ {\lambda_{y} } \\ {\lambda_{xy} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\frac{{\partial \phi_{x} }}{\partial x}} \\ {\frac{{\partial \phi_{y} }}{\partial y}} \\ {\frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x}} \\ \end{array} } \right), $$

(9)

3.2 Constitutive Relations

The nonlinear stress–strain relations of FSDT with porosity are based on the generalized Hooke's law (Keleshteri and Jelovica 2020):

$$ \begin{gathered} \left( {\begin{array}{*{20}c} {\sigma_{x}^{sh} } \\ {\sigma_{y}^{sh} } \\ {\tau_{xy}^{sh} } \\ {\tau_{xz}^{sh} } \\ {\tau_{yz}^{sh} } \\ \end{array} } \right) = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & 0 & 0 & 0 \\ {C_{12} } & {C_{22} } & 0 & 0 & 0 \\ 0 & 0 & {C_{44} } & 0 & 0 \\ 0 & 0 & 0 & {C_{55} } & 0 \\ 0 & 0 & 0 & 0 & {C_{66} } \\ \end{array} } \right]\left( {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{xy} } \\ {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right) \hfill \\ C_{11} = C_{22} = \frac{E(z)}{{1 - \nu^{2} }},C_{12} = \frac{\nu E(z)}{{1 - \nu^{2} }},C_{44} = C_{55} = C_{66} = \frac{E(z)}{{2(1 + \nu )}} \hfill \\ \end{gathered} $$

(10)

The resultant of the forces and moments is gained as follows:

$$ N_{x} = I_{10} \varepsilon_{x}^{ \circ } + I_{20} \varepsilon_{y}^{ \circ } + I_{11} \frac{{\partial \phi_{x} }}{\partial x} + I_{21} \frac{{\partial \phi_{y} }}{\partial y}, $$

(11a)

$$ N_{y} = I_{20} \varepsilon_{x}^{ \circ } + I_{10} \varepsilon_{y}^{ \circ } + I_{21} \frac{{\partial \phi_{x} }}{\partial x} + I_{11} \frac{{\partial \phi_{y} }}{\partial y}, $$

(11b)

$$ N_{xy} = I_{30} \gamma_{xy}^{ \circ } + 2I_{31} \left( {\frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x}} \right), $$

(11c)

$$ M_{x} = I_{11} \varepsilon_{x}^{ \circ } + I_{21} \varepsilon_{y}^{ \circ } + I_{12} \frac{{\partial \phi_{x} }}{\partial x} + I_{22} \frac{{\partial \phi_{y} }}{\partial y}, $$

(11d)

$$ M_{y} = I_{21} \varepsilon_{x}^{ \circ } + I_{11} \varepsilon_{y}^{ \circ } + I_{22} \frac{{\partial \phi_{x} }}{\partial x} + I_{12} \frac{{\partial \phi_{y} }}{\partial y}, $$

(11e)

$$ M_{xy} = I_{31} \gamma_{xy}^{ \circ } + I_{32} \left( {\frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x}} \right), $$

(11f)

$$ Q_{x} = K_{s} I_{30} \gamma_{xz} , $$

(11g)

$$ Q_{y} = K_{s} I_{30} \gamma_{yz} , $$

(11h)

where

$$ \begin{gathered} \left\{ {\begin{array}{*{20}c} {N_{x} } & {N_{y} } & {N_{xy} } & {Q_{x} } & {Q_{y} } \\ \end{array} } \right\} = \int\limits_{ - h/2}^{h/2} {\left\{ {\begin{array}{*{20}c} {\sigma_{x}^{sh} } & {\sigma_{y}^{sh} } & {\tau_{xy}^{sh} } & {K_{s} Q_{x} } & {K_{s} Q_{y} } \\ \end{array} } \right\}} dz, \hfill \\ \left\{ {\begin{array}{*{20}c} {M_{x} } & {M_{y} } & {M_{xy} } \\ \end{array} } \right\} = \int\limits_{ - h/2}^{h/2} {\left\{ {\begin{array}{*{20}c} {\sigma_{x}^{sh} } & {\sigma_{y}^{sh} } & {\tau_{xy}^{sh} } \\ \end{array} } \right\}z} dz, \hfill \\ E_{i} = \left\{ \begin{gathered} \int_{{ - \frac{{(h_{FG} + h_{L} )}}{2}}}^{{ - \frac{{(h_{FG} )}}{2}}} {E(z)dz + \int\limits_{{ - \frac{{(h_{FG} )}}{2}}}^{{\frac{{(h_{FG} )}}{2}}} {\left[ {E_{m} - \beta .E_{m} \left( {\frac{z}{h} + \frac{1}{2}} \right)^{r} } \right]dz} } \hfill \\ + \int_{{\frac{{(h_{FG} )}}{2}}}^{{\frac{{(h_{FG} + h_{U} )}}{2}}} {E(z)dz} \hfill \\ \end{gathered} \right\}\left( {1,z,z^{2} } \right), \hfill \\ {\rm I}_{i} = \int_{{ - \frac{{(h_{FG} + h_{L} )}}{2}}}^{{ - \frac{{(h_{FG} )}}{2}}} {\rho \left( z \right)dz + \int\limits_{{ - \frac{{(h_{FG} )}}{2}}}^{{\frac{{(h_{FG} )}}{2}}} {\left[ {\rho_{m} - \beta .\rho_{m} \left( {\frac{z}{h} + \frac{1}{2}} \right)} \right]\left( {1,z,z^{2} } \right),dz} } \hfill \\ \quad + \int_{{\frac{{(h_{FG} )}}{2}}}^{{\frac{{(h_{FG} + h_{U} )}}{2}}} {\rho \left( z \right)dz} , \hfill \\ \end{gathered} $$

(12)

where ${K}_{s}$ denotes the shear correction characteristic of (FSDT) $({K}_{s} = \frac{5}{6})$ (Kumar and Harsha 2021). All coefficients in Eqs. (11) and (12) are explained in the appendix. Through Eqs. (11a–c), one produces:

$$ \varepsilon_{x}^{ \circ } = A_{22} N_{x} - A_{12} N_{y} - B_{11} \frac{{\partial \phi_{x} }}{\partial x} - B_{12} \frac{{\partial \phi_{y} }}{\partial y}, $$

(13a)

$$ \varepsilon_{y}^{ \circ } = A_{11} N_{y} - A_{12} N_{x} - B_{21} \frac{{\partial \phi_{x} }}{\partial x} - B_{22} \frac{{\partial \phi_{y} }}{\partial y}, $$

(13b)

$$ \gamma_{xy}^{ \circ } = A_{66} N_{xy} - B_{66} \left( {\frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x}} \right), $$

(13c)

3.3 Equations of Motion

Hamilton’s principal approach consists of three terms (strain energy, kinetic energy, and work done). It describes one of the most important aspects of variation principle in mechanical science used for dynamic systems. To illustrate mathematically, the following form is described as follows (Trinh and Kim 2019):

$$ 0 = \int\limits_{0}^{T} {\left( {\delta U + \delta V - \delta K} \right)} {\text{d}}t $$

(14)

The variation of strain energy, kinetic energy, and work done of the cylindrical shell is obtained as the following expression (Jweeg et al. 2010; Hassan Hadi and Aziz Ameen 2011):

$$ \delta U = \int_{V} {\left( {\sigma_{x}^{sh} \delta \varepsilon_{x} + \sigma_{y}^{sh} \delta \varepsilon_{y} + \sigma_{xy}^{sh} \delta \gamma_{xy} + \sigma_{xz}^{sh} \delta \gamma_{xz} + \sigma_{yz}^{sh} \delta \gamma_{yz} } \right)} {\text{d}}V $$

(15a)

$$ \delta K = \int_{V} {\rho \left( z \right)\left( {u^{ \cdot } \delta u^{ \cdot } + v^{ \cdot } \delta v^{ \cdot } + w^{ \cdot } \delta w^{ \cdot } } \right)} {\text{d}}V $$

(15b)

$$ \delta W = \int_{A} {q \delta w } {\text{d}}A $$

(15c)

where $q$ is uniformly distributed pressure (UDP). Substituting Eqs. (8), (9), and (10) into Eq. (15a), substituting Eqs. (7) into (15b), and after the integration by part through the thickness of the shell, the governing equations of the motion of the porous FG sandwich cylindrical panels are derived from Eq. (14), as the following procedures (Kumar et al. 2021):

$$ \delta u:\frac{{\partial N_{x} }}{\partial x} + \frac{{\partial N_{xy} }}{\partial y} = {\rm I}_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} + {\rm I}_{1} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }}, $$

(16a)

$$ \delta v:\frac{{\partial N_{xy} }}{\partial x} + \frac{{\partial N_{y} }}{\partial y} = {\rm I}_{0} \frac{{\partial^{2} v}}{{\partial t^{2} }} + {\rm I}_{1} \frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }}, $$

(16b)

$$ \delta w:\frac{{\partial Q_{x} }}{\partial x} + \frac{{\partial Q_{y} }}{\partial y} + N_{x} \frac{{\partial^{2} w}}{{\partial x^{2} }} + 2N_{xy} \frac{{\partial^{2} w}}{\partial x\partial y} + N_{y} \frac{{\partial^{2} w}}{{\partial y^{2} }} + q + \frac{{N_{y} }}{R} = {\rm I}_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }}, $$

(16c)

$$ \delta \phi_{x} :\frac{{\partial M_{x} }}{\partial x} + \frac{{\partial M_{xy} }}{\partial y} - Q_{x} = {\rm I}_{2} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} + {\rm I}_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }}, $$

(16d)

$$ \delta \phi_{y} :\frac{{\partial M_{xy} }}{\partial x} + \frac{{\partial M_{y} }}{\partial y} - Q_{y} = {\rm I}_{2} \frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} + {\rm I}_{1} \frac{{\partial^{2} v}}{{\partial t^{2} }}, $$

(16e)

3.4 Stress Function Method

The membrane strains of cylindrical panels are also related to the compatibility equations.

$$ \frac{{\partial^{2} \varepsilon_{x}^{ \circ } }}{{\partial y^{2} }} + \frac{{\partial^{2} \varepsilon_{y}^{ \circ } }}{{\partial x^{2} }} - \frac{{\partial^{2} \gamma_{xy}^{ \circ } }}{\partial x\partial y} = \frac{{\partial^{2} w^{2} }}{\partial x\partial y} - \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial y^{2} }} - \frac{1}{R}\frac{{\partial^{2} w}}{{\partial x^{2} }}, $$

(17)

The Airy stress function f (x, y) satisfies Eqs. (16a) and (16b) can be determined as: (Singh and Harsha 2019; Mouthanna et al. 2022b):

$$ N_{x} = \frac{{\partial^{2} f}}{{\partial y^{2} }},N_{y} = \frac{{\partial^{2} f}}{{\partial x^{2} }},N_{xy} = - \frac{{\partial^{2} f}}{\partial x\partial y}, $$

(18)

Substituting Eq. (18) into Eqs. (16a) and (16b) yields the following:

$$ \frac{{\partial^{2} u}}{{\partial t^{2} }} = - \frac{{{\rm I}_{1} }}{{{\rm I}_{0} }}\frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }}, $$

(19a)

$$ \frac{{\partial^{2} v}}{{\partial t^{2} }} = - \frac{{{\rm I}_{1} }}{{{\rm I}_{0} }}\frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }}, $$

(19b)

Substituting Eq. (19) into Eqs. (16c–e) results:

$$ \delta w:\frac{{\partial Q_{x} }}{\partial x} + \frac{{\partial Q_{y} }}{\partial y} + N_{x} \frac{{\partial^{2} w}}{{\partial x^{2} }} + 2N_{xy} \frac{{\partial^{2} w}}{\partial x\partial y} + N_{y} \frac{{\partial^{2} w}}{{\partial y^{2} }} + q + \frac{{N_{y} }}{R} = {\rm I}_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }}, $$

(20a)

$$ \delta \phi_{x} :\frac{{\partial M_{x} }}{\partial x} + \frac{{\partial M_{xy} }}{\partial y} - Q_{x} = \left( {{\rm I}_{2} - \frac{{{\rm I}_{1}^{2} }}{{{\rm I}_{0} }}} \right)\frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }}, $$

(20b)

$$ \delta \phi_{y} :\frac{{\partial M_{xy} }}{\partial x} + \frac{{\partial M_{y} }}{\partial y} - Q_{y} = \left( {{\rm I}_{2} - \frac{{{\rm I}_{1}^{2} }}{{{\rm I}_{0} }}} \right)\frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }}, $$

(20c)

Inserting Eq. (13) into Eqs. (11d–h) and then into Eq. (20) leads to:

$$ {\rm T}_{11} \left( w \right) + {\rm T}_{12} \left( {\phi_{x} } \right) + {\rm T}_{13} \left( {\phi_{y} } \right) + R_{1} \left( {w,f} \right) + q = {\rm I}_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }}, $$

(21a)

$$ {\rm T}_{21} \left( w \right) + {\rm T}_{22} \left( {\phi_{x} } \right) + {\rm T}_{23} \left( {\phi_{y} } \right) + R_{2} \left( f \right) = \left( {{\rm I}_{2} - \frac{{{\rm I}_{1}^{2} }}{{{\rm I}_{0} }}} \right)\frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }}, $$

(21b)

$$ {\rm T}_{31} \left( w \right) + {\rm T}_{32} \left( {\phi_{x} } \right) + {\rm T}_{33} \left( {\phi_{y} } \right) + R_{3} \left( f \right) = \left( {{\rm I}_{2} - \frac{{{\rm I}_{1}^{2} }}{{{\rm I}_{0} }}} \right)\frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }}, $$

(21c)

When Eq. (15) is substituted into Eq. (7) along with the equation of stress functions, one gets the following equation for the compatibility of porous FGM sandwich cylindrical panels:

$$ \begin{aligned} & A_{11} \frac{{\partial^{4} f}}{{\partial x^{4} }} + A_{22} \frac{{\partial^{4} f}}{{\partial y^{4} }} + \left( {A_{66} - 2A_{12} } \right)\frac{{\partial^{4} f}}{{\partial x^{2} \partial y^{2} }} - B_{21} \frac{{\partial^{3} \phi_{x} }}{{\partial x^{3} }} - B_{12} \frac{{\partial^{3} \phi_{y} }}{{\partial y^{3} }} \\ & \quad + \left( {B_{66} - B_{11} } \right)\frac{{\partial^{3} \phi_{x} }}{{\partial x\partial y^{2} }} + \left( {B_{66} - B_{22} } \right)\frac{{\partial^{3} \phi_{y} }}{{\partial x^{2} \partial y}} - \left( {\frac{{\partial^{2} w^{2} }}{\partial x\partial y} - \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial y^{2} }} - \frac{1}{R}\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) = 0, \\ \end{aligned} $$

(22)

3.5 The Solution of Problem

The exact solution of Eq. (21) for cylindrical porous FGM sandwich panels with simply supported edges and evenly distributed pressure intensity can be written, as the following formula:

$$ \begin{gathered} w = N_{xy} = \phi_{y} = 0,at \, x = 0,a, \hfill \\ w = N_{xy} = \phi_{x} = 0,at \, y = 0,b, \hfill \\ \end{gathered} $$

(23)

In the current cases, the corresponding formulations are meant to represent the displacements that conform to the presumed boundary conditions.

$$ w\left( {x,y,t} \right) = W\left( t \right)\sin \lambda_{m} x\sin \delta_{n} y, $$

(24a)

$$ \phi_{x} \left( {x,y,t} \right) = \Phi_{x} \left( t \right)\cos \lambda_{m} x\sin \delta_{n} y, $$

(24b)

$$ \phi_{y} \left( {x,y,t} \right) = \Phi_{y} \left( t \right)\sin \lambda_{m} x\cos \delta_{n} y, $$

(24c)

where ${\lambda }_{m}=\frac{m\pi }{a},{\mathrm{and \delta }}_{\mathrm{n}}=\frac{n\pi }{b}.$

Substituting Eqs. (24) into (22) to find the stress function's coefficients:

$$ f\left( {x,y,t} \right) = \tilde{A}_{1} \left( t \right)\cos 2\lambda_{m} x + \tilde{A}_{2} \left( t \right)\cos 2\delta_{n} y + \tilde{A}_{3} \left( t \right)\sin \lambda_{m} x\sin \delta_{n} y, $$

(25a)

$$ \begin{gathered} \tilde{A}_{1} \left( t \right) = \frac{{\delta_{n}^{2} }}{{32A_{11} \lambda_{m}^{2} }}W^{2} ,\tilde{A}_{2} \left( t \right) = \frac{{\lambda_{m}^{2} }}{{32A_{22} \delta_{n}^{2} }}W^{2} , \hfill \\ \tilde{A}_{3} \left( t \right) = \frac{1}{{\left[ {A_{11} \lambda_{m}^{4} + A_{22} \delta_{n}^{4} + \left( {A_{66} - 2A_{12} } \right)\lambda_{m}^{2} \delta_{n}^{2} } \right]}}\frac{W}{R} \hfill \\ + \frac{{\left[ {B_{21} \lambda_{m}^{3} + \left( {B_{11} - B_{66} } \right)\lambda_{m} \delta_{n}^{2} } \right]\Phi_{x} \left( t \right) + \left[ {\delta_{n}^{3} B_{12} + \left( {B_{22} - B_{66} } \right)\lambda_{m}^{2} \delta_{n} } \right]\Phi_{y} \left( t \right)}}{{\left[ {A_{11} \lambda_{m}^{4} + A_{22} \delta_{n}^{4} + \left( {A_{66} - 2A_{12} } \right)\lambda_{m}^{2} \delta_{n}^{2} } \right]}}, \hfill \\ \end{gathered} $$

(25b)

Substituting Eqs. (24) and (25) into Eq. (21) and applying the Galerkin approach give:

$$ \begin{gathered} t_{11} W + t_{12} \Phi_{x} + t_{13} \Phi_{y} + t_{14} W\Phi_{x} + t_{15} W\Phi_{y} + t_{16} W \hfill \\ + t_{17} W^{2} + t_{18} W^{3} + L_{32} q = {\rm I}_{0} \frac{{d^{2} W}}{{dt^{2} }}, \hfill \\ \end{gathered} $$

(26a)

$$ t_{21} W + t_{22} \Phi_{x} + t_{23} \Phi_{y} + n_{1} W + n_{2} W^{2} = \tilde{\rho }_{1} \mathop {\Phi_{x} }\limits^{..} , $$

(26b)

$$ t_{31} W + t_{32} \Phi_{x} + t_{33} \Phi_{y} + n_{3} W + n_{4} W^{2} = \tilde{\rho }_{1} \mathop {\Phi_{y} }\limits^{..} , $$

(26c)

The natural frequencies can be derived by solving the below equation:

$$ \left| {\begin{array}{*{20}c} {t_{11} + t_{16} + {\rm I}_{0} \omega^{2} } & {t_{12} } & {t_{13} } \\ {t_{21} + n_{1} } & {t_{22} + \tilde{\rho }_{1} \omega^{2} } & {t_{23} } \\ {t_{31} + n_{3} } & {t_{32} } & {t_{33} + \tilde{\rho }_{1} \omega^{2} } \\ \end{array} } \right| = 0, $$

(27)

3.6 Nonlinear Dynamic Responses

Consider that the cylindrical shell of the FGM sandwich with porosity is under the effect of a uniformly distributed transverse load $\left(q=Q sin\Omega t\right)$. The nonlinear Eq. (26) becomes:

$$ \begin{aligned} & {\rm I}_{0} \frac{{{\text{d}}^{2} W}}{{{\text{d}}t^{2} }} - t_{11} W - t_{12} \Phi_{x} - t_{13} \Phi_{y} - t_{14} W\Phi_{x} \\ & \quad - t_{15} W\Phi_{y} - t_{16} W - t_{17} W^{2} - t_{18} W^{3} = L_{32} Q\sin \Omega t, \\ \end{aligned} $$

(28a)

$$ t_{21} W + t_{22} \Phi_{x} + t_{23} \Phi_{y} + n_{1} W + n_{2} W^{2} = \tilde{\rho }_{1} \mathop {\Phi_{x} }\limits^{..} , $$

(28b)

$$ t_{31} W + t_{32} \Phi_{x} + t_{33} \Phi_{y} + n_{3} W + n_{4} W^{2} = \tilde{\rho }_{1} \mathop {\Phi_{y} }\limits^{..} , $$

(28c)

By using Eq. (28) which takes into consideration three characteristics: nonlinear free vibration, frequency-amplitude relationship, and fundamental frequencies of cylindrical pore FGM sandwich panels, the nonlinear dynamical responses of FGM panels can be derived by solving Eq. (28) with the initial conditions $W\left(0\right)=0$ by applying the Runge–Kutta method. For further study, next, the virtual case of rotations $\left({\Phi }_{x},{\Phi }_{y}\right)$ is examined. The inertial forces produced by the rotation angles $\left({\Phi }_{x},{\Phi }_{y}\right)$ are small, so they can be neglected. Equation (28) can be rewritten as:

$$ \begin{aligned} & {\rm I}_{0} \frac{{{\text{d}}^{2} W}}{{{\text{d}}t^{2} }} - t_{11} W - t_{12} \Phi_{x} - t_{13} \Phi_{y} - t_{14} W\Phi_{x} \\ & \quad - t_{15} W\Phi_{y} - t_{16} W - t_{17} W^{2} - t_{18} W^{3} = L_{32} Q\sin \Omega t, \\ \end{aligned} $$

(29a)

$$ t_{21} W + t_{22} \Phi_{x} + t_{23} \Phi_{y} + n_{1} W + n_{2} W^{2} = 0, $$

(29b)

$$ t_{31} W + t_{32} \Phi_{x} + t_{33} \Phi_{y} + n_{3} W + n_{4} W^{2} = 0 $$

(29c)

From Eq. (29), solving the second and third equations concerning ${(\Phi }_{x}$,${\Phi }_{y})$ and then substituting the outcomes into the first equation give:

$$ {\rm I}_{0} \frac{{{\text{d}}^{2} W}}{{{\text{d}}t^{2} }} - \left( {a_{1} + a_{2} } \right)W - \left( {a_{3} + a_{4} + a_{6} + r_{17} } \right)W^{2} - \left( {a_{5} + r_{18} } \right)W^{3} = L_{32} Q\sin \Omega t, $$

(30)

For an ideal shell, the fundamental frequencies can be obtained as:

$$ \omega_{mn} = \sqrt {\frac{{ - \left( {a_{1} + a_{2} } \right)}}{{{\rm I}_{0} }}} , $$

(31)

4 Finite Element Modeling

Usually, numerical methods are used to verify the analytical study (Al-Waily et al. 2020b; Njim et al. 2021a). Among numerous mathematical techniques, the FEA approach is the most accurate (Burlayenko and Sadowski 2020; Sadiq et al. 2020). ANSYS (version 2021 R1) was used in this investigation as a model of the finite element approach. In this study, the SOLID186 element was selected as the default choice. SOLID186 is a widely utilized element in structural modeling due to its reliability and accuracy. It is known for providing quadratic interpolation functions within the element, enabling precise results. The element's capability to capture complex deformations and stress distributions makes it suitable for a wide range of applications, including solid mechanics, structural analysis, and finite element modeling. Figure 4 illustrates the element, which consists of 20 nodes and possesses quadratic spatial characteristics. It offers three degrees of freedom (DOF) for translations in the normal axes (Kadum Njim et al. 2021a).

Fig. 4

Structural design of the SOLID 186 element type

Figure 5 displays the 3D model of the FGM constructed using SOLID 186 and 8-node fine grid size. This meshing approach has resulted in a total of 19,360 slices and 137,922 nodes in the numerical. In the FE modeling, Eq. 6 is utilized to determine the characteristics of porous metal materials, and then, using Excel 2020, the obtained data are added to the model examined. The mesh refinement was investigated for convergence to achieve the best numerical outcome feasible with further mesh refinement (Rasheed Ismail et al. 2018). The boundary conditions are applied to each cylindrical panel edge. According to modal analysis, the natural frequency in the cylindrical sandwich FGM panel at stability can be calculated.

Fig. 5

Simulation of the sandwich porous FGM cylindrical shell using the ANSYS model

5 Experimental Investigation

5.1 Specimen Manufacturing

The manufacturing process of FGM specimens depends on the specific materials and properties required for the application. One of the most important ways is to use 3D printing techniques to build up the FGM specimen layer by layer. In this case, the printer nozzle deposits different materials with varying compositions or properties, following a predetermined pattern. Polylactic acid (PLA) is a prominent biomaterial in the medical technology, and its properties are causing it to replace the petrochemical-based plastics. The SolidWorks program was used to design the PLA samples with the porosity for expressing the distribution pattern, then saving the design model as a (.stl) file, and eventually using it to make the sample via the CR-10 Max 3D printer, as illustrated in Fig. 6. Aluminum alloy (AA6061-T6) cylindrical panel having a thickness of 1 mm was employed for the face sheet layers, designated as being extremely appropriate for a variety of technical and structural uses in aviation. The face sheet layers were bonded to the FGM core using epoxy adhesive. Table 2 lists the material characteristics of the FG core and the face sheet layers.

Fig. 6

Fabricating FG specimens employing 3D printing

Table 2 Material characteristics utilized in the FG sandwich shell

5.2 Experimental Design and Technique

The performing of free vibration tests is a viable method to determine the fundamental natural frequency of sandwich cylindrical panels composed of functionally graded porous metal. A test bench for vibration analysis was created and produced specifically for performing modal analysis techniques to identify the properties of a sandwich cylindrical panel featuring a functionally graded porous metal core. The samples used in the tests had a (0.3 m × 0.3 m) and (0.2 m × 0.2 m) cross-sectional area and were composed of FG porous metal with varying core heights of 6, 8, and 14 mm. The cylindrical panel was affixed to the fixtures, and the experiment was carried out using simply supported boundary conditions. The electronic system consists of a data acquisition device (NI-6009 DAQ) and two ADXL accelerometers that are affixed to different locations on the upper and lower surfaces of the cylindrical shell of the FG porous metal sandwich. The free vibration measurements were conducted using LabVIEW and SIGVIEW software on a computer PC. The setup for the DAQ, accelerometer, and impact hammer connections is manifested in Fig. 7. The cylindrical sandwich panel specimen was excited using an IH-01 piezoelectric impulse force hammer model, which immediately applied an impact force, thereby generating an electrical signal that corresponded to the intensity of the impact. The specimen was then allowed to oscillate freely. The signals generated by the sensors and impact hammer are transmitted to a PC via the NI-6009 data acquisition device, which interfaces with LabVIEW software. The results were displayed using OriginPro 8.5. The SIGVIEW software was used to convert the signals from the time domain into the frequency domain by employing the fast Fourier transform (FFT) method (Njim et al. 2021a). The natural frequency of plate construction with various parameters was determined through modal analysis. The numerical results obtained were compared with the analytical outcomes, which were derived from the general equation of motion for cylindrical shell structures. The discrepancies between the two sets of results were evaluated, as described in (Abbas et al. 2020). The agreement between the analytical and numerical solutions was found to be satisfactory, indicating that a sandwich cylindrical shell panel structure with a functionally graded material (FGM) core and a porous effect is a suitable choice. The experimental results were compared with the other results obtained by analytical or numerical techniques, taking into account the effect of various porous and shell parameters. The degree of agreement between the experimental and other results was evaluated to determine the validity and reliability of the chosen parameters (Al-Waily et al. 2020b; Jebur et al. 2021).

Fig. 7

Experimental design for free vibration examination

6 Results and Discussion

This study conducted an analytical investigation of free vibration in a sandwich cylindrical panel composed of a single-phase functionally graded porous metal core. The analysis considered several parameters clarified in Fig. 8. And, the shells' lower and upper were supposed to be prepared of uniform materials, whereas the section of FGM possessed a metal having a gradient of porosity throughout its thickness. As well, a numerical study employing ANSYS program was utilized for validating their results. Additionally, an investigational program was conducted for verifying the analytical as well as numerical solutions accuracy. Figure 9 presents the experimental outcomes of the free vibration test performed upon the specimens of FG sandwich shell with a height (6, 8 and 14 mm) of core, $\left(\beta =10, 20 \mathrm{and} 30\%\right), (k=0.5 \mathrm{and} 2),$ and sheet of the face sheet of (1 mm).

Fig. 8

Parameters investigated in the present work

Fig. 9

Experimental results for (FFT)

Table 3 presents a comparison of the results obtained using analytical, numerical, and experimental methods for the fundamental natural frequency with a gradient index of 0.5 and 2 and three porosity parameters ($\beta$ = 0.1, 0.2, and 0.3). The comparison was done for various core heights, ranging from 6 to 14 mm. The results elucidated that an increase in the gradient index and a decrease in the porous parameter led to a decrease in natural frequencies due to the reduced stiffness of the material. This is due to a reduction in the bending rigidity and elasticity modulus of the cylindrical shell, leading to a decrease in material strength. Additionally, the findings indicated that a greater shell thickness and higher frequency modes may lead to smaller errors in the FSDT calculations. The analytical and numerical solutions exhibited an acceptable level of error, with a maximum deviation of 6.7503% at a core thickness of 8 mm. The properties, such as material stiffness, density, and other relevant parameters, were accurately defined and applied consistently, which help in minimizing the discrepancies between the two solutions. However, the maximum discrepancy between the experimental and numerical results was 14.21%, which occurred at a core thickness of 6 mm and was influenced by the material gradient and porous factor for a given FG shell thickness. This suggests that the behavior of the system is more sensitive to variations in the core thickness in that range. The analytical model might accurately capture this sensitivity, resulting in better agreement with the experimental observations for that particular core thickness. At a porosity ratio of 0.3, the largest difference between the analytical and experimental results was 13.6923%. This indicates that there is a good level of agreement between the analytical solution proposed and the one obtained through the experimentation.

Table 3 Analytical, numerical, and experimental fundamental natural frequency values (Hz)

Table 4 illustrates the results of the analytical method and finite element analysis for the frequency parameter of sandwich shells simply supported with an FG polyethylene core (8 mm thick) and different porosity factors (0.1, 0.2, and 0.3), volume fraction index (0.5, 1, and 5), wave numbers m = n = 1, and skins of 1 mm. The data evinced that as the gradient index increases and the porous parameter decreases, the natural frequencies of the sandwich shells decrease due to the reduction in material rigidity. This trend can be explained by the fact that the presence of voids or pores reduces the material's overall density, resulting in a decrease in its stiffness. Thus, an increase in the porous parameter would mean a decrease in the stiffness of the material, which in turn leads to an increase in the natural frequencies. In the case of sandwich shells with FG Polyethylene core, the gradient index was achieved by varying the volume fraction index of the FG core along the thickness direction. When the gradient index was increased, the rigidity of material reduced due to the presence of more compliant materials at the core, which in turn led to a decrease in the natural frequencies. In addition, the void content can be controlled by adjusting the porosity factor, which is a measure of the size and distribution of voids in the FG core. This result helps design sandwich shells with desired natural frequencies for specific applications, by controlling the material properties by adjusting the gradient index and porosity factor.

Table 4 Numerical and analytical results of the fundamental natural frequency of the sandwich shell with a PLA core height of 8 mm

The first six mode shapes of sandwich (SSSS) cylindrical shells with a porous single-phase metal core porosity of 10%, material gradient k = 0.5, FG core thickness of 10 mm, face sheet layers of 1 mm, a = b = 0.5, and radius of curvature of 3 m are presented in Fig. 10. From Fig. 10, the radial mode ${\omega }_{1}= 488.22$ Hz: In this mode, the shell deforms radially inward and outward. The deformation is symmetrical about the axis of the shell, with the metal core remaining stationary. The circumferential mode ${\omega }_{2}= 1102.2$ Hz: In this mode, the shell deforms in a circumferential direction. The deformation is symmetrical about the axis of the shell, with the metal core remaining stationary. The axial mode ${\omega }_{3}= 1109.9$ Hz: In this mode, the shell deforms in an axial direction, with the ends of the shell moving in opposite directions. The deformation is symmetrical about the axis of the shell, with the metal core remaining stationary. The first bending mode ${\omega }_{4}= 1639.3$ Hz: In this mode, the shell deforms in a bending motion, with the ends of the shell moving in opposite directions. The deformation is asymmetrical about the axis of the shell, with the metal core also deforming. The second bending mode ${\omega }_{5}= 1959.4$ Hz: In this mode, the shell deforms in a more complex bending motion, with the ends of the shell moving in opposite directions and the center of the shell also deforming. The deformation is asymmetrical about the axis of the shell, with the metal core also deforming. The torsional mode ${\omega }_{6}= 1964.7$ Hz: In this mode, the shell twists about its axis, with one end of the shell rotating clockwise and the other end rotating counterclockwise. The deformation is symmetrical about the axis of the shell, with the metal core also deforming. These mode shapes are important to understand because they can affect the performance and behavior of the cylindrical shell under different types of loading and operating conditions.

Fig. 10

The first six mode shapes of porous single-phase metal core cylindrical shells at β = 0.1 and k = 0.5

The influence of porosity distribution on the transient deflection response of a single-phase sandwich cylindrical shell is portrayed in Fig. 11. Three different values of pore volume fractions (β = 10, 20, and 30%) were utilized at gradient index 0.5 and q = 2000 sin200t. The results demonstrated that as the pore volume fraction in the sandwich core material increases, the transient deflection response of the FG single-phase sandwich cylindrical shell decreases. This decrease in the transient deflection response can be attributed to the fact that an increase in porosity could lead to a decrease in the mass of material, which would decrease the transient deflection response, while the stiffness remains constant. However, the changes in stiffness and damping could also play a role in affecting the transient deflection response, as could other factors, such as the geometry and boundary conditions of material. On the other hand, the gradient index is a measure of the variation in material composition along the thickness direction of the sandwich cylindrical shell structure. The gradient index affects the natural frequencies of the sandwich structure in the opposite way to the porous parameter. Figure 12 represents the effect of material gradients (0.5, 2, and 10) on the amplitude deflection for the FG porous sandwich cylindrical shell at porosity of 10%. The result illustrated that as the gradient index increases, the amplitude deflection of sandwich structure increases. This is because a higher gradient index means a higher variation in material composition, leading to a stiffer sandwich structure, and hence to a higher amplitude deflection.

Fig. 11

Effect of the porosity parameter on the transient deflection response of the FG single-phase sandwich cylindrical shell

Fig. 12

Influence of material gradient on the transient deflection response of the FG single-phase sandwich cylindrical shell

Figure 13 provides numerical data on the frequency parameter of imperfect cylindrical shell panels of a FG sandwich with various porous factors and a PLA core height of 10 mm, under the influence of various boundary conditions. The shell has a skin thickness of 1 mm, a power index of 0.5, 2, and 5, and equal side lengths (a = b = 300 mm). The data in the table depict the frequency parameter for each combination of porous factor and boundary condition. The influence of porous parameters and gradient indices was investigated. This investigation found that the natural frequency of the selected model increased as the number of constraints was increased. For example, when the porous factor was 0.3 and the gradient index was 0.5, the natural frequency for the CCCC model was 869.6, while for the CCCS model, it was 796.42, for the CSCS model it was 738.22, for the SSSS model it was 565.32, and for FFFF it was 512.87. When the FG porous shell is free on all edges (free-free-free-free boundary conditions), it has more flexibility compared to other boundary conditions. The absence of constraints allows for more modes of vibration and greater deformation possibilities. In essence, the free boundary conditions provide the shell with more freedom to move and deform in various ways. In this mode, the entire shell moves and deforms uniformly, resulting in the lowest frequency of vibration. This indicates that the number of constraints in the model has a significant impact on the natural frequency of the structure. Increasing the number of constraints in a model results in a stiffer and more stable structure; this, in turn, leads to an increase in the natural frequency. This is because the additional constraints increase the amount of energy required to excite the structure, and as a result, the natural frequency of the structure increases.

Fig. 13

Numerical results of the natural frequency for the cylindrical shell of the FG sandwich with different boundary conditions

Figures 14, 15 and 16 reveal the influence of modifying the thickness of the FG core and skin on the fundamental natural frequency and nonlinear time-deflection curve of sandwich cylindrical panels. The cylindrical shell has dimensions of a = b = 0.3 and a radius of curvature of R = 3 m. Furthermore, the shell has a material gradient of 0.5 and a porosity coefficient of 10%, indicating the amount of vacant space that presents within the material. The thickness of the FGM core in the cylindrical panels under investigation varies between 10 and 25 mm, while the thickness of the face sheet ranges from 1 to 2.5 mm. According to the figures, there is a clear relationship between the thickness of the FGM core or the face sheet and the natural frequency or amplitude deflection of the sandwich shells and increasing the thickness of either component leads to a significant increase in the natural frequency and a decrease in the nonlinear dynamic response. Increasing the thickness of the FGM core or the face sheet increases the stiffness and strength of the sandwich shells, resulting in higher natural frequency and lower deflection. This is because the added material increases the resistance of the shell to bending and deformation, making it less susceptible to vibration.

Fig. 14

Analytical results of the fundamental natural frequency for various FG core and face sheet thicknesses

Fig. 15

Impact of FG core thickness on the dynamic behavior of the porous single-phase sandwich cylindrical shell

Fig. 16

Result of skin thickness on the time-deflection curve of a porous FG single-phase sandwich cylindrical shell

Figure 17 explains how the dynamic behavior of a FG single-phase porous sandwich cylindrical shell is affected by changes in its radius of curvature (R = 1, 2, and 3 m). The results manifested that the deflection curve increased as the radius of curvature was increased. As the radius of curvature of the cylindrical shell increases, the shell becomes less stiff and more flexible, which can lead to increased deflection. This is because a larger radius of curvature causes the shell to experience less bending stress, which reduces its resistance to deformation. Regardless, the effect of changes in the radius of curvature on the deflection of the cylindrical shell can also depend on various other factors, including the thickness and material properties of shell, the type of loading, and the boundary conditions. Additionally, the changes in radius of curvature may also affect the other properties of shell, such as its natural frequency, which can, in turn, affect its dynamic behavior. Consequently, while the results suggest a correlation between the radius of curvature and the deflection of cylindrical shell, it is important to consider other factors and limitations to fully understand the dynamic behavior of shell.

Fig. 17

Effects of the radius of curvature on the dynamic behavior of FG single-phase porous sandwich cylindrical shell

Since one of the boundary conditions is a uniform distributed load, it is important to analyze how the excitation force affects the time displacement curve of the cylindrical FG single-phase porous sandwich shell. To do this, the study investigated three different cases of excitation force amplitude (Q), specifically 1000, 2000, and 3000 Pa, using a cylindrical shell with a radius of 3 m, a FG core thickness of 10 mm, and a face sheet thickness of 1 mm. The shell also had a porosity coefficient of 10% and a volume fraction index of 0.5. The results, as elucidated in Fig. 18, indicated that as the excitation force amplitude decreases, the amplitude of the cylindrical shell panel also decreases. In other words, the magnitude of the external load that is applied to the cylindrical shell affects its dynamic behavior. This finding has important implications for the design and engineering of structures, as it highlights the need to carefully consider the amplitude of the external load when analyzing and predicting the dynamic behavior of cylindrical shells. By understanding the relationship between the excitation force and the shell response, engineers can design structures that are more resilient and less likely to fail due to dynamic loads. Additionally, this information can be used to optimize the performance of cylindrical shell structures by adjusting the excitation force to achieve the desired dynamic response.

Fig. 18

Impacts of the amplitude on the dynamic behavior of FG single-phase porous sandwich cylindrical shell at $\Omega =200 {\mathrm{s}}^{-1}$

7 Conclusions

This study analyzes the nonlinear free vibration behavior of a sandwich cylindrical shell consisting of a single-phase FG core metal and two isotropic panels. The governing equation is derived from the nonlinear constitutive relationship of the shell using first-order shear deformation theory (FSDT). The properties of the material are determined based on the recommended mixing rules. To ensure the accuracy of the analytical solution, a comprehensive comparative study is conducted using numerical and experimental techniques. The results of the study include the natural frequencies and the nonlinear time-deflection curve expressed in essential parameters, such as power-law index, porosity coefficient, FG core thickness, skin thickness, boundary conditions, and excitation force. The results of analytical, numerical, and experimental investigations indicate that the natural frequencies of the system increase as the porosity factor increases and decrease as the gradient index increases. The accuracy of the observed natural frequency is influenced by various factors, including the noise and deviations in frequency response, which can affect the reliability of experimental results.

Appendix

$$ \begin{gathered} I_{10} = \frac{{E_{1} }}{{1 - \upsilon^{2} }},I_{20} = \frac{{\upsilon E_{1} }}{{1 - \upsilon^{2} }},I_{30} = \frac{{E_{1} }}{{2\left( {1 + \upsilon } \right)}}, \hfill \\ I_{11} = \frac{{E_{2} }}{{1 - \upsilon^{2} }},I_{21} = \frac{{\upsilon E_{2} }}{{1 - \upsilon^{2} }},I_{31} = \frac{{E_{2} }}{{2\left( {1 + \upsilon } \right)}}, \hfill \\ I_{12} = \frac{{E_{3} }}{{1 - \upsilon^{2} }},I_{22} = \frac{{\upsilon E_{3} }}{{1 - \upsilon^{2} }},I_{32} = \frac{{E_{3} }}{{2\left( {1 + \upsilon } \right)}}, \hfill \\ \end{gathered} $$

(32)

$$ A_{11} = \frac{{I_{10} }}{\Delta },A_{22} = \frac{{I_{10} }}{\Delta },A_{12} = \frac{{I_{20} }}{\Delta },A_{66} = \frac{1}{{I_{30} }}, $$

(33)

$$ \Delta = I_{10}^{2} - I_{20}^{2} ,B_{11} = A_{22} I_{11} - A_{12} I_{21} ,B_{22} = A_{11} I_{11} - A_{12} I_{21} , $$

(34)

$$ \begin{gathered} B_{12} = A_{22} I_{21} - A_{12} A_{12} , \hfill \\ B_{21} = A_{11} I_{21} - A_{12} I_{11} , \hfill \\ B_{66} = \frac{{I_{31} }}{{I_{30} }}, \hfill \\ \end{gathered} $$

(35)

$$ \begin{gathered} D_{11} = I_{12} - B_{11} B_{12} - I_{21} B_{21} , \hfill \\ D_{22} = I_{22} - B_{22} I_{11} - I_{21} B_{12} , \hfill \\ D_{12} = I_{22} - B_{12} I_{11} - I_{21} B_{22} , \hfill \\ D_{21} = I_{22} - B_{21} I_{11} - I_{21} B_{11} , \hfill \\ D_{66} = I_{32} - I_{31} B_{66} , \hfill \\ \end{gathered} $$

(36)

$$ \begin{gathered} {\rm T}_{11} \left( w \right) = K_{s} I_{30} \frac{{\partial^{2} w}}{{\partial x^{2} }} + K_{s} I_{30} \frac{{\partial^{2} w}}{{\partial y^{2} }}, \hfill \\ {\rm T}_{12} \left( {\phi_{x} } \right) = K_{s} I_{30} \frac{{\partial \phi_{x} }}{\partial x}, \hfill \\ {\rm T}_{13} \left( {\phi_{y} } \right) = K_{s} I_{30} \frac{{\partial \phi_{y} }}{\partial y}, \hfill \\ {\rm T}_{21} \left( w \right) = - K_{s} I_{30} \frac{\partial w}{{\partial x}}, \hfill \\ {\rm T}_{22} \left( {\phi_{x} } \right) = D_{11} \frac{{\partial^{2} \phi_{x} }}{{\partial x^{2} }} + D_{66} \frac{{\partial^{2} \phi_{y} }}{{\partial y^{2} }} - K_{s} I_{30} \phi_{x} , \hfill \\ {\rm T}_{23} \left( {\phi_{y} } \right) = \left( {D_{12} + D_{66} } \right)\frac{{\partial^{2} \phi_{y} }}{\partial x\partial y}, \hfill \\ {\rm T}_{33} \left( {\phi_{y} } \right) = D_{22} \frac{{\partial^{2} \phi_{y} }}{{\partial y^{2} }} + D_{66} \frac{{\partial^{2} \phi_{y} }}{{\partial x^{2} }} - K_{s} I_{30} \phi_{y} , \hfill \\ \end{gathered} $$

(37)

$$ \begin{gathered} R_{1} \left( {w,f} \right) = \frac{{\partial^{2} f}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial x^{2} }} - 2\frac{{\partial^{2} f}}{\partial x\partial y}\frac{{\partial^{2} w}}{\partial x\partial y} + \frac{{\partial^{2} f}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{1}{R}\frac{{\partial^{2} f}}{{\partial x^{2} }}, \hfill \\ R_{2} \left( f \right) = B_{21} \frac{{\partial^{3} f}}{{\partial x^{3} }} + \left( {B_{11} - B_{66} } \right)\frac{{\partial^{3} f}}{{\partial x\partial y^{2} }}, \hfill \\ R_{3} \left( f \right) = B_{12} \frac{{\partial^{3} f}}{{\partial y^{3} }} + \left( {B_{22} - B_{66} } \right)\frac{{\partial^{3} f}}{{\partial x^{2} \partial y}}, \hfill \\ \end{gathered} $$

(38)

$$ \begin{gathered} t_{11} = - \frac{{\lambda_{m}^{4} }}{{L_{26} R^{2} }},t_{12} = - \lambda_{m}^{2} \frac{{L_{27} }}{{L_{26} R}} - K_{s} I_{30} \lambda_{m} ,t_{13} = - \lambda_{m}^{2} \frac{{L_{28} }}{{L_{26} R}} - K_{s} I_{30} \delta_{n} , \hfill \\ t_{14} = \left( {L_{12} + L_{13} } \right) - \frac{{L_{25} L_{27} }}{{L_{26} }} - \frac{{L_{27} L_{29} }}{{L_{26} }},t_{15} = \left( {L_{14} + L_{15} } \right) - \frac{{L_{25} L_{28} }}{{L_{26} }} - \frac{{L_{28} L_{29} }}{{L_{26} }}, \hfill \\ t_{16} = \left( {L_{23} + L_{24} } \right)\Phi_{1} - K_{s} I_{30} \lambda_{m}^{2} - K_{s} I_{30} \delta_{n}^{2} ,t_{17} = \left( {L_{16} + L_{17} } \right) - \frac{{L_{25} \lambda_{m}^{2} }}{{L_{26} R}} - \frac{{L_{29} \lambda_{m}^{2} }}{{L_{26} R}} - L_{31} , \hfill \\ t_{18} = - \left( {L_{18} + L_{19} } \right) - \frac{1}{16}\left( {\frac{{\lambda_{m}^{2} }}{{A_{22} }} + \frac{{\delta_{n}^{2} }}{{A_{11} }}} \right),t_{21} = - B_{21} \frac{1}{S}\frac{{\lambda_{m}^{2} }}{R}\lambda_{m}^{3} - \left( {B_{11} - B_{66} } \right)\frac{1}{S}\frac{{\lambda_{m}^{2} }}{R}\lambda_{m} \delta_{n}^{2} , \hfill \\ t_{22} = - D_{11} \lambda_{m}^{2} - D_{66} \delta_{n}^{2} - K_{s} I_{30} - B_{21} \frac{\zeta }{S}\lambda_{m}^{3} - \left( {B_{11} - B_{66} } \right)\frac{\zeta }{S}\lambda_{m} \delta_{n}^{2} , \hfill \\ t_{23} = - \left( {D_{12} + D_{66} } \right)\lambda_{m} \delta_{n} - B_{21} \frac{\Psi }{S}\lambda_{m}^{3} - \left( {B_{11} - B_{66} } \right)\frac{\Psi }{S}\lambda_{m} \delta_{n}^{2} , \hfill \\ t_{31} = - B_{12} \frac{1}{S}\frac{{\lambda_{m}^{2} }}{R}\delta_{n}^{3} - \left( {B_{22} - B_{66} } \right)\frac{1}{S}\frac{{\lambda_{m}^{2} }}{R}\delta_{n} \lambda_{m}^{2} , \hfill \\ t_{32} = - \left( {D_{21} + D_{66} } \right)\lambda_{m} \delta_{n} - B_{12} \frac{\zeta }{S}\delta_{n}^{3} - \left( {B_{22} - B_{66} } \right)\frac{\zeta }{S}\lambda_{m}^{2} \delta_{n} , \hfill \\ t_{33} = - D_{22} \delta_{n}^{2} - D_{66} \lambda_{m}^{2} - K_{s} I_{30} - B_{12} \frac{\Psi }{S}\delta_{n}^{3} - \left( {B_{22} - B_{66} } \right)\frac{\Psi }{S}\lambda_{m}^{2} \delta_{n} , \hfill \\ \end{gathered} $$

(39)

$$ \begin{gathered} n_{1} = - K_{s} I_{30} \lambda_{m} ,n_{2} = - \frac{8}{3}\frac{{B_{21} }}{{A_{11} }}\frac{{\delta_{n} }}{ab}, \hfill \\ n_{3} = - K_{s} I_{30} \delta_{n} ,n_{4} = - \frac{8}{3}\frac{{B_{12} }}{{A_{22} }}\frac{{\lambda_{m} }}{ab}, \hfill \\ \end{gathered} $$

(40)

$$ \tilde{\rho }_{1} = \left( {{\rm I}_{2} - \frac{{{\rm I}_{1}^{2} }}{{{\rm I}_{0} }}} \right) $$

(41)

$$ \zeta = B_{21} \lambda_{m}^{3} + \left( {B_{11} - B_{66} } \right)\lambda_{m} \delta_{n}^{2} , $$

(42)

$$ \Psi = B_{12} \delta_{n}^{3} + \left( {B_{22} - B_{66} } \right)\lambda_{m}^{2} \delta_{n} , $$

(43)

$$ S = A_{11} \lambda_{m}^{4} + A_{22} \delta_{n}^{4} + \left( {A_{66} - 2A_{12} } \right)\lambda_{m}^{2} \delta_{n}^{2} , $$

(44)

$$ \begin{gathered} a_{1} = t_{11} + t_{12} \frac{{t_{23} t_{31} - t_{21} t_{33} }}{{t_{22} t_{33} - t_{32} t_{23} }} + t_{13} \frac{{t_{32} t_{21} - t_{22} t_{31} }}{{t_{22} t_{33} - t_{32} t_{23} }}, \hfill \\ a_{2} = t_{12} \frac{{n_{3} t_{23} - n_{1} t_{33} }}{{t_{22} t_{33} - t_{32} t_{23} }} + t_{13} \frac{{n_{1} t_{32} - n_{3} t_{22} }}{{t_{22} t_{33} - t_{32} t_{23} }} + t_{16} , \hfill \\ a_{3} = t_{14} \frac{{t_{23} t_{31} - t_{21} t_{33} }}{{t_{22} t_{33} - t_{32} t_{23} }} + t_{15} \frac{{t_{32} t_{21} - t_{22} t_{31} }}{{t_{22} t_{33} - t_{32} t_{23} }}, \hfill \\ a_{4} = t_{12} \frac{{n_{4} t_{23} - n_{2} t_{33} }}{{t_{22} t_{33} - t_{32} t_{23} }} + t_{13} \frac{{n_{2} t_{32} - n_{4} t_{22} }}{{t_{22} t_{33} - t_{32} t_{23} }}, \hfill \\ a_{5} = t_{14} \frac{{n_{4} t_{23} - n_{2} t_{33} }}{{t_{22} t_{33} - t_{32} t_{23} }} + t_{15} \frac{{n_{2} t_{32} - n_{4} t_{22} }}{{t_{22} t_{33} - t_{32} t_{23} }}, \hfill \\ a_{6} = t_{14} \frac{{n_{3} t_{23} - n_{1} t_{33} }}{{t_{22} t_{33} - t_{32} t_{23} }} + t_{15} \frac{{n_{1} t_{32} - n_{3} t_{22} }}{{t_{22} t_{33} - t_{32} t_{23} }}, \hfill \\ \end{gathered} $$

(45)

$$ \begin{gathered} L_{11} = \left( {A_{11} A_{22} - A_{12}^{2} } \right),L_{12} = \frac{{4\lambda_{m}^{2} \left( {B_{21} A_{12} + A_{11} B_{11} } \right)}}{{\delta_{n} abL_{11} }},L_{13} = \frac{{4\delta_{n} \left( {B_{11} A_{12} + A_{11} A_{22} B_{21} } \right)}}{{abL_{11} }}, \hfill \\ L_{14} = \frac{{4\lambda_{m} \left( {B_{22} A_{12} + A_{11} B_{12} } \right)}}{{abL_{11} }},L_{15} = \frac{{4\delta_{n}^{2} \left( {B_{12} A_{12} + A_{22} B_{22} } \right)}}{{\lambda_{m} abL_{11} }},L_{16} = \frac{{4\lambda_{m} A_{12} }}{{\delta_{n} RL_{11} }},L_{17} = \frac{{4\delta_{n} A_{22} }}{{\lambda_{m} RL_{11} }}, \hfill \\ L_{18} = \frac{{\lambda_{m}^{3} \delta_{n} \left( {\delta_{n}^{2} A_{12} + \lambda_{m}^{2} A_{22} } \right)}}{{8abL_{11} }},L_{19} = \frac{{\delta_{n}^{3} \lambda_{m} \left( {\lambda_{m}^{2} A_{12} + \delta_{n}^{2} A_{22} } \right)}}{{8abL_{11} }},L_{21} = \frac{{\lambda_{m}^{3} \delta_{n} \left( {\delta_{n}^{2} A_{12} + \lambda_{m}^{2} A_{11} } \right)}}{{4abL_{11} }}, \hfill \\ L_{22} = \frac{{\lambda_{m} \delta_{n}^{3} \left( {\lambda_{m}^{2} A_{12} + \delta_{n}^{2} A_{22} } \right)}}{{4abL_{11} }},L_{25} = \frac{{8\lambda_{m} \delta_{n} }}{ab}, \hfill \\ L_{26} = A_{11} \lambda_{m}^{4} + A_{22} \delta_{n}^{4} + \left( {A_{66} - 2A_{12} } \right)\lambda_{m}^{2} \delta_{n}^{2} ,L_{27} = B_{21} \lambda_{m}^{3} + \left( {B_{11} - B_{66} } \right)\lambda_{m} \delta_{n}^{2} , \hfill \\ L_{28} = B_{12} \delta_{n}^{3} + \left( {B_{22} - B_{66} } \right)\lambda_{m}^{2} \delta_{n} ,L_{29} = \frac{{16\lambda_{m}^{2} \delta_{n}^{2} }}{{3mn\pi^{2} }},L_{31} = \frac{{\delta_{n}^{2} }}{{3A_{11} mn\pi^{2} R}},L_{32} = \frac{16}{{mn\pi^{2} }}, \hfill \\ \end{gathered} $$

(46)