Introduction

Over the past decades, nonlinear modal coupling through internal resonances and parametric excitation in microelectromechanical systems (MEMS) has been widely researched to investigate many practical applications, such as sensors [1], bandpass filters [2, 3], logic gates [4], and energy harvesting [5]. Parametric excitation is the external forced manipulation of effective stiffness and coupling coefficients to achieve intermodal coupling [6, 7]. On the other hand, internal resonance occurs when two or more frequencies of a multi-degree-of-freedom MEMS resonator are commensurate or nearly commensurate and interact when one of the modes is externally excited [7,8,9]. Here, we study a bandpass filter based on nonlinear intermodal coupling via 2:1 internal resonance of an electrostatically actuated clamped-guided microbeam.

Mechanical bandpass filters based on MEMS resonators have received a lot of attention in recent decades because of their narrow bandwidth, low loss, and good stability [9, 10]. Earlier, bandpass filters were developed by coupling several MEMS resonators through an additional connected mechanical beam to generate the desired bandpass [11, 12]. For example, Greywall and Busch [13] used 20 mechanically connected drumhead resonators in a closed ring to demonstrate bandpass filter characteristics. In a later work, Chivukula and Rhoads [14] demonstrated bandpass filters based on cyclically coupled MEMS resonators and compared the results with open-chain resonator-based filters. Furthermore, Zhu and Kirby [15] proposed a bandpass filter model based on two mechanically coupled silicon cantilevers, where the coupling is induced by a silicon linkage. Similarly, Motiee et al. [16] investigated bandpass filters in two MEMS resonators: two coupled cantilevers and two coupled doubly clamped beams. To generate coupling, they used a connected flexural-mode beam for coupled cantilevers and a V-shaped element for coupled doubly clamped beams. On the other hand, Hammad et al. [17] presented an analytical model for a tunable MEMS filter based on two coupled electrostatic resonators by a weak microbeam.

Parallelly, the electrical coupling has been used between MEMS resonators to achieve the bandpass filter characteristics and eliminate the need for any physical coupling between resonators. For example, Pourkamali et al. [18] presented passive and active filter synthesis approaches using the electrical coupling of capacitive MEMS resonators. In the follow-up works, they demonstrated high-order narrow-bandwidth bandpass filters using an electrostatic force as a coupling source between closely spaced microresonators [19, 20]. In another work, Galayko et al. [21] reported fourth- and sixth-order bandpass filters using controlled electrostatic coupling through bias voltage in coupled electromechanical resonators. Recently, Behzadi and Baghelani [22] investigated weakly connected radial contour mode disk MEMS resonators to demonstrate tunable narrowband filters.

Later, researchers utilised both mechanical and electrical coupling together to enhance the response of bandpass filters. For example, Kharrat et al. [23] proposed a tuning strategy for mechanically coupled NEMS arrays resonator based on the modal control by adjusting actuation and detection configurations separately. Giner et al. [24] reported the CMOS-MEMS bandpass filter in two mechanically and electrically coupled clamped–clamped beam resonators. To demonstrate a tunable narrowband micromechanical filter, Hajhashemi et al. [25] used two electrostatically coupled microresonators through a third coupling beam. They also showed independent tunability of the centre frequency and bandwidth by applying DC voltage on an electrode and axial stress on one resonator. In another work, Ilyas et al. [26] investigated an H-shaped coupled MEMS resonator to demonstrate a wideband tunable filter using mixed-frequency external electrostatic excitation. Their subsequent research studied the same resonator with mixed-frequency external excitation to demonstrate low-frequency filtering characteristics in the air [27]. Simultaneously, they also demonstrated a bandpass filter using the nonlinear behaviour of two electrically coupled microbeam resonators [28]. Recently, Syms and Bouchaala [29] proposed MEMS bandpass filters based on arrays of electrostatically driven coupled beams. They modified the outer beams of the coupled resonator by adding masses to them to overcome the DC tuning problems and achieve a synchronised AC response. In addition, Luo et al. [30] reported a dual-passband filter with bandwidths of 66 MHz and 112 MHz using a dual-mode lamb wave resonator. Hou et al. [31] presented a frequency–amplitude independently tunable bandpass filter in substrate integrated waveguide resonator. Wu et al. [32] designed and fabricated a compact fifth-order microstrip interdigital filter for aggressive space mapping applications. Widaa et al. [33] presented a compact, high-Q, tunable coaxial filter based on an inset resonator. Very recently, multimode resonators have also been used to demonstrate multiband bandpass filters based on parallel coupled split structures [34, 35].

To obtain bandpass behaviour in MEMS resonators, researchers have lately tried to use internal modal coupling rather than external mechanical and electrical coupling [2, 3]. The modal coupling can be achieved through either internal resonance [7, 36,37,38,39] or external parametric excitation [6, 7]. Hajjaj et al. [2] demonstrated bandpass filter characteristics in an electrostatically actuated MEMS arch resonator through electrothermal tuning. Moreover, they observed a bandpass filter with a sharp roll-off from the passband to the stopband using nonlinear softening, hardening, and veering phenomena. On the other hand, Liu et al. [3] investigated a bandpass filter based on two magnetically coupled orthogonal cantilevers. They used modal coupling based on 1:2 internal resonance to drive the second cantilever while externally driving the first one. In addition, recently, Wang et al. [40] proposed a narrow bandpass filter using 2:1 internal resonance in an inverted T-shaped beam resonator. To the best of our knowledge, only a few studies have demonstrated bandpass filters based on nonlinear modal coupling induced by internal resonance and parametric excitation. However, there are not any studies on bandpass filters based on modal coupling through internal resonance in single-beam MEMS resonators. Hence, in the present work, we attempt to observe the bandpass filter characteristics through modal coupling induced by 2:1 internal resonance in electrostatically actuated clamped-guided microbeams.

In our recent work, we studied the nonlinear modal coupling due to 2:1 internal resonance between the second and third modes of electrostatically actuated clamped–clamped beams [36]. Further analysis revealed that the dynamical modal coupling between these modes through 2:1 internal resonance could be exploited to produce a bandpass filter for a specific electrode gap and thickness ratio (\({\alpha }_{1}=1\)). We also found that the value \({\alpha }_{1}=1\) is challenging to achieve experimentally for electrostatically actuated clamped–clamped beams. To solve this difficulty, we convert the one-clamped end into a guided end using a number of flexural beams arranged in a specific way to provide axial stiffness sufficient to ensure \({\alpha }_{1}=1.\) Then, taking into account the axial spring effect, we first drive the governing equation of motion for an electrostatically actuated clamped-guided beam. Following that, we present the analytical calculation for the axial stiffness of the guided end as well as use finite-element analysis in COMSOL to confirm the outcome of the analytical expression for a set of parameters. Next, we investigate the dynamic analysis of the bandpass filter based on nonlinear intermodal coupling between the second and third modes via 2:1 internal resonance when the third mode is externally excited. Finally, we show the dimensional values of axial stiffness and bandwidth of the bandpass filter using a particular set of beam dimensions and material properties from the literature.

Mathematical Modelling and Problem Formulation

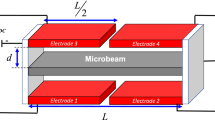
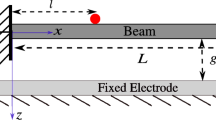
A schematic of an electrostatically actuated clamped-guided microbeam for a bandpass filter is shown in Fig. 1a. The guided end of the beam is modelled using a series of flexural beams by arranging them in a certain orientation. These flexural beams can be used to tune the total axial stiffness and coefficient of the mid-plane stretching nonlinearity. Hence, to ensure \({\alpha }_{1}=1,\) the dimensions of each flexural beam can be modified, so that they can produce desired axial stiffness when combined. Figure 1b shows equivalent schematics of an electrostatically actuated clamped-guided beam with an axial spring of stiffness Ka representing the combined axial spring effect of flexural beams. We first systematically derive the reduced-order model (ROM) for n-coupled modes, taking into account the effects of axial spring, mid-plane stretching, and electrostatic force. We then provide the estimation of total axial stiffness Ka of the guided end using analytical technique and finite-element analysis (FEA) in COMSOL.

Fig. 1
figure 1

a Schematic of an electrostatically actuated clamped-guided microbeam. b An axial spring is accounted for the guided end of the resonator to approximate the total axial stiffness Ka of flexural beams in an equivalent model

Full size image

Equation of Motion

The mechanical beam vibrates transversely as a result of applied external electrostatic force, which is a combination of DC and AC voltages, as shown in Fig. 1a and b. The governing equation of motion for the transverse displacement of the beam \(w\left(x,t\right)\) can be expressed as [36, 41, 42]

$$\begin{gathered} \rho A\ddot{\hat{w}} + EI\hat{w}^{{{{\prime\prime\prime}}}} + c\dot{\hat{w}} = \frac{{K_{a} EA}}{{2\left( {EA + K_{a} L} \right)}}\mathop \int \limits_{0}^{L} \hat{w}^{{\prime2}} dx \hfill \\ \hat{w}^{{\prime\prime}} + \frac{{ \in _{0} b\left[ {V_{{dc}} + V_{{ac}} {\text{cos}}\left( {\Omega t} \right)} \right]^{2} }}{{2\left( {g - \hat{w}} \right)^{2} }}, \hfill \\ \end{gathered}$$
(1)

with the following boundary conditions:

$$\begin{array}{cc}& \widehat{w}\left(0,t\right)=0, {\widehat{w}}^{\mathrm{^{\prime}}}\left(0,t\right)=0, \widehat{w}\left(L,t\right)=0,\\ & {\widehat{w}}^{\mathrm{^{\prime}}}\left(L,t\right)=0.\end{array}$$
(2)

Here, · and ʹ represent time, t, and space, x, derivatives, respectively (for derivation see Appendix). The first term on the right side of Eq. 1 describes the effect of mid-plane stretching and axial spring. The beam dimension and material properties parameters are length L, thickness h, width B, cross-section area A, second moment of area I, mass density ρ, and Young’s modulus of the beam E. The effective damping experienced by the beam is represented by c. In the second term on the right-hand side, the external electrostatic force is expressed as a combination of DC (Vdc) and AC (Vac) voltages, where g and ϵ0 represent the electrode gap and free space permittivity, respectively. The total axial stiffness of the spring or guided end is indicated by Ka. The effective axial spring allows tuning the mid-plane stretching nonlinearity.

The transverse displacement w, spatial x, and time t in Eq. 1 are non-dimensionalized with respect to length scales g and L, and a time scale \(T=\sqrt{\rho A{L}^{4}/EI}\), respectively, as follows:

$$\begin{array}{c}\widehat{w}=\frac{w}{g}, \widehat{x}=\frac{x}{L}, \widehat{t}=\frac{t}{T}.\end{array}$$
(3)

Next, we obtain the following non-dimensionalized equation by substituting Eq. 3 into Eq. 1

$$\begin{gathered} \ddot{w} + w^{{\prime\prime\prime}} + c\dot{w} = \left( {\alpha _{1} \mathop \int \limits_{0}^{1} w^{{\prime2}} dx} \right)w^{{\prime\prime}} \hfill \\ + \alpha _{2} \frac{{\left[ {V_{{dc}} + V_{{ac}} {\text{cos}}\left( {\Omega t} \right)} \right]^{2} }}{{\left( {1 - w} \right)^{2} }}, \hfill \\ \end{gathered}$$
(4)

with boundary conditions

$$\begin{array}{cc}& w\left(0,t\right)=0,{w}^{\mathrm{^{\prime}}}\left(0,t\right)=0,w\left(1,t\right)=0,\\ & {w}^{\mathrm{^{\prime}}}\left(1,t\right)=0.\end{array}$$
(5)

The non-dimensionalized parametersof Eqs. 4 and 5 are

$$\begin{array}{cc}& {\alpha }_{1}=6{\left(\frac{g}{h}\right)}^{2}\frac{{K}_{a}L}{EA+{K}_{a}L}, \quad {\alpha }_{2}=\frac{6{\epsilon }_{0}{L}^{4}}{E{g}^{3}{h}^{3}},\\ & \mathrm{and}\quad c=\frac{c{L}^{4}}{ETI}.\end{array}$$
(6)

The total transverse displacement \(w\left(x,t\right)={w}_{dc}\left(x\right)+{w}_{ac}\left(x,t\right)\) is the sum of static displacement \({w}_{dc}\left(x\right)\) and dynamic motion \({w}_{ac}\left(x,t\right)\) induced by DC and AC voltages, respectively. Similar to the clamped–clamped beam, the static displacement of an electrostatically actuated clamped-guided beam can be obtained using the same procedure [36, 43]. Now, for the dynamic motion, we obtain the multimode coupled reduced-order model (ROM) from Eq. 4 using the standard procedure of assuming a solution as \({w}_{ac}\left(x,t\right)=\sum_{i=1}^{p}{u}_{i}\left(t\right)\) \({\phi }_{i}\left(x\right)\), where \({\phi }_{i}\left(x\right)\) is the \({i}^{th}\) mode shape of a clamped-guided straight beam and \(p\) is the total number of modes [36, 43]. The resulting \(n\)-mode coupled ROM equations are

$$\ddot{u}_{n} + c_{n} \dot{u}_{n} + \omega_{n}^{2} u_{n} + \mathop \sum \limits_{i = 1}^{4} \mathop \sum \limits_{j = 1}^{4} \beta_{ijn} u_{i} u_{j} + \mathop \sum \limits_{i = 1}^{4} \mathop \sum \limits_{j = 1}^{4} \mathop \sum \limits_{k = 1}^{4} \Gamma_{ijkn} u_{i} u_{j} u_{k} = f_{n} {\text{cos}}\left( {\Omega t} \right),$$
(7)

where · represents derivative with respect to time. The coefficients of quadratic and cubic nonlinear terms are expressed as

$$\begin{gathered} \beta_{ijn} = \left[ {\alpha_{1} \mathop \int \limits_{0}^{1} w_{dc}^{{^{\prime\prime}}} \phi_{n} dx\mathop \int \limits_{0}^{1} \phi_{i} \phi_{j} dx + \alpha_{1} \mathop \int \limits_{0}^{1} \phi_{i}^{{^{\prime\prime}}} } \right. \hfill \\ \left. {\phi_{n} dx\mathop \int \limits_{0}^{1} 2\phi_{j}{\prime} w_{dc}{\prime} dx + 3\alpha_{2} V_{dc}^{2} \mathop \int \limits_{0}^{1} \frac{{\phi_{i} \phi_{j} \phi_{n} }}{{\left( {1 - w_{dc} } \right)^{4} }}dx} \right] \hfill \\ {\text{and}}\,\Gamma_{ijkn} = \left[ {\alpha_{1} \mathop \int \limits_{0}^{1} \phi_{i}^{{^{\prime\prime}}} \phi_{n} dx\mathop \int \limits_{0}^{1} \phi_{j}{\prime} \phi_{k}{\prime} dx + 4\alpha_{2} V_{dc}^{2} \mathop \int \limits_{0}^{1} \frac{{\phi_{i} \phi_{j} \phi_{k} \phi_{n} }}{{\left( {1 - w_{dc} } \right)^{5} }}} \right] \hfill \\ \end{gathered}$$

Equation 7 describes \(n\)-modes coupled nonlinear ordinary differential equations of electrostatically actuated clamped-guided microbeams. From Eq. 7, we can obtain the dynamical governing equations of two coupled modes based on 2:1 internal resonance condition, which later use to observe dynamical modal coupling between these modes for bandpass filter behaviour. In the following section, we present the calculation of the total axial stiffness (\({K}_{a}\)) of the guided end, which is essential for maintaining \({\alpha }_{1}=1\).

Estimation of Axial Stiffness

We found from our previous study that the modal interaction based on \({\omega }_{3}=2{\omega }_{2}\) internal resonance can further be used to develop bandpass filters based on electrostatically actuated clamped–clamped microbeams when \({\alpha }_{1}=1\) [36]. However, to achieve \({\alpha }_{1}=1\), the resonator electrode gap must be less than the beam thickness, which is difficult to do experimentally. To overcome this challenge, we use a set of flexural beams to change one end of the beam, such that it functions as a guided end [44, 45]. As a result, the total axial stiffness of the flexible guided end allows us to achieve \({\alpha }_{1}=1\) for a variety of electrode gap and thickness ratios.

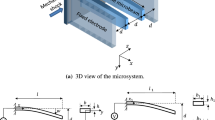
To calculate the axial stiffness of the flexible guided end, we first obtain the tip displacement of bent beam ABCD due to applied force \(P\), as shown in Fig. 2a. In this analysis, we assume that the guided support only allows the axial motion and constrains the transverse and rotational motions. To determine the deflection, we consider reaction force \(R\) and moment \(M\) at the tip of the beam due to guided support. The tip displacement of the beam in \(x\)-directions is

Fig. 2
figure 2

a Three flexural beams’ combination from the axially guided mechanism as shown in Fig. 1a. This combination is used to modify the axial stiffness by varying the length of each flexural beam. b The axial displacement distribution of three flexural beams is estimated using finite-element analysis (FEA) in COMSOL

Full size image
$$\begin{array}{cc}{\delta }_{x}=& \frac{P{a}^{3}}{3EI}+\frac{Pb}{EA}+\frac{P{a}^{2}b}{3EI}+\frac{Pa{c}^{2}}{EI}+\frac{P{a}^{2}c}{2EI}+\\ & \frac{Ra{b}^{2}}{2EI}+\frac{Rb{c}^{2}}{2EI}+\frac{Rabc}{EI}+\frac{M{a}^{2}}{2EI}+\\ & \frac{Mba}{EI}+\frac{M{c}^{2}}{2EI}+\frac{Mca}{2EI}.\end{array}$$

The tip displacement of the beam in \(z\)-direction is

$$\begin{array}{cc}{\delta }_{z}=& \frac{Pa{b}^{3}}{2EI}+\frac{P{c}^{2}b}{2EI}+\frac{Pacb}{EI}+\frac{R\left(a+c\right)}{EA}+\\ & \frac{R{b}^{3}}{3EI}+\frac{R{b}^{2}c}{EI}+\frac{M{b}^{2}}{2EI}+\frac{Mcb}{EI}.\end{array}$$

The slope of the beam is

$$\begin{array}{cc}{\theta }_{y}=& \frac{P{c}^{2}}{2EI}+\frac{Pac}{EI}+\frac{Pab}{EI}+\frac{P{a}^{2}}{2EI}+\frac{Rbc}{EI}+\\ & \frac{R{b}^{2}}{2EI}+\frac{Mc}{EI}+\frac{Mb}{EI}+\frac{Ma}{EI}.\end{array}$$

To satisfy the boundary conditions, the displacement \({\delta }_{z}\) and slop \({\theta }_{y}\) must both be zero. The reaction force and moment are calculated using \({\delta }_{z}=0\) and \({\theta }_{y}=0\) and substituted in \({\delta }_{x}\) equation to obtain the \(x\)-axial stiffness (\({K}_{I}\)) of the ABCD beam. After mathematical manipulation, the \({K}_{I}\) can be expressed as

$$\begin{array}{c}{K}_{I}=\frac{3AEI\left(\begin{array}{c}A{b}^{2}\left(4a\left(b+3c\right)+b\left(b+4c\right)\right)\\ +12I\left(a+c\right)\left(a+b+c\right)\end{array}\right)}{\begin{array}{c}\left(a+b+c\right)({A}^{2}{b}^{2}\left({a}^{2}-ac+{c}^{2}\right)(a\left(b+3c\right)+\\ bc)+3AI({a}^{4}+3{a}^{3}b-3{a}^{2}{b}^{2}+c(4{a}^{3}-3{a}^{2}\\ b+6a{b}^{2}+3{b}^{3})+3a{b}^{3}+{c}^{3}\left(4a+3b\right)+3{c}^{2}\\ \left(a-b\right)\left(2a+b\right)+{b}^{4}+{c}^{4})+36b{I}^{2}\left(a+c\right))\end{array}}.\end{array}$$

In addition, for example, we also independently verify the value of \({K}_{I}\) and axial tip displacement \({\delta }_{x}\) using the finite-element analysis in COMSOL. For the COMSOL calculation, we choose parameters such as \(a=200\) \(\upmu\)m, \(b=100\) \(\upmu\)m, \(c=100\) \(\upmu\)m, cross-section \(60\times 4\) \(\upmu\)m2, and Young’s modulus \(E=160\times {10}^{9}\) N/m2. Based on these parameters, we calculate the tip displacement of ABCD beam \({\delta }_{x}\) and \({K}_{I}\) using Eq. 10 and COMSOL. The values of \({\delta }_{x}\) and \({K}_{I}\) for both analytical and COMSOL approaches are shown in Table 1. Although, here, we show the calculation of axial stiffness (\({K}_{I}\)) for one set of beam dimensions and material properties, this approach can be used further for any other combination of beam parameters to get the desired \({K}_{I}\) for the total axial stiffness of guided end.

Table 1 The value of tip displacement \({\delta }_{x}\) and axial stiffness \({\mathrm{K}}_{\mathrm{I}}\) of the ABCD beam
Full size table

Similarly, the axial stiffness of the other three identical bent beams can also obtain using the above approach. However, these beams have the same axial stiffness as the ABCD beam due to their same dimensions, as shown in Fig. 1(a). To obtain the total axial stiffness (\({K}_{a}\)) of guided support, the rigidity of the first two cantilever flexural beams is also taken into account with four ABCD types of beams. Hence, the total axial stiffness can be written as

$$\begin{array}{c}{K}_{a}=4{K}_{I}+2\left(\frac{3EI}{{\left(a+c\right)}^{3}}\right).\end{array}$$
(8)

The total axial stiffness described in Eq. 8 can be used \({\alpha }_{1}=1\) with experimentally feasible electrode gap and beam thickness, which is essential to observe the bandpass characteristics in the resonator. Next, we obtain the first three frequencies as a function of \({\alpha }_{1}\) and axial stiffness \({K}_{a}\).

Frequencies of the Beam at Various \({\boldsymbol{\alpha }}_{1}\) and \({{\varvec{K}}}_{{\varvec{a}}}\)

To obtain the first three frequencies of the beam as a function of \({\alpha }_{1}\) and axial stiffness \({K}_{a}\), we obtain a system of linear-coupled differential equations from three-mode ROM of Eq. 4 by eliminating the damping and nonlinear terms as

$$\bar{\omega }_{n}^{2} = \omega _{n}^{2} - \left[{\mathop \int \limits_{0}^{1} \phi _{i}^{{''}} \phi _{n} dx} { + 2\alpha _{1} \mathop \int \limits_{0}^{1} w_{{dc}}^{{''}} \phi _{n} dx} {\mathop \int \limits_{0}^{1} \phi _{i}^{'} w_{{dc}}^{'} dx + 2\alpha _{2} V_{{dc}}^{2} } {\mathop \int \limits_{0}^{1} \frac{{\phi _{i} \phi _{n} }}{{\left( {1 - w_{{dc}} } \right)^{3} }}dx}\right]$$
(9)

Solution of the linearized eigenvalue problem associated with these coupled equations gives the first \(n\) natural frequencies, which are a function of the non-dimensional parameters \({\alpha }_{1}\), \({\alpha }_{2}{V}_{dc}^{2}\), static deflection \({w}_{dc}\left(x\right)\), and mode shapes \({\phi }_{n}\left(x\right)\).

Figure 3a shows the variation of the first three frequencies of the beam with \({\alpha }_{1}\), which is obtained using three-mode ROM and FEA in COMSOL. Next, to see the role axial stiffness \({K}_{a}\) on the frequencies of the beam, we first calculate the \({K}_{a}\) using \({\alpha }_{1}\) expression described in Eq. 6 with beam dimensions (L = 800 μm, b = 30 μm, h = 2 μm, and electrode gap \(g = 2\) μm) and material properties (E = 169 GPa and \(\rho = 2332\) kg/m3). Figure 3b shows the first three-dimensional frequencies of the beam as a function of axial stiffness \({K}_{a}\) for an applied DC voltage \({V}_{dc}=3.5259\) V. However, the variation of the frequencies is the same for both \({\alpha }_{1}\) and \({K}_{a}\), but values are different due to dimensional conversion. In the next section, we investigate the dynamic analysis of the coupled second and third modes due to \({\omega }_{3}=2{\omega }_{2}\) internal resonance to analyse bandpass filter characteristics in electrostatically actuated clamped-guided microbeams.

Fig. 3
figure 3

The first three frequencies of the beam as a function of a non-dimensional parameter α1 and b axial stiffness Ka

Full size image

Dynamic Analysis of Bandpass Filter

In this section, to observe bandpass filter characteristics, we study the dynamic of the coupled second and third modes through \({\omega }_{3}=2{\omega }_{2}\) internal resonance when the third mode is externally excited. We also examine the effect of mid-plane stretching nonlinearity, damping, and excitation amplitude and frequency on the frequency bandwidth of the bandpass filter.

For the dynamic analysis, we obtain the coupled governing equations corresponding to the second and third modes from multimode Eq. 7 by neglecting the terms linking with uncoupled modes. As a result, the final coupled equations are as follows:

$$\begin{array}{cc}& {\ddot{u}}_{2}+{c}_{2}{\dot{u}}_{2}+{\omega }_{2}^{2}{u}_{2}+{\alpha }_{21}{u}_{2}^{2}+{\alpha }_{22}{u}_{2}{u}_{3}+{\alpha }_{23}{u}_{3}^{2}\\ & +{\alpha }_{211}{u}_{2}^{3}+{\alpha }_{212}{u}_{2}^{2}{u}_{3}+{\alpha }_{213}{u}_{3}^{2}{u}_{2}+{\alpha }_{214}{u}_{3}^{3}=0,\end{array}$$
(10)
$$\begin{gathered} \ddot{u}_{3} + c_{3} \dot{u}_{3} + \omega_{3}^{2} u_{3} + \alpha_{31} u_{2}^{2} + \alpha_{32} u_{2} u_{3} + \alpha_{33} u_{3}^{2} \hfill \\ + \alpha_{311} u_{2}^{3} + \alpha_{312} u_{2}^{2} u_{3} + \alpha_{313} u_{3}^{2} u_{2} + \alpha_{314} u_{3}^{3} \hfill \\ = f_{3} {\text{cos}}\left( {\Omega t} \right), \hfill \\ \end{gathered}$$
(11)

where ⋅ represents derivative with time, and the coefficients of quadratic and cubic terms are expressed as \({\alpha_{n1}} = {\beta_{22n}} ,{\alpha_{n2}} = {\beta_{23n}} + {\beta_{32n}} ,{\alpha_{n3}}= {\beta_{33n}} ,{\alpha_{n11}} = {\Gamma_{222n}} ,{\alpha_{n12}} = {\Gamma_{223n}} + {\Gamma_{232n}} + {\Gamma_{322n}} ,{\alpha_{n13}} = {\Gamma_{233n}} + {\Gamma_{323n}} + {\Gamma_{332n}} ,{\alpha_{n14}} = {\Gamma_{333n}} ,\) where \(n = 2\) and \(3\) corresponding mode-2 and 3. The quantities \(\beta_{ijn}\) and \(\Gamma_{ijkn}\) were stated above.

To observe the existence of intermodal coupling between the second and third modes due to internal resonance, we first obtain the time history of the coupled modes by numerically integrating Eqs. 10 and 11. Figure 4 shows the time history of the second and third modes when the third mode is externally excited with different excitation frequencies around its normalized frequency \({\omega }_{3}\). It can be observed that the third mode only shows the steady-state response, while the second mode response dies out with time when \(\Omega =120.1\). When the excitation frequency further increases to \(\Omega =120.2\), the response amplitude of the second mode increases due to intermodal coupling with the third mode and the steady-state amplitude is higher than the driving mode. Then, the response amplitude of the second mode is almost constant for a specific range of excitation frequency before sharply decreasing near zero due to the end of the intermodal coupling, whereas the third mode response amplitude initially decreases for a certain range before gradually increasing until it reaches back to the single-mode response. In addition, we also obtain the frequency spectra of the second and third modes using MATLAB fft function, which we display alongside the time history in Fig. 4.

Fig. 4
figure 4

Time history of the second and third mode of the beam at various excitation frequencies when the third mode is externally excited while the second mode is driven by intermodal coupling due to ω3 = 2ω2 internal resonance. The frequency spectrum corresponding to time history is also plotted, which supports the coupling through internal resonance

Full size image

It can be noted that the frequency spectra also confirm the range of intermodal coupling and response amplitude variation with excitation frequency. Next, the steady-state amplitude is extracted from the time history as a function of the excitation frequency to determine whether or not the coupled response can exhibit bandpass behaviour.

First, we investigate the amplitude–frequency response curves of the second and third modes under different excitation amplitudes \({f}_{3}\) when the third mode is externally excited and normalize damping \(c=0.\) Figure 5 shows the amplitude–frequency response curves of the second and third modes at varied \({f}_{3}\). From Fig. 5, we can note that the intermodal coupling due to \(2:1\) internal resonance does not initiate till \({f}_{3}=0.8\) and after it continues. Interestingly, we observe that the second mode response shows bandpass in the amplitude–frequency curve for a certain range of excitation amplitude, while the third mode response curve shows concave-like behaviour for all values of \({f}_{3}\), but the range of this concave varies with increasing \({f}_{3}\). However, the perfect bandpass flatness does not observe at the initial value of \({f}_{3}\); instead, it appears at some specific value of \({f}_{3}\) and then continues for a range of \({f}_{3}\) until ripple starts appearing in the bandpass. It can also be noted that the frequency bandwidth of bandpass and modal interaction is also increased with increasing \({f}_{3}\). Therefore, the bandpass filter can be realized without distortion within specific range parameters via intermodal coupling based on internal resonance. Furthermore, to check bandpass performance, we examine a specific amplitude–frequency response curve of the second and third modes from Fig. 5, which shows an almost flat bandpass.

Fig. 5
figure 5

The amplitude–frequency response curve of the second and third modes at various excitation amplitudes f3 for c = 0.2. The bandpass characteristic is seen in the amplitude–frequency response of the second mode for the range of f3

Full size image

The bandpass ripple is an important aspect in determining the performance of a filter. Hence, to check the flatness behaviour of bandpass, we investigate an amplitude–frequency curve of the second mode corresponding to \({f}_{3}=1.5\) from Fig. 5. Figure 6 shows the amplitude–frequency response curve of the second and third modes when normalized excitation amplitude \({f}_{3}=1.5\) and damping \(c=0.2\). It can observe that the amplitude–frequency response curve of the second mode exhibits the flat bandpass when the second mode is driven through intermodal coupling with the externally excited third mode. Moreover, the response amplitude of the second mode is stable in the intermodal coupling region (passband) and sharply decreases to zero outside the coupling region (stopband). As a result, the frequencies of external excitation in the bandpass range can be seen in the output, while those in the stopband zone can be filtered away.

Fig. 6
figure 6

The amplitude–frequency response curve of the second and third modes when external excitation is applied around the third mode frequency ω3 with excitation amplitude f3 = 1.5 and damping c = 0.2. The solid blue line represents the results of numerical time integration, the red solid points represent the findings of the method of multiple scales, and the dotted blue line represents the bandpass boundaries

Full size image

In addition, we also use the method of multiple scales (MMS) to check the numerical integration computation of bandpass behaviour in the amplitude–frequency response curve of the second mode. For MMS calculation, we solve the following coupled equation of amplitudes and phases [36]:

$$\begin{array}{cc}{\dot{a}}_{2}& \,=\,-\,\frac{1}{2}{c}_{2}{a}_{2}-\frac{{\alpha }_{22}}{4{\omega }_{2}}{a}_{2}{a}_{3}\mathrm{sin}{\gamma }_{2},\\ \dot{{\gamma }_{2}}& ={\sigma }_{1}+{\sigma }_{2}-\frac{{\alpha }_{22}{a}_{3}}{2{\omega }_{2}}\mathrm{cos}{\gamma }_{2}-\left(\frac{3{\alpha }_{211}}{4{\omega }_{2}}-\frac{{\alpha }_{22}{\alpha }_{31}}{2{\omega }_{3}^{2}{\omega }_{2}}\right)\\ & {a}_{2}^{2}-\left(\frac{{\alpha }_{213}}{2{\omega }_{2}}-\frac{{\alpha }_{22}{\alpha }_{33}}{2{\omega }_{3}^{2}{\omega }_{2}}+\frac{{\alpha }_{22}^{2}}{4{\omega }_{2}{\omega }_{3}\left(2{\omega }_{2}+{\omega }_{3}\right)}\right){a}_{3}^{2},\\ {\dot{a}}_{3}& =-\frac{{c}_{3}}{2}{a}_{3}+\frac{{\alpha }_{31}}{4{\omega }_{3}}{a}_{2}^{2}\mathrm{sin}{\gamma }_{2}+\frac{{f}_{3}}{2{\omega }_{3}}\mathrm{sin}{\gamma }_{3},\\ \dot{{\gamma }_{3}}& ={\sigma }_{2}-\frac{{\alpha }_{31}{a}_{2}^{2}}{4{\omega }_{3}{a}_{3}}\mathrm{cos}{\gamma }_{2}-\left(\frac{3{\alpha }_{314}}{8{\omega }_{3}}-\frac{5{\alpha }_{33}^{2}}{12{\omega }_{3}^{3}}\right){a}_{3}^{2}\\ & -\left(\frac{{\alpha }_{312}}{4{\omega }_{3}}-\frac{{\alpha }_{31}{\alpha }_{33}}{2{\omega }_{3}^{3}}+\frac{{\alpha }_{22}{\alpha }_{31}}{4{\omega }_{3}^{2}\left(2{\omega }_{2}+{\omega }_{3}\right)}\right){a}_{2}^{2}\\ & +\frac{{f}_{3}}{2{\omega }_{3}{a}_{3}}\mathrm{cos}{\gamma }_{3},\end{array}$$
(12)

where \({a}_{2}\) (\({a}_{3}\)) and \({\gamma }_{2}\) (\({\gamma }_{3}\)) represent the amplitude and phase of the second (third) mode. The steady-state response amplitudes of both modes are obtained by equating the \({a}_{n}^{\mathrm{^{\prime}}}\) and \({\gamma }_{n}^{\mathrm{^{\prime}}}\) to zero. Therefore, the resulting four coupled nonlinear algebraic equations are solved using the Newton–Raphson method with an appropriate initial guess.

For the same set of parameters, the MMS results are presented alongside the numerical time integration calculation in Fig. 6, and they match well with time integration findings. As we can see from Fig. 6, the MMS results are denoted by solid red circles, while the time integration findings are represented by a combination of the blue dotted line and solid circles. It can be noted that the MMS results are also shown the bandpass characteristics in the second mode amplitude–frequency response curve. Moreover, the MMS data also demonstrate a passband region with a sharp transition from stable response amplitude to zero. The bandpass has the same frequency bandwidth as time integration computations. The third mode response amplitude produced by both approaches matches the intermodal coupling region.

The basic parameters of the bandpass filter also estimate based on the amplitude–frequency response of the second mode. Figure 6 shows \(-3\) dB level, \(3\) dB bandwidth, centre frequency (\({f}_{c}\)), and start (\({f}_{L}\)) and end (\({f}_{H}\)) frequencies of passband. The maximum amplitude is represented by \(0\) dB level, and \(-3\) dB level is about \(0.707\) or \(1/\sqrt{2}\) relative to the maximum amplitude. The non-dimensional centre frequency (\({f}_{c}\)) is \(120.2685\). In addition, the non-dimensional \(3\) dB bandwidth of the passband is \(0.321\). The start frequency (\({f}_{L}\)) of passband is \(120.108\) and end frequency (\({f}_{H}\)) is \(120.429\). The centre frequency is an average of \({f}_{L}\) and \({f}_{H}\).

So far, we investigate the response of the second and third modes as a function of the excitation frequency \(\Omega\) around the third mode \({\omega }_{3}\). Now, we examine the involvement of the second mode response in the bandpass characteristics while varying \(\Omega\) about \({\omega }_{3}\). To do so, we obtain the frequency spectrum of the second mode at different \(\Omega\) from time history using MATLAB function fft. Figure 7 shows the frequency spectrum of the second mode around \({\omega }_{2}\) at different \(\Omega\) as well as the range of modal coupling or bandpass around the second mode frequency \({\omega }_{2}\) (see inset Fig. 7). It can be observed that the frequency bandwidth of intermodal coupling is almost half around the second mode frequency compared to its range with the third mode frequency. Interestingly, the frequency bandwidth of the bandpass with excitation frequency is twice what it was around the second mode frequency, implying \(2:1\) internal resonance between bandpass frequencies. The frequency spectrum results also support the bandpass frequency bandwidth with respect to \(\Omega\) (see Figs. 6 and 7). Next, we investigate the role of non-dimensional parameter \({\alpha }_{1}\) and damping \(c\) in the bandpass characteristics.

Fig. 7
figure 7

Frequency spectrum of the second mode at different excitation frequencies as well as shows the range of intermodal coupling with the third mode. The frequency range of modal interaction around the second mode frequency ω2 is also plotted in the inset figure

Full size image

Effects of \({\boldsymbol{\alpha }}_{1}\) and Damping \({\varvec{c}}\) on Bandpass

In this section, we investigate the effects of \({\alpha }_{1}\) and \(c\) on the bandpass characteristics by obtaining the amplitude–frequency response curves of the second and third modes over a range of these parameters. Thus far, to observe the bandpass characteristics, we used \({\alpha }_{1}=1\) and \(c=0.2\) throughout the investigation. However, it is challenging to obtain these parameters precisely through experimentation, because they are so particular. Therefore, we now explore the coupled response for additional values of \({\alpha }_{1}\) and \(c\) to see how robust the bandpass behaviour is when these variables are changed.

Figure 8 shows the amplitude–frequency response curves of the second and third modes for six different values of \({\alpha }_{1}\) around \({\alpha }_{1}=1\) when the third mode is externally excited with \({f}_{3}=1.5\) and \(c=0.2\). It can be observed that the flatness of the bandpass starts deviating when \({\alpha }_{1}\) is decreased to \(0.9\) from \(1\). On the other hand, the bandpass characteristics continue to hold as \({\alpha }_{1}\) increases until the flatness of the bandpass disappears due to emergent ripple behaviour in the second-mode response at a given letter value of \({\alpha }_{1}\). Moreover, the amplitude–frequency response of both modes shifts right side with increasing the value of \({\alpha }_{1}\). It can be noted that the symmetry in the amplitude–frequency response curve of the third mode breaks away from \({\alpha }_{1}=1\), and this asymmetry shift changes the flatness behaviour of the bandpass in the second mode response. We can conclude that the \({\alpha }_{1}\) plays a very crucial role in generating the bandpass behaviour in the coupled response due to intermodal coupling via \(2:1\) internal resonance. However, in the current analysis, to overcome this challenge, we propose modifying the one-clamped end of the beam as flexible support to tune the \({\alpha }_{1}\) parameter by utilising the axial stiffness of flexible support.

Fig. 8
figure 8

The amplitude–frequency response curves of the second and third modes for six different α1 when the third mode is externally excited with f3 = 1.5 and c = 0.2

Full size image

In addition to \({\alpha }_{1}\), we found that the damping \(c\) also plays an essential role in the bandpass characteristics, and it is also a critical design parameter for MEMS resonators [46]. Therefore, to see the feasible experimental range of the bandpass with respect to damping \(c\), we now study the amplitude–frequency response of the second mode for a range of \(c.\) Figure 9 shows bandpass characteristics in the second-mode response for four different values of \(c\). It can be seen that the bandpass behaviour in the second-mode response is observed for each case of damping with different \({f}_{3}\) ranges. We also see that a low initial value of \({f}_{3}\) is required for lower \(c\) and vice versa for higher \(c\). Furthermore, the frequency bandwidth of the bandpass increases with increasing \(c\) as well as required \({f}_{3}\) for respective \(c\). We conclude that bandpass characteristics can be achieved using our analysis for any feasible value of damping \(c\) and adequate excitation amplitude \({f}_{3}\).

Fig. 9
figure 9

The amplitude–frequency response curve of the second mode for four different damping c values as a function of excitation amplitude. The frequency bandpass behaviour is seen for a certain range of excitation amplitude in each case

Full size image

Using the similar process describe in Fig. 6, we also estimate the centre frequency and \(3\) dB bandwidth of passband at various \({\alpha }_{1}\) and combination of damping \(c\) and excitation amplitude \({f}_{3}\) from Figs. 8 and 9. Table 2 shows the centre frequency \({f}_{c}\) and \(3\) dB bandwidth of passband at different \({\alpha }_{1}\) and combination of \(c\) and \({f}_{3}\). It can be noted that the centre frequency \({f}_{c}\) and \(3\) dB bandwidth increase with increasing \({\alpha }_{1}\) and \(c\).

Table 2 The centre frequency and 3 dB bandwidth of bandpass filter at various α1 and combination of damping c and excitation amplitude f3
Full size table

Numerical Estimates of the Axial Stiffness \({{\varvec{K}}}_{{\varvec{a}}}\) of Guided End and Frequency Bandwidth \(\boldsymbol{\Delta }\boldsymbol{\Omega }\) of Bandpass

Up to this point, we have presented the bandpass characteristics in terms of the normalized parameters \({\alpha }_{1}\), \({f}_{3}\), and \(\Omega\). To investigate how the current analysis might be better applied in actual bandpass filter applications, we collect typical experimental dimensions (\(L = 800\) μm, \(B = 30\) μm, and \(h = 2\) μm) and material properties (\(E = 160\) GPa and \(\rho = 2332\) kg/m3) from Hajjaj et al. [2]. Additionally, the electrode gap \(g\) is chosen to be between \(2\) and \(6\) μm to provide a practical range for the axial stiffness of the guided end with retaining \({\alpha }_{1}=1\). For each electrode gap, we calculate the values of total axial stiffness (\({K}_{a}\)) and show them in Table 3. However, the required axial stiffness value might be generated by an infinite number of different combinations of length, width, and thickness of the guided end’s flexural beams. The combination of length, width, and thickness of each flexural beam of flexible guided support can thus be estimated using these axial stiffnesses in Eq. 8. For example, to show the exact dimensions of flexural beams, here, we assume the width (\({B}_{f}\)) and thickness (\({h}_{f}\)) of all flexural beams of the guided end are the same as well as

Table 3 The axial stiffness (\({K}_{a}\)) of the guided end at various electrode gap \(g\)
Full size table
$$\begin{array}{c}b=a/2, c=a/2, {B}_{f}=a/5, \,{\text{and}}\, {h}_{f}={B}_{f}/5.\end{array}$$
(13)

Now, we can calculate the value of a by solving Eq. 8 after inserting expressions of Eq. 13 and value of Ka from Table 3. The obtained value of a corresponding to the axial stiffness of the guided end is also shown in Table 3.

Above, we saw the dimensional conversion of axial stiffness and dimensions of flexural beams of the guided end from non-dimensional quantities. Now, we obtain the dimensional value of frequency bandwidth \(\Delta \Omega\) of bandpass using frequency dimensional conversion factor \(1/2\pi {L}^{2}\left(\sqrt{EI/\rho A}\right)\). The cross-section area \(A\) and second moment of area \(I\) are calculated using the previously specified beam dimensions. Table 4 shows real frequency bandwidth \(\Delta \Omega\) of bandpass filter for different combination of excitation amplitude \({f}_{3}\) and damping \(c\) that are chosen from Figs. 6 and 9. We also note that the frequency bandwidth \(\Delta \Omega\) of the filter increases with increasing the value of \({f}_{3}\) and \(c\) combinations. It can be noted from Table 5 that the bandwidth observed in the current analysis using \(2:1\) internal resonance is less than that observed in parametric excitation-based veering phenomena in an electrostatically driven arch clamped–clamped beam [2]. However, the fabrication of the arch beams is more challenging than the fabrication of the straight electrostatically driven clamped-guided beams. On the other hand, Liu et al. [3] reported 6.2 Hz bandwidth of bandpass using \(1:2\) internal resonance in coupled \(35\times 5\times 0.8\) mm3 size cantilevers, whereas we observed \(954.97\) Hz bandwidth of bandpass through \(2:1\) internal resonance in an electrostatically actuated \(0.8\times 0.03\times 0.002\) mm3 size clamped-guided beam, as shown in Table 5. Based on these dimensional conversions and findings, future experiments may be designed to measure bandpass filter bandwidth.

Table 4 The frequency bandwidth \(\Delta \Omega\) of bandpass filter at different combinations of excitation amplitude \({f}_{3}\) and damping \(c\)
Full size table
Table 5 Comparison of the 3 dB bandwidth obtained in the current analysis and achieved by Liu et al. [3] and Hajjaj et al. [2]
Full size table

Conclusion

In this paper, we investigated the bandpass filter based on intermodal coupling due to \(2:1\) internal resonance of electrostatically actuated clamped-guided microbeam. We modelled the guided end using a set of flexural beams structured in a certain way to tune and obtain the necessary mid-plane stretching nonlinearity. We found that the axial stiffness of the guided end allowed us to choose any experimentally feasible electrode gap and thickness combinations. We also provided a thorough calculation of the axial stiffness of the guided end using COMSOL’s finite-element analysis and analytical methods.

We then comprehensively investigated the dynamics of the coupled second and third modes for \({\omega }_{3}=2{\omega }_{2}\) internal resonance by solving coupled governing equations (Eqs. 10 and 11) using numerical integration and the method of multiple scales. We found that the amplitude–frequency response curve of the second mode exhibits bandpass characteristics for a range of excitation amplitudes when the third mode is externally excited and subject to particular damping (Figs. 5 and 6). We also noted the ripple effect on the bandpass for higher excitation amplitude (Fig. 5). The second mode’s frequency spectrum showed similar bandpass behaviour as a function of excitation frequency; however, to internal \(2:1\) resonance, the second mode’s bandpass frequency bandwidth is half that of excitation frequency (Fig. 7). Additionally, we found that the exact bandpass characteristics’ manifestation strongly depends on the mid-plane stretching nonlinearity and the combination of excitation amplitude and damping (Figs. 8 and 9). We presented dimensional conversions of the frequency bandwidth \(\Delta \Omega\) of the bandpass, the axial stiffness \({K}_{a}\) of the guided end, and length of flexible beams corresponding \({K}_{a}\) (Tables 3 and 4), and compared the 3 dB bandwidth of the current analysis with the literature (Table 5).

To the best of our knowledge, this is the first time a bandpass filter based on intermodal coupling via internal resonance of an electrostatically actuated clamped-guided microbeam is proposed and analysed in detail. The bandpass characteristics of the resonator are also presented in a most general manner for any combination of beam dimensions and material properties via non-dimensional parameters. The internal resonance-based bandpass filter demonstrated here illustrates a novel method for building filters using a single MEMS resonator. Here, we consider electrostatically actuated clamped–guided beams, but the concept can be applied to any MEMS resonator that exhibits modal coupling based on internal resonance. In addition, it is more durable than contemporary electronic filters and is temperature robust. The work presented here might potentially serve as a guide for investigating more MEMS resonators to create bandpass filters based on internal resonances.