Introduction

Vibration is an unavoidable phenomenon in people's production and life. The existence of vibration makes fatigue in industrial production equipment damage, affect the accuracy of equipment and even shorten the life of the equipment. In general, vibration-damping and vibration-isolating equipment are installed in the forced components to reduce the vibration [1,2,3,4,5,6] and ensure the normal operation of the components. Tuned mass damper is a device that uses the tuned resonance effect between the damping device and the component to achieve energy absorption, energy dissipation and vibration reduction. This classic method of vibration reduction is not only applicable to macro-scale projects, but it is still a great advantage compared to other methods of vibration reduction in micro-precision instruments, especially in electromechanical devices [7,8,9,10]. Roberson [11] studied the dynamic response of a TMD and an un-damped Duffing spring system. Studies have shown that the controllable frequency bandwidth of the nonlinear absorber is much wider than the linear TMD. Srinivasan [12] researched the parallel damping TMD and found that when the damping frequency coincides with the excitation frequency, the main system remains stationary, but the control bandwidth of TMD becomes narrower. However, sometimes the input energy of the vibration device is too large, and the TMD cannot absorb so much energy to ensure the normal work of the main component. Then, another vibration-damping device, nonlinear energy sink (NES) passive vibration absorbers are needed to consume the excess energy of the main component. NES extracts unwanted vibrations from the system to reduce component amplitude by moving energy from the directly excited primary system to the ancillary system. Thus, a wide variety of NES designs have been proposed. Some scholars aimed at choosing the different types of nonlinear stiffness, for example, non-smooth [13, 14], non-polynomial [15], cubic [16], vibro-impact [17,18,19] to optimize of NES system. Ohtori et al. [20] and Nucera et al. [17, 21] studied NES contribution to the overall system and found that it can reduce the time of energy dissipation or energy decay, and mitigate the lateral reaction force applied on the tank wall. Gendelman et al. [22] and Sapsis et al. [23] researched the effect of a NES with relatively small mass on the dynamics of a coupled system under periodic forcing in the vicinity of a main resonance theoretically and experimentally. They pointed that the quasi-periodic regime response provide efficient vibration suppression. Kerschen et al. [24] studied a two-degree-of-freedom master system with an attached NES, and found that this system may have more sequences of resonance transitions possible due to initial conditions than the single-degree-of-freedom case. Though the phenomenon of NES has been extensively studied in the references, the parameter selection and optimization problem for multiple-degree-of-freedom systems are still a challenge [25,26,27].

In addition, many researchers have conducted dynamic research on different micro shock absorbers. For example, Malhotra et al. [28] showed that mass-spring damping systems are more common in engineering design regulations. Nagurka and Huang [29] compared the vertical drop ball to the mass-spring-damping system and studied its physical properties. Hamamoto et al. [30] conducted a controller design study on a mass-spring system with two degrees of freedom.

Motivated by these ideas, in this paper, we describe the TMD and NES system coupled to the equivalent model of the micro-electro-mechanical damping component. To study the dynamic characteristics of the micro-damper, we use the Hamiltonian variational principle to derive the nonlinear vibration equations of 3 freedom degrees (3-DOF) of a spring-mass-damping system. Moreover, the multiscale method [31,32,33,34,35,36] is used to obtain an approximate analytical solution to the derived nonlinear set of differential equations and the corresponding numerical results and discussion of the nonlinear dynamics are presented. Through the analysis of the parameters of the micro-damper, the dynamical behaviors of the shock absorber were examined.

Mathematical Model

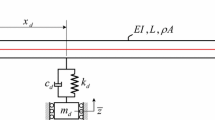
Micro-electro-mechanical damping component, as shown in Fig. 1, with cylindrical tank with height, radius and wall thickness of \(H,{\kern 1pt} {\kern 1pt} R\) and \(t_{{\text{w}}}\) on the left side of the micro device is an electrostatic excitation \(u_{{\text{g}}} = A\cos \left( {\omega t} \right)\).

Fig. 1
figure 1

Micro-electro-mechanical damping component schematic

Full size image

Here the excitation frequency is \(\omega_{1}\). The component \(L\) and the main component are connected by a spring \(K\). There is a damping symbol \(C\) between the component \(L\) and the main component \(M\). The mass of the main component is denoted by \(M\), and the length of the inner hollow part of \(M\) is \(2R\). Place a coordinated damping element of mass \(m_{1}\) inside the main component. It is connected with the main component using spring \(k_{1}\), \(m_{1}\) and \(k_{1}\) form TMD, and the inter-component damping parameter is \(c_{1}\). The right side of the main component has a mass block of mass \(m_{2}\). Springs \(k_{2}\) and \(k_{3}\) connect with the main component. \(m_{2}\) and springs \(k_{2}\), \(k_{3}\) work together to form NES for absorbing the excess energy of the main component. There are no displacement changes in the vertical direction and the elongation and compression of the springs \(k_{1}\), \(k_{2}\) and \(k_{3}\) are all in the horizontal direction. All the micro-components except the spring in the Fig. 1 are considered to be rigid materials and do not deform. In addition, for the sake of generality, we assume that \(K\), \(k_{1}\), \({\kern 1pt} k_{2}\), \(k_{3}\) are stiffness of springs and \(C\), \(c_{1}\), \({\kern 1pt} c_{2}\) are damping.

The system Lagrangian is written as follows [37]:

$$\begin{aligned} L & = \frac{M}{2}\left( {\dot{u}_{{\text{g}}} + \dot{x}} \right)^{2} + \frac{{m_{1} }}{2}\left( {\dot{u}_{{\text{g}}} + \dot{y}} \right)^{2} + \frac{{m_{2} }}{2}\left( {\dot{u}_{{\text{g}}} + \dot{z}} \right)^{2} \\ & \quad - \frac{K}{2}x^{2} - \frac{{k_{1} }}{2}\left( {y - x} \right)^{2} - \frac{{k_{2} }}{2}\left( {z - x} \right)^{2} - \frac{{k_{3} }}{2}\left( {z - x} \right)^{4} , \\ \end{aligned}$$
(1)

where \(x\), \(y\), \({\kern 1pt} z\) are horizontal displacements of \(M\), \({\kern 1pt} m_{1}\) and \(m_{2}\), respectively.

There are 7 items in Eq. (1). Among them, the first three items are the kinetic energy of the main component, the kinetic energy of the mass damper, the kinetic energy of the mass damper, and the kinetic energy of the mass damper of the passive energy absorber. The last four items are spring elastic energy. \(\frac{K}{2}x^{2}\) is the elastic potential energy between the main component and the excitation part, \(\frac{{k_{1} }}{2}\left( {y - x} \right)^{2}\) is the elastic potential energy between the main component and TMD, \(\frac{{k_{2} }}{2}\left( {z - x} \right)^{2}\) and \(\frac{{k_{3} }}{4}\left( {z - x} \right)^{4}\) is the elastic potential energy between the main component and NES.

The energy consumed by the system can be expressed by the following equation:

$$D = \frac{C}{2}\dot{x}^{2} + \frac{{c_{1} }}{2}\left( {\dot{y} - \dot{x}} \right)^{2} + \frac{{c_{2} }}{2}\left( {\dot{z} - \dot{x}} \right)^{2} ,$$
(2)

where \(\frac{C}{2}\dot{x}^{2}\) represents the energy consumption of the damping between the main component and the excitation portion, \(\frac{{c_{1} }}{2}\left( {\dot{y} - \dot{x}} \right)^{2}\) represents the energy consumed by the damping between the main component and TMD, \(\frac{{c_{2} }}{2}\left( {\dot{z} - \dot{x}} \right)^{2}\) represents the energy consumed by the damping between the main component and NES. Excitation item \(u_{{\text{g}}}\) is \(A\cos \left( {\omega t} \right)\). The dimensional system dynamics equations obtained from Eqs. (1, 2) using the Hamiltonian variational principle are as follows:

$$M\left( {\ddot{u}_{{\text{g}}} + \ddot{x}} \right) + Kx - k_{2} \left( {z - x} \right) - k_{3} \left( {z - x} \right)^{3} - k_{1} \left( {y - x} \right) + C\dot{x} - c_{1} \left( {\dot{y} - \dot{x}} \right) - c_{2} \left( {\dot{z} - \dot{x}} \right) = 0,$$
(3)
$$m_{1} \left( {\ddot{u}_{{\text{g}}} + \ddot{y}} \right) + k_{1} \left( {y - x} \right) + c_{1} \left( {\dot{y} - \dot{x}} \right) = 0,$$
(4)
$$m_{2} \left( {\ddot{u}_{{\text{g}}} + \ddot{z}} \right) + k_{2} \left( {z - x} \right) + k_{3} \left( {z - x} \right)^{3} + c_{2} \left( {\dot{z} - \dot{x}} \right) = 0.$$
(5)

Introduce dimensionless parameters: \(t_{N} = \Omega t\), here \(\Omega^{2} = \frac{K}{M}\), \(\Omega\) is the natural frequency of main component system. Dimensionless parameters are: \(\overline{x} = \frac{x}{R}\), \(\overline{y} = \frac{y}{R}\), \(\overline{z} = \frac{z}{R}\), \(\omega_{1}^{2} = \frac{{k_{1} }}{{m_{1} }}\), \(\omega_{2}^{2} = \frac{{k_{2} }}{{m_{2} }}\), \(\beta_{1} = \frac{{\omega_{1} }}{\Omega }\), \(\beta_{2} = \frac{{\omega_{2} }}{\Omega }\), \(\overline{k}_{2} = \frac{{k_{3} R^{2} }}{{m_{2} \Omega^{2} }}\), \(\varepsilon_{1} = \frac{{m_{1} }}{M}\), \(\varepsilon_{2} = \frac{{m_{2} }}{M}\), \(\overline{Z} = \frac{C}{2M\Omega }\), \(\overline{\varsigma }_{1} = \frac{{c_{1} }}{{2m_{1} \omega_{1} }}\), \(\overline{\varsigma }_{2} = \frac{{c_{2} }}{{2m_{2} \omega_{2} }}\).

Simplification Eqs. (3–5) gives the system dimensionless equation of motion as:

$$\begin{aligned} & \overline{x}^{\prime\prime} + 2\overline{Z}\overline{x}^{\prime} + \overline{x} - \varepsilon_{1} \beta_{1}^{2} \left( {\overline{y} - \overline{x}} \right) - 2\varepsilon_{1} \beta_{1} \overline{\varsigma }_{1} \left( {\overline{y}^{\prime} - \overline{x}^{\prime}} \right) - \varepsilon_{2} \beta_{2}^{2} \left( {\overline{z} - \overline{x}} \right) - \varepsilon_{2} \overline{k}_{2} \left( {\overline{z} - \overline{x}} \right)^{3} \\ & \quad - 2\varepsilon_{2} \beta_{2} \overline{\varsigma }_{2} \left( {\overline{z}^{\prime} - \overline{x}^{\prime}} \right) = - \frac{1}{{R\Omega^{2} }}\ddot{u}_{{\text{g}}} \left( t \right), \\ \end{aligned}$$
(6)
$$\overline{y}^{\prime\prime} + \beta_{1}^{2} \left( {\overline{y} - \overline{x}} \right) + 2\beta_{1} \overline{\varsigma }_{1} \left( {\overline{y}^{\prime} - \overline{x}^{\prime}} \right) = - \frac{1}{{R\Omega^{2} }}\ddot{u}_{{\text{g}}} \left( t \right),$$
(7)
$$\overline{z}^{\prime\prime} + \beta_{2}^{2} \left( {\overline{z} - \overline{x}} \right) + \overline{k}_{2} \left( {\overline{z} - \overline{x}} \right)^{3} + 2\beta_{2} \overline{\varsigma }_{2} \left( {\overline{z}^{\prime} - \overline{x}^{\prime}} \right) = - \frac{1}{{R\Omega^{2} }}\ddot{u}_{{\text{g}}} \left( t \right),$$
(8)

\(\left( {} \right)^{\prime \prime }\) denote the differentiation of \(t_{N}\).

In the above equations, parameters such as \(\beta_{2}\), \(\overline{\zeta }_{2}\) and \(\overline{k}_{2}\) can be determined based on the properties of TMD and NES.

Next, we simplify the calculation of the Eqs. (6–8). Let: \(u = \overline{x} + \varepsilon_{1} \overline{y}\), \(v = \overline{x} - \overline{y}\) and \(w = \overline{z} - \overline{x}\), then \(\overline{x} = \left( {u + \varepsilon_{1} v} \right)/\left( {1 + \varepsilon_{1} } \right)\), \(\overline{y} = \left( {u - v} \right)/\left( {1 + \varepsilon_{1} } \right)\), \(\overline{z} = \left( {u + \varepsilon_{1} v} \right)/\left( {1 + \varepsilon_{1} } \right) + w\).

To simplify the calculation, we introduce a new time parameter \(\tau\) for conversion. Here \(\tau = \frac{{t_{N} }}{{\sqrt {1 + \varepsilon_{1} } }}\).

The transformation of the Eqs. (6–8) into the following equation can be achieved by the parameter transformation:

$$\ddot{u} + u + \varepsilon_{1} v + Z\dot{u} + \varepsilon_{1} Z\dot{v} - \varepsilon_{2} \left( {1 + \varepsilon_{1} } \right)\beta_{2}^{2} w - \varepsilon_{2} k_{2} w^{3} - 2\varepsilon_{2} \beta_{2} \varsigma_{2} \dot{w} = \frac{{1 + \varepsilon_{1} }}{R}A\cos \left( {\omega^{*} \tau } \right),$$
(9)
$$\begin{aligned} & \ddot{v} + u + \left( {\varepsilon_{1} + \left( {1 + \varepsilon_{1} } \right)^{2} \beta_{1}^{2} } \right)v + Z\dot{u} + \left( {\varepsilon_{1} Z + 2\left( {1 + \varepsilon_{1} } \right)\beta_{1} \varsigma_{1} } \right)\dot{v} - \varepsilon_{2} \left( {1 + \varepsilon_{1} } \right)\beta_{2}^{2} w \\ & \quad - \varepsilon_{2} k_{2} w^{3} - 2\varepsilon_{2} \beta_{2} \varsigma_{2} \dot{w} = 0, \\ \end{aligned}$$
(10)
$$\begin{aligned} & \ddot{w} - u - \varepsilon_{1} \left( {1 + \left( {1 + \varepsilon_{1} } \right)\beta_{1}^{2} } \right)v + \left( {1 + \varepsilon_{1} } \right)\left( {1 + \varepsilon_{2} } \right)\beta_{2}^{2} w + \left( {1 + \varepsilon_{2} } \right)k_{2} w^{3} - Z\dot{u} \\ & \quad - \varepsilon_{1} \left( {Z + 2\beta_{1} \varsigma_{1} } \right)\dot{v} + 2\left( {1 + \varepsilon_{2} } \right)\beta_{2} \varsigma_{2} \dot{w} = 0. \\ \end{aligned}$$
(11)

Among them, dimensionless parameters are: \(Z = \frac{{2\overline{Z}}}{{\sqrt {1 + \varepsilon_{1} } }}\), \(\varsigma_{1} = \sqrt {1 + \varepsilon_{1} } \overline{\varsigma }_{1}\), \(\varsigma_{2} = \sqrt {1 + \varepsilon_{1} } \overline{\varsigma }_{2}\), \(k_{2} = \left( {1 + \varepsilon_{1} } \right)\overline{k}_{2} ,\)\(\omega^{*} = \frac{{\omega \sqrt {1 + \varepsilon_{1} } }}{\Omega }\).

Multiscale Method

In this section, to obtain numerical solution of the micro shock absorbers model by the multiscale method, we transform the Eq. (9). Let the system (9) except for \(\ddot{u}\) and \(u\) be multiplied by the small parameter \(\varepsilon\):

$$\begin{aligned} & \ddot{u} + u + \varepsilon \cdot \varepsilon_{1} v + \varepsilon \cdot Z\dot{u} + \varepsilon \cdot \varepsilon_{1} Z\dot{v} - \varepsilon \cdot \varepsilon_{2} \left( {1 + \varepsilon_{1} } \right)\beta_{2}^{2} w - \varepsilon \cdot \varepsilon_{2} k_{2} w^{3} - 2\varepsilon \cdot \varepsilon_{2} \beta_{2} \varsigma_{2} \dot{w} \\ & \quad = \frac{{1 + \varepsilon_{1} }}{R}\varepsilon A\cos \left( {\omega^{*} \tau } \right). \\ \end{aligned}$$
(12)

In the same way, the same transformations can be made for Eqs. (10) and (11). Equations (10) and (11) can be rewritten as follows:

$$\begin{aligned} & \ddot{v} + \varepsilon u + \left( {\varepsilon_{1} + \left( {1 + \varepsilon_{1} } \right)^{2} \beta_{1}^{2} } \right)v + \varepsilon \cdot Z\dot{u} + \varepsilon \cdot \left( {\varepsilon_{1} Z + 2\left( {1 + \varepsilon_{1} } \right)\beta_{1} \varsigma_{1} } \right)\dot{v} \\ & \quad - \varepsilon \cdot \varepsilon_{2} \left( {1 + \varepsilon_{1} } \right)\beta_{2}^{2} w - \varepsilon \cdot \varepsilon_{2} k_{2} w^{3} - 2\varepsilon \cdot \varepsilon_{2} \beta_{2} \varsigma_{2} \dot{w} = 0, \\ \end{aligned}$$
(13)
$$\begin{aligned} & \ddot{w} - \varepsilon u - \varepsilon \cdot \varepsilon_{1} \left( {1 + \left( {1 + \varepsilon_{1} } \right)\beta_{1}^{2} } \right)v + \left( {1 + \varepsilon_{1} } \right)\left( {1 + \varepsilon_{2} } \right)\beta_{2}^{2} w + \varepsilon \cdot \left( {1 + \varepsilon_{2} } \right)k_{2} w^{3} \\ & \quad - \varepsilon \cdot Z\dot{u} - \varepsilon \cdot \varepsilon_{1} \left( {Z + 2\beta_{1} \varsigma_{1} } \right)\dot{v} + 2\varepsilon \cdot \left( {1 + \varepsilon_{2} } \right)\beta_{2} \varsigma_{2} \dot{w} = 0. \\ \end{aligned}$$
(14)

Next, apply the multiscale method. Let:

$$u = x_{11} \left( {T_{0} ,T_{1} } \right) + \varepsilon x_{12} \left( {T_{0} ,T_{1} } \right),$$
(15)
$$v = x_{21} \left( {T_{0} ,T_{1} } \right) + \varepsilon x_{22} \left( {T_{0} ,T_{1} } \right),$$
(16)
$$w = x_{31} \left( {T_{0} ,T_{1} } \right) + \varepsilon x_{32} \left( {T_{0} ,T_{1} } \right),$$
(17)
$$\dot{u} = \left( {D_{0} + \varepsilon D_{1} } \right)\left( {x_{11} + \varepsilon x_{12} } \right) = D_{0} x_{11} + \varepsilon \left( {D_{0} x_{12} + D_{1} x_{11} } \right),$$
(18)
$$\dot{v} = \left( {D_{0} + \varepsilon D_{1} } \right)\left( {x_{21} + \varepsilon x_{22} } \right) = D_{0} x_{21} + \varepsilon \left( {D_{0} x_{22} + D_{1} x_{21} } \right),$$
(19)
$$\dot{w} = \left( {D_{0} + \varepsilon D_{1} } \right)\left( {x_{31} + \varepsilon x_{32} } \right) = D_{0} x_{31} + \varepsilon \left( {D_{0} x_{32} + D_{1} x_{31} } \right).$$
(20)

Substituting the Eqs. (15–20) into (12)–(14) yields Eq. (21)–(23):

$$\begin{aligned} & D_{0}^{2} x_{11} + \varepsilon \left( {D_{0}^{2} x_{12} + 2D_{0} D_{1} x_{11} } \right) + \left( {x_{11} + \varepsilon x_{12} } \right) \\ & \quad \; + \varepsilon \left[ \begin{gathered} \varepsilon_{1} \left( {x_{21} + \varepsilon x_{22} } \right) + Z\left( {D_{0} x_{11} + \varepsilon \left( {D_{0} x_{12} + D_{1} x_{11} } \right)} \right) \hfill \\ + \varepsilon_{1} Z\left( {D_{0} x_{21} + \varepsilon \left( {D_{0} x_{22} + D_{1} x_{21} } \right)} \right) \hfill \\ - \varepsilon_{2} \left( {1 + \varepsilon_{1} } \right)\beta_{2}^{2} \left( {x_{31} + \varepsilon x_{32} } \right) - \varepsilon_{2} k_{2} \left( {x_{31} + \varepsilon x_{31} } \right)^{3} \hfill \\ - 2\varepsilon_{2} \beta_{2} \varsigma_{2} \left( {D_{0} x_{31} + \varepsilon \left( {D_{0} x_{32} + D_{1} x_{31} } \right)} \right) \hfill \\ \end{gathered} \right] \\ & \quad = \frac{{1 + \varepsilon_{1} }}{R}\varepsilon A\cos \left( {\omega^{*} \tau } \right), \\ \end{aligned}$$
(21)
$$\begin{aligned} & D_{0}^{2} x_{21} + \varepsilon \left( {D_{0}^{2} x_{22} + 2D_{0} D_{1} x_{21} } \right) + \left( {\varepsilon_{1} { + }\left( {1 + \varepsilon_{1} } \right)^{2} \beta_{{1}}^{{2}} } \right)\left( {x_{21} + \varepsilon x_{22} } \right) \\ & \quad + \varepsilon \left[ \begin{gathered} \left( {x_{11} + \varepsilon x_{12} } \right) + Z\left( {D_{0} x_{11} + \varepsilon \left( {D_{0} x_{12} + D_{1} x_{11} } \right)} \right) + \hfill \\ \left( {\varepsilon_{1} Z + 2\left( {1 + \varepsilon_{1} } \right)\beta_{1} \varsigma_{1} } \right)\left( {D_{0} x_{21} + \varepsilon \left( {D_{0} x_{22} + D_{1} x_{21} } \right)} \right) \hfill \\ - \varepsilon_{2} \left( {1 + \varepsilon_{1} } \right)\beta_{2}^{2} \left( {x_{31} + \varepsilon x_{21} } \right) - \varepsilon_{2} k_{2} \left( {x_{31} + \varepsilon x_{32} } \right)^{3} \hfill \\ - 2\varepsilon_{2} \beta_{2} \varsigma_{2} \left( {D_{0} x_{31} + \varepsilon \left( {D_{0} x_{32} + D_{1} x_{31} } \right)} \right) \hfill \\ \end{gathered} \right] = 0, \\ \end{aligned}$$
(22)
$$\begin{aligned} & D_{0}^{2} x_{31} + \varepsilon \left( {D_{0}^{2} x_{32} + 2D_{0} D_{1} x_{31} } \right) + \left( {1 + \varepsilon_{1} } \right)\left( {1 + \varepsilon_{2} } \right)\beta_{2}^{2} \left( {x_{31} + \varepsilon x_{32} } \right) \\ & \quad + \varepsilon \left[ \begin{gathered} - \left( {x_{11} + \varepsilon x_{12} } \right) - \varepsilon_{1} \left( {1 + \left( {1 + \varepsilon_{1} } \right)\beta_{1}^{2} } \right)\left( {x_{21} + \varepsilon x_{22} } \right) \hfill \\ + \left( {1 + \varepsilon_{2} } \right)k_{2} \left( {x_{31} + \varepsilon x_{32} } \right)^{3} - Z\left( {D_{0} x_{11} + \varepsilon \left( {D_{0} x_{12} + D_{1} x_{11} } \right)} \right) \hfill \\ - \varepsilon_{1} \left( {Z + 2\beta_{1} \varsigma_{1} } \right)\left( {D_{0} x_{21} + \varepsilon \left( {D_{0} x_{22} + D_{1} x_{21} } \right)} \right) \hfill \\ + 2\left( {1 + \varepsilon_{2} } \right)\beta_{2} \varsigma_{2} \left( {D_{0} x_{31} + \varepsilon \left( {D_{0} x_{32} + D_{1} x_{31} } \right)} \right) \hfill \\ \end{gathered} \right] = 0. \\ \end{aligned}$$
(23)

Considered the Eq. (21), let \(\omega_{10}^{2} = 1\) and equating the coefficients of \(\varepsilon\), we have:

$$\varepsilon^{0} :D_{0}^{2} x_{11} + \omega_{10}^{2} x_{11} = 0,$$
(24)
$$\begin{aligned} & \varepsilon^{1} :{\kern 1pt} D_{0}^{2} x_{12} + 2D_{0} D_{1} x_{11} + \omega_{10}^{2} x_{12} + \varepsilon_{1} x_{21} + ZD_{0} x_{11} + \varepsilon_{1} ZD_{0} x_{21} - \varepsilon_{2} k_{2} x_{31}^{3} \\ {\kern 1pt} & \quad - \varepsilon_{2} \left( {1 + \varepsilon_{1} } \right)\beta_{2}^{2} x_{31} - 2\varepsilon_{2} \beta_{2} \varsigma_{2} D_{0} x_{31} = \frac{{1 + \varepsilon_{1} }}{R}A\cos \left( {\omega^{*} \tau } \right). \\ \end{aligned}$$
(25)

Considered the Eq. (22), let \(\omega_{20}^{2} = (\varepsilon_{{1}} + \left( {1 + \varepsilon_{1} } \right)^{2} )\beta_{1}^{2}\) and equating the coefficients of \(\varepsilon\), we have:

$$\varepsilon^{0} :D_{0}^{2} x_{21} + \omega_{20}^{2} x_{21} = 0,$$
(26)
$$\begin{aligned} & \varepsilon^{1} :D_{0}^{2} x_{22} + 2D_{0} D_{1} x_{21} + \omega_{{_{20} }}^{2} x_{22} + x_{11} + ZD_{0} x_{11} + \left( {\varepsilon_{1} Z + 2\left( {1 + \varepsilon_{1} } \right)\beta_{1} \varsigma_{1} } \right)D_{0} x_{21} \\ {\kern 1pt} & \quad - \varepsilon_{2} k_{2} x_{31}^{3} - \varepsilon_{2} \left( {1 + \varepsilon_{1} } \right)\beta_{2}^{2} x_{31} - 2\varepsilon_{2} \beta_{2} \varsigma_{2} D_{0} x_{31} = 0. \\ \end{aligned}$$
(27)

Considered the Eq. (23), let \(\omega_{30}^{2} = \left( {1 + \varepsilon_{1} } \right)\left( {1 + \varepsilon_{2} } \right)\beta_{2}^{2}\) and equating the coefficients of \(\varepsilon\), we have:

$$\varepsilon^{0} :D_{0}^{2} x_{31} + \omega_{30}^{2} x_{31} = 0,$$
(28)
$$\begin{aligned} & \varepsilon^{1} D_{0}^{2} x_{32} + 2D_{0} D_{1} x_{31} + \omega_{{_{30} }}^{2} x_{32} - x_{11} - ZD_{0} x_{11} - \varepsilon_{1} \left( {1 + \left( {1 + \varepsilon_{1} } \right)\beta_{1}^{2} } \right)x_{21} \\ {\kern 1pt} & \quad - \varepsilon_{1} \left( {Z + 2\beta_{1} \varsigma_{1} } \right)D_{0} x_{21} + \left( {1 + \varepsilon_{2} } \right)k_{2} x_{31}^{3} + 2\left( {1 + \varepsilon_{2} } \right)\beta_{2} \varsigma_{2} D_{0} x_{31} = 0. \\ \end{aligned}$$
(29)

According to (24), (26), and (28), we can get (30):

$$x_{11} = A_{1} \left( {T_{1} } \right)e^{{i\omega_{10} T_{0} }} + \overline{A}_{1} \left( {T_{1} } \right)e^{{ - i\omega_{10} T_{0} }} ,$$
$$x_{21} = A_{2} \left( {T_{1} } \right)e^{{i\omega_{20} T_{0} }} + \overline{A}_{2} \left( {T_{1} } \right)e^{{ - i\omega_{20} T_{0} }} ,$$
(30)
$$x_{31} = A_{3} \left( {T_{1} } \right)e^{{i\omega_{30} T_{0} }} + \overline{A}_{3} \left( {T_{1} } \right)e^{{ - i\omega_{30} T_{0} }} .$$

Substituting Eq. (30) into Eqs. (25), (27), and (29), we get Eqs. (31), (32), and (33), as follows:

$$\begin{aligned} D_{0}^{2} x_{12} + \omega_{{_{10} }}^{{2}} x_{12} & = - 2\left( {\omega_{10} D_{1} A_{1} ie^{{i\omega_{10} T_{0} }} - \omega_{10} D_{1} \overline{A}_{1} ie^{{ - i\omega_{10} T_{0} }} } \right) \\ & \quad - \varepsilon_{1} \left( {A_{2} e^{{i\omega_{20} T_{0} }} + \overline{A}_{2} e^{{ - i\omega_{20} T_{0} }} } \right) \\ & \quad - Z\left( {\omega_{10} A_{1} ie^{{i\omega_{10} T_{0} }} - \omega_{10} \overline{A}_{1} ie^{{ - i\omega_{10} T_{0} }} } \right) \\ & \quad - \varepsilon_{1} Z\left( {\omega_{20} A_{2} ie^{{i\omega_{20} T_{0} }} - \omega_{20} \overline{A}_{2} ie^{{ - i\omega_{20} T_{0} }} } \right) \\ & \quad + \varepsilon_{2} \left( {1 + \varepsilon_{1} } \right)\beta_{2}^{2} \left( {A_{3} e^{{i\omega_{30} T_{0} }} + \overline{A}_{3} e^{{ - i\omega_{30} T_{0} }} } \right) \\ & \quad + \varepsilon_{2} k_{2} \left( {A_{3} e^{{i\omega_{30} T_{0} }} + \overline{A}_{3} e^{{ - i\omega_{30} T_{0} }} } \right)^{3} \\ & \quad + 2\varepsilon_{2} \beta_{2} \varsigma_{2} \left( {\omega_{30} A_{3} ie^{{i\omega_{30} T_{0} }} - \omega_{30} \overline{A}_{3} ie^{{ - i\omega_{30} T_{0} }} } \right) \\ & \quad { + }\frac{{1 + \varepsilon_{1} }}{2R}Ae^{{i\omega^{*} T_{0} }} , \\ \end{aligned}$$
(31)
$$\begin{aligned} D_{0}^{2} x_{22} + \omega_{{_{20} }}^{{2}} x_{22} & = - 2\left( {\omega_{20} D_{1} A_{2} ie^{{i\omega_{20} T_{0} }} - \omega_{20} D_{1} \overline{A}_{2} ie^{{ - i\omega_{20} T_{0} }} } \right) \\ & \quad - \left( {A_{1} e^{{i\omega_{10} T_{0} }} + \overline{A}_{1} e^{{ - i\omega_{10} T_{0} }} } \right) - Z\left( {\omega_{10} A_{1} ie^{{i\omega_{10} T_{0} }} - \omega_{10} \overline{A}_{1} ie^{{ - i\omega_{10} T_{0} }} } \right) \\ & \quad - \left( {\varepsilon_{1} Z + 2\left( {1 + \varepsilon_{1} } \right)\beta_{1} \varsigma_{1} } \right)\left( {\omega_{20} iA_{2} e^{{i\omega_{20} T_{0} }} - \omega_{20} i\overline{A}_{2} e^{{ - i\omega_{20} T_{0} }} } \right) \\ & \quad + \varepsilon_{2} \left( {1 + \varepsilon_{1} } \right)\beta_{2}^{2} \left( {A_{3} e^{{i\omega_{30} T_{0} }} + \overline{A}_{3} e^{{ - i\omega_{30} T_{0} }} } \right) \\ & \quad + \varepsilon_{2} k_{2} \left( {A_{3} e^{{i\omega_{30} T_{0} }} + \overline{A}_{3} e^{{ - i\omega_{30} T_{0} }} } \right)^{3} \\ & \quad + 2\varepsilon_{2} \beta_{2} \varsigma_{2} \left( {\omega_{30} iA_{3} e^{{i\omega_{30} T_{0} }} - \omega_{30} i\overline{A}_{3} e^{{ - i\omega_{30} T_{0} }} } \right), \\ \end{aligned}$$
(32)
$$\begin{aligned} D_{0}^{2} x_{32} + \omega_{{_{30} }}^{{2}} x_{32} & = - 2\left( {\omega_{30} D_{1} A_{3} ie^{{i\omega_{30} T_{0} }} - \omega_{30} D_{1} \overline{A}_{3} ie^{{ - i\omega_{30} T_{0} }} } \right) \\ & \quad + \left( {A_{1} e^{{i\omega_{10} T_{0} }} + \overline{A}_{1} e^{{ - i\omega_{10} T_{0} }} } \right) \\ & \quad + \varepsilon_{1} \left( {1 + \left( {1 + \varepsilon_{1} } \right)\beta_{1}^{2} } \right)\left( {A_{2} e^{{i\omega_{20} T_{0} }} + \overline{A}_{2} e^{{ - i\omega_{20} T_{0} }} } \right) \\ & \quad - \left( {1 + \varepsilon_{2} } \right)k_{2} \left( {A_{3} e^{{i\omega_{30} T_{0} }} + \overline{A}_{3} e^{{ - i\omega_{30} T_{0} }} } \right)^{{3}} \\ & \quad + Z\left( {\omega_{10} A_{1} ie^{{i\omega_{10} T_{0} }} - \omega_{10} \overline{A}_{1} ie^{{ - i\omega_{10} T_{0} }} } \right) \\ & \quad + \varepsilon_{1} \left( {Z + 2\beta_{1} \varsigma_{1} } \right)\left( {\omega_{20} iA_{2} e^{{i\omega_{20} T_{0} }} - \omega_{20} i\overline{A}_{2} e^{{ - i\omega_{20} T_{0} }} } \right) \\ & \quad - 2\left( {1 + \varepsilon_{2} } \right)\beta_{2} \varsigma_{2} \left( {\omega_{30} iA_{3} e^{{i\omega_{30} T_{0} }} - \omega_{30} i\overline{A}_{3} e^{{ - i\omega_{30} T_{0} }} } \right). \\ \end{aligned}$$
(33)

In the following, we discuss the primary resonance with the frequency of external excitation approaches the main component, in other words, \(\omega^{*} = \omega_{10} + \varepsilon \sigma\), where \(\sigma\) is the nonlinear detuning parameter.

Case 1: when \(\omega_{20}\) and \(\omega_{30}\) are far from \(\omega_{10}\), substituting \(\omega^{*} = \omega_{10} + \varepsilon \sigma\) into the Eqs. (31–33) and eliminating the secular terms, the following equations are obtained:

$$- 2\omega_{10} D_{1} A_{1} i - Z\omega_{10} A_{1} i{ + }\frac{{1 + \varepsilon_{1} }}{2R}Ae^{{i\varepsilon \sigma T_{0} }} = 0,$$
(34)
$$- 2\omega_{20} D_{1} A_{2} i - \left( {\varepsilon_{1} Z + 2\left( {1 + \varepsilon_{1} } \right)\beta_{1} \varsigma_{1} } \right)\omega_{20} iA_{2} = 0,$$
(35)
$$- 2\omega_{30} D_{1} A_{3} i - 3\left( {1 + \varepsilon_{2} } \right)k_{2} A_{3}^{2} \overline{A}_{3} - 2\left( {1 + \varepsilon_{2} } \right)\beta_{2} \varsigma_{2} \omega_{30} iA_{3} = 0.$$
(36)

By assuming:

$$A_{1} = \frac{1}{2}a_{1} \left( {T_{1} } \right)e^{{i\varphi_{1} \left( {T_{1} } \right)}} ,\overline{A}_{1} = \frac{1}{2}a_{1} \left( {T_{1} } \right)e^{{ - i\varphi_{1} \left( {T_{1} } \right)}} ,$$
(37a)
$$A_{2} = \frac{1}{2}a_{2} \left( {T_{1} } \right)e^{{i\varphi_{2} \left( {T_{1} } \right)}} ,\overline{A}_{2} = \frac{1}{2}a_{2} \left( {T_{1} } \right)e^{{ - i\varphi_{2} \left( {T_{1} } \right)}} ,$$
(37b)
$$A_{3} = \frac{1}{2}a_{3} \left( {T_{1} } \right)e^{{i\varphi_{3} \left( {T_{1} } \right)}} ,\overline{A}_{3} = \frac{1}{2}a_{3} \left( {T_{1} } \right)e^{{ - i\varphi_{3} \left( {T_{1} } \right)}} ,$$
(37c)

and substituting it into (34–36), we have the result:

$$\dot{a}_{1} + a_{1} i\dot{\varphi }_{1} = - \frac{Z}{2}a_{1} - \frac{{i\left( {1 + \varepsilon_{1} } \right)A}}{{2R\omega_{10} }}\left( {\cos \left( {\sigma T_{1} - \varphi_{1} } \right) + i\sin \left( {\sigma T_{1} - \varphi_{1} } \right)} \right),$$
(38a)
$$\dot{a}_{2} + a_{2} i\dot{\varphi }_{2} = \frac{{\varepsilon_{1} Z + 2\left( {1 + \varepsilon_{1} } \right)\beta_{1} \varsigma_{1} }}{2}a_{2} ,$$
(38b)
$$\dot{a}_{3} + a_{3} i\dot{\varphi }_{3} = \frac{{3i\left( {1 + \varepsilon_{2} } \right)k_{2} a_{3}^{3} }}{{8\omega_{30} }} - \left( {1 + \varepsilon_{2} } \right)\beta_{2} \varsigma_{2} a_{3} .$$
(38c)

Let \(\theta_{1} = \sigma T_{1} - \varphi_{1}\), separating real and imaginary parts can be obtain:

$$\dot{a}_{1} = - \frac{Z}{2}a_{1} + \frac{{\left( {1 + \varepsilon_{1} } \right)A}}{{2R\omega_{10} }}\sin \theta_{1} ,$$
(39a)
$$\dot{a}_{1} \dot{\varphi }_{1} = - \frac{{\left( {1 + \varepsilon_{1} } \right)A}}{{2R\omega_{10} }}\cos \theta_{1} ,$$
(39b)
$$\dot{a}_{2} = \frac{{\varepsilon_{1} Z + 2\left( {1 + \varepsilon_{1} } \right)\beta_{1} \varsigma_{1} }}{2}a_{2} ,$$
(39c)
$$a_{2} \dot{\varphi }_{2} = 0,$$
(39d)
$$\dot{a}_{3} = - \left( {1 + \varepsilon_{2} } \right)\beta_{2} \varsigma_{2} a_{3} ,$$
(39e)
$$a_{3} \dot{\varphi }_{3} = \frac{{3\left( {1 + \varepsilon_{2} } \right)k_{2} a_{3}^{3} }}{{8\omega_{30} }}.$$
(39f)

In order to obtain a steady state solution, let \(\dot{a}_{1} = \dot{\theta }_{1} = \dot{a}_{2} = \dot{\varphi }_{2} = \dot{a}_{3} = \dot{\varphi }_{3} = 0\), we can obtained the Eq. (40) as follow:

$$\frac{{\left( {1 + \varepsilon_{1} } \right)^{2} A^{2} }}{{4R^{2} \omega_{10}^{2} }} = \frac{{Z^{2} a_{1}^{2} }}{4} + a_{1}^{2} \sigma^{2} .$$
(40)

Substituting Eqs. (34–36, 37) into Eqs. (31–33) and Eqs. (15–17), finally, the approximate solutions of the shock absorbers \(\overline{x}\), \(\overline{y}\), \(\overline{z}\) are obtained.

Case 2: when \(\omega_{20} = \omega_{10} + \varepsilon \sigma_{1}\) (\(\sigma_{1}\) is the nonlinear detuning parameter) and \(\omega_{30}\) is far from \(\omega_{10}\), substituting the expressions of \(\omega^{*}\) and \(\omega_{20}\) into the Eqs. (31–33) and eliminating the secular terms, one obtained:

$$- 2\omega_{10} D_{1} A_{1} i - \varepsilon_{1} A_{2} e^{{i\varepsilon \sigma_{1} T_{0} }} - Z\omega_{10} A_{1} i - \varepsilon_{1} {\text{Z}}\omega_{20} A_{2} ie^{{i\varepsilon \sigma_{1} T_{0} }} { + }\frac{{1 + \varepsilon_{1} }}{2R}Ae^{{i\varepsilon \sigma T_{0} }} = 0,$$
(41)
$$- 2\omega_{20} D_{1} A_{2} i - A_{1} e^{{ - i\varepsilon \sigma_{1} T_{0} }} - Z\omega_{10} A_{1} ie^{{ - i\varepsilon \sigma_{1} T_{0} }} - \left( {\varepsilon_{1} Z + 2\left( {1 + \varepsilon_{1} } \right)\beta_{1} \varsigma_{1} } \right)\omega_{20} iA_{2} = 0,$$
(42)
$$- 2\omega_{30} D_{1} A_{3} i - 3\left( {1 + \varepsilon_{2} } \right)k_{2} A_{3}^{2} \overline{A}_{3} - 2\left( {1 + \varepsilon_{2} } \right)\beta_{2} \varsigma_{2} \omega_{30} iA_{3} = 0.$$
(43)

Substituting (37) into (41–43), we have:

$$\begin{aligned} \dot{a}_{1} + a_{1} i\dot{\varphi }_{1} & = \frac{{i\varepsilon_{1} a_{2} }}{{2\omega_{10} }}\left( \begin{gathered} \cos \left( {\varphi_{2} - \varphi_{1} + \sigma_{1} T_{1} } \right) + \hfill \\ i\sin \left( {\varphi_{2} - \varphi_{1} + \sigma_{1} T_{1} } \right) \hfill \\ \end{gathered} \right) - \frac{Z}{2}a_{1} \\ & \quad - \frac{{\varepsilon_{1} Z\omega_{20} a_{2} }}{{2\omega_{10} }}\left( \begin{gathered} \cos \left( {\varphi_{2} - \varphi_{1} + \sigma_{1} T_{1} } \right) + \hfill \\ i\sin \left( {\varphi_{2} - \varphi_{1} + \sigma_{1} T_{1} } \right) \hfill \\ \end{gathered} \right) \\ & \quad - \frac{{\left( {1 + \varepsilon_{1} } \right)A}}{{2R\omega_{10} }}i\left( \begin{gathered} \cos \left( {\sigma T_{1} - \varphi_{1} } \right) + \hfill \\ i\sin \left( {\sigma T_{1} - \varphi_{1} } \right) \hfill \\ \end{gathered} \right), \\ \end{aligned}$$
(44a)
$$\begin{aligned} \dot{a}_{2} + a_{2} i\dot{\varphi }_{2} & = \frac{{ia_{1} }}{{2\omega_{20} }}\left( \begin{gathered} \cos \left( {\varphi_{2} - \varphi_{1} + \sigma_{1} T_{1} } \right) - \hfill \\ i\sin \left( {\varphi_{2} - \varphi_{1} + \sigma_{1} T_{1} } \right) \hfill \\ \end{gathered} \right) \\ & \quad - \frac{{Z\omega_{10} a_{1} }}{{2\omega_{20} }}\left( \begin{gathered} \cos \left( {\varphi_{2} - \varphi_{1} + \sigma_{1} T_{1} } \right) - \hfill \\ i\sin \left( {\varphi_{2} - \varphi_{1} + \sigma_{1} T_{1} } \right) \hfill \\ \end{gathered} \right) \\ & \quad - \frac{{\varepsilon_{1} Z + 2\left( {1 + \varepsilon_{1} } \right)\beta_{1} \varsigma_{1} }}{2}a_{2} , \\ \end{aligned}$$
(44b)
$$\dot{a}_{3} + a_{3} i\dot{\varphi }_{3} = \frac{{3i\left( {1 + \varepsilon_{2} } \right)k_{2} a_{3}^{3} }}{{8\omega_{30} }} - \left( {1 + \varepsilon_{2} } \right)\beta_{2} \varsigma_{2} a_{3} .$$
(44c)

Let \(\theta_{2} = \varphi_{2} - \varphi_{1} + \sigma_{1} T_{1}\), the calculation process is as in case 1, the frequency response equation of the steady-state solutions is obtained:

$$\left( {\frac{{a_{1} }}{{2\omega_{20} }}} \right)^{2} + \left( {\frac{{Z\omega_{10} }}{{2\omega_{20} }}a_{1} } \right)^{2} = \left( {\frac{{\varepsilon_{1} Z + 2\left( {1 + \varepsilon_{1} } \right)\beta_{1} \varsigma_{1} }}{2}a_{2} } \right)^{2} + a_{2}^{2} \left( {\sigma - \sigma_{1} } \right)^{2} .$$
(45)

Case 3: when \(\omega_{30} = \omega_{10} + \varepsilon \sigma_{2}\) (\(\sigma_{2}\) is the nonlinear detuning parameter) and \(\omega_{20}\) is far from \(\omega_{10}\), substituting the expressions of \(\omega^{*}\) and \(\omega_{30}\) into the Eqs. (31–33) and eliminating the secular terms, we have the result:

$$\begin{aligned} & - 2\omega_{10} D_{1} A_{1} i - Z\omega_{10} A_{1} i + \varepsilon_{2} \left( {1 + \varepsilon_{1} } \right)\beta_{2}^{2} A_{3} e^{{i\varepsilon \sigma_{2} T_{0} }} { + 3}\varepsilon_{2} k_{2} A_{3}^{2} \overline{A}_{3} e^{{i\varepsilon \sigma_{2} T_{0} }} \\ & \quad + 2\varepsilon_{2} \beta_{2} \varsigma_{2} \omega_{30} A_{3} ie^{{i\varepsilon \sigma_{2} T_{0} }} { + }\frac{{1 + \varepsilon_{1} }}{2R}Ae^{{i\varepsilon \sigma T_{0} }} = 0, \\ \end{aligned}$$
(46)
$$- 2\omega_{20} D_{1} A_{2} i - \left( {\varepsilon_{1} Z + 2\left( {1 + \varepsilon_{1} } \right)\beta_{1} \varsigma_{1} } \right)\omega_{20} iA_{2} = 0,$$
(47)
$$\begin{aligned} & - 2\omega_{30} D_{1} A_{3} i + A_{1} e^{{ - i\varepsilon \sigma_{2} T_{0} }} - 3\left( {1 + \varepsilon_{2} } \right)k_{2} A_{3}^{2} \overline{A}_{3} + Z\omega_{10} A_{1} ie^{{ - i\varepsilon \sigma_{2} T_{0} }} \\ & \quad - 2\left( {1 + \varepsilon_{2} } \right)\beta_{2} \varsigma_{2} \omega_{30} iA_{3} = 0. \\ \end{aligned}$$
(48)

Substituting (37) into (46–48), we have:

$$\begin{aligned} \dot{a}_{1} + a_{1} i\dot{\varphi }_{1} & = \frac{Z}{2}a_{1} - \frac{{i\varepsilon_{2} \left( {1 + \varepsilon_{1} } \right)\beta_{2}^{2} a_{3} }}{{2\omega_{10} }}\left( \begin{gathered} \cos \left( {\varphi_{3} - \varphi_{1} + \sigma_{2} T_{1} } \right) + \hfill \\ i\sin \left( {\varphi_{3} - \varphi_{1} + \sigma_{2} T_{1} } \right) \hfill \\ \end{gathered} \right) \\ & \quad - \frac{{i3\varepsilon_{2} k_{2} a_{3}^{3} }}{{8\omega_{10} }}\left( \begin{gathered} \cos \left( {\varphi_{3} - \varphi_{1} + \sigma_{2} T_{1} } \right) + \hfill \\ i\sin \left( {\varphi_{3} - \varphi_{1} + \sigma_{2} T_{1} } \right) \hfill \\ \end{gathered} \right) \\ & \quad + \frac{{\varepsilon_{2} \beta_{2} \varsigma_{2} \omega_{30} a_{3} }}{{\omega_{10} }}\left( \begin{gathered} \cos \left( {\varphi_{3} - \varphi_{1} + \sigma_{2} T_{1} } \right) + \hfill \\ i\sin \left( {\varphi_{3} - \varphi_{1} + \sigma_{2} T_{1} } \right) \hfill \\ \end{gathered} \right) \\ & \quad - \frac{{\left( {1 + \varepsilon_{1} } \right)A}}{{2R\omega_{10} }}i\left( \begin{gathered} \cos \left( {\sigma T_{1} - \varphi_{1} } \right) + \hfill \\ i\sin \left( {\sigma T_{1} - \varphi_{1} } \right) \hfill \\ \end{gathered} \right), \\ \end{aligned}$$
(49a)
$$\dot{a}_{2} + a_{2} i\dot{\varphi }_{2} = \frac{{\varepsilon_{1} Z + 2\left( {1 + \varepsilon_{1} } \right)\beta_{1} \varsigma_{1} }}{2}a_{2} ,$$
(49b)
$$\begin{aligned} \dot{a}_{3} + a_{3} i\dot{\varphi }_{3} & = - \frac{{ia_{1} }}{{2\omega_{30} }}\left( \begin{gathered} \cos \left( {\varphi_{3} - \varphi_{1} + \sigma_{2} T_{1} } \right) - \hfill \\ i\sin \left( {\varphi_{3} - \varphi_{1} + \sigma_{2} T_{1} } \right) \hfill \\ \end{gathered} \right) + \frac{{i3\left( {1 + \varepsilon_{2} } \right)k_{2} a_{3}^{3} }}{{8\omega_{30} }} \\ & \quad + \frac{{Z\omega_{10} a_{1} }}{{2\omega_{30} }}\left( \begin{gathered} \cos \left( {\varphi_{3} - \varphi_{1} + \sigma_{2} T_{1} } \right) - \hfill \\ i\sin \left( {\varphi_{3} - \varphi_{1} + \sigma_{2} T_{1} } \right) \hfill \\ \end{gathered} \right) - \left( {1 + \varepsilon_{2} } \right)\beta_{2} \varsigma_{2} a_{3} . \\ \end{aligned}$$
(49c)

Let \(\theta_{3} = \varphi_{3} - \varphi_{1} + \sigma_{2} T_{1}\), similarly, the frequency response equation of the steady-state solutions is obtained:

$$\left( {\frac{{a_{1} }}{{2\omega_{30} }}} \right)^{2} + \left( {\frac{{Z\omega_{10} }}{{2\omega_{30} }}a_{1} } \right)^{2} = \left( {\left( {1 + \varepsilon_{2} } \right)\beta_{2} \varsigma_{2} a_{3} } \right)^{2} + \left( {\frac{{3\left( {1 + \varepsilon_{2} } \right)k_{2} a_{3}^{3} }}{{8\omega_{30} }} + a_{3} \left( {\sigma - \sigma_{2} } \right)} \right)^{2} .$$
(50)

Repeat the same procedures for case 2 and 3, then, the approximate solutions of the shock absorbers \(\overline{x}\), \(\overline{y}\), \(\overline{z}\) are obtained.

Results and Discussion

In this section, numerical simulations are used to study the nonlinear vibration of electrostatically excited miniature shock absorbers based on 3 degrees of freedom model. The tank is made of an aluminum sheet with a thickness \(t_{w} = 1\;{\text{mm}}\) and mass density \(\rho = 2700\;{{{\text{kg}}} \mathord{\left/ {\vphantom {{{\text{kg}}} {{\text{m}}^{3} }}} \right. \kern-\nulldelimiterspace} {{\text{m}}^{3} }}\). In addition, the non-dimensionless parameter values are taken as \(Z = 3.7 \times 10^{ - 2}\) and \(k_{2} = 1\)[37]. In the following, the non-dimensionless parameter values are \(\varepsilon_{1} = 0.17\), \(\varepsilon_{2} = 0.01\), \(\beta_{1} = \beta_{2} = 0.1\), \(\sigma = \sigma_{1} { = }\sigma_{2} { = }0.1\), \(\varsigma_{1} { = }0.1\), \(\varsigma_{2} { = }0.001\) [37] when they are not listed specifically.

The relations among the amplitudes of main component and dampers are present in Figs. 2, 3 and 4 for case 1, case 2 and case 3 correspondingly. It can be observed that the main component amplitude \(\overline{x}\) is much smaller than those of the dampers \(\overline{y}\) and \(\overline{z}\). Obviously, the dampers absorb energy of system, which makes the amplitude of main component is reduced. From Fig. 3, It is clearly noted that when \(\omega^{*} = \omega_{10} + \varepsilon \sigma\) and \(\omega_{20} = \omega_{10} + \varepsilon \sigma_{1}\), the association of external and internal resonances causes the energy of the external excitation moves to the TMD, and the amplitude \(\overline{y}\) improves. From Fig. 4, we also get that the amplitude \(\overline{z}\) improves.

Fig. 2
figure 2

Diagram of amplitude relationship among main component and dampers for case 1

Full size image
Fig. 3
figure 3

Diagram of amplitude relationship among main component and dampers for case 2

Full size image
Fig. 4
figure 4

Diagram of amplitude relationship among main component and dampers for case 3

Full size image

To better show the damping effect of the dampers, the amplitude diagram of the main component under different dampers for case 1 is shown in Fig. 5. Obviously, with a damper, whether it is TMD or NES, the amplitude of the main component will be deskilled. Moreover, a combination of both can make a largely reduction. This indicates that TMD and /or NES play an important role in the shock absorption system.

Fig. 5
figure 5

Time response of main component amplitude for case 1

Full size image

Moreover, comparisons of the TMD mass ratio on the amplitude of the main component for case 2 and case 3 in Figs. 6 and 7 show that as the mass ratio increases, time response of main component amplitude is remarkably decreased. This indicates that the effect of TMD mass ratio on the amplitude of the main component is significant. Therefore, adjusting the mass ratio of the TMD can be used to reliably control the vibration characteristics of the system. The results in this paper accord well with those in Ref. [38].

Fig. 6
figure 6

Time response of main component amplitude with different TMD mass ratio for case 1

Full size image
Fig. 7
figure 7

Time response of main component amplitude with different TMD mass ratio for case 2

Full size image

We now turn our attention to the influence of the TMD damping ratio on the system amplitude as shown in Fig. 8. Studies have shown that as the damping ratio increases, the amplitude of the system decreases mostly, and at some point, the situation is just the opposite which is agreement with Ref. [38].

Fig. 8
figure 8

Time response of main component amplitude with different TMD damping ratio for case 2

Full size image

To clear how the amplitude varies with the different values of NES mass ratio, the case 3 are plotted in Fig. 9. Clearly, the larger the mass ratio is, the lower amplitude of the main component is, which is consistent with that of the TMD.

Fig. 9
figure 9

Time response of main component amplitude with different NES mass ratio for case 3

Full size image

In addition, Fig. 10 shows variation of main component amplitude of system with different NES damping ratio. It is clear from Fig. 10 that the component amplitude decreases as the NES damping ratio coefficient increases, which is consistent with that of the TMD.

Fig. 10
figure 10

Time response of main component amplitude with different NES damping ratio for case 3

Full size image

Finally, the results in Figs. 2, 3, 4, 5, 6, 7, 8, 9 and 10 reveal that the amplitudes of main component and dampers may be in the same or the opposite direction as the parameter values vary.

Conclusion

To study the dynamic characteristics of the miniature shock absorber, the 3 DOF nonlinear forced vibration equations are established by Hamiltonian variational principle. A numerical approximate solution is obtained using a multiscale method. The main results of the study may be listed as:

  • TMD and/or NES play an important role in the shock absorption system which can kill the amplitude of the main component magically.

  • The vibration amplitude of the main components can be largely decreased by increasing the mass ratio and damping ratio of TMD and NES.

  • The association of external and internal resonances causes the energy of the external excitation moves to the TMD or NES, thus reducing the amplitude of main component.

  • The amplitudes of main component and dampers may be in the same or opposite direction by adjusting the parameter values.

It is hoped that the nonlinear vibration presented herein will be useful for research work on micro shock absorbers.