Introduction

The membrane is widely used in building structures. As its weight, thickness and stiffness are less, the sensitivity of the membrane structure to external excitation is great. Under the external excitation, the vibration amplitude of the membrane structure is much larger than its thickness, which makes the vibration problem of membrane structures have strongly geometric nonlinearity. Meanwhile, the membrane materials used in construction field are woven by fibres in the two orthogonal directions. Its elastic modulus in two orthogonal directions is different compared with that of isotropic materials, which means the membranes are orthotropic [1,2,3,4].

In recent years, a large number of studies on the dynamic problems of membranes have been performed. Pan and Gu [5, 6] established the discrete square tensioned membrane's nonlinear vibration equations using D'Alembert's principle, and deduced the free oscillating system's equivalent fundamental frequency. The effects of membrane's prestrain, size, elastic ratio, density, relative amplitude and dead load of square tensioned membrane on the structure's nonlinearity were also studied. Zheng et al. [7] obtained the governing equations of orthotropic membrane using the large deflection theory, and got the power series formula of nonlinear vibration frequency of a rectangular membrane with four edges fixed. Liu et al. [8] took an orthotropic membrane with four edges fixed as the research object, got the approximate solution of the frequency of nonlinear vibration of the membrane and its displacement function by employing the L–P perturbation method. Liu et al. [9] calculated the frequency of the nonlinear vibration of a simply supported rectangular membrane using the assumed mode method and the finite element method, and compared the two methods. The results indicated that the natural frequency obtained by the finite element method is larger than that obtained by the assumed mode method. Li et al. [10] proposed the modified multi-scale method based on the traditional multi-scale method, and used this method to solve the approximate solution of the strong nonlinear vibration frequency and displacement of clamped membrane structures. The method was verified by experiments. Lu et al. [11] gave the approximate solution and theoretical solution of the nonlinear frequency of the membrane during the study of the nonlinear vibration control of membrane structures. Song et al. [12] solved the strongly nonlinear vibration of orthotropic membrane using the improved multi-scale method. The results showed that its accuracy is higher than that of the traditional perturbation methods. Zhang [13, 14] calculated the vibration frequencies of rectangular membrane and strip membrane when studying the equivalent principle of them. Although there are many reports in the literature on the outcome of vibration of the membrane, most are restricted to the small deflection theory and traditional perturbation method, which is not suitable for large amplitude vibration of the membrane. When the amplitude of the membrane increases to a certain extent, the strong nonlinearity of the membrane emerges, and the error of the calculation results of these previous methods exceeds the allowable range of engineering, which cannot be used. Meanwhile, some scholars assumed that the membrane is an isotropic material, which ignored the influence of the orthogonal anisotropy of the membrane on its dynamic characteristics to facilitate the calculation.

In view of the limitations of the traditional perturbation method, He [14,15,16,17] proposed the homotopy perturbation method. It has been proved that it is applicable to strongly nonlinear vibration problems by applied in many actual engineering problems. Ganji et al. [18] applied the homotopy perturbation method to solve nonlinear partial differential equations of fractional orders. Andrianov et al. [19] proposed an analytical solution of the problem of free in-plane vibration of rectangular plates with complicated boundary conditions using the homotopy perturbation method. Shakeri and Dehghan [20] presented the solution of a delay differential equation by means of the homotopy perturbation method and listed some numerical illustrations. Ozturk et al. [21] applied the homotopy perturbation method for free vibration analysis of a beam with an elastic foundation. Liu et al. [22] investigated the geometric nonlinear vibrations of pretensioned orthotropic membrane with four edges fixed via the homotopy perturbation. However, its solution that has to be squared twice is too complex to use.

In this paper, the strongly nonlinear vibration of the orthotropic membrane under displacement excitation is investigated using the homotopy perturbation method and the improved homotopy perturbation method, respectively. The results compared with other traditional perturbation methods are also shown. The results reveal that the improved homotopy perturbation method has an amount of capability to apply in strongly nonlinear vibration of orthotropic membranes. The form of the solution is simpler and more convenient to use in engineering. In addition, the dynamic characteristics of membrane structures are also studied parametrically. This research is beneficial to the vibration control and dynamic design of membrane structures.

Solution of Nonlinear Transverse Vibration of Orthotropic Membrane

Governing Equations

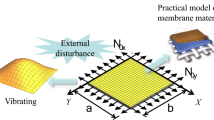
The cross section of a membrane is shown in Fig. 1. The length and width of the shown cross section in the main directions of the coordinates x and y are indicated with two parameters a and b, respectively. The initial tensile stresses in the main directions of the coordinates x and y are N0x and N0y, respectively.

Fig. 1
figure 1

Rectangle membrane with four edges simply supported

Full size image

According to the Von Karman large deflection theory and D’Alembert’s principle, the vibration partial differential equations for strongly nonlinear vibration of orthotropic membranes will be

$$\frac{\rho }{h}\frac{{\partial^{2} {\text{w}}}}{{\partial t^{2} }} - \left( {\sigma_{0x} + \frac{{\partial^{2} \varphi }}{{\partial y^{2} }}} \right)\frac{{\partial^{2} {\text{w}}}}{{\partial {\text{x}}^{2} }} - \left( {\sigma_{0y} + \frac{{\partial^{2} \varphi }}{{\partial x^{2} }}} \right)\frac{{\partial^{2} {\text{w}}}}{{\partial y^{2} }} = 0,$$
(1)
$$\frac{1}{{E_{1} }}\frac{{\partial^{4} \varphi }}{{\partial y^{4} }} + \frac{1}{{E_{2} }}\frac{{\partial^{4} \varphi }}{{\partial x^{4} }} = (\frac{{\partial^{2} {\text{w}}}}{{\partial {\text{x}}\partial y}}) - \frac{{\partial^{2} {\text{w}}}}{{\partial {\text{x}}^{2} }}\frac{{\partial^{2} {\text{w}}}}{{\partial y^{2} }},$$
(2)

where ρ is aerial density of membrane. h denotes membrane thickness. E1 and E2 suggest the Young’s modulus in the X and Y directions, respectively. σ0x and σ0y represent the normal stress in the X and Y directions, respectively. φ = φ(x,y,t) denotes the stress function, and w = w(x,y,t) denotes deflection.

The corresponding boundary conditions of a rectangle membrane with four immovable edges simply supported are as follows [23]:

$$\left\{ \begin{gathered} w\left( {0,y,t} \right) = w\left( {a,y,t} \right) = w\left( {x,0,t} \right) = w\left( {x,b,t} \right) = 0 \hfill \\ \frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {a,y,t} \right) = \frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {0,y,t} \right) = \frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {x,0,t} \right) = \frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {x,b,t} \right) = 0 \hfill \\ \end{gathered} \right.$$
(3)
$$\left\{ \begin{gathered} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }}\left( {0,y,t} \right) = \frac{{\partial^{2} \varphi }}{{\partial y^{2} }}\left( {x,0,t} \right) = 0,\;\;\;\frac{{\partial^{2} \varphi }}{{\partial x^{2} }}\left( {a,y,t} \right) = 0,\frac{{\partial^{2} \varphi }}{{\partial y^{2} }}\left( {x,b,t} \right) = 0 \hfill \\ \frac{{\partial^{2} \varphi }}{{\partial x^{2} }}\left( {x,0,t} \right) = 0,\frac{{\partial^{2} \varphi }}{{\partial y^{2} }}\left( {0,y,t} \right) = 0, \frac{{\partial^{2} \varphi }}{{\partial x^{2} }}\left( {x,b,t} \right) = 0,\frac{{\partial^{2} \varphi }}{{\partial y^{2} }}\left( {a,y,t} \right) = 0 \hfill \\ \end{gathered} \right.$$
(4)

Functions that satisfy the boundary conditions (3) and (4) are expressed as follows:

$$w(x,y,t) = u_{mn} (t)W_{mn} (x,y),$$
(5)
$$\varphi (x,y,t) = u^{2}_{mn} (t)\Phi_{mn} (x,y),$$
(6)

where Wmn(x,y) is the mode shape function, φ(x,y,t), umn(t) and Φ(x,y) are the unknown functions.

By assuming the mode function is an orthogonal trigonometric function [24], then

$$W_{mn} (x,y) = \sin \frac{m\pi x}{a}\sin \frac{n\pi y}{b},$$
(7)

where m and n are positive integers, which denote the sinusoid half wave number.

By substituting Eqs. (5), (6) and (7) into (2), yields:

$$\frac{1}{{E_{1} }}\frac{{\partial^{4} \Phi }}{{\partial y^{4} }} + \frac{1}{{E_{2} }}\frac{{\partial^{4} \Phi }}{{\partial x^{4} }} = \frac{{m^{2} n^{2} \pi^{4} }}{{2a^{2} b^{2} }}\left(\cos \frac{2m\pi x}{a} + \cos \frac{2n\pi y}{b}\right).$$
(8)

The form of the construction solution of Eq. (8) can be assumed as

$$\Phi (x,y) = \alpha \cos \frac{2m\pi x}{a} + \beta \cos \frac{2n\pi y}{b} + \gamma_{1} x^{3} + \gamma_{2} x^{2} + \gamma_{3} y^{3} + \gamma_{4} y^{2} .$$
(9)

By substituting Eq. (9) into (8) and (4), yields

$$\Phi (x,y) = \left(\frac{{E_{2} n^{2} a^{2} }}{{32m^{2} b^{2} }}\cos \frac{2m\pi x}{a} + \frac{{E_{1} m^{2} b^{2} }}{{32n^{2} a^{2} }}\cos \frac{2n\pi y}{b} + \frac{{E_{2} n^{2} \pi^{2} }}{{16b^{2} }}x^{2} + \frac{{E_{1} m^{2} \pi^{2} }}{{16a^{2} }}y^{2} \right)u^{2} \left(t\right).$$
(10)

Substituting Eqs. (5), (6) and (10) into (1) and simplified, we gain Eq. (11) by the Galerkin method:

$$\frac{{d^{2} u(t)}}{{dt^{2} }} + \lambda u(t) + \varepsilon u^{3} (t) = 0,$$
(11)

where

$$\lambda = \frac{{h\pi^{2} }}{\rho }\left(\frac{{m^{2} }}{{a^{2} }}\sigma_{0x} + \frac{{n^{2} }}{{b^{2} }}\sigma_{0y} \right),$$
$$\varepsilon = \frac{{3h\pi^{4} }}{16\rho }\left(\frac{{E_{1} m^{4} }}{{a^{4} }} + \frac{{E_{2} n^{4} }}{{b^{4} }}\right).$$

Take the ZZF membrane as an illustration, which commonly used in China, its aerial density is 0.95 kg/m2; the thickness is 0.72 mm, the Young’s modulus in the X and Y directions are E1 = 1590 MPa, E2 = 1360 MPa, respectively; the length and width of the membrane are a = 5 m, b = 5 m, respectively.

Substituting those parameters into the nonlinear term in Eq. (11), we gain the following results:

$$\varepsilon = \frac{{3h\pi^{4} }}{16\rho }\left(\frac{{E_{1} m^{4} }}{{a^{4} }} + \frac{{E_{2} n^{4} }}{{b^{4} }}\right) = \frac{291.64 \times 0.72}{{16 \times 0.95}} \times \left( {\frac{1590}{{625}} + \frac{1360}{{625}}} \right) = 65.20 \gg 1.$$

The formula shows that the coefficient of the nonlinear term in Eq. (11) is much larger than 1. It is easy to see that Eq. (11) is a strongly nonlinear differential equation with respect to u(t).

At the initial moment, the out-of-plane displacement of the membrane surface is 0. The membrane surface begins to vibrate under the displacement excitation after an initial displacement is applied to the center point of the membrane surface as shown in Fig. 2. The following initial conditions can be applied.

$$u(0) = a_{0} ,u^{\prime}(t) = 0.$$
(12)
Fig. 2
figure 2

Initial condition of membrane’s vibration

Full size image

In reference [11], Lu has given the power series frequency solution of the strongly nonlinear vibration of the orthotropic membrane with large amplitude as follows:

$$\omega = \frac{{\sqrt {\lambda + (\varepsilon /2){\text{a}}_{0}^{2} } }}{{\sum\limits_{{{\text{p}} = 0}}^{\infty } {\left( { - 1} \right)^{{\text{p}}} \left[ {\frac{{\left( {2{\text{p}} - 1} \right)!!}}{(2p)!!}} \right]^{2} \left( {\frac{{\varepsilon a_{0}^{2} }}{{2\lambda + \varepsilon a_{0}^{2} }}} \right)^{P} } }}.$$
(13)

The Homotopy Perturbation Solution for Vibration Governing Equations

According to the homotopy perturbation method, we obtain:

$$L(v) - L(u_{0} ) + pL(u_{0} ) + p\varepsilon v^{3} = 0,$$
(14)

where \(L(u) = \frac{{d^{2} u}}{{dt^{2} }} + \lambda u.\)

The solution of formula (11) can be rewritten as follows:

$$v(t) = v_{0} (t) + pv_{1} (t) + p^{2} v_{2} (t) + \ldots \ldots$$
(15)

By substituting Eq. (15) into (14) and comparing the coefficients of p1 and p2, yields

$$L(v_{0} ) - L(u_{0} ) = 0,v_{0} (0) = {\text{a}}_{0} ,{\text{v}}_{0} ^{\prime}(0) = 0,$$
(16)
$$L(v_{1} ) + L(u_{0} ) + \varepsilon v_{0}^{3} = 0,v_{1} \left( 0 \right) = {\text{v}}_{0} ^{\prime}(0) = 0.$$
(17)

By assuming the solution of formula (16), yields

$$u_{0} (t) = a_{0} \cos \sqrt \lambda \alpha t.$$
(18)

From Eqs. (16), (17) and (18), we can obtain

$$v_{0} (t) = u_{0} (t) = a_{0} \cos \sqrt \lambda \alpha t,$$
(19)
$$\frac{{dv_{1} }}{dt} + \lambda v_{1} + a_{0} (\lambda - \lambda \alpha^{2} + \frac{3}{4}\varepsilon a_{0}^{2} )\cos \sqrt \lambda \alpha t + \frac{3}{4}\varepsilon a_{0}^{3} \cos \sqrt \lambda \alpha t = 0.$$
(20)

Obviously, Eq. (20) is a linear differential equation, and its solution is

$$\begin{gathered} v_{1} = (\lambda - \lambda \alpha^{2} + \frac{3}{4}\varepsilon a_{0}^{2} )\frac{{a_{0} }}{{\lambda (\alpha^{2} - 1)}}(\cos \sqrt \lambda \alpha t - \cos \sqrt \lambda t) \\ + \frac{{\varepsilon a_{0}^{3} }}{{4\lambda (9\alpha^{2} - 1)}}(\cos 3\sqrt \lambda \alpha t - \cos \sqrt \lambda t). \\ \end{gathered}$$
(21)

Here we set the coefficient of \(\cos \sqrt \lambda t\) to zero to eliminate the secular term which may occur in the next iteration

$$- (\lambda - \lambda \alpha^{2} + \frac{3}{4}\varepsilon a_{0}^{2} )\frac{{a_{0} }}{{\lambda (\alpha^{2} - 1)}} - \frac{{\varepsilon a_{0}^{3} }}{{4\lambda (9\alpha^{2} - 1)}} = 0.$$
(22)

We can get

$$\alpha = \sqrt {\frac{{10\lambda + 7\varepsilon a_{0}^{2} + \sqrt {64\lambda^{2} + 104\lambda \varepsilon a_{0}^{2} + 49\varepsilon^{2} a_{0}^{4} } }}{18\lambda }} .$$
(23)

Thus, the homotopy perturbation ((hereinafter, HPM for short)) solution of the vibration frequency of the membrane can be obtained as

$$\omega = \sqrt \lambda \alpha = \sqrt {\frac{{10\lambda + 7\varepsilon a_{0}^{2} + \sqrt {64\lambda^{2} + 104\lambda \varepsilon a_{0}^{2} + 49\varepsilon^{2} a_{0}^{4} } }}{18}} .$$
(24)

The Improved Homotopy Perturbation Solution for Vibration Governing Equations

We construct a homotopy as follows for Eq. (11):

$$\frac{{d^{2} u(t)}}{{dt^{2} }} + \lambda u(t) + p\varepsilon u^{3} (t) = 0,$$
(25)

where p ∈ (0,1), when p = 0, Eq. (25) is a linear differential equation; when p = 1, Eq. (25) is equal to Eq. (11).

Then we expand u(t) and λ into a power series [25]:

$$u(t) = u_{0} (t) + pu_{1} (t) + p^{2} u_{2} (t) + \cdots \cdots$$
(26)
$$\lambda = \omega^{2} + \omega_{1} p + \omega_{2} p^{2} + \cdots \cdots$$
(27)

Substituting Eq. (26) into (27) and comparing the coefficients of p1 and p2, yields

$$u_{0} ^{\prime\prime} + \omega^{2} u_{0} = 0,u(0) = a_{0} ,u^{\prime}(0) = 0,$$
(28)
$$u_{1} ^{\prime\prime} + \omega u_{1} + \omega_{1} u_{0} + \varepsilon u_{0}^{3} = 0,u_{1} = a_{0} ,u_{1} ^{\prime}(0) = 0.$$
(29)

We assume the initial approximation of Eq. (28) has the form

$$u_{0} = a_{0} \cos \omega t.$$
(30)

Substituting Eq. (30) into (29), yields

$$u_{1} ^{\prime\prime} + \omega u_{1} + \omega_{1} a_{0} \cos \omega t + \frac{{\varepsilon a_{0}^{2} }}{4}(\cos 3\omega t + 3\cos \omega t) = 0.$$
(31)

Setting the coefficient of \(\cos \sqrt \lambda t\) to zero to eliminate the secular term, we can get

$$\omega_{1} = - \frac{{3\varepsilon a_{0}^{2} }}{4}.$$
(32)

Omitting the higher order term, we can get from Eq. (27)

$$\lambda = \omega^{2} + \omega_{1} .$$
(33)

From Eqs. (32) and (33), we can obtain

$$\omega = \sqrt {\lambda + \frac{{3\varepsilon a_{0}^{2} }}{4}} .$$
(34)

It is the improved homotopy perturbation (hereinafter, IHPM for short) solution of the vibration frequency for strongly nonlinear vibration of orthotropic membranes.

Example Analysis

To verify the strength of the improved homotopy perturbation method, the orthotropic membrane applied in engineering is investigated. Simplified sketch is shown in Fig. 1. Its material properties under consideration are the aerial density is ρ = 1.7 kg/m2; the thickness is h = 1.0 mm; the pretension is σ0x = σ0y = 5 × 103 KN/m2, the length and width are a = 1 m and b = 1 m; the Young’s modulus in the X and Y directions are E1 = 1.4 × 106 KN/m2 and E2 = 0.9 × 106 KN/m2.

Comparison with the Two Power Series Solutions

In reference [7], Zheng has given the power series solution of nonlinear vibration of prestressed orthotropic membranes as follows:

$$\omega = \frac{{\sqrt {M + (N/2){\text{a}}_{0}^{2} } }}{{\sum\limits_{{{\text{p}} = 0}}^{\infty } {( - 1)^{{\text{p}}} \left[ {\frac{{(2{\text{p}} - 1)!!}}{(2p)!!}} \right]^{2} \left( {\frac{{Na_{0}^{2} }}{{2M + Na_{0}^{2} }}} \right)^{P} } }},$$
(35)

where \(M = \frac{{h\pi^{2} }}{\rho }\left( {\frac{{m^{2} }}{{a^{2} }}\sigma_{0x} + \frac{{n^{2} }}{{b^{2} }}\sigma_{0y} } \right)\),\(N = \frac{{h\pi^{4} }}{16\rho }\left( {\frac{{E_{1} m^{4} }}{{a^{4} }} + \frac{{E_{2} n^{4} }}{{b^{4} }}} \right).\)

The formula of the vibration of rectangular orthotropic membranes in small deflection (hereinafter, SL for short) is

$$\omega = \pi \sqrt {\frac{{\text{h}}}{\rho }} .\sqrt {\frac{{\sigma_{0x} {\text{m}}^{2} }}{{{\text{a}}^{2} }} + \frac{{\sigma_{{0{\text{y}}}} {\text{n}}^{2} }}{{{\text{b}}^{2} }}} .$$
(36)

The first-order frequencies of the membranes under different displacement excitations are obtained by Eqs. (13) and (35), which are listed in Table 1. The results are also illustrated in Fig. 3.

Table 1 Series solution of vibration frequency of the membranes under different displacement excitations
Full size table
Fig. 3
figure 3

Series solution of vibration frequency of the membranes under different displacement excitations

Full size image

As it can be seen, the frequency grows with the displacement excitation increasing. The frequency of Lu’s method grows faster than that of Zheng’s method. The difference between Lu’s method and Zheng’s method is minuscule when the displacement excitation is small. When the displacement excitation grows, Zheng’s method displays a profound error. The reason leading to the phenomenon will be talked about. In reference [7], Zheng assumed the stress function as follows:

$$\Phi (x,y) = \alpha \cos \frac{2m\pi x}{a} + \beta \cos \frac{2n\pi y}{b}.$$

Compared with Eq. (9), this function has not the polynomial terms of x and y. It leads to the coefficient of the nonlinear term of the governing equations is different, which means that ε is 3 times as much as N. Thus, the solution of Zheng’s method is closer to the solution of small deflection theory. The lack of polynomials of x and y weakens the nonlinearity of Zheng’s method and enhances its linearity. Because formula (13) is more accurate than formula (35) in theory, this paper will discuss formula (13) as the theoretical solution.

Comparisons with Other Methods

The results of Eqs. (24), (34) and the L–P perturbation method solution are compared in this section for verifying the improved homotopy perturbation method. In reference [8], Liu has given the L–P perturbation method solution of nonlinear vibration of a prestressed orthotropic membrane with large amplitude as follows:

$$\omega = \sqrt \lambda + \frac{{3\varepsilon a_{0}^{2} }}{8\sqrt \lambda }.$$
(37)

It should be noted in particular that the coefficients of the nonlinear term governing equation of the membrane are the same as reference [7], which is smaller. Herein, the coefficients in formula (11) are used in this equation.

The frequencies of the membrane under different displacement excitations and orders obtained by various methods are displayed in Table 2, and the curves are also shown in Fig. 4.

Table 2 The results calculated by various methods
Full size table
Fig. 4
figure 4

Vibration frequencies of the membranes under different displacement excitations

Full size image

As shown in Table 2, the results calculated by various methods are almost same as the results obtained by the small deflection theory when the displacement excitation is close to 0. With the displacement excitation increasing, the frequency grows and the high-order frequency grows faster than low-order frequency. However, the results obtained by the small deflection theory do not change with displacement excitation. The reasons for this situation are also discussed. From the view of formula construction, the formulas obtained by large deflection theory include pretension and displacement excitation, that is, the results obtained by large deflection theory are influenced by pretension and displacement excitation, while the formula obtained by small deflection theory only contains pretension, which is not affected by displacement excitation. From the view of theory, the large deflection theory takes into account the strong nonlinearity of the membrane. The displacement excitation of the membrane affects the internal stress of the membrane. The greater the displacement excitation, the greater the internal stress of the membrane, the higher lateral stiffness of the membrane and the higher the vibration frequency. However, the small deflection theory ignores the nonlinearity of the membrane. No matter how the displacement excitation changes, the internal stress of the membrane is equal to the initial pretension, so the frequency of the small deflection formula is only related to the pretension, but not to the displacement excitation. This confirms that the strong nonlinearity of the membrane cannot be ignored in practical engineering.

It can be seen that the frequency increases with the order growing from Table 2. It is worth noting that when m = 1, n = 2 and m = 2, n = 1, the frequency calculated by the small deflection formula is the same, while the frequency calculated by the large deflection formula is different. m and n represent the half wave numbers of displacement functions in X and Y directions of the membrane, respectively. In the small deflection formula, the positions of m and n are symmetrical, and the participation degree in calculation is the same. In the large deflection formula, m and n have different weights. This proves that the influence of orthogonal anisotropy of the membrane on its mechanical properties cannot be ignored. This is also the reason for the different calculation results after exchange m and n.

It can be seen that the results obtained by HPM and IHPM are almost same as the theoretical solution from Fig. 4. What’s more, the discrepancy between L–P solution and the theoretical solution grows with the increase of the order and displacement excitation. L–P method cannot get rid of the boundedness that the traditional perturbation methods can only be applied to weakly nonlinear equations. When the displacement excitation is small, the L–P solution is close to the theoretical solution and it can be the approximate solution of frequency of the membrane under displacement excitation. However, the errors between the L–P solution and the theoretical solution become vast when the displacement excitation increases and the vibration of the membrane displays strong geometrically nonlinearity. It is out of the accepted field in engineering. In view of the limitation of the traditional perturbation methods, He proposed the homotopy perturbation method [14,15,16,17]. The adaptability to strongly nonlinear problems of this method is strong. It can be observed that the homotopy solution is almost the same as the theoretical solution and its accuracy is better than L–P method. Moreover, there is a minuscule amount of discrepancy between the improved homotopy solution and the theoretical solution. It is closer to the theoretical solution than the homotopy solution.

One can observe that the improved homotopy solution is always a bit bigger than the theoretical solution. And the difference between the improved homotopy solution and the theoretical solution increases with the increase of the displacement excitation. To demonstrate the accuracy of the improved homotopy perturbation method, set a0 → ∞, and the error between the improved homotopy solution and the theoretical solution is as follows:

$$\mathop {\lim }\limits_{{a_{0} \to \infty }} 1 - \frac{{\frac{{\sqrt {\lambda + (\varepsilon /2){\text{a}}_{0}^{2} } }}{{\sum\limits_{{{\text{p}} = 0}}^{\infty } {\left( { - 1} \right)^{{\text{p}}} \left[ {\frac{{\left( {2{\text{p}} - 1} \right)!!}}{(2p)!!}} \right]^{2} \left( {\frac{{\varepsilon a_{0}^{2} }}{{2\lambda + \varepsilon a_{0}^{2} }}} \right)^{P} } }}}}{{\sqrt {\lambda + \frac{{3\varepsilon a_{0}^{2} }}{4}} }} = 2.54\% .$$
(38)

It shows that the maximum error between the improved homotopy solution and the theoretical solution is not more than 2.54%. Thus, the strength of the improved homotopy perturbation method is meeting the demand of the engineering. The solution obtained by the improved homotopy perturbation method can be the approximate solution of frequency of the membrane under displacement excitation.

From the results obtained, the improved homotopy perturbation method has an amount of capacity to apply in the nonlinear vibration of orthotropic membrane. It may have the potential to apply in other nonlinear systems such as shell.

Parametric Study

The size, the pretension, the thickness, the Young’s modulus and the aerial density of the membrane have leverage on the nonlinear vibration of orthotropic membrane. The effect of those parameters on the vibration of the membrane under different displacement excitations is analyzed in this section. The results are obtained by the improved homotopy perturbation method.

Impact of Membrane Size

To analyze the impact of membrane size, three cases have investigated: 1. the length and width of the membrane increase together; 2. at fixed the length a = 1 m, the width b is set to vary from 1 to 5 m; 3. at fixed b = 1 m, a gain from 1 to 5 m. The other parameters are taken as follows: E1 = 1.4 × 106 KN/m2, E2 = 0.9 × 106 KN/m2, ρ = 1.7 kg/m2, h = 1.0 mm, σ0x = σ0y = 5 × 103 KN/m2. The results are shown in Fig. 5.

Fig. 5
figure 5

Frequency of the membrane under different displacement excitations with different membrane sizes

Full size image

As shown in Fig. 5, the frequency decreases with the hike of membrane size under the same displacement excitation. Frequency grows with the increase of the displacement excitation. However, the enhancement effect on the frequency of the membrane declines with the escalation of membrane size. It is noteworthy that the frequency of a = 1 and b = 2 and the frequency of a = 2 and b = 1 is not same. This also exists in other condition that a and b exchange. The reason resulting in the situation may be the orthogonal anisotropy of the membrane. If the orthogonal anisotropy of the membrane is ignored, it is considered isotropic. Then the frequency of the membrane surface is the same after exchanging a and b. This once proved that the orthogonal anisotropy of the membrane cannot be ignored.

Impact of Membrane Thickness

To study the effect of thickness of the membrane on the vibration of the membrane under different displacement excitations, the frequencies of the membrane with different thicknesses are calculated. The thickness of the membrane varies from 1 to 5 mm. The other parameters include E1 = 1.4 × 106 KN/m2, E2 = 0.9 × 106 KN/m2, ρ = 1.7 kg/m2, a = 1.0 m and b = 1 m, σ0x = σ0y = 5 × 103 KN/m2. The results are displayed in Fig. 6.

Fig. 6
figure 6

Frequency of the membrane under different displacement excitations with different thickness

Full size image

It can be seen that the frequency escalates with the hike of the thickness of the membrane under the same displacement excitation. The frequency grows nonlinearly with the displacement excitation gain.

Impact of Aerial Density

To research the effect of the aerial density of the membrane on the vibration of the membrane under different displacement excitations, the frequencies of the membrane with different aerial densities are calculated. The aerial density of the membrane changes from 1.6 to 2.0 kg/m2. The other parameters include E1 = 1.4 × 106 KN/m2, E2 = 0.9 × 106 KN/m2, a = 1.0 m and b = 1.0 m, σ0x = σ0y = 5 × 103 KN/m2. The results are shown in Fig. 7

Fig. 7
figure 7

Frequency of the membrane under different displacement excitation with different aerial densities

Full size image

As it can be seen, the frequency reduces with the escalation of the thickness of the membrane under the same displacement excitation. The frequency grows nonlinearly with the displacement excitation gain.

Impact of Pretension

To investigate the effect of the pretension of the membrane on the vibration of the membrane under different displacement excitations, the frequencies of the membrane with different pretension are calculated. The pretensions of the membrane are σ0x = σ0y = 1 KN/m2, 2 KN/m2, 3 KN/m2, 4 KN/m2, 5 KN/m2. The other parameters include E1 = 1.4 × 106 KN/m2, E2 = 0.9 × 106 KN/m2, a = 1.0 m and b = 1.0 m, h = 1 mm, ρ = 1.7 kg/m2. The results are shown in Fig. 8

Fig. 8
figure 8

Frequency of the membrane under different displacement excitation with different pretensions

Full size image

According to Fig. 8, the frequency increases with the escalation of the pretension of the membrane under the same displacement excitation. The discrepancy between frequencies with different pretension of the membrane decreases with the displacement excitation gain. The reason resulting in this condition may be that the increase of the pretension of the membrane enhances the lateral stiffness of the membrane. When the displacement excitation is large, the effect of the pretension on the lateral stiffness of the membrane becomes smaller with the comparison of the impact of the displacement excitation on the lateral stiffness of the membrane.

Impact of Young’s Modulus

To investigate the effect of the Young’s modulus of the membrane on the vibration of the membrane under different displacement excitations, the frequencies of the membrane with different pretension are calculated. This is a change in the ratio of E1 and E2. When E1 > E2, set E2 = 0.9 × 106 KN/m2, when E1 < E2, set E1 = 0.9 × 106 KN/m2. The other parameters are a = 1.0 m and b = 1.0 m, h = 1 mm, ρ = 1.7 kg/m2, σ0x = σ0y = 1 KN/m2. The results are shown in Fig. 9

Fig. 9
figure 9

Frequency of the membrane with different Young’s modulus and ao = 0.1 m

Full size image

When E1 > E2, the frequency of the membrane decreases with the decline of the ratio of E1 and E2, and the frequency of m = 2, n = 1 is greater than the frequency of m = 1, n = 2. When E1 < E2, the frequencies of the membrane escalate with the decline of the ratio of E1 and E2, and the frequency of m = 2, n = 1 is smaller than the frequency of m = 1, n = 2. The curve of m = n = 1 and m = n = 2 is symmetrical. Especially, when the ratio of E1 and E2 = 1, the membrane degenerates into an isotropic material and their frequency is the same. This demonstrates that the orthotropy of the membrane is the reason why the calculation results of large deflection and small deflection are different after exchange of m and n in “Comparisons with Other Methods”.

Conclusions

  • This paper draws on the homotopy method and the improved homotopy method to study the strongly nonlinear vibration of the orthotropic membrane under displacement excitation, respectively. The result indicates that the improved homotopy solution is closer to the theoretical solution than the homotopy solution. In addition, although the error between the improved homotopy solution and the theoretical solution increases with the increase of the displacement excitation, the maximum error is less than 2.54%. The improved homotopy solution is simpler in form and more suitable for application in engineering.

  • The frequency of the membrane increases with the increase of the thickness, the pretension, the Young’s modulus of the membrane and the decrease of membrane size, aerial density. In engineering, it is recommended to adjust the dynamic characteristics of the membrane structures by adjusting the size and thickness of the membrane.

  • The frequencies after exchanges a and b are different. In addition, the impact of Young’s modulus on ω12 and ω21 is different. The results demonstrate that the orthogonal anisotropy and geometrical nonlinearity of the membrane have a great influence on the membrane vibration.