Introduction

Flexible membranes are widely used in various fields of technology with different mechanics and material properties, such as PVDF membrane in the field of construction [1]; semiconductor membrane in the field of machinery [2], and so on. The membrane material used in the construction field is a woven membrane composed of base material and coating [3]. The base material is woven by fiber orthogonal [3], which makes the elastic modulus of the membrane material different in two directions and shows orthotropy. Woven membranes are usually smaller in thickness, stiffness and damping, so they tend to vibrate under external loads. Even the vibration amplitude is much larger than its thickness, which shows obvious geometric non-linearity in essence. The exact solution of the nonlinear vibration problem of membranes is complex, even impossible to get the exact solution when considering various material characteristics of the membrane (such as orthotropic, damping coefficient, etc.) [4,5,6,7,8,9].

In recent decades, a number of investigations on vibration of membranes have been performed. Sato et al. [10] took the compound elliptical membrane composed of confocal ellipse as the research object, analyzed its free vibration with small deflection; Shin et al. [11] studied the nonlinear vibration of the moving membrane in the axial direction, then the influence of parameters (such as velocity, boundary, geometry and so on) of membranes on the vibration frequency was summarized; Goncalves et al. [12] applied nonlinear finite element method to the study of physical non-linearity of hyper-elastic stretched membrane, and analyzed the influence of stretching ratio on linear and nonlinear vibration. Lin and Chen [13] studied the free vibration of circular membrane, the analytical expression of frequency and mode shape was obtained and was further verified by numerical calculation. Different from the study of scholars above, some scholars have done some researches on the weakly nonlinear vibration of membrane using the traditional perturbation method, some meaningful results were further obtained [14,15,16,17]. However, these studies are basically based on the theory of small deflection or the method of weak nonlinear perturbation, such as Lindestedt–Poincaré method (LP), Krylov–Bogoliubov–Mitropolsky method (KBM), Multi-Scale method and so on. That is to say, the coefficient of the nonlinear term of the vibration equation was omitted or weakened. In fact, it is not accurate when the membrane amplitude is large. For example, in Liu's paper [18], with the increase of the initial displacement, the frequency error of the membrane obtained by Krylov–Bogoliubov–Mitropolsky perturbation method is getting larger and larger. In this case, the dynamic characteristics of membranes are estimated incorrectly, which may increase their risk of use. Therefore, it is worth studying the analytical method for calculating the strongly nonlinear vibration of membranes; furthermore, the accurate vibration characteristics of membranes can be obtained.

In view of the limitations of traditional perturbation method and theory of small deflection in solving problems of strongly nonlinear vibration of membranes, this paper introduces the transformation parameter to modify the traditional multi-scale method, and an improved multi-scale method suitable for strongly nonlinear dynamic systems is proposed. This improved method can consider the strongly geometrically nonlinear vibration characteristics of flexible membrane. Based on this method, the strongly nonlinear vibration control equation of membrane is established and solved. Consequently, a series of statistical results including function of displacement and frequency are obtained. Furthermore, the theoretical model is validated by the numerical computation method. In addition, the results are compared with those of the traditional perturbation method, which shows the limitations of the traditional perturbation method in solving strongly nonlinear vibration problems. Finally, the experiment of membrane vibration is carried out to further verify the theory. In addition, the economic pretension of membrane material in engineering is obtained. The method and conclusions of this paper provide a theoretical references for the refined dynamic design of flexible membrane.

Solution of Strongly Nonlinear Vibration of Membranes

Stress and Displacement Solution

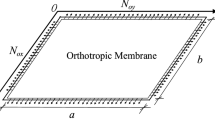
The calculation model of membrane material is shown in Fig. 1. The effect of shear stress is very small in the vibration of flexible membrane, so the shear stress is not considered in the study, and the governing equations for nonlinear vibration of orthotropic membranes are as follows [18]:

$$\rho \frac{{\partial^{2} w}}{{\partial t^{2} }} + c\frac{\partial w}{{\partial t}} = h\left( {\sigma_{0x} + \frac{{\partial^{2} \varphi }}{{\partial y^{2} }}} \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} + h\left( {\sigma_{0y} + \frac{{\partial^{2} \varphi }}{{\partial x^{2} }}} \right)\frac{{\partial^{2} w}}{{\partial y^{2} }}$$
(1)
$$\frac{1}{{E_{1} }}\frac{{\partial^{4} \varphi }}{{\partial y^{4} }} + \frac{1}{{E_{2} }}\frac{{\partial^{4} \varphi }}{{\partial x^{4} }} = \left( {\frac{{\partial^{2} w}}{\partial x\partial y}} \right)^{2} - \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial y^{2} }}$$
(2)
Fig. 1
figure 1

Calculation model of membrane material

Full size image

where \(\varphi = \varphi \left( {x,y,t} \right)\) is the stress function; \(\sigma_{x}\) and \(\sigma_{y}\) are normal stresses in the X direction and Y direction, respectively; h is the thickness of the membrane; The Young's modulus of elasticity in X and Y directions are \(E_{1}\) and \(E_{2}\), respectively; w is the normal vibration displacement; \(\rho\) is the surface density; c is the damping coefficient.

The four sides of the membrane are fixed, and there is only horizontal tension in the vibration. Therefore, the boundary conditions can be expressed as

$$w\left( {0,y,t} \right) = w\left( {a,y,t} \right) = w\left( {x,0,t} \right) = w\left( {x,b,t} \right) = 0$$
(3)
$$\frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {a,y,t} \right) = \frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {0,y,t} \right){ = }\frac{{\partial^{2} w}}{{\partial y^{2} }}\left( {x,0,t} \right) = \frac{{\partial^{2} w}}{{\partial y^{2} }}\left( {x,b,t} \right) = 0$$
(4)

Let the mode function of the vibration be an orthogonal trigonometric function. Then, the displacement function and stress function of the vibration satisfying the boundary conditions are [19]:

$$w\left( {x,y,t} \right) = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {Q_{mn} \left( t \right) \cdot \sin \frac{m\pi x}{a}} } \sin \frac{n\pi y}{b}$$
(5)
$$\varphi \left( {x,y,t} \right) = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {Q_{mn}^{2} \left( t \right) \cdot } } \phi_{mn} \left( {x,y} \right)$$
(6)

where m and n are positive integers, which denote sinusoidal half wave number, \(Q_{mn} \left( t \right)\) is the time-dependent function.

By assuming the expression structure of stress function, we substitute Eqs. (5) and (6) into Eq. (2). The form of the construction solution can be assumed as:

$$\phi \left( {x,y} \right) = \beta_{1} \cdot \cos \frac{2m\pi x}{a} + \beta_{2} \cdot \cos \frac{2n\pi y}{b} + \gamma_{1} x^{3} + \gamma_{2} x^{2} + \gamma_{3} y^{3} { + }\gamma_{4} y^{2}$$
(7)

By substituting (7) and (5) into (2) and comparing the coefficients of \(\cos \left( {{{2m\pi x} \mathord{\left/ {\vphantom {{2m\pi x} a}} \right. \kern-\nulldelimiterspace} a}} \right)\) and \(\cos \left( {{{2n\pi y} \mathord{\left/ {\vphantom {{2n\pi y} b}} \right. \kern-\nulldelimiterspace} b}} \right)\) on both sides of the equation, yields:

$$\beta_{1} = \frac{{E_{2} }}{32}\left( \frac{n}{m} \right)^{2} \left( \frac{a}{b} \right)^{2} ,\quad \beta_{2} = \frac{{E_{1} }}{32}\left( \frac{m}{n} \right)^{2} \left( \frac{b}{a} \right)^{2}$$

The stress boundary conditions of membranes with four sides fixed can be expressed as

$$\frac{{\partial^{2} \varphi }}{{\partial x^{2} }}\left( {0,y,t} \right) = \frac{{\partial^{2} \varphi }}{{\partial x^{2} }}\left( {a,y,t} \right){ = }\frac{{\partial^{2} \varphi }}{{\partial y^{2} }}\left( {x,0,t} \right) = \frac{{\partial^{2} \varphi }}{{\partial y^{2} }}\left( {x,b,t} \right) = 0$$
(8)

By substituting (7) into (8), then,

$$\gamma_{1} = \gamma_{3} = 0,\quad \gamma_{2} = \frac{{\pi^{2} E_{2} n^{2} }}{{16b^{2} }},\quad \gamma_{4} = \frac{{\pi^{2} E_{1} m^{2} }}{{16a^{2} }}$$

By substituting the obtained expressions of \(\alpha\),\(\beta\),\(\gamma_{1}\),\(\gamma_{2}\),\(\gamma_{3}\),\(\gamma_{4}\) into (7), yields:

$$\phi \left( {x,y} \right) = \frac{{E_{2} n^{2} a^{2} }}{{32m^{2} b^{2} }}\cos \frac{2m\pi x}{a} + \frac{{E_{1} m^{2} b^{2} }}{{32n^{2} a^{2} }}\cos \frac{2n\pi y}{b} + \frac{{\pi^{2} E_{2} n^{2} }}{{16b^{2} }}x^{2} + \frac{{\pi^{2} E_{1} m^{2} }}{{16a^{2} }}y^{2}$$
(9)

By substituting (6) and (9) into (1), the governing Eq. (1) can be decoupled by the Galerkin method [20, 21] and expressed as

$$\begin{gathered} \iint\limits_{S} {\left[ {\frac{\rho }{h}\frac{{\partial^{2} w}}{{\partial t^{2} }} + \frac{c}{h}\frac{\partial w}{{\partial t}} - \left( {\sigma_{0x} + \frac{{\partial^{2} \varphi }}{{\partial y^{2} }}} \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} - \left( {\sigma_{0y} + \frac{{\partial^{2} \varphi }}{{\partial x^{2} }}} \right)\frac{{\partial^{2} w}}{{\partial y^{2} }}} \right] \cdot } \hfill \\ \sin \frac{m\pi x}{a}\sin \frac{n\pi y}{b}ds = 0 \hfill \\ \end{gathered}$$
(10)

After (10) is solved and simplified, the inhomogeneous partial differential equation can be obtained as

$$\begin{gathered} \frac{{d^{2} Q(t)}}{{dt^{2} }} + \frac{c}{\rho }\frac{dQ(t)}{{dt}}{ + }\frac{{\pi^{2} h}}{\rho }\left( {\frac{{m^{2} }}{{a^{2} }}\sigma_{0x} + \frac{{n^{2} }}{{b^{2} }}\sigma_{0y} } \right)Q(t) + \hfill \\ \frac{{3\pi^{4} h}}{16\rho }\left( {\frac{{E_{1} m^{4} }}{{a^{4} }} + \frac{{E_{2} n^{4} }}{{b^{4} }}} \right)Q^{3} (t) = 0 \hfill \\ \end{gathered}$$
(11)

Take the commonly used ZZF membrane made in China as an example (the material parameters are provided by the manufacturer), the surface density of the membrane is 0.95 kg/m2, the thickness is 0.72 mm, elastic modulus in x and y directions are E1 = 1590 MPa, E2 = 1360 MPa, respectively, the length and width of the membrane are a = 5 m and b = 5 m, respectively.

After introducing the parameter into the coefficient of the nonlinear term in Eq. (11), the following results can be calculated as follows:

$$\frac{{3\pi^{4} h}}{16\rho }\left( {\frac{{E_{1} m^{4} }}{{a^{4} }} + \frac{{E_{2} n^{4} }}{{b^{4} }}} \right) = \frac{291.64 \times 0.72}{{16 \times 0.95}} \times (\frac{1590}{{625}} + \frac{1360}{{625}}) = 65.20 \gg 1$$

The inequation shows that the coefficient of the nonlinear term in Eq. (11) is much larger than 1. Obviously, Eq. (11) is a strongly nonlinear vibration equation [19].

Improved Multi-scale Solution for Vibration Control Equation

For nonlinear vibration systems, many scholars have proposed some applicable methods, Lai et al. [22] applied Newton-Harmonic balance method for solving accurate approximate analytical higher-order solutions for strong nonlinear Duffing oscillators with cubic-quintic nonlinear restoring force. Accurate higher-order approximate analytical expressions for period and periodic solution are established. Li et al. [23] used a perturbation method investigated the transverse vibration of a simply supported nanobeam with an initial axial tension based on the nonlocal stress field theory with a nonlocal size parameter. Wu et al. [24] proposed a modified Newton-Harmonic balance approach to strongly odd nonlinear oscillators. Gao et al. [25] studied the nonlinear phenomena of a simple dual-rotor system in the case of primary resonances by the multi-scale method. Li et al. [26] investigated the natural frequency, steady-state resonance and stability for the transverse vibrations of a nanobeam subjected to a variable initial axial force by multi-scale method. In addition, Li [27] applied the multi-scale method to the dynamic response research of axially travelling carbon nanotubes considering nonlocal weakening effect. In addition, the frequency-incremental method [28], the modified Lindstedt–Poincaré (MLP) method [29] and so on, also provide great convenience for solving the nonlinear system. Based on the above works, the parameter transformation is introduced into the multi-scale method, and an improved multi-scale method is proposed in this paper.

By letting \(\varepsilon = \frac{{3\pi^{4} h}}{16\rho }\left( {\frac{{E_{1} m^{4} }}{{a^{4} }} + \frac{{E_{2} n^{4} }}{{b^{4} }}} \right)\), \(Q = Q(t)\), Eq. (11) can be simplified as

$$\frac{{{\text{d}}^{2} Q}}{{{\text{d}}t^{2} }} + \omega_{0}^{2} Q + \varepsilon \left( {\mu \frac{{{\text{d}}Q}}{{{\text{d}}t}} + Q^{3} } \right) = 0$$
(12)

where \(\omega_{0}^{2} = \frac{{h\pi^{2} }}{\rho }\left( {\frac{{m^{2} }}{{a^{2} }}\sigma_{0x} + \frac{{n^{2} }}{{b^{2} }}\sigma_{0y} } \right)\), \(\mu = \frac{{16a^{4} b^{4} c}}{{3\pi^{4} h(E_{1} m^{4} b^{4} + E_{2} n^{4} a^{4} )}}\).

Let ω be the vibration frequency of membranes, then expand \(\omega^{2}\) to the power series of \(\varepsilon\) as follows:

$$\omega^{2} = \omega_{0}^{2} + \varepsilon \omega_{1} + \varepsilon^{2} \omega_{2} + \cdots$$
(13)

The transformation parameter α is as follows:

$$\alpha = \frac{{\varepsilon \omega_{1} }}{{\omega_{0}^{2} + \varepsilon \omega_{1} }}$$
(14)

Then,

$$\omega^{2} = \omega_{0}^{2} + \varepsilon \omega_{1} \left[ {1 + \frac{1}{{\omega_{0}^{2} + \varepsilon \omega_{1} }}\left( {\varepsilon^{2} \omega_{2} + \varepsilon^{3} \omega_{3} + \cdots } \right)} \right] = \frac{{\omega_{0}^{2} }}{1 - \alpha }\left( {1 + \delta_{2} \alpha^{2} + \delta_{3} \alpha^{3} + \cdots } \right)$$
(15)
$$\omega = \omega_{0} \left[ {1 + \frac{1}{2}\alpha + \left( {\frac{3}{8} + \frac{{\delta^{2} }}{2}} \right)\alpha^{2} + \cdots } \right]$$
(16)

The perturbation solution of (12) can be expressed as:

$$Q(t,\alpha ) = Q_{0} (t,\alpha t) + \alpha Q_{1} (t,\alpha t) + \alpha^{2} Q_{2} (t,\alpha t) + \cdots$$
(17)

Differential operators can be obtained as:

$$\begin{aligned} \frac{{\text{d}}}{{{\text{d}}t}} = & D_{0} + \alpha D_{1} + \alpha^{2} D_{2} + \ldots , \\ \frac{{{\text{d}}^{2} }}{{{\text{d}}t^{2} }} = & D^{2}_{0} + 2\alpha D_{0} D_{1} + \alpha^{2} (D_{1}^{2} + 2D_{0} D_{2} ) + \ldots \\ \end{aligned}$$
(18)

By substituting Eqs. (14), (15) and (18) into Eq. (12) and then simplifying, yields:

$$\begin{gathered} (1 - \alpha )\left[ {D^{2}_{0} + 2\alpha D_{0} D_{1} + \alpha^{2} (D_{1}^{2} + 2D_{0} D_{2} )} \right](Q_{0} + \alpha Q_{1} + \alpha^{2} Q_{2} + \cdots ) \hfill \\ + (1 - \alpha )\omega_{0}^{2} (Q_{0} + \alpha Q_{1} + \alpha^{2} Q_{2} + \cdots ) + \frac{{\alpha \omega_{0}^{2} }}{{\omega_{1}^{2} }}\left[ \begin{gathered} (Q_{0} + \alpha Q_{1} + \alpha^{2} Q_{2} + \cdots )^{3} + \hfill \\ (D_{0} + \alpha D_{1} + \alpha^{2} D_{2} ) \cdot \hfill \\ (Q_{0} + \alpha Q_{1} + \alpha^{2} Q_{2} + \cdots ) \hfill \\ \end{gathered} \right] \hfill \\ = 0 \hfill \\ \end{gathered}$$
(19)

After expanding Eq. (19), the coefficient of each power of α in the equation can be zero, and the following equation can be obtained as

$$\begin{array}{ll} {\alpha^{0} } & {D_{0}^{2} Q_{0} + \omega_{0}^{2} Q_{0} = 0} \\ {\alpha^{1} } & {D_{0}^{2} Q_{1} + \omega_{0}^{2} Q_{1} + 2D_{0} D_{1} Q_{0} + \frac{{\omega_{0}^{2} }}{{\omega_{1} }}(D_{0} Q_{0} + x_{0}^{3} ) = 0} \\ {\alpha^{2} } & {D_{0}^{2} Q_{2} + Q_{2} + 2D_{0} D_{1} Q_{1} + (D_{1}^{2} + 2D_{0} D_{2} )Q_{0} + \frac{{\omega_{0}^{2} }}{{\omega_{1} }}3Q_{0}^{2} Q_{1} = 0} \\ \end{array}$$
(20)

The solution of the first equation in the system of Eq. (20) can be expressed as

$$Q_{0} = A(\alpha t){\text{e}}^{{i\omega_{0} t}} + \overline{A}(\alpha t){\text{e}}^{{ - i\omega_{0} t}}$$
(21)

Further, the following equation will be established by substituting (21) into the second equation of (20).

$$D_{0}^{2} Q_{1} + \omega_{0}^{2} Q_{1} + \left( {2i\omega_{0} D_{1} A + 3\frac{{\omega_{0}^{2} }}{{\omega_{1} }}A^{2} \overline{A} + i\mu \frac{{\omega_{0}^{3} }}{{\omega_{1} }}A} \right){\text{e}}^{it} + \frac{1}{{\omega_{1} }}A^{3} {\text{e}}^{3it} + cc = 0$$
(22)

where \(cc\) is the conjugate complex term. Eliminate the term of immortality in Eq. (34), then

$$2D_{1} A + 3\frac{{\omega_{0} }}{{\omega_{1} }}A_{{}}^{2} \overline{A} + i\mu \frac{{\omega_{0}^{3} }}{{\omega_{1} }}A = 0$$
(23)

Finally, the solution of (23) can be obtained as

$$Q_{1} = \frac{1}{{8\omega_{1} }}(A^{3} {\text{e}}^{3it} + \overline{A}^{3} {\text{e}}^{ - 3it} )$$
(24)

Let \(A = \frac{1}{2}f{\text{e}}^{i\phi }\), and bring it into Eq. (23), then separate the imaginary part from the real part, yields

$$\begin{array}{*{20}c} {\frac{{{\text{d}}f}}{{\alpha {\text{d}}t}} = - \frac{1}{2}\mu \frac{{\omega_{0}^{2} }}{{\omega_{1} }}f,} & {f\frac{{{\text{d}}\phi }}{{\alpha {\text{d}}t}} = - \frac{{3\omega_{0} }}{{8\omega_{1} }}} \\ \end{array} f^{3}$$
(25)

By substituting \(A = \frac{1}{2}fe^{i\phi }\) into (21), yields

$$Q_{0} = f\cos (\omega t + \phi_{0} )$$
(26)

By comparing the angular frequency in Eq. (26) with that in Eq. (16), the equation under the first-order approximation can be obtained as

$$\frac{{{\text{d}}\phi }}{{\alpha {\text{d}}t}} = \frac{{\omega_{0} }}{2}$$
(27)

By substituting (27) into (25), yields

$$\omega_{1} = \frac{3}{4}f^{2}$$
(28)

After substituting (28) into (25) and omitting the higher-order term, the approximate expression of vibration frequency of the membrane can be obtained as

$$\omega = \sqrt {\omega_{0}^{2} + \frac{3}{4}\varepsilon f^{2} }$$
(29)

By substituting (29) into (25), yields:

$$\frac{{{\text{d}}f}}{{{\text{d}}t}} = - \frac{1}{2}\varepsilon \mu f\frac{1}{{1 + \varepsilon \frac{{3f^{2} }}{{4\omega_{0}^{2} }}}}$$
(30)

where f is the vibration amplitude, and its specific expression can be obtained as

$$f = c_{0} \sqrt {\frac{{{\text{Product}}\log [\zeta \cdot {\text{e}}^{ - \varepsilon \mu t} ]}}{\zeta }}$$
(31)

where \(\zeta = \frac{3\varepsilon }{{4\omega_{0}^{2} }}\), the Productlog[x] is the Lambert W function, which is the inverse of \(x{\text{e}}^{x}\) on interval \(\left[ { - \frac{1}{e}, + \infty } \right]\), usually written as W(x). \(c_{0}\) is the integral constant related to the initial condition. Therefore, the first-order perturbation solution of (12) is obtained as:

$$Q(t) = c_{0} \sqrt {\frac{{{\text{W}}(\zeta \cdot {\text{e}}^{ - \varepsilon \mu t} )}}{\zeta }} \cdot \cos \left( {\sqrt {\omega_{0}^{2} + \frac{3}{4}\varepsilon a^{2} } t + \phi_{0} } \right)$$
(32)

here \(\phi_{0}\) is the initial phase angle, and its value is determined according to the initial conditions as well as \(c_{0}\). Assume that the membrane surface is in a static equilibrium state in the horizontal position at t = 0. Then, an initial normal displacement is applied to the surface of the membrane as shown in Fig. 2, and finally it begins to vibrate.

Fig. 2
figure 2

Initial condition of membrane’s vibration

Full size image

The initial vibration conditions can be expressed as

$$\left. {Q(t)} \right|_{t = 0} = a_{0} , \, \left. {\frac{{{\text{d}}Q(t)}}{{{\text{d}}t}}} \right|_{t = 0} = 0$$
(33)

where \(a_{0}\) is the initial displacement.

In view of the initial vibration conditions, the values of \(c_{0}\) and \(\phi_{0}\) can be easily obtained as follows:

$$a_{0} = c_{0} \sqrt {\frac{{W(\zeta \cdot {\text{e}}^{ - \varepsilon \mu t} )}}{\zeta }} \cos \phi_{0}$$
(34)
$$\left. {\frac{{{\text{d}}Q(t)}}{{{\text{d}}t}}} \right|_{t = 0} = 0$$
(35)

Finally, by substituting (32), (34) and (35) into (5), the displacement response expression of strongly nonlinear vibration of orthotropic membrane is obtained as

$$w\left( {x,y,t} \right) = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\left( \begin{gathered} \sin \frac{m\pi x}{a}\sin \frac{n\pi y}{b}a_{0} \sqrt {\frac{{{\text{W}}(\zeta \cdot {\text{e}}^{ - \varepsilon \mu t} )}}{{{\text{W}}(\zeta )}}} \cdot \hfill \\ \cos \left( {\sqrt {\omega_{0}^{2} + \frac{3}{4}\varepsilon f^{2} } t} \right) \hfill \\ \end{gathered} \right)} }$$
(36)

The lateral vibration displacement of any point on the membrane can be obtained according to (36). Where a0 is the single-order vibration amplitude of the membrane, which is determined by the initial vibration conditions. The initial normal displacement of the membrane at t = 0 is expressed as:

$$w\left( {x,y,0} \right) = w_{0} \left( {x,y} \right)$$
(37)

By substituting (37) into (36), yields:

$$w_{0} \left( {x,y} \right) = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {a_{0} \cdot \sin \frac{m\pi x}{a}\sin \frac{n\pi y}{b}} }$$
(38)

Multiply by \(\rho hW_{kl}\) on both sides of (38) and integrate along the membrane area. Finally, the relationship between w0 and a0 can be obtained as:

$$\begin{aligned} a_{0} = & \frac{{\iint\limits_{s} {\rho hw_{0} \left( {x,y} \right)}\sin \frac{m\pi x}{a}\sin \frac{n\pi y}{b}{\text{d}}s}}{{\iint\limits_{s} {\rho h}\sin^{2} \frac{m\pi x}{a}\sin^{2} \frac{n\pi y}{b}{\text{d}}s}} \\ = & \frac{4}{ab}\int_{0}^{a} {\int_{0}^{b} {w_{0} \left( {x,y} \right)\sin \frac{m\pi x}{a}\sin \frac{n\pi y}{b}{\text{d}}x} } {\text{d}}y \\ \end{aligned}$$

Consequently,

$$a_{0} = \left\{ \begin{gathered} \frac{{16w_{0} }}{{mn\pi^{2} }} \, \left( {m,n = 1,3,5 \cdots } \right) \hfill \\ \, 0 \, \left( {m,n = 2,4,6 \cdots } \right) \hfill \\ \end{gathered} \right.$$

where \(w_{0} \left( {x,y} \right) = w_{0}\).

Obviously, it can be seen from Eq. (29) that when the amplitude of strongly nonlinear vibration of the membrane is determined, the frequency value is not related to the damping. Therefore, we remove the damping term in (12), then use the separation variable method to carry out the analytical calculation of the vibration frequency, so as to verify the accuracy of the improved multi-scale method for the calculation of the vibration frequency. In this way, (12) will be transformed into the standard Duffing equation as [30]

$$\frac{{{\text{d}}^{2} Q}}{{{\text{d}}t^{2} }} + \omega_{0}^{2} Q + \varepsilon Q^{3} = 0$$
(39)

By integrating both sides of (39), yields:

$$\left( {\frac{{{\text{d}}Q}}{{{\text{d}}t}}} \right)^{2} + \omega_{0}^{2} Q^{2} + \frac{\varepsilon }{2}Q^{4} = A$$
(40)

where A is obtained from the initial conditions.

Then, suppose f is the amplitude, which is the initial normal displacement of the central point of the membrane surface when t = 0.

The initial vibration conditions can be expressed as

$$x(0) = f,\quad \dot{x}(0) = 0$$
(41)

According to the initial conditions, the expression of A can be obtained as

$$A = \omega_{0}^{2} f^{2} + \frac{\varepsilon }{2}f^{4}$$
(42)

By substituting (42) into (40), yields:

$$\frac{{{\text{d}}Q}}{{{\text{d}}t}} = \lambda \cdot \sqrt {\left( {1 - \frac{{Q^{2} }}{{f^{2} }}} \right) \cdot \left( {1 + k^{2} \cdot \frac{{Q^{2} }}{{f^{2} }}} \right)}$$
(43)

where \(\lambda = f^{2} \sqrt {\frac{{\omega_{0}^{2} }}{{f^{2} }} + \frac{\varepsilon }{2}}\), \(k^{2} = \frac{{\varepsilon f^{2} }}{{2\omega_{0}^{2} + \varepsilon f^{2} }}\).

By integrating (43) with the method of separating variables, the results can be obtained as

$$Z = \frac{4}{\lambda }\int_{0}^{f} {\sqrt {\left( {1 - \frac{{x^{2} }}{{f^{2} }}} \right)\left( {1 + k^{2} \cdot \frac{{x^{2} }}{{f^{2} }}} \right)} {\text{d}}x}$$
(44)

Let \(x = f\sin \theta\), and bring it into (44), yields:

$$Z = \frac{4f}{\lambda }\int_{0}^{{\frac{\pi }{2}}} {\left( {1 + k^{2} \cdot \sin^{2} \theta } \right)^{{ - \frac{1}{2}}} d\theta } \, \left( {0 \le k \cdot \sin \theta \le 1} \right)$$
(45)

where \(\left( {1 + k^{2} \cdot \sin^{2} \theta } \right)^{{ - \frac{1}{2}}}\) can be expanded into a power series of \(k \cdot \sin \theta\), that is

$$\left( {1 + k^{2} \cdot \sin^{2} \theta } \right)^{{ - \frac{1}{2}}} = 1 - \frac{1}{2}k^{2} \sin^{2} \theta + \frac{1 \cdot 3}{{2 \cdot 4}}k^{4} \sin^{4} \theta + \cdots \left( { - 1} \right)^{n} \frac{{\left( {2i - 1} \right){!!}}}{{\left( {2i} \right)!!}}\left( {k\sin \theta } \right)^{2p}$$
(46)

By substituting (46) into (45), then integrating them item by item, the equation is obtained as

$$Z = \frac{2\pi f}{\lambda }\sum\limits_{i = 0}^{\infty } {\left( { - 1} \right)^{i} \left( {\frac{{\left( {2i - 1} \right)!!}}{{\left( {2i} \right)!!}}} \right)^{2} k^{2i} }$$
(47)

where \(i = 0,1,2,3 \ldots\).

Finally, the series solution of the vibration frequency of the membrane can be obtained as

$$\omega = \frac{2\pi }{Z} = \frac{{\sqrt {\omega_{0}^{2} + \frac{\varepsilon }{2}f^{2} } }}{{\sum\limits_{i = 0}^{\infty } {\left( { - 1} \right)^{i} \left( {\frac{{\left( {2i - 1} \right)!!}}{{\left( {2i} \right)!!}}} \right)^{2} \left( {\frac{{\varepsilon f^{2} }}{{2\omega_{0}^{2} + \varepsilon f^{2} }}} \right)^{i} } }}$$
(48)

It should be noted that since the exact series solution of the vibration frequency can be obtained, why do we have to work hard to solve the control equation of membrane vibration? Obviously, this idea is one-sided. This is because we can only get the information of vibration frequency through series derivation, other vibration characteristics (such as vibration mode, attenuation speed, etc.) are not available to us. Therefore, it is not enough to master the vibration characteristics of membrane materials only by series solution.

Validation of Theoretical Model

Comparisons with Numerical Solutions

Analytical results of Eq. (36) are compared with numerical results. The orthotropic membrane applied in engineering is analyzed, membrane parameters are as follows: w0 = 0.05 m; ρ = 1.2 kg/m2; h = 1.0 mm; E1 = 1400 MPa; E2 = 900 MPa; a = b = 1.2 m; c = 90 N·s/m3.

By comparison, it can be found that the first-order approximate solutions obtained by the improved multi-scale method are in good agreement with the numerical solutions as shown in Fig. 3. With the increase of the vibration mode order, the maximum vibration amplitude between the improved multi-scale solution and the numerical solution shows a small deviation, but all are within the acceptable range of the engineering error. Therefore, the theoretical derivation process in this paper is applicable.

Fig. 3
figure 3

Comparison between numerical solution and improved multi-scale solution

Full size image

The curve of the vibration amplitude of orthotropic membrane varying with the mode shape is shown in Fig. 4. It can be clearly obtained from the figure that the amplitude of the membrane decreases gradually with the increase of the mode number. When m and n are >5, the amplitude value is almost zero. That is to say, the contribution of the high-order mode shape of the membrane vibration to the overall dynamic response of the structure decreases with the increase of the mode number.

Fig. 4
figure 4

The amplitude of vibration varies with the mode shape

Full size image

According to the mathematical calculation of Eq. (36), the mode shape of each stage and superimposed mode of the membrane at t = 0.03 are obtained, as shown in Fig. 5. Obviously, mode shapes and superposition mode are symmetric along the longitudinal and latitudinal axes of the membrane, which is consistent with the reference [18]. So indirectly, it also proves the correctness of the theoretical analysis in this paper.

Fig. 5
figure 5

Vibration mode. a First mode (t = 0.03 s). b Second mode (t = 0.03 s). c Third mode (t = 0.03 s). d Superposed mode (t = 0.03 s)

Full size image

Comparisons with Traditional Perturbation Method

Next, the results of (29), (48) and the Krylov–Bogoliubov–Mitropolsky perturbation solutions in reference [18] are compared in this paper. The membrane parameters required for the calculation are as follows: w0 = 0.05 m; ρ = 1.2 kg/m2; h = 1.0 mm; E1 = 1400 MPa; E2 = 900 MPa; a = b = 1.2 m; c = 90 N·s/m3; σ0x = σ0y = σ.

The frequency amplitude response calculated by the improved multi-scale method is close to the series solution as shown in Fig. 6. The difference between the improved multi-scale results, Krylov–Bogoliubov–Mitropolsky method results and the series solution results is small when the initial displacement is small. However, with the increase of the initial displacement, the results of KBM perturbation method show a large error. The reason is that with the increase of the initial normal displacement at zero time, the vibration of the membrane presents more and more strong geometrically nonlinear characteristics. However, the KBM perturbation method is only applicable to weakly nonlinear vibration systems, and its applicability to strongly nonlinear vibrations is poor. Obviously, the improved multi-scale method in this paper can more accurately describe the strongly nonlinear vibration characteristics of the membrane, and is not limited by the initial displacement of the membrane.

Fig. 6
figure 6

Amplitude–frequency response curve

Full size image

The vibration frequency of the membrane increases nonlinearly with the increase of the initial normal displacement at zero time, showing the geometric nonlinear characteristics of the vibration. At the same initial normal displacement, the vibration frequency of the membrane increases with the increase of the mode shape, and the vibration frequency of the high-order mode is higher than that of the low-order mode. When the initial normal displacement is close to zero, the frequencies calculated by the improved multi-scale solutions, series solutions, and KBM perturbation solutions are the same as those calculated by the linear (small deflection) method.

Experimental Study

In this paper, a cross screw-type membrane tension device is made to apply pretension to the membrane material. The high-pressure centrifugal blower is used as the power equipment, and the wind guiding device is designed to blow the wind to the surface of the membrane instantaneously and evenly and then stop suddenly. The initial vertical disturbance is produced uniformly on the membrane surface, and then the free vibration begins. Of course, the whole process described above is controlled by a computer. Finally, the experimental results are compared with the theoretical results to verify the applicability of the multi-scale method in the strongly nonlinear vibration of orthotropic membrane, and the most economical value of pretension is found.

Experimental Materials

Heytex and ZZF membrane materials were used in the test. Each kind of membrane material had two test pieces, the sizes were 1200 * 800 mm and 1200 * 1200 mm, respectively. The cross-shaped membrane specimens were cut at four ends. Further, the four corners are rounded. The cross-shaped membrane specimens were cut at four ends, Further, the four corners are rounded. For the specimen with square central membrane surface area, the small squares with side length of 650 mm are cut from the square membrane surface with side length of 2500 mm at four corners, and then the four sides are cut with a width of 100 mm, and the four small corners are chamfered with a half diameter of 200 mm. Finally, fold, lock and drill holes in the four tension directions as shown in Fig. 7. The purpose of slit treatment is to ensure that the pretension can be transferred to the membrane material in the middle area [31].

Fig. 7
figure 7

The photos of the experiment membrane material

Full size image

The physical properties of membrane materials are given in Table 1.

Table 1 Physical parameters of membrane materials
Full size table

Tensioning and Measuring Device

Referring to the experimental tensioning device in reference [32], a new type of reinforced cross-shaped membrane biaxial tension support is designed and manufactured. Its plane size is 3800 × 4160 mm, the central square area size is 1200 × 1200 mm, and the height is 1600 mm. The test bracket is welded by square steel tube with size of 60 × 60 mm. To ensure that the strength of the test frame can meet the test requirements, diagonal braces are added to the four pillars of the test frame and the four ends of its table. The diagonal braces are made of 60 × 60 mm square steel pipes. As shown in Fig. 8.

Fig. 8
figure 8

Reinforced biaxial tensioning support

Full size image

The test measuring device includes a dynamometer and a displacement sensor. Hp-10K digital display push–pull meter was placed between the tension screw and the membrane splint to measure the tensile force of membrane material. ZLDS100 laser distance sensor is used to measure the vibration of film surface. The specific arrangement is shown in Fig. 9.

Fig. 9
figure 9

The digital display pull-and-push dynamometer and ZLDS100 laser displacement sensor

Full size image

Loading Scheme

The initial pretension of the membrane is applied by adjusting the tension screw. In the test, the grading tension was adopted. Let the tensile force in X and Y directions be equal, and its values are 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0 and 8.0 kN, respectively. First, under the determined pretension, the air blower is used to impact the membrane surface vertically through the air supply device, and then the fan is turned off immediately. Through this process, the membrane surface is simulated to be impacted and vibrated uniformly. Finally, by changing the fans of different power to adjust the size of uniform impact load, the loading device is shown in Fig. 10.

Fig. 10
figure 10

The loading device

Full size image

Experimental Results and Verification

To further reveal the characteristics of the strong nonlinear vibration of membrane materials, and strictly verify the theoretical calculation results, we completed the experiment. Obviously, the free vibration of the membrane starts after the initial displacement is generated by the impact. The displacement time history data obtained are compared with the theoretical calculation results and shown in Fig. 11.

Fig. 11
figure 11

Comparison between theoretical time history curve and test time history curve. a Heytex/1kN/C1/CZR-CZT, b Heytex/2kN/C1/CZR-CZT, c ZZF/1kN/C1/CZR-CZT, d ZZF/6kN/C1/CZR-CZT

Full size image

The results of theoretical calculation are basically consistent with the experimental results. Because the mode function in the theoretical calculation comes from the plate shell theory, it is only a simple spatial vibration model, and the shape of the mode is full. However, as a flexible material, the simple mode function cannot accurately reflect the actual complex vibration situation. Therefore, the amplitude and frequency of theoretical calculation are larger than the experimental results.

Discussion

The experimental and theoretical results of the membrane under the same displacement excitation are analyzed to seek some common and interesting conclusions. Figures 12, 13, 14, 15, 16, 17 show the theoretical and experimental values of vibration amplitude and frequency of each measuring point under different pretensions.

Fig. 12
figure 12

Dynamic response parameters on C1 point of square Heytex membrane

Full size image
Fig. 13
figure 13

Dynamic response parameters on C2 point of square Heytex membrane

Full size image
Fig. 14
figure 14

Dynamic response parameters on C3 point of square Heytex membrane

Full size image
Fig. 15
figure 15

Dynamic response parameters on C1 point of square ZZF membrane

Full size image
Fig. 16
figure 16

Dynamic response parameters on C2 point of square ZZF membrane

Full size image
Fig. 17
figure 17

Dynamic response parameters on C3 point of square ZZF membrane

Full size image

By analyzing the results of amplitude and frequency of membrane vibration under different pretensions, it can be revealed that at lower pretensions, the membrane surface has a little relaxation, and its elastic restoring force is smaller. Obviously, the velocity and acceleration of membrane surface vibration are smaller, but the vibration amplitude is larger under displacement excitation. With the increase of pretension, the elastic restoring force of membrane increases gradually, which leads to the decrease of the transverse deformation ability of membrane under the same displacement excitation. It is found that when the initial pretension is about 6 kN, the change of membrane amplitude tends to be smooth with the increase of the initial pretension.

The original intention of pre-tensioning membrane is to form stiffness for the membrane to resist external load. The results show that when the pretension is more than 6 kN, the increasing of the pretension has little effect on the membrane stiffness. In addition, too much tension will increase the difficulty of construction technology. Of course, the economy is unreasonable. Through the above analysis, our paper gives the maximum initial stress of membrane surface considering economy. The length of the membrane used in the analysis is 1.2 m, and the thickness of the common membrane in the market is about 0.8 mm as shown in Table 2. Therefore, the economic limit of the maximum initial stress on the membrane surface is about 6.25 × 106 N/m2.

Table 2 Thickness of the membrane
Full size table

Conclusion

In this paper, the parameter transformation idea of the improved Lindestedt–Poincaré method is introduced into the multi-scale method, and the improved multi-scale method is proposed. Then, strongly non-linear damped vibration of orthotropic membrane under initial displacement is solved using this method, and the explicit expression of the first-order perturbation solution of the strongly non-linear vibration system of membrane with damping is derived, which is compared with the numerical calculation results and experimental results. The main conclusions can be summarized as follows:

  • Compared with the traditional perturbation method, the improved multi-scale method can solve the large deflection vibration problem effectively, and the result is more accurate. Furthermore, the improved multi-scale method proposed in this paper is not limited by the initial excitation energy (such as the initial vertical displacement applied on the membrane surface).

  • The orthotropic and geometrical non-linearity of the membrane has a great influence on the vibration frequency of the membrane. The vibration frequency of each order calculated by the strongly non-linearity theory is less than that calculated by the weak non-linearity theory.

  • Pretension can increase the stiffness of membrane. However, the increase of membrane stiffness is limited when the pretension increases to a certain extent. According to the theoretical analysis and successful experimental results, the economic limit of the maximum initial stress on the membrane surface is about 6.25 × 106 N/m2.