Effects of Vibration Isolator on Compound Planetary Gear Train with Marine Twin-Layer Gearbox Case: a Dynamic Load Analysis

Abstract

Purpose

This study aims to take the compound planetary gear train as an example to investigate how the vibration isolator affects the dynamic characteristics of the gear system.

Methods

The dynamic parameters are obtained from the finite element model of the gearbox case with the vibration isolators by the substructure method. The lumped mass method is used to construct the systematic coupled dynamic model of the compound planetary gear train with the marine twin-layer gearbox case. The dynamic response of the coupled system is calculated by the numerical calculation method of the Fourier series.

Results

The number of vibration isolators negatively affects the bearing forces of the input shaft, output shaft, and planets. The influence of the number of vibration isolators on LSCs is different in the differential stage and the encased stage. When the vibration isolators stiffness is less than 200 N/μm, the stiffness of the vibration isolator has a significant effect on the bearing forces of the input shaft, output shaft, and planets. The increase in the stiffness of the vibration isolator would increase the LSCs of the differential stage and decrease the LSCs of the encased stage.

Conclusions

The number and stiffness of the vibration isolator have influences on the bearing forces and the LSCs. Compared with the LSCs in the differential stage, the LSCs in the encased stage are more sensitive to the number and stiffness of vibration isolators.

Introduction

Excessive vibration of the gearbox in ship equipment not only reduces the reliability of the compound planetary gear train, but also weakens the acoustical stealth of ship [1]. To reduce the vibration noise, vibration isolation, also called elastic components, is generally used in rotating machinery equipment [2, 3]. However, the influence of the vibration isolator on the dynamic behavior of the gear system has not received enough attention. The purpose of this study is to explore how the vibration isolator affects the dynamic behavior of the gear system by taking the compound planetary gear train as an example.

The existing literature on the dynamic characteristics of the planetary gear train focuses on time-varying meshing stiffness, piecewise backlash, planet bearing stiffness, and comprehensive gear errors [4,5,6,7,8]. Considering the flexible support and multiple manufacturing errors, Mo et al. [9] established the refined dynamic model of the compound planetary gear train to calculate the loading sharing coefficient and floating orbits of center gears. Zhang et al. [10] studied the modal properties of the planetary gear train of the helicopter under the gyroscopic effect. Besides, some researchers have considered the flexibility of the gearbox case. Lin et al. [11] utilized the experimental modal analysis method to identify the joint parameters of the gearbox case, and then used modal superposition method to analyze the coupling dynamics model of the full finite element gearbox. To investigate the vibration response of the gearbox case, Zhou et al. [3] and Guo et al. [12] applied the bearing dynamic load calculated by the gear system dynamics model to the gearbox case finite element model. Using the mode mechanical impedance synthesis analysis, Ren et al. [13] established the coupled impedance dynamic model of the gear-shaft-bearing-housing to analyze the system dynamic characteristics. To improve the accuracy of the investigation, Wang et al. [14] considered the basic admittance characteristics in the dynamic model of marine gear system. Using the dynamic substructuring method, Abbes et al. [15] analyzed the overall dynamic behavior of the parallel helical gear transmission. Zhu et al. [16] obtained the stiffness of the wind turbine gearbox case using the substructure method, and then coupled it to the dynamics model of the planetary gear system with flexible pins.

Besides, some scholars pay attention to the vibration transmission path of gearbox. Zhou et al. [17] added spring elements between the marine gearbox and the installation base to study the dynamic response of the gearbox, but they overlooked the flexibility of the gearbox when calculating the dynamic load of the gearbox. Wang et al. [18] found that the design of a new compounded periodic struts between the helicopter cabin and the gearbox can alleviate the cabin noise caused by the gearbox. Luan et al. [2] coupled the double-layer gearbox case with the planetary gear transmission system through MASTA software, and they found that adding vibration isolators between the double gearbox case can effectively reduce the vibration noise of the gearbox.

Considering all of the above evidence, many studies regard planet bearings as isotropic spring units when constructing system dynamics models, while the asymmetry and interaction of stiffness and damping of planet bearing are overlooked. Moreover, most of the researches focus on the optimization of gear transmission system, while few researches investigate the optimization of gearbox-case dynamic parameters. It would, therefore, be interesting to investigate the role of vibration isolator in marine twin-layer gearbox case. The purpose of this study is to address the following two questions: (a) how the system dynamics model incorporates the asymmetry and interaction of the stiffness and damping of planet bearings; (b) how the number and stiffness of the vibration isolator affect the dynamic characteristics of the compound planetary gear train.

This study is organized as follows. First, the dynamic parameters are extracted from the finite element model of the gearbox case by the substructure method. Second, the systematic coupled dynamic model of the compound planetary gear train with the gearbox case is established by the lumped mass method. The dynamic response of the coupled system is solved by the numerical calculation method of the Fourier series. Third, the influences of the number and stiffness of the vibration isolators on the dynamic behavior of the compound planetary gear train are explored. This finding may expand the literature on vibration isolators and rotating machinery equipment, and provide guidance for the optimization of the marine gearbox case structure.

Systematic Coupled Dynamic Model

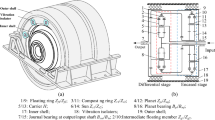
Figure 1 shows a schematic diagram of the compound planetary gear train with a marine twin-layer gearbox case, which consists of a differential stage and an encased stage. The numbers in Fig. 1 represent the elements of the compound planetary gear train with marine twin-layer gearbox case, and the names of their corresponding elements are listed in Table 1. The cylindrical vibration isolators are placed radially between the inner and outer shells.

Fig. 1

Schematic diagram of compound planetary gear train with marine twin-layer gearbox case

Table 1 Names of the elements of the compound planetary gear train with marine twin-layer gearbox case

Figure 2 illustrates the dynamic model of the compound planetary gear train with the marine twin-layer gearbox case. The differential stage uses the rotational coordinate system. In Fig. 2, H_I, V_I, H_p, and V_p are the rotating coordinate systems based on the rotation angular velocity ω_c of carrier H. The encased stage is fixed on the inner shell of gearbox. The encased stage uses the fixed coordinate system. H_II, V_II, H_m, and V_m are the fixed coordinate systems. X, Y, and Z in the global coordinate system mean axial, vertical, and horizontal directions, respectively. The Z and Y directions in the global coordinate system are the same as the H_II and V_II directions in the fixed coordinate system. The displacement vector X for the coupling system is defined as follows:

$$ {\mathbf{X}} = \left\{ {{\mathbf{X}}_{s1} \;,} \right.\;{\mathbf{X}}_{pi} \;,{\mathbf{X}}_{r1} \;\;,x_{g1} \;,x_{f1} \;,{\mathbf{X}}_{s2} \;,{\mathbf{X}}_{mj} \;\;,{\mathbf{X}}_{r2} \;,x_{g2} \;,x_{f2} \;,{\mathbf{X}}_{c} \;,\left. {\;{\mathbf{X}}^{g}_{\text{in}} \;,{\mathbf{X}}^{g}_{\text{out}} \;,{\mathbf{X}}^{g}_{mj} \;} \right\}^{\text{T}} , $$

(1)

where X_s1, X_pi, X_r1, and X_c are the displacement vectors of the sun, planet, ring gear, and carrier in the differential stage, respectively. X_s2, X_mj, and X_r2 are the displacement vectors of the sun, planet, and ring gear in the encased stage, respectively. These displacement vectors include torsion and two translational degrees of freedom. x_g1, x_f1, x_g2, and x_f2 are torsional line displacements along the pitch circle radius of Z_g1, Z_f1, Z_g2, and Z_f2, respectively. X ^g_in and X ^g_out are the displacement vectors of the gearbox case at the input and output, respectively. X ^g_mj is the displacement vectors of the carrier of the encased stage. There are two degrees of translational freedom in X ^g_in , X ^g_out , and X ^g_mj .

Fig. 2

Dynamic model of the compound planetary gear train with marine twin-layer gearbox case

Calculation of Journal Bearing Forces

The oil film force of journal bearing can be expressed by four stiffness coefficients and four damping coefficients when the displacement and velocity of journal shaft remain small disturbance near the static equilibrium position [19]. The stiffness and damping matrices of the journal bearing can be expressed as follows:

$$ {\mathbf{K}}_{b} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & {k_{xx} } & {k_{xy} } \\ 0 & {k_{yx} } & {k_{yy} } \\ \end{array} } \right],\;{\mathbf{C}}_{b} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & {c_{xx} } & {c_{xy} } \\ 0 & {c_{yx} } & {c_{yy} } \\ \end{array} } \right], $$

(2)

where k_ij and c_ij (i, j = x, y) are the stiffness coefficient and damping coefficient of journal bearing, respectively.

Fig.ure illustrates the relationships among the components of the differential stage. In Fig. 3, ψ_pi is the phase angle of the ith planet, ψ_pi= 2π(i − 1)/N. N denotes the number of differential stage planetary gears. α_rp (α_sp) represents the pressure angle of the internal (external) mesh pair.

Fig. 3

Schematic diagram of the geometric relationship among components in the differential stage

Based on the Eq. (2), the ith planet bearing force in the differential stage can be obtained as follows:

$$ {\mathbf{F}}_{pi}^{b} = {\mathbf{K}}_{pi}^{b} \left( {{\mathbf{T}}_{pi}^{D} {\mathbf{X}}_{c} - {\mathbf{X}}_{pi} } \right) + {\mathbf{C}}_{pi}^{b} \left( {{\mathbf{T}}_{pi}^{D} {\dot{\mathbf{X}}}_{c} - {\dot{\mathbf{X}}}_{pi} } \right), $$

(3)

where K ^b_pi denotes the stiffness matrix of planet bearing. C ^b_pi means the damping matrix of planet bearing.${\dot{\mathbf{X}}}_{c}$ is the velocity vector of the carrier. ${\dot{\mathbf{X}}}_{pi}$ is the velocity vector of the ith planet in the differential stage. T ^D_pi is the transfer matrix, which can be obtained from Eq. (4):

$$ \varvec{T}_{pi}^{D} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & {\cos \psi_{pi} } & {\sin \psi_{pi} } \\ 1 & { - \sin \psi_{pi} } & {\cos \psi_{pi} } \\ \end{array} } \right] $$

(4)

The bearing forces on the input and output shafts can be defined by Eq. (5):

$$ \left\{ \begin{aligned} {\mathbf{F}}_{\text{in}}^{b} = {\mathbf{K}}_{\text{in}}^{b} \left( {{\mathbf{X}}_{c} - {\mathbf{X}}_{\text{in}}^{g} } \right) + {\mathbf{C}}_{\text{in}}^{b} \left( {{\dot{\mathbf{X}}}_{c} - {\dot{\mathbf{X}}}_{\text{in}}^{g} } \right) \hfill \\ {\mathbf{F}}_{\text{out}}^{b} = {\mathbf{K}}_{\text{out}}^{b} \left( {{\mathbf{X}}_{c} - {\mathbf{X}}_{\text{out}}^{g} } \right) + {\mathbf{C}}_{\text{out}}^{b} \left( {{\dot{\mathbf{X}}}_{c} - {\dot{\mathbf{X}}}_{\text{out}}^{g} } \right) \hfill \\ \end{aligned} \right., $$

(5)

where K ^b_in (K ^b_out ) is the bearing stiffness matrix of the input (output) shaft. C ^b_in (C ^b_out ) is the bearing damping matrix of the input (output) shaft. ${\dot{\mathbf{X}}}_{\text{in}}^{g}$(${\dot{\mathbf{X}}}_{\text{out}}^{g}$) is the velocity vector of the planetary gearbox at the input (output).

The jth planet bearing force in the encased stage can be expressed by Eq. (6):

$$ {\mathbf{F}}_{mj}^{b} = {\mathbf{K}}_{mj}^{b} \left( {{\mathbf{T}}_{mj}^{D} {\mathbf{X}}_{mj}^{g} - {\mathbf{X}}_{mj} } \right) + {\mathbf{C}}_{mj}^{b} \left( {{\mathbf{T}}_{mj}^{D} {\dot{\mathbf{X}}}_{mj}^{g} - {\dot{\mathbf{X}}}_{mj} } \right), $$

(6)

where K ^b_mj is the stiffness matrix of the planet bearing in the encased stage. C ^b_mj represents the damping matrix of planet bearing in the encased stage. ${\dot{\mathbf{X}}}^{g}_{mj}$ is the velocity vector of the carrier. ${\dot{\mathbf{X}}}_{mj}$ is the velocity vector of the jth planet. T ^D_mj is the transfer matrix, which is calculated by Eq. (7):

$$ \varvec{T}_{mj}^{D} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & {{ \cos }\psi_{mj} } & {\sin \psi_{mj} } \\ 0 & { - \sin \psi_{mj} } & {\cos \psi_{mj} } \\ \end{array} } \right], $$

(7)

where ψ_mj is the phase angle of the jth planet, ψ_mj= 2π(j − 1)/M. M represents the number of gears in encased stage planetary gears. The matrices in Eq. (3) and Eq. (6) are listed in the “Appendix”.

Calculation of the Meshing Force

The Fourier series method is used to calculate the time-varying meshing stiffness of herringbone gears as follows:

$$ K(t) = 2k_{0} \left( {1 + \sum\limits_{k = 1}^{5} {\left[ {A_{k} \cos \left( {2\pi k\frac{t}{{T_{m} }} - \gamma } \right) + B_{k} \sin \left( {2\pi k\frac{t}{{T_{m} }} - \gamma } \right)} \right]} } \right)\frac{{b\varepsilon_{\alpha } }}{{2\cos \beta_{b} }}, $$

(8)

where k₀ represents the mean value for the time-varying meshing stiffness. ε_α, β_b, and b denote end-face contact ratio, helical angle, and gear tooth width, respectively. t and T_m represent the meshing time and meshing period. γ means the mesh phasing facto [20]. A_k and B_k are obtained from Eq. (9):

$$ \left\{ \begin{aligned} A_{k} = \frac{1}{{2\varepsilon_{\alpha } \varepsilon_{\beta } \pi^{2} k^{2} }}\left[ {\cos \left( {2\pi k\varepsilon_{\beta } } \right) + \cos \left( {2\pi k\varepsilon_{\alpha } } \right) - \cos \left[ {2\pi k(\varepsilon_{\alpha } + \varepsilon_{\beta } )} \right] - 1} \right] \hfill \\ B_{k} = \frac{1}{{2\varepsilon_{\alpha } \varepsilon_{\beta } \pi^{2} k^{2} }}\left[ {\sin \left( {2\pi k\varepsilon_{\beta } } \right) + \sin \left( {2\pi k\varepsilon_{\alpha } } \right) - \sin \left( {2\pi k(\varepsilon_{\alpha } + \varepsilon_{\beta } )} \right)} \right] \hfill \\ \end{aligned} \right., $$

(9)

where ε_β denotes axial contact ratio for the herringbone gear.

According to Fig. 3, the equivalent displacement for each gear pair is projected into the meshing line direction, which is expressed as follows:

$$ \left\{ \begin{aligned} S_{rpi} (t) = \left( {x_{pi} + H_{pi} \sin \alpha_{rp} - V_{pi} \cos \alpha_{rp} } \right) - \left( {x_{r1} + H_{r1} \sin \psi_{{rp_{i} }} - V_{r1} \cos \psi_{{rp_{i} }} } \right) - e_{rpi} (t) \hfill \\ S_{spi} (t) = \left( {x_{s1} - H_{s1} \sin \psi_{{sp_{i} }} + V_{s1} \cos \psi_{{sp_{i} }} } \right) - \left( {x_{pi} + H_{pi} \sin \alpha_{sp} + V_{pi} \cos \alpha_{sp} } \right) - e_{spi} (t) \hfill \\ \end{aligned} \right., $$

(10)

where e_rpi (e_spi) is the equivalent error of the internal (external) mesh pair along meshing line direction. x_s1, x_pi, and x_r1 denote the torsional line displacements of Z_s1, Z_pi, and Z_r1, respectively. H_s1, H_pi, and H_r1 represent the horizontal displacements of Z_s1, Z_pi, and Z_r1, respectively. V_s1, V_pi, and V_r1 mean the vertical displacements of Z_s1, Z_pi, and Z_r1, respectively. ψ_rpi (ψ_spi) denotes the position angles of the internal (external) mesh pair, which can be calculated by Eq. (11)

$$ \left\{ \begin{aligned} \psi_{rpi} = \psi_{pi} { + }\alpha_{rp} \hfill \\ \psi_{spi} = \psi_{pi} - \alpha_{sp} \hfill \\ \end{aligned} \right.. $$

(11)

Based on Eq. (12), the equivalent displacement in the encased stage is obtained by Eq. (12):

$$ \left\{ \begin{aligned} S_{rmj} (t) = \left( {x_{mj} + H_{mj} \sin \alpha_{rm} - V_{mj} \cos \alpha_{rm} } \right) - \left( {x_{r2} + H_{r2} \sin \psi_{rmj} - V_{r2} \cos \psi_{rmj} } \right) - e_{rmj} (t) \hfill \\ S_{smj} (t) = \left( {x_{s2} - H_{s2} \sin \psi_{smj} + V_{s2} \cos \psi_{smj} } \right) - \left( {x_{mj} + H_{mj} \sin \alpha_{sm} + V_{mj} \cos \alpha_{sm} } \right) - e_{smj} (t) \hfill \\ \end{aligned} \right., $$

(12)

where x_s2, x_mj, and x_r2 denote the torsional line displacements of Z_s2, Z_mj, and Z_r2, respectively. H_s2, H_mj, and H_r2 represent the horizontal displacements of Z_s2, Z_mj, and Z_r2, respectively. V_s2, V_mj, and V_r2 mean the vertical displacements of Z_s2, Z_mj, and Z_r2, respectively. ψ_rmj (ψ_smj) is the position angles of the internal (external) mesh pair, which can be expressed by Eq. (13):

$$ \left\{ \begin{aligned} \psi_{rmj} = \psi_{mj} { + }\alpha_{rm} \hfill \\ \psi_{smj} = \psi_{mj} - \alpha_{sm} \hfill \\ \end{aligned} \right.. $$

(13)

The resultant meshing force for elasticity and damping is defined by Eq. (14):

$$ P_{i} (t) = K_{i} \left( t \right)S_{i} (t) + C_{i} \dot{S}_{i} (t),\;\;i = spi,rpi,smj,\;{\text{and }}rmj, $$

(14)

where $\dot{S}_{i} (t)$ represents the first-order derivative of equivalent displacement. C_i denotes the meshing damping factor.

Dynamic Equation of Compound Planetary Gear Train

According to Fig. 2, differential equations of the compound planetary gear train are constructed by Newton’s second law.

In the differential stage, differential equations can be expressed by

• 1. Sun gear Z_s1:

  $$ \left\{ \begin{aligned} m_{s1} \ddot{x}_{s1} + \sum\limits_{i = 1}^{N} {P_{spi} (t)} = \frac{{T_{D} }}{{r_{s1b} }} \hfill \\ M_{s1} \left( {\ddot{H}_{s1} - 2\omega_{c} \dot{V}_{s1} - \omega_{c}^{2} H_{s1} } \right) - \sum\limits_{i = 1}^{N} {P_{spi} (t)} \sin \psi_{spi} = - M_{s1} g\sin (\omega_{c} t) \hfill \\ M_{s1} \left( {\ddot{V}_{s1} + 2\omega_{c} \dot{H}_{s1} - \omega_{c}^{2} V_{s1} } \right) + \sum\limits_{i = 1}^{N} {P_{spi} (t)} \cos \psi_{spi} = - M_{s1} g\cos (\omega_{c} t) \hfill \\ \end{aligned} \right. $$

  (15)

  where T_D is the input torque on the sun gear Z_s1. r_s1b represents the base circle radius of the sun gear Z_s1. m_s1 means the equivalent mass of the sun gear Z_s1. M_s1 is the actual mass of the sun gear Z_s1.

• 2. Planet gear Z_pi:

  $$ \left\{ \begin{aligned} m_{p} \ddot{x}_{pi} - P_{spi} (t) + P_{rpi} (t) = 0 \hfill \\ M_{p} \left( {\ddot{H}_{pi} - 2\omega_{c} \dot{V}_{pi} - \omega_{c}^{2} H_{pi} } \right) - P_{spi} (t)\sin \alpha_{sp} + P_{rpi} (t)\sin \alpha_{rp} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - F_{Hcpi} (t) = - M_{p} g\sin (\omega_{c} t + \psi_{pi} ) + F_{pi} \hfill \\ M_{p} \left( {\ddot{V}_{pi} + 2\omega_{c} \dot{H}_{pi} - \omega_{c}^{2} V_{pi} } \right) - P_{spi} (t)\cos \alpha_{sp} - P_{rpi} (t)\cos \alpha_{rp} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - F_{Vcpi} (t) = - M_{p} g\cos (\omega_{c} t + \psi_{pi} ) \hfill \\ \end{aligned} \right. $$

  (16)

  where m_p means the equivalent mass of the ith planet Z_pi. M_p is the actual mass of the ith planet Z_pi. F_Hcpi(t) (F_Vcpi(t)) denotes the ith planet bearing force in the horizontal (vertical) direction, which can be obtained by the Eq. (5). F_pi means the centrifugal force of the ith planet.

• 3. Composting ring gear Z_r1:

  $$ \left\{ \begin{aligned} m_{r1} \ddot{x}_{r1} - \sum\limits_{i = 1}^{N} {P_{rpi} (t)} + k_{g1q} \left( {x_{r1} - x_{g1} } \right) = 0 \hfill \\ M_{r1} \left( {\ddot{H}_{r1} - 2\omega_{c} \dot{V}_{r1} - \omega_{c}^{2} H_{r1} } \right) - \sum\limits_{i = 1}^{N} {P_{rpi} (t)} \sin \psi_{rpi} + K_{r1} H_{r1} = - M_{r1} g\sin (\omega_{c} t) \hfill \\ M_{r1} \left( {\ddot{V}_{r1} + 2\omega_{c} \dot{H}_{r1} - \omega_{c}^{2} V_{r1} } \right) + \sum\limits_{i = 1}^{N} {P_{rpi} (t)} \cos \psi_{rpi} + K_{r1} V_{r1} = - M_{r1} g\cos (\omega_{c} t) \hfill \\ \end{aligned} \right. $$

  (17)

  where m_r1 means the equivalent mass of the composting ring gear Z_r1. M_r1 is the actual mass of the composting ring gear Z_r1.

• 4. Intermediate floating member Z_g1 and floating ring Z_f1:

  $$ \left\{ \begin{aligned} m_{g1} \ddot{x}_{g1} - K_{g1q} \left( {x_{r1} - x_{g1} } \right) + K_{f1q} \left( {x_{g1} - x_{f1} } \right) = 0 \hfill \\ m_{f1} \ddot{x}_{f1} - K_{f1q} \left( {x_{g1} - x_{f1} } \right) + \frac{{K_{f1s2} }}{{r_{f1b} }}\left( {\frac{{x_{f1} }}{{r_{f1b} }} - \frac{{x_{s2} }}{{r_{s2b} }}} \right) = 0 \hfill \\ \end{aligned} \right. $$

  (18)

  where m_g1 represents the equivalent mass of the intermediate floating member Z_g1. m_f1 denotes the equivalent mass of the floating ring Z_f1. r_s2b is the base circle radius of the sun gear Z_s2. r_f1b means the pitch circle radius of the floating ring gear Z_f1.

In the encased stage, differential equations can be expressed by

• 1. Sun gear Z_s2:

  $$ \left\{ \begin{aligned} m_{s2} \ddot{x}_{s2} - \frac{{K_{f1s2} }}{{r_{s2b} }}\left( {\frac{{x_{f1} }}{{r_{f1b} }} - \frac{{x_{s2} }}{{r_{s2b} }}} \right) + \sum\limits_{j = 1}^{M} {P_{smj} (t)} = 0 \hfill \\ M_{s2} \ddot{H}_{s2} - \sum\limits_{j = 1}^{M} {P_{smj} (t)} \sin \psi_{smj} + K_{s2} H_{s2} = 0 \hfill \\ M_{s2} \ddot{V}_{s2} + \sum\limits_{j = 1}^{M} {P_{smj} (t)} \cos \psi_{smj} + K_{s2} V_{s2} = - M_{s2} g \hfill \\ \end{aligned} \right. $$

  (19)

  where m_s2 means the equivalent mass of the sun gear Z_s2. M_s2 is the actual mass of the sun gear Z_s2.

• 2. Planet gear Z_mj:

  $$ \left\{ \begin{aligned} m_{m} \ddot{x}_{mj} - P_{smj} (t) + P_{rmj} (t) = 0 \hfill \\ M_{m} \ddot{H}_{mj} - P_{smj} (t)\sin \alpha_{sm} { + }P_{rmj} (t)\sin \alpha_{rm} - F_{Hmj} (t) = - M_{m} g\sin \psi_{mj} \hfill \\ M_{m} \ddot{V}_{mj} - P_{smj} (t)\cos \alpha_{sm} - P_{rmj} (t)\cos \alpha_{rm} - F_{Vmj} (t) = - M_{m} g\cos \psi_{mj} \hfill \\ \end{aligned} \right. $$

  (20)

  where F_Hmj(t) (F_Vmj(t)) denotes the jth planet bearing force in the horizontal (vertical) direction. m_m means the equivalent mass of the jth planet Z_mj. M_m is the actual mass of the jth planet Z_mj.

• 3. Composting ring gear Z_r2:

  $$ \left\{ \begin{aligned} m_{r2} \ddot{x}_{r2} - \sum\limits_{j = 1}^{M} {P_{rmj} (t)} + k_{g2q} \left( {x_{r2} - x_{g2} } \right) = 0 \hfill \\ M_{r2} \ddot{H}_{r2} - \sum\limits_{j = 1}^{M} {P_{rmj} (t)} \sin \psi_{rmj} + K_{r2} H_{r2} = 0 \hfill \\ M_{r2} \ddot{V}_{r2} + \sum\limits_{i = 1}^{M} {P_{rmj} (t)} \cos \psi_{rmj} + K_{r2} V_{r2} = - M_{r2} g \hfill \\ \end{aligned} \right. $$

  (21)

  where m_r2 means the equivalent mass of the composting ring gear Z_r2. M_r2 is the actual mass of the composting ring gear. Z_r2

• 4. Intermediate floating member Z_g2 and floating ring Z_f2:

  $$ \left\{ \begin{aligned} m_{g2} \ddot{x}_{g2} - K_{g2q} \left( {x_{r2} - x_{g2} } \right) + K_{f2q} \left( {x_{g2} - x_{f2} } \right) = 0 \hfill \\ m_{f2} \ddot{x}_{f2} - K_{f2q} \left( {x_{g2} - x_{f2} } \right) + \frac{{K_{f2L} }}{{r_{f2b} }}\left( {\frac{{x_{f2} }}{{r_{f2b} }} - \frac{{x_{c} }}{{r_{L} }}} \right) = 0 \hfill \\ \end{aligned} \right. $$

  (22)

  where m_g1 represents the equivalent mass of the intermediate floating member Z_g2. m_f2 denotes the equivalent mass of the floating ring Z_f2. r_f2b denotes pitch circle radius of floating ring gear Z_f2. r_L represents the rotation radius of the carrier.

Besides, the differential equation of carrier H can be expressed by

$$ \left\{ \begin{aligned} m_{\text{c}} \ddot{x}_{\text{c}}& + \sum\limits_{i = 1}^{N} {F_{Hcpi} } + \frac{{K_{cL} }}{{r_{\text{c}} }}\frac{{x_{c} }}{{r_{\text{c}} }} - \frac{{K_{f2L} }}{{r_{f2b}^{2} }}\left( {x_{f2} - \frac{{x_{c} }}{{r_{L} }}r_{f2b} } \right) = - P_{L} \\& M_{\text{c}} \left( {\ddot{H}_{\text{c}} - 2\omega_{\text{c}} \dot{V}_{\text{c}} - \omega_{\text{c}}^{2} H_{\text{c}} } \right) + F_{H}^{\text{in}} + F_{H}^{\text{out}}\hfill \\& + \sum\limits_{i = 1}^{N} {\left( {F_{Hcpi} \cos \psi_{pi} - F_{Vcpi} \sin \psi_{pi} } \right)} = - M_{\text{c}} g\sin (\omega_{\text{c}} t) \hfill \\& M_{\text{c}} \left( {\ddot{V}_{\text{c}} + 2\omega_{\text{c}} \dot{H}_{\text{c}} - \omega_{\text{c}}^{2} V_{\text{c}} } \right) + F_{V}^{\text{in}} + F_{V}^{\text{out}}\hfill \\& +\sum\limits_{i = 1}^{N} {\left( {F_{Hcpi} \sin \psi_{pi} + F_{Vcpi} \cos \psi_{pi} } \right)} = - M_{\text{c}} g\cos (\omega_{\text{c}} t) \hfill \\ \end{aligned} \right., $$

(23)

where F ⁱⁿ_H (F ^out_H ) represents the bearing force of the input (output) shaft in the horizontal direction. F ⁱⁿ_V (F ^out_V ) denotes the bearing force of the input (output) shaft in the vertical direction. m_c is the equivalent mass of the carrier. M_c is the actual mass of the carrier. P_L represents the equivalent force of the output torque.

Dynamic Equation of the Marine Twin-Layer Gearbox Case

The substructure method that can effectively reduce the degree of freedom of the gearbox model is used to calculate the mass, stiffness and damping matrices for the marine twin-layer gearbox case. This gearbox case is made of alloy steel with a density of 7900 kg/m³, an elastic modulus of 2.05 × 10⁵ MPa, and Poisson’s ratio of 0.3. The finite element model of the twin-layer gearbox case includes 828,873 nodes and 585,756 elements, as shown in Fig. 4.

Fig. 4

Finite-element model of the marine twin-layer gearbox case, a the integral structure of the gearbox case, b the carrier of the encased stage mounted in the inner shell. c The output end of the gearbox case. d The input end of the gearbox case

The spring element with stiffness and damping is used to simulate the cylindrical vibration isolator placed between the inner and outer shells. The stiffness and damping of the spring element are 7.3 × 10⁶ N/m and 6.6 × 10⁵ N s/m, respectively. The master node is built in the center of the bearing hole and is rigidly coupled to the slave node on the surface of the bearing hole (see Fig. 4b–d). The bolt holes at the bottom of the gearbox case are given a fixed constraint. When solving, the mass, stiffness, and damping matrices of the slave nodes are all condensed to the master node. Therefore, the dynamic parameters of the gearbox case can be characterized by the mass matrix, stiffness matrix and damping matrix on the master node.

After condensing, the dynamic equation of twin-layer gearbox case is expressed as

$$ {\mathbf{M}}_{g} {\mathbf{X}}_{g} + {\mathbf{C}}_{g} \left( {{\dot{\mathbf{X}}}_{g} - {\dot{\mathbf{X}}}_{cm} } \right) + {\mathbf{K}}_{g} \left( {{\mathbf{X}}_{g} - {\mathbf{X}}_{cm} } \right) = {\mathbf{F}}_{g} $$

(24)

where M_g, K_g, and C_g are mass, stiffness, and damping matrices of the master nodes on the twin-layer gearbox case, respectively. X_g is the displacement vector of the master nodes on the twin-layer gearbox case, ${\mathbf{X}}_{g} \, = \,\left\{ {{\mathbf{X}}^{\text{g}}_{\text{in}} ,{\mathbf{X}}^{g}_{\text{out}} ,{\mathbf{X}}^{\text{g}}_{mj} } \right\}$. X_cm is the displacement vector in the gear system, X_cm= {X_c, X_mj}. F_g is the force vector of the journal bearing force and gravity.

Systematic Coupled Dynamic Equation

Based on the above equation, the coupled dynamic equation of the compound planetary gear train with the twin-layer gearbox case can be expressed with the following matrix–vector form as

$$ {\mathbf{M\ddot{X}}}(t) + \left( {{\mathbf{K}}_{b}^{{}} + {\mathbf{K}}_{m}^{{}} (t) - \omega_{c}^{2} {\mathbf{K}}_{\omega } } \right)\left[ {{\mathbf{X}}(t) - {\mathbf{e}}(t)} \right] + \left( {{\mathbf{C}}_{b}^{{}} + {\mathbf{C}}_{m}^{{}} + \omega_{c} {\mathbf{G}}} \right)\left[ {{\dot{\mathbf{X}}}(t) - {\dot{\mathbf{e}}}(t)} \right] = {\mathbf{F}}\left( t \right) $$

(25)

where M and G denote the mass and gyroscopic matrices, respectively. K_b and C_b are the bearing stiffness and damping matrices, respectively. ${\mathbf{K}}_{\omega }^{{}}$ is the centripetal stiffness matrix.

K_m(t) and C_m are the meshing stiffness and damping matrices, respectively. F(t) represents the exciting force vector.

Dynamic Characteristics

Solution of Systematic Coupled Dynamic Equation

In Eq. (25), K_m(t) and X (t) can be written as Eq. (26):

$$ \left\{ \begin{aligned} {\mathbf{K}}_{m} \left( t \right) = {\bar{\mathbf{K}}}_{m} + \Delta {\mathbf{K}}_{m} \left( t \right) \hfill \\ {\mathbf{X}}\left( t \right) = {\bar{\mathbf{X}}} + \Delta {\mathbf{X}}\left( t \right) \hfill \\ \end{aligned} \right. $$

(26)

where ${\bar{\mathbf{K}}}_{m}$ is the average stiffness matrix.${\bar{\mathbf{X}}}$ is the static displacement vector. ∆K_m(t) and ∆X(t) are the fluctuating parts of ${\bar{\mathbf{K}}}_{m}$ and ${\bar{\mathbf{X}}}$, respectively.

After substituting Eq. (26) into Eq. (25), the periodic excitation forces on the left side of the Eq. (25) are divided into two parts. One is that the average value remains to the left of Eq. (25). The other is that the fluctuation value is moved to the right of Eq. (25). Thus, systematic coupled dynamic equation is written as Eq. (27), which can be solved by numerical calculation of the Fourier series in Ref. [21]:

$$ [{\mathbf{M}}]\{ \Delta \ddot{X}\} + [{\mathbf{D}}]\{ \Delta \dot{X}\} + [{\bar{\mathbf{K}}}]\{ \Delta X\} = \{ P\} $$

(27)

where {P} is the exciting force vector, including stiffness, error, gravity, planetary centrifugal force, and load.

Calculation of Load Sharing Coefficient

In the differential stage, the external and internal LSCs are defined as Eq. (28):

$$ \left\{ \begin{aligned} b_{spi} = \left| {{{N\left( {P_{spik1} } \right)_{\hbox{max} } } \mathord{\left/ {\vphantom {{N\left( {P_{spik1} } \right)_{\hbox{max} } } {\sum\limits_{i = 1}^{3} {\left( {P_{spik1} } \right)_{\hbox{max} } } }}} \right. \kern-0pt} {\sum\limits_{i = 1}^{3} {\left( {P_{spik1} } \right)_{\hbox{max} } } }} - 1} \right|_{\hbox{max} } + 1 \hfill \\ b_{rpi} = \left| {{{N\left( {P_{rpik2} } \right)_{\hbox{max} } } \mathord{\left/ {\vphantom {{N\left( {P_{rpik2} } \right)_{\hbox{max} } } {\sum\limits_{i = 1}^{3} {\left( {P_{rpik2} } \right)_{\hbox{max} } } - 1}}} \right. \kern-0pt} {\sum\limits_{i = 1}^{3} {\left( {P_{rpik2} } \right)_{\hbox{max} } } - 1}}} \right|_{\hbox{max} } + 1 \hfill \\ \end{aligned} \right.,\;\left\{ \begin{aligned} k_{1} = 1,2, \ldots ,n_{1} \hfill \\ k_{2} = 1,2, \ldots ,n_{2} \hfill \\ \end{aligned} \right., $$

(28)

where (P_spik1)_max ((P_rpik2)_max) denotes the maximum value of the external (internal) dynamic meshing force in the k₁th (k₂th) meshing period. n₁ (n₂) represents the total number of the meshing period for the external (internal) gear pairs.

Based on Eq. (29), the external and internal LSCs for the encased stage can be constructed by Eq. (29):

$$ \left\{ \begin{aligned} b_{smj} = \left| {{{M\left( {P_{smjk3} } \right)_{\hbox{max} } } \mathord{\left/ {\vphantom {{M\left( {P_{smjk3} } \right)_{\hbox{max} } } {\sum\limits_{i = 1}^{M} {\left( {P_{spmj3} } \right)_{\hbox{max} } } - 1}}} \right. \kern-0pt} {\sum\limits_{i = 1}^{M} {\left( {P_{spmj3} } \right)_{\hbox{max} } } - 1}}} \right|_{\hbox{max} } + 1 \hfill \\ b_{rmj} = \left| {{{M\left( {P_{rmjk4} } \right)_{\hbox{max} } } \mathord{\left/ {\vphantom {{M\left( {P_{rmjk4} } \right)_{\hbox{max} } } {\sum\limits_{i = 1}^{M} {\left( {P_{rmjk4} } \right)_{\hbox{max} } } - 1}}} \right. \kern-0pt} {\sum\limits_{i = 1}^{M} {\left( {P_{rmjk4} } \right)_{\hbox{max} } } - 1}}} \right|_{\hbox{max} } + 1 \hfill \\ \end{aligned} \right.,\;\left\{ \begin{aligned} k_{3} = 1,2, \ldots ,n_{3} \hfill \\ k_{4} = 1,2, \ldots ,n_{4} \hfill \\ \end{aligned} \right., $$

(29)

where (P_smjk3)_max ((P_rpik4)_max) represents the maximum value of the external (internal) dynamic meshing force in the k₃th (k₄th) meshing period. n₃ (n₄) denotes the total number of the meshing period for the external (internal) gear pairs.

According to Eqs. (28) and (29), the LSCs of the coupled system can be expressed by Eq. (30):

$$ \left\{ \begin{aligned} B_{p} = \hbox{max} (b_{spi} ,\;b_{rpi} ) \hfill \\ B_{m} = \hbox{max} (b_{smj} ,\;b_{rmj} ) \hfill \\ \end{aligned} \right. $$

(30)

where B_p is the LSC in the differential stage. B_m is the LSC in the encased stage.

The input torque of the coupling system is 3183 N m, and the input speed is 3000 r/min. Table 2 lists the parameters of the compound planetary gear train with marine twin-layer gearbox case.

Table 2 Parameters of the differential stage

Journal Bearing Forces

Dynamic meshing excitation is transmitted to the gearbox case through bearings in the transmission system, causing the gearbox case to vibrate [12]. Therefore, investigating the bearing dynamic load characteristics can effectively evaluate the vibration isolation performance of the marine twin-layer gearbox case. The vibration responses of compound planetary gear train are obtained by Eq. (27).

The number of vibration isolators in this gearbox case is 18. Figure 5 shows the time and frequency response of the bearing force at the output shaft. The bearing force in the Z direction is ranged between − 2300 and 2440 N, while the bearing force in the Y direction is ranged between − 2109 N and 1770 N. It could be concluded that the amplitude of the bearing force in the Z direction is greater than that in the Y direction. Besides, the frequency responses of the bearing forces in the Z and Y directions are dominated by the meshing frequency f₁ of the differential stage, since the time-varying meshing stiffness of the differential stage is fluctuating. In Fig. 5b–c, f_H, f_p, and f_r1 are the rotation frequencies of the carrier, planet, and ring gear of the differential stage, respectively.

Fig. 5

Bearing force at the output shaft. a Time response in the Z and Y directions, b frequency response in the Z direction, c frequency response in the Y direction

Figure 6 illustrates the time–frequency response of the first planet bearing force in the encased stage. The amplitude of the first planet bearing force in the Z direction is greater than that in the Y direction. In Fig. 6b, c, the frequency responses of the first planet bearing force in both the Z and Y directions are the superposition of the rotation frequencies (i.e., f_m, f_p, f_s2, and f_r2) and the meshing frequency f₂, f_m, f_s2, and f_r2 represent the rotation frequencies of the planet, sun and ring gear of the encased stage, respectively. It’s worth noting that the rotation frequency f_p of the differential stage planet appears in the frequency responses of the planet bearing force of the encased stage.

Fig. 6

First planet bearing force of the encased stage, a time response in the Z and Y directions, b frequency response in the Z direction, c frequency response in the Z direction

Load Sharing Characteristics

The LSCs in the compound planetary gear train with the twin-layer gearbox case are calculated by Eqs. (28) and (29). The results are obtained from the three meshing pairs of the differential stage, as shown in Fig. 7. In the differential stage, the external LSCs range from 0.974 to 1.032 and internal LSCs range from 0.917 to 1.133. Moreover, the (external and internal) LSCs in the differential stage differ significantly among the three meshing pairs. For example, the sp3 LSC is greater than the sp1 and sp2 LSCs (see Fig. 7a).

Fig. 7

LSCs of the differential stage, a external meshing, b internal meshing

It can be drawn from the Eqs. (28) and (29) that the torque of the encased sun gear is Z_r1/Z_s1 times that of the differential sun gear. In other words, the load in the encased stage is greater than load the in the differential stage. Figure 8 shows that the external LSCs in the encased stage are close to 1, with a range of 0.957–1.029; the internal LSCs in the encased stage are varied from 0.966 to 1.018. Besides, the LSCs difference among the five meshing pairs in the encased stage is smaller compared with the differential stage. It is useful to note that the maximum value of LSCs in the differential stage is larger than that of the encased stage. This result is consistent with the conclusion in the literature [22] that the encased stage has a larger load than the differential stage, and thus its balanced load capacity is stronger.

Fig. 8

LSCs of the encased stage, a external meshing, b internal meshing

Impact of Vibration Isolators on the System

According to Eq. (24), the dynamic parameters of the marine twin-layer gearbox case affect the dynamic characteristics of the compound planetary gear train. The stiffness and damping of the marine twin-layer gearbox case are affected by the number and stiffness of the vibration isolators. Therefore, how the number and stiffness of vibration isolator affect the bearing force and load sharing characteristics in the compound planetary gear train is investigated. The effective value of the bearing forces is characterized by the root mean square of the resultant bearing force in the Y and Z directions as follows:

$$ F_{bi} = {\text{RMS}}\left( {\sqrt {F_{biy}^{2} (t) + F_{biz}^{2} (t)} } \right), $$

(31)

where F_bi is the effective value of each journal bearing force. The function RMS() represents taking the root mean square. F_biy and F_biz are the bearing forces in the Y and Z directions, respectively.

Number of the Vibration Isolator

The vibration isolator is radially arranged between the inner and outer shells of the gearbox (see Fig. 1), and its number ranges from 3 to 18. Figure 9 shows the variation of bearing force with the number of vibration isolators on the input and output shafts. In general, when the number of vibration isolators becomes larger, the bearing forces on the output and input shafts become smaller. It’s worth noting that with increasing the number of vibration isolators, the bearing force of the input shaft (Fig. 9a) is generally smaller than that of the output shaft (Fig. 9b). Therefore, the stiffness and damping of the output should be increased in the marine gearbox.

Fig. 9

Influence of the number of the vibration isolator on bearing force, a bearing force of input shaft. b Bearing force of output shaft

Figure 10 illustrates the relationship between the number of vibration isolators and the bearing forces of planet bearings in the encased stage. With the increase of the number of vibration isolators, the bearing forces gradually decreases. This is because the increase in the number of vibration isolators would increase the stiffness and damping of the marine twin-layer gearbox case.

Fig. 10

Influence of the number of vibration isolators on the bearing forces of planet bearings in the encased stage. a The 1st planet bearing. b The 2nd planet bearing, c the 3rd planet bearing, d the 4th planet bearing, e the 5th planet bearing

Figure 11 shows how the LSCs vary with the number of vibration isolators in the compound planetary gear train with the twin-layer gearbox case. Increasing the number of vibration isolators could enhance the LSCs of the differential stage, while the LSCs of the encased stage would decrease with the increase of the number of vibration isolators. This result indicates that compared with the differential stage, the LSCs in the encased stage is more sensitive to the number of vibration isolators.

Fig. 11

Influence of the number of vibration isolators on LSCs of the system, a the differential stage, b the encased stage

Stiffness of the Vibration Isolator

In addition to the number of vibration isolators, the stiffness of vibration isolators is also an important dynamic parameter that affects marine twin-layer gearbox case. In this section, we investigate the effects of isolator stiffness on bearing force and load sharing characteristics. The number of vibration isolators in the gearbox is 18. The stiffness of vibration isolators is discrete in the range of 10–800 N/μm.

Figure 12 shows the influence of the stiffness of the vibration isolator on bearing force of the output and input shafts. When the stiffness of vibration isolators is less than 30 N/μm, the bearing forces on the output and input shafts display the downward trend. This result is because the natural frequency of the system is far from the excitation frequency. At this time, the vibration isolators present better effects of vibration reduction. When the stiffness of vibration isolators ranges from 30 to 200 N/μm, bearing forces on the output and input shafts show an increasing trend. This finding is because the natural frequency of the system is gradually approaching the excitation frequency within the corresponding vibration isolator stiffness range. The vibration reduction effect of the vibration isolator is weakened. When the stiffness of the vibration isolators exceeds 200 N/μm, the bearing forces on the output and input shafts gradually increase and tend to be stable. This is because the natural frequency of the system is greater than the excitation frequency. The vibration isolators fail to reduce vibration within the corresponding vibration isolator stiffness range.

Fig. 12

Influence of the stiffness of the vibration isolator on bearing force of the output and input

Figure 13 shows the relationship between the stiffness of vibration isolators and planet bearing force in the encased stage during the stiffness range of 10–800 N/μm. The bearing forces of planet bearings in the encased stage decrease obviously when the stiffness of the vibration isolators increases from 10 to 200 N/μm. In addition, the bearing forces of planet bearings in the encased stage tend to be stable when the stiffness of vibration isolators is greater than 200 N/μm. This result indicates that when the stiffness of the vibration isolator exceeds 200 N/μm, the performance of the vibration isolator in the marine twin-layer gearbox case would be weakened.

Fig. 13

Influence of vibration isolator stiffness on planet bearing force of the encased stage. a The 1st and 4th planet bearing, b the 2nd, 3rd, and 5th planet bearing

Figure 14 reveals how the stiffness of vibration isolators affects the LSCs in the compound planetary gear train with the twin-layer gearbox case. When the stiffness of vibration isolators is ranged between 10 and 800 N/μm, the LSCs in the differential stage is varied from 1.133082 to 1.133143, and the LSCs in the encased stage is varied from 1.04256 to 1.04336. This result suggests that compared with the differential stage, the LSCs in the encased stage is more sensitive to the stiffness of vibration isolators. Moreover, the LSCs in the differential stage show an upward trend with increasing stiffness of vibration isolators. In contrast, when the stiffness of vibration isolators becomes larger, the LSCs in the encased stage becomes smaller. The LSCs in the differential and encased stages tend to be stable with the increase of vibration isolator stiffness. These results suggest that to improve the performance of the vibration isolator, the stiffness of the vibration isolator could be appropriately reduced in the vibration isolation design.

Fig. 14

Influence of the stiffness of vibration isolators on LSCs of the system, a the differential stage, b the encased stage

Conclusions

The dynamic model of the twin-layer gearbox case with the vibration isolator is constructed, and then coupled with the dynamic model of the compound planetary gear train. The time–frequency responses of journal bearing forces are investigated, and the load sharing characteristics in both differential and encased stages are studied. Besides, the impact of vibration isolators on the bearing force and LSC are explored.

The number and stiffness of vibration isolators could affect the bearing forces and LSC of the compound planetary gear train with the twin-layer gearbox case. As the number of vibration isolators increases, the bearing forces of the input shaft, output shaft, and planets decrease. Besides, the influence of the number of vibration isolators on LSCs is different in the differential stage and the encased stage.

The bearing force curve of the input shaft has a “inflection point” when the stiffness of vibration isolators is 30 N/μm. The variation trend of the bearing force curve of the output shaft is basically the same as that of the input shaft. When the vibration isolators stiffness is less than 200 N/μm, the stiffness of the vibration isolator has a significant negative effect on the bearing force of the planet bearing.

The increase in the stiffness of the vibration isolator would increase the LSCs of the differential stage and decrease the LSCs of the encased stage. Compared with the LSCs in the differential stage, the LSCs in the encased stage is more sensitive to the number and stiffness of vibration isolators. When the stiffness of the vibration isolators is greater than 200 N/μm, it has little effect on the bearing forces and LSCs.

Appendix

$$ \varvec{K}_{pi}^{b} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & {k_{xx}^{p} } & {k_{xy}^{p} } \\ 0 & {k_{yx}^{p} } & {k_{yy}^{p} } \\ \end{array} } \right],\;\varvec{C}_{pi}^{b} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & {c_{xx}^{p} } & {c_{xy}^{p} } \\ 0 & {c_{yx}^{p} } & {c_{yy}^{p} } \\ \end{array} } \right], $$

(32)

$$ \left\{ {\begin{array}{*{20}c} {\varvec{F}_{pi}^{b} = \left[ {\begin{array}{*{20}c} 0 & {F_{Hcpi} } & {F_{Vcpi} } \\ \end{array} } \right]^{\text{T}} } \\ {\varvec{X}_{c} = \left[ {\begin{array}{*{20}c} {x_{c} } & {H_{c} } & {V_{c} } \\ \end{array} } \right]^{\text{T}} } \\ {\varvec{X}_{pi} = \left[ {\begin{array}{*{20}c} {x_{pi} } & {H_{pi} } & {V_{pi} } \\ \end{array} } \right]^{\text{T}} } \\ \end{array} } \right., $$

(33)

$$ \varvec{K}_{\text{in}}^{b} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & {k_{xx}^{\text{in}} } & {k_{xy}^{\text{in}} } \\ 0 & {k_{yx}^{\text{in}} } & {k_{yy}^{\text{in}} } \\ \end{array} } \right],\varvec{C}_{\text{in}}^{b} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & {c_{xx}^{\text{in}} } & {c_{xy}^{\text{in}} } \\ 0 & {c_{yx}^{\text{in}} } & {c_{yy}^{\text{in}} } \\ \end{array} } \right], $$

(34)

$$ \varvec{K}_{\text{out}}^{b} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & {k_{xx}^{\text{out}} } & {k_{xy}^{\text{out}} } \\ 0 & {k_{yx}^{\text{out}} } & {k_{yy}^{\text{out}} } \\ \end{array} } \right],\;\varvec{C}_{\text{in}}^{b} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & {c_{xx}^{\text{out}} } & {c_{xy}^{\text{out}} } \\ 0 & {c_{yx}^{\text{out}} } & {c_{yy}^{\text{out}} } \\ \end{array} } \right], $$

(35)

$$ \left\{ {\begin{array}{*{20}c} {\varvec{F}_{\text{in}}^{b} = \left[ {\begin{array}{*{20}c} 0 & {F_{H}^{\text{in}} } & {F_{V}^{\text{in}} } \\ \end{array} } \right]^{\text{T}} } \\ {\varvec{X}_{\text{in}}^{g} = \left[ {\begin{array}{*{20}c} 0 & {H_{\text{in}}^{g} } & {V_{\text{in}}^{g} } \\ \end{array} } \right]^{\text{T}} } \\ {\varvec{F}_{\text{out}}^{b} = \left[ {\begin{array}{*{20}c} 0 & {F_{H}^{\text{out}} } & {F_{V}^{\text{out}} } \\ \end{array} } \right]^{\text{T}} } \\ {\varvec{X}_{\text{out}}^{g} = \left[ {\begin{array}{*{20}c} 0 & {H_{\text{out}}^{g} } & {V_{\text{out}}^{g} } \\ \end{array} } \right]^{\text{T}} } \\ \end{array} } \right., $$

(36)

$$ \varvec{K}_{mj}^{b} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & {k_{xx}^{m} } & {k_{xy}^{m} } \\ 0 & {k_{yx}^{m} } & {k_{yy}^{m} } \\ \end{array} } \right],\;\varvec{C}_{mj}^{b} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & {c_{xx}^{m} } & {c_{xy}^{m} } \\ 0 & {c_{yx}^{m} } & {c_{yy}^{m} } \\ \end{array} } \right], $$

(37)

$$ \left\{ {\begin{array}{*{20}c} {\varvec{F}_{mj}^{b} = \left[ {\begin{array}{*{20}c} 0 & {F_{Hbmj} } & {F_{Vbmj} } \\ \end{array} } \right]^{\text{T}} } \\ {\varvec{X}_{mj}^{g} = \left[ {\begin{array}{*{20}c} 0 & {H_{b}^{j} } & {V_{b}^{j} } \\ \end{array} } \right]^{\text{T}} } \\ {\varvec{X}_{mj} = \left[ {\begin{array}{*{20}c} {x_{mj} } & {H_{mj} } & {V_{mj} } \\ \end{array} } \right]^{\text{T}} } \\ \end{array} } \right.. $$

(38)