Introduction

The planetary gear transmission system has the advantages of high safety performance, long service life, and large transmission ratio. It is widely used in aviation, shipbuilding, electric power and other mechanical fields. As a key component carried by the planetary gear transmission system, the ring gear is simultaneously subjected to multiple meshing excitation sources, which causes it to become the main component of gear tooth cracks and fatigue damage in the planetary gear system. With the development of precision machinery, planetary gear transmission systems tend to be lightweight. To reduce the quality of the transmission system to meet the needs of the project, the thin-walled ring gear has gradually become popular for practical applications. Therefore, analysis of the vibration characteristics and stress characteristics of the thin-walled ring gear under meshing excitation is of great significance to prevent the occurrence of fatigue damage and ensure the safety of the planetary gear train.

Early research on planetary gear sets focused on system analysis. For example, in the work of Kahraman et al. [1], the torsion model of the planetary gear transmission system was established, and the natural frequency of the planetary gear system was analyzed. Lin and Parker et al. [2] established the analysis model of the planetary gear transmission system and studied its natural frequency and vibration mode. Subsequently, Wu and Parker [3] analyzed the inherent characteristics of the equidistant planetary gear flexible ring gear model by perturbation and a candidate mode method. Tsai and Shyi-Jeng [4] introduced the meshing analysis method of floating sun–planet gear pair, and discussed the influence of assembly and manufacturing error of planetary gear on the backlash and performance the sun gear. Liu et al. [5, 6] calculated the vibration characteristics of herringbone planetary gears and the influence of centrifugal force on the planetary gear transmission system at high speed. Fan et al. [7] calculated and analyzed the dynamic characteristics of the planetary gear transmission system considering the flexibility of the ring gear. In the analysis of the ring gear, the ring is usually used instead of the analysis. Literature [8,9,10,11] employed different methods to study the inherent characteristics of the ring and its vibration characteristics. Tanna et al. [12] used the finite element method to analyze the inherent characteristics of three-dimensional unconstrained ring gear. Subsequently, Wang et al. [13] studied the influence of Meshing Effect on ring gear vibration. Hidaka et al. [14] analyzed that the displacement of the ring gear mainly came from the elastic deformation, and studied the resonance conditions of the ring gear.

Fortunately, many scholars have completed extensive research on gear stress, providing a lot of theoretical support for the research in this work. Argyris et al. [15] proposed a numerical calculation method for the stress analysis of spiral bevel gears. Kahraman et al. [16] calculated the effect of different rim thicknesses on the tooth root stress by taking into account the flexibility of the ring gear. Ming-Jong Wang [17] used a digital photoelastic system to determine the maximum bending stress of spur gears. Wang et al. [18] proposed a finite element analysis method for high contact ratio gears, and calculated tooth root stress and contact stress. Wu et al. [19] proposed a contact stress analysis method for the bevel gear tooth surface considering the influence of tooth contact deformation and tooth bending deflection. Tesfahunegn, Y et al. [20] analyzed the influence of tooth profile modification on transmission error and contact stress. Li et al. [21, 22] used the finite element method to analyze the contact stress of the spur gears and the stress of the thin-sided spur gears with oblique webs in high-speed rotation. Lias et al. [23] studied the influence of spur gears on the bending stress of gears in the case of radial misalignment. Gonzalezperez et al. [24] proposed a finite element model for the calculation of gear contact stress and bending stress, and obtained accurate results. Literature [25, 26] calculated the contact stress and bending stress with the finite element method to provide theoretical guidance for the gears.

Experimental measurement has also been focused of the majority of scholars. Patil et al. [27] used a gear dynamic stress tester (GDSTR) to measure the contact stress of the gear pair and employed the finite element method for simulation comparisons. Dai et al. [28] used the finite element method to calculate the tooth root strain at different speeds, and compared this with the experimental results to obtain a large change in the strain curve under resonance. Literature [29, 30] used fiber Bragg grating (FBG) sensors to measure the dynamic strain of gears under external and internal gearing.

In summary, most of literatures focuses on the dynamic characteristics of planetary gear transmission system. For the gear stress, the analysis mostly concentrates on the external-gear, especially the change in the contact and bending stress of the cylindrical gear under static conditions. The stress analysis of the internal meshing-gear is relatively less. At the same time, the dynamic stress under load is the direct factor affecting the fatigue life of ring gear, and the thin-walled ring gear has greater flexibility, with many uncertainties regarding practical applications. In past research, relatively few studies have been conducted on the thin-walled ring gear.

In this work, a new numerical calculation method for the vibration and stress characteristics of ring gear is proposed. Establishing the dynamic model of planetary gear transmission system, the dynamic load of planet-ring gear meshing element is extracted. Then, the load distribution relationship between the ring gear and the meshing-gear teeth is determined by combining with the load tooth contact analysis method [31]. Finally, the modal superposition method and Newmark β integration method are used to solve the dynamic characteristics of the ring gear. Compared with the traditional ring gear, the thin-walled ring gear will have greater bending deformation due to its flexible structure, which will directly affect its vibration mode and stress distribution. On the basis of verifying the method proposed in this paper, the vibration and stress characteristics of thin-walled ring gear are further analyzed.

Calculation Method for Dynamic Stress of Flexible Ring Gear

The planetary gear transmission system is a complex gear train composed of sun gears, planet gears, and ring gears. In the past, the mechanics of materials approximation method and the finite element method have commonly been used to calculate the gear stress. The former is usually used for strength check at the theoretical design stage, and cannot effectively reflect the dynamic change process of tooth root stress during operation. The latter is widely used, but there are still many difficulties in accurately simulating the complex process of planetary gear transmission, such as the need for a very fine mesh on the gear tooth contact surface, which will greatly increase calculation time and reduce calculation efficiency. Therefore, under careful consideration of the situation that the ring gear is subjected to meshing excitation, this paper proposes a comprehensive method for calculating the dynamic stress of the ring gear as shown in Fig. 1.

Fig. 1
figure 1

Dynamic stress calculation process of flexible ring gear

Full size image

First, the dynamic transmission process of the planetary gear system is analyzed synthetically, the dynamic model of translation–torsion coupling of the planetary gear transmission system is established, and the dynamic load time history of planet-ring gear meshing element is extracted. Second, the dynamic load cycle is divided into n impact loads, and the load distribution relationship between teeth is determined by LTCA. Then, the n modes of the ring gear under the initial condition are extracted, and the dynamic equations of the ring gear are decoupled using the modal matrix. Finally, the stress time history of the ring gear under the dynamic load is solved step by step using the Newmark-β time integration method.

To verify the effectiveness of the above calculation method, the time-domain strain history of the root of the ring gear in the planetary gear set of the wind turbine test bed is extracted using an FBG sensor and is then compared with the theoretical calculation results.

The Construction of System Dynamics Model

Basic parameters of planetary gear transmission system are shown in Table 1.

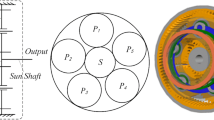
Table 1 Planetary gear transmission system parameters
Full size table

The model of planetary gear transmission system is shown in Fig. 2. The planetary gear system is 2K-H planetary gear set, and the four planets are evenly distributed along the circumference. In the process of planetary gear transmission, the motion process is more complicated than that of fixed-shaft transmission. Also, the analysis is much more difficult. Therefore, considering the complex coupling relationship among various components, the translation–torsion coupling dynamic model of the planetary gear transmission system is established. In the modeling, the center of the model is taken as the coordinate origin, the horizontal direction is X, and the vertical direction is Y. The model uses springs to simulate the meshing stiffness of the meshing element, where kspi and krpi are the meshing stiffness of the i-th planet with the sun and the ring gear (i = 1, 2, 3, 4).

Fig. 2
figure 2

Planetary gear set and system dynamics model

Full size image

In the transmission process of planetary gear train, the periodic change of meshing stiffness is also the main internal excitation of system vibration. According to reference [32], the time-varying stiffness of meshing element can be extracted effectively. The meshing stiffness curve of meshing element is shown in Fig. 3. To facilitate subsequent analysis, each gear tooth is numbered in the counterclockwise direction of the Y-axis. A total of 100 gear teeth are numbered from 1 to 100.

Fig. 3
figure 3

Meshing element dynamics model

Full size image

In Fig. 3, ws, vs, θs, wr, vr and θr are respectively the sun gear, ring gear translation and torsional micro displacement. wpi, vpi and θpi are each the radial, tangential and torsional micro displacements of the planet respectively. In practical applications, the sun gear and planet are supported by bearings, while the ring gear is fixed by bolts. The spring is used to simulate the supporting structure of each component in the system modeling. ks, kp and kr are the supporting stiffness of sun, planet and ring gear, respectively. According to the literature [33], the equivalent damping coefficient of the system is related to the adjacent mass and stiffness, and its values are shown in Table 2.

Table 2 Modeling parameters of planetary gear transmission
Full size table

Taking the meshing element of planet-ring gear in Fig. 3. as an example to analyze the force situation, the projection vector of the translation and torsion micro displacement of meshing element along the direction of the line of action is

$$ \left. \begin{gathered} {\overline{x}}_{{r}} = v_{{r}}\cos (\alpha_{i} + \varphi_{{{\text{pi}}}} ) - w_{{\text{r}}} \sin (\alpha_{i} + \varphi_{pi} ) + \theta_{{\text{r}}} R_{{\text{r}}} \hfill \\ \overline{{x_{{{\text{pi}}}} }} = - w_{{{\text{pi}}}} \sin (\alpha_{i} + \varphi_{{{\text{pi}}}} ) + v_{{{\text{pi}}}} \cos (\alpha_{i} + \varphi_{{{\text{pi}}}} ) + \theta_{{{\text{pi}}}} R_{{{\text{pi}}}} \hfill \\ \end{gathered} \right\}, $$
(1)

where αi is the engagement angle between the ith planet and the ring gear. φpi is the phase angle of the planet i. Rr and Rpi are the base circle radius of the ring gear and the planet, respectively.

The meshing force can be expressed as

$$ F_{{{\text{rpi}}}} = k_{{{\text{rpi}}}} (v_{{{\text{pi}}}} \cos (\alpha_{i} + \varphi_{{{\text{pi}}}} ) - w_{{{\text{pi}}}} \cos (\alpha_{i} + \varphi_{pi} ) + \theta_{{{\text{pi}}}} R_{{{\text{pi}}}} - v_{{\text{r}}} \cos (\alpha_{i} + \varphi_{{{\text{pi}}}} ) + w_{{\text{r}}} \sin (\alpha_{i} + \varphi_{{{\text{pi}}}} ) - \theta_{{\text{r}}} R_{{\text{r}}} ){\kern 1pt} . $$
(2)

According to Newtonian mechanics theory, the dynamic differential equation of the meshing element of the planet and the ring gear can be obtained

$$ \left. \begin{gathered} m_{{\text{r}}} \ddot{v}_{{\text{r}}} - \sum\limits_{i = 1}^{n} {k_{{{\text{rpi}}}} \eta_{{{\text{rpi}}}} \sin (\alpha_{i} + \varphi_{{{\text{pi}}}} )} + k_{{\text{r}}} v_{{\text{r}}} = 0 \hfill \\ m_{{\text{r}}} \ddot{w}_{{\text{r}}} + \sum\limits_{i = 1}^{n} {k_{{{\text{rpi}}}} \eta_{{{\text{rpi}}}} \cos (\alpha_{i} + \varphi_{{{\text{pi}}}} )} + k_{{\text{r}}} w_{{\text{r}}} = 0 \hfill \\ (I_{{\text{r}}} /R_{{\text{r}}}^{2} )\ddot{\theta }_{{\text{r}}} R_{{\text{r}}} + \sum\limits_{i = 1}^{n} {k_{{{\text{rpi}}}} \eta_{{{\text{rpi}}}} } + k_{{{\text{r}}\theta }} \theta_{{\text{r}}} R_{{\text{r}}} = 0 \hfill \\ \end{gathered} \right\}, $$
(3)

where n = 1, 2, 3, 4. ηrpi is the elastic deformation of the planet-ring gear meshing element along the line of action. mr is the mass of the ring gear. Ir is the moment of inertia of the ring gear.

In the same way, the dynamic equation of the sun-planet gear meshing element can be expressed as follows:

$$ \left. \begin{gathered} m_{{\text{s}}} \ddot{v}_{{\text{s}}} + \sum\limits_{i = 1}^{n} {k_{{{\text{spi}}}} \eta_{{{\text{spi}}}} \sin (\varphi_{{{\text{pi}}}} - \alpha_{i} )} + k_{{\text{s}}} v_{{\text{s}}} = 0 \hfill \\ m_{{\text{s}}} \ddot{w}_{{\text{s}}} + \sum\limits_{i = 1}^{n} {k_{{{\text{spi}}}} \eta_{{{\text{spi}}}} \cos (\varphi_{{{\text{pi}}}} - \alpha_{i} )} + k_{{\text{s}}} w_{{\text{s}}} = 0 \hfill \\ (I_{{\text{s}}} /R_{{\text{s}}}^{2} )\ddot{\theta }_{{\text{s}}} R_{{\text{s}}} - \sum\limits_{i = 1}^{n} {k_{{{\text{spi}}}} \eta_{{{\text{spi}}}} } + k_{{{\text{s}}\theta }} \theta_{{\text{s}}} R_{{\text{s}}} = T_{{{\text{in}}}} /R_{{\text{s}}} \hfill \\ \end{gathered} \right\}, $$
(4)

where n = 1, 2, 3, 4. ηspi is the elastic deformation of the sun-planet gear meshing element along the line of action. ms is the mass of the sun gear. Is is the moment of inertia of the sun gear.

Extraction and Analysis of Dynamic Load of Meshing Element

Due to the symmetry of the planetary gear system structure, the meshing force of planet-ring gear meshing element changes periodically. In the transmission process of planetary gear train, the meshing element of planet-ring gear is in multi-tooth meshing state, although the force of a single tooth of the ring gear fluctuates periodically. Due to the complex meshing situation, therefore, it is difficult to extract the time-domain load history of a single tooth of ring gear effectively. To sum up, this work extracts the total meshing force of meshing elements through the system dynamics program. In the subsequent analysis, the LTCA method is used to determine the load distribution relationship between teeth.

When the input speed of the sun gear is 600 r/min and the load is 59 N·m, the dynamic load time history and spectrum analysis are calculated as shown in Fig. 4.

Fig. 4
figure 4

Dynamic load and frequency spectrum analysis of the meshing element of the planet ring

Full size image

According to Fig. 4a, the dynamic load fluctuation amplitude is 2.6 N. In the spectrum analysis of Fig. 4b, the main excitation frequency is the energy of the meshing frequency of the planet-ring meshing element (218.65 Hz) and its frequency doubling component energy. As the frequency increases, the energy gradually decreases.

Finite element analysis of dynamic stress of ring gear

In an ideal state, during the meshing process of the planet and the ring gear, each participating tooth pair will always be in line contact. Therefore, to effectively simulate the planet-ring gear meshing process, the contact surface of the ring gear is divided into n contact lines along the direction of the tooth profileas shown in Fig. 5b (Fdi is the impact load when the ith contact line participates in meshing), which will effectively reduce the mesh refinement degree of the contact surface of the ring gear, and at the same time reduce the calculation time and the storage to improve the efficiency.

Fig. 5
figure 5

Schematic diagram of discretized dynamic load and ring gear loading

Full size image

The planet-ring meshing element is a continuous dynamic meshing process. Hence, the dynamic load can be discretized into n impact loads for each period of meshing of the gear teeth. As shown in Fig. 5a, the curve A is dispersed into 12 impact loads. From meshing in to meshing out, the action time of each impact load is Δt, and the action position successively changes from the first contact line entering into meshing to the exit of meshing.

When meshing the ring gear, the traditional meshing method has dense mesh in the contact area, which will greatly increase the calculation time and storage. To avoid the above situation, when meshing the ring gear teeth, it is divided into n equal parts along the tooth profile, that is, n + 1 contact lines are divided, and the discrete load is applied to the corresponding contact lines, and then the vibration and stress characteristics of the ring gear under the meshing excitation are obtained.

Load Distribution Relationship Between Teeth

When multiple teeth are meshed at the same time, there is also a problem of dynamic load distribution between teeth. In this paper, the LTCA method is used to discretize one period of the dynamic load on the ring gear, and the deformation of each participating gear along the contact line direction in a period is determined Δij(t) (the deformation along the ith contact line of the jth engaged gear at t time), as shown in Fig. 5. Fij(t) is the component force of the dynamic load on the jth engaged tooth along the ith contact line at time t, as shown in Fig. 5b. And the meshing element of the planet-ring gear is single tooth and double tooth alternately meshing. According to the calculation Eq. (5) of gear theoretical coincidence degree, in a meshing cycle, 93% of the time is in double tooth meshing, and 7% of the time is in single tooth meshing.

The theoretical calculation formula of the coincidence degree of the planet-ring gear meshing element is

$$ \varepsilon_{a} = \frac{1}{2\pi }[z_{1} (\tan \alpha_{a1} - \tan \alpha^{\prime}) - z_{2} (\tan \alpha_{a2} - \tan \alpha^{\prime})], $$
(5)

where αa1, αa2 and α′ are the planet, the ring gear tip pressure angle and the indexing circle pressure angle, respectively, z1 and z2 are the number of teeth of the planet gear and the ring gear.

Figure 6 shows, at time tq, the planet and the ring gear are in the state of double tooth meshing, and the loads borne by the double tooth are defined as Fi and Fj, respectively. The elasticity and bending deformation of each participating meshing tooth in the direction of the contact line under the load can be expressed as δi, δj, νi and νj, respectively. Assuming that the total load on the ring gear at this time is Fq, the relationship between the meshing teeth and the total load can be obtained according to the vector and superposition of the force

$$ F_{{\text{q}}} = F_{i} + F_{j} . $$
(6)
Fig. 6
figure 6

t = tq Load distribution and stress nephogram

Full size image

At this moment, the total deformation of each tooth along the direction of the contact line is Δq, then the relationship of the deformation of each tooth is

$$ \Delta_{j} = \delta_{j} + \nu_{j} , $$
(7)
$$ \Delta_{{\text{q}}} = \Delta_{i} + \Delta_{j} . $$
(8)

According to Eqs. (6), (7) and (8), the load of the j-th meshing gear tooth can be expressed as

$$ F_{j} = \frac{{\Delta_{j} }}{{\Delta_{{\text{q}}} }}F_{{\text{q}}} . $$
(9)

Since the load on the ring gear changes with time in actual work, the dynamic load can be expressed as Fq(t), then Eq. (8) can be rewritten as

$$ F_{j} (t) = \frac{{\Delta_{j} (t)}}{{\Delta_{{\text{q}}} (t)}}F_{{\text{q}}} (t), $$
(10)

where Fq(t), Fj(t), Δq(t) and Δj(t) are the total load and deformation of the ring gear and the load and deformation of the j-th meshing gear at time t.

The dynamic load of the ring gear presents periodic fluctuation, and it is divided into n sub-steps. The deformation of each sub-step along the contact line of the meshing teeth is shown in Fig. 8.

According to Fig. 7, when the jth tooth enters into meshing, the meshing position is located at the tooth root, and the meshing force is small. Its bending deformation and elastic deformation are small. With the revolution of the planet, the load on the jth tooth increases gradually, and the elastic deformation increases, and the bending deformation also presents an increasing trend from the root to the top of the tooth. In the same way, the elastic deformation and bending deformation of ith tooth decrease gradually when the ith tooth is out of meshing. Figure 7 shows that the horizontal axis X represents the revolution angle of the planet, and the vertical axis Y represents the normalized deformation of the teeth engaged along the contact line direction.

Fig. 7
figure 7

Deformation of meshing gear along contact line under dynamic load

Full size image

Analysis Of Inherent Characteristics Of Ring Gear

The finite element method is used to build the dynamic model of the ring gear. The matrix form is as follows:

$$ [M]\{ \ddot{q}\} + [C]\{ \dot{q}\} + [K]\{ q\} = \{ F^{a} \} , $$
(11)

where [M] is the mass matrix of the ring gear.[K] is the stiffness matrix of the ring gear. {q} is the displacement vector of the node. {Fa} is the external load matrix. Its damping matrix [C] can be considered as a linear combination of the mass matrix [M] and the stiffness matrix [K].

$$ [C] = a[M] + b[K]. $$
(12)

From a mathematical point of view, the above-mentioned mass, damping, and stiffness matrices are all high-order matrices, so it takes a lot of calculation time using the general method. Because the modal superposition method is convenient to calculate and is widely used in engineering, this article uses the modal superposition method decouples Eq. (11).

From Eq. (11), the undamped free vibration equation of the ring gear is

$$ [M]\{ \ddot{q}\} + [K]\{ q\} = 0. $$
(13)

The undamped free vibration equation should satisfy

$$ q = \{ \delta_{i} \} \cos \omega_{i} t, $$
(14)

where δi is the eigenvector of the i-th mode. ωi is the i-th natural vibration frequency. t is time.

From Eqs. (11) and (12), the vibration characteristic equation of the structure can be obtained.

$$ \left| { - \omega_{i}^{2} M + K} \right| = 0. $$
(15)

where the natural vibration frequency ωi of the i-th order can be obtained, and then the eigenvector {δi} of the ith order modal shape can be obtained.

Dynamic Stress Solution

After the modal matrix [Φ] of the ring gear is obtained, the coordinate transformation is carried out using the modal matrix.

$$ \{ q(t)\} = [\Phi ]\{ Y(t)\} , $$
(16)

where {Y(t)} is the principal coordinate matrix Y1 (t), Y2 (t), … Yp(t). Taking Eq. (14) into account

$$ [M][\Phi ]\{ Y(t)\} + (a[M] + b[K])[\Phi ]\{ Y(t)\} + [K][\Phi ]\{ Y(t)\} = \{ F^{a} \} . $$
(17)

According to the orthogonality of modal matrix, Eq. (17) is decoupled, and the motion equation in the main coordinate system can be obtained.

$$ \ddot{Y}_{i} (t) + (a + b\omega_{i}^{2} )\dot{Y}_{i} (t) + \omega_{i}^{2} Y_{i} (t) = N_{i} (t), $$
(18)

where i = 1, 2, … p, \((a + b\omega_{i}^{2} )\) is the modal damping coefficient of the i-th main mode. Ni (t) is the time vector varying with load in principal coordinate system.

When solving the dynamic equation in the principal coordinate system, because of the good convergence of the Newmark-β time integration method, this paper uses the Newmark-β time integration method to solve the Eq. (18) and then obtains the displacement field of each element of the inner gear ring.

After the displacement field of each element of the ring gear is obtained, the tooth root stress of the ring gear at any time can be further obtained according to the literature [34].

$$ \{ \sigma \} = [D][B]Y(t + \Delta t) = [S]Y(t + \Delta t), $$
(19)

where [D] is the elastic constant matrix, [B] is the strain matrix, [S] = [D]·[B] is the stress matrix. The matrix forms of [D] and [B] are shown in the appendix.

Fiber Bragg Grating Measurement Principle

Fiber Bragg grating sensor is a kind of structure which is made of fiber core by means of ultraviolet illumination. This structure can reflect the light of specific wavelength. The resonance wavelength of reflected light is related to the period of fiber grating and the effective refractive index of the fiber core. According to reference [35], the axial deformation of FBG will cause the reflection wavelength to shift, and the strain in the measurement area can be further obtained.

The key to the detection and diagnosis of the planetary gearbox is to obtain the change of strain in this position with time. Compared with the radial direction, the circumferential direction of the ring gear side should be changed significantly, reaching the maximum value near the root circle and between the two adjacent teeth, and the measurement of the circumferential strain can better reflect the health state of the planetary gearbox. So, the FBG is arranged in the area with the maximum circumferential strain of the ring gear side, and the strain value of this part is more sensitive to the change of the state of the planetary gearbox.

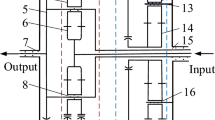
In this paper, the wind turbine test bed produced by SQI company is taken as the research object, as shown in Fig. 8. The motor provides the input speed, and the magnetic powder brake provides the load of the planetary gearbox.

Fig. 8
figure 8

Wind turbine test bench and fiber grating monitoring system

Full size image

The fiber grating used in the experiment is 2 mm in length and 0.125 mm in diameter. According to the above analysis, the fiber is pasted on the position of the tooth root at the middle side of the 6th and 7th tooth anticlockwise in the direction perpendicular to the ground, as shown in Fig. 8c; the fiber is led out from the side of the planetary gearbox, as shown in Fig. 8b; the dynamic monitoring system of the fiber grating is shown in Fig. 8d.

Time Domain Analysis of Dynamic Strain

In the experimental data collection, FBG sensor is pasted on the position of the middle root of the 6th and 7th tooth of the counterclockwise (Y-axis) perpendicular to the ground, as shown in Fig. 8b (circumferential direction). Therefore, this position should also be taken as the dynamic strain output point (as shown in Fig. 3) when extracting the simulation results. And, the simulation results are, respectively, obtained under the condition that the motor output frequency is 7.5 Hz and the load torque is 59 N·m The strain time history of the ring gear root under the experimental conditions is shown in Fig. 9.

Fig. 9
figure 9

Circumferential dynamic strain time-domain curve

Full size image

To effectively extract the time-domain strain history of the gear root in the working process, this paper uses NI USB 6009 acquisition card (sampling frequency: 5000 Hz, system detection accuracy: 4.8 mV/με). A sensor is pasted at the position of 1 mm at the root of the tooth space (number of sensors: 1), and then the time-domain strain history of the tooth root is obtained, as shown in Fig. 9a.

The dynamic strain time history can be divided into two parts by analyzing the above figure, that is, the meshing area and non-meshing area when teeth 6 and 7 (Fig. 5b) participate in meshing. It can be seen from Fig. 9 that in the meshing area, the meshing action leads to the complex meshing process from compression to tension at the tooth root, and the dynamic strain will also appear sudden change. It can be seen from Fig. 9a, b, the maximum dynamic strain measured by the experiment is 26.2 με, and the maximum dynamic strain calculated by simulation is 28.5 με. There is a certain error between the experimental measurement result and the simulation result, which is due to the numerical error caused by the test method and other factors.

In the non-meshing area, it can be seen from Fig. 9a, the dynamic strain measured by the experiment shows a gradual decrease of smoothness, which is due to the recovery of ring gear deformation after the tooth are meshed and the attenuation process of FBG sensor in signal transmission. In the simulation calculation (Fig. 9b), the dynamic strain curve is reduced to 0 in a step manner.

According to the calculation results in the reference [16], when the planet is meshed to the stress extraction position, its stress curve has a sudden change process from positive to negative in each cycle; and when the planet leaves the stress extraction position, its stress value also decreases to 0 by step, which is consistent with the fluctuation trend of the dynamic stress curve obtained by the simulation algorithm in this paper.

Comparative Analysis Of Strain Under Different Loads

To effectively demonstrate the consistency of simulation and experimental test results under different loads, the dynamic strain of ring gear under various load conditions are calculated and tested in this paper. During the experimental measurement, the load is provided by the magnetic powder brake, so the motor frequency is 7.5 Hz, the load current of the magnetic powder brake is 0.6A, 1.0A, 1.5A, and 2.0A, respectively, and the corresponding load torque is 16 N·m, 34 N·m, 59 N·m and 79 N·m.

Take the mean value of the absolute value of the strain fluctuation when the teeth on both sides of the strain characteristic point participate in the meshing under different loads, and draw the curve as shown in Fig. 10. It can be seen that under four load cases, the simulation results of the root strain are basically consistent with the experimental test results, the strain increases linearly with the load, and the maximum error between the simulation results and the experimental results is 8.88%.

Fig. 10
figure 10

Strain of tooth root under different loads

Full size image

Dynamic Characteristics of Thin-Walled Ring Gear

In the analysis of thin-walled ring gear, according to reference [16], the rim thickness coefficient can be defined as:

$$ \lambda = \frac{{r_{0} - r_{{\text{f}}} }}{{r_{{\text{f}}} - r_{{\text{a}}} }}, $$
(20)

where r0, rf and ra are the radius of the gear rim, the radius of the tooth root circle and the radius of the tooth top circle, respectively.

The smaller the rim thickness coefficient, the thinner the ring gear wall thickness, and with the decrease of the rim thickness coefficient, the mass of the ring gear decreases, but its flexibility will increase.

To sum up, this paper defines the rim thickness coefficient in the analysis of thin-walled ring gear λ = 0.55. Compared with the traditional ring gear, its flexibility is greater, and in practical work, due to the effect of load and meshing excitation, the thin-walled ring gear will produce greater bending deformation, and the bending stiffness will also become the main factor affecting the vibration and stress distribution of the ring gear. Therefore, the vibration and stress characteristics of the thin-walled gear ring are further analyzed by the method proposed in this paper.

Analysis of Ring Gear Vibration Characteristics

The input speed is the direct factor that affects the vibration and noise of the planetary gear transmission system. At high speed, the dynamic characteristics of planetary gear system are more obvious. In this paper, the vibration characteristics of ring gear at different speeds are calculated. In terms of vibration, the radial vibration of the ring gear is more representative of its vibration characteristics than the circumferential vibration. Therefore, the radial amplitude of the ring gear at 600–10800 r/min and the vibration amplitude of nodes 1–25 at different speeds are calculated and extracted as shown in Fig. 11.

Fig. 11
figure 11

Radial vibration amplitude of ring gear

Full size image

Figure 11a shows the amplitude of the ring gear radial vibration at different speeds. In the low-speed area, the ring gear radial vibration amplitude fluctuates less. As the speed increases, it is located in the medium and high-speed area, and the ring gear vibration is significantly enhanced. When the input speed of the sun gear is 4200 r/min, the sixth frequency of the meshing frequency is close to the first natural frequency of the ring gear, which causes obvious vibration of the ring gear. When the speed is 8800 r/min, the third meshing frequency is close to the fourth natural frequency of ring gear. Similarly, when the input speed of the sun gear is 7600 r/min, the fourth octave of the meshing frequency is close to the ninth natural frequency of the ring gear.

The structure and boundary conditions of the ring gear have symmetry. To more effectively respond to the vibration of the ring gear under the meshing excitation, 25 nodes on the 1/4 circumference of the ring gear are extracted as the output points of the vibration response. The vibration amplitude at 600, 4200, 7600 and 8800r/min is shown in Fig. 11b.

According to Fig. 11b, when the input speed of the sun gear is 600 r/min, the meshing excitation does not cause the ring gear resonance, and the ring gear deformation tends to static deformation. The radial vibration amplitude of the ring gear on both sides of the support position presents an inverted U-shape and is symmetrical with respect to the constraint position. The maximum amplitudes on the left and right sides of the constraint position are 6.5 μm and 7.6 μm, respectively. With the increase of the rotational speed, the vibration of the ring gear gradually tends to its natural mode due to the influence of the meshing excitation. When the input rotational speed of the sun gear is 7600 r/min, the vibration of the ring gear is particularly obvious due to the quadruple frequency of the meshing excitation, and the vibration amplitude is 15.4 μm. When the input speed of the sun gear is 4200 r/min and 8800 r/min, respectively, according to Fig. 11b, the amplitudes are 11.2 μm and 14.3 μm, respectively, The amplitudes of 8800 r/min are obviously larger than those of 4200 r/min because the energy of the sixth harmonic of the meshing frequency is obviously weaker than that of the third harmonic.

Stress Analysis of Ring Gear

It is of great significance to study the stress distribution of the ring gear during the operation of the planetary gear train for predicting the location of fatigue occurrence and ensuring the safety of engineering, while the influence of resonance on the stress of the ring gear is particularly significant. Given the above problems, this paper calculates and analyzes the stress of the ring gear at different speeds. For a more intuitive response to the stress fluctuation process of the ring gear, the time-domain history of the circumferential stress at the root of the ring gear at different speeds is extracted in this paper, as shown in Fig. 12.

Fig. 12
figure 12

Circumferential dynamic stress of ring gear at different speeds

Full size image

By analyzing the time-domain history of the ring gear at different speeds shown in Fig. 12 and taking the input speed of the sun gear at 600 r/min as an example, the time-domain history of dynamic stress can be divided into the stress fluctuation due to meshing deformation and the stress fluctuation caused by vibration. Due to the effect of meshing force and the flexibility of thin-walled ring gear, when the planet is close to the stress extraction position, obvious ring gear compression deformation occurs before the teeth on both sides of the stress extraction position engaged in meshing. This leads to a large fluctuation of the root stress, and the magnitude of the compressive stress is σc = 35.6 MPa. Similarly, when the planet is meshed out of the stress extraction position, the stress extraction position is in the state of tensile deformation due to the effect of the meshing force, and the tensile stress of the ring gear is σt = 61.5 MPa. The compressive stress at the root of the tooth is obviously smaller than the tensile stress. When the planet is far away from the stress extraction position, it can be seen that the dynamic stress fluctuates near 0, which is caused by the vibration deformation of the thin-walled ring gear caused by meshing excitation.

Rotation speed is the direct factor affecting the meshing excitation. As illustrated in Fig. 12b, it can be seen that the dynamic stress of the tooth root increases significantly at 4200 r/min. This is due to the increase of rotation speed and the increase of the deformation of the ring gear, which is caused by the close relationship between the excitation frequency and the natural frequency. When the input speed of the sun gear continues to increase to 7600 r/min and 8800 r/min, the dynamic stress fluctuation of the ring gear is particularly obvious. Taking 8800r/min as an example, due to the influence of resonance, the stress fluctuation of the ring gear is significantly increased. With the rotation of the planet gear, the vibration at the stress extraction position gradually increases from strong to weak and then to strong. The stress also increases at first, then decreases and then increases. The magnitude of compressive stress is σc = 83.9 MPa, the magnitude of tensile stress is σt = 126 MPa, and the magnitude of tensile stress is twice that under non-resonant conditions.

To further verify the relationship between stress and ring gear deformation under resonance and non-resonance conditions, the deformation of ring gear under the sun gear input speed of 600 r/min and 8800 r/min is taken as an example, as shown in Fig. 13. (ring gear deformation magnified 10,000 times).

Fig. 13
figure 13

Deformation of gear ring at different speeds

Full size image

To reflect the deformation of the ring gear in the meshing process more intuitively, the ring gear is deformed once every 15°revolution of the planet. As shown in Fig. 13a, the deformation of the gear ring is analyzed when the input speed of the sun gear is 600 r/min. When the angle between the centerline of planet 1, the sun gear, and the vertical direction is 0°, the meshing tooth pair of the planet and the ring gear is located near the constraint position. Due to the action of the meshing force, the gear ring between the two constraints gradually changes from convex deformation to concave deformation, the stress extraction position is just in the state of tension, and the stress is positive. When the angle between the central line of planet 1, the sun gear, and the vertical direction is 15°, the stress extraction position is located at the convex deformation position, the outer side of the ring gear is in tension state, the inner side is in compression state, and the stress is negative. With the revolution of the planet, when the angle between the central line of the planet 1, the sun gear, and the vertical direction is 30°, the gear ring at the stress extraction position is concave deformation, the outer side of the gear ring is in the compression state, the inner side is in the tension state, and the stress is positive. As the planet continues to rotate, when the angle between the central line of planet 1, the sun gear and the vertical direction is 45°, 60°, and 75°, no planet is engaged between constraint 1 and constraint 2. At this time, the stress fluctuates near 0, which is caused by micro deformation due to ring gear vibration.

Similarly, the deformation of the ring gear is analyzed when the input speed of the sun gear is 8800 r/min. It can be seen that when the angle between the central line of the planet gear 1 and the sun gear and the vertical direction is 0°, 15°, and 30°, there is no obvious difference except that the deformation of the ring gear increases obviously. But when the angle between the centerline of planet 1 and sun gear and the vertical direction is 45°, there is no planet between constraint 1 and constraint 2, but the resonance effect caused by the meshing excitation increases the overall deformation of the ring gear, resulting in a large fluctuation of the stress. However, with increased distance of planet 1, the deformation caused by its vibration decreases gradually, which leads to a stress fluctuation from strong to weak in the non-meshing deformation area. In conclusion, the deformation trend is consistent with the dynamic stress time history.

Influence of Meshing Deformation on Stress Field Distribution

From the above analysis, it can be seen that the meshing deformation is a direct factor affecting the stress fluctuation. However, compared with the dynamic strain time-domain curve in Fig. 9., the range of stress fluctuation is significantly expanded, and the compressive stress σc at the tooth root position is significantly smaller than the tensile stress σt. Due to the above problems, to further explore the influence of the deformation of the thin-walled ring gear caused by meshing excitation on the stress, the stress cloud diagram near the meshing deformation of the ring gear and the trend of the stress fluctuation along the circumferential direction are shown in Fig. 14. This is a more intuitive way to show the meshing deformation, and in which the effect of force takes the equivalent stress as the output stress.

Fig. 14
figure 14

Stress nephogram of gear ring and stress fluctuation curve of one eighth circle (600r/min)

Full size image

As shown in Fig. 14a, the stress cloud diagram of the ring gear can be divided into three areas, namely, the concave deformation area caused by the tension on the left side of the meshing tooth, the convex deformation area caused by extrusion near the meshing area, and the right side of the meshing tooth, and the concave deformation zone caused by the deformation of the side wheel body. According to the stress cloud diagram, the stress concentration position from the constrained position 1 to the constrained position 2 gradually transitions from the root position to the edge of the wheel body and then to the root position. According to the stress fluctuation curve at the tooth root of Fig. 14b, it can be seen that the maximum stress position is on the left side of the meshing gear tooth, and the magnitude is 63 MPa, while the stress at the meshing position is 32.1 MPa. The magnitude is much greater than the stress generated by the compression deformation at the meshing position. These results are consistent with the results obtained in the time domain history of the circumferential stress. At the same time, it can be seen that the stress between two adjacent peaks experiences large fluctuations, which is due to the influence of the spacing distribution of the gear tooth–tooth groove–tooth on the stress. Analysis of the stress fluctuation curve of the outer side of the ring gear in Fig. 14c shows that the stress at the meshing position experiences a sharp increase and the stress on both sides is relatively small. This is because the extrusion caused by the meshing excitation leads to convex warpage. The stress of the rim ring body of the ring gear is more concentrated relative to the position of the inner root. At this time, the maximum stress is 35 MPa. As illustrated in Fig. 14c, the stress at the restraint position 1 shows a sharp drop. This is because the constraint prevents the deformation of the ring gear, so the stress concentration occurs at the intersection of the constraint positions.

Conclusion

Considering the dynamic characteristics of the planetary gear transmission system, ring gear vibration characteristics and dynamic stress calculation method are proposed, and the vibration and stress of the thin-walled ring gear are analyzed.

  1. (1)

    In the calculation results of thin-walled ring gear, at the resonance speed, the vibration shapes of the ring gear is more complex than at the non-resonant speed. The root stress increases by 100% compared to the non-resonant speed.

  2. (2)

    The deformation of ring gear tends to static deformation at the non-resonance speed, while it tends to its natural vibration mode at the resonance speed, and the vibration shape is more complex.

  3. (3)

    In the calculation results of thin-walled ring gear, in the meshing position, due to the influence of the flexibility of the thin-walled ring gear, the stress on the rim position of the ring gear is more concentrated than the root position; the stress of the tooth root of the tension deformation side is more concentrated than that of the meshing position.