Introduction

Feedback control [1,2,3,4] allows a system dynamic response to be modified without changing any system components. However, in an open-loop controller, also called a non-feedback controller, the control action from the controller is independent of the “process output”, which is the process variable that is being controlled [5,6,7]. It does not use feedback to determine if its output has achieved the desired goal of the input command or process. In these control methods, the periodicity and the stability condition of the chaos controlled in nonlinear dynamical systems by periodic perturbation [8, 9] have been investigated in many experiments and models from chemistry, physics and neuroscience [10,11,12].

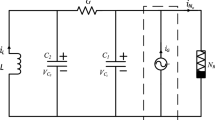
The Murali–Lakshmanan–Chua (MLC) circuit is a two-dimensional dissipative circuit system introduced by Murali et al. [13, 14] which is a classic configuration of electronic circuit having a Chua’s diode as its nonlinearity and the bi-stability nature clarified by two discontinuous boundaries. Bifurcations of equilibriums in non-smooth MLC circuit system are related to piecewise smooth maps, which lead to a large variety of nonlinear phenomena such as the coexistence of several stable states, jump behavior of periodic responses, quasiperiodic response and chaotic attractors [15,16,17,18]. We restrict our discussion to the MLC circuit shown in Fig. 1 with periodic perturbation expressed by the set of differential equations,

$$C\frac{dV}{dt} = i_{L} - G\left( V \right)$$
$$L\frac{{di_{L} }}{dt} = - Ri_{L} - v + f\sin \left( {\varOmega t} \right)$$
(1)

where \(C\) is the capacitor, \(R\) is a linear resistor and \(L\) is an inductor while the nonlinear resistor \(R_{N}\) is the Chua’s diode, and the corresponding \(V - i\) characteristic is given by

Fig. 1
figure 1

MLC circuit diagram with periodic alternating current source \(V_{G}\)

Full size image
$$G\left( V \right) = P_{2} V + \frac{1}{2}\left( {P_{2} - P_{1} } \right)\left( {\left| {V + E_{0} } \right| - \left| {V - E_{0} } \right|} \right)$$
(2)

The periodic power source is \(V_{G} = f\sin \left( {\varOmega t} \right)\).

By suitably rescaling the variables and parameters, the MLC circuit system can be written in dimensionless form

$$\dot{x} = y - g\left( x \right)$$
$$\dot{y} = - \alpha y - \beta x + F_{1} \kappa + F_{2} \sin \left( {\omega_{2} t} \right)$$
(3)

where \(\omega \ll 1\) is the frequency of the periodic signal and \(g\left( x \right) = bx + \frac{1}{2}\left( {a - b} \right)\left( {\left| {x + 1} \right| - \left| {x - 1} \right|} \right)\). \(\alpha\), \(\dot{x} = y - g\left( x \right)\), \(a\) and \(b\) are rescaled circuit parameters. \(F > 0\) is the forcing amplitude. If the frequency of periodic perturbation is of order 1, the MLC circuit consisting with the piecewise linear element has been reported to possess rich nonlinear dynamical behaviors and observed numerically and experimentally [19,20,21].

All through this paper, we fix the parameter values at \(\beta = 1.0\), \(a = - 1.02\) and \(b = - 0.55\) in system (3) to reveal the dynamical evolutions in the circuit system. For example, chaotic behaviors are presented from the one-parameter bifurcation diagram in Fig. 2a for increasing values of the driving amplitude \(F\) with the specific choice of the parameter \(\alpha { = 1} . 0 1 5\) and the external frequency \(\omega = 0.75\). As shown in Fig. 2a, one can identify different attractors as starting from the equilibrium branch to a limit cycle, period-\(3T\) orbit and then period-doubling sequences to a double-scroll chaotic attractors with the variation \(F\) in the range \(\left( {0,0.5} \right)\). Further, fixing the driving amplitude at \(F = 0. 45\), we can present a typical double-scroll chaotic attractor as shown in Fig. 2b.

Fig. 2
figure 2

Numerical simulations of the MLC circuit with constant forcing frequency at \(\omega { = 0} . 7 5\) and \(\alpha = 1.015\). a One-parameter bifurcation diagram of \(\left( {F,x} \right)\) showing an infinite period bubble and chaotic structure by fixing other parameter values of \(\beta = 1.0\), \(a = - 1.02\), \(b = - 0.55\) and \(\omega = 0.75\). b Chaotic attractor at \(F = 0. 4 5\)

Full size image

What are the mechanisms of the complex trajectories appearing the small amplitude oscillations that alternate with large relaxation-like oscillations [22,23,24,25] in a non-smooth dissipative and non-autonomous circuit is still an open question. The number, amplitude and shape of small and large excursions may vary depending on the bifurcation of state for various types of periodic response influenced by the discontinuous boundaries, which play an important role in the analysis of the transition process about the variation equations. The goal of this paper is to study such complex oscillation patterns under periodic perturbation with multiple frequency signal as well as the understanding of the underlying characteristic properties in the non-smooth MLC circuit.

The rest of this paper is organized as follows. In Sect. 2, the non-smooth bifurcation for the layer equation and its switching properties are discussed. Some computational results are given to determine the later localized structures of large amplitude oscillations on a background of small amplitude oscillations. In Sect. 3, we investigate the generation of some novel periodic attractors with clearly separated amplitudes in each periodic cycle. The associated oscillation mechanisms are also revealed. Section 4 is devoted to the study of the influence on the MLC circuit by the addition of the second periodic signal. Irregular periodic oscillation modes are found to occur for a wide range of frequencies of the additive force. The DeMoivre expansion method and the variable replacing technique are used to illustrate two different oscillation mechanisms in the non-smooth circuit system. A brief conclusion and possibilities of further studies are discussed in Sect. 5.

Non-Smooth Bifurcation Analysis for the Layer Equations

Complicated nonlinear behaviors in the dissipative chaotic MLC circuit may be discussed by the geometric properties of non-smooth differential equations. Using the technique of fast–slow analysis method combined with the geometrical properties [26,27,28], several distinct mechanisms may be revealed. We can present the fast system as an autonomous form, and the discontinuous bifurcations can be discussed by using Clarke’s generalized Jacobian matrix [34, 35] in the following.

Assume \(\kappa = \sin \left( {\omega t} \right)\) in system (3) for \(\omega \ll 1\) and give the autonomous layer equations (fast system),

$$\dot{x} = y - g\left( x \right)$$
$$\dot{y} = - \alpha y - \beta x + F\kappa$$
(4)

Referring to the non-smooth or piecewise smooth characteristics represented by \(G\left( V \right)\) in Eq. (2), two non-smooth boundaries \(\varSigma_{1,2} = \left\{ {\left( {x,y} \right) \in R^{2} \left| {x = \pm 1} \right.} \right\}\) can be obtained. Consequently, the phase space for the layer equations can be divided into three subspaces:

$$I = \left\{ {\left( {x,y} \right) \in R^{2} \left| {x < - 1} \right.} \right\},II = \left\{ {\left( {x,y} \right) \in R^{2} \left| {\left| x \right| < 1} \right.} \right\},\,{\text{and}},\,III = \left\{ {\left( {x,y} \right) \in R^{2} \left| {x > 1} \right.} \right\}$$

with two non-smooth boundaries \(\varSigma_{1,2} = \left\{ {\left( {x,y} \right) \in R^{2} \left| {x = \pm 1} \right.} \right\}\). If the variable \(x\) passes across \(\varSigma_{1,2}\), non-smooth bifurcation on the dynamics will appear, which plays an effective role for leading to qualitative properties of the nonlinear circuit system.

Equilibrium Points and Their Stability

The details of the equilibrium points in each domain can be described as: the only equilibrium point \(E_{0} \left( {\frac{F\kappa }{a\alpha + \beta },\frac{aF\kappa }{a\alpha + \beta }} \right)\) in space II and the two equilibrium points \(E_{ \pm } \left( {\frac{{F\kappa \mp \alpha \left( {a - b} \right)}}{b\alpha + \beta },\frac{{bF\kappa \pm \beta \left( {a - b} \right)}}{b\alpha + \beta }} \right)\) in spaces I and III, respectively, the stability of which can be determined by the corresponding eigenvalues of the Jacobian matrix.

For \(E_{ 0}\), the Jacobian matrix of \(J_{0}\) at this equilibrium state is given by

$$J_{0} = \left( {\begin{array}{*{20}c} { - a} & 1 \\ { - \beta } & { - \alpha } \\ \end{array} } \right)$$
(5)

which yields the characteristic polynomial

$$P_{0} \left( \lambda \right) = \lambda^{2} + \left( {a + \alpha } \right)\lambda + a\alpha + \beta$$
(6)

The eigenvalues that characterize the equilibrium states are given as

$$\lambda_{0}^{1,2} = \frac{{ - \left( {a + \alpha } \right)}}{2} \pm \frac{{\sqrt {\left( {a - \alpha } \right)^{2} - 4\beta } }}{2}$$
(7)

Depending on the eigenvalues, the nature of the equilibrium states differs. Obviously, if \(\left( {a - \alpha } \right)^{2} > 4\beta\), the equilibrium \(E_{0}\) will be a saddle, and while if \(\left( {a - \alpha } \right)^{2} < 4\beta\), \(E_{0}\) will be a focus whose stability may depend on whether \(a + \alpha\) is positive or not.

Then, we consider \(E_{ \pm }\), whose Jacobian matrix can be expressed as

$$J_{ \pm } = \left( {\begin{array}{*{20}c} { - b} & 1 \\ { - \beta } & { - \alpha } \\ \end{array} } \right)$$
(8)

which results in the characteristic polynomial

$$P_{ \pm } \left( \lambda \right) = \lambda^{2} + \left( {b + \alpha } \right)\lambda + b\alpha + \beta$$
(9)

The eigenvalues that characterize the equilibrium states are given as

$$\lambda_{ \pm }^{1,2} = \frac{{ - \left( {b + \alpha } \right)}}{2} \pm \frac{{\sqrt {\left( {b - \alpha } \right)^{2} - 4\beta } }}{2}$$
(10)

One may derive the stability conditions related to \(E_{ \pm }\), from which \(E_{ \pm }\) will be stable foci when \(\left( {b - \alpha } \right)^{2} < 4\beta\) and \(b + \alpha > 0\). At this case, the circuit admits self-oscillations with natural frequency of \(\frac{{\sqrt {\left( {b - \alpha } \right)^{2} - 4\beta } }}{2}\). It means that at two subspaces of \(S_{ \pm }\), the MLC circuit system has the trajectory orbits with the same frequency.

When we fix \(\alpha = 1.015\), \(F = 0.5\) and \(\kappa { = } \pm 1\) in the layer Eq. (4), the distribution of equilibrium points is shown in Fig. 3. Depending on the eigenvalues by Jacobian matrix, the equilibrium points \(E_{ \pm }\) in spaces of I and III are stable foci, and \(E_{0}\) in space of II is a saddle as depicted in Fig. 3. Furthermore, for the equilibrium point which is located by the non-smooth boundaries as \(\varSigma_{1,2} = \left\{ {\left( {x,y} \right) \in R^{2} \left| {x = \pm 1} \right.} \right\}\), the dynamics in the vicinity of the equilibrium point cannot only be determined by the eigenvalues defined in \(P_{0} \left( \lambda \right)\) or \(P_{ \pm } \left( \lambda \right)\), respectively.

Fig. 3
figure 3

Phase portraits for \(\alpha = 1.015\) of layer equations (4) in the different subspaces about the switching manifolds \(\varSigma_{1,2}\), as we choose \(\kappa = \pm 1\), respectively

Full size image

The switching manifolds \(\varSigma_{1,2}\) will result in the trajectories behaving as a piecewise smooth flows that admit different types of non-smooth bifurcations such as boundary equilibrium bifurcations, grazing bifurcations or sliding bifurcations et al [29,30,31,32,33]. In order to investigate the evolution of the fast system dynamics near the switch boundaries, we next consider the occurrence of a discontinuity-induced Hopf bifurcation leading to limit cycle motion.

Discontinuity Hopf Bifurcation by the Switching Manifolds

The evolution of non-smooth dynamics near the switching discontinuities may be investigated by a generalized Jacobian matrix \(J_{q}\) expressed as the following set-valued matrix.

$$J_{q} = qJ_{0} + \left( {1 - q} \right)J_{ \pm } ,\,q \in \left[ {0,1} \right]$$
(11)

Written explicitly, we have

$$J_{q} = \left( {\begin{array}{*{20}c} { - aq + bq - b} & 1 \\ { - \beta } & { - \alpha } \\ \end{array} } \right)$$
(12)

which results in the generalized characteristic polynomial equation

$$P_{q} \left( \lambda \right) = \lambda^{2} + \left( {aq - bq + b + \alpha } \right)\lambda + aq\alpha - bq\alpha + b\alpha + \beta = 0$$
(13)

Obviously, discontinuous bifurcations may occur at the non-smooth boundaries when the eigenvalues defined in (13) pass zero point or pure imaginary axis. When the auxiliary variable \(q = 1\) by fixing the parameter values of \(\alpha = 1.015\), we have \(P_{q} \left( \lambda \right) = P_{0} \left( \lambda \right)\) and the eigenvalues \(\lambda_{q}\) deduced by the Jacobian matrices \(J_{0}\) are \(\lambda_{0}^{1} = 0.1904\) and \(\lambda_{0}^{2} = - 0.1854\) for the subspace II in the central region. On the other hand, at \(q = 0\), we have \(P_{q} \left( \lambda \right) = P_{ \pm } \left( \lambda \right)\), and the eigenvalues \(\lambda_{q}\) deduced by the Jacobian matrices \(J_{ \pm }\) are \(\lambda_{ \pm }^{1,2} = - 0.2325 \pm 0.6227i\) for the spaces of I and III in the both symmetric side regions (as seen in Fig. 4).

For other intermediate values in \(0 < q < 1\), the eigenvalues \(\lambda\) from the Jacobian matrices \(J_{q}\) form a one-dimensional path in the complex plane shown as the blue tracks in Fig. 3. These generalized eigenvalues are found that they have not crossed through the imaginary axis as a conjugate complex pair. At the critical value of \(q = 0.9255\), the fixed points will lose the stability and a saddle-node bifurcation occurs suggesting that the two fixed points of the nonlinear dynamical system collide and annihilate each other. Following that one-dimensional path at that point, we can find the eigenvalue of \(\lambda_{q} = - 0.015\), thereby suggesting the only one stable equilibrium point in the fast system.

Fig. 4
figure 4

Schematic diagram of the discontinuous-fold bifurcation for \(\alpha = 1.015\) showing the path of eigenvalues \(\lambda\) in the complex plane parameterized with auxiliary variable of \(q\) described by Eq. (13)

Full size image

As the parameter \(\alpha\) is reduced maintaining all other parameters unchanged, the generalized eigenvalues may cross the pure imaginary axis at the non-smooth boundaries which leads to the occurrence of discontinuous Hopf bifurcations. As an example of Fig. 5 for \(\alpha = 0.8\), these generalized eigenvalues \(\lambda_{q}\) are observed to jump through the imaginary axis as a conjugate pair at the critical value. As shown in Fig. 5, the fast system has the stable foci \(E_{ \pm }\) in the subspaces I and III with the eigenvalues of \(\lambda_{q} = - 0.1250 \pm 0.7378i\) for the Jacobian matrix \(J_{q}\) at \(q = 0\), while the eigenvalues of \(\lambda_{q} = 0.11 \pm 0.4146i\) for the Jacobian matrix \(J_{q}\) at \(q = 1\) indicate an unstable focus, the equilibrium point \(E_{0}\) in the center space II repelling the trajectories away.

Fig. 5
figure 5

Schematic diagram of the discontinuous Hopf bifurcation for \(\alpha = 0.8\) showing the path of eigenvalues \(\lambda\) in the complex plane parameterized with auxiliary variable of \(q\) described by Eq. (13)

Full size image

Following that one-dimensional path at that critical point of \(q = 0.532\), we can find the eigenvalues of \(\lambda_{q} = \pm 0.6i\), and the fast system will lose the stability of the fixed points and generate the stable periodic motions via the discontinuity. For the phase portrait of system (4) at \(\alpha = 0.8\) and \(\kappa = 0\) plotted in Fig. 6, the trajectory starting from the basin of attraction may cycle around the equilibrium point of \(E_{0}\) and cross the non-smooth boundaries of \(\varSigma_{1,2}\) according to the frequency approximated by the discontinuous Hopf bifurcation. Such combined effect of the two different vector fields clarified by the switching manifolds is so as to cause the birth of periodic orbits.

Fig. 6
figure 6

Phase portraits for \(\alpha = 0.8\) of layer equations (4) crossing the different subspaces about the switching manifolds by discontinuous singular Hopf as we choose \(\kappa = 0\) in Eq. (4)

Full size image

Periodic Vibrations in the Perturbed System

Based on the results of the stability and bifurcations discussed above, we begin to investigate periodic cascades of oscillations with clearly separated amplitudes [36, 37] in the MLC circuit system. Since the periodic force frequency is far smaller than the natural frequency of the unperturbed system, system (3) may possess the fast variable of \(x\) (or \(y\)) and exhibit different types of flow relaxations. To reveal the non-smooth dynamics in this double-scroll circuit in the presence of the perturbation, we fix the parameters at \(F = 0.5\) and \(\omega = 0.01\) in this section.

Figure 7 shows the relaxation flows at \(\alpha = 1.015\) in the perturbed system (3) by numerical simulation, in which relaxation excursions and small peaks appear alternately in one period. Another type of oscillation patterns, an example for \(\alpha { = 0} . 8\), is presented in Fig. 8, in which the trajectories clearly move back and forth periodically between the foci and the large amplitude cycles controlled by the non-smooth boundaries. Non-smooth critical manifolds can be developed to compute and visualize geometric structures that shape such dynamics in the following.

Fig. 7
figure 7

Relaxation flows in system (3) for \(\alpha = 1.015\) with fixed parameter values \(\beta = 1.0\), \(a = - 1.02\), \(b = - 0.55\), \(F = 0. 5\) and \(\omega = 0.01\). a Phase portraits. b Time series

Full size image
Fig. 8
figure 8

Oscillation patterns in system (3) for \(\alpha = 0. 8\) with fixed parameter values at \(\beta = 1.0\), \(a = - 1.02\), \(b = - 0.55\), \(F = 0. 5\) and \(\omega = 0.01\). a Phase portraits. b Time series

Full size image

Mechanism of Relaxation Flows by Fold Singularities

Non-smooth critical manifold from the fast system (4) can be expressed by

$$S_{1} = \left\{ {\left( {x,\kappa } \right) \in R^{2} \left| { - \alpha g\left( x \right) - \beta x + F\kappa = 0} \right.} \right\}$$
(14)

where \(g\left( x \right) = bx + \frac{1}{2}\left( {a - b} \right)\left( {\left| {x + 1} \right| - \left| {x - 1} \right|} \right)\). Due to the existence of two non-smooth boundaries, \(S_{ 1}\) may have singularities with three normally hyperbolic pieces of I, II and III.

Figure 9a gives a critical manifold with piecewise linear shape on the plane of \(\left( {x,\kappa } \right)\) at \(\alpha = 1.015\) according to Eq. (14), where the branches \(Sa_{ \pm }\) are attracting, and \(Sr\) is repelling. However, the discontinuity-induced Hopf singularities are not observed in this case, while the two generic-fold bifurcation points may occur on the non-smooth boundaries and separate attracting and repelling sheets of the non-smooth critical manifold into three areas. Such generic-fold points are also called as jump points \(J_{1,2}\) (see Fig. 9), where the fast and slow segments are concatenated and the trajectory flow is directed away from the boundaries on the critical manifold.

Fig. 9
figure 9

Oscillation mechanism in the MLC circuit system at \(\alpha = 1.015\) with other fixed parameter values at \(\beta = 1.0\), \(a = - 1.02\), \(b = - 0.55\), \(F = 0. 5\) and \(\omega = 0.01\). a Fast–slow decomposition on critical manifold \(S_{ 1}\) with piecewise linear shape. b The periodic vibration combined with the switching manifold \(S_{ 1}\)

Full size image

We now clarify the mechanism of periodic relaxation flows observed in the perturbed system at \(\alpha { = 1} . 0 1 5\) with the other parameter values of \(F = 0.5\) and \(\omega { = 0} . 0 1\). As shown in Fig. 9b, the orbits are drawn in the phase space of \(\left( {x,\kappa } \right)\) combined with the manifold \(S_{ 1}\) and the attracting branch appears the focus form. Such closed curve is a singular orbit composed of two fast trajectories indicated by the horizontal double arrows as depicted in Fig. 9b. Meanwhile, the slow flow indicated by single arrows surrounding the attracting branch of \(Sa_{ \pm }\) forms the continuous concatenation flanked the non-smooth boundaries, the process of which is belong to the rest state.

This slow drift persists until approaching the fold point of \(J_{1}\), where the trajectory flows lose the stability and go into the fast process. Upon that, the system jumps toward another stable branch with damped oscillations. Then, the trajectories slow drift is back to the manifold when the slow variable of \(\kappa\) reaches the other fold point of \(J_{2}\) which leads to the second fast process with the quick jump and another cluster of the fast damped oscillations.

Oscillation Mechanism Induced by Discontinuous Singular Hopf Bifurcations

Previous studies show that the structures of the attracting branch may change with the variation in the parameter values of \(\alpha\). The stable limit cycle can exist and affect the oscillation modes of the layer Eq. (4). Here, Fig. 10a gives another critical manifold with piecewise linear shape at \(\alpha = 0.8\) based on Eq. (14). The discontinuous Hopf bifurcation may occur at points \(H_{1,2}\) (see Fig. 10) on the non-smooth boundaries which lead to the birth of large amplitude oscillations as the return mechanism involved in the formation of complex oscillation modes.

Fig. 10
figure 10

Oscillation mechanism in the MLC circuit system at \(\alpha = 0.8\) with other fixed parameter values of \(\beta = 1.0\), \(a = - 1.02\), \(b = - 0.55\), \(F = 0. 5\) and \(\omega = 0.01\). a Fast–slow decomposition with a critical manifold \(S_{ 1}\) with piecewise linear shape. b The periodic vibration combined with the switching manifold \(S_{ 1}\)

Full size image

Figure 10b gives numerical simulations about the mechanism of complex oscillation patterns when the discontinuous Hopf bifurcation occurs on the non-smooth boundaries. Firstly, the system converges toward the slow manifold in the area of I belonging to the part of the rest state. When the slow-varying variable of \(\kappa\) reaches the non-smooth boundaries and the discontinuous Hopf bifurcation at point \(H_{1}\) appears, the trajectory undergoes a transition to the limit cycle attractor according to the frequency approximated by the discontinuous Hopf bifurcation. The corresponding spiking orbits are drawn in the phase space of \(\left( {x,\kappa } \right)\) combined with the manifold of \(S_{ 1}\), in which a continuation of stable limit cycles born between the two Hopf bifurcations at \(H_{1,2}\) is detected.

Such large amplitude oscillations persist until approaching the next switching boundary at \(H_{2}\), where the trajectories lose stability and go back into the damped oscillations. Then, the trajectories slow drift is back to the critical manifold, and the attracting branch displays the focus form. Such closed curve is due to symmetric singular Hopf bifurcations clarified by the two non-smooth boundaries. These trajectories consisting of small amplitude oscillations that alternate with large relaxation-like oscillations during each period indicate that the transition behaviors are both depended on the singular Hopf point found in the non-smooth boundaries as it allows the reduced flow to cross from the attractive region of I to the other attractive region of III repeatedly.

Effect of the Second Periodic Force

A prime advantage of addition of the second sinusoidal force is its easy implementability in actual application. One can also add a second periodic signal in series with the existing one of the MLC circuit model as shown in Fig. 1. Then, the system becomes a quasiperiodically driven one with the forcing item of \(f_{1} \sin \left( {\varOmega_{1} t} \right) + f_{2} \sin \left( {\varOmega_{2} t} \right)\), where the corresponding dimensionless form can be represented by,

$$\dot{x} = y - g\left( x \right)$$
$$\dot{y} = - \alpha y - \beta x + F_{1} \sin \left( {\omega_{1} t} \right) + F_{2} \sin \left( {\omega_{2} t} \right)$$
(15)

where \(F_{1} = 0.5\) and \(\omega_{1} = 0.01\). Some investigations have been carried out in Eq. (15) for a fixed amplitude value of the second force \(F_{2} = 0.2\) and varying the frequency \(\omega_{2}\) over a range. In order to give the description of the distinction that occurs in the system’s dynamics under the second forcing frequency variation, two representative periodic forces in values of frequency of the second force can be clarified. One case is when the two periodic signals in series have the resonant ratio. The other is when there exists a significant order gap between \(\omega_{1}\) and \(\omega_{2}\).

Oscillation Mechanisms with Two Low-Frequency Periodic Forces

Due to the resonant frequency ratio of the same order, the total force can be interpreted as slow-varying incentive under the action of periodic effect which leads to complex oscillations with apparent fast and slow flows. The decomposition technique applied here is based on the formula of DeMoivre expansion [38]. Without loss of generality, we can assume \(\omega_{2} = n\omega_{1}\) and give the expression as,

$$\sin \left( {\omega_{2} t} \right) = \sum\limits_{k = 0}^{n} {\left( \begin{aligned} n \hfill \\ k \hfill \\ \end{aligned} \right)} \cos^{k} \left( {\omega_{1} t} \right)\sin^{{\left( {n - k} \right)}} \left( {\omega_{1} t} \right)$$
(16)

where the integer \(k \le n\).

Here are the concrete instances based on Eq. (16) for \(\omega_{2} = 2\omega_{1}\) or \(\omega_{2} = 3\omega_{1}\) as \(\sin \left( {\omega_{2} t} \right) = 2\sin \left( {\omega_{1} t} \right)\cos \left( {\omega_{1} t} \right)\) or \(\sin \left( {\omega_{2} t} \right) = 3\sin \left( {\omega_{1} t} \right) - 4\sin^{3} \left( {\omega_{1} t} \right)\). An appropriate scaling of the parameters will help us magnify the transition process and offer some more perspective. As an example of \(\omega_{2} = 2\omega_{1}\), we assume \(\sin \left( {\omega_{1} t} \right) = \kappa\) and obtain that \(\sin \left( {\omega_{2} t} \right) = \pm 2\kappa \sqrt {1 - \kappa^{2} }\), which leads to the complex critical manifold,

$$S_{2} = \left\{ {\left( {x,\kappa } \right) \in R^{2} \left| { - \alpha g\left( x \right) - \beta x + F_{1} \kappa \pm 2F_{2} \kappa \sqrt {1 - \kappa^{2} } = 0} \right.} \right\}$$
(17)

where \(g\left( x \right) = bx + \frac{1}{2}\left( {a - b} \right)\left( {\left| {x + 1} \right| - \left| {x - 1} \right|} \right)\). Due to the existence of two non-smooth boundaries, \(S_{2}\) gives a non-smooth manifold and may have more complex singularities with three normally hyperbolic pieces of I, II and III.

At \(\alpha = 1.015\), the sketch of the time series of the oscillation modes in system (15) with two low-frequency forces is presented in Fig. 11a. The fast and slow oscillation parts connected by catastrophic jumps clarified by the non-smooth boundaries appear irregularly in one period. Although the attracting branch still appears the form of stable foci, such closed curve combined with the non-smooth manifold is composed of more complex dynamical properties due to the complexity of the critical manifold as shown in Fig. 11b.

Fig. 11
figure 11

Complex relaxation flows with multiple frequency signals of system (15) at \(\alpha = 1. 0 1 5\), with other parameter values of \(\beta = 1.0\), \(a = - 1.02\), \(b = - 0.55\), \(F_{1} = 0. 5\), \(\omega_{1} = 0.01\), \(F_{2} = 0.2\) and \(\omega_{2} = 0.02\). a Time series. b The periodic vibration combined with the complex manifold \(S_{ 2}\)

Full size image

As shown in Fig. 11b, when the slow variable of \(\kappa\) passes through the singular-fold bifurcation clarified by the non-smooth boundaries at \(J_{1,2}\), the system undergoes catastrophic transitions between area I and area III. One revolution of fast and slow flows on such complex critical manifold is illustrated in detail of Fig. 11b. What is noteworthy is that due to the characteristic of the more complicated manifold depicted by Eq. (17), the system will undergo one periodic movement with the joint of distinct segments showing small oscillations interspersed with large amplitude jumps.

Previous studies have shown that the eigenvalues for the generalized Jacobian matrix in the fast system may change with the bifurcation coefficient of \(\alpha\). More precisely, the repelling part still has saddle properties which are independent, while the transition process is by means of the discontinuous Hopf bifurcation which induces dense cycle motions. In the case of \(\alpha { = 0} . 8\), Fig. 12 shows the sketch of phase portraits of another type of oscillation modes with two resonant low-frequency signals as well as time series.

Fig. 12
figure 12

Complex oscillation patterns with multiple frequency signals of system (15) at \(\alpha = 0. 8\), with other parameter values of \(\beta = 1.0\), \(a = - 1.02\), \(b = - 0.55\), \(F_{1} = 0. 5\), \(\omega_{1} = 0.01\), \(F_{2} = 0.2\), and \(\omega_{2} = 0.02\). a Phase portraits. b Time series

Full size image

The cycle trajectories are repelled by the saddle causing them to cross the non-smooth boundaries and settle down to the bilateral equilibrium points of \(E_{ \pm }\), the mechanism of which is associated with the singular discontinuous Hopf bifurcations. Thus, the system exhibits the oscillation motions involving parts of small damped oscillations and parts of large limit cycles bifurcated by the discontinuous Hopf bifurcation due to the two non-smooth boundaries.

Quasiperiodic Spiking for an Order Gap Between Two Frequencies

When an order gap exists between the two external periodic forces, the transformation method by expansion formula of Eq. (16) can no longer be used for the DeMoivre polynomial in the much higher order of \(n\). We can rewrite the system (15) into the following fast system by still introducing \(\kappa = \sin \left( {\omega_{1} t} \right),\)

$$\dot{x} = y - g\left( x \right)$$
$$\dot{y} = - \alpha y - \beta x + F_{1} \kappa + F_{2} \sin \left( {\omega_{2} t} \right)$$
(18)

Introducing the two new variables \(u = \cos \left( {\omega_{2} t} \right)\) and \(v = \sin \left( {\omega_{2} t} \right)\) into Eq. (15) gives autonomous four-dimensional layer equations with an additional equation of \(u^{2} + v^{2} = 1\),

$$\dot{x} = y - g\left( x \right)$$
$$\dot{y} = - \alpha y - \beta x + F_{1} \kappa + F_{2} v$$
$$\dot{u} = - \omega_{2} v$$
$$\dot{v} = \omega_{2} u$$
(19)

where \(\left( {x,y,u,v} \right) \in R^{4}\) and \(g\left( x \right) = bx + \frac{ 1}{ 2}\left( {a - b} \right)\left( {\left| {x + 1} \right| - \left| {x - 1} \right|} \right)\). Obviously, the critical manifold is decided by

$$S_{3} = \left\{\left({x,\kappa }\right) \in R^{2} \left| { - \alpha g\left( x \right) - \beta x + F_{1} \kappa = 0} \right.\right\}$$
(20)

We remark that the critical manifold defined by \(S_{3}\) depicted by Eq. (20) has the similar form as \(S_{1}\) depicted by Eq. (14). This means that the intersection between the stable branch and the slow unstable manifolds (through the fold or the discontinuous Hopf singularities) can exist in the same way. Moreover, something should be pointed out that the existence of the second signal will introduce additional frequency as well as the harmonics, which leads to the occurrence of local cycles as slow stable branches with the second frequency of \(\omega_{ 2}\).

As an example of \(\omega_{2} = 1\) and \(\alpha = 1.015\) in the fast system (18), the distribution of two stable local limit cycles is shown in Fig. 13. We can easily find that the area of the local cycle orbits scale is in accordance with the variation in the second signal. When we further investigate such multiple frequency signal-driven system (15), the phase portraits of non-smooth dynamics by the addition of the second periodic force are presented in Fig. 14a.

Fig. 13
figure 13

Phase portraits showing two symmetric local cycles at \(\alpha = 1.015\) in fast system (18) with the second frequency at \(\omega_{2} = 1\) clarified by the switching manifolds as we choose \(\kappa { = } \pm 1\), respectively

Full size image
Fig. 14
figure 14

Periodic oscillations with multiple frequency signals of system (15) at \(\alpha = 1. 0 1 5\), with other parameter values of \(\beta = 1.0\), \(a = - 1.02\), \(b = - 0.55\), \(F_{1} = 0. 5\), \(\omega_{1} = 0.01\), \(F_{2} = 0.2\) and \(\omega_{2} = 1\). a Phase portraits. b The periodic vibration combined with the manifold \(S_{ 3}\) on the plane of \(\left( {x,\kappa } \right)\)

Full size image

One may easily find that there is an oscillation of large amplitude with fast transitions between the two clusters of local cycle orbits. Moreover, we can find that in addition to the second signal, the two local cycles will go through saddle-node bifurcation of period orbits (fold-cycle bifurcation) at the non-smooth boundaries. This resulting singularity-induced dynamics can be called as discontinuous fold-cycle bifurcation \(Sa_{1,2}\) for the local cycle orbits which cross the boundaries and evolve to large amplitude oscillations (see Fig. 14b).

Figure 14b shows one revolution of the trajectories in detail. Before the left of the fold-cycle point (\(Sa_{1}\)) induced by the boundary \(\varSigma_{1}\), the periodic oscillation in the area I is the only attractor corresponding to the quasi-stationary manifold. Beyond \(Sa_{1}\), the local cycle orbits become unstable causing the oscillations to increase until the orbits are finally attracted by the local cycles in the area III. When the trajectories pass the other fold-cycle point (\(Sa_{2}\)) induced by the boundary \(\varSigma_{2}\), the orbits with the small amplitude oscillations will increase again and jump back to the left to begin the next revolution. The large amplitude oscillations are indicated by the double arrows corresponding to the spiking process.

According to the classification scheme of oscillation mechanisms given by Izhikevich et al. [39,40,41,42], the nature of such dynamical behaviors is associated with the symmetric discontinuous fold-cycle spiking mode since the large amplitude oscillations terminate at discontinuous fold-cycle bifurcations.

Previous studies have shown that as the bifurcation parameter \(\alpha\) is reduced, the generalized eigenvalues of fast system (18) without regard to the second force may cross the pure imaginary axis at the non-smooth boundaries which leads to the occurrence of a discontinuous Hopf bifurcation. As we take into account the second periodic force and fetch values at \(\alpha = 0. 8\) in fast system (18) of the second frequency of \(\omega_{2} = 1\), we can present quasiperiodic behaviors in Fig. 15 at \(\kappa { = 0}\) as well as the two stable local cycle orbits at \(\kappa = \pm 1\) distributed in regions I and III. These quasiperiodic trajectories pass through all the three regions of the state space and enclose the two local cycle orbits.

Fig. 15
figure 15

Phase portraits showing the quasiperiodic orbits and local cycle orbits at \(\alpha = 0.8\) in fast system (18) with the second frequency at \(\omega_{2} = 1\) clarified by the switching manifolds as we choose \(\kappa = 0\) and \(\kappa { = } \pm 1\), respectively

Full size image

The quasiperiodic oscillations exhibited by the non-autonomous fast system can be explained by the discontinuous Hopf bifurcation as suggested by the eigenvalues for the Jacobian matrices. This discontinuous Hopf bifurcation leads to the birth of periodic motion which is combined with the periodically forced vibration introduced by the second signal with the frequency of \(\omega_{ 2}\) and the harmonic, thereby forming the quasiperiodic motions.

In order to determine the nature of the non-smooth dynamics affected by the second periodic force, we present the sketch of phase portraits as well as time series in Fig. 16 for \(\alpha = 0.8\) in system (15). Note that, the fast transitions will happen near the neighborhood of the non-smooth boundaries causing the quasiperiodic oscillations via the discontinuous Hopf bifurcation. More precisely, the clusters of large cycle oscillations still remain in the area of II along with the two non-smooth boundaries, while the small cycle oscillations occur and go around the bilateral equilibrium points on the areas of both sides. From such dynamical system structure, the difference is that these driven dynamics are more sophisticated than those observed previously because the quasiperiodic spiking modes exist due to discontinuity-induced Hopf bifurcations.

Fig. 16
figure 16

Complex quasiperiodic spiking behaviors with multiple frequency signals of system (15) at \(\alpha = 0. 8\), with other parameter values of \(\beta = 1.0\), \(a = - 1.02\), \(b = - 0.55\), \(F_{1} = 0. 5\), \(\omega_{1} = 0.01\), \(F_{2} = 0.2\) and \(\omega_{2} = 1\). a Phase portraits. b Time series

Full size image

Conclusions

The transitions through the sets of non-smooth bifurcation values may lead to complicated dynamics such as the coexistence of bilateral local cycles and the abrupt jumps or hysteresis cycles in the MLC electronic circuit. Relaxation trajectories with complicated waveforms are observed under the influence of periodic perturbation during one period. A small number of well-chosen examples of various kinds of nonlinear dynamics have been followed by a discussion of the non-smooth bifurcation phenomena in hand, and a brief introduction to the mathematical tools associated with the MLC electronic circuit has been developed to study these phenomena.

The discontinuous bifurcations in layer equations associated with the switching manifolds are analyzed by the generalized Jacobian matrix. A prime advantage of periodic perturbations is that they can evoke so complex oscillatory patterns consisting of large amplitude oscillations that alternate with slight oscillations. It could be easy to observe this phenomenon and implement in many actual electronic systems as the MLC circuit. The addition of second periodic signal will provide more parameter condition, namely amplitude and frequency. One can choose suitable values of the second perturbation to acquire more desired periodic vibrations. To investigate the feature of such complex oscillation patterns in more non-smooth and non-autonomous chaotic systems is one of our attractive following research topics.