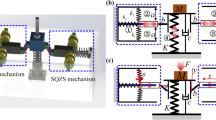
Abstract
In this study, a novel criterion known as the comprehensive transmissibility is proposed to estimate the isolation performance of nonlinear isolation systems under complex loading excitations. A combined quasi-zero-stiffness (QZS) isolator is enumerated, and the comprehensive performance of other common isolator systems and the existing QZS system is analyzed. Based on the normalized differential equations of the isolation system, the isolation performances of different isolation systems are studied by using the comprehensive transmissibility criterion, showing that the combined QZS isolator has better isolation performance than others. In addition, the output frequency response function (OFRF) representation of the comprehensive transmissibility is derived, and the optimal design of the QZS isolation system is developed by using the OFRF. The simulation results demonstrate that the design can meet the requirements of the vibration isolator with both the force and displacement excitations and is promised to be applied to the design of nonlinear isolation systems in engineering practice.
Graphic abstract
To solve the issue of the analysis and design of nonlinear vibration isolation systems under multi-excitation, a new criterion known as comprehensive transmissibility is proposed. Based on the comprehensive transmissibility, the isolation performance of the combined vibration isolation system is analyzed, and the output frequency response function (OFRF) method is applied to conduct the design of the isolation system.

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Vibration isolation systems have been widely applied to reduce the vibration transmission between the foundation and the equipment in engineering practice [1,2,3]. For example, Rao [4] introduced the theory and application of vibration isolation technology. Liu et al. [5] introduced the research progress of micro-vibration isolation in recent years. Basically, the limitations of linear isolation systems are obvious to have narrow isolation range and unsatisfied isolation performance over frequency wideband frequency ranges [6]. In order to solve the aforementioned issues, various nonlinear isolation systems were discussed to solve the problems in recent years [7, 8].
In general, the nonlinear isolation system is combined with nonlinear stiffness and nonlinear damping to achieve more abundant dynamic properties than a linear isolation system [5]. For instance, Kink [9] examined the influence of cubic spring and tangent spring on the performance of the vibration isolator. Dutta and Chakraborty [10] investigated the performance of the nonlinear vibration isolator, in which the softened nonlinear spring was proved to have a good isolation performance. Reducing the stiffness of the system would contribute to obtaining the low frequency vibration isolation performance and the low carrying capacity. The quasi-zero-stiffness (QZS) concept was proposed with the aim of achieving the improvement in both the isolation range and the carrying capacity of the system. Basically, buckled beams [11], inclined springs [12], etc., can all be applied to achieve the QZS property to build a nonlinear isolation system [13,14,15]. Although such nonlinear stiffness can be applied to broaden the isolation range, it is difficult to suppress the resonant vibration. In order to address this issue, geometric nonlinear damping [16], nonlinear viscous damping [17, 18], etc., were applied to isolate the vibration over the resonant frequency range but they do not affect the isolation performance over the high frequency range. However, the applicability of vibration isolators with damping nonlinearity is still limited. For example, the Coulomb friction applied in the vehicles' suspension would result in the poor experience of driving on the flat surface of the small amplitude excitation [19]. And for the cubic damping, when the strength of the disturbing force is related to the square of the frequency, increasing the cubic damping would increase the force transmissibility in the high frequency region [20]. To address the above issues, researchers paid their attention to sophisticated nonlinear technologies and used them in nonlinear vibration isolation systems. Sun et al. [21] analyzed and designed a scissor system with nonlinear stiffness and damping for the advantageous isolation effect. Ho et al. [22] designed a vibration isolator with two auxiliary springs and viscous damping, which increased the vibration isolation range and the vibration isolation capability at the resonance.
In practice, vibration isolators may be subjected to different types of excitation signals [1], but vibration isolators are usually designed and analyzed based on the force and the base displacement excitations [23, 24]. In order to investigate the integral characterizes of the system under complex excitations including both the force and displacement excitations, scholars have completed many research works [25,26,27,28]. For example, Carrella et al.[25] investigated the force and displacement transmissibility of the QZS system with auxiliary springs. Lv and Yao [26] studied the performance of vibration isolation systems which are based on the harmonic force and base excitations. Xiao et al. [27] investigated the transmissibility of vibration isolators with cubic nonlinear damping under the complex load. Guo et al. [28] investigated both the force and displacement transmissibility of the force isolation systems and displacement isolation systems. However, given the multifarious input loads, using the force transmissibility and the base displacement transmissibility is not comprehensive to estimate and design vibration isolator systems, which needs a new evaluation indicator to consider the vibration isolation effect of the force and displacement at the same time.
The desired isolation performance of a nonlinear isolation system is usually achieved by properly designing the system characteristic parameters [22, 29]. In general, the design of linear vibration isolation systems is conducted by using the frequency response function (FRF) approach in the frequency domain [30,31,32]. For nonlinear systems, many techniques have been applied for the analysis and design of nonlinear systems [33,34,35,36,37]. For example, the generalized frequency response function (GFRFs) can facilitate the analysis of the nonlinear in the frequency domain [33, 34]. However, the GFRFs method is multidimensional, which causes the GFRFs to be difficult to be used in practice [35]. To address these issues, the OFRF was proposed and applied to formulate a one-dimensional relationship between the output responses and nonlinear characteristic parameters of a general class of nonlinear Volterra systems [36], so as to be applied for the design of nonlinear systems [37]. Lv and Yao [26] used the OFRF to study the effect of damping on the force and displacement transmissibility.
In this paper, a new criterion named as the comprehensive transmissibility is proposed to assess the isolation performance by considering both the force and the base displacement excitations. A QZS isolator combined with both QZS and horizontal damping is introduced. A comparison study is conducted based on the comprehensive transmissibility criterion, showing that the combined QZS isolator has better isolation performance than other nonlinear isolators. Moreover, the design of the combined QZS isolator is discussed based on the comprehensive transmissibility criterion, where the OFRF representation of the comprehensive transmissibility of the vibration isolation system is derived, so as to conduct the design of the nonlinear isolation system.
This paper is organized as follows. In Sect. 2, a new criterion known as the comprehensive transmissibility for vibration isolators subject to complex excitations is described. The isolation effect of a combined QZS isolator is asserted by using the new criterion in Sect. 3. The OFRF expression of the comprehensive transmissibility and the detailed system design procedure using the OFRF method are discussed in Sect. 4. Next, a numerical example of the design process is described in Sect. 5. Finally, in Sect. 6, conclusions are drawn.
2 Assessment and design of vibration isolators
2.1 A comprehensive transmissibility criterion
A single-degree-of-freedom (SDOF) vibration isolation system is illustrated in Fig. 1, where the input excitation displacement signal d in(t) or the force signal fin(t) can be considered as a force \(u(t)\) to the system, the absolute displacement of the mass is \(d_{{{\text{out}}}} (t)\), and the relative displacement of the mass generated by the excitation is \(x(t)\). M is the total mass, and the nonlinear force in the isolation system is defined by \(f_{n} (x,t)\). The system dynamics equation can be written as
where the force transferred to the foundation denoted by \(f_{{{\text{out}}}} (t)\) is written as
In practice, a vibration isolator can have beneficial effects on the input signals of the displacement [17] and the force[38] from the base, respectively. The vibration isolator can be excited by different kinds of loadings, wherein this study, both the displacement and force input loadings, which are usually used to study vibration isolators [25,26,27,28], are considered.
When the input excitation of the system in Fig. 1 is the harmonic displacement signal \(d_{{{\text{in}}}} (t) = H_{\rm D} \sin (\omega t)\), u(t) in Eq. (1) can be obtained that
where \(H_{\rm D}\) is the amplitude of the excitation and \(\omega\) is the excitation frequency. The input force \(u(t)\) in Eq. (1) is achieved from the second-order derivative of the displacement \(d_{{{\text{in}}}} (t)\) and the mass M.
When the input is \(d_{{{\text{in}}}} (t)\), the displacement \(x(t)\) of the mass in Eq. (1) generated by the displacement input signal is obtained as \(x(t) = d_{{{\text{out}}}} (t) - d_{{{\text{in}}}} (t)\). And the system dynamics equation can be written as
where the right-hand side of Eq. (4) \(\hbox{MH}_{\rm D} \omega^{2} sin(\omega t)\) is the equivalent for \(- M\ddot{d}_{{{\text{in}}}} (t)\).
The displacement input excitations are usually evaluated from uneven roads [39], etc. Both the Displacement–force (DF) transmissibility \(T_{{{\text{DF}}}} (\omega )\) and the displacement–displacement (DD) transmissibility \(T_{{{\text{DD}}}} (\omega )\) are considered to assess the isolation performance of a vibration isolator on the system output force and displacement, respectively, defined as
and
where DD is expressed by absolute displacement transmissibility and the absolute displacement is \(d_{{{\text{out}}}} (t)\) under displacement excitation [13].\(F\left\{ . \right\}\) represents the Fourier Transform, and \(F_{{{\text{out}}}} (j\omega )\) and \(D_{{{\text{out}}}} (j\omega )\) are the spectra of \(f_{{{\text{out}}}} (t)\) and \(d_{{{\text{out}}}} (t)\), respectively.
When the input excitation of the system in Fig. 1 is the harmonic force loading
where HF is the amplitude of the excitation, for the force input systems, there is \(u(t) = f_{{{\text{in}}}} (t) = H_{{\text{F}}} sin(\omega t)\).
When inputting the pure force signal \(f_{{{\text{in}}}} (t)\) [38], so \(d_{{{\text{in}}}} (t) = 0\), then in Eq. (1) the vibration relative displacement generated by the force input signal is \(x(t) = d_{{{\text{out}}}} (t)\). Therefore, the system dynamics equation can be written as
The force input excitations are usually evaluated from wind or water wave loadings [28], etc. Both the force–displacement (FD) transmissibility \(T_{\rm FD} (\omega )\) [28] and the force–force (FF) transmissibility \(T_{\rm FF} (\omega )\) are considered to assess the isolation performance of a vibration isolator on the system output displacement and force, respectively, defined as [28]
where \(X(j\omega )\) is the Fourier transform of \(x(t)\), and for the force input system \(x(t) = d_{{{\text{out}}}} (t)\) and
In general, the force and displacement transmissibilities are separately discussed to study the displacement isolation performance and the force isolation performance [13,14,15, 25], respectively. However, it is a fact that both the displacement and force output exist in either the displacement or force loading input, and both the displacement and force transmissibility should be considered to assess the performance of a vibration isolator. A more comprehensive criterion is therefore needed in practice to solve this issue. In the present study, considering the displacement and force input signals on both the displacement and force vibration isolation and the effect of the energy of different input signals, we use the energy of E1 and E2 of the displacement and force input signals and the energy ratio E2/E1 of both to determine the proportional coefficient of the two signals in the overall criterion, and based on these, a new comprehensive transmissibility criterion is defined as TC (ω), which is proposed below to assess the isolation performance of a vibration isolator systematically
where \(\Xi = E_{2} /E_{1}\), \(E_{1}\) and \(E_{2}\) represent the energy of the displacement signal and force signal defined as
with \(v_{i} (t)\) being either a displacement signal or a force signal, \(T_{i}\) is the period of the signals of the displacement or force, respectively.
2.2 The comprehensive design of the vibration isolator
In order to achieve good vibration isolation performance for both output force and displacement, the parameters of the vibration isolation system can be designed based on the comprehensive transmissibility proposed in Eq. (11). The comprehensive transmissibility curve of a system that meets all design requirements in Fig. 1 can be generally represented in Fig. 2. In Fig. 2, \(T_{\rm m}\) is the maximum allowable value of the comprehensive transmissibility at the resonance frequency. Point \(L\) is the limiting position of the high frequency transmissibility. Point s is the limiting positions at the beginning isolation frequency of the corresponding linear system; the value of \(f_{n} (x,t)\) in Eq. (1) is assumed zero. The design of the comprehensive transmissibility should meet the following design requirements to ensure a good isolation performance.
-
(1)
In the resonance region: \(\max T_{\rm C} \le T_{\rm m}\).
-
(2)
When \(\omega = \omega_{\rm s} ,\;T_{\rm C} \le T_{\rm s}\).
-
(3)
When \(\omega = \omega_{\rm l} ,{\kern 1pt} \;T_{\rm C} \le T_{\rm l}\).
Remark 1
The high frequency comprehensive transmissibility may begin to increase because the DF transmissibility is related to the input frequency. However, in practice, the input signal frequency is not very large, especially for the displacement excitation. Therefore, according to the actual excitation conditions, the comprehensive transmissibility can be designed and evaluated within a certain frequency range.
The OFRF derived from the Volterra series gives the direct relationship between the output frequency response and the nonlinear parameters of the system, and the Volterra series is based on the weak nonlinear systems; therefore, OFRF method is suitable for the weakly nonlinear systems. By using the OFRF method, the values of system parameters can be determined to achieve the desired output frequency response of the system. In the following studies, the OFRF representation will also be applied to conduct the design of the nonlinear isolation system.
3 Analysis of vibration isolators with damping and stiffness nonlinearities
3.1 Limitations of the linear isolation systems
The isolation performance of force and displacement signals of linear vibration isolation systems has been studied extensively. For the DD and FF transmissibility, linear systems start isolation at the cutoff frequency that is the \(\sqrt 2\) times of natural frequency of the systems; large linear damping can reduce the resonance peak, but it will increase the value of the displacement and force transmissibility at high frequencies [1,2,3,4,5,6].
An SDOF linear vibration isolation system is illustrated in Fig. 3, where the input force excitation is defined as \(u(t)\), and the relative displacement of the mass is \(x(t)\). M is the total mass. The system dynamics equation can be written as
Let \(\Xi = 1\), the influence of linear damping and stiffness on the comprehensive transmissibility of the linear isolator is shown in Fig. 4. From Fig. 4, it can be seen that: (1) increasing the damping of the linear system can reduce the peak of the transmissibility at the resonance frequency, but can increase the comprehensive transmissibility at the high frequency, (2) increasing the stiffness of the linear system can increase the cutoff frequency of the vibration isolation system and reduce the vibration isolation interval of the system. In order to overcome the limitations of linear isolation systems, the study of nonlinear systems is increasing.
Comprehensive transmissibility of the linear system. a Change in the damping coefficient of the linear system, where \(C = 50\, \hbox{N}\,\hbox{sm}^{ - 1}\) (solid), \(C = 7\, \hbox{N}\,\hbox{sm}^{ - 1}\) (dashed), \(C = 90\, \hbox{N}\,\hbox{sm}^{ - 1}\) (dot-dashed). b Change in the stiffness coefficient of the linear system, where \(K = 1500\,\hbox{Nm}^{ - 1}\) (solid), \(K = 1800\,\hbox{Nm}^{ - 1}\) (dashed), \(K = 2000\,\hbox{Nm}^{ - 1}\) (dot-dashed)
3.2 Mathematical modeling for the nonlinear isolator systems
3.2.1 Horizontal stiffness and damping elements
For the nonlinear stiffness vibration isolator with a vertical spring and two auxiliary springs [12], when the vibration isolator is in the balanced position, the negative stiffness provided by the inclined spring and the positive stiffness provided by the vertical spring make the whole mechanism in the state of near-zero stiffness; that is, the isolator is a QZS isolation system; because of its low dynamic stiffness, this type of vibration isolation system can decrease the frequency which starts isolation compared with cubic nonlinear stiffness and linear stiffness isolation system. For the nonlinear damping vibration isolators, when the excitation is the displacement signal, comparing the displacement isolation performance of the horizontal damping vibration isolator with the equivalent vertical cubic damping vibration isolator, the vibration isolator with the horizontal damping has a superior isolation performance at high frequencies, and the isolation effect of the vibration isolator with the vertical cubic damping is not good because the damping force generated by the equivalent cubic damping is related to the frequency [23]. For obtaining the vibration isolator systems with excellent integrated isolation performance, it is necessary to analyze the effects of nonlinear stiffness [12] and damping [23] on the comprehensive transmissibility.
Figure 5 shows the schematic modes with two nonlinear stiffness and the nonlinear damping, respectively, where \(f_{n\rm s} (x,t)\) and \(f_{\rm nd} (x,t)\) are the nonlinear stiffness and damping force, respectively, \(K_{\rm h}\) is the spring stiffness coefficient, \(C_{\rm h}\) is the damping coefficient, \(l\) is the horizontal distance between the ends of each element and \(l_{0}\) is the original length of the spring.
In Fig. 5a, the nonlinear spring force along the vertical direction is described by [22]
And in Fig. 5b, the nonlinear damping force along the vertical direction is expressed as [23]
3.2.2 Nonlinear isolation systems
To study the vibration isolation performance of the two nonlinear components demonstrated above, three types of nonlinear isolation systems composed of horizontal springs and damping shown in Fig. 6 are discussed. System (a) described in Fig. 6a is the nonlinear stiffness and damping system [40], which has a vertical spring \(K_{\rm v}\), a pair of horizontal auxiliary spring \(K_{\rm h}\), a vertical damping \(C_{\rm v}\) and the horizontal linear damping \(C_{\rm h}\). Systems (b) and (c) illustrated in Fig. 6b, c are the nonlinear isolation systems composed of horizontal stiffness and damping, respectively.
Consequently, given the harmonic displacement of Eq. (3), the dynamic equation of the nonlinear Systems (a), (b), and (c) can be obtained according to Eq. (4) as
where given the harmonic displacement input of Eq. (3) \(u(t) = H_{\rm D} \omega^{2} \sin (\omega t)\) and the harmonic force of Eq. (7) \(u(t) = H_{\rm F} \sin (\omega t)\), the dynamic equations of Systems (b) and (c) are obtained by setting \(K_{\rm h} = 0\) and \(C_{\rm h} = 0\) in Eq. (16), respectively.
3.2.3 Approximate analysis of the mathematical modeling
The system parameters can be designed based on the design requirements of the comprehensive transmissibility by utilizing the OFRF method, because the OFRF method can establish the polynomial function between output spectrum and nonlinear coefficients; for facilitating the design of system parameters by using the OFRF method, it is necessary to simplify the nonlinear force as the polynomial function of the displacement and velocity to the power of n. Therefore, the equations of the nonlinear stiffness, nonlinear damping force and the system dynamic are simplified, respectively, in this section.
Rewrite Eq. (16) in a dimensionless form as follows
where
where the normalized dynamic equation of system (b) is obtained by setting \(k = 0\) in Eq. (17) and the normalized dynamic equation of system (c) is obtained by setting \(\xi_{2} = 0\) in Eq. (17). When the system is stimulated the by harmonic displacement \(r = \Omega {}^{2}\), \(\sigma = \chi = \frac{{H_{\rm D} }}{{l_{\rm o} }}\), \(\hat{x}(\tau ) = \frac{x(t)}{{H_{\rm D} }}\), when the system is excited by the harmonic force \(r = 1\), \(\sigma = \lambda = \frac{{H_{\rm F} }}{{K_{\rm v} l_{\rm o} }}\), \(\hat{x}(\tau ) = \frac{{K_{\rm v} x(t)}}{{H_{\rm F} }}\).
The dimensionless nonlinear spring force of spring in Eq. (14) can be expressed by the Taylor formula for small \(\hat{x}(\tau )\)
where \(\hat{f}_{\rm ns} (\hat{x},\tau )\) is the dimensionless expression for \(f_{\rm ns} (x,t)\). The superscript (i) represents the i derivative of the function.
In order to use the OFRF to design the system parameters under displacement and force excitations, for the simplified system dynamics equation, the system parameters designed need to be independent of the type of excitation. Therefore, the expressions are simplified as follows.
When \(\left| {x(t)/l} \right| < 0.2\), the dimensionless nonlinear damping force in Eq. (15) can be approximated as [23]
where \(\xi_{3} = \xi_{2} /\hat{l}^{2}\).
Assuming the nonlinear stiffness is expanded by a fifth-order Taylor series, the dimensionless nonlinear force and output force of system (a) are simplified as
where
and
where
where the nonlinear force and output force of system (b) are obtained by setting \(\alpha = 1,\;\alpha_{2} = 0,\;\alpha_{3} = 0\), and the nonlinear force and the output force of system (c) are obtained by setting \(\xi_{3} = 0\). When the harmonic displacement signal stimulates the system, \(\sigma = \chi\). When the system is excited by the harmonic force, \(\sigma = \lambda\).
Substituting Eq. (24) into Eq. (17), the dynamic equation of the nonlinear systems (a), (b) and (c) can be written as
where the normalized dynamic equation of system (b) is obtained by setting \(\alpha = 1,\;\alpha_{2} = 0,\;\alpha_{3} = 0\) in Eq. (26), and the normalized dynamic equation of system (c) is obtained by setting \(\xi_{3} = 0\) in Eq. (26). When the input signal is the displacement, \(\sigma = \chi\), \(r = \Omega {}^{2}\), \(\hat{x}(\tau ) = \frac{x(t)}{{H_{\rm D} }}\); when the input signal is the force, \(\sigma = \lambda\), \(r = 1\), \(\hat{x}(\tau ) = \frac{{K_{\rm v} x(t)}}{{H_{\rm F} }}\).
Remark 2
When the direction of the excitations to the system is horizontal, this is equivalent to the system being rotated. For this condition, the structure of system (a) subjected to the horizontal inputs is the same as that of Eq. (26) of the system subjected to the vertical input, except that the coefficients in front of each term are different. Therefore, the vibration isolation effect of the system with horizontal input excitation is similar to the vertical ones. The specific content will be discussed in a future paper.
3.3 Analysis of the nonlinear force on the comprehensive transmissibility
By using the fourth-order Runge–Kutta method, the transmissibility curves of \(T_{\rm DF} (\Omega )\), \(T_{\rm DD} (\Omega )\), \(T_{\rm FD} (\Omega )\), \(T_{\rm FF} (\Omega )\) and \(T_{\rm C} (\Omega )\) are shown in Figs. 7 and 8, where systems (a), (b) and (c) are, respectively, the systems described in Fig. 6a–c, and for comparing the performance of linear and nonlinear vibration isolators, an SDOF linear vibration isolation system is defined as system (d) which is illustrated in Fig. 3. Weak and strong nonlinear systems belong to two kinds of common nonlinear problems [41]. The OFRF can be used for the design of weakly nonlinear systems, so this section only compares the systems in the weakly nonlinear region and then selects the best isolation effect system, so as to design the selected system in the area using the OFRF method and the fourth-order Runge–Kutta.
In Fig. 7, compared with systems (b) and (d), system (a) with nonlinear stiffness and damping has beneficial performance as shown by (1) a large isolation frequency range, (2) the low energy of the mass at high frequency and (3) a relatively small resonance peak.
Figure 8 shows the comprehensive transmissibility of the four systems. Compared with the resonance of systems (b), (c) and (d), system (a) in Eq. (26) has lower maximum transmissibility in the resonance interval and a larger vibration isolation interval. So the type of vibration isolation system with the nonlinear stiffness and damping force has good isolation performance on the whole. Based on the beneficial effects of horizontal stiffness and damping, parameters of system (a) can be designed by using the OFRF method according to actual vibration isolation requirements and excitation amplitude.
For the convenience of the design of system (a) by the OFRF method, system parameters on the vibration isolation effect on the comprehensive transmissibility curves of system (a) are analyzed by the Runge–Kutta method as shown in Fig. 9. Figure 9a, b shows the effect of the linear and nonlinear damping on the comprehensive transmissibility of the system expressed in Eq. (26). At the high frequency, the increase in linear damping will cause the improvement in the comprehensive transmissibility, and when the value of the nonlinear damping increases, the comprehensive transmissibility is unaffected. Figure 9c shows the effect of the nonlinear stiffness on the comprehensive transmissibility; nonlinear stiffness can decrease the peak value and the vibration isolation range. The effect of both the nonlinear stiffness and damping is shown in Fig. 9d. It can be seen that the combination of them can reduce the initial frequency of vibration isolation, the degree of system nonlinearity and the peak value of the system.
Effects of system parameters on the comprehensive transmissibility for system (a), where \(\Xi = 1\), \(\chi = 0.04,\;{\kern 1pt} \lambda = 0.05\). In a, \(\xi_{1} = 0.2,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.5\) and \(0.8\). In b, \(\xi_{3} = 2,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 5\) and \(8\). In c, \(k = 0.2,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.8\) and \(1.4\). In d, \(k = 0.2,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.8,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1.4\) and \(\xi_{3} = {\kern 1pt} {\kern 1pt} {\kern 1pt} 5,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 10,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 15\)
4 Optimization design
For letting the comprehensive transmissibility to meet the design requirements described in Sect. 2, it needs to establish the relationship between both system parameters and the comprehensive transmissibility first, and then by using the OFRF design the system according to requirements. In the paper, the OFRF method is suitable for the design of the mentioned weakly nonlinear system. In this section, the representation of the OFRF method will be introduced at first. Then, the expression of the OFRF of the comprehensive transmissibility is derived, and the design process of the weakly QZS isolation system is developed based on the OFRF method. Due to the good comprehensive isolation performance of system (a), system (a) is selected as the system designed.
4.1 The OFRF representation
For nonlinear systems, the OFRF method defines the explicit analytic relationship between the output spectrum of the system and the nonlinear parameters of the system; the expression can be described by a polynomial differential equation model, which is written as [36]
where the polynomial \(Q_{{j_{1} \ldots j_{\rm s} }} (j\omega )\) is the function of frequency. \(M_{1} \ldots \;M_{\rm s}\) are the orders of the nonlinear parameter with \(\eta_{1} \ldots {\kern 1pt} \;\eta_{\rm s}\), respectively, \(j_{i} = 0,1, \ldots ,M_{i} ,\) for \(i = 1 \ldots \;s\).
Defining M as the number of \(Q_{{j_{1} \ldots j_{\rm s} }} (j\omega )\), then \(M\) can be obtained from the following equations
The evaluation values of \(Q_{{j_{2} j_{3} \ldots j_{\rm s} }} (j\omega )\) can be calculated by
where
4.2 The OFRF-based design of the isolation system
In the design of system (a), the values of the mass of the system \(M\), the vertical spring \(K_{\rm v}\) and the original length of spring \(l_{0}\) are preset. The system physical parameters to be designed are the horizontal stiffness \(K_{\rm h}\), the horizontal damping \(C_{\rm h}\), the vertical spring \(C_{\rm v}\) and the horizontal length between two ends of the nonlinear element \(l\). According to Eq. (26), these design parameters are combined in dimensionless parameters \(\xi_{1}\), \(\xi_{3}\), \(\alpha\), \(\alpha_{2}\) and \(\alpha_{3}\), where \(\xi_{1}\) and \(\alpha\) are linear parameters, while \(\xi_{3}\), \(\alpha_{2}\) and \(\alpha_{3}\) are nonlinear parameters. The basic process of the parameters’ design can be summarized into two parts: firstly, using the frequency response function (FRF) approaches [30, 31] to design linear parameters and secondly, designing nonlinear parameters by using the OFRF approach [36]. The flowchart of the design process of system (a) is illustrated in Fig. 10.
The program process is divided into four stages, and detailed discussions of each stage are studied as follows.
4.2.1 Stage 1: Determine the preset values
In this stage, the values of requirements and part of the parameters are determined. The determination of the preset values follows two steps. First, the thresholds of the design, given as \(T_{\rm m}\), \(T_{\rm l}\) and \(\Omega_{\rm s}\), \(\Omega_{\rm l}\), are designed. Next, the input signals used for the design are prepared by taking the input force and displacement amplitudes \(H_{\rm F}\) and \(H_{\rm D}\), respectively, under a specific energy ratio \(\Xi\). Moreover, presetting the physical parameters of \(M\), \(K_{\rm v}\) and \(l_{0}\), then the values of dimensionless parameters \(\chi\) and \(\lambda\) in Eq. (26) are determined.
4.2.2 Stage 2: The FRF-based design of linear parameters
In the second stage of the design, the linear parameters \(\alpha\) and \(\xi_{1}\) are determined by using the FRF of the vibration isolation system (a) as below.
Without considering the nonlinear effects of \(\alpha_{2}\), \(\alpha_{3}\) and \(\xi_{3}\), the FRF on the comprehensive transmissibility is obtained as
where \(T_{DD,0} (\Omega )\), \(T_{DD,0} (\Omega )\), \(T_{DF,0} (\Omega )\), \(T_{FD,0} (\Omega )\) are the FRF on the DD, FF, DF, FD transmissibility obtained as
The linear parameters can be designed by considering the following steps.
Step 1: Design the value of \(\alpha\).
According to Eqs. (32)–(34), when \(\Omega = \Omega_{\rm s}\) which is defined as the cutoff frequency of the linear system, four linear transmissibilities are \(T_{DD,0} (\Omega_{\rm s} ) = T_{DD,0} (0) = 1\), \(T_{FF,0} (\Omega_{\rm s} ) = T_{FF,0} (0) = 1\), \(T_{\rm DF} (\Omega_{\rm s} ) = T_{DF,0} (0) = \Omega_{\rm s}^{2}\) and \(T_{FD,0} (\Omega_{\rm s} ) = T_{FD,0} (0) = \frac{1}{\alpha }\).
Therefore, the comprehensive transmissibility at the cutoff frequency \(\Omega_{\rm s}\) can be obtained as
In practice, the linear damping ratio in isolation systems is usually small to achieve desired isolation performance over the isolation frequency range [1,2,3,4,5,6], and \(\xi_{1}^{2}\) is extremely small. As illustrated in Appendix A, the value of \(\alpha\) can be evaluated as \(\alpha \approx \frac{{\Omega_{\rm s}^{2} }}{2}\).
Step 2. Design the value of \(\xi_{1}\).
According to the design requirement, \(\xi_{1}\) can then be evaluated by substituting the estimated value of \(\alpha\) into Eqs. (32), (33), (34) and (11) which gives
where 0.9 is to compensate for the possible influence of nonlinear parameters on the comprehensive transmissibility.
4.2.3 Stage 3: The OFRF-based design of nonlinear parameters
According to the OFRF theory [36], it is known that when linear parameters \(\alpha\) and \(\xi_{1}\) are determined in Stage 2, the transmissibilities of system (a) can be represented using the OFRF as
Substituting Eq. (37) to Eq. (40) into Eq. (11), the OFRF equation of the comprehensive transmissibility can be written as
where \(Q_{{C_{{j_{1} j_{2} j_{3} }} }} (\Omega ) = \frac{{Q_{{DF_{{j_{1} j_{2} j_{3} }} }} (\Omega ) + Q_{{DD_{{j_{1} j_{2} j_{3} }} }} (\Omega )}}{2(\Xi + 1)} + \frac{{Q_{{FD_{{j_{1} j_{2} j_{3} }} }} (\Omega ) + Q_{{FF_{{j_{1} j_{2} j_{3} }} }} (\Omega )}}{{2(\Xi^{ - 1} + 1)}}\).
Then, the value of \(\hat{l}\)is selected and the values of \(\xi_{3}\), \(\alpha_{2}\) and \(\alpha_{3}\) are determined. Moreover, the value of \(k\) is calculated. The specific design process is described as follows.
Step 1. Prepare a set of simulation data for use in the OFRF calculations.
First, the order of the OFRF \(M\) is determined according to Eq. (28). Second, the \(M\) groups of \(\hat{l}\),\(\xi_{3}\), \(\alpha_{2}\) and \(\alpha_{3}\) are set. Third, \(M\) groups of \(T_{DF(i)} (\Omega )\), \(T_{DD(i)} (\Omega )\), \(T_{FD(i)} (\Omega )\) and \(T_{FF(i)} (\Omega )\) are obtained by taking the values of \(M\) groups of parameters, and then the \(M\) sets of values of \(T_{C(i)} (\Omega )\) are obtained by using Eq. (11), for \(i = 1,2 \ldots M\). Finally, the values of \(Q_{{C_{{j_{1} j_{2} j_{3} }} }} (\Omega )\) are calculated according to Eqs. (41) and (29).
Step 2. Determine the value of \(\alpha_{2}\) and \(\alpha_{3}\).
Rearranging Eq. (25), \(k\) can be written as
Substituting Eq. (42) into Eq. (22) and Eq. (23) gives,
Then, the value of \(\hat{l}\) is selected within the range of the above \(M\) groups values, and the values of \(\alpha_{2}\) and \(\alpha_{3}\) are calculated by using Eqs. (43) and (44).
Step 3. Find \(\Omega_{\max }\) and determine \(\xi_{3}\).
The value of comprehensive transmissibility \(T_{\rm C} (\Omega )\) is obtained, and the value of \(\Omega_{\max }\)is found, which is the frequency at the maximum comprehensive transmissibility in the resonance region, where \(\xi_{3}\) is the maximum value of \(\xi_{3} (i)\) for \(i = 1,2 \ldots M\).
Then, \(\xi_{3}\) is defined by calculating Eq. (45).
where 0.9 is to compensate for the inaccurate value of \(\Omega_{\max }\).
Step 4. Determine \(k\).
The value of \(k\) can be obtained by substituting the values determined in the above steps into Eq. (42)
4.2.4 Stage 4: Validation requirements
The parameters of the system are obtained through the above stages, and the value of \(T_{\rm s}\) is calculated according to Eq. (35). Then, it is checked whether the system can meet the design requirement after obtaining all design parameters. If the comprehensive transmissibility cannot meet requirements at the same time, the iteration is repeated until the design requirements are met simultaneously; the specific process can be described as below.
-
(i)
If it does not meet requirement 2), repeat from stage 3 to get a smaller value of \(\hat{l}\). If it still cannot satisfy requirement 2) when \(\hat{l}\) is the minimum value in the range, repeat from Stage 2 to reduce the value of \(\alpha\).
-
(ii)
If it does not meet requirement 3), repeat from step 3 to get a smaller value of \(\xi_{1}\).
5 Numerical simulation study
In this section, in order to obtain parameters that can meet the requirements, a numerical example of the design of system (a) following the steps in the previous section will be carried out to prove the effectiveness of the above design steps. The specific process of the numerical example is as follows.
Stage 1: Determine the preset values
-
1.
Let \(T_{\rm m} = 2.5\), \(T_{\rm l} = 0.55\) and \(\Omega_{\rm s} = 1.12\), \(\Omega_{\rm l} = 3.1\).
-
2.
Define \(\chi = 0.12\), \(\lambda = 0.1\), \(\Xi = {{\Xi_{2} } \mathord{\left/ {\vphantom {{\Xi_{2} } \Xi }} \right. \kern-\nulldelimiterspace} \Xi }_{1} = 0.8\).
Stage 2: The FRF-based design of linear parameters
Calculating the value of \(\alpha\) gives \(\alpha { = }\frac{{\Omega_{\rm s}^{2} }}{2}{ = 0}{\text{.627}}\). Then, substituting \(\alpha\) into Eq. (36) gives \(\xi_{1} = 0.38\).
Stage 3: The OFRF-based design of nonlinear parameters
Step 1. Prepare a set of simulation data for use in the OFRF calculations.
First, set \(M_{{\alpha_{2} }} = M_{{\alpha_{3} }} = M_{{\xi_{3} }} = 1\), and get \(M = 2^{3} = 8\). Next, give the eight groups of the parameters’ value. Because \(\alpha_{2}\) and \(\alpha_{3}\) are dependent on \(\hat{l}\) and \(\alpha\), eight groups of \(\hat{l}\) are given first, and then eight groups of \(\alpha_{2}\) and \(\alpha_{3}\) are obtained which are calculated by substituting \(\hat{l}\) and \(\alpha\) into Eqs. (43) and (44). The values of these parameters are shown in Table 1. Then, the eight groups values of \(T_{{\rm DF}(i)} (\Omega )\), \(T_{{\rm DD}(i)} (\Omega )\), \(T_{{\rm FD}(i)} (\Omega )\), \(T_{{\rm FF}(i)} (\Omega )\) and \(T_{{\rm C}(i)} (\Omega )\) are obtained, for \(i = 1,2 \ldots 8\) by taking the values of the parameters shown in Table 1. Finally, the values of \(Q_{{C_{{j_{1} j_{2} j_{3} }} }} (\Omega )\) are obtained according to Eqs. (41) and (29).
Step 2. Determine the value of \(\alpha_{2}\) and \(\alpha_{3}\).
Let \(\hat{l} = 0.61\), get \(\alpha_{2} = 1.463\) and \(\alpha_{3} = - 4.217\).
Step 3. Find \(\Omega_{\max }\) and determine \(\xi_{3}\).
Taking these values of the parameters obtained so far, the value of \(T_{\rm C} (\Omega )\) is calculated by using Eq. (11), and get \(\Omega_{\max } = 0.781\) as presented in Fig. 11. Next, the value \(\xi_{3} = 7.266\) is obtained by calculating Eq. (45).
Step 4. Determine \(k\).
By substituting the values of \(\alpha\) and \(\hat{l}\) into Eq. (42), the value of \(k\) can be obtained as \(k = 0.194\).
Stage 4: Validation requirements
Get the value of \(T_{\rm s} = \frac{{1 + 0.8 + 1.12^{2} }}{3.6} + \frac{1}{4.5\alpha } = 1.202\). The curve of the comprehensive transmissibility when \(\alpha = 0.627\), \(\xi_{1} = 0.38\), \(\hat{l} = 0.61\), \(k = 0.194\), \(\xi_{3} = 7.266\), \(\alpha_{2} = 1.463\) and \(\alpha_{3} = - 4.217\) is presented in Fig. 12.
Comparing the result in Fig. 12 with the design requirements, it can be seen that all requirements are satisfied. The values of other physical parameters can be obtained according to these dimensionless parameters and preset values of the physical parameter values set before programming.
Figure 13 compares the designed final optimized system by using the comprehensive transmissibility with an arbitrary undesigned system. The two systems are evaluated by DD, DF, FD and FF to highlight the superiority of the design using the comprehensive transmissibility. In Fig. 13, the coefficients of the suboptimal system are set as 4 in Table 1.
In Fig. 13, for DD, FF, FD and DF, the system using the comprehensive transmissibility to design has a lower amplitude than the unoptimized one at the resonance frequency, and the isolation range of the optimized one is greater than the other. At high frequency, the vibration isolation level of the suboptimal system is slightly improved due to the increase in the nonlinear stiffness, but the performance difference between the two is very small. For DF, the reason for the slightly larger gap is as mentioned in Remark1 and the DF transmissibility is related to the frequency. Therefore, in general, the performance of the system designed with the comprehensive transmissibility is good for four transmissibilities.
The final design results illustrate that the nonlinear parameters of the vibration isolator system can be designed according to the requirements under the multi-input condition by the OFRF method and the comprehensive transmissibility. In the case of multi input in reality, if using one or two kinds of the transmissibilities to design system, which leads to that a final designed system cannot concurrently have good overall vibration isolation effect under the complex input, using the comprehensive transmissibility is more effective. The use of the OFRF method can effectively design the parameters of the nonlinear vibration isolation system under multiple inputs. The method can also be applied to the design of the other type of nonlinear isolator system.
6 Conclusions
For linear isolators, it is necessary to make a choice between good-resonance suppression effect and high-frequency isolation effect, and the cutoff frequency of the linear vibration isolators is also large. Nonlinear stiffness and damping can be used to address these issues. Nonlinear damping can address the first issue mentioned. Nonlinear stiffness can solve the last problem.
When analyzing and designing the nonlinear vibration isolator, it is hoped that the vibration isolator has a good isolation effect of both the displacement and force. However, the performance of the vibration isolator is usually evaluated by methods based on one kind of transmissibility, which is not well adapted to the actual usage situation. In order to solve this problem, it is necessary to evaluate the comprehensive isolation effect of the system by the new criterion.
There are many ways to analyze nonlinear systems, and some traditional analytical methods such as the harmonic balance method can establish implicit expressions of the output spectrum and system parameters. But the OFRF method can provide the explicit expression characterization for the output frequency response of nonlinear isolator systems, so as to offer the convenience for the analysis and design of the nonlinear systems.
In this paper, a new criterion is proposed to evaluate the isolation effect of the vibration isolator under the displacement and force excitations. Then, a combined nonlinear isolator system is introduced, and several vibration isolators with other different nonlinear forces are listed. The normalized mathematical differential equations of the systems are established, and the isolation performances are studied with the new criterion. It is theoretically shown that the system with the nonlinear stiffness and damping has a good isolation effect. Moreover, the polynomial function of the OFRF of the comprehensive transmissibility is derived, and the design procedure of the combined vibration system by using the OFRF method is proposed. Simulation results demonstrate that the system can meet the proposed requirements. In the case of multiple input signals, the vibration isolation system can be designed easily to meet the specified design requirements by using the OFRF approach. Future studies will examine the method in real applications and study the isolation performance of other nonlinear damping and stiffness forms under the displacement and force excitations.
References
Rivin, E.I.: Passive Vibration Isolation. ASME Press, New York (2003)
Snowdon, J.C.: Vibration isolation: use and characterization. J. Acoust. Soc. Am. 66(5), 1245–1274 (1979)
Kelly, S.G.: Fundamentals of Mechanical Vibrations Any Text on Mechanical Vibrations. Mcgraw-Hill College, New York (2000)
Rao, S.S.: Mechanical Vibrations (več izdaj). Addison-Wesley Publishing Company, Boston (1990)
Ibrahim, R.: Recent advances in nonlinear passive vibration isolators. J. Sound Vib. 314(3–5), 371–452 (2008)
Graham, D., McRuer, D.T.: Analysis of Nonlinear Control Systems. Wiley, New York (1961)
Wang, K., Zhou, J.X., Chang, Y.P., Ouyang, H.J., Xu, D., Yang, Y.: A nonlinear ultra-low-frequency vibration isolator with dual quasi-zero-stiffness mechanism. Nonlinear Dyn. 101(2), 755–773 (2020)
Wang, Q., Zhou, J.X., Xu, D.L., Ouyang, H.J.: Design and experimental investigation of ultra-low frequency vibration isolation during neonatal transport. Mech. Syst. Signal. Pr. 139, 106633 (2020)
Kirk, C.: Non-linear random vibration isolators. J. Sound Vib. 124(1), 157–182 (1988)
Dutta, S., Chakraborty, G.: Performance analysis of nonlinear vibration isolator with magneto-rheological damper. J. Sound Vib. 333(20), 5097–5114 (2014)
Tseng, W.Y., Dugundji, J.: Nonlinear Vibrations of a Beam Under Harmonic Excitation. ASME Press, New York (1970)
Alabuzhev, P.: Vibration Protection and Measuring Systems with Quasi-Zero Stiffness. CRC Press, Boca Raton (1989)
Carrella, A., Brennan, M., Kovacic, I., Waters, T.: On the force transmissibility of a vibration isolator with quasi-zero-stiffness. J. Sound Vib. 322(4–5), 707–717 (2009)
Xu, D.L., Zhang, Y.Y., Zhou, J.X., Lou, J.J.: On the analytical and experimental assessment of the performance of a quasi-zero-stiffness isolator. J. Vib. Control. 20(15), 2314–2325 (2014)
Liu, X.T., Huang, X.C., Hua, H.X.: On the characteristics of a quasi-zero stiffness isolator using Euler buckled beam as negative stiffness corrector. J. Sound Vib. 332(14), 3359–3376 (2013)
Sun, J.Y., Huang, X.C., Liu, X.T., Xiao, F., Hua, H.X.: Study on the force transmissibility of vibration isolators with geometric nonlinear damping. Nonlinear Dyn. 74(4), 1103–1112 (2013)
Sun, X.J., Zhang, J.R.: Displacement transmissibility characteristics of harmonically base excited damper isolators with mixed viscous damping. Shock. Vib. 20(5), 921–931 (2013)
Mokni, L., Belhaq, M., Lakrad, F.: Effect of fast parametric viscous damping excitation on vibration isolation in sdof systems. Commun. Nonlinear. Sci. 16(4), 1720–1724 (2011)
Dixon, J.C.: The Shock Absorber Handbook. Wiley, Hoboken (2008)
Peng, Z.K., Meng, G., Lang, Z.Q., Zhang, W.M., Chu, F.L.: Study of the effects of cubic nonlinear damping on vibration isolations using harmonic balance method. Int. J. Nonlinear Mech. 47(10), 1073–1080 (2012)
Liu, Y.Q., Xu, L.L., Song, C.F., Gu, H.S., Ji, W.: Dynamic characteristics of a quasi-zero stiffness vibration isolator with nonlinear stiffness and damping. Arch. Appl. Mech. 89(9), 1743–1759 (2019)
Ho, C., Lang, Z.Q., Billings, S.A.: Design of vibration isolators by exploiting the beneficial effects of stiffness and damping nonlinearities. J. Sound Vib. 333(12), 2489–2504 (2014)
Tang, B., Brennan, M.: A comparison of two nonlinear damping mechanisms in a vibration isolator. J. Sound Vib. 332(3), 510–520 (2013)
Cheng, C., Li, S.M., Wang, Y., Jiang, X.X.: Force and displacement transmissibility of a quasi-zero stiffness vibration isolator with geometric nonlinear damping. Nonlinear Dyn. 87(4), 2267–2279 (2017)
Carrella, A., Brennan, M., Waters, T., Lopes, V., Jr.: Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic-stiffness. Int. J. Mech. Sci. 55(1), 22–29 (2012)
Lv, Q., Yao, Z.: Analysis of the effects of nonlinear viscous damping on vibration isolator. Nonlinear Dyn. 79(4), 2325–2332 (2015)
Xiao, Z.L., Jing, X.J., Cheng, L.: The transmissibility of vibration isolators with cubic nonlinear damping under both force and base excitations. J. Sound Vib. 332(5), 1335–1354 (2013)
Guo, P.F., Lang, Z.Q., Peng, Z.K.: Analysis and design of the force and displacement transmissibility of nonlinear viscous damper based vibration isolation systems. Nonlinear Dyn. 67(4), 2671–2687 (2012)
Sun, X.T., Zhang, S., Xu, J.: Parameter design of a multi-delayed isolator with asymmetrical nonlinearity. Int. J. Mech. Sci. 138, 398–408 (2018)
Pavlov, A., van de Wouw, N., Nijmeijer, H.: Frequency response functions for nonlinear convergent systems. IEEE Trans. Autom. Control 52(6), 1159–1165 (2007)
Garbuio, L., Lallart, M., Guyomar, D., Richard, C., Audigier, D.: Mechanical energy harvester with ultralow threshold rectification based on SSHI nonlinear technique. IEEE Trans. Ind. Electron. 56(4), 1048–1056 (2009)
Yang, X.M., Guo, X.L., Ouyang, H.J., Li, D.S.: A new frequency matching technique for FRF-based model updating. J. Phys. Conf. Ser. 842(1), 1–10 (2017)
Ran, Q., Xiao, M.L., Hu, Y.X.: Nonlinear vibration with volterra series method used in civil engineering: the bouc-wen hysteresis model of generalized frequency response. Appl. Mech. Mater. 530, 561–566 (2014)
Zhang, J.L., Cao, J.F.: Nonlinear circuit fault diagnosis based on simplified estimation of generalized frequency response function. In: 32th CCDC, pp. 698–702 (2020)
Peng, Z.K., Lang, Z.Q., Billings, S.A., Tomlinson, G.: Comparisons between harmonic balance and nonlinear output frequency response function in nonlinear system analysis. J. Sound Vib. 311(1–2), 56–73 (2008)
Lang, Z.Q., Billings, S.A., Yue, R., Li, J.: Output frequency response function of nonlinear Volterra systems. Automatica. 43(5), 805–816 (2007)
Zhu, Y.P., Lang, Z.Q.: Design of nonlinear systems in the frequency domain: an output frequency response function-based approach. IEEE Trans. Control Syst. Technol. 26(4), 1358–1371 (2017)
Chang, Y.P., Zhou, J.X., Wang, K., Xu, D.L.: A quasi-zero-stiffness dynamic vibration absorber. J. Sound Vib. 494, 115859 (2021)
Kuo, C.M., Fu, C.R., Chen, K.Y.: Effects of pavement roughness on rigid pavement stress. J. Mech. 27(1), 1–8 (2011)
Dong, Y.Y., Han, Y.W., Zhang, Z.J.: On the analysis of nonlinear dynamic behavior of an isolation system with irrational restoring force and fractional damping. Acta. Mech. 230(7), 2563–2579 (2019)
Worden, K., Tomlinson, G.R.: Nonlinearity in structural dynamics detection, identification and modelling. Institute of Physics Publishing, Bristol and Philadelphia (2001)
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 11872148) and the Fundamental Research Funds for the Central Universities of China (Grant Nos. N2003012, N2003013).
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A
Appendix A
The greater value of linear damping ratio \(\xi_{1}\) causes the greater beginning isolation frequency; usual systems are the little linear damping ratio systems; if the reasonable formulas for \(\xi_{1}^{2}\) are neglected, Eq. (35) is rewritten as
Simplifying Eq. (A.1) gives
In order for Eq. (A.2) to be true, \(2\alpha - \Omega_{\rm s}^{2} \approx 0\). From this, the value of \(\alpha\) can be written as
On the other hand, \(\alpha \approx \frac{{\Omega_{\rm s}^{2} }}{2}\) can be also drawn. For the DD, FF and DF transmissibilities, note that \(T_{{\rm DD},0} (\Omega_{\rm s} ) = T_{{\rm DD},0} (0) = 1\), \(T_{{\rm FF},0} (\Omega_{\rm s} ) = T_{{\rm FF},0} (0) = 1\) and \(T_{{\rm DF},0} (\Omega_{\rm s} ) = T_{{\rm DF},0} (0) = \Omega_{\rm s}^{2}\), and the transmissibilities at the cutoff frequency \(\Omega_{\rm s}\) can be obtained as
Equations (A.4) and (A.5) can be simplified as
And for FD transmissibility, when \(\Omega = \Omega_{\rm s}\), \(T_{{\rm FD},0} (\Omega_{\rm s} ) = T_{{\rm FD},0} (0) = \frac{1}{\alpha }\), then substituting the value into Eq. (34) gives
Equation (A.7) can be simplified as
Because the usual systems are the little linear damping ratio systems, the greater value of \(\alpha\) causes the greater beginning isolation frequency; therefore, the value of \(\xi_{1}^{2} /2\) can be ignored. So for the comprehensive transmissibility, the value of \(\alpha\) is considered as \(\alpha \approx \frac{{\Omega_{\rm s}^{2} }}{2}\).
Rights and permissions
About this article
Cite this article
Qiu, Y., Zhu, Y., Luo, Z. et al. The analysis and design of nonlinear vibration isolators under both displacement and force excitations. Arch Appl Mech 91, 2159–2178 (2021). https://doi.org/10.1007/s00419-020-01875-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00419-020-01875-0