Dynamic analysis and experiment of Quasi-zero-stiffness system with nonlinear hysteretic damping

Abstract

Nonlinear Quasi-zero-stiffness (QZS) vibration isolation systems with linear damping cannot lead to displacement isolation with different excitation levels. In this study, a QZS system with nonlinear hysteretic damping is investigated. The Duffing-Ueda equation with a coupling nonlinear parameter $\eta$ is proposed to describe the dynamic motion of the QZS system. By using the harmonic balance method (HBM), the primary and secondary harmonic responses are obtained and verified by numerical simulations. The results indicate that nonlinear damping can guarantee a bounded response for different excitation levels. The one-third subharmonic response is found to affect the isolation frequency range even when the primary response is stable. To evaluate the performance of the QZS system, the effective isolation frequency ${\Omega }_{e}$ and maximum transmissibility $T_{p}$ are proposed to represent the vibration isolation range and isolation effect, respectively. By discussing the effect of $\eta$ on ${\Omega }_{e}$ and $T_{p}$, the conditions to avoid nonlinear phenomena and improve the isolation performance are provided. A prototype of the QZS system is then constructed for vibration tests, which verified the theoretical analysis.

1 Introduction

In recent decades, there has been a significant increase in the application of quasi-zero stiffness (QZS) vibration isolators [1,2,3,4], which are essential for systems sensitive to low-frequency vibrations, such as ultra-precision manufacturing systems, ultra-high-precision measuring systems, and optical instruments for gravitational wave detection [5,6,7]. In general, for a payload of mass m, a linear isolator with stiffness k can function only for an excitation frequency greater than $\sqrt {2k/m}$ [8]. Therefore, ultra-low-stiffness isolators are required for isolating the frequency range to low and ultra-low frequencies. However, for traditional linear spring systems, low stiffness may cause a large static displacement due to the weight of the payload, which is generally impractical considering the installation space restrictions and stability of the system. Thus, nonlinear QZS isolators have been proposed to overcome this limitation; these isolators possess a localized zero stiffness at equilibrium by combining a matched nonlinear negative-stiffness structure in parallel with a positive spring. Hence, the positive spring has relatively high stiffness to reduce the static deflection due to the weight of the payload.

The design of a structure to obtain negative stiffness is essential to QZS isolators, and can be traced back to a conceptual design introduced by Molyneux with two oblique linear springs to provide negative stiffness [9]. The fundamental theory and design methodology of this type of isolator was comprehensively studied by Alabuzhev et al. [1], Carrella et al. [10,11,12,13,14], Kovacic et al. [15], Hao and Cao [16], and Lan. et al. [17]. Similar mechanisms have been introduced by applying electromagnets or magnet springs to form tunable QZS isolators [14, 18,19,20,21,22]. Meanwhile, various other mechanisms have been exploited to construct negative-stiffness elements, including inverse pendulums [23], bulking beams [24,25,26], and roll-cam-springs or ball-roller-spring [27, 28], as reviewed in detail by Ibrahim [2], Mizuno [3], and recently Li et al. [4].

However, the nonlinearity of a QZS system may cause the occurrence of subharmonic, superharmonic, and sometimes chaotic behavior, and the jump-through phenomenon, which can degrade the performance of the system. The transmissibility defined by the linear theory of vibration isolation is not quite applicable for demonstrating above phenomena [2]. Theoretical studies on Duffing oscillators [27, 29] have shown that as the excitation level increases, secondary harmonic responses other than the principle harmonic response may dominate the response. Then, chaotic motion may appear with the loss of stability of the secondary harmonic response and the separation of two periodic solutions with different periods. However, the boundaries between the principle and secondary harmonic responses and the effect of the onset of the secondary harmonic response on the isolation region have rarely been reported.

Moreover, almost all studies on QZS systems have adopted linear viscous damping with a damping force proportional to the velocity, which implies that the energy dissipated per cycle is dependent on the frequency and becomes infinitely small as this is reduced to zero [24]. Previous studies in refs. [13, 15, 17] have indicated that for a system with viscous damping, an unbounded response may appear with an increase in the excitation level, which may cause a deterioration in the isolation system. Therefore, hysteretic damping is adopted in this study to accurately describe the physical system and safety of the isolation system. A recent study by Liu and Yu [30] revealed that a large damping nonlinearity factor is beneficial for improving the vibration isolation performance.

Inspired by the theoretical research of Liu and Yu [30], a QZS system with nonlinear hysteretic damping is investigated in this study. The complex dynamic behavior of the system, including the primary, superharmonic, and subharmonic responses, is analyzed theoretically and numerically. Based on the dynamic analysis, parameter optimization is performed to improve the isolation performance. The isolation performance of the QZS system is evaluated using two indicators, i.e., the effective isolation frequency ${\Omega }_{e}$ and maximum transmissibility $T_{p}$. To verify the theoretical results, a prototype QZS system with nonlinear hysteretic damping is designed, and experiments are conducted with the prototype.

2 Dynamic analysis of QZS system with hysteretic damping

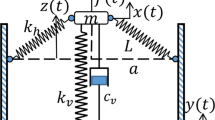
Figure 1 illustrates the idealized lumped parameter model to be considered, in which the mass $m$ is supported by a three-spring QZS isolator and two lateral hysteretic dampers with coefficients $c_{l}$. The structure is similar to that in Ref. [30], damping force applied on the object can be written as

$$ F_{d} = - 2F_{1} sin\theta $$

(1)

where $F_{1}$ is the damping force and $\theta$ is the angle of the lateral spring. Since the effect of lateral hysteretic damper is independent of frequency, the damping force $F_{1}$ can be obtained according to Ref.[30], which is

$$ F_{1} = \frac{{C_{l} \dot{\delta }_{l} }}{\omega } $$

(2)

where $\delta_{l}$ is the compressed deformations of the lateral spring. When the isolated object experiences a vertical displacement $y$, the deformation $\delta_{l}$ of the lateral spring is

$$ \delta_{l} = L_{0} - \sqrt {D^{2} + y^{2} } $$

(3)

where $L_{0}$ is the original length of the lateral spring without deformation and ${\text{D}}$ is the horizontal distance between the two ends of the lateral spring. And $sin\theta$ can be written as $\frac{y}{{\sqrt {D^{2} + y^{2} } }}$. Substituting Eq. (2), Eq. (3) and $sin\theta$ into Eq. (1) gives

$$ F_{d} = \frac{{2C_{l} y^{2} \dot{y}}}{{\omega \left( {D^{2} + y^{2} } \right)}} $$

(4)

Fig. 1

Idealized lumped parameter QZS model with a lateral hysteretic damper, m represents mass, $c_{l}$ represents the lateral hysteretic damping, Y is the response displacement of mass and Z is the excitation displacement from the base

Considering vertical displacement y is much less than length D of the lateral spring, and omitting higher order nonlinear items, $F_{d}$ can be rewritten as

$$ F_{d} = 2\frac{{C_{l} }}{{D^{2} \omega }}y^{2} \dot{y} $$

(5)

Let us assume that the vertical displacement $y$ of the static equilibrium position is small and the system is well tuned such that the effective linear stiffness is zero. Then, the equation of motion of the system about the static equilibrium position can be approximated using Duffing’s equation with no linear term [10,11,12,13,14]. Thus, combined with Eq. (5), the equation of motion for harmonic base excitation, is

$$m\mathop y\limits + 2\frac{{C_{l} }}{{D^{2} \omega }}y^{2} \dot{y} + k_{3} y^{3} = mz\omega^{2} \cos \left( {\omega t} \right) $$

(6)

where $m$ is the mass of the payload, $k_{3}$ is the cubic stiffness of the QZS system, and $z$ is the displacement excitation. To facilitate the analysis, Eq. (6) is rewritten in non-dimensional form as a Duffing-Ueda oscillator [31] with hysteretic damping,

$$ \frac{{\partial^{2} \overline{y}}}{{\partial \tau^{2} }} + \frac{2\eta }{\Omega }\frac{{\partial \overline{y}}}{\partial \tau }\overline{y}^{2} + \overline{y}^{3} = \Omega^{2} \cos \left( {\Omega \tau } \right) $$

(7)

where $\overline{y} = \frac{y}{z}$, $\omega^{*2} = \frac{{k_{3} z^{2} }}{m}$,$\tau = \omega^{*} t$, $\eta = \frac{{c_{l} }}{{D^{2} k_{3} }}$, and $\Omega = \omega /\omega^{*}$. It is important to note that $\omega^{*}$ is proportional to the displacement level. It can be observed in Eq. (7) that through the above non-dimensional transformation, the dynamic characteristics of the system are mainly governed by the non-dimensional parameter$\eta$.

Hassan [32] pointed out that the linear, undamped, and unforced oscillator corresponding to the system described by Eq. (7) is neutrally stable. In this situation, the system described by Eq. (7) does not represent a small perturbation of a stable linear system. Therefore, standard perturbation methods cannot be used directly. Consequently, for solving the periodic response in this situation, we rely on the harmonic balance method (HBM) and numerical simulations.

This study aims to investigate the isolation effect of the proposed isolation system, which is evaluated using the transmissibility parameter. Herein, we focus on the absolute displacement transmissibility. According to numerous previous studies [33,34,35], there are two possibilities for the steady-state response. The first is the harmonic solution alone, which has the same frequency as the excitation frequency, resulting in primary resonance in the amplitude-frequency curve. The second is the harmonic solution, which has the same frequency as the excitation frequency, and a permanent harmonic term whose frequency is a fraction $\left( \frac{1}{3} \right)$ or three times that of the excitation frequency (the former is called the one-third subharmonic resonance and the latter is called the superharmonic resonance of order three). The initial conditions determine the possibilities that may occur in the actual response. Thus, we separately present three cases to discuss the transmissibility of the proposed QZS system. The following analysis is aimed at obtaining the effective isolation frequency ranges by examining the transmissibility of the system through the HBM and numerical simulations. These frequency ranges are established by examining the boundaries of the operational regime of the isolator with respect to the primary and secondary responses.

2.1 Primary resonance

In the region of the primary resonance, the lowest harmonic dominates, whereas the higher harmonics are relatively small and can be omitted. Hence, the response of the system at the excitation frequency is assumed to be of the form $\overline{y} = \overline{A}\cos \left( {\Omega \tau + \varphi } \right)$. According to ref. [36], the harmonic balance method is an effective method for obtaining approximate analytic solutions of strongly nonlinear vibrations. Thus, the primary resonance was investigated by applying the harmonic balance method. Substituting $\overline{y} = \overline{A}\cos \left( {\Omega \tau + \varphi } \right)$ into Eq. (7) yields

$$ \begin{gathered} \left( {\frac{3}{4}\overline{A}^{ 3} - \Omega^{2} \overline{A}} \right)\cos \left( {\Omega \tau + \varphi } \right) + \frac{1}{2} \eta \overline{A}^{ 3} \sin \left( {\Omega \tau + \varphi } \right) \hfill \\ + \frac{1}{2} \eta \overline{A}^{ 3} \sin 3\left( {\Omega \tau + \varphi } \right) + \frac{1}{4}\overline{A}^{ 3} \cos 3\left( {\Omega \tau - \varphi } \right) - \Omega^{2} \cos \left( {\Omega \tau } \right) = 0 \hfill \\ \end{gathered} $$

(8)

Equating the coefficient of $\cos \left( {\Omega \tau } \right)$ and $\sin \left( {\Omega \tau } \right)$ to zero, we obtain

$$ \left\{ {\begin{array}{*{20}c} {\left( {\frac{3}{4}\overline{A}^{ 3} - \Omega^{2} \overline{A}} \right)\cos \varphi + \frac{1}{2} \eta \overline{A}^{ 3} \sin \varphi - \Omega^{2} = 0} \\ { - \left( {\frac{3}{4}\overline{A}^{ 3} - \Omega^{2} \overline{A}} \right)\sin \varphi + \frac{1}{2} \eta \overline{A}^{ 3} \cos \varphi = 0 } \\ \end{array} } \right. $$

(9)

Rearranging Eq. (9) by eliminating the parameter $\varphi$ yields the implicit amplitude-frequency (${\overline{A}}$-Ω) relationship

$$ \left( {\frac{{\overline{A}^{ 3} \eta }}{{2\Omega^{2} }}} \right)^{2} + (\frac{{3\overline{A}^{ 3} - 4\Omega^{2} \overline{A}}}{{4\Omega^{2} }}{ })^{2} = 1 $$

(10)

This can be expanded as

$$ \left( {\overline{A}^{ 2} - 1} \right)\Omega^{4} - \frac{3}{2}\overline{A}^{ 4} \Omega^{2} + \frac{9}{16}\overline{A}^{ 6} + \frac{1}{4}\eta^{2} \overline{A}^{ 2} = 0 $$

(11)

Solving for $\Omega$, the two positive solutions are

$$ \Omega_{1} = \sqrt {\frac{1}{{4\left( {\overline{A}^{ 2} - 1} \right)}}\left( {3\overline{A}^{ 4} + \sqrt {\Delta_{1} } } \right)} $$

(12a)

$$ \Omega_{2} = \sqrt {\frac{1}{{4\left( {\overline{A}^{ 2} - 1} \right)}}\left( {3\overline{A}^{ 4} - \sqrt {\Delta_{1} } } \right)} $$

(12b)

where ${ }\Delta_{1} = \overline{A}^{ 6} { }\left[ {9 + 4\eta^{2} \left( {1 - \overline{A}^{ 2} } \right)} \right]$. Equation (12a) and (12b) yields two real values of $\Omega$, which are used to plot the relative displacement transmissibility-frequency ($\overline{A}$-Ω) curves with different values of η in Fig. 2. ${\Omega }_{1}$ represents the lower branch of the $\overline{A}$-Ω curve while ${\Omega }_{2}$ represents the upper branch $\overline{A} = T_{r}$. Figure 2 also depicts the trend of the relative displacement transmissibility. Similar to the viscous damping QZS system, owing to the existence of nonlinearity, the $\overline{A}$-Ω curve behaves as a hardening curve characterizing bending to the right. This nonlinear characteristic leads to the physical jump phenomenon [16]. The curve of the phenomena depicted by the lower branch of the $\overline{A}$ vs Ω curve determined by Eq. (12b), is concave when $\eta$ is weak [20]. The occurrence of the inflection point leads to the jump-up phenomenon when

$$ \frac{{\partial \Omega_{1} }}{{\partial \overline{A}}} = - 9\overline{A}^{{{ }5}} \left( {3 - \overline{A}^{{{ }2}} } \right) + 4\left( {5\overline{A}^{{{ }2}} - 2\overline{A}^{{{ }4}} - 3} \right)\eta^{2} \overline{A}^{{{ }5}} + 6\left( {\overline{A}^{{{ }2}} - 2} \right)\overline{A}^{3} \sqrt {\Delta_{1} } = 0 $$

(13)

Fig. 2

Non-dimensional amplitude—frequency (${\overline{\varvec{A}}} {-} {{\varvec{\Omega}}}$) curves with stable solutions (solid line) and unstable solutions (dashed line) under ${\varvec{\eta}} =$ 0.2 (black), $0.5$ (red), 1 (blue) and 2 (green)

The frequency and amplitude of the jump-up point can be obtained by solving Eq. (13) as

$$ \Omega_{u} = \sqrt {\frac{{3\left( {\left( {9 + 12\eta^{2} } \right)\Delta_{2} + 24\eta^{4} - 90\eta^{2} + 2\eta^{2} \Delta_{3} } \right)}}{{16\eta^{2} \Delta_{2} }}} $$

(14a)

$$ \overline{A}_{u} = \frac{\sqrt 6 }{4}\sqrt {4 + \frac{3}{{\eta^{2} }} - \frac{{\sqrt {3\left( {3 - 4\eta^{2} } \right)} }}{{\eta^{2} }}} $$

(14b)

where $\Delta_{2} = 9 + 4\eta^{2} - 3\sqrt {9 - 12\eta^{2} }$ and $\Delta_{3} = \sqrt {6(\left( {3 + 8\eta^{2} - 16\eta^{4} } \right)\Delta_{1} + 2\eta^{2} \left( {200\eta^{2} + 16\eta^{4} - 15} \right)}$. The threshold value of $\eta$ for the appearance of the unstable jump phenomenon can be solved using Eq. (14),

$$ \eta_{cr\_1} = 0.866 $$

(15)

above which no jump phenomenon occurs and the whole $\overline{A}$-Ω curve is similar to that of a linear system.

Jumping down occurs at the interaction of the two branches of the $\overline{A}$-${\Omega }$ curves as $\Delta_{1} = A^{6} { }\left[ {9 + 4\eta^{2} \left( {1 - A^{2} } \right)} \right] = 0$. From Eq. (12), the peak amplitude and frequency can be solved as

$$ {\overline{A}}_{p} = \sqrt {\frac{{9 + 4\eta^{2} }}{{4\eta^{2} }}} $$

(16a)

$$ {\Omega }_{p} = \frac{{9 + 4\eta^{2} }}{4\sqrt 3 \eta } $$

(16b)

For the QZS system with hysteretic damping, the backbone curve is given by ${\Omega }_{backbone} = \sqrt {\frac{{3A^{4} }}{{4\left( {A^{2} - 1} \right)}}}$. It should be noted that from Eq. (16a), unlike the linear damping QZS system [12], the response of the present nonlinear hysteretic damping system always has a limited response. Furthermore, as the non-dimensional damping coefficient $\eta$ is independent of the excitation amplitude, the peak response defined by the primary resonance is constant for different excitation levels. However, for a linear damping system, the non-dimensional damping is inversely proportional to the excitation amplitude and causes a weak damping effect with high excitation.

As transmissibility is the key parameter to evaluate the vibration isolation effect, the displacement transmissibility is expressed in absolute form:

$$ T = \sqrt {1 + A^{2} + 2Acos\left( \varphi \right){ }} $$

(17)

where $\varphi$ can be determined from Eq. (9) as

$$ \cos \varphi = \frac{{3\overline{A}^{3} - 4\Omega^{2} \overline{A}}}{{4\Omega^{2} }} $$

(18)

The transmissibility curves with different values of $\eta$ are plotted in Fig. 3. The transmissibility curves increase from 1 to the peak and then decrease as the frequency increases. When an unstable area exists in the response $\overline{A}$-${\Omega }$ curves, the transmissibility curve exhibits the same hardening trend (as depicted by the curves for $\eta = 0.2$ and 0.5). The curves reach the peak point and jump down to the lower branch. The peak transmissibility can be obtained by solving $\frac{\partial T}{{\partial \overline{A}}} = 0$, which yields ${\overline{A}} = \frac{3}{2\eta }$ and the corresponding frequency ${\Omega }_{T} = \frac{3\sqrt 3 }{{4\eta }}$. The frequency of the peak transmissibility ${\Omega }_{T}$ is different from that of the peak relative amplitude response $\Omega_{p}$ determined by Eq. (16).) Thus, the peak transmissibility is

$$ T_{p} = \sqrt {1 + \frac{9}{{4\eta^{2} }}} $$

(19)

As $\eta \to + \infty$, the peak transmissibility $T_{p} { }$ tends to be close to 1, and the corresponding frequency ${\Omega }_{T}$ tends to be close to 0. Thus, a large damping ratio suppresses the peak transmissibility and decreases the effective isolation frequency.

Fig. 3

Non-dimensional transmissibility-frequency (${\varvec{T}} - {{\varvec{\Omega}}}$) curves defined by primary resonance with stable solutions (solid line) and unstable solutions (dashed line) under ${\varvec{\eta}} =$ 0.2 (black), $0.5$ (red), 1 (blue) and 2 (green); the effective frequency point is represented by the black dot

As effective isolation of the system implies $T < 1$, we define the frequency corresponding to $T = 1$ as the effective frequency ${\Omega }_{e}$. Solving for $T = 1$,

$$ \Omega = 0{ }or{ }\Omega = \sqrt {\frac{54}{{9 + 4\eta^{2} }}} { } $$

(20)

As shown in Fig. 3, the stable isolation frequency range of the transmissibility curves without an unstable area starts from $\Omega_{C} = \sqrt {\frac{54}{{9 + 4\eta^{2} }}}$. However, when an unstable area exists, the stable isolation frequency range of the transmissibility curves starts from $\Omega_{T}$. The transmissibility after this ${\Omega }_{T}$ point is close to 0. This indicates that when the frequency exceeds the peak point, the vibration isolator exhibits an excellent stable isolation effect. Therefore, the effective frequency $\Omega_{e}$ can be determined by

$$ \Omega _{e} = \left\{ {\begin{array}{*{20}l} {\frac{{3\sqrt 3 }}{{4\eta }}{\text{ }}\quad \left( {\eta \le 0.866} \right)} \hfill \\ {\sqrt {\frac{{54}}{{9 + 4\eta ^{2} }}} \quad (\eta > 0.866)} \hfill \\ \end{array} } \right. $$

(21)

${\Omega }_{e}$ depends only on the damping ratio $\eta$. Figure 4 depicts the effect of the damping ratio $\eta$ on the effective vibration isolation frequency, as defined by Eq. (21). As demonstrated previously, the effective frequency decreases significantly as $\eta$ increases. When $\eta$ is larger than the critical value $\eta_{cr\_1} = 0.866$, the nonlinearity of the system is suppressed. The transmissibility beyond ${\Omega }_{e}$ is lesser than 0.01, and approaches zero as the frequency increases. Therefore, when the primary resonance is suppressed, the proposed system can achieve an excellent isolation effect.

Fig. 4

Effective isolation frequency ${{\varvec{\Omega}}}_{{\varvec{e}}}$ defined by primary resonance under various values of the damping ratio $\eta$

2.2 One-third subharmonic resonance

2.2.1 Response components

Previous numerical studies have revealed that in harmonically excited oscillators with symmetric nonlinearity and single degree-of-freedom, as in system (b), the second harmonic response of odd order may grow steadily to a significant value without any bifurcation of periodic solutions of one type to another [32]. The approximate solution of the subharmonic response assumes the form [34]

$$ \overline{y} = \overline{A}_{1/3} \cos \left( {\Omega \tau /3} \right) + \overline{A}_{0} \cos \left( {\Omega \tau } \right) + \overline{B}_{0} \sin \left( {\Omega \tau } \right){ } $$

(22)

For convenience, the differential equation in Eq. (7) is written in the form

$$ \overline{y}^{^{\prime\prime}} + \frac{2\eta }{\Omega }\overline{y}^{2} \overline{y}^{^{\prime}} + \overline{y}^{3} = H\Omega^{2} \cos \left( {\Omega \tau } \right) - G\Omega^{2} \sin \left( {\Omega \tau } \right) $$

(23)

where $H^{2} + G^{2} = 1$. Substituting Eq. (22) into Eq. (23) yields the following four equations, when the harmonic term higher than $\cos \left( {{\Omega }\tau } \right)$ is neglected.

$$ \overline{A}_{1/3} \left( { - 4\Omega^{2} + 27\left( {2\overline{A}_{0} ^{2} + \overline{A}_{1/3} \overline{A}_{0} + \overline{A}_{1/3} ^{2} + 2\overline{B}_{0}^{2} } \right) + 6\eta \overline{A}_{1/3} \overline{B}_{0} } \right) = 0 $$

(24a)

$$ \overline{A}_{1/3} \left( { - 9\overline{A}_{1/3} \overline{B}_{0} + 2\eta \left( {2\overline{A}_{0}^{2} + \overline{A}_{1/3} ^{2} + \overline{A}_{0} \overline{A}_{1/3} + 2\overline{B}_{0}^{2} } \right)} \right) = 0 $$

(24b)

$$ \left( {\overline{A}_{0} ^{2} + 2\overline{A}_{1/3} ^{2} + \overline{B}_{0}^{2} } \right)\left( {3\overline{A}_{0} + 2\eta \overline{B}_{0} } \right) - 4\Omega^{2} \overline{A}_{0} + \overline{A}_{1/3} ^{3} = 4H\Omega^{2} $$

(24c)

$$ \left( {\overline{A}_{0} ^{2} + 2\overline{A}_{1/3} ^{2} + \overline{B}_{0}^{2} } \right)\left( {9\overline{B}_{0} - 6\eta \overline{A}_{0} } \right) - 12\Omega^{2} \overline{B}_{0} - 2\eta \overline{A}_{1/3} ^{3} = - 12G\Omega^{2} $$

(24d)

when $\overline{A}_{1/3} = 0$ is satisfied identically in Eq. (24a) and Eq. (24b), Eq. (24c) and (24d) are reduced to Eq. (9) for the primary resonance harmonic case. For $\overline{A}_{1/3} \ne 0$, by simplifying Eq. (24a) and Eq. (24b), $\overline{A}_{0}$ and $\overline{B}_{0}$ can be rewritten in the form

$$ \overline{A}_{0} = \frac{{ - \left( {2\overline{A}_{1} { }^{2} + \overline{A}_{1/3} { }^{2} } \right)\left( {81 + 4\eta^{2} } \right) + 12\Omega^{2} { }}}{{\left( {81 + 4\eta^{2} } \right)\overline{A}_{1/3} }} $$

(25a)

$$ \overline{B}_{0} = \frac{{8{ }\eta \Omega^{2} }}{{3\left( {81 + 4\eta^{2} } \right)\overline{A}_{1/3} }} $$

(25b)

where $\overline{A}_{1} ^{2} = \overline{A}_{0} ^{2} + \overline{B}_{0}^{2}$ is the square of the amplitude of the harmonic whose frequency is the same as that of the excitation. Substituting Eq. (24a) and Eq. (24b) into Eq. (24c) and Eq. (24d) yields the relationship between the frequency $\Omega$ and amplitude, $\overline{A}_{1}$ and $\overline{A}_{1/3}$:

$$ \frac{1}{{\overline{A}_{1/3} { }^{2} }}\left[ {4\eta^{2} \left( {\frac{{\Delta_{4} { }}}{{12\Omega^{2} }} - \frac{{24\Delta_{5} + 16\Omega^{2} { }}}{{12\left( {81 + 4\eta^{2} } \right)}}} \right)^{2} + \left( {\frac{{\Delta_{4} { }}}{{4\Omega^{2} }} + \frac{{ - 4\Delta_{6} + 144\Omega^{2} { }}}{{12\left( {81 + 4\eta^{2} } \right)}}} \right)^{2} } \right] = 1 $$

(26)

where $\Delta_{4} = 5\overline{A}_{1/3} ^{2} + 15\overline{A}_{1/3} ^{2} \overline{A}_{1} ^{2} + 6\overline{A}_{1} ^{2}$ and $\Delta_{5} = 2\overline{A}_{1/3} ^{2} + \overline{A}_{1} ^{2}$,$\Delta_{6} = \overline{A}_{\frac{1}{3}} ^{2} \left( {297 + 20\eta^{2} } \right) + \overline{A}_{1} ^{2} \left( {513 + 28\eta^{2} } \right)$. Noting that $\overline{A}_{1}$ is a function of $\overline{A}_{1/3}$, Eq. (26) can be regarded to represent the relationship between the frequency $\Omega$ and the one-third subharmonic amplitude $\overline{A}_{1/3}$, and $\overline{A}_{1/3}$ can be obtained with a certain $\Omega$ value. Thus, the solution to Eq. (22) can now be written as

$$ \overline{y} = \overline{A}_{1/3} \cos \left( {{\Omega }\tau /3} \right) + \overline{A}_{1} \cos \left( {{\Omega }\tau + \theta } \right) $$

(27)

where $\theta = arctan\frac{{\overline{A}_{0} }}{{\overline{B}_{0} }} - \frac{\pi }{2}$. Thus, the natural amplitude of the response is $\left| {\overline{A}} \right| = \left| {\overline{A}_{1/3} + \overline{A}_{1} \cos \left( \theta \right)} \right|$.

Figure 5a shows the two possible response curves, one-third subharmonic resonance $\left| {\overline{A}} \right|_{1/3}$ ($\overline{A}_{1/3} \ne 0$) and primary resonance $\left| {\overline{A}} \right|_{1}$ ($\overline{A}_{1/3} = 0$) under $\eta = \eta_{cr\_1} = 0.866$. Noting although the primary harmonic resonance curve $\left| {\overline{A}} \right|_{1}$ has no unstable jump-up region, one-third of the subharmonic resonance $\left| {\overline{A}} \right|_{1/3}$ may still occur. (This phenomenon does not exist in the viscous QZS system). Unlike the primary harmonic resonance, the curve of the one-third subharmonic resonance forms a loop and assumes a limited frequency range, from point M to point N. In this frequency region, the occurrence of the two response cases is determined by the initial condition. Figure 5b shows the $\overline{A}_{1/3}$ and $\overline{A}_{1}$ components of $\left| {\overline{A}} \right|_{1/3}$. Point P in Fig. 5a is the intersection point of the two curves, and the corresponding frequency of that subharmonic also corresponds to the intersection point in Fig. 5b. According to refs. [32, 34], the subharmonic vibration results from the bifurcation of the harmonic vibration. Point P is the bifurcation point. The corresponding point R in the lower branch is the minimum amplitude point. The bifurcation point P symbolizes the minimum frequency at which the response is dominated by the one-third subharmonic resonance. Although point Q in the lower graph is also an intersection point, the corresponding one-third subharmonic and primary harmonic components are different (shown in the upper graph). Thus, point Q is not a bifurcation point.

Fig. 5

a The two possible response curves, one-third subharmonic resonance $\left| {\overline{A}} \right|_{1/3}$ and primary resonance $\left| {\overline{A}} \right|_{1}$, point P and Q present the intersections of the two curves, and point P is the bifurcation point; b) One-third harmonic component amplitude-frequency curve of the response (red), compared with the primary harmonic component amplitude-frequency curve of the response (black) under ${\varvec{\eta}} = 0.866$

2.2.2 Stability of the solution

Figure 5a reveals that the nonlinear solutions originate from the linear solution, which is also verified by the results of other researchers [37,38,39], and for different types of oscillators. Similar to the treatment used in ref. [40], the steady-state displacement amplitude of the primary harmonic under displacement harmonic excitation is approximately 1, and the phase is approximately $\pi$. Thus, we assume $\overline{A}_{1} \approx - 1$ to simplify the expression of the response amplitude $\left| {\overline{A}} \right|$ to analyze the isolation performance when a one-third subharmonic exists. Considering the phase between the primary and one-third harmonics, the response in Eq. (27) can be rewritten as

$$ \overline{y} = \overline{A}_{1/3} \cos \left( {{\Omega }\tau /3 + \theta { }} \right) - \cos \left( {{\Omega }\tau } \right) $$

(28)

Substituting Eq. (28) into Eq. (7) and by comparing the coefficients of the terms containing $\cos \left( {\Omega \tau } \right)$ and $\sin \left( {\Omega \tau } \right)$, we can obtain the relationship between $\left| {\overline{A}_{1/3} } \right|$ and $\Omega$ as

$$ \left( {\frac{{8\eta {\Omega }^{2} }}{{3\overline{A}_{1/3} \left( {81 + 4\eta^{2} } \right)}}} \right)^{2} + \left( {\frac{2}{{\overline{A}_{1/3} }} + \overline{A}_{1/3} - \frac{{12{\Omega }^{2} }}{{\overline{A}_{1/3} \left( {81 + 4\eta^{2} } \right)}}} \right)^{2} = 1 $$

(29)

Thus, the amplitude of $\left| {\overline{A}_{1/3} } \right|$ can be solved as:

$$ \left| {\overline{A}_{1/3\_1} } \right| = \sqrt { - \frac{3}{2} + \frac{{12{\Omega }^{2} }}{{81 + 4\eta^{2} }} - \frac{1}{6}\sqrt { - 63 + \frac{{16{\Omega }^{2} \left( {2187 + 4\eta^{2} \left( {26 - 4{\Omega }^{2} } \right)} \right)}}{{\left( {81 + 4\eta^{2} } \right)^{2} }}} } $$

(30a)

$$ \left| {\overline{A}_{1/3\_2} } \right| = \sqrt { - \frac{3}{2} + \frac{{12{\Omega }^{2} }}{{81 + 4\eta^{2} }} + \frac{1}{6}\sqrt { - 63 + \frac{{16{\Omega }^{2} \left( {2187 + 4\eta^{2} \left( {26 - 4{\Omega }^{2} } \right)} \right)}}{{\left( {81 + 4\eta^{2} } \right)^{2} }}} } $$

(30b)

To discuss the stability of the two solutions of the response, we assume that ${\overline{A} }_{1/3}$ and $\theta$ are functions of time $\tau$. Substituting Eq. (28) into Eq. (7), ${\dot{\overline{A}} }_{1/3}$ and $\dot{\theta }$ can be obtained by integrating in the period from $\tau = 0$ to $2\pi$. The results are

$$ \mathop {\overline{A}}\limits_{1/3} = - \frac{{3A_{1/3} \left( {2\left( {2 + A_{1/3}^{2} } \right)\eta - 2A_{1/3} \eta cos\left( {3\theta } \right) + 9A_{1/3} sin\left( {3\theta } \right)} \right)}}{{8{\Omega }^{2} }} $$

(31a)

$$ \dot{\theta } = - \frac{{ - 54 - 27A_{1/3}^{2} + 4{\Omega }^{2} + 27A_{1/3} cos\left( {3\theta } \right) + 6A_{1/3} \eta sin\left( {3\theta } \right)}}{{8{\Omega }^{2} }} $$

(31b)

As singularity exists when $\dot{\theta } = 0$ and $\mathop {\overline{A}}\limits_{1/3} = 0$, $cos\left( {3\theta } \right)$ and $sin\left( {3\theta } \right)$ can be obtained, and we assume that

$$ M = cos\left( {3\theta } \right) = \frac{2}{{\overline{A}_{1/3} }} + \overline{A}_{1/3} - \frac{{12{\Omega }^{2} }}{{\overline{A}_{1/3} \left( {81 + 4\eta^{2} } \right)}} $$

(32a)

$$ N = sin\left( {3\theta } \right) = - \frac{{8\eta {\Omega }^{2} }}{{3\overline{A}_{1/3} \left( {81 + 4\eta^{2} } \right)}} $$

(32b)

By introducing the disturbance variables $\Delta \overline{A}_{1/3} = \overline{A}_{1/3} - \overline{A}_{1/3\_0} ,{ }\Delta \theta = \theta - \theta_{0}$ into Eq. (32), the first approximation of Eq. (31), close to the singularity ($\overline{A}_{1/3\_0}$,$\theta_{0}$) yields

$$ \Delta \overline{{\dot{A}}}_{1/3} = - \frac{{3\left( {\left( {2\left( {2 + 3\overline{A}_{1/3\_0}^{2} } \right)\eta + 2\left( {9N_{0} - 2\eta M_{0} } \right)\overline{A}_{1/3\_0} } \right)\Delta \overline{A}_{1/3} + 3\left( {2\eta N_{0} + 9M_{0} } \right)\overline{A}_{1/3\_0} \Delta \theta } \right)}}{{8{\Omega }^{2} }} $$

(33a)

$$ \Delta \dot{\theta } = - \frac{{\left( { - 54\overline{A}_{1/3\_0} + 27M_{0} + 6\eta N_{0} } \right)\Delta \overline{A}_{1/3} + 9\left( {2\eta M_{0} - 9N_{0} } \right)\overline{A}_{1/3\_0} \Delta \theta }}{{8{\Omega }^{2} }} $$

(33b)

The Jacobian matrix of the right-hand function of Eq. (33) is

$$ \left| {\begin{array}{*{20}c} { - 3\left( {2\left( {2 + 3\overline{A}_{{\frac{1}{{3_{0} }}}}^{2} } \right)\eta + 2\left( {9N_{0} - 2\eta M_{0} } \right)\overline{A}_{{\frac{1}{{3_{0} }}}} } \right) - \lambda } & { - 9\left( {2\eta N_{0} + 9M_{0} } \right)\overline{A}_{{\frac{1}{{3_{0} }}}} } \\ { - \left( { - 54\overline{A}_{{\frac{1}{{3_{0} }}}} + 27M_{0} + 6\eta N_{0} } \right)} & { - 9\left( {2\eta M_{0} - 9N_{0} } \right)\overline{A}_{{\frac{1}{{3_{0} }}}} - \lambda { }} \\ \end{array} } \right| $$

$$ = \lambda^{2} + a_{1} \lambda + a_{2} = 0 $$

(34)

where $a_{1}$ and $a_{2}$ can be written as

$$ \left\{ {\begin{array}{*{20}c} {a_{1} = 24\eta \left( {1 + \overline{A}_{1/3\_0}^{2} } \right)} \\ {a_{2} = \frac{{27\left( {\overline{A}_{1/3\_0}^{4} - 4} \right)\left( {4\eta^{2} \overline{A}_{1/3\_0} - 81} \right) - 1296{\Omega }^{2} + 48{\Omega }^{4} }}{{\overline{A}_{1/3\_0} }}} \\ \end{array} } \right. $$

(35)

The Lyapunov linearized stability theory indicates that the instability of a nonlinear system coincides with that of the corresponding linear system [41]. Hence, the stability of the system can be demonstrated based on the first-order Lyapunov approximation stability theory and the Routh–Hurwitz criterion [42, 43]. When $a_{1} > 0$ and ${ }a_{2} > 0$, the singularity is asymptotically stable. In contrast, when ${ }a_{1} > 0$ and $a_{2} < 0$, the singularity is asymptotically unstable. We note that $a_{1} > 0$ is always satisfied in Eq. (35). Thus, $a_{2}$ is a critical criterion.

Combined with Eq. (29), the one-third subharmonic amplitude-frequency ($\overline{A}_{1/3} - {\Omega }$) curves are plotted in Fig. 6 by identifying the stable solution. The solution in the upper branch (solid lines in Fig. 6) of the $\left| {\overline{A}_{1/3} } \right| - {\Omega }$ curve is stable, whereas that in the lower branch (dotted lines in Fig. 6) is unstable. The results indicate that in the actual experiment, the response amplitude solution in the upper branch of the $\left| {\overline{A}_{1/3} } \right| - {\Omega }$ curve can be observed in the response. As the frequency increases, the lower branch of the $\left| {\overline{A}_{1/3} } \right| - {\Omega }$ curve first drops to a turning point R. Exceeding the turning point R, the $\left| {\overline{A}_{1/3} } \right| - {\Omega }$ curve rises with increasing frequency ${\Omega }$ until it reaches the peak point. According to Sect. 2.2.1, the turning point R corresponds to the bifurcation point R. As the lower branch is unstable, a one-third subharmonic resonance can be observed from the turning point P in the upper branch, which corresponds to R. The frequency of the turning point ${\Omega }_{TP}$ can be solved by $\frac{{\partial \overline{A}_{1/3\_1} }}{{\partial {\Omega }}} = 0$

$$ {\Omega }_{TP} = \frac{1}{2}\sqrt {\frac{27}{{8\eta^{2} }}\left( {\left( {81 + 4\eta^{2} } \right) - \sqrt {\Delta_{7} } } \right)} $$

(36)

Fig. 6

One-third harmonic component amplitude-frequency curve of the response under ${\varvec{\eta}} =$ 0.5 (black), $0.866$ (red), 1 (blue), and 1.5 (green); the turning point P is marked by the black dot while R is marked by the square dot

$\Delta_{7} = \left( {81 + 4\eta^{2} } \right)\left( {81 - 28\eta^{2} } \right)$. The corresponding amplitude is

$$ \left| {\overline{{\text{A}}}_{TP} } \right| = \sqrt { - \frac{3}{2} + \frac{{\sqrt {\Delta_{6} } }}{{81 + 4\eta^{2} }} + \frac{{81 - \sqrt {\Delta_{7} } }}{{8\eta^{2} }}} $$

(37)

This is approximately 1, as shown in Fig. 6. The frequency range of the one-third subharmonic resonance is determined by the turning point and peak point, which we refer to as the start and end points. Noting the one-third subharmonic $\overline{A}_{1/3} - {\Omega }$ curve forms a loop and there are two intersections of the upper branch and the lower branch. By solving $\left| {\overline{A}_{1/3\_1} \left| = \right|\overline{A}_{1/3\_2} } \right|$, we can obtain the expressions for the two intersections. The frequencies of the two intersections are

$$ {\Omega }_{1/3\_min} = \sqrt {\frac{{3\left( {9 - \sqrt {\left( {81 - 28\eta^{2} } \right)} } \right)\left( {81 + 4\eta^{2} } \right)}}{{32\eta^{2} }}} $$

(38a)

$$ {\Omega }_{1/3\_max} = \sqrt {\frac{{3\left( {9 + \sqrt {\left( {81 - 28\eta^{2} } \right)} } \right)\left( {81 + 4\eta^{2} } \right)}}{{32\eta^{2} }}} $$

(38b)

and the corresponding amplitudes of the two points are

$$ \overline{{\text{A}}}_{1/3\_min} = \sqrt { - \frac{3}{2} - \frac{{9\left( { - 9 + \sqrt {\left( {81 - 28\eta^{2} } \right)} } \right)}}{{8\eta^{2} }}} $$

(39a)

$$\overline{{\text{A}}}_{1/3p\_max} = \sqrt { - \frac{3}{2} + \frac{{9\left( {9 + \sqrt {\left( {81 - 28\eta^{2} } \right)} } \right)}}{{8\eta^{2} }}} $$

(39b)

Noting the peak exists at the intersection with maximum value of the two branches of the $\left| {\overline{A}_{1/3} } \right| - {\Omega }$ curve, which is also the end point. Since $\frac{{d\overline{{\text{A}}}_{1/3p\_max} }}{d\eta } < 0$ and $\frac{{d{\Omega }_{1/3\_max} }}{d\eta } < 0$, the frequency and amplitude of peak decrease as $\eta$ increases. The effects of $\eta$ on ${\Omega }_{TP}$ and ${\text{A}}_{TP}$ are opposite. Hence, as shown in Fig. 6, the frequency range of the subharmonic resonance decreases as $\eta$ increases. It can be observed from Fig. (6), when $\eta$ reaches the critical value $\eta_{cr\_1/3}$, the one-third subharmonic resonance disappears. By solving ${\Omega }_{1/3\_min} = {\Omega }_{1/3\_max}$, $\eta_{cr\_1/3}$ can be obtained as

$$ \eta_{cr\_1/3} = 1.701 $$

(40)

In Sect. 2.1, we obtained the critical condition for avoiding the jump phenomena in the existing primary harmonic resonance as $\eta_{cr\_1} = 0.866$. By combining the results in Eq. (15), although the jump phenomenon is suppressed when $\eta > 0.866$, one-third subharmonic resonance may exist and degrade the effective isolation frequency to a higher frequency when $\eta \left( {0.866,1.701} \right)$.

2.2.3 Transmissibility and effective isolation frequency

As this study focuses on the isolation performance of the proposed QZS system, we attempted to obtain the transmissibility with the natural amplitude. Considering that the phase difference between the excitation and the primary harmonic in the response is approximately $\pi$, the absolute response $\overline{A}_{a}$ is

$$ \overline{A}_{a} = \overline{A}_{1/3} \cos \left( {\frac{{{\Omega }\tau }}{3} + \theta { }} \right) - \cos \left( {{\Omega }\tau } \right) + \cos \left( {{\Omega }\tau } \right) = \overline{A}_{1/3} \cos \left( {\frac{{{\Omega }\tau }}{3} + \theta { }} \right) $$

(41)

Thus, the absolute displacement transmissibility can be written in the form

$$ T_{a} = \overline{A}_{1/3} $$

(42)

As only a stable solution exists in the actual experiment, the transmissibility is plotted in Fig. 7. As $\eta$ increases, the frequency range of the transmissibility is narrowed. The transmissibility curve increases with increasing frequency ${\Omega }$ until it reaches the peak point. Moreover, the transmissibility peak corresponds to the end point in Sect. 2.2.2, which is

$$ {\text{T}}_{p} = \sqrt { - \frac{3}{2} + \frac{{9\left( {9 + \sqrt {\left( {81 - 28\eta^{2} } \right)} } \right)}}{{8\eta^{2} }}} $$

(43)

With the existing condition of the one-third subharmonic resonance $\eta \in \left( {0,1.701} \right)$, the value range of ${\text{T}}_{p}$ is $\left( {1.414, + \infty } \right)$. The minimum value of 1.414 is obtained with $\eta = 1.701$. The result indicates that when one-third subharmonic resonance is possible, the maximum value of the transmissibility-frequency curve always exceeds 1 and occurs at the maximum frequency point. Hence, the isolation effect of the system fails when the excitation frequency approaches ${\Omega }_{1/3\_max}$. Comparing ${\Omega }_{1/3\_max}$ with ${\Omega }_{e}$, we obtain

$$ {\Omega }_{1/3\_max} - {\Omega }_{e} = \left\{ {\begin{array}{*{20}c} {\sqrt {\frac{{3\left( {9 + \sqrt {\left( {81 - 28\eta^{2} } \right)} } \right)\left( {81 + 4\eta^{2} } \right)}}{{32\eta^{2} }}} - \frac{3\sqrt 3 }{{4\eta }} > 0} & {\left( {\eta \le 0.866} \right)} \\ {\sqrt {\frac{{3\left( {9 + \sqrt {\left( {81 - 28\eta^{2} } \right)} } \right)\left( {81 + 4\eta^{2} } \right)}}{{32\eta^{2} }}} - \sqrt {\frac{54}{{9 + 4\eta^{2} }}} > 0} \quad{(0.866 < \eta < 1.701)} \\ \end{array} } \right. $$

(44)

Therefore, the effective isolation frequency is extended from ${\Omega }_{e}$ in the primary resonance to ${\Omega }_{1/3\_max}$ in the one-third subharmonic resonance. Figure 8 presents the possible transmissibility response-frequency curve when $\eta = 0.5,{ }0.866$, 1.5, and 2. In the curves of $\eta = 0.5,{ }0.866$, and 1.5 ($\eta < \eta_{cr\_1/3}$), there are two observations for the transmissibility curves. The two curves both reach the first resonance and then drop from the peak point $P_{1}$ until the turning point ${\text{S}}$. The difference appears after crossing the turning point S. The initial condition determines whether the curve continues to decline or experiences secondary resonance. If the latter occurs, the curve continues to rise until it reaches the end point $P_{2}$ and then drops again to the primary resonance curve. Exceeding the end point, the transmissibility is lesser than 1 in a stable manner. When $\eta > \eta_{cr\_1/3}$, as shown in the curve of $\eta = 2$, there is only one possible transmissibility response-frequency curve. Thus, the effective isolation frequency in Eq. (21) is modified as

$$ \Omega _{e} = \left\{ {\begin{array}{*{20}l} {\sqrt {\frac{{3\left( {9 + \sqrt {\left( {81 - 28\eta ^{2} } \right)} } \right)\left( {81 + 4\eta ^{2} } \right)}}{{32\eta ^{2} }}} \quad \left( {\eta \le 1.701} \right)} \hfill \\ {\sqrt {\frac{{54}}{{9 + 4\eta ^{2} }}} \quad (\eta > 1.701)} \hfill \\ \end{array} } \right. $$

(45)

Fig. 7

One-third subharmonic resonance transmissibility-frequency curve under ${\varvec{\eta}} =$ 0.5 (black), 0.866 (red), 1 (blue), and 1.5 (green)

Fig. 8

Two possible resonance response curves under ${\varvec{\eta}} =$ 0.5 in a, 0.866 in b, 1.5 in c, and 2 in d. The red curve represents the one-third subharmonic resonance and the black curve represents the primary resonance. Points ${\varvec{P}}_{1}$ and ${\varvec{P}}_{2}$, respectively, denotes the peak points in primary resonance and one-third subharmonic resonance, and point S represents the turning point

Moreover, it is observed that the transmissibility curve exhibits a weaker hardening characteristic in the first resonance with increasing $\eta$ under $\eta < \eta_{cr\_1}$, as shown in the curves of $\eta = 0.5,{ }0.866$. Comparing the figure of $\eta = 0.5,{ }0.866,$ and 1.5, it can be noted that the frequency region of the secondary resonance is narrowed down with increasing $\eta$ under $\eta < \eta_{cr\_1/3} .$

2.3 Superharmonic resonance of order 3

Numerous studies have demonstrated [32, 44] that the superharmonic may exist in the response of a nonlinear system. Noting that Eq. (8) has a superharmonic term, the second approximation of the solution can be written in the form

$$\overline{y }={\overline{A} }_{1}\mathrm{cos}\left(\Omega \tau \right)+{\overline{M} }_{3}\mathrm{cos}\left(3\Omega \tau \right)+{\overline{N} }_{3}\mathrm{sin}\left(3\Omega \tau \right)$$

(46)

where $\overline{M}_{3}^{2} + \overline{N}_{3}^{2} = \overline{A}_{3}^{2} . \overline{A}_{3}$ is the amplitude of the superharmonic of order 3. Substituting Eq. (46) into Eq. (23), we expand the resulting expression in trigonometric series and obtain

$$ \frac{{\overline{A}_{1}^{2} }}{{16{\Omega }^{4} }}\left( {\Delta_{10}^{2} + \Delta_{11}^{2} } \right) = 1 $$

(47a)

$$ \left( {1 + 4\eta^{2} } \right)\Delta_{12} = 1296\overline{A}_{3}^{2} {\Omega }^{4} $$

(47b)

where $\Delta_{8} = 2\overline{A}_{1}^{2} + \overline{A}_{3}^{2}$, $\Delta_{9} = \overline{A}_{1}^{2} + 2\overline{A}_{3}^{2}$_,

$\Delta_{10} = \frac{{2\eta (\Delta_{7} \left( {5\left( {\overline{A}_{1}^{2} + \overline{A}_{3}^{2} } \right)\Delta_{8} - 4\overline{A}_{3}^{2} } \right)\left( {1 + 4\eta^{2} } \right) - 24\left( {\left( {4\overline{A}_{1}^{2} + 7\overline{A}_{3}^{2} } \right)\Delta_{8} - 8\overline{A}_{3}^{2} } \right){\Omega }^{2} + 432\Delta_{8} {\Omega }^{4} )}}{{3\Delta_{7}^{2} \left( {1 + 4\eta^{2} } \right) - 72\Delta_{7} {\Omega }^{2} + 432{\Omega }^{4} }}$ _,

$\Delta_{11} = 3\Delta_{8} - 4{\Omega }^{2} + \frac{{\overline{A}_{1}^{4} \left( { - \Delta_{7} \left( {1 + 4\eta^{2} } \right) + 4\left( {3 - 4\eta^{2} } \right){\Omega }^{2} } \right)}}{{\Delta_{7}^{2} \left( {1 + 4\eta^{2} } \right) - 24\Delta_{7} {\Omega }^{2} + 144{\Omega }^{4} }}$, $\Delta_{12} = \overline{A}_{1}^{6} + 9\Delta_{7}^{2} \overline{A}_{3}^{2} + \frac{{2\overline{A}_{1}^{6} \Delta_{7} \left( { - \Delta_{7} \left( {1 + 4\eta^{2} } \right) + 12{\Omega }^{2} } \right)}}{{\Delta_{7}^{2} \left( {1 + 4\eta^{2} } \right) - 24\Delta_{7} {\Omega }^{2} + 144{\Omega }^{4} }}$.

Equation (47b) indicates the relationship between $\overline{A}_{1} ,\overline{A}_{3}$ and the excitation frequency ${\Omega }$. As $\overline{A}_{1}$ is a function of $\overline{A}_{3}$ and ${\Omega }$, Eq. (47a) can be rewritten using $\overline{A}_{3}$ and ${\Omega }$. Then, the relationship between $\overline{A}_{3}$ and ${\Omega }$ is obtained and plotted as shown in Fig. 9. As ${\Omega }$ increases, $\overline{A}_{3}$ increases until the peak point is reached, and then gradually decreases. The damping ratio $\eta$ can suppress the behavior of the third superharmonic. To discuss the relationship between the third superharmonic and the primary harmonic, the two curves of $\overline{A}_{3}$ and $\overline{A}_{1}$ under $\eta = 0.866$ are plotted in Fig. 10a. We note that the trend of the curve $\overline{A}_{3}$ is the same as that of the curve $\overline{A}_{1}$, but with a smaller value. The amplitude of the third harmonic is always 1/24 of the primary harmonic in the steady-state response [45].

Fig. 9

Superharmonic component amplitude of the response-frequency curve under ${\varvec{\eta}}=0.5$ (black), $0.866$ (red), 1 (blue), and 1.5 (green)

Fig. 10

a Superharmonic of order 3 component amplitude-frequency curve (red), compared with the primary harmonic component amplitude-frequency curve (black) of the response $\left| {\overline{A}} \right|_{3}$ under ${\varvec{\eta}} = 0.866$; b the natural response $\left| {\overline{A}} \right|_{3}$ with the superharmonic of order 3 compared with the primary resonance response $\left| {\overline{A}} \right|_{1}$ under ${\varvec{\eta}} = 0.866$

As in the preceding section, the solution of Eq. (47) can be written as

$$ \overline{y} = \overline{A}_{1} \cos \left( {{\Omega }\tau } \right) + \overline{A}_{3} \cos \left( {3{\Omega }\tau + \theta_{2} } \right) $$

(48)

where $\theta_{2} = arctan\frac{{\overline{M}_{3} }}{{\overline{N}_{3} }} - \frac{\pi }{2}$. Thus, the natural amplitude of the response is $\left| {\overline{A}} \right|_{3} = \left| {\overline{A}_{1} + \overline{A}_{3} \cos \left( \theta \right)} \right|$. Figure 10b shows the natural response-frequency curve compared with the primary resonance curve. The third superharmonic only affects the response near the resonance peak, and this effect is slight. Thus, when the third superharmonic exists without the one-third subharmonic, the response of the system is still dominated by the primary harmonic. In this case, the first approximation with the primary harmonic can describe the behavior of the system. Hence, the effect of the third superharmonic on the isolation performance and effective isolation frequency can be ignored.

2.4 Effect of ${\varvec{\eta}}$ on effective frequency and maximum transmissibility

According to the above analysis, the critical points of the main resonance and one-third subharmonic resonance can be expressed as a function of the damping ratio $\eta$. With the existing conditions of the jump phenomena $\eta \in \left( {0,0.866} \right)$ and the one-third subharmonic resonance $\eta \in \left( {0,1.701} \right)$, the value range of the critical points can be obtained in the non-dimensional form, which are summarized in Table 1.

Table 1 The expression of the critical point in primary resonance and one-third subharmonic resonance

The effective isolation frequency is presented in Fig. 11. The corresponding maximum transmissibility of the QZS system can be summarized as

$$ {\text{T}}_{p} = \left\{ {\begin{array}{*{20}l} {\sqrt { - \frac{3}{2} + \frac{{9\left( {9 + \sqrt {\left( {81 - 28\eta ^{2} } \right)} } \right)4\quad (\eta < 1.701)}}{{8\eta ^{2} }}} } \hfill \\ {{\text{ }}\sqrt {1 + \frac{9}{{4\eta ^{2} }}} \quad \left( {\eta \ge 1.701} \right)} \hfill \\ \end{array} } \right.{\text{ }} $$

(49)

Fig. 11

Effective isolation frequency ${{\varvec{\Omega}}}_{{\varvec{e}}}$ (red) and the transmissibility peak ${\mathbf{T}}_{{\varvec{p}}}$(blue) under various values of damping ratio ${\varvec{\eta}}$ considering the one-third harmonic resonance and primary resonance

Figure 11 shows the effect of the damping ratio $\eta$ on the effective isolation frequency and the corresponding transmissibility peak. The damping ratio $\eta$ can reduce the effective isolation frequency; thus, the vibration isolation frequency band is expanded. Moreover, the damping ratio $\eta$ can dampen the transmissibility peak to a lower value, which results in an improvement in isolation performance. The value of the effective frequency and maximum transmissibility experience a substantial decline from ${\Omega } = 0$ to ${\Omega } = 1.7$. After exceeding ${\Omega } = 1.7$, the two curves experience a further decrease at a slow rate, and the value gradually stabilizes close to 0. Therefore, to improve the stability of the response and avoid complex nonlinear dynamic behavior, the condition of the damping ratio can be determined using

$$ \eta \ge 1.701 $$

(50)

2.5 Numerical analysis of nonlinear dynamic response

The details of numerical simulations are provided in this section to conduct theoretical analysis. The simulations implement a vibration experiment under sine-sweep frequency excitation. The non-dimensional excitation frequency ${\Omega }$ varies from 0.01 to 20, with a sweep time of $\frac{{2000{\uppi }}}{{\Omega }}$ and a sweep rate of $\frac{{\uppi }}{{50{\Omega }}}$. The initial conditions at the initial frequency ${\Omega } = 0.01$ are ${\text{y}}\left( 0 \right) = 0$ and ${\text{y}}^{\prime } \left( 0 \right) = 0$. At the subsequent frequency, the initial conditions are set as the response results ${\text{y}}\left( {\frac{{2000{\uppi }}}{{\Omega }}} \right)$ and ${\text{y}}^{\prime } \left( {\frac{{2000{\uppi }}}{{\Omega }}} \right)$ obtained from the simulation at the previous frequency. The parameters of the damping ratio are fixed at $\eta = 0.866$ (the condition for the existence of the one-third subharmonic resonance) and $\eta = 2$ (the condition for the non-existence of the one-third subharmonic resonance). The ODE45 method in MATLAB software was used to obtain the numerical results.

Figure 12 depicts the transmissibility of the QZS system described in Eq. (7) using numerical simulations and theoretical analysis with ${\upeta } = 0.866$. The numerical results in Fig. 12 are in good agreement with the theoretical results. The transmissibility first increases with increasing frequency until it reaches the peak point of the primary resonance and then decreases. The reduction ends at a critical point where the frequency Ω = 3.79, with T = 1.025, and then the numerical result jumps up to the one-third resonance transmissibility curve. The frequency value and the transmissibility correspond to those of the turning point in Table 1 at $\eta = 0.866$, which are Ω = 3.82 and T = 1.006. Thus, the obtained turning point can predict the start point of the one-third resonance. The transmissibility increases again along with the one-third resonance until the peak point, and then jumps down to the main resonance curve. It is observed that error exists and increases between the numerical and theoretical results from Ω = 9.15 to Ω = 13.15. This phenomenon is caused by the error in the approximate assumption in Eq. (28). We have obtained the numerical frequency of the peak point as 13.15, which is close to the theoretical solution Ω = 13.26 from Table 1. The corresponding numerical transmissibility of the peak is 5.18, while that obtained from Eq. (49) is 4.88. Although there are small errors in the solution, the effective isolation frequency and maximum transmissibility can approximately determine the peak point of transmissibility. Moreover, the results again indicate that the effective isolation frequency depends on the jump-down frequency of the one-third subharmonic resonance, even when the primary resonance is stable. Figure 13a presents a Fourier analysis of the point ${\Omega } = 10$. We note that there exists not only the excitation frequency ${\Omega } = 10$ with an amplitude close to 1, but also the one-third excitation frequency harmonic of ${\Omega } = 3.333$ with a larger amplitude of 3.88. Thus, the harmonic component ${\Omega } = 3.333$ dominates the response, which verifies the theoretical analysis. The time-domain response diagram at the excitation frequency ${\Omega } = 10$ is compared with the time-domain excitation diagram, as shown in Fig. 13b.

Fig. 12

Transmissibility curve from the numerical results compared with the theoretical results under ${\varvec{\eta}} = 0.866$; the green curve represents the theoretical one-third resonance, the blue curve represents the theoretical primary resonance, and the red dashed curve represents the numerical result

Fig.13

a Fourier analysis diagram at frequency ${{\varvec{\Omega}}} = 10$; b time domain diagram of the response and excitation at frequency ${{\varvec{\Omega}}} = 10$

Figure 14 presents the effect of initial conditions on the transmissibility at a frequency of ${\Omega } = 1{\text{ and }}10$, respectively. At ${\Omega } = 1$, i.e., the frequency in the stable region, it is noted that the response of the system is independent of the initial conditions and has only one certain solution. When the external excitation frequency is in the unstable frequency range, as ${\Omega } = 10$, the solution of the transmissibility is determined by the initial conditions. As shown in Fig. 15b, the solutions under various initial conditions lie on either the primary resonance close to 0 or 1/3 subharmonic resonance close to 3.91. Attractor-basin phase portraits of Fig. 15b is shown in Fig. 15c. As the result in ref.[16], we could control the initial value condition of the QZS dynamic system to make the steady-state motion settle into the non-resonant period-1 motion, even if the subharmonic solutions exist, which would extend the effective isolation frequency to low and ultra-low frequency. The range of vibration isolation is thus in a large extent theoretically beyond the traditional understand for nonlinear vibration isolation.

Fig. 14

Dynamic response under various initial conditions at a ${{\varvec{\Omega}}} = 1{\text{ and b}}){ }{{\varvec{\Omega}}} = 10$; the blue dots represent the solution in primary resonance, and the red dots represent that in one-third subharmonic resonance; c) attractor-basin phase portraits of b, yellow basin represents the non-resonant period-1 motion, red basin represents the one-third subharmonic resonant period-1 motion

Fig. 15

Transmissibility curve from numerical results compared with the theoretical results under ${\varvec{\eta}} = 2$. The blue curve represents the theoretical primary resonance, and the red dashed line represents the numerical result

Figure 15 shows the transmissibility for the damping ratio $\eta = 2$. Similar to the theoretical result, only the primary resonance exists in the transmissibility curve. Figure 16 shows the transmissibility response at the frequencies of ${\Omega } = 1{\text{ and }}10$ under various initial conditions. As the damping ratio $\eta = 2 > \eta_{cr\_1/3}$, the transmissibility response is independent of the initial conditions and has only one stable solution.

Fig. 16

Dynamic response under various initial conditions at a)${ }{{\varvec{\Omega}}} = 1{\text{ and }}{\mathbf{b}}){ }{{\varvec{\Omega}}} = 10{ }$. The blue dot represents the solution in primary resonance

As the system is dominated by nonlinear stiffness, chaos may be triggered when the damping is small. Under chaos, the response of the system cannot be predicted, and the QZS system may fail to realize the predicted isolation effect. Thus, the effective frequency in Eq. (45) cannot effectively estimate the vibration isolation frequency range of the system owing to chaos. To discuss the effect of $\eta$ on the nonlinear behavior of the system, a bifurcation diagram at $\Omega =$ 5.195 is presented in Fig. 17. According to Table 1, the frequency $\Omega =$ 5.195 is the maximum start point frequency and the minimum end point frequency. Hence, when the existing condition of the one-third subharmonic resonance is satisfied, the response at ${\Omega } =$ 5.195 always has a solution of the one-third subharmonic. Hence, ${\Omega } = { }$ 5.195 is used in the analysis. When the damping ratio is less than 0.003, the response of the system exhibits chaos. Exceeding 0.003, the response of the system alternates between multi-period motion and 1-period motion until the damping ratio increases to 0.013. The response of the system exhibits a stable 1-period motion when the damping ratio is within (0.013, 0.25). As the damping ratio increases from 0.25 to 1.66, the response exhibits 3-period motion with a maximum amplitude close to 2.25. Therefore, to avoid the existence of chaos, the damping ratio must be larger than 0.003. When the damping ratio is in the interval (0.25, 1.701), the response exhibits 3-period motion. According to the analysis of the one-third subharmonic resonance in Sect. 2.2, the damping ratio range (0.25, 1.701) corresponds to the existing condition of the one-third subharmonic resonance. Therefore, when the damping ratio is in the range (0.25, 1.701), the effective isolation can be determined by Eq. (45).

Fig.17

Bifurcation diagram at ${{\varvec{\Omega}}} = 5.195$

By implementing the numerical simulation, the theoretical analysis of the QZS system described in the previous section can be verified. When the damping ratio is smaller than the critical damping ratio of 1.701, one-third subharmonic resonance occurs owing to nonlinearity. In the transmissibility curve, as the frequency increases, the 1/3 harmonic leads to a second peak with a larger value after the main resonance peak frequency (as shown in Fig. 17). Therefore, the effective frequency is pushed to a higher frequency. When the damping ratio is larger than 1.701, there exists only a main resonance peak in the response. After reaching the peak, the transmissibility curve decreases as the frequency increases, and gradually approaches zero with superior vibration isolation performance.

3 Experiment and design for QZS isolator

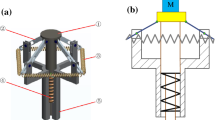
To evaluate the above results of the QZS system, an experimental prototype was constructed for the vibration tests. Considering the stability of the system, the horizontal springs in Fig. 1 are replaced by two slightly rectangular steel bar as the negative-stiffness structure, as illustrated in Fig. 18 The two bars were hinged by ball bearings at one end and connected in parallel with the vertical spring at the other end. Various experiments [46,47,48,49,50] have revealed that bearings contribute a significant amount of damping in comparison with other structural components, and the damping ratio is constant under low sinusoidally varying loads. Thus, it is reasonable to conclude that the presented prototype can be applied to the idealized model shown in Fig. 1.

Fig. 18

Engineering design drawing of the proposed QZS system time-domain, and the prototype in the vibration tests

3.1 Static test and results

The prototype of the QZS system was tested using an INSTRON universal testing machine to obtain the actual static characteristics. To obtain the force–displacement characteristic of only the negative-stiffness element and that of the entire QZS system, the tests were conducted with one group without a vertical spring and the other with a vertical spring. Figure 19a presents the experimental results of the force–displacement characteristic of the negative stiffness element alone, which are compared with the theoretical results presented in the previous section and the simulation predictions. Owing to the occurrence of a snap-through, the prototype and the machine were separated, and the static test could not be continued after a displacement of 3.6. From the F-D curve, the stiffness–displacement (S–D) relationship can be obtained, and the stiffness of the vertical spring can be determined from the value of the equilibrium position, which is 9.17 N/mm.

Fig. 19

Force–displacement characteristic of the a negative stiffness structure from the static test and, b the entire QZS system from the static test, in comparison with the theoretical curves

Figure 19b shows the force–displacement characteristics of the entire QZS system based on the experimental results and comparison with theoretical results. The two curves agree qualitatively. By fitting the experimental curve, the value of the nonlinear cubic stiffness ${k}_{3}$ k3can be obtained, which is 2.38 N/${mm}^{3}$. At the equilibrium position, the force is 31.7 N. Hence, the system can support a mass of 3.17 kg.

3.2 Vibration test and results

The isolated system with the payload was fixed on a shake table, and sine sweep tests were conducted to evaluate the performance of the isolation system. The excitation frequency range was set to sweep from 0.1 Hz to 70 Hz with 0.05 Hz resolution. Three swept sine tests were produced with the excitation amplitudes of 0.15, 0.5, and 1 mm. The vibration response was measured by an accelerometer attached to the payload, and another accelerometer was fixed on the shaker platform.

To directly compare the dynamic response under various displacement amplitudes, the response curve is presented in the form of the acceleration transmissibility with respect to the excitation frequency. The experimental results of the transmissibility of the QZS vibration isolation system are shown in Fig. 20. Here, the orange, purple, and green curves depict the excitation levels of 0.15 mm, 0.5 mm, and 1 mm, respectively. It can be observed that the transmissibility increases rapidly at first and reaches the peak point, after which a sharp decrease occurs and it drops below 1. Then, the curve rises again and approaches another peak. After exceeding the second peak, the transmissibility of the system decreases to a low value close to zero and continues to decrease as the excitation frequency increases. Thus, the frequency of the second peak corresponds to the effective isolation frequency. It is noted from Fig. 20 that the effective isolation frequencies are 7.55 Hz, 23.9 Hz, and 43.5 Hz at the points $P_{e\_1} ,P_{e\_2} ,$ and $P_{e\_3}$ for the excitation levels of 0.15 mm, 0.5 mm, and 1 mm, respectively.

Fig. 20

Results of the proposed QZS system design in vibration tests in comparison with the numerical simulation results under the displacement excitation of 0.15 mm (red), 0.5 mm (blue), and 1 mm (green). The effective isolation frequency point of each line is denoted by the black dots

To compare the results with the previously presented numerical analysis, the simulation results have been obtained in the form of the acceleration transmissibility. Based on the numerical simulation with parameters specified by the prototype experimental system with an excitation level of z = 0.15 mm, the damping ratio $\eta$ obtained by curve fitting is 1.05. With $\eta = 1.05$, the numerical simulations are implemented with the same swept sine excitation process as the experimental tests under z = 0.15,0.5, and 1 mm. As shown in Fig. 20, the numerical curves closely match the experimental measurements. Hence, according to the previous section analysis, the results reveal that.

• (1) The response model predicted by the theoretical analysis can describe the experimental results. When the damping ratio is smaller than $\eta_{cr\_1/3} = 1.701$, two peaks exist in the transmissibility-frequency curve. The first peak is caused by the primary resonance, and the second is due to the one-third subharmonic resonance.

• (2) The nonlinearity of the system is stronger with the increase in the excitation displacement, which results in the effective isolation frequency extending to a higher frequency. Exceeding the effective isolation frequency, the transmissibility remains at an ultra-low value (< 0.01). Thus, the proposed QZS system can achieve a good vibration isolation effect at stable frequencies, which is consistent with the theoretical results. According to the theoretical results, the isolation effect at low frequencies can be improved by increasing the damping ratio.

• (3) ${\Omega }_{e}$ obtained in the previously described theoretical analysis can predict the effective isolation frequency. Based on the experimental results at $\eta = 1.05$, the theoretical non-dimensional effective isolation frequency ${\Omega }_{e}$ can be calculated as 10.74. We substitute ${\Omega } = 10.74$ into the definition of the actual frequency $f = \frac{{\sqrt {\frac{{k_{3} {\text{z}}^{2} }}{m}} {\Omega }}}{2\pi }$. The theoretical actual effective isolation frequency can be obtained as 7.03 Hz, 23.43 Hz, and 46.87 Hz at $z =$ 0.15 mm, 0.5 mm, and 1 mm, respectively. The results are close to the experimental results of 7.55, 23.9, and 43.5 Hz.

It is noted that the numerical and experimental results at $z = 1$ mm do not fit as well as those at $z = 0.15$ mm and 0.5 mm. This behavior may have been caused by the self-locking of the system. When the displacement transmissibility is larger than 3.6, the displacement response at $z = 1$ mm is larger than 3.6 mm, which is the maximum deformation of the system. Thus, the structure may self-lock and result in the transmissibility remaining at 1, as shown in the experimental curve.

Figure 21a shows the time-domain diagram under the displacement excitation of 0.5 mm at 20 Hz in Fig. 20. It can be observed under the sweep mode, the one-third subharmonic resonance is excited in the response. Figure 21b shows the time-domain diagram of the system with the same excitation parameters under the initial condition of $y = 0$ and $\dot{y} = 0$. Noting the response is in non-resonant steady state with smaller amplitude than the excitation. Hence as demonstrated in Sect. 2.5, controlling the initial value condition of the QZS dynamic system can make the steady-state motion settle into the non-resonant period-1 motion and widen the isolation frequency range.

Fig. 21

Time-domain diagrams of the vibration tests under the displacement excitation of 0.5 mm at 20 Hz, a under the sweep mode, b under the initial condition of ${\varvec{y}} = 0$ and $\dot{\user2{y}} = 0$

4 Conclusion

In this study, the vibration isolation effect of a QZS system with nonlinear hysteretic damping was studied theoretically and experimentally. Considering the QZS characteristics, the Duffing-Ueda equation was used to describe the dynamic motion of the system. By non-dimensional transformation, the nonlinear dynamic equation of the system was determined using only one key parameter, the effective damping ratio $\eta$. As the system was dominated by nonlinear stiffness, theoretical analysis was performed for the complex nonlinear responses including the primary and secondary harmonic responses by employing the HBM method. Since the paper focused on the isolation effect of the system, the analysis was discussed based on transmissibility. Then, the analytical solutions for the nonlinear equation were confirmed by numerical simulations. The results reveal that the isolation system with nonlinear hysteretic damping exhibits several characteristics.

• (1) Unlike the linear damping model adopted in previous studies, the response of the present QZS system is always bounded for different damping ratios $\eta$, which implies that the system can always achieve an isolation effect when exceeding the critical frequency point, which we term as the effective isolation frequency point ${\Omega }_{e} .$

• (2) The $\eta$ value for the present system is independent of the excitation level, which implies that the present QZS can provide a stable isolation effect.

• (3) For the damping ratio $\eta < 1.701$, one-third subharmonic resonance may occur in the response and degrade the effective isolation frequency to a higher frequency, although the primary response is stable.

• (4) When the damping ratio $\eta > 1.701$, the jump phenomena in the primary resonance and one-third subharmonic resonance are suppressed, and the system has the advantage of guaranteeing a sufficient damping effect at low frequency and extremely low transmissibility at high frequencies.

To evaluate the actual isolation effect, we proposed two critical parameters, i.e., the effective isolation frequency ${\Omega }_{e}$ and maximum transmissibility $T_{p}$. The theoretical and numerical results indicate that ${\Omega }_{e}$ can predict the start excitation frequency at which the system achieves a stable isolation effect, while $T_{p}$ predicts the maximum transmissibility of the system under different excitations.

To verify the above theoretical results, an experiment using a prototype of the QZS system was constructed for the vibration test. As predicted, two peaks were observed in the experimental transmissibility curve. According to the theoretical analysis, the first peak was due to the primary harmonic resonance, and the second was due to the one-third subharmonic resonance. In addition, the frequency range of the one-third resonance was narrowed down as the excitation displacement decreases. When compared with the numerical results, the experimental curve also verified that the effective isolation frequency ${\Omega }_{e}$ could effectively predict the start frequency of the stable isolation frequency range.