Quantitative Stability Analysis of an Unmanned Tethered Quadrotor

Abstract

Tethered quadrotors, unmanned aerial quadrotors connected to a fixed point via tether cables, have been widely applied in numerous aerial tasks. However, their structural parameters and external disturbances give rise to dynamic stability issues, resulting in uncontrolled autonomous flight, shaking, and vibrating. Thus, this article investigates the quantitative stability of a tethered quadrotor using the Lyapunov exponent approach. First, a mathematical model of the tethered quadrotor is developed, and its dynamic stability is quantified to verify the rationality of the designed physical prototype and enhance the aerial system’s stability. Both simulation and experimental results show that the dynamic stability during the landing phase is better than that during takeoff. Finally, optimizing the structural parameters enhances the dynamic stability, which is sensitive to cable length, wind gusts, and yaw angle.

1 Introduction

In recent years, there were numerous progressive advancements in the field of rotorcraft unmanned aerial vehicles (RUAVs) due to their broad application in daily life. RUAVs have been promoted in both civilian and military missions, including aerial manipulation [1], aerial photography [2], agricultural spraying [3], and military reconnaissance [4]. However, RUAVs’ potential is limited by several crucial characteristics, including endurance time, computational efficiency, and load capacity [5].

One feasible approach to mitigating these limitations is to connect an RUAV to a ground station via a tether cable to supply energy, apply forces, and transmit flight information. Fortunately, the tethered quadrotor is of this type RUAV, which is novel aerial robots consisting of a ground mooring unit, tether cables, and a rotorcraft. However, like other aerial robots, tethered quadrotors are prone to fuselage vibration, instability, crashing, loss of the command and control link, and other dynamic stability problems in the presence of internal uncertainties and external disturbances [6]. Furthermore, the tether cable significantly influences the tethered quadrotor’s dynamics. Thus, safe deployment of a tethered quadrotor requires the analysis of their structural stability and dynamic stability.

Stability analysis inspects whether the system states remain stable under the influences of internal uncertainties and external disturbances. As such, it promotes optimization of the system’s structural parameters and control commands. Generally, there are two stability analysis methods for nonlinear dynamic systems. The first relies on analyzing the dynamics model, whereas the second utilizes Lyapunov stability theory [7, 8]. More precisely, the first method analyzes the stability of the dynamics model established via parameter identification. However, this method depends on the model accuracy and the efficiency of solving dynamic equations. For the tethered quadrotor system with noise interference, nonlinearity, and strong coupling, the dynamic model is very complicated, and the Lyapunov function cannot be accurately constructed or even obtained.

The second method constructs a Lyapunov function for nonlinear systems. The Lyapunov exponent can describe the average exponential rate of divergence or convergence of the states when the system is subjected to disturbances, so it can be used to quantitatively analyze the motion stability of the tethered quadrotor system. Compared with the first method, the Lyapunov exponent method is easier to construct and more suitable for the stability analysis of complex nonlinear system dynamics models [9, 10]. For instance, Amiri et al. [11] utilized the Newton–Euler equations to derive the dynamics model of a small-scale unmanned helicopter and analyzed its stability by applying Lyapunov stability theory. Pfimlin et al. [12] adopted the Lyapunov method to analyze the stability of the dynamics model for a ducted-fan unmanned aerial vehicle. However, the authors omitted the influence of external disturbances to decrease the algorithm complexity. Under the assumption that all system states are measurable, Islam and Liu [13] used a Lyapunov-like energy function to evaluate a quadrotor’s controller design with uncertain parameters, unknown environmental effects, and unmodeled dynamics.

Nevertheless, while the discussed works provide an approach to analyze the aerial robots' stability, they are usually constrained by the dynamics model’s calculation efficiency. Meanwhile, the stability of the tethered quadrotors executing complex flight missions in a dynamic environment is hampered by their inherent instability, strong coupling of their dynamics, and high nonlinearity. Furthermore, tethered quadrotors are susceptible to underactuated behavior, modeling errors, and external disturbances. Hence, there is a need for an efficient and practical method for the tethered quadrotor’s stability analysis.

The Lyapunov exponent approach has attracted significant attention from the research community, because it enables quantitative dynamic stability analysis [14, 15]. For example, Chen et al. [16] aimed to improve the dynamic stability of a ducted-fan unmanned aerial vehicle using the Lyapunov exponent. Similarly, Liu et al. used the Lyapunov exponent to analyze the dynamic stability of quadrotors during takeoff, landing, yawing, rolling, and pitching [7, 17, 18]. Moreover, the Lyapunov exponent has been identified as the prominent approach for the stability analysis of other robots, such as mobile vehicles [19], underwater robots [20], and biped robots [21].

The discussed works optimized the structural parameters to improve the movement stability of the robotic systems. Furthermore, the effect of external disturbances on robots' dynamic stability was studied by evaluating it via the Lyapunov exponent method [22]. These works suggest the suitability of the Lyapunov exponent method for quantitative analysis of the tethered quadrotors’ dynamical stability when subjected to parametric uncertainties and external disturbances.

Therefore, this study utilizes the Lyapunov exponent method in dynamic stability analysis of the tethered quadrotor, demonstrating its efficacy and efficiency. Extensive simulations in the virtual environment are performed to evaluate the performance of the proposed Lyapunov exponent approach. In addition, real-world flight experiments are conducted to validate the proposed approach further. Although the Lyapunov exponent theory is a proven effective method for stability analysis of nonlinear systems, to the best of the authors’ knowledge, it has never been used for dynamic stability analysis of tethered quadrotors. This aspect constitutes one of the main contributions and novelties of the present work. Another contribution is reflected in the rationality of the designed physical prototype, which has been verified through both simulation and experiments. The main contributions and features of this work can be summarized as follows:

• (1) Compared with the existing works [7,8,9,10,11,12,13], this paper extends the previous theoretical work by providing Lyapunov exponent approach for stability analysis. Meanwhile, theoretical results are first experimentally verified using a tethered quadrotor.

• (2) This work develops a novel tethered quadrotor which addresses the shortcomings of conventional drones, such as endurance time, computational efficiency, and load capacity. Compared with the conventional drones, the stability analysis of the tethered quadrotor has more challenging due to the flexible ropes.

• (3) This work analyzes the stability of the tethered aircraft in different flight stages, which is conducive to the design of a reasonable aircraft. In particular, the effects of cable length and wind gusts on system stability are explored.

The remainder of this paper is organized as follows. Section 2 introduces the tethered quadrotor's design concepts. System modeling is presented in Sect. 3, establishing the quadrotor dynamics model and tether cable model. Section 4 describes the Lyapunov exponents’ calculation method. Then, the simulation and experiment results are shown in Sect. 5. Finally, the main conclusions are given in Sect. 6.

2 Design Concepts

In this section, a tethered quadrotor is designed to increase endurance time, critical for a classical aerial robot. The tethered quadrotor consists of an X450 quadrotor and a ground mooring unit, which communicate via a tether cable and wirelessly. Its architecture is illustrated in Fig. 1. The aircraft comprises the following modules: a global positioning system (GPS), gyroscope, accelerometer, magnetometer/compass, inertial measurement unit (IMU), wireless modem, and embedded control processor. The ground mooring unit contains a diesel generator connected to a cable capstan and a power conversion module to boost 220 V alternating current (AC) to 380 V direct current (DC) through the tether cable. The tether cable is wrapped around the cable capstan (Fig. 2), which adopts a reciprocating screw mechanism to ensure the cable neatly rolls on the drum. The unit tether cable has one core 1550 nm single-channel optical fiber and two 0.75 mm² aviation wire cores, covered with high-temperature resistant Teflon composite film and woven aramid fibers (Fig. 3). Finally, a computer serves as the ground station, running programs for retrieving information regarding the aircraft's status.

Fig. 1

The system architecture of the tethered quadrotor

Fig. 2

The cable capstan

Fig. 3

Sketch map of the cable wheel

3 System Modeling

3.1 Quadrotor Dynamics Model

The model of quadrotor dynamics is established by representing the aircraft as a solid body evolving in a 3D space while subjected to the thrust and three moments: pitch, roll, and yaw. The two coordinate frames of the tethered quadrotor, namely the body-fixed frame ($\left\{ {O_{B} } \right\}$) and earth-fixed frame ($\left\{ {O_{E} } \right\}$), are depicted in Fig. 4. Frame $\left\{ {O_{B} } \right\}$ is fixed at the center of the aircraft, whereas frame $\left\{ {O_{E} } \right\}$ is fixed at the center of the ground mooring unit. The quadrotor’s generalized coordinates are

$$ {\mathbf{q}} = [x,y,z,\phi ,\theta ,\psi ]^{T} , $$

(1)

where $[x,y,z] \in R^{3}$ is the position vector of the aircraft’s center of mass relative to frame $\left\{ {O_{E} } \right\}$. Euler angles $[\phi ,\theta ,\psi ]^{T} \in R^{3}$ capture the quadrotor's orientation, where $\phi$ is the roll angle about the $X_{B}$-axis, $\theta$ is the pitch angle about the $Y_{B}$-axis, and $\psi$ is the yaw angle about the $Z_{B}$-axis.

Fig. 4

Structure sketch of the tethered quadrotor

In tethered quadrotor system, the dynamics model of quadrotor subsystem is established via the Euler–Lagrange method [25]

$$ \left\{ {\begin{array}{*{20}l} {{\mathbf{\dot{q} = V}}\left( {\mathbf{q}} \right){\mathbf{p}}} \hfill \\ {{\mathbf{M}}\left( {\mathbf{q}} \right){\mathbf{\dot{p} + C}}\left( {{\mathbf{q,p}}} \right){\mathbf{p + F}}\left( {{\mathbf{p,q,u}}} \right){\mathbf{ = 0}}} \hfill \\ \end{array} } \right., $$

(2)

where ${\mathbf{p}} = [u,v,w,p,q,r]^{T}$ denotes the vector of the generalized linear and angular velocities. Further, ${\mathbf{V}}\left( {\mathbf{q}} \right)$ captures the relationship between generalized coordinates and generalized velocities and consists of a transformation matrix ${\mathbf{R}}_{1}$ from $\left\{ {O_{B} } \right\}$ to $\left\{ {O_{E} } \right\}$ and an orientation transformation matrix ${\mathbf{R}}_{2}$ [26], which is described as

$$ {\mathbf{V}}\left( {\mathbf{q}} \right) = \left[ {\begin{array}{*{20}c} {{\mathbf{R}}_{1} } & 0 \\ 0 & {{\mathbf{R}}_{2} } \\ \end{array} } \right], $$

(3)

where

$$ {\mathbf{R}}_{1} = \left[ {\begin{array}{*{20}c} {C_{\theta } C_{\psi } } & {S_{\phi } S_{\theta } C_{\psi } - C_{\phi } S_{\psi } } & {C_{\phi } S_{\theta } C_{\psi } + S_{\phi } S_{\psi } } \\ {C_{\theta } S_{\psi } } & {S_{\phi } S_{\theta } S_{\psi } + C_{\phi } C_{\psi } } & {C_{\phi } S_{\theta } S_{\psi } - S_{\phi } C_{\psi } } \\ { - S_{\theta } } & {S_{\phi } C_{\theta } } & {C_{\phi } C_{\theta } } \\ \end{array} } \right], $$

(4)

and

$$ {\mathbf{R}}_{2} = \left[ {\begin{array}{*{20}c} 1 & {S_{\phi } S_{\theta } /C_{\theta } } & {C_{\phi } S_{\theta } /C_{\theta } } \\ 0 & {C_{\phi } } & { - S_{\phi } } \\ 0 & {S_{\phi } /C_{\theta } } & {C_{\phi } /C_{\theta } } \\ \end{array} } \right], $$

(5)

where $S\left( \cdot \right)$ and $C\left( \cdot \right)$ are abbreviations of $\sin \left( \cdot \right)$ and $\cos \left( \cdot \right)$, respectively.

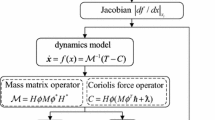
${\mathbf{M}}\left( {\mathbf{q}} \right) \in R^{6 \times 6}$ denotes the inertial matrix, which is described as

$$ {\mathbf{M}}\left( {\mathbf{q}} \right) = \left[ {\begin{array}{*{20}c} m & 0 & 0 & 0 & 0 & 0 \\ 0 & m & 0 & 0 & 0 & 0 \\ 0 & 0 & m & 0 & 0 & 0 \\ 0 & 0 & 0 & {I_{xx} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {I_{yy} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {I_{zz} } \\ \end{array} } \right], $$

(6)

where $m$ is the quadrotor’s mass, and $I_{xx}$, $I_{yy}$, and $I_{zz}$ are the moment of inertia.

${\mathbf{C}}\left( {{\mathbf{q}},{\mathbf{p}}} \right) \in R^{6 \times 6}$ is the gyroscopic matrix that includes the Coriolis and centrifugal forces and can be expressed as

$$ {\mathbf{C(q,p)}} = \left[ {\begin{array}{*{20}c} 0 & { - mr} & {mq} & 0 & 0 & 0 \\ {mr} & 0 & { - mp} & 0 & 0 & 0 \\ { - mq} & {mp} & 0 & 0 & 0 & 0 \\ 0 & { - mw} & {mv} & 0 & {I_{yy} r} & { - I_{zz} q} \\ {mw} & 0 & { - mu} & {I_{zz} r} & 0 & { - I_{xx} p} \\ { - mv} & {mu} & 0 & {I_{xx} q} & { - I_{yy} p} & 0 \\ \end{array} } \right]. $$

(7)

Finally,${\mathbf{F}}\left( {{\mathbf{p}},{\mathbf{q}},{\mathbf{u}}} \right)$ denotes an input matrix containing active forces/moments (e.g., motor drive force and motor drive moments) and passive forces/moments (e.g., gravity, the tension of the cable, and air drag). The quadrotor motor's driving force/moments ${\mathbf{u}} = \left[ {U_{1} ,U_{2} ,U_{3} ,U_{4} } \right]^{\rm T}$ can be calculated as [27]

$$ \left\{ \begin{gathered} U_{1} = F_{1} + F_{2} + F_{3} + F_{4} \hfill \\ U_{2} = \left( {\frac{\sqrt 2 }{2}F_{1} - \frac{\sqrt 2 }{2}F_{2} - \frac{\sqrt 2 }{2}F_{3} + \frac{\sqrt 2 }{2}F_{4} } \right)L \hfill \\ U_{3} = \left( {\frac{\sqrt 2 }{2}F_{1} + \frac{\sqrt 2 }{2}F_{2} - \frac{\sqrt 2 }{2}F_{3} - \frac{\sqrt 2 }{2}F_{4} } \right)L \hfill \\ U_{4} = M_{2} + M_{4} - M_{1} - M_{3} \hfill \\ \end{gathered} \right., $$

(8)

where $L$ is the distance between the center of the propeller hub and the center of the quadrotor's mass, and $U_{1}$, $U_{2}$, $U_{3}$, and $U_{4}$ are the thrust input, pitch moment input, roll moment input, and yaw moment input, respectively. $F_{i}$ and $M_{i}$ ($i = 1,2,3,4$) are the force and momnet produced by each propeller, which are expressed as [23, 24]

$$ \left\{ {\begin{array}{*{20}l} {F_{i} = \rho_{a} C_{T} AR^{2} \Omega_{i}^{2} } \hfill \\ {M_{i} = \rho_{a} C_{M} AR^{3} \Omega_{i}^{2} } \hfill \\ \end{array} } \right., $$

(9)

where $\Omega_{i}$ denotes the propeller speed, $\rho_{a}$ is the air density, $A$ is the propeller disk area, $R$ is the propeller's radius, and $C_{T}$ and $C_{M}$ are the thrust coefficient and the moment coefficient, respectively.

3.2 Tether Cable Model

Remark 1

Assuming the cable only bears tension and gravity, the angle between the cable and longitudinal plane $O_{E} Y_{E} Z_{E}$ is set as $\beta$. Since the $\beta$ is almost unchanged during the takeoff and landing process, it can be taken as a particular vale. Therefore, the force analysis of the entire system can be restricted to the longitudinal plane $O_{E} Y_{E} Z_{E}$.

Remark 2

Assuming the cable tension in 3D space is set as $T_{h}$, the cable tension $T_{1}$ in the longitudinal plane $O_{E} Y_{E} Z_{E}$ can be calculated as $T_{1} = T_{h} \cos \beta$.

The planar model of the tethered quadrotor is illustrated in Fig. 5. The tether cable is subject to gravity acceleration $g$ and the aircraft's tension $T_{1}$. Similar analysis can be found in [5]. The forces acting on the cable can be expressed as

$$ \left\{ \begin{gathered} T_{1} \sin \Upsilon = T_{0} \hfill \\ T_{1} \cos \gamma = g \cdot \rho sl = G_{c} \hfill \\ \end{gathered} \right., $$

(10)

where $\Upsilon$ is the angle between the gravity and cable tension, $\rho$ is the cable density, $s$ denotes the sectional area of the cable, and $l$ is the cable length.

Fig. 5

Tether cable longitudinal simplified scheme

Consider the following equation:

$$ \frac{dz}{{dy}} = \frac{{G_{c} }}{{T_{0} }}. $$

(11)

Using Eq. (9), one obtains

$$ g\rho sl = T_{0} \frac{dz}{{dy}}. $$

(12)

Then, the derivative of Eq. (12) satisfies

$$ g\rho sdl = T_{0} \frac{{d^{2} z}}{dy}, $$

(13)

where the infinitesimal $dl$ is defined as

$$ dl = \sqrt {\left( {dy} \right)^{2} + \left( {dz} \right)^{2} } = \sqrt {1 + \left( {\frac{dz}{{dy}}} \right)^{2} } dy. $$

(14)

Equation (13) can now be transformed into

$$ \rho sg\sqrt {1 + (\frac{dz}{{dy}})^{2} } = T_{0} \frac{{d^{2} z}}{{dy^{2} }} = T_{0} \frac{{d\left( {\frac{dz}{{dy}}} \right)}}{dy}. $$

(15)

Since $\varepsilon = dz/dy$, integrating Eq. (15) yields

$$ \int {\frac{\rho sg}{{T_{0} }}} dy = \int {\frac{1}{{\sqrt {1 + \varepsilon^{2} } }}} d\varepsilon . $$

(16)

Solving the integral equation results in

$$ \varepsilon = \frac{dz}{{dy}} = \sinh \left( {\frac{\rho sg}{{T_{0} }}y - c_{1} } \right). $$

(17)

Since $y = 0$ and $\dot{z} = 0$, one obtains $c_{1} = 0$. Then, the integration of Eq. (16) is

$$ z = \frac{{T_{0} }}{\rho sg}\cosh \left( {\frac{\rho sg}{{T_{0} }}y} \right) + c_{2} . $$

(18)

Again, since $y = 0$ and $\dot{z} = 0$, $c_{2} = - T_{0} /\rho sg$. Using the catenary theory [28], the tether cable length model can be formulated as

$$ z = D\cosh \left( {\frac{1}{D}y} \right) - D, $$

(19)

where $D = T_{0} /\rho sg$ denotes the equivalent cable length.

By combining Eqs. (10) and (19) with the Euler formula $\cosh \left( x \right) = \left( {e^{x} + e^{ - x} } \right)/2$, the tether cable tension model is

$$ T = T_{1} = T_{0} \frac{1}{\cos \alpha } = T_{0} \sqrt {1 + \dot{z}^{2} } = T_{0} + \rho szg, $$

(20)

where $\alpha$ represents the angle between the tension $T_{1}$ and the axis $Y_{E}$.

Let symbol $\beta$ represent the angle between the cable and the longitudinal plane. Now, the cable tension in 3D space can be expressed using a $6 \times 1$ column vector

$$ {\mathbf{T}} = \left[ {\begin{array}{*{20}c} { - TS_{\beta } /C_{\beta } } & { - TC_{\alpha } } & {TS_{\alpha } } & 0 & 0 & 0 \\ \end{array} } \right]^{\rm T} . $$

(21)

3.3 State-Space Model

In control engineering, a state-space representation is a mathematical model of a physical system that relates input, output, and state variables via first-order differential equations [29]. Under the state-space representation, the dynamical model of the tethered quadrotor can be expressed as

$$ {\dot{\mathbf{X}}} = f({\mathbf{X}}), $$

(22)

where ${\mathbf{X}} = [{\mathbf{q}},{\mathbf{p}}]^{T}$.

Remark 3

The variation Eq. (22) is a matrix-valued time-varying linear differential equation. It is derived by linearization of the vector field along the trajectory ${\mathbf{X}}(t)$.

Combining Eqs. (4), (21), and (22), one obtains the first-order derivative of the state variables as

$$ {\dot{\mathbf{q}}} = \left[ {\begin{array}{*{20}c} {w\left( {S_{\phi } S_{\psi } + C_{\phi } C_{\psi } S_{\theta } } \right) - v\left( {C_{\phi } S_{\psi } - C_{\psi } S_{\phi } S_{\theta } } \right) + C_{\psi } C_{\theta } u} \\ {v\left( {C_{\phi } C_{\psi } + S_{\phi } S_{\psi } S_{\theta } } \right) - w\left( {C_{\psi } S_{\phi } - C_{\phi } S_{\psi } S_{\theta } } \right) + C_{\theta } uS_{\psi } } \\ {C_{\phi } C_{\theta } w - uS_{\theta } + C_{\theta } vS_{\phi } } \\ {p + \frac{{C_{\phi } S_{\theta } r}}{{C_{\theta } }} + \frac{{S_{\phi } S_{\theta } q}}{{C_{\theta } }}} \\ {C_{\phi } q - S_{\phi } r} \\ {\frac{{C_{\phi } r + S_{\phi } q}}{{C_{\theta } }}} \\ \end{array} } \right], $$

(23)

$$ {\dot{\mathbf{P}}} = \left[ {\begin{array}{*{20}c} {\frac{{U_{1} \left( {S_{\phi } S_{\psi } + C_{\phi } C_{\psi } S_{\theta } } \right) - mqw + mrv - TS_{\beta } /C_{\beta } }}{m}} \\ { - \frac{{U_{1} \left( {C_{\psi } S_{\phi } - C_{\phi } S_{\psi } S_{\theta } } \right) - mpw + mru + T_{1} S_{\Upsilon } }}{m}} \\ { - \frac{{mg + mpv - mqu - U_{1} C_{\phi } C_{\theta } + T_{1} C_{\Upsilon } }}{m}} \\ {\frac{{U_{2} - I_{yy} qr + I_{zz} qr}}{{I_{xx} }}} \\ {\frac{{U_{3} - I_{zz} pr + I_{xx} pr}}{{I_{yy} }}} \\ {\frac{{U_{4} - I_{xx} pq + I_{yy} pq}}{{I_{zz} }}} \\ \end{array} } \right]. $$

(24)

4 Lyapunov Exponent Method

Dynamic stability analysis assumes that convergence (or divergence) of motion trajectories with close starting points continues as time approaches infinity. Such a behavior can be analyzed by the Lyapunov exponent proposed in [30]. Given a continuous dynamical system in an n-dimensional phase space, we track the long-term development of an infinitesimal n-sphere of starting conditions. Due to the flow’s locally deforming character, the sphere will deform into an $n{\text{ - ellipsoid}}$. Define the $i{\text{th}}$ one-dimensional Lyapunov exponent in term of the length of the ellipsoidal principal axis $\left\| {\delta x_{i} \left( t \right)} \right\|$ as

$$ \gamma_{i} = \mathop {\lim }\limits_{t \to \infty } \frac{1}{t}\ln \frac{{\left\| {\delta x_{i} \left( t \right)} \right\|}}{{\left\| {\delta x_{i} \left( {t_{0} } \right)} \right\|}}\quad \left( {i = 1, \ldots ,n} \right), $$

(25)

where $x_{i} \left( {t_{0} } \right)$ and $x_{i} \left( t \right)$ denote the state variables at the initial and the current time, $t_{0}$ and $t$, respectively. The function (25) of Lyapunov exponents indicates the stability property of the dynamic system. If $\gamma_{i} < 0$, the system is stable, and the lower the exponent, the more stable the system. If $\gamma_{i} > 0$, the system implies instability. If $\gamma_{i} { = }0$, the system is asymptotically stable.

Remark 4

The Lyapunov exponents are proportional to the expanding or contracting character of certain phase space directions. Due to the fact that the ellipsoid's orientation changes continually as it evolves, the directions associated with a particular exponent fluctuate in a complex manner along the attractor. As a result, one cannot talk of an exponent having a well-defined direction.

The Jacobian matrix of Eq. (22) can be calculated as

$$ \left| {\frac{{df\left( {\mathbf{X}} \right)}}{{d{\mathbf{X}}}}} \right| = \left| {\begin{array}{*{20}c} {\frac{{\partial \dot{X}_{1} }}{{\partial X_{1} }}} & {\frac{{\partial \dot{X}_{2} }}{{\partial X_{1} }}} & \cdots & {\frac{{\partial \dot{X}_{12} }}{{\partial X_{1} }}} \\ {\frac{{\partial \dot{X}_{1} }}{{\partial X_{2} }}} & {\frac{{\partial \dot{X}_{2} }}{{\partial X_{2} }}} & \cdots & {\frac{{\partial \dot{X}_{12} }}{{\partial X_{2} }}} \\ \vdots & \vdots & {} & \vdots \\ {\frac{{\partial \dot{X}_{1} }}{{\partial X_{12} }}} & {\frac{{\partial \dot{X}_{2} }}{{\partial X_{12} }}} & \cdots & {\frac{{\partial \dot{X}_{12} }}{{\partial X_{12} }}} \\ \end{array} } \right| = \eta^{^{\prime}} , $$

(26)

where $\dot{X}_{i} \left( {i = 1,2, \ldots ,12} \right)$ is the derivative of the system state variables.

To calculate the Lyapunov exponents based on the dynamical model (22), fiducial trajectories are constructed by integrating nonlinear equations of motion for some post-transient initial conditions. Meanwhile, an arbitrarily oriented frame of $n$ orthonormal vectors is constructed by simultaneously integrating the linearized equations of motion for $n$ different initial conditions. On the initial frame of orthonormal vectors, let the linearized equations of motion create the set of vectors $[\delta x_{1} \left( t \right),\delta x_{2} \left( t \right), \cdots ,\delta x_{n} \left( t \right)]$. The Gram–Schmidt reortho-normalization (GSR) is applied to avoid a misalignment of all vectors along the direction of maximal expansion [31]. GSR provides the orthonormal set $[\eta_{1}^{^{\prime}} ,\eta_{2}^{^{\prime}} , \cdots ,\eta_{n}^{^{\prime}} ]$ shown below

$$ \begin{gathered} \eta_{1}^{\prime } = \frac{{\eta_{1} }}{{\left\| {\eta_{1} } \right\|}}, \hfill \\ \eta_{2}^{\prime } = \frac{{\eta_{2} - \left\langle {\eta_{2} ,\eta_{1}^{\prime } } \right\rangle \eta_{1}^{\prime } }}{{\left\| {\eta_{2} - \left\langle {\eta_{2} ,\eta_{1}^{\prime } } \right\rangle \eta^{\prime } } \right\|}}, \hfill \\ \cdots \hfill \\ \eta_{n}^{\prime } = \frac{{\eta_{n} - \left\langle {\eta_{n} ,\eta_{n - 1}^{\prime } } \right\rangle \eta_{n - 1}^{\prime } - \cdots - \left\langle {\eta_{n} ,\eta_{1}^{\prime } } \right\rangle \eta_{1}^{\prime } }}{{\left\| {\eta_{n} - \left\langle {\eta_{n} ,\eta_{n - 1}^{\prime } } \right\rangle \eta_{n - 1}^{\prime } - \cdots - \left\langle {\eta_{n} ,\eta_{1}^{\prime } } \right\rangle \eta_{1}^{\prime } } \right\|}}, \hfill \\ \end{gathered} $$

(27)

where $\left\langle \cdot \right\rangle$ denotes the inner product. GSR procedure allows the integration of the vector frame for as long as required for the convergence of Lyapunov spectrum.

Combining Eqs. (22), (25) and (27), the Lyapunov exponent for the tethered quadrotor can be written as [32]

$$ \gamma = \mathop {\lim }\limits_{n \to \infty } \frac{1}{n}\sum\limits_{i = 0}^{n - 1} {\ln \left| {\eta^{^{\prime}} } \right|} , $$

(28)

describing the quantitative relation between the quadrotor's structural parameters and the dynamic stability.

Figure 6 summarizes the tethered quadrotor's motion stability analysis based on the Lyapunov exponent concept in a block diagram.

Fig. 6

Flowchart of the dynamic stability analysis based on the Lyapunov exponent

5 Simulation and Experiments

5.1 Parameters’ Identification

Structure parameters of the tethered quadrotor can be assessed through direct and indirect measurement. Several physical parameters (such as the quadrotor’s mass $m$ and length $L$) can be obtained using standard measurement tools. However, specific physical parameters cannot be directly obtained unless specialized testing platforms are utilized. Such parameters include the rotational inertia, thrust coefficient, and moment coefficient.

The aircraft's rotational inertia can be measured using the bifilar pendulum method [33]. As seen in Fig. 7, the aircraft is suspended with two thin wires of the same length. Taking the rotational inertia ($I_{xx}$) as an example, the aircraft is rotated manually about $OX$ axis by a small angle. Once released, the aircraft proceeds to periodically move back-and-forth about $OX$ axis.

Fig. 7

The test platform designed to assess rotational inertia

The rotational inertia is calculated as

$$ I = \frac{{mgr^{2} }}{{\omega^{2} a}}, $$

(29)

where $r$ denotes the distance between the aircraft mass and the wire, $a$ is the wire length, and $\omega$ is the oscillation period. The calculated rotational inertia parameters are listed in Table 1.

Table 1 Parameters of rotational inertia of the quadrotor

The propeller’s thrust and moment coefficients assessment is conducted on a specific test platform shown in Fig. 8. One propeller is fixed on the support frame, and its thrust and moment are collected by a tension sensor (model MT1022-15, METTLER TOLEDO) and a torque sensor (model MT1022-3, METTLER TOLEDO). The electrical signals from the sensors are converted into 0–5 V voltage signals through the transducer, and an acquisition board samples the voltage signals at a frequency of 500 Hz. These sensors have a measurement sensitivity from 1.8 to 2.2 mV. Figure 9 shows the relation between the propeller speed and thrust. Similarly, the connection between moment and propeller speed is estimated in Fig. 10.

Fig. 8

The test platform designed to assess the propeller's parameters

Fig. 9

The thrust coefficient assessment results

Fig. 10

The moment coefficient assessment results

The derived intrinsic parameters of the tethered quadrotor are listed in Table 2.

Table 2 Tethered quadrotor intrinsic parameters

5.2 Simulation Results

This section presents four simulation cases conducted to investigate the proposed tethered quadrotor's dynamic stability under different conditions.

Case 1. The aircraft flied from the ground to a hovering altitude of 100 m, increasing the propeller speed from 0 to 10,800 rpm. Then, the aircraft returned to the ground, and the propeller speed dropped to zero. As seen in Fig. 11, the Lyapunov exponents during takeoff are smaller than those during landing. Therefore, the tethered quadrotor has better dynamic stability during landing. This result stems from the tether cable's shortening, revealing the stability performance’s sensitivity to the tether cable tension.

Fig. 11

The Lyapunov exponents during takeoff and landing

Furthermore, the stability performance during takeoff and landing was quantified using evaluation Eq. (30), and the results are listed in Table 3

$$ \Delta \gamma \left( \cdot \right) = \frac{{\gamma_{i} \left( \cdot \right) - \gamma_{j} \left( \cdot \right)}}{{\left| {\gamma_{i} \left( \cdot \right) + \gamma_{j} \left( \cdot \right)} \right|}} \times 100\% . $$

(30)

Table 3 Final Lyapunov exponents during takeoff and land

The results show that the stability is higher during landing than during takeoff, which contradicts the stability analysis results for conventional free-flying vehicles [7, 16]. If channel $x$ is taken as an example, the Lyapunov exponent for landing is 100.35% higher than that for takeoff.

In addition, Fig. 12 displays a variation in the Lyapunov exponents for different cable tensions. It can be observed that the cable tension’s effect on the tethered quadrotor’s takeoff phase is greater than that on the landing phase. As the cable tension increases, the Lyapunov exponents of $\theta$ channel and $\psi$ channel approach either zero or a negative value. More precisely, when the cable tension exceeds 150 N, the convergence speed of these two channels is almost zero. These results demonstrate that the channels are not sensitive to the variation in the cable tension. Furthermore, the overlarge cable tension leads to an unstable aircraft position, which is not allowed in practice.

Fig. 12

The Lyapunov exponents for different cable tensions

Case 2. This case provides three scenarios to investigate the propeller’s impact on stability performance during the yawing phase. Three cases with varying propeller speeds are selected as follows:

Scenario 1: $\Omega_{2} = \Omega_{4} = 10800\;{\text{rpm}}$, $\Omega_{1} = \Omega_{3} = 5800\;{\text{rpm}}$,

Scenario 2: $\Omega_{2} = \Omega_{4} = 10800\;{\text{rpm}}$, $\Omega_{1} = \Omega_{3} = 7800\;{\text{rpm}}$,

Scenario 3: $\Omega_{2} = \Omega_{4} = 10800\;{\text{rpm}}$, $\Omega_{1} = \Omega_{3} = 9800\;{\text{rpm}}$.

From the results in Fig. 13, it can be seen that the channels display the quickest convergence to zero or a negative value for Scenario 1. Furthermore, the Lyapunov exponents of Scenario 1 are the smallest when the algorithm reaches the iteration maximum. The larger the yaw angle, the better the aircraft’s stability at yawing phase. In practice, the system’s stability at the yawing phase is sensitive to the speed difference between two propeller pairs. Thus, the system’s stability can be enhanced by expanding the speed difference.

Fig. 13

The Lyapunov exponents during yawing phase

Case 3. This case studies the influence of different propeller radius on the tethered quadrotor’s stability when hovering. Three different propellers are selected:

Scenario 1: $R = 0.226{\text{m}}$, $\Omega_{1} = \Omega_{2} = \Omega_{3} = \Omega_{4} = 10800\;{\text{rpm}}$.

Scenario 2: $R = 0.200{\text{m}}$, $\Omega_{1} = \Omega_{2} = \Omega_{3} = \Omega_{4} = 10800\;{\text{rpm}}$.

Scenario 3: $R = 0.165{\text{m}}$, $\Omega_{1} = \Omega_{2} = \Omega_{3} = \Omega_{4} = 10800\;{\text{rpm}}$, while the rest of the intrinsic parameters remain unchanged.

The Lyapunov exponents’ spectrum is depicted in Fig. 14. The results demonstrate that the Lyapunov exponents of Scenario 1 are smaller than those in Scenario 2 and Scenario 3 when the algorithm reaches the maximum iteration. Therefore, the stability performance of the tethered quadrotor can be improved when the propeller radius increases within the motor load capacity. Of considered, 0.226 m radius propeller is the most appropriate choice for the tethered quadrotor.

Fig. 14

The Lyapunov exponents for different propeller radius

Case 4. The tethered quadrotor’s stability decreases in real-world flights due to environmental uncertainties (e.g., wind gusts). Thus, this case investigates the effect of wind gusts on the tethered quadrotor's stability performance when hovering. The wind components along the $x$ and $y$ axes ($\left[ {W_{x} ,W_{y} } \right]^{T}$) are modeled as [34, 35]

$$ \left[ {\begin{array}{*{20}c} {W_{x} } \\ {W_{y} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {k_{x} } & 0 \\ 0 & {k_{y} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {V_{x} } \\ {V_{y} } \\ \end{array} } \right], $$

(31)

where $k_{x}$ and $k_{y}$ are correlation coefficients of the wind, and $V_{x}$ and $V_{y}$ are wind speeds.

Again, three scenarios are considered.

Scenario 1: $V_{x} = V_{y} = 0.2{\text{m/s}}$, hovering state with the propeller speed of 10,800 rpm;

Scenario 2: $V_{x} = V_{y} = 6{\text{m/s}}$, hovering state with the propeller speed of 10,800 rpm;

Scenario 3: $V_{x} = V_{y} = 6{\text{m/s}}$, hovering state with the optimized propeller speed.

The simulation results are shown in Fig. 15. One can observe that the stability performance displayed in Scenario 2 is significantly poorer than in other cases. Nevertheless, the system stability can be recovered by adjusting the propeller speeds according to the results of Scenario 3. Additionally, the system subjected to the wind gusts in the horizontal direction has a superior stability performance than that in the vertical direction, which stems mainly from the tether cable tension acting along the $y$ axis.

Fig. 15

The Lyapunov exponents under wind gusts

5.3 Experimental Results

The purpose of the real-world flight experiments is to test whether the structural parameters of the designed prototype are well chosen. Furthermore, the dynamic stability of the tethered quadrotor will be evaluated through the experiments. It should be noted that since the outdoor experimental environment cannot be controlled, only part of the simulation cases can be verified. In addition, a conventional cascade PID controller is designed for the tethered quadrotor, as shown in Fig. 16.

Fig. 16

Control structure of the tethered quadrotor

Several results are shown to demonstrate the theoretical analysis validity. The flight experiments were conducted on an empty area with an average wind speed of 1.6 m/s and a maximum wind speed equal to 5.1 m/s (as measured by an anemometer). The snapshots in Fig. 17 present the flight fragments of the tethered quadrotor. The experimental data were collected via the ground control station through wireless communication.

Fig. 17

Snapshots of the flight experiments

Test 1. The tethered quadrotor was controlled from the ground to a hovering altitude of 100 m. During takeoff, the experimental data were collected in the 20 s time intervals (0–20 s). Then, the quadrotor returned to the ground, and the experimental data with the same time intervals (93–113 s) were collected during the landing phase.

The collected experimental data are depicted in Figs. 18 and 19. It can be observed that the stability performance during landing is better than that during takeoff. Therefore, these results correspond to the theoretical results in Case 1. Such correspondence in the results and derived conclusions demonstrates the validity of the mathematical model of the quadrotor. Furthermore, the stability performance during takeoff deteriorates notably when the tethered quadrotor rises in a windy environment. Wind speed increases with the rise in flight altitude, and the tethered quadrotor's stability is sensitive to the wind speed. In addition, the increasing cable tension might be another factor decreasing the stability performance during landing.

Fig. 18

Position response during takeoff and landing

Fig. 19

Attitude response during takeoff and landing

Test 2. While the tethered quadrotor was hovering in Test 1, the yaw angle was varied. The experimental results are shown in Figs. 20, 21, 22. As seen in the time intervals 46–55 s, with the increase in the yaw angle, the stability of both position and attitude channels (except for the yaw angle) also increases. This result is consistent with that obtained in the second simulated case (Case 2) and demonstrates the effectiveness of the proposed Lyapunov exponent method.

Fig. 20

Motor speeds during yawing phase

Fig. 21

Position response during yawing phase

Fig. 22

Attitude response during yawing phase

Test 3. Finally, the tethered quadrotor was controlled to hover with propellers of three different sizes ($R = 0.226\,{\text{m}}$, $R = 0.200\,{\text{m}}$, and $R = 0.165\,{\text{m}}$). The position response was recorded with 10 s sampling intervals. Based on the experimental results, the standard deviation (std) can be calculated. The results in Fig. 23 show that as the propeller radius increases, the stability of position channels also rises, thus complying with the results of Case 3.

Fig. 23

Standard deviation of the position for different propeller radius

Furthermore, of the three channels, the variation is most significant for $x$. This discrepancy might be due to the propeller radius affecting the tethered quadrotor's power system, thus affecting the force of the cable on the $x$ axis. Therefore, the appropriate propeller should be selected to ensure the tethered quadrotor's stable flight.

6 Conclusion

This work studies the dynamic stability of the tethered quadrotor during takeoff, landing, and yawing phases. Furthermore, its structural parameters and the conditions in the presence of wind gusts are considered to improve the tethered quadrotor's dynamic stability. The overarching goal is to develop a Lyapunov exponent approach that enables quantitative stability analysis for a tethered quadrotor. Therefore, extensive simulations are conducted to evaluate the efficacy of this quantitative stability analysis method. Additionally, the real-world flight experiments further validate the reliability of the simulation results. Both simulation and experimental results have highlighted that:

• (1) Dynamic stability of the tethered quadrotor during landing is better than that during takeoff. Such discrepancies mainly stem from cable length and wind gusts.

• (2) The dynamic stability at yawing phase is sensitive to the yaw angle. Namely, the larger the yaw angle, the more stable the system.

• (3) High stability depends on a large propeller radius.

• (4) Compared to the vertical direction, the horizontal dynamic stability is more influenced by wind gusts.

• (5) The plausibility of the designed prototype's structural parameters has been verified.

Nevertheless, several aspects of the presented work require further investigation to improve the confidence in the derived results. Thus, future studies will consider more complex nonlinear systems, extending the quantitative stability analysis method based on the Lyapunov exponents. In addition, an advanced intelligent control technique will be further explored to improve the dynamic stability of the tethered quadrotor.