1 Introduction

The excellent properties of quadrotor unmanned aerial vehicles, such as small volume, strong maneuverability, vertical takeoff and landing, have made them attractive candidate performer for bomb attacking, atmospheric sounding, goods delivery and so on [1]. However, the dynamics stability problems, such as shaking and losing the tracking accuracy of command, and out of control of unmanned aerial vehicles often happened, which results from the gyroscopic effect and other unpredictable effects due to the atmospheric disturbance. The huge cost of the device and the security risk of crashing have made the unmanned aerial vehicles important object of study for the dynamics stability [2].

Dynamics stability refers to the performance to keep stability under the external disturbance [3]. Dynamics stability reflects the dynamics characteristics of the whole systems, which is mainly affected by the structural parameters and control moment [4,5,6]. Therefore, it is of great importance to optimize the structural parameters for improving dynamics stability of vehicles. In the early years, NASA DFRC had made analysis and technical research of flight stability of Grumman X-29 A 1, 2, which includes the analysis of the manual technique of frequency sweeping and the stability [7, 8]. The analysis of stability is achieved by adding a signal stimulus before the steering engine controller and then calculating the transfer function with excitation response of the vehicles. The main problem of this method is that the frequency components of the signal stimulus are required to form the harmonic sequence and the signal need to stay independent with each other. Presently, the dynamics stability is mainly analyzed with two traditional methods: the direct solution to dynamics equation and Lyapunov approach. However, the two methods are difficult to analyze the nonlinear system of quadrotor unmanned aerial vehicles with multiple variables, high coupling and underactuation. It is difficult to calculate the complex dynamics equation and establish the Lyapunov function. Meanwhile, the quantitative relationship between the structural parameters and the dynamics stability of systems is hard to build [9,10,11,12]. For example, Pflimlin applied Newton–Euler equations to establish a dynamics equation of the system for unmanned aerial vehicles and analyzed the stability with Lyapunov approach. But, he failed to express the equation due to the fact that the influence of atmospheric disturbance and the algorithm complexity are ignored [13]. Islam presented the nonlinear adaptive tracking system based on Lyapunov energy function for the uncertain problem on the modeling mistakes and disturbance uncertainties of small unmanned aerial vehicles. The algorithms have been developed using Lyapunov energy function by assuming that all the states are available for measurement [14]. Therefore, it is of important scientific significance and practical value that the quantitative relationship between structural parameters and the dynamics stability is established [15].

Lyapunov exponent provides an effective quantitative analysis method of dynamics stability, which is normally used to quantitatively describe the exponential divergence or convergence degree of initial value and original initial value of the system after disturbed over time. Dingwell et al. [16], based on Lyapunov exponent, investigated the stability of biped robots during movement; Yang and Wu et al. applied Lyapunov exponent method in biomechanics field to study the dynamics stability of the upper part of the body during walking [17,18,19,20]; Abdulwahab et al. [21], using Lyapunov exponent method, analyzed the lateral flight stability of unmanned aerial vehicles. Therefore, it is reasonable to adopt Lyapunov exponent method to implement quantitative analyse for the dynamics stability of quadrotor unmanned aerial vehicles. Ershkov [22] introduced a new exact solution of Euler’s equations (rigid body dynamics), which assumed that the center of mass of rigid body was located at meridional plane along the main principal axis of inertia of rigid body and the principal moments of inertia were satisfied to a simple algebraic equality. Liu put emphasis on the system optimization by controlling the input parameters, which focuses on the optimization to the control moment by varying the input parameters (e.g., the motor speed and the length of the rotor). This analysis process is accomplished after the mechanical design of the quadrotor unmanned aerial vehicles [23]. In the present paper, the quadrotor unmanned aerial vehicle is assumed as a particle, which is located in the center of the structure. Compared with Lyapunov direct method, the advantage of this method lies in its buildability, especially the ability to describe the relationship between structural parameters and dynamics stability quantitatively.

2 Mathematical preliminary

As is well known to us, Lyapunov exponent can be used to describe the average exponential rate of convergence between the divergence of initial value and the original initial value of the system after the system disturbance. Therefore, it can be applied to implement the quantitative analysis of the dynamics stability of systems. When the value of Lyapunov exponent is less than zero, the whole systems remain stable. The basic characteristic of Lyapunov exponent with negative numbers indicates that the system is dissipative or non-conservative (such as damped harmonic oscillator). The convergence rate of phase trajectory increases with increasing of negative value. When the negative number of Lyapunov exponent tends to infinity, the system moves toward a extraordinary degree of stability. On the contrary, when the value of Lyapunov exponent is larger than zero, the system is unstable or chaotic. When the value of Lyapunov exponent is fixed at zero, the phase trajectory is periodic with time [24,25,26].

Lyapunov exponent can be obtained through the dynamics equation, and the formula is written as

$$\begin{aligned} \lambda =\mathop {\lim }\limits _{n\rightarrow \infty } \frac{1}{n}\sum _{i=0}^{n-1} {\ln } \left| {\frac{\hbox {d}f(X)}{\hbox {d}X}} \right| _{X_i} \end{aligned}$$
(1)

where the state equation is obtained through transformation of the dynamics equation of the nonlinear system. The value of Lyapunov exponent is defined by Jacobian matrix \({\vert }\hbox {d} f/\hbox {d} X{\vert }\) of Function f(X) at \(X_{i}\). The calculation details are represented by

  1. (i)

    Dynamics model with the standard form is written as

    $$\begin{aligned}&\dot{q}=V(q)p\\&M(q)\dot{p}+C(q,p)p+F(p,q,u)=0 \end{aligned}$$
  2. (ii)

    Transforming model equation into state equation

    $$\begin{aligned}&{\hbox {d}X(t)}/{\hbox {d}t}=f\left( {X(t)} \right) \end{aligned}$$
  3. (iii)

    Calculating Jacobian

    $$\begin{aligned}&\left| {\hbox {d}f\left( X \right) /\hbox {d}X} \right| _{X_i} \end{aligned}$$
  4. (iv)

    Calculating Lyapunov exponent

    $$\begin{aligned}&\lambda =\mathop {\lim }\limits _{n\rightarrow \infty } \frac{1}{n}\sum _{i=0}^{n-1} {\ln } \left| {\hbox {d}f(X)/\hbox {d}X} \right| _{X_i} \end{aligned}$$
Fig. 1
figure 1

Main parameters affecting the Lyapunov exponent

Full size image

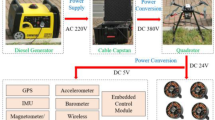
Lyapunov exponent can be applied to implement the quantitative analysis of the dynamics stability of systems. The main factors affected the value of Lyapunov exponent can be derived by Fig. 1, which includes structural parameters (e.g., L), the mass of system (m), rotational inertia (\(I_{x}, I_{y}, I_{z}\)) and the initial value (\(x_{0}\)). Therefore, the main factors affected the stability of quadrotor unmanned aerial vehicles are \(L, m, I_{x}, I_{y}, I_{z}\) and \(x_{0}\).

3 Methodology

3.1 Dynamics model

Assuming the quadrotor unmanned aerial vehicle is a rigid body and four propeller axes are all perpendicular to the surface of vehicle body (see Fig. 2). B(x, y, z) represents body-fixed coordinate frame and E(X, Y, Z) indicates the earth-fixed coordinate frame. Four situations exist with the different value of \(F_{1}, F_{2}, F_{3}\) and \(F_{4}\), as follows.

When \(F_{1}=F_{2}=F_{3}=F_{4}\), the quadrotor unmanned aerial vehicle stays the state of rising, descending or hovering;

When \(F_{2}=F_{4}\) and \(F_{1}\ne F_{3}\), the system stays the state of pitching;

When \(F_{1}=F_{3}\) and \(F_{2}\ne F_{4}\), the system stays the state of rolling;

When \(F_{1}=F_{3}\ne F_{2}=F_{4}\), the system stays the state of yawing.

Fig. 2
figure 2

System diagram

Full size image

The dynamics model of quadrotor unmanned aerial vehicles based on Euler–Poincare equation is written as

$$\begin{aligned}&\dot{q}=V(q)p\end{aligned}$$
(2)
$$\begin{aligned}&M(q)\dot{p}+C(q,p)p+F(p,q,u)=0 \end{aligned}$$
(3)

where V(q), M(q) and C(q, p) are kinematics matrix, inertia matrix and gyroscopic matrix, respectively. F(p, q, u) is the sum of aerodynamics force, gravity and control input, as follows:

$$\begin{aligned}&p=(p_1, q_1, r, u, v, w)^\mathrm{T}\\&q=(\phi , \theta , \psi , x, y, z)^\mathrm{T}\\&V(q)= \left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1&{} 0&{} 0&{} 0&{} 0&{} 0 \\ {S_\phi T_\theta }&{} {C_\phi }&{} {S_\phi C_\theta ^{-1}}&{} 0&{} 0&{} 0 \\ {C_\phi T_\theta }&{} {-S_\phi }&{} {C_\phi C_\theta ^{-1}}&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} {C_\theta C_\psi }&{} {C_\theta S_\psi }&{} {-S_\theta } \\ 0&{} 0&{} 0&{} {S_\phi S_\theta C_\psi -C_\phi S_\psi }&{} {S_\phi S_\theta S_\psi +C_\phi C_\psi }&{} {S_\phi C_\theta } \\ 0&{} 0&{} 0&{} {C_\phi S_\theta C_\psi +S_\phi S_\psi }&{} {C_\phi S_\theta S_\psi -S_\phi C_\psi }&{} {C_\phi C_\theta } \\ \end{array}}} \right] \\ \end{aligned}$$
$$\begin{aligned}&C(q,p)\\&=\left[ {{\begin{array}{cccccc} 0&{}\quad {-I_y r}&{}\quad {I_z q_1}&{}\quad 0&{}\quad {-mw}&{}\quad {mv} \\ {I_x r}&{}\quad 0&{}\quad {-I_z p_1}&{}\quad {mw}&{}\quad 0&{}\quad {-mu} \\ {-I_x q_1}&{}\quad {I_y p_1}&{}\quad 0&{}\quad {-mv}&{}\quad {mu}&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {-mr}&{}\quad {mq_1} \\ 0&{}\quad 0&{}\quad 0&{}\quad {mr}&{}\quad 0&{}\quad {-mp_1} \\ 0&{}\quad 0&{}\quad 0&{}\quad {-mq_1}&{}\quad {mp_1}&{}\quad 0 \\ \end{array}}} \right] \\ \end{aligned}$$
$$\begin{aligned}&F(p,q,u)\\&=\left[ {{\begin{array}{c} {-LU_2} \\ {-LU_3} \\ {-U_4} \\ {mgS_\theta -U_1 \left( {C_\phi C_\psi S_\theta +S_\phi S_\psi } \right) } \\ {-mgC_\theta S_\phi -U_1 \left( {-S_\phi C_\psi +C_\phi S_\theta S_\psi } \right) } \\ {-mgC_\theta C_\phi -U_1 C_\phi C_\theta } \\ \end{array}}} \right] \\&M(q)=\left[ {{\begin{array}{cccccc} {I_x}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad {I_y}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad {I_z}&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad m&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad m&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad m \\ \end{array}}} \right] \\&\left\{ {\begin{array}{l} U_1 =F_1 +F_2 +F_3 +F_4 \\ U_2 =F_2 +F_4 \\ U_3 =F_1 +F_3 \\ U_4 =K\left( {F_1 +F_2 +F_3 +F_4} \right) \\ \end{array}} \right. \\&F=1/2\rho AC_\mathrm{T} R^{2}\Omega ^{2} \end{aligned}$$

where \(I_{x}, I_{y}\) and \(I_{z}\) are rotational inertia of axis x, y and z of systems, respectively; \(A=\pi R^{2}\), with R being the rotor radius; \(\rho \) is air density; \(K=C_{Q}\)/\(C_\mathrm{T}\), and \(C_{Q}\) is the coefficient of the rotor torque; \(C_\mathrm{T}\) is rotor tensile force coefficient; \(\Omega \) is the rotor speed; \(U_{l}, U_{2}, U_{3}\) and \( U_{4}\) are vertical speed control, roll input control, pitching control input and yawing control, respectively; F is the tensile force acting on each rotor; m is the mass of systems; g is the acceleration of gravity; \(\phi \) is the roll angle of the system around Axis x (rad), \(\theta \) is the pitching angle of the system around Axis y (rad), \(\psi \) is the yawing angle of the system around Axis z (rad); \(S_{\phi }=\hbox {sin} \phi , C_{\phi }=\hbox {cos} \phi , S_{\theta }=\hbox {sin} \theta , C_{\theta }=\hbox {cos} \theta , C^{-1}_{\theta }=\hbox {sec} \theta , T_{\theta } =\hbox {tan}\theta , S_{\psi }=\hbox {sin} \psi , C_{\psi }=\hbox {cos} \psi \).

Seen from Eqs. (2) and (3), the vectors can be written as

$$\begin{aligned}&\dot{q}= \left[ {{\begin{array}{c} {p_1 +rC_\phi T_\theta +q_1 S_\phi T_\theta } \\ {q_1 C_\phi -rS_\phi } \\ {rC_\phi C_\theta ^{-1} +q_1 S_\phi C_\theta ^{-1}} \\ uC_\theta C_\psi +v\left( {C_\psi S_\theta S_\phi -C_\phi S_\psi } \right) \\ +\,w\left( {C_\phi C_\psi S_\theta +S_\phi S_\psi } \right) \\ uC_\theta S_\psi +v\left( {C_\phi C_\psi +S_\theta S_\phi S_\psi } \right) \\ +\,w\left( {-C_\psi S_\phi +C_\phi S_\theta S_\psi } \right) \\ {wC_\theta C_\phi -uS_\theta +vC_\theta S_\phi } \\ \end{array}}} \right] \end{aligned}$$
(4)
$$\begin{aligned}&\dot{p}= \left[ {{\begin{array}{c} {-(-I_y q_1 r+I_z q_1 r-LU_2)/I_x} \\ {-(I_x p_1 r-I_z p_1 r-LU_3)/I_y} \\ {-(-I_x p_1 q_1 +I_y p_1 q_1 -U_4)/I_z} \\ -\left[ (\right. -mrv+mq_1 w+mgS_\theta \\ \qquad \quad -U_1 (C_\phi C_\psi S_\theta +S_\phi S_\psi \left. ) \right] /m \\ -\left[ (\right. mru-mp_1 w-mgC_\theta S_\phi \\ \quad \qquad -U_1 (-C_\psi S_\phi +C_\phi S_\theta S_\psi \left. ) \right] /m \\ -\left[ (\right. -mq_1 u+mp_1 v-mgC_\theta \\ C_\phi -U_1 C_\theta C_\phi \left. ) \right] /m \\ \end{array}}} \right] \end{aligned}$$
(5)

3.2 Calculation of Lyapunov exponents

Equations (4) and (5) could be transformed as:

$$\begin{aligned} \dot{X}=f\left( X \right) \end{aligned}$$
(6)

where \(X=[q p]^\mathrm{T}=(\phi , \theta ,\psi , x, y,z, p_{1}, q_{1},r,u, v, w)^\mathrm{T}\).

Fig. 3
figure 3

Calculation process of Lyapunov exponent

Full size image

Based on the dynamics model established, the Lyapunov exponent spectrum of the whole system can be calculated according to Eqs. (6) and (1).

In order to calculate Lyapunov exponent \(\lambda _{1}, \lambda _{2}, {\ldots }, \lambda _{6}\), the time T is fixed as 0.1 and iterations K is 100. For kth iteration (\(k=1, 2, {\ldots }, K\)), the initial condition of matrix variation Eq. (6) is {\(u_{1}^{(k-1)}, u_{2}^{(k-1)}, {\ldots }, u_{6}^{(k-1)}\)}. After Ts integration, one can obtain the vector values {\(w_{1}^{(k-1)},w_{2}^{(k-1)},{\ldots },w_{6}^{(k-1)}\)}, orthogonalize Gram–Schmidt, convert the above vector values into {\(v_{1}^{(k-1)}, v_{2}^{(k-1)}, {\ldots },v_{6}^{(k-1)}\)}, normalize them, then obtain vector values {\(u_{1}^{k}, u_{2}^{k},{\ldots }, u_{6}^{k}\)}. This process is repeated until Lyapunov exponent reaches the maximum number of iterations K and the mentioned exponent \(\lambda _{1}, \lambda _{2}, {\ldots }, \lambda _{6}\) would form the Lyapunov exponent spectrum.

Figure 3 displays the specific calculation process.

4 Simulation results

4.1 Parameterization

According to the simulation analysis, Mathematica is used to develop the dynamics model for quadrotor unmanned aerial vehicles during takeoff, landing and yawing stage, respectively. Meanwhile, Lyapunov exponent spectrum of attitude and total input energy spectra under different circumstances in Mathematica are systematically simulated. Then, the quantitative relation between structural parameters and stability of the system is obtained. Therefore, it can be summarized that the system stability is remarkably improved by changing structural parameter, so as the reduction of the system energy consumption.

Table 1 Structural parameters of systems
Full size table

Based on the previous study, the parameters, such as \(m, g, L, I_{x}, I_{y}, I_{z}, C_\mathrm{T}, C_{Q}, R\) and K, should be obtained to develop the dynamics model for quadrotor unmanned aerial vehicles. Detailed structural parameters of quadrotor unmanned aerial vehicles are listed in Table 1.

The parameters, such as the system mass m, center distance from rotor to vehicle body L and rotor radius R, can be obtained through measurement. The local acceleration of gravity g and the air density \(\rho \) are got easily. At the some time, other parameters can be calculated with the experimental method.

4.1.1 The measured of the rotational inertia

Two-line method is shown in Fig. 4a, which is used to measure the rotational inertia of the X axis and Y axis.

The rotational inertia of the Z axis is measured with the four-line method shown in Fig. 4b.

Fig. 4
figure 4

Measurement method of rotational inertia. a Two-line method. b Four-line method

Full size image

The rotational inertia can be calculated with the following formula:

$$\begin{aligned} I=\frac{mgr^{2}}{\omega ^{2}a} \end{aligned}$$
(7)

where \(m=0.8754\) kg, \(g=9.8\) m s\(^{-2}\), r represents the distance between the suspension point and the center of mass of the rotor, the parameter a is the length of the string, \(\omega \) is the oscillation period.

If \(\omega \) is known, values of the rotational inertia are obtained. Parameters of the rotational inertia are listed in Table 2.

Table 2 Parameters of the rotational inertia
Full size table
Fig. 5
figure 5

Test results of rotor tensile force

Full size image
Fig. 6
figure 6

Test results of rotor torque

Full size image

4.1.2 The coefficient of rotor tensile force and torque

The results of rotor tensile force test are shown in Fig. 5, \(C_\mathrm{T}=1.0792\)E−005.

The results of rotor torque test are shown in Fig. 6, \(C_{Q}=1.8992\)E−007.

4.2 Case study

4.2.1 Takeoff stage

The total tensile force increases with the increasing of the rotation speed of four rotors of quadrotor unmanned aerial vehicles simultaneously. When total tensile force is larger than force of gravity, quadrotor unmanned aerial vehicles take off and the tendency of the curve x(t), y(t) and z(t) will be monotonically increasing, as shown in Fig. 7.

Fig. 7
figure 7

Attitude curve during takeoff stage. a \(\phi (t)\), b \(\theta (t)\), c \(\psi (t)\), d x(t), e y(t), f z(t)

Full size image
Fig. 8
figure 8

Lyapunov exponent spectrum of attitude during takeoff stage. a LE (\(\phi \)), b LE (\(\theta \)), c LE (\(\psi \)), d LE (x), e LE (y), f LE (z)

Full size image

4.2.2 Landing stage

When the rotation speed of four rotors of quadrotor unmanned aerial vehicles decreases, the quadrotor unmanned aerial vehicles appears the stage of landing (Fig. 8). In this case, the Curve of x(t) and z(t) will be on rise and the Curve of y(t) will be declining, as shown in Figs. 9 and 10.

According to the comparison of Figs. 8 and 10, it can be drawn that the convergence speed of Lyapunov exponent spectrum during the takeoff stage is faster than that of the landing stage, which reveals that the stability performance of quadrotor unmanned aerial vehicles of takeoff stage is better. It should be admit the fact that the unmanned aerial vehicles take off stably and have difficulty in stable landing, which explains the phenomenon that many civil aircrafts are more likely to crash during the landing stage perfectly.

Seen from Figs. 11 and 12, the center distance from rotor to vehicle body stays 0.5m alone during the landing stage of quadrotor unmanned aerial vehicles.

According to the comparison of Figs. 10 and 12, when the value of L changes, it can be concluded that the convergence speed of Lyapunov exponent spectrum during the landing stage is faster with the increasing of the value of L. Therefore, the dynamics stability of the system can be properly improved by optimizing structural parameters.

Fig. 9
figure 9

Attitude curve during landing stage. a \(\phi (t)\), b \(\theta (t)\), c \(\psi (t)\), d x(t), e y(t), f z(t)

Full size image
Fig. 10
figure 10

Lyapunov exponent spectrum of attitude during landing stage. a LE (\(\phi \)), b LE (\(\theta \)), c LE (\(\psi \)), d LE (x), e LE (y), f LE (z)

Full size image
Fig. 11
figure 11

Improved attitude curve during landing stage. a \(\phi (t)\), b \(\theta (t)\), c \(\psi (t)\), d x(t), e y(t), f z(t)

Full size image
Fig. 12
figure 12

Improved Lyapunov exponent spectrum of attitude during landing stage. a LE (\(\phi \)), b LE (\(\theta \)), c LE (\(\psi \)), d LE (x), e LE (y), f LE (z)

Full size image

Seen from Fig. 13, the total input energy spectra under different conditions of center distance from rotor to vehicle body (\(L=0.225\) m and \(L=0.5\) m, respectively) is established using Mathematica during landing stage.

A peak value of energy consumption exists in Fig. 13 due to the disturbance and the unsteadiness of the whole system at the initial stage of landing (\(0 \leqq t \leqq 20\) s). This phenomenon can be explained that it is necessary for the system to overcome disturbance in movement and the motor current increases instantaneously during this stage while the voltage remains constant.

When the value of L increases from 0.225 to 0.5 m, the dynamics stability is improved due to the less work to overcome the disturbance and the less energy consumption. When the time is fixed at 70 s and the value of L is 0.225 and 0.5 m, the energy consumption of systems is reduced by 51.78%. This present study verifies the feasibility and accuracy by analyzing the system dynamics stability with the method of Lyapunov exponent, and also shows the possibility to solve energy consumption and dynamics stability of the system by changing structural parameter of quadrotor unmanned aerial vehicles.

Fig. 13
figure 13

Total input energy spectra

Full size image
Fig. 14
figure 14

Lyapunov exponent spectrum of system attitude. a LE (\(\phi \)), b LE (\(\theta \)), c LE (\(\psi \)), d LE (x), e LE (y), f LE (z)

Full size image

4.2.3 Yawing stage

Optimization of control input Figure 1 illustrates the control inputs \(U_{1}, U_{2}\), \(U_{3}\) and \(U_{4}\) have an influence on the Lyapunov exponent spectrum of system attitude. The control inputs are related to the rotation speed of motor. Therefore, Lyapunov exponent spectrum of system attitude can be calculated according to different rotation speeds of motor. The scenes of quadrotor unmanned aerial vehicles under the condition of different rotation speeds of motor are shown as follows:

Scene 1: When the rotation speed of Motor 1 and 3 is fixed at 3500 rpm (revolutions per minute) and that of Motor 2 and 4 is set to 1000 rpm, the system is at the state of yawing.

Scene 2: When the rotation speed of Motor 1 and 3 is fixed at 3000 rpm and that of Motor 2 and 4 is set to 1500 rpm, the system is at the state of yawing. The simulation results are shown as in the Fig. 14.

It can be drawn from Fig. 14, when the quadrotor unmanned aerial vehicles stay at the state of yawing, the system stability in Scene 2 is better than that of Scene 1.The system stability can be improved by controlling the difference between the input values of two groups of motors during the flight of quadrotor unmanned aerial vehicles. The smaller the difference between input values of the two groups of motors within a certain range, the better the dynamics stability of the system at yawing is.

Optimization of structural parameter Figure 1 demonstrates the structural parameter of the system L has an influence on Lyapunov exponent of attitude of quadrotor unmanned aerial vehicles. Meanwhile, the calculation results of Lyapunov exponent spectrum of system attitude are emerged under the different values of L.

In Scene 2, when the system input and other parameters stay a constant, the simulation results are shown in Fig. 15 with different values of L.

Fig. 15
figure 15

Lyapunov exponent spectrum of system attitude. a LE (\(\phi \)), b LE (\(\theta \)), c LE (\(\psi \)), d LE (x), e LE (y), f LE (z)

Full size image
Fig. 16
figure 16

Influence of different parameters on the energy spectrum

Full size image
Fig. 17
figure 17

Online interface of flight performance of the quadrotor unmanned aerial vehicles

Full size image
Fig. 18
figure 18

Location parameters of the system in the X-axis. a \(L=0.225\) m, b \(L=0.5\) m

Full size image
Fig. 19
figure 19

Location parameters of the system in the Y-axis. a \(L=0.225\) m, b \(L=0.5\) m

Full size image
Fig. 20
figure 20

Location parameters of the system in the Z-axis. a \(L=0.225\) m, b \(L=0.5\) m

Full size image

It can be drawn from Fig. 15, when the value of L is the only variable of the quadrotor unmanned aerial vehicles, the converges to zero is faster with the increasing of the value of L within a certain range and then the better performance of the system stability is displayed at yawing state. Therefore, the dynamics stability of quadrotor unmanned aerial vehicles can be improved by changing the value of L at yawing state.

Optimization of energy consumption Based on the previous study, Mathematica is used to develop the total input energy spectra at the stage of yawing. Figure 16 presents the influence of different system parameters with the total input energy spectra.

Seen from Fig. 16, it reveals that the quadrotor unmanned aerial vehicle (\(0 \leqq t \leqq 5\) s) at an initial landing stage appears unstable due to the disturbance. On the one hand, it is necessary to overcome the disturbance of system at the stage of movement; on the other hand, when the motor current increases instantaneously and the voltage remains unchanged, the energy consumption of the system will be increased remarkably. Therefore, a peak value of energy consumption can be found in the figure as well.

Seen from Fig. 16a, the energy consumption grows exponentially with the increasing of the rotation speed of brushless motor. When the time t is fixed at 50 s, the energy consumption of the system in scene 2 is 19.27% lower than that in scene 1. The smaller the difference between the input values of these two groups of motors, the more stable the system become and the lower the energy consumption would be.

Seen from Fig. 16b, the time t is fixed at 50 s, when the value of L is increased from 0.225 to 0.5 m, the energy consumption of the system is decreased about 7.27%. When the value of L is increased from 0.225 to 1 m, the energy consumption of the system is decreased about 50.17%.

When the value of L is increased from 1 to 0.225 m and other conditions of the system are constant, the dynamics stability of the system is improved and the work due to the overcoming disturbance. Meanwhile, the energy consumption is also reduced correspondingly.

In general, the results of simulation analysis in Figs. 13 and 16 verify the feasibility and accuracy of system dynamics stability with Lyapunov exponent method, and also show the possibility to solve the problems of energy consumption and dynamics stability by changing structural parameter of systems.

5 Experimental results

In this section, the experimental results of different structural parameters are revealed. When the value of L is 0.5 m, the flight performance of the quadrotor unmanned aerial vehicles is much better than that of the lower value of L (0.225 m) during the flight experiment. Seen from Fig. 17, the location parameters of the system are obtained from the online interface of flight performance of the quadrotor unmanned aerial vehicles. The location parameters of the system in the X-axis, Y-axis and Z-axis is shown in Figs. 18, 19 and 20, respectively.

The results reveal that the quadrotor unmanned aerial vehicle has better flight performance with the larger value of L (see Figs. 18, 19 and 20), which can be confirmed by the results of Figs. 11, 12 and 15. Therefore, the conclusion can be summarized that the structural parameters have a significant influence on the dynamics stability of quadrotor unmanned aerial vehicles.

6 Conclusions

To solve problems of dynamics stability for quadrotor unmanned aerial vehicles during takeoff, landing and yawing stage, this paper establishes a quantitative relationship between dynamics stability of the vehicles and the system with Lyapunov exponent method from the viewpoint of optimizing the structural parameters. The present approach relies on a theory foundation for optimization of structural parameter of the system and control of dynamics stability. Compared with Lyapunov direct method, the present method has the features of buildability and simple calculation process, etc. By first developing a signal dynamics model for unmanned aerial vehicles, then proposing a model for the quantitative relationship between structural parameters and dynamics stability of the system according to the dynamics model, and finally verifying the effectiveness and buildability of the whole theory through simulation analysis of examples, several conclusions are made as follows:

  1. (1)

    Results illustrate a quantitative relation between input torque of quadrotor unmanned aerial vehicles and dynamics stability of the system, which provides a theoretical basis for control of system optimization. As for the yawing state, it is found out the system would become more stable when the difference between input values of any two groups of motors is smaller;

  2. (2)

    The dependence of dynamics stability on structural parameter of the system also constructed, which is believed to have great significance in guiding optimization of structural parameter of the system.