1 Introduction

Electro-hydraulic actuators (EHAs) are widely applied in mechanical engineering as they have power density and large load capacity, which have been used in fatigue test device [1], wheel loader [2], exoskeleton [3], and shaking tables [4]. However, there exist lumped uncertain disturbances in the EHA including hydraulic parametric uncertainties and the external load, which are unknown constant or time-varying. These uncertainties may degrade the dynamic performance of the EHA. Thus, many novel controllers have been developed such as parametric adaptive controllers [5,6,7,8], robust controllers [9,10,11,12], RBFNN controller [13], geometric controller [14], output regulation controller [15], backstepping controller with the high-gain disturbance observer [16], adaptive robust controllers [17,18,19], and robust controller with the extended state observer [20, 21].

The aforementioned controllers used in EHAs only achieve the asymptotic convergence of the output responses. However, to the authors’ best knowledge, the finite-time stability [22] of EHAs has not be addressed yet. Recently, the finite-time stabilization control has been employed in manipulator motion control [23] and strict-feedback control plant [24]. Yu et al. [25] proposed a fast terminal sliding mode control (TSMC) for SISO nonlinear systems and adopted the TSMC in robotic manipulator to achieve faster and higher precision tracking performance [26]. Chen et al. [27] used the terminal sliding mode technique in both the controller design of SISO nonlinear system and the disturbance observer design. Sun et al. [28] investigated a finite-time adaptive stabilization strategy for a class of high-order uncertain nonlinear systems. Liu [29] proposed a finite-time \(H_{\infty }\) controller of uncertain robotic manipulator to improve the response and the performance of the output tracking. Then He et al. [30, 31] proposed an adaptive NN control to estimate the unknown modelling uncertainty and environmental disturbance. In addition, Shao et al. [32, 33] also adopted many advanced control methods in quadrotors UAV to handle parametric uncertainty and external disturbance. Therefore, for many motion plants with unknown uncertainties and disturbances, these finite-time convergence controllers can be used in the industrial practice to obtain the fast and high-precision performance.

Thanks to the research development of finite-time convergent control, the study is supplied valuable intention. The main contributions of the proposed approach are given by

  1. (i)

    A terminal sliding mode control is tried in the velocity feedback control of EHS to improve the fast and high-precision tracking performance. Different from [27], the hydraulic parametric uncertainties integrated with unknown external load are considered as the mismatched uncertain disturbance in the EHS model, which are extended by a disturbance observer with terminal sliding mode effect.

  2. (ii)

    The effectiveness of the proposed controller is verified by comparative simulation results with the other two controllers.

2 Plant description

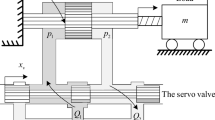
The EHA is a typical double-rod actuator, which is composed of a servo valve, a symmetrical cylinder, a fixed displacement pump with a servo motor and a relief valve as shown in Fig. 1. The pump is driven by the motor and outputs the supply pressure \(p_\mathrm{{s}}\). The pressure threshold of the relief valve is set as \(p_\mathrm{{s}}\). As the spool position of the servo valve \(x_\mathrm{{v}} > 0\), the hydraulic oil passes the servo valve and enters the left chamber. The forward channel flow \(Q_\mathrm{{L}}\) and the cylinder load pressure \(p_\mathrm{{L}}\) are controlled by \(x_\mathrm{{v}}\). The right chamber is connected to the return channel and the return pressure is \(p_\mathrm{{r}}\). On the other hand, the right chamber is connected to the forward channel where the load flow and pressure \(Q_\mathrm{{L}}\), \(p_\mathrm{{L}}\) are controlled by the servo valve when \(x_\mathrm{{v}} < 0\). The channel flow is cut off as \(x_\mathrm{{v}} = 0\) where the load pressure can be steadily maintained.

Fig. 1
figure 1

The control mechanism of double-rod EHA

Full size image

First, the servo model is given by [34]

$$\begin{aligned} x_\mathrm{{v}} = K_\mathrm{{sv}} u, \end{aligned}$$
(1)

where \(K_\mathrm{{sv}}\) and u are the gain and the control voltage of the servo valve, respectively.

Second, the load flow \(Q_\mathrm{{L}}\) is related to the cylinder load pressure \(p_\mathrm{{L}}\) as follows [35]:

$$\begin{aligned} Q_\mathrm{{L}} = C_\mathrm{{d}} wx_\mathrm{{v}} \sqrt{(p_\mathrm{{s}} - {\mathop \mathrm{sgn}} (x_\mathrm{{v}})p_\mathrm{{L}} )/\rho }, \end{aligned}$$
(2)

where \(C_\mathrm{{d}}\) is the discharge coefficient, w is the area gradient of the servo valve spool, \({\rho }\) is the density of the hydraulic oil.

According to the flow conservation law, the hydraulic pressure behavior for a compressible fluid volumes, i.e., the flow-pressure continuous model, is given by [9]

$$\begin{aligned} Q_\mathrm{{L}} = A_\mathrm{{p}} \dot{y} + C_\mathrm{{tl}} p_\mathrm{{L}} + V_\mathrm{{t}} \dot{p}_\mathrm{{L}} /4\beta _\mathrm{{e}}, \end{aligned}$$
(3)

where \(\dot{y}\) is the piston velocity, \(C_\mathrm{{tl}}\) is the coefficient of the total leakage of the cylinder, \(\beta _\mathrm{{e}}\) is the effective bulk modulus, \(A_\mathrm{{p}}\) is the annulus area of the cylinder chamber, \(V_\mathrm{{t}}\) is the half-volume of cylinder.

Then the mechanical dynamic equation can be described as [36]

$$\begin{aligned} m\ddot{y} = p_\mathrm{{L}} A_\mathrm{{p}} - b\dot{y} - F_\mathrm{{L}} (t), \end{aligned}$$
(4)

where m is the load mass, b is the viscous damping coefficient of the hydraulic oil, \(F_\mathrm{{L}}\) is the external load on the hydraulic actuator.

From (1) to (4), if we define \(X=[x_1, x_2]^\mathrm{{T}}=[\dot{y}, A_\mathrm{{p}} p_\mathrm{{L}}]^\mathrm{{T}}\), then the state space model of the electro-hydraulic velocity control system is given by

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} \begin{aligned} \dot{x}_1 &{} = \frac{1}{m}( - bx_1 + x_2 - F_\mathrm{{L}} ) \\ \dot{x}_2 &{} = - \frac{{4\beta _\mathrm{{e}} A_\mathrm{{p}}^2 }}{{V_\mathrm{{t}} }}x_1 - \frac{{4\beta _\mathrm{{e}} A_\mathrm{{p}} C_\mathrm{{tl}} }}{{V_\mathrm{{t}} }}x_2 \\ &{} \quad + \frac{{4\beta _\mathrm{{e}} C_\mathrm{{d}} wK_\mathrm{{sv}} A_\mathrm{{p}} }}{{V_\mathrm{{t}} \sqrt{\rho }}}\sqrt{p_\mathrm{{s}} - {\mathop \mathrm{sgn}} (u)x_2 /A_\mathrm{{p}} } u \\ \end{aligned} \end{array}} \right. . \end{aligned}$$
(5)

The external load disturbance \(F_\mathrm{{L}}(t)\) is unknown [37]. However, \(F_\mathrm{{L}}(t)\) is often assumed to be bounded in practice. The two states \(x_1\) and \(x_2\) can be measured by the pressure transducer and the encoder.

Generally, the hydraulic parameters \(C_\mathrm{{d}}\), \(\rho \), w, K, b, \(\beta _\mathrm{{e}}\), \(C_\mathrm{{tl}}\) are often perturbed by different hydraulic physical characteristics [8]. Hence, these parameters can be written as \(C_\mathrm{{d}} = \bar{C}_\mathrm{{d}} + \Delta C_\mathrm{{d}}\), \(\rho = \bar{\rho }+ \Delta \rho \), \(w = \bar{w} + \Delta w\), \(b = \bar{b} + \Delta b\), \(\beta _\mathrm{{e}} = \bar{\beta }_\mathrm{{e}} + \Delta \beta _\mathrm{{e}}\), \(C_\mathrm{{tl}} = \bar{C}_\mathrm{{tl}} + \Delta C_\mathrm{{tl}}\), where \(\bar{*}\) is the nominal value of \(*\), \(\Delta *\) is the parametric uncertainty.

Then, in view of parametric uncertainties, the model in (5) can be formulated as

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} \begin{aligned} \dot{x}_1 &{} = f_1 (x_1 ) + g_1 x_2 + d_{\mathrm{{L}}1} \\ \dot{x}_2 &{} = f_2 (x_1 ,x_2 ) + g_2 (x_2, u)u + d_{\mathrm{{L}}2} \\ \end{aligned} \end{array}} \right. , \end{aligned}$$
(6)

where

$$\begin{aligned} \begin{array}{l} \begin{aligned} &{}f_1 = - \frac{{\bar{b}x_1 }}{m}, \ \ g_1 = \frac{1 }{m}, \ d_{\mathrm{{L}}1} = \frac{- F_\mathrm{{L}} - \Delta b x_1}{m} \\ &{}f_2 = - \frac{{4\bar{\beta }_\mathrm{{e}} A_\mathrm{{p}}^2 }}{{V_\mathrm{{t}} }}x_1 - \frac{{4\bar{\beta }_\mathrm{{e}} A_\mathrm{{p}} \bar{C}_\mathrm{{tl}} }}{{V_\mathrm{{t}} }}x_2 \\ &{}g_2 = \frac{{4\bar{\beta }_\mathrm{{e}} \bar{C}_\mathrm{{d}} \bar{w}K_\mathrm{{sv}} A_\mathrm{{p}} }}{{V_\mathrm{{t}} \sqrt{\bar{\rho }} }}\sqrt{p_\mathrm{{s}} - {\mathop \mathrm{sgn}} (u)x_2 /A_\mathrm{{p}} } \\ &{}d_{\mathrm{{L}}2} = \Delta f_2 (x_1 ,x_2 ,\Delta \beta _\mathrm{{e}} ,\Delta C_\mathrm{{tl}}) \\ &{} \ \ \qquad + \Delta g_2 (x_1 ,x_2 ,\Delta C_\mathrm{{d}} ,\Delta w,\Delta \rho )\\ \end{aligned} \end{array}. \end{aligned}$$
(7)

Remark 1

The two lumped uncertain disturbances \(d_{\mathrm{{L}}1}\) and \(d_{\mathrm{{L}}2}\) are caused by parametric uncertainties and unknown external load.

Assumption 1

These two disturbances \(d_{\mathrm{{L}}i}(i=1,2)\) are bounded by \(\left| {d_{\mathrm{{L}}i} } \right| \le d_{\mathrm{{L}}i\max }\), where \(d_{\mathrm{{L}}i\max }\) is a known value for \(i=1,2\).

3 Terminal sliding mode control

3.1 Preliminaries

Lemma 1

[26, 38] If a positive definite Lyapunov function \(V(x,t) \ge 0\) yields that

$$\begin{aligned} \dot{V}(x,t) + \mu V(x,t) + \delta V^\alpha (x,t) \le 0,\forall t \ge t_0, \end{aligned}$$
(8)

then V(t) converges to the equilibrium point \(x_0\) in finite time \(t_f\) bounded by

$$\begin{aligned} t_f \le t_0 + \frac{1}{{\mu (1 + \alpha )}}\ln \frac{{\mu V^{1 - \alpha } (t_0 ) + \delta }}{\delta }, \end{aligned}$$
(9)

where \(\mu , \delta > 0\), \(0< \alpha < 1\) are positive constants, \(t_0\) is the initial time with respect to \(x_0\).

Definition 1

[25] For the low-triangle strict-feedback nonlinear system

$$\begin{aligned} \left\{ {\begin{array}{*{20}l} {\dot{x}_1 = f(x_1 ) + g_1 (x_1 )x_2 } \\ { \cdots \cdots } \\ {\dot{x}_i = f(\bar{x}_i ) + g_i (\bar{x}_i )x_{i + 1} } \\ { \cdots \cdots } \\ {\dot{x}_n = f(\bar{x}_n ) + g_n (\bar{x}_n )u} \\ \end{array}} \right. , \end{aligned}$$
(10)

where \(\bar{x}_i = [x_1 , \ldots ,x_i ]\), the terminal sliding mode surface has n orders form, which can be derived by the recursive procedure given by

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} \begin{aligned} s_1 &{} = x_1 - y_\mathrm{{d}} \\ s_2 &{} = \dot{s}_1 + \mu _1 s_1 + \delta _1 s_1^{p_1 /q_1 } \\ \vdots &{} \\ s_n &{} = \dot{s}_{n - 1} + \mu _{n - 1} s_{n - 1} + \delta _{n - 1} s_{n - 1}^{p_{n - 1} /q_{n - 1} } \\ \end{aligned} \end{array}} \right. , \end{aligned}$$
(11)

where \(s_i(i=1,\ldots ,n)\) are the n orders terminal sliding mode surfaces, \(p_i < q_i(i=1,\ldots ,n-1)\) are positive odd integers, \(y_\mathrm{{d}}\) is the desirable output.

3.2 TSM disturbance observer

The sliding mode surfaces of two lumped uncertain disturbances \(d_{\mathrm{{L}}i}(i=1,2)\) are designed as follows:

$$\begin{aligned} s_i = \nu _i - x_i , \quad i = 1,2, \end{aligned}$$
(12)

where \(\nu _i(i=1,2)\) are two disturbance observer variables.

To guarantee the finite time convergence to the disturbances, \(\nu _i(i=1,2)\) are designed to satisfy the following forms:

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} \begin{aligned} \dot{\nu }_1 &{}= - k_{\mathrm{{d}}1} s_1 - D_1 {\mathop \mathrm{sgn}} (s_1 ) - \varepsilon _1 s_1 ^{p_0 /q_0 } + f_1 + g_1 x_2 \\ \dot{\nu }_2 &{}= - k_{\mathrm{{d}}2} s_2 - D_2 {\mathop \mathrm{sgn}} (s_2 ) - \varepsilon _2 s_2 ^{p_1 /q_1 } + f_2 + g_2 u \\ \end{aligned} \end{array}} \right. , \end{aligned}$$
(13)

where \(k_{\mathrm{{d}}i}(i=1,2)\) are the observer gains, \(\varepsilon _i, D_i(i=1,2) > 0\) are positive constants, \(p_i<q_i(i=0,1)\) are positive odd integers.

Then the estimates of the two disturbances are written as

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} \begin{aligned} \hat{d}_{\mathrm{{L}}1} &{} = - k_{\mathrm{{d}}1} s_1 - D_1 {\mathop \mathrm{sgn}} (s_1 ) -\varepsilon _1 s_1 ^{p_0 /q_0 } \\ \hat{d}_{\mathrm{{L}}2} &{} = - k_{\mathrm{{d}}2} s_2 - D_2 {\mathop \mathrm{sgn}} (s_2 ) -\varepsilon _2 s_2 ^{p_1 /q_1 } \\ \end{aligned} \end{array}} \right. . \end{aligned}$$
(14)

Lemma 2

[27] Consider the disturbance observer (13) and the velocity control system (5) under Assumption 1. If the positive constants \(D_i > d_{\mathrm{{L}}i\max } (i=1,2)\), then disturbance observer is convergent in finite time.

Proof

To begin with, the following Lyapunov functions are considered:

$$\begin{aligned} V_i = \frac{1}{2}s_i^2, \quad i=1,2. \end{aligned}$$
(15)

Then the time derivative of \(V_i\) takes the form

$$\begin{aligned} \begin{array}{l} \begin{aligned} \dot{V}_i &{} = s_i \dot{s}_i = s_i (\dot{\nu }_i - \dot{x}_i ) \\ &{} = s_i ( - k_{\mathrm{{d}}i} s_i - D_i {\mathop \mathrm{sgn}} (s_i ) - \varepsilon _i s_i ^{p_{i-1} /q_{i-1} } + f_i \\ &{} \quad + g_i x_{i+1} - f_i - g_i x_{i+1} - d_{\mathrm{{L}}i} ) \\ &{} \le - k_{\mathrm{{d}}i} s_i ^2 - D_i s_i {\mathop \mathrm{sgn}} (s_i ) - \varepsilon _i s_i ^{p_{i-1} + q_{i-1} /q_{i-1} } \\ &{} \quad + \left| {s_i } \right| \left| {d_{\mathrm{{L}}i} } \right| \\ \end{aligned} \end{array}. \end{aligned}$$
(16)

Due to \(D_i > d_{\mathrm{{L}}i\max } (i=1,2)\), and by Assumption 1, (16) is rewritten as

$$\begin{aligned} \begin{array}{l} \begin{aligned} \dot{V}_i &{} \le - k_{\mathrm{{d}}i} s_i ^2 - D_i\left| {s_i } \right| - \varepsilon _i s_i ^{p_{i-1} + q_{i-1} /q_{i-1} } + \left| {s_i } \right| \left| {d_{\mathrm{{L}}i} } \right| \\ &{} \le - k_{\mathrm{{d}}i} s_i ^2 - \varepsilon _i s_i ^{p_{i-1} + q_{i-1} /q_{i-1} } \\ &{} \le - k_{\mathrm{{d}}i} V_i - 2^{(p_{i-1} + q_{i-1} )/2q_{i-1} } \varepsilon _i V_i^{(p_{i-1} + q_{i-1} )/2q_{i-1} } \\ \end{aligned} \end{array}, \end{aligned}$$
(17)

for \(i=1,2\). For the convenience of derivation, we assume the virtual variable \(x_3 = u\).

According to Lemma 1, two sliding mode surfaces \(s_i(i=1,2)\) converge to the origin in a finite time. Meanwhile, from (14), the observation errors take the form

$$\begin{aligned} \begin{array}{*{20}c} \begin{array}{l} \begin{aligned} \tilde{d}_{\mathrm{{L}}i} &{}= \hat{d}_{\mathrm{{L}}i} - d_{\mathrm{{L}}i} \\ &{}= - k_{\mathrm{{d}}i} s_i - D_i {\mathop \mathrm{sgn}} (s_i )- \varepsilon _i s_i ^{p_{i - 1} /q_{i - 1} } \\ &{} \quad + f_i + g_i x_{i + 1} - \dot{x}_i \\ &{}= \dot{\nu }_i - \dot{x}_i = \dot{s}_i \\ \end{aligned} \end{array} \\ \end{array}, \end{aligned}$$
(18)

for \(i=1,2\).

Since \(s_i(i=1,2)\) are finite-time stable at the origin, \(\dot{s}_i(i=1,2)\) approach zero in finite time. Hence, the two disturbance observer errors \(\tilde{d}_{\mathrm{{L}}i}(i=1,2)\) converges to zero in finite time.

3.3 Terminal sliding mode controller design

Assumption 2

[39] It is assumed that \(y_\mathrm{{d}}(t)\) and its ith order derivatives \(y_\mathrm{{d}}^{(i)}(t),i=1,2,3\) satisfy \(\left| {y_\mathrm{{d}} (t)} \right| \le Y_0 < k_{\mathrm{{c}}1}\) and \(\left| {y_\mathrm{{d}}^{(i)}(t)} \right| \le Y_i\), where \(Y_i(i=0,1,2,3)\) are positive constants.

To achieve the finite-time velocity control of the EHA, two sliding mode surfaces are designed as follows:

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} \begin{aligned} \xi _1 &{} = x_1 - \dot{y}_\mathrm{{d}} + s_1 \\ \xi _2 &{} = \dot{\xi }_1 + \mu _1 \xi _1 + \delta _1 \xi _1^{p_1 /q_1 } + g_1 s_2 - \frac{{\bar{b}}}{m}s_1 \\ \end{aligned} \end{array}} \right. . \end{aligned}$$
(19)

Substituting the time derivative of \(\xi _1\) into \(\xi _2\), we have

$$\begin{aligned} \begin{array}{l} \begin{aligned} \xi _2 &{}= \dot{x}_1 - \ddot{y}_\mathrm{{d}} + \dot{s}_1 + \mu _1 \xi _1 + \delta _1 \xi _1^{p_1 /q_1 } + g_1 s_2 - \frac{{\bar{b}}}{m}s_1 \\ &{}= f_1 + g_1 x_2 + d_{\mathrm{{L}}1} - \ddot{y}_\mathrm{{d}} + \tilde{d}_{\mathrm{{L}}1} \\ &{} \quad + \mu _1 \xi _1 + \delta _1 \xi _1^{p_1 /q_1 } + g_1 s_2 - \frac{{\bar{b}}}{m}s_1 \\ &{}= f_1 + g_1 x_2 + \hat{d}_\mathrm{{L}} - \ddot{y}_\mathrm{{d}} + \mu _1 \xi _1 \\ &{}\quad + \delta _1 \xi _1^{p_1 /q_1 } + g_1 s_2 - \frac{{\bar{b}}}{m}s_1 \\ \end{aligned} \end{array}. \end{aligned}$$
(20)

Then the time derivative of \(\xi _2\) takes the form

$$\begin{aligned} \begin{array}{l} \begin{aligned} \dot{\xi }_2 &{}= - \frac{{\bar{b}}}{m}(f_1 + g_1 x_2 + d_{\mathrm{{L}}1} ) + g_1 (f_2 + g_2 u + d_{\mathrm{{L}}2} ) \\ &{} \quad + \dot{\hat{d}}_{\mathrm{{L}}1} - \dddot{y}_\mathrm{{d}} + \mu _1 \dot{\xi }_1 + \delta _1 \frac{{\mathrm{{d}}(\xi _1^{p_1 /q_1 } )}}{{\mathrm{{d}}t}} + g_1 \dot{s}_2 - \frac{{\bar{b}}}{m}\dot{s}_1 \\ &{}= - \frac{{\bar{b}}}{m}(f_1 + g_1 x_2 + \hat{d}_{\mathrm{{L}}1} ) + g_1 (f_2 + g_2 u + \hat{d}_{\mathrm{{L}}2} ) \\ &{} \quad + \dot{\hat{d}}_{\mathrm{{L}}1}- \dddot{y}_\mathrm{{d}} + \mu _1 \dot{\xi }_1 + \delta _1 \frac{{\mathrm{{d}}(\xi _1^{p_1 /q_1 } )}}{{\mathrm{{d}}t}} \\ \end{aligned} \end{array}. \end{aligned}$$
(21)

Lemma 3

Consider the two sliding mode surfaces (19) and the velocity control system (5). Based on the disturbance observer (13), if the terminal sliding mode controller (TSMC) is designed by

$$\begin{aligned} \begin{array}{l} \begin{aligned} u &{} = - \frac{1}{{g_1 g_2 }}\Bigg [ - \frac{b}{m}(f_1 + g_1 x_2 + \hat{d}_{\mathrm{{L}}1} ) + g_1 (f_2 + \hat{d}_{\mathrm{{L}}2} ) \\ &{} \quad + \dot{\hat{d}}_{\mathrm{{L}}1} - \dddot{y}_\mathrm{{d}} + \mu _1 \dot{\xi }_1 + \delta _1 \frac{{\mathrm{{d}}(s_1^{p_1 /q_1 } )}}{{\mathrm{{d}}t}} + \mu _2 \xi _2 + \delta _2 \xi _2^{p_2 /q_2 } \Bigg ] \\ \end{aligned} \end{array}, \end{aligned}$$
(22)

then all closed-loop signals of the EHA are stable in the finite time \(t_f\) and the EHA velocity satisfies \(\left| x_1(t) - \dot{y}_\mathrm{{d}}(t) \right| \rightarrow 0, t \rightarrow t_f\) for any given velocity command \(y_\mathrm{{d}}\).

Proof

Consider the following candidate Lyapunov function

$$\begin{aligned} V_3 = \frac{1}{2}\xi _2^2. \end{aligned}$$
(23)

Substituting (21) into the time derivative of \(V_3\), we can obtain that

$$\begin{aligned} \begin{array}{l} \begin{aligned} \dot{V}_3 &{}= \xi _2 \Bigg [ - \frac{{\bar{b}}}{m}(f_1 + g_1 x_2 + \hat{d}_{\mathrm{{L}}1} ) + g_1 (f_2 + g_2 u + \hat{d}_{\mathrm{{L}}2} ) \\ &{} \quad + \dot{\hat{d}}_{\mathrm{{L}}1}- \dddot{y}_\mathrm{{d}} + \mu _1 \dot{\xi }_1 + \delta _1 \frac{{\mathrm{{d}}(\xi _1^{p_1 /q_1 } )}}{{\mathrm{{d}}t}}\Bigg ] \\ \end{aligned} \end{array}. \end{aligned}$$
(24)

Then consider the controller u in (22), and we have

$$\begin{aligned} \begin{array}{l} \begin{aligned} \dot{V}_3 &{} \le - \mu _2 \xi _2^2 - \delta _2 \xi _2^{p_2 + q_2 /q_2 } \\ &{} \le - 2\mu _2 V_3 - 2^{(p_2 + q_2 )/2q_2 } \delta _2 V_3^{(p_2 + q_2 )/2q_2 } \\ \end{aligned} \end{array}. \end{aligned}$$
(25)

According to Lemma 1, the sliding mode variable \(\xi _2\) is finite-time stable. Furthermore, from (19), \(\xi _2\) a function of \(\xi _1\), \(s_1\) and \(s_2\). Since the two observer sliding mode variables \(s_i(i=1,2)\) converge to zero in a finite time by Lemma 2, \(\xi _1\) is also convergent in a finite time. Due to \(\dot{y}_\mathrm{{d}}\) is bound by Assumption 2 and \(s_1 \rightarrow 0, t \rightarrow t_\mathrm{{f}}\), \(x_1\) is also bounded from \(\xi _1\). Hence, \(\nu _1\) is bounded from the definition of \(s_1\) in (12). Then \(\dot{\nu }_1\) is bounded which, in turn, derives \(x_2\) converge to zero in finite-time using (13). By (19), since \(\xi _2 \rightarrow 0, t \rightarrow t_\mathrm{{f}}\), \(\xi _1 \rightarrow 0\) and \(\left| x_1(t) - \dot{y}_\mathrm{{d}}(t) \right| \rightarrow 0\) as \(t \rightarrow t_\mathrm{{f}}\).

The block diagram of the terminal sliding mode control scheme is shown in this Fig. 2. The whole closed-loop system includes two sliding mode surfaces \(s_i, \xi _i(i=1,2)\) for the disturbance observe \(\hat{d}_{\mathrm{{L}}i} (i=1,2)\) and the TSMC u. According to the TSM stable condition (8), u is designed to guarantee the EHA (1) is finite-time stable. The block diagram of the terminal sliding mode control scheme

Fig. 2
figure 2

The block diagram of the terminal sliding mode control scheme

Full size image
Fig. 3
figure 3

The cylinder velocity response of three controllers in simulation for the demand \(\dot{y}_\mathrm{{d}} = 30 \sin (0.5\pi t)\) mm/s

Full size image
Fig. 4
figure 4

The tracking errors of the cylinder velocity in simulation for the demand \(\dot{y}_\mathrm{{d}} = 30 \sin (0.5\pi t)\) mm/s

Full size image

4 Simulation results

To verify the TSMC, some nominal hydraulic parameters of the EHA are given by \(\bar{C}_\mathrm{{d}}\) = 0.62, \(\Delta C_\mathrm{{d}} = 0.1 \bar{C}_\mathrm{{d}}\), \(\bar{w}\) = 0.024 m, \(\Delta w = 0.1 \bar{w}\), \(\bar{C}_\mathrm{{tl}}\) = \(2.5\times 10^{-11}\, \mathrm{m}^3/(\mathrm{{s}}\, \mathrm{{Pa}})\), \(\Delta C_\mathrm{{tl}} = 0.3\bar{C}_\mathrm{{tl}}\), \(\bar{\beta }_\mathrm{{e}} = 7000\) bar, \(\Delta \beta _\mathrm{{e}} = 0.1 \bar{\beta }_\mathrm{{e}}\), \(\bar{\rho }= 850\) kg/\(\mathrm{m}^3\), \(\Delta \rho = 0.15 \bar{\rho }\), \(\bar{b}\) = 50 Ns/m, \(\Delta b = 0.2 \bar{b}\), \(K_\mathrm{{sv}}\) = \(5\times 10^{-4}\) m/V, \(T_\mathrm{{sv}}\) = 10 ms, \(x_\mathrm{{v max}}\) = 5 mm, \(L_\mathrm{max}\) = 78 mm, \(p_\mathrm{{s}}\) = 40 bar, \(p_\mathrm{{r}}\) = 2 bar, \(A_\mathrm{{p}}\) = 4.91 \(\mathrm{cm}^2\), \(V_\mathrm{{t}}\) = \(8.74\times 10^{-5}\, \mathrm{m}^3\). The manipulator load mass is \(m = 6\) kg. The disturbance observer parameters are \(k_{\mathrm{{d}}1}=k_{\mathrm{{d}}2}=1000\), \(D_1=30\), \(D_2 = 100\), \(\varepsilon _1 = 100\), \(\varepsilon _2 = 10\), \(p_0 = p_1 = 5\), \(q_0 = q_1 = 7\). The TSM controller parameters \(\mu _1 = 10^4\), \(\mu _2 = 100\), \(\delta _1 = \delta _2 = 1\), \(p_2 = 5\), \(q_2 = 9\) are set. The cylinder velocity demands are chosen as \(\dot{y}_\mathrm{{d}} = 30 \sin (0.5\pi t)\) mm/s and \(\dot{y}_\mathrm{{d}}\) = square(\(\pm 30\)) mm/s, respectively. The corresponding external load of the EHA is assumed to be \(F_\mathrm{{L}}(t) = 100 \sin (0.5\pi t)\) N and \(F_\mathrm{{L}}(t) = 100\) N. To make a comparison, the other two controllers are also applied for the EHA:

Fig. 5
figure 5

The cylinder velocity response of three controllers in simulation for the demand \(\dot{y}_\mathrm{{d}} = \text {square} ~(\pm 30)\) mm/s

Full size image
Fig. 6
figure 6

The tracking errors of the cylinder velocity in simulation for the demand \(\dot{y}_\mathrm{{d}} = \text {square} ~(\pm 30)\) mm/s

Full size image
Fig. 7
figure 7

The two disturbance estimations by the TSM controller in simulation for the demand \(\dot{y}_\mathrm{{d}} = 30 \sin (0.5\pi t)\) mm/s

Full size image
Fig. 8
figure 8

The two disturbance estimations by the TSM controller in simulation for the demand \(\dot{y}_\mathrm{{d}} = \text {square} ~(\pm 30)\) mm/s

Full size image
Fig. 9
figure 9

The two sliding mode surfaces and the TSM controller output in simulation for the demand \(\dot{y}_\mathrm{{d}} = 30 \sin (0.5\pi t)\) mm/s

Full size image
Fig. 10
figure 10

The two sliding mode surfaces and the TSM controller output in simulation for the demand \(\dot{y}_\mathrm{{d}} = \text {square} ~(\pm 30)\) mm/s

Full size image
  1. 1)

    PI controller \(u = k_p (\dot{y}_\mathrm{{d}} - x_1 ) + k_i \int {(\dot{y}_\mathrm{{d}} - x_1 )\mathrm{{d}}t}\), where the control gains \(k_\mathrm{{p}}\) = 100 and \(k_i\) = 10 are chosen to guarantee the fast response of EHA.

  2. 2)

    the traditional backstepping controller (TBC), given by

    $$\begin{aligned} \left\{ {\begin{array}{*{20}c} \begin{aligned} \zeta _1 &{} = (- k_1 z_1 -f_1 + \ddot{y}_\mathrm{{d}})/g_1 \\ u &{} = ( - k_2 z_2 - f_2 - g_1 z_1+ \dot{\zeta }_1 )/g_2 \\ \end{aligned} \end{array}} \right. , \end{aligned}$$
    (26)

where \(z_1 = x_1 - \dot{y}_\mathrm{{d}}\) and \(z_2 = x_2 - \zeta _1\), \(\zeta _1\) is the virtual control variable, \(f_1 = \bar{b} x_1/m\), \(g_1 = 1/m\), \(f_2 = - 4\bar{\beta }_\mathrm{{e}} A_\mathrm{{p}}^2 x_1/ V_\mathrm{{t}} - 4\bar{\beta }_\mathrm{{e}} \bar{C}_\mathrm{{tl}} A_\mathrm{{p}} x_2/ V_\mathrm{{t}}\), \(g_2 = 4\bar{\beta }_\mathrm{{e}} \bar{C}_\mathrm{{d}} \bar{w} K_\mathrm{{sv}} A_\mathrm{{p}} \sqrt{p_\mathrm{{s}} - \text {sgn} (\eta u)x_2 /A_\mathrm{{p}} } / (V_\mathrm{{t}} \sqrt{\bar{\rho }})\), \(k_1 = 2000\), \(k_2 = 1000\).

The simulation results under the two types of demands are shown in Figs. 3, 4, 5, 6, 7, 8, 9 and 10. All the three controllers guarantee that the cylinder velocity can track the two types of demands with performance. However, the tracking performance subject to the TSMC is better than the PI and backstepping controllers in both scenarios, as shown in Figs. 4 and 6. Meanwhile, the disturbance estimates generated by the proposed observer are shown in Figs. 7 and 8, which are employed in the TSM controller (22). By a further inspection, these disturbance estimates are consistent with the dynamics of the external load \(F_\mathrm{{L}}\) and the model functions \(f_2\), \(g_2\). The two sliding mode surfaces and the corresponding TSM controller output of two demands are shown in Figs. 9 and 10, which guarantee the electrohydraulic system stable by the proposed TSM controller.

5 Conclusions

In this study, a terminal sliding mode control (TSMC) strategy is used in the electro-hydraulic actuator under lumped uncertain disturbance. Based on the strict-feedback nonlinear model of the electro-hydraulic velocity control loop, the proposed controller is designed based on the sliding mode control and the. By proposing a new disturbance TSM observer, the lumped uncertain disturbances are estimated and compensated in the TSMC design. The simulation results with comparisons demonstrate that the proposed control strategy achieves faster responses and better tracking performance. In the future work, the experimental bench of the manipulator driving by EHA will verify the proposed control scheme.