Robust output feedback control of electro-hydraulic system

Abstract

This paper presents output feedback second order sliding mode control to achieve robust finite time position control for Electro-Hydraulic Servo System (EHSS). The system is subjected to inherent uncertainties, parametric perturbations and disturbances. A nonlinear dynamics of EHSS is represented by linear uncertain dynamics for the sake of control design. A relative degree one sliding surface is proposed. It is shown that super twisting controller using this relative degree one sliding surface attains finite time positioning. Further disturbance estimation is used to augment the control for getting desired performance with less control effort. The method is validated in simulation and experiment both. The performance of the proposed controller is compared with the super twisting controller devised using non singular terminal sliding surface which also yields finite time positioning.

1 Introduction

Electro-Hydraulic Servo System (EHSS) is well known for high torque to weight ratio and faster response. These features resulted in its use in many applications such as manufacturing systems, suspension systems, mining machinery, robotics, automotive industries and many more. In EHSS electrical signal plays an important role to accomplish flexible and accurate hydraulic actuation. Various methods of modeling have been examined by many researchers see for example [1,2,3,4] and the references therein.

Various control strategies have been reported in the literature for position control of EHSS. Proportional Integral Derivative (PID) controller is the classical controller and is widely used [5]. It has advantages such as simplicity, good stability, high reliability etc. However, tuning of PID gains and robustness of controller are the issues. Therefore, the conventional PID controller often cannot ensure the desired performance. Many methods have been proposed for improving PID controller. Still disturbance rejection and plant uncertainties tolerance beg a question.

For position control of EHSS neural network [6], fuzzy logic [7], feedforward [8] and Lyapunov [9] based control algorithms have been designed and implemented. Advanced control methods such as QFT [10], $H_{\infty }$ [11] have been examined for EHSS. However, controller order becomes large and tuning of controller parameter becomes cumbersome. Adaptive control yields robust performance but needs exact knowledge of uncertainties and nonlinearities. Some authors combined adaptive control schemes with other techniques which include feedback linearization [12], backstepping [13], model reference adaptive control (MRAC) [14]. However, these control methods require linear parameterizations of the unknown parameters and exact knowledge of the nonlinear functions. Sliding mode control (SMC) is one of the robust control techniques reported in [15,16,17,18,19]. Although SMC gives robust performance against matched uncertainties and disturbances, chattering is the issue which is addressed using Higher Order Sliding Modes (HOSM) [20, 21]. For the EHS system, the proposed HOSM control is complimented with disturbance observer (DO) for an efficient control design. DO is mathematically an inversion of system dynamics and is one of the simplest disturbance estimator designed to estimate disturbance and accommodating control strategy proposed by Johnson [22]. The origin of DO can be traced to [23] by Ohishi, in which estimation using disturbance decoupling has been proposed. A similar basic DO is proposed for EHS system, in this paper.

1.1 Motivation

Research on the modeling and control of electro-hydraulic systems has received sustained attention due to their several advantages. Need to provide desired performance in the presence of nonlinearities in the valve, spool, pressure dynamics of EHSS has been motivation for investigation of a robust control method. Often model approximation is used to simplify control design. However, it leads to performance degradation. It is required to design a control which takes care of wide varieties of uncertainties. SMC is robust. However, it suffers a drawback of chattering. Higher Order Sliding Mode Control (HOSMC) has evolved to yield robust performance and smooth control. This has been motivated us to examine HOSM controller.

The Super-Twisting Algorithm (STA) is one of the best Second Order Sliding Mode Control (SOSMC) algorithms [24]. Some of the researchers have examined SOSMC for EHSS [25, 26]. However, while developing mathematical modeling the authors have not considered the solenoid coil nonlinearities which has been considered in the present work. The preliminary version of this work has been presented in [27]. In this paper, experimental results are presented. Also, disturbance estimation is considered to augment HOSM control. The approach to combat any kind of disturbance is to use a large gain for the designed control. This leads to conservative control and also amplifies the inherent disadvantage of chattering due to discontinuity in control. Use of disturbance estimation results in reducing amplitudes of discontinuous component of control, leading to the less conservative control. With this motivation, the designed STA controller is complemented with a simple DO.

To the best of our knowledge, this has been done for the first time for EHSS. The main contributions of the paper are as below:

• Detailed modeling of EHSS.

• Output feedback STA controller using relative degree one surface.

• Detailed stability proof.

• Control implementation using disturbance estimation in simulation and experimentation both.

1.2 Structure of paper

The rest of the paper is organized as follows. The mathematical modeling of the Electro-Hydraulic Servo System is elaborated in Sect. 2. Section 3 describes model validation. The control development and disturbance estimation is presented in Sect. 4. Detailed stability proof is presented in Sect. 5. The simulation results are shown in Sect. 6. Experimental set up is described in Sect. 7. Experimental results are presented in Sect. 8. Section 9 concludes the work.

2 Mathematical modeling of electro-hydraulic servo system

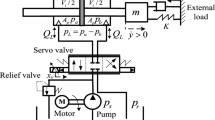
A typical EHSS comprises of hydraulic fluid tank, hydraulic pump, pressure relief valve, hydraulic valve, hydraulic double actuating cylinder with single rod, load connected to hydraulic cylinder and controller. Schematic of EHSS is shown in Fig. 1.

Fig. 1

Schematic of a typical EHSS

When solenoid coil of the hydraulic valve is energized, current sets up in the coil establishes a flux. The magnetic field sets up around the coil results in an electromagnetic force ($F_{mag}$) on the spool of the valve. This $F_{mag}$ causes spool displacement which in turn opens orifice. This results in pressurized fluid flow from the reservoir to the pressure ports through the proportional valve. Fluid flow in hydraulic cylinder builds up pressure on the piston. That pressure head drives the piston and subsequently the load attached to it. The load displacement is controlled by controlling voltage applied to the solenoid coil.

In [27], the mathematical model developed by Shailaja et al. [28, 29] has been modified to reduce the complexity and to solve singularity issue. The model reported in [27] has been revisited here. Total EHSS dynamics include Solenoid Valve Dynamics, Spool Dynamics, Pressure Dynamics and Load Dynamics.

2.1 Assumptions in modeling

Following assumptions are considered while developing the model.

• Return line pressure is neglected.

• Orifices are matched and symmetrical.

• Fluid flow is incompressible and laminar.

• Frictional force between the cylinder wall and the piston is neglected. This is due to the fact that frictional forces acting on piston are very small in magnitude as compared to load forces on cylinder.

• Leakage flow of fluid in the cylinder and the valve is neglected. Decrease in the flow rate due to these leakages are very less hence those leakages can be overlooked.

2.2 Solenoid valve dynamics

The electro-hydraulic valve comprises of the solenoid coil and spool-plunger arrangement as shown in Fig. 2. The energized solenoid coil creates a $F_{mag}$ on the plunger. When plunger moves, reluctance offered to flux varies and hence inductance varies as a function of spool displacement [2].

Fig. 2

Flux established in the solenoid coil

Looking at the geometry as shown in Fig. 2, length of air gap hence reluctance offered by it changes as spool gets displaced. Thus the total reluctance offered by an air gap and the ferromagnetic plunger is,

$$\begin{aligned} R_l = \frac{l_a-x_s}{{{\mu }_0}{A_p}} + \frac{l_p}{{{\mu }_0}{{\mu }_r}{A_p}}=\frac{-\,x_s}{{{\mu }_0}{A_p}} + \frac{l_a{\mu }_r+l_p}{{{\mu }_0}{{\mu }_r}{A_p}}, \end{aligned}$$

(1)

which can be written as,

$$\begin{aligned} R_l = R_2-R_1x_s. \end{aligned}$$

(2)

where $R_1 = \frac{1}{{{\mu }_0}{A_p}}$ and $R_2 = \frac{l_a{\mu }_r+l_p}{{{\mu }_0}{{\mu }_r}{A_p}}$.

Since $R_l$ is the function of $x_s$, inductance is also function of $x_s$ and is given by [2],

$$\begin{aligned} L_{x_s} =\frac{N^2}{R_l}=\frac{N^2}{R_2-R_1x_s}. \end{aligned}$$

(3)

Therefore,

$$\begin{aligned} \frac{dL_{x_s}}{dx_s} = \frac{{R_1}{N^2}}{({R_2-R_1x_s})^2} . \end{aligned}$$

(4)

Kirchhoff’s Voltage Law is applied to coil having above inductance and resistance R, with v as applied voltage,

$$\begin{aligned} v = iR + L_{x_s}\frac{di}{dt} + i\frac{dL_{x_s}}{dx_s}\frac{dx_s}{dt}, \end{aligned}$$

(5)

substituting $L_{x_s}$ and $\frac{dL_{x_s}}{dx_s}$ from Eqs. (3) and (4) in above equation,

$$\begin{aligned} v = iR + \frac{N^2}{({R_2}{-R_1}{x_s})}\frac{di}{dt}+ i\frac{{R_1}N^2}{({R_2}{-R_1}{x_s})^2}\frac{dx_s}{dt}. \end{aligned}$$

(6)

Rearranging above equation to get,

$$\begin{aligned} \frac{di}{dt} = {\frac{({R_2}{-R_1}{x_s})}{N^2}\left[ v-iR- i\frac{{R_1}N^2}{({R_2}{-R_1}{x_s})^2}\frac{dx_s}{dt}\right] }. \end{aligned}$$

(7)

Using Eq. (2), the dynamic equation becomes,

$$\begin{aligned} \frac{di}{dt} = {\frac{R_l}{N^2}\left[ v-iR- i\frac{{R_1}N^2}{{R_l}^2}\frac{dx_s}{dt}\right] }. \end{aligned}$$

(8)

2.3 Spool dynamics

Excited coil produces $F_{mag}$ on the spool-plunger assembly. This force is given by,

$$\begin{aligned} {F_{mag}}=\frac{{{i^2}{N^2}{R_1}}}{{2{({R_2}{-R_1}{x_s})^2}}}. \end{aligned}$$

(9)

Using Eq. (2), the above equation becomes,

$$\begin{aligned} {F_{mag}}=\frac{{{i^2}{N^2}{R_1}}}{2{R_l}^2}. \end{aligned}$$

(10)

This ${F_{mag}}$ displaces the spool to initiate orifice opening. This motion is opposed by flow forces. The spool motion is given by,

$$\begin{aligned} {F_{mag}}= m_s\frac{{d^2x_s}}{{dt}^2} + b\frac{{dx_s}}{{dt}} + k{x_s} + F_{flow}, \end{aligned}$$

(11)

where $F_{flow}$ are flow forces which are negligible and hence neglected in dynamics.

From Eqs. (10) and (11) spool dynamics is,

$$\begin{aligned} \frac{d^2{x_s}}{{dt}^2}= \frac{{{i^2}{N^2}{R_1}}}{{2(R_l)^2}{m_s}}-\frac{b}{m_s}{\frac{d{x_s}}{dt}}- \frac{k}{m_s}{x_s}. \end{aligned}$$

(12)

2.4 Pressure dynamics

When orifice opening is initiated, pressurized fluid flows from reservoir to hydraulic cylinder as shown in Fig. 3. This results in variation of volume in the hydraulic cylinder which further results in change in pressure.

Fig. 3

Pressure and flow dynamics in EHSS

Due to pressurized fluid flow through pressure port A, differential pressure is established in the cylinder. This exerts a force on the piston. During this process volume, flow rate and pressure in chamber 1 and 2 of the hydraulic cylinder varies.

Flow rates in the cylinder that vary due to variations in $x_s$ are,

$$\begin{aligned} {q_1}= {c_d}{\omega }{x_s}\sqrt{\left( {\frac{{{p_s} - {p_1}}}{\rho }} \right) } \hbox { and} ~~{q_2}={c_d}{\omega }{x_s}\sqrt{\left( {\frac{{p_2}}{\rho }}\right) }. \end{aligned}$$

The pressure dynamics in chamber 1 and 2 are,

$$\begin{aligned} {\dot{p}}_1= & {} \frac{\beta }{{v_1}+{v_{p_1}}}\left( {{q_1}-{A_a}\frac{d{x_l}}{dt}} \right) , \end{aligned}$$

(13)

$$\begin{aligned} {\dot{p}}_2= & {} \frac{\beta }{{v_2}+{v_{p_2}}}\left( {-{q_2}+{A_b}\frac{d{x_l}}{dt}} \right) , \end{aligned}$$

(14)

where ${v_1}= {v_i} + {A_a}{x_l}$  and  ${v_2}= {v_f} - {A_b}{x_l}.$

Since the cylinder used is asymmetrical double acting cylinder, the differential pressure is,

$$\begin{aligned} \varDelta p = p_1-np_2. \end{aligned}$$

(15)

where $n=\frac{A_b}{A_a}$

$$\begin{aligned} \frac{d\varDelta p}{dt}= {\dot{p}}_1-n{\dot{p}}_2. \end{aligned}$$

(16)

Substituting for ${\dot{p}}_1$ and ${\dot{p}}_2$ from Eqs. (13) and (14),

$$\begin{aligned} \frac{d\varDelta p}{dt}&= \frac{{\beta }{c_d}{\omega }{x_s}}{\sqrt{\rho }}\left[ {\frac{\sqrt{{p_s} - {p_1}}}{{v_1}+{v_{p_1}}}}-{\frac{n\sqrt{{p_2}}}{{v_2}+{v_{p_2}}}}\right] \nonumber \\&-\,{\beta \frac{d{x_l}}{dt}\left[ {\frac{A_a}{{v_1}+{v_{p_1}}}}- {\frac{n A_b}{{v_2}+{v_{p_2}}}}\right] }. \end{aligned}$$

(17)

2.5 Load dynamics

The force exerting on load $m_{l}$ is,

$$\begin{aligned} F_g = {A_a}{p_1}-{A_b}{p_2}. \end{aligned}$$

(18)

This force causes the load motion, the governing dynamic equation is,

$$\begin{aligned} F_g = {m_l}\frac{d^2{x_l}}{{dt}^2} + {b_l}\frac{d{x_l}}{dt}, \end{aligned}$$

(19)

where $b_l$ is coefficient of friction.

From Eqs. (18) and (19) load dynamics is given by,

$$\begin{aligned} \frac{d^2x_l}{dt^2} = \frac{A_a(p_1-np_2)}{m_l}-\frac{b_l}{m_l}{\frac{d{x_l}}{dt}} \end{aligned}$$

(20)

This can be written as,

$$\begin{aligned} \frac{d^2 x_l}{dt^2} = \frac{A_a}{m_l}\varDelta p-\frac{b_l}{m_l}\frac{d{x_l}}{dt}. \end{aligned}$$

(21)

It may be noted that, if applied voltage becomes zero, due to spring action, $x_s$ becomes zero. As soon as $x_s=0$, ports A, B, P and T in spool plunger assembly shown in Fig. 1 are remain intact. Hence $\varDelta P$ remain constant even if control voltage is removed. Therefore, load will not sink and its position will be maintained.

Defining $i ={x_1}$, ${x_s} = {x_2}$, ${{\dot{x}}}_s = {x_3}$, $\varDelta p = {x_4}$, ${x_l} = {x_5}$, ${{\dot{x}}}_l = {x_6}$, and $v = u$. From Eqs. (8), (12), (17) and (21) the complete plant dynamics in state space can be represented as,

$$\begin{aligned} {{\dot{x}}}_{1}&= {\frac{R_l}{N^2}\left[ u-x_1R- x_1\frac{{R_1}N^2}{{R_l}^2}x_3\right] } \end{aligned}$$

(22a)

$$\begin{aligned} {{\dot{x}}}_{2}&= x_{3} \end{aligned}$$

(22b)

$$\begin{aligned} {{\dot{x}}}_{3}&= \frac{{{x_1^2}{N^2}{R_1}}}{{2{{R_l}^2}}{m_s}}-\frac{b}{m_s}x_3- \frac{k}{m_s}{x_2} \end{aligned}$$

(22c)

$$\begin{aligned} {{\dot{x}}}_{4}&= \frac{{\beta }{c_d}{\omega }{x_2}}{\sqrt{\rho }}\left[ {\frac{\sqrt{{p_s} - {p_1}}}{{v_1}+{v_{p_1}}}}- {\frac{n\sqrt{{p_2}}}{{v_2}+{v_{p_2}}}}\right] \nonumber \\&\quad - {\beta x_6\left[ {\frac{A_a}{{v_1}+{v_{p_1}}}}- {\frac{n A_b}{{v_2}+{v_{p_2}}}}\right] } \end{aligned}$$

(22d)

$$\begin{aligned} {{\dot{x}}}_{5}&=x_{6} \end{aligned}$$

(22e)

$$\begin{aligned} {{\dot{x}}}_{6}&= \frac{A_a}{m_l} x_4-\frac{b_l}{m_l}x_6 \end{aligned}$$

(22f)

Remark I

This model is generalized model for 1 DoF EHSS. It does not consider state and control constraints. The physical parameters and constants of the system are given in Table 1.

Table 1 Physical parameters and constants of system

3 Model validation

The mathematical model developed in Eq. (22) has been validated. The proposed model was simulated in Matlab. The system model was excited by the step input of amplitude 5 V. The actual plant was also excited by same input of 5 V. Figure 4 shows the response of the model and actual system for the step input. To validate the model simulated performance is compared with the experimental performance by exciting the actual system using the same step command. It is observed that system excitation delay of the order of 0.7751 s. is negligible compared to system time constant i.e. 5.985 s. and desired settling time. Hence it is neglected while designing the controller. Further pulse input of amplitude 5 V and time period 10 and pulse width 20% of the time period was considered as an input. Figure 5 shows the response of the model and actual plant to pulse input. It can be seen that the proposed model fairly captures system dynamics.

Fig. 4

Response of system to step input

Fig. 5

Response of system to pulse input

Remark II

Model in Eq. (22) is detailed and general. Consideration of constraints due to geometry and design constraints, this model can be simplified as explained subsequently.

It may be noted that due to geometry of valve when plunger movement is initiated the spool can move a maximum distance of $\pm ~2.5$ mm. Hence spool position $x_2 \in [-~2.5 \times {10^{-3}}$, $+~2.5 \times {10^{-3}}]$. Therefore $R_l$ which is $(R_2-R_1x_s)$ lies in [7124.41, 7159.59]. Using this information and system parameters and constants given in Table 1 we get,

$$\begin{aligned}&\frac{R_l}{N^2}\equiv a_1 \in [7.124, 7.159]\times 10^{-3},\\&R\left[ {\frac{R_l}{N^2}}\right] \equiv a_2 \in [22.79, 22.91]\times 10^{-3},\\&\frac{R_1}{R_l}\equiv a_3 \in [0.9828, 0.9876],\\&\frac{{{N^2}{R_1}}}{{2{{R_l}^2}}{m_s}} \equiv a_4 \in [137.268, 138.628],\\&\frac{b}{m_s}\equiv a_5 = 200,\\&\frac{k}{m_s}\equiv a_6= 2400. \end{aligned}$$

Similarly pressures $p_1$ and $p_2$ can vary from 0 to $p_s$ due to variation in $x_s$. Therefore

$$\begin{aligned}&\frac{{\beta }{c_d}{\omega }}{\sqrt{\rho }}\left[ {\frac{\sqrt{{p_s}- {p_1}}}{{v_1}+{v_{p_1}}}}- {\frac{n\sqrt{{p_2}}}{{v_2}+{v_{p_2}}}}\right] \equiv a_7 \in [315.55, 0]\times 10^{7},\\&\beta \left[ {\frac{A_a}{{v_1}+{v_{p_1}}}}-{\frac{n A_b}{{v_2}+{v_{p_2}}}}\right] \equiv a_8\in 1.64\times 10^{6}[2.9,1.4]. \end{aligned}$$

Other constants are

$$\begin{aligned} \frac{A_a}{m_l}\equiv & {} a_9 = 0.0001256,\\ \frac{b_l}{m_l}\equiv & {} a_{10} = 40. \end{aligned}$$

Therefore Eq. (22) is represented as interval system with $a_1$ to $a_4$, $a_7$ and $a_8$ being parameters lying in certain interval. Further $a_5$, $a_6$, $a_9$ and $a_{10}$ are constants. The dynamics is

$$\begin{aligned} {{\dot{x}}}_{1}&= a_1 u- a_2x_1 - a_3x_1x_3 \end{aligned}$$

(23a)

$$\begin{aligned} {{\dot{x}}}_{2}&= x_3 \end{aligned}$$

(23b)

$$\begin{aligned} {{\dot{x}}}_{3}&= a_4{x_1}^2-a_5 x_3- a_{6}{x_2} \end{aligned}$$

(23c)

$$\begin{aligned} {{\dot{x}}}_{4}&= a_7{x_2}-a_8 x_6 \end{aligned}$$

(23d)

$$\begin{aligned} {{\dot{x}}}_{5}&=x_6 \end{aligned}$$

(23e)

$$\begin{aligned} {{\dot{x}}}_{6}&= a_9 x_4- a_{10} x_6 \end{aligned}$$

(23f)

The sixth order model in Eq. (23) is nonlinear and uncertain.

Remark III

Control design for this uncertain system is hard. Control becomes complex and unimplementable if such model is considered for control design. Moreover all the states are not measurable. This creates problem in implementing modern control which needs information of all the states.

The model in Eq. (23) is further simplified as described below:

Substituting $x_6$ from Eq. (23d) in Eq. (23f),

$$\begin{aligned} \dot{x_6}= a_9 x_4-a_{10}\left[ \left( \frac{a_7}{a_8}\right) {x_2}-\left( \frac{1}{a_8}\right) {{\dot{x}}}_4\right] . \end{aligned}$$

(24)

From Eq. (23c), $x_2$ is represented as,

$$\begin{aligned} x_2= -\frac{1}{a_6}\left( -a_4{x_1}^2+a_5x_3+{\dot{x_3}}\right) . \end{aligned}$$

Now substituting $x_2$ in Eq. (24),

$$\begin{aligned} \dot{x_6} = a_9 x_4 +\left( \frac{{a_{10}}{a_7}}{{a_8}{a_6}}\right) \left( -a_4 {x_1}^2+a_5x_3+{{\dot{x}}}_3\right) + \left( \frac{a_{10}}{a_8}\right) {{\dot{x}}}_4. \end{aligned}$$

(25)

Multiplying Eq. (23a) by $x_1$, and rearranging to get,

$$\begin{aligned} {x_1}^2= -\left( \frac{1}{a_2}\right) x_1 {{\dot{x}}}_1 -\left( \frac{a_3}{a_2}\right) {x_1}^2 x_3+\left( \frac{a_1}{a_2}\right) ux_1. \end{aligned}$$

Defining $\frac{a_{10}{a_7}}{{a_8}{a_6}}=a_{12}$, $\frac{a_{10}}{a_8}=a_{13}$ and substituting $x_1^2$ in Eq. (25) we get,

$$\begin{aligned} \dot{x_6}= & {} a_9 x_4+ a_{12}\left[ -a_4\left( -\frac{1}{a_2}x_1 {{\dot{x}}}_1 -\frac{a_3}{a_2}{x_1}^2 x_3+\frac{a_1}{a_2}ux_1\right) \right] \nonumber \\&+\,a_{12}a_5x_3+a_{12}{{\dot{x}}}_3+ a_{13}{{\dot{x}}}_4. \end{aligned}$$

(26)

Substituting ${{\dot{x}}}_3$ from Eq. (23c) and ${{\dot{x}}}_4$ from Eq. (23d) in Eq. (26) to get,

$$\begin{aligned} \dot{x_6}= & {} a_9 x_4-a_{12}a_4\left( -\frac{1}{a_2}x_1{{\dot{x}}}_1 -\frac{a_3}{a_2}{x_1}^2 x_3+\frac{a_1}{a_2}u x_1\right) \nonumber \\&+\,a_{12}a_5x_3+a_{12}( a_4{x_1}^2-a_5 x_3- a_6x_2)\nonumber \\&+\, a_{13}(a_7x_2-a_8x_6). \end{aligned}$$

(27)

Rearranging the above equation to get,

$$\begin{aligned} {{\dot{x}}}_6= & {} a_{12}a_4{x_1}^2-(a_{12}a_6-a_{13}a_7)x_2 -a_{13}a_8x_6\nonumber \\&+\, \left( \frac{a_{12}a_4}{a_2}\right) x_1{{\dot{x}}}_1+\left( \frac{a_{12}a_4a_3}{a_2}\right) {x_1}^2x_3+a_9 x_4 \nonumber \\&-\,\left( \frac{a_{12}a_4a_1}{a_2}\right) u x_1. \end{aligned}$$

(28)

Now defining $\frac{a_{12}a_4}{a_2}=a_{14}$ the above can be written as,

$$\begin{aligned} {{\dot{x}}}_6= & {} a_{12}a_4{x_1}^2-(a_{12}a_6-a_{13}a_7)x_2 -a_{13}a_8x_6 \nonumber \\&+\,a_{14}x_1{{\dot{x}}}_1+a_{14}a_3{x_1}^2x_3+a_9 x_4 -a_{14}a_1 x_1 u. \end{aligned}$$

(29)

Equation (29) can be rearranged as below:

$$\begin{aligned} x_6= & {} \frac{1}{a_{13}a_8}(a_{12}a_4{x_1}^2-(a_{12}a_6-a_{13}a_7)x_2-{{\dot{x}}}_6\nonumber \\&+\,a_{14}x_1{{\dot{x}}}_1+a_{14}a_3{x_1}^2x_3+a_9 x_4-a_{14}a_1 x_1 u). \end{aligned}$$

(30)

Now substituting $\frac{1}{a_{13}a_8}=a_{15}$ and using Eq. (23e), above becomes,

$$\begin{aligned} {{\dot{x}}}_5= & {} a_{15}a_{12}a_4{x_1}^2-a_{15}(a_{12}a_6-a_{13}a_7)x_2 -a_{15}{{\dot{x}}}_6 \nonumber \\&+\,a_{15}a_{14}x_1{{\dot{x}}}_1+a_{15}a_{14}a_3{x_1}^2x_3+a_{15}a_9 x_4 \nonumber \\&-\,a_{15}a_{14}a_1 x_1 u. \end{aligned}$$

(31)

It may be noted that supply pressure is constant ($3\times 10^{6}$ Pa). Volume of cylinder is also bounded. Therefore differential pressure hence force acting on load is bounded. The term $a_{15}$ is also bounded.

Therefore $a_{15} {{\dot{x}}}_6$ defined as $\psi$, where $\psi$ is bounded.

Defining,

$$\begin{aligned}&a_{15}a_{12}a_4{x_1}^2-a_{15}(a_{12}a_6-a_{13}a_7)x_2+a_{15}a_{14}x_1{{\dot{x}}}_1\\&\quad +\,a_{15}a_{14}a_3{x_1}^2x_3+a_{15}a_9 x_4=f(x_1,{{\dot{x}}}_1, x_2, x_3,x_4). \end{aligned}$$

The above equation can be written as,

$$\begin{aligned} {\dot{x}}_5= f(x_1,{{\dot{x}}}_1, x_2, x_3,x_4)-\psi -a_{15}a_{14}a_1x_1u, \end{aligned}$$

Since $a_{14},a_{15},a_1, x_1$ are bounded. Hence $(-a_{15}a_{14}a_1x_1u)$ can be written as $u+\varDelta u.$

Therefore,

$$\begin{aligned} {\dot{x}}_5= & {} f(x_1,{{\dot{x}}}_1, x_2, x_3,x_4)-\psi +u+\varDelta u,\nonumber \\ \dot{x_5}= & {} u+\rho . \end{aligned}$$

(32)

where $\rho =f(x_1,{{\dot{x}}}_1, x_2, x_3,x_4)-\psi +\varDelta u$.

It may be noted that $\rho$ takes account of parametric uncertainties which includes effect of variation of temperature, pressure, etc. In presence of external matched disturbance, above equation takes the form

$$\begin{aligned} {{\dot{x}}}_5=u+\rho + d, \end{aligned}$$

(33)

where d is used to represent neglected dynamics such as time delay. Also, d is assumed to be smooth and bounded.

Remark IV

EHSS exhibits time delay of the order of 0.7751 s. which is very much less than desired settling time which is order of 15–17 s.

The system in Eq. (33) is relative degree one system and is considered for control design under the valid assumption of bounded acceleration. Therefore Super Twisting Algorithm (STA) can be applied.

It may be noted that state $x_1$ i.e. input current is bounded hence resulting Fmag acting on the spool is bounded. Similarly spool displacement $x_s$ i.e. state $x_2$ and spool velocity ${{\dot{x}}}_s$ i.e. $x_3$ are bounded due to the geometry of spool plunger assembly and bounded magnetizing force respectively. Moreover, due to finite port opening $p_1$, $p_2$ and hence $\varDelta p$ =$x_4$ is bounded. Due to the geometry of cylinder and piston force acting on the piston is bounded hence load velocity ($x_6$) is bounded. Maximum load displacement ($x_5$) is equal to piston length which is finite hence the load displacement is bounded. Thus it is evident that all states are bounded.

4 Control development

The control objective is to design second order sliding mode controller for complex EHSS described in Eq. (22) to move 10 kg mass through 0.1 m in 17 s. The state $x_5$ i.e. actual load position is measurable whereas other states $x_1$, $x_2$, $x_3$, $x_4$ and $x_6$ are not measurable. A simple linear sliding variable is proposed.

$$\begin{aligned} \sigma _{l} = e_{x_5}, \end{aligned}$$

(34)

where  ${e_{{x_5}}}={x_5} - {x_{{5_d}}}.$

Here, ${x_{{5_d}}}$ is desired load position. Differentiating Eq. (34),

$$\begin{aligned} {\dot{\sigma }}_{l} = {\dot{e}}_{x_5}, \end{aligned}$$

(35)

Now surface in Eq. (34) is relative degree one surface with respect to Eq. (32). Therefore Super Twisting Algorithm (STA) can be applied.

According to STA [24], the variable $\sigma _1$ and its derivative ${\dot{\sigma }}_l$ converge to zero in finite time if ${\dot{\sigma }}_l=-{k_1}{\left| \sigma _l \right| ^{0.5}}sgn(\sigma _l)-{k_2}\int {sgn}(\sigma _l )+\rho _l$  with $k_2>|\rho _l|_{max}$, $k_1>k_2$.

Differentiating Eq. (34) to get

$$\begin{aligned} {\dot{\sigma }}_l={{\dot{x}}}_{5}=x_6. \end{aligned}$$

(36)

Therefore using Eq. (32)

$$\begin{aligned} {\dot{\sigma }}_l = u + \rho + d. \end{aligned}$$

(37)

With the choice of u as

$$\begin{aligned} u= & {} -\,{k_1}{\left| \sigma _l \right| ^{0.5}}sgn(\sigma _l)-{k_2}\int _{0}^{t}{sgn}(\sigma _l )d\tau , \end{aligned}$$

(38)

$\sigma _l$ and ${\dot{\sigma }}_l$ converges to zero in finite time if $k_2>(|\rho |_{max}+|{d}|_{max})$ and $k_1>k_2$. $|\rho |_{max}$ can be calculated using worst case analysis and $|{d}|_{max}$ is assumed to be known [24]. Other methods such as evolutionary algorithm can also be found to arrive at controller gains $k_1$ and $k_2$.

4.1 Disturbance estimation

The STA based control designed in Eq. (38) is developed to compensate for the disturbance via appropriately assumed gains. These high gains can be avoided if an approximate estimate of the disturbance is available. In this section Disturbance Observer (DO) is designed to estimate the unknown lumped disturbance. The Eq. (33) can be represented as,

$$\begin{aligned} {{\dot{x}}}_5= u + x_5+\rho + d-x_5 \end{aligned}$$

Defining $\rho + d-x_5=\rho _d$,

$$\begin{aligned} {{\dot{x}}}_5= u + x_5+\rho _{d} \end{aligned}$$

The estimate of $\rho _{d}$ is obtained with simple inversion of dynamics i.e.;

$$\begin{aligned} \hat{\rho }_{d}= {{\dot{x}}}_5- x_5- u \end{aligned}$$

(39)

Here $\hat{\rho }_{d}$ is the estimate of the disturbance. $x_5$ is measurable and u is the known input. However, ${{\dot{x}}}_5$ is unknown. It is proposed to obtain information of ${{\dot{x}}}_5$ using a HOSM exact differentiator. The exact first order differentiator as proposed by Levant in [30] is used as follows;

$$\begin{aligned} \begin{aligned} \dot{\hat{x}}_5&=\nu +w_1\\ \dot{\nu }&=w_2, \end{aligned} \end{aligned}$$

(40)

The correction variables $w_1$ and $w_2$ are output injections of the form;

$$\begin{aligned} w_1= & {} \lambda |x_5-\hat{x}_5|^{1/2}sign(x_5-\hat{x}_5)\\ w_2= & {} \alpha sign(x_5-\hat{x}_5) \end{aligned}$$

$\lambda$ and $\alpha$ are the tuning parameters. The DO is thus modified to have the form

$$\begin{aligned} \hat{\rho }_d=\dot{\hat{x}}_5-x_5-u \end{aligned}$$

(41)

The HOSM differentiator provides exact, finite time convergent derivative of $x_5$. It thus removes the necessity of filter and its allied disadvantages as in a conventional DO.

$\hat{\rho }_d$ is estimate of $\rho +d-x_5$.

Therefore, estimate of $(\rho +d)$ i.e. $\hat{\rho }+\hat{d}=\hat{\rho }_d+x_5$.

4.2 Proposed controller with disturbance estimation

The proposed controller in Eq. (38) is augmented to compensate the disturbance. The control law therefore becomes

$$\begin{aligned} u_1 = -{k_1}{\left| \sigma _l \right| ^{0.5}}sgn(\sigma _l)-{k_2}\int _{0}^{t}{sgn}(\sigma _l)d\tau -(x_5+\hat{\rho }_d), \end{aligned}$$

(42)

This is proposed controller with proposed disturbance estimator. This controller is compared with the STA controller using non-singular terminal sliding surface [31], which is also finite time controller.

4.3 Controller with non-singular terminal sliding surface

Non-singular terminal sliding surface is

$$\begin{aligned} \sigma _2 = e_{x_5}+{\beta _1{\dot{e}}_{x_5}}^ \frac{5}{3}, \end{aligned}$$

(43)

where ${\dot{e}}_{x_5}={\dot{x}}_5- \dot{x}_{5_d}= \dot{x}_5.$

Here ${\dot{x_5}}$  and  ${{{\dot{x}}}_{{5_d}}}$ are actual and desired load velocity respectively. Now STA controller using surface $\sigma _2$ is

$$\begin{aligned} u_2 = -\,{k_3}{\left| \sigma _2 \right| ^{0.5}}sgn(\sigma _2)-{k_4}\int _{0}^{t}{sgn}(\sigma _2)d\tau , \end{aligned}$$

(44)

where $k_3$ and $k_4$ are controller gains so chosen to ensure sliding. Proposed output feedback finite time controller in Eq. (42) is compared with finite time controller in Eq. (44). Finite time convergence is explained in next subsection for the sake of ready reference.

4.4 Existence of sliding

Theorem 1

Control in Eq. (38) ensures $\sigma _l={\dot{\sigma }}_l=0$ in finite time if $k_1>k_2>|\rho |_{max}+|d|_{max}.$

Proof

Define $\sigma _l=z_1$.

Differentiating the above

$$\begin{aligned} {\dot{\sigma }}_l=\dot{z}_1. \end{aligned}$$

Using Eq. (37) and substituting u from Eq. (38), the above equation becomes $\dot{z}_1=-{k_1}{\left| z_1 \right| ^{0.5}}sgn(z_1)-{k_2}\int {sgn}(z_1 )+\rho _l$.

Defining $\rho +d=\rho _l$,

$$\begin{aligned} \dot{z}_1= & {} -\,k_1 |z_1|^{0.5}sgn(z_1)+z_2+ \rho _l\\ \dot{z}_2= & {} -\,k_2sgn(z_1) \end{aligned}$$

This is classical STA in $z_1$. Therefore $z_1$ and $\dot{z}_1$ (i.e. $\sigma _l$  and  ${\dot{\sigma }}_l$) converge to zero in finite time [32] if $k_1>k_2>|\rho _l|_{max}$.

Similarly, it can be proved that controller in Eq. (44) ensures sliding if $k_3>k_4>|\rho _l|_{max}$. $\square$

5 Stability analysis

This section illustrates stability analysis of system with the proposed controller.

STA controller ensures $\sigma _l$ and ${\dot{\sigma }}_1$ zero in finite time.

Therefore from Eqs. (34) and (35),

$$\begin{aligned} e_{x_5}= e_{x_l}= & {} 0, \end{aligned}$$

(45)

$$\begin{aligned} \dot{e}_{x_5}= \dot{e}_{x_l}= & {} 0. \end{aligned}$$

(46)

With this $x_l$ acquires ${x_l}_{d}$ and $\dot{x_l}=0$ in finite time. Since, $\dot{x_l}=0$; forcing function exerting on load is zero i.e. $A_a\varDelta p \rightarrow 0$. This implies that $\varDelta p \rightarrow 0$ and $\varDelta \dot{p} \rightarrow 0$. When $\varDelta p \rightarrow 0$, $p_1 \cong p_2$ and change in volume of chamber 1 ($v_1$) and chamber 2 $(v_2)$ tends to zero. There is no further change in orifice area hence $q_1 \cong q_2$. Constant flow means no further spool motion. This implies that forcing function acting on spool i.e. $Fmag \rightarrow 0$ which in turn implies that $i \rightarrow 0$. From Eq. (12), $x_s$ and $\dot{x_s}$ converges to zero asymptotically. Thus $\dot{x_l}$ converges to zero in finite time and all remaining states converge asymptotically.

Another method is proposed to prove stability of the system.

Theorem 2

Finite time convergence of the proposed sliding surface in Eq. (34) with control in Eq. (42) ensures the convergence of all the states with finite time convergence of load to desired position and its velocity to zero if $k'> 2.018$.

Proof

Choosing the Lyapunov function as below.

$$\begin{aligned} V =\frac{a_4 {x_1}^{2}}{2a_3}+a_6 \frac{{x_2}^{2}}{2}+ \frac{{x_3}^{2}}{2}+\frac{{x_4}^{2}}{2}+k'|\sigma _l|+ \frac{{x_6} ^{2}}{2}, \end{aligned}$$

Since $a_3, a_4, a_6$ and $k'$ are positive the above is valid Lyapunov function.

Differentiating the above

$$\begin{aligned} {\dot{V}}= & {} \left( \frac{a_4}{a_3}\right) {x_1} \dot{x_1}+ a_6 {x_2}\dot{x_2}+{x_3}\dot{x_3}+{x_4}\dot{x_4}+k'(sgn{\sigma _l}){\dot{\sigma }}_l\nonumber \\&+\,x_6 {{\dot{x}}}_6. \end{aligned}$$

Using Eq. (23), the above becomes,

$$\begin{aligned} {\dot{V}}= & {} \left( \frac{a_4}{a_3}\right) {x_1}(a_1u-a_2 x_1-a_3x_1x_3)+ a_6{x_2}{x_3}\nonumber \\&+\, {x_3}(a_4{{x_1}^2}-a_5x_3-a_6x_2)+ {x_4}(a_7x_2-a_8x_6 )\nonumber \\&+\,k'(sgn{\sigma _l}){\dot{\sigma }}_l+ x_6(a_9x_4-a_{10}x_6). \end{aligned}$$

Simplifying the above to get,

$$\begin{aligned} {\dot{V}}= & {} \left( \frac{a_4 a_1}{a_3}\right) x_1u-\left( \frac{a_4 a_2}{a_3}\right) {x_1}^{2}-a_5 {x_3}^{2}+a_7 x_2 x_4\nonumber \\&+\, (a_9-a_8) x_4 x_6 + k'(sgn \sigma _l){\dot{\sigma }}_l -a_{10} {x_6}^{2}. \end{aligned}$$

All parameters from $a_1$ to $a_{10}$ are positive uncertain constants. When $x_2>0$, $x_4>0$ and $a_7<0$ also when $x_2<0$, $x_4>0$ and $a_7>0$. Therefore $a_ 7x_2x_4$ is either zero or negative definite. Similarly when $x_4>0$, $x_6>0$ and when $x_4<0$, $x_6<0$. Therefore $x_4x_6>0$. Further $a_8>>a_9$ therefore the term $(a_9-a_8)x_4x_6$ is always negative definite. Therefore  ${\dot{V}} < 0$ if

$$\begin{aligned} \left( \frac{a_4 a_1}{a_3}\right) x_1u+k'sgn(\sigma _l){\dot{\sigma }}_l <0. \end{aligned}$$

Now defining $\left( \frac{a_4a_1}{a_3}\right) =a_{11}$ and substituting for u from Eq. (38) in above, ${\dot{V}} < 0$ if

$$\begin{aligned}&a_{11}x_1(-{k_1}{\left| \sigma _l \right| ^{0.5}}sgn(\sigma _l)-{k_2}\int _{0}^{t}{sgn}(\sigma _l )d\tau )\nonumber \\&\quad +\,k'sgn(\sigma _l){\dot{\sigma }}_l <0. \end{aligned}$$

It may be noted that for positive $\sigma _l$, $\dot{\sigma _l}$ is negative and for negative $\sigma _l$, $\dot{\sigma _l}$ is positive leading to $k' sgn \sigma _l \dot{\sigma _l}$ negative. Therefore ${\dot{V}}<0$ if

$$\begin{aligned} |k'sgn(\sigma _l){\dot{\sigma }}_l| >|a_{11}x_1u|. \end{aligned}$$

(47)

Since $k'>0$ and $|sgn \sigma _l|=1$, the above condition becomes

$$\begin{aligned} k'|{\dot{\sigma }}_l|>|a_{11}x_1|_{max}|u| \end{aligned}$$

Considering maximum rated value of current i.e. $x_{1_{max}}=2A$ and the parameters $a_1,a_3$ and $a_4$ from Table I, $a_{11 _{max}}=1.009$. For ${\dot{V}}<0$,

$$\begin{aligned} k'|{\dot{\sigma }}_l|>2.018|u| \end{aligned}$$

(48)

If condition in Eq. (48) is satisfied for any controller then that controller stabilizes all the states which implies that during reaching (i.e. $\sigma _l\rightarrow 0$) all other states also converge.

Controller in Eqs. (38), (42) and (44) can be analyzed for stability by verifying condition in Eq. (48) for possibility of negative definiteness of ${\dot{V}}$.

Substituting Eq. (38) in Eq. (48), ${\dot{V}}<0$ if

$$\begin{aligned} k'|{\dot{\sigma }}_l| >2.018\left| -{k_1}{\left| \sigma _l \right| ^{0.5}}sgn(\sigma _l)-{k_2}\int _{0}^{t}{sgn}(\sigma _l )d\tau \right| . \end{aligned}$$

As per STA, ${\dot{\sigma }}_l=-{k_1}{\left| \sigma _l \right| ^{0.5}}sgn(\sigma _l)-{k_2}\int _{0}^{t}{sgn}(\sigma _l )d\tau +\rho _l$.

Therefore, ${\dot{V}}<0$ if,

$$\begin{aligned} k'|{\dot{\sigma }}_l| >2.018|({\dot{\sigma }}_l-\rho _l)|. \end{aligned}$$

where $\rho _l$ is total lumped disturbance.

If $k'|{\dot{\sigma }}_l| >2.018|{\dot{\sigma }}_l|$ then $k'|{\dot{\sigma }}_l| >2.018|{\dot{\sigma }}_l|-2.018|\rho _l|_{max}$.

Therefore for ${\dot{V}}<0$; $k'|{\dot{\sigma }}_l| >2.018|{\dot{\sigma }}_l|$ , it implies that if $k'>2.018$ then stability is assured. Hence with $k'> 2.018$ proposed output feedback controller without estimation ensures convergence of all states.

Similarly stability with controller in Eq. (42) is verified.

Substituting Eq. (42) in Eq. (48),

$$\begin{aligned}&{\dot{V}}<0,\text {if}\\&k'|{\dot{\sigma }}_l|>\eta \left| -{k_1}{\left| \sigma _l \right| ^{0.5}}sgn(\sigma _l) -{k_2}\int _{0}^{t}{sgn}(\sigma _l)-(x _5+\hat{\rho }_{d})\right| \end{aligned}$$

where $\eta =2.018.$ Now, $\hat{\rho }_d$ is estimate of $\rho +d+x_5$ hence $x_5+\hat{\rho }_d= \hat{\rho }+\hat{d}$.

Therefore ${\dot{V}}<0$ if

$$\begin{aligned}&k'|{\dot{\sigma }}_l| >2.018|-{k_1}{\left| \sigma _l \right| ^{0.5}}sgn(\sigma _l)\\&-\,{k_2}\int _{0}^{t}{sgn}(\sigma _l )d\tau -(\hat{\rho }+\hat{d})|. \end{aligned}$$

$(\rho +d)$ is lumped disturbance is equal to $\rho _l$. Therefore for ${\dot{V}}<0$,

$$\begin{aligned}&k'|{\dot{\sigma }}_l|>2.018\left| -{k_1}{\left| \sigma _l \right| ^{0.5}}sgn(\sigma _l)\right. \\&\left. -\,{k_2}\int _{0}^{t}{sgn}(\sigma _l )d\tau -\rho _l\right| . \end{aligned}$$

According to STA,

$$\begin{aligned} -{k_1}{\left| \sigma _l \right| ^{0.5}}sgn(\sigma _l)-{k_2}\int _{0}^{t}{sgn}(\sigma _l )d\tau +\rho _l={\dot{\sigma }}_l. \end{aligned}$$

Hence for ${\dot{V}}<0$, $k'|{\dot{\sigma }}_l|>2.018|{\dot{\sigma }}_l|$ which means $k'>2.018$ ensures stability. Thus with $k'> 2.018$ proposed output feedback controller with proposed estimation ensures convergence of all states.

For devising controller in Eq. (44), sliding variable is $\sigma _2$ instead of $\sigma _l$. Accordingly derivation of Lyapunov function is negative definite if $k'|{\dot{\sigma }}_2|>2.018|u_2|$.

Substituting $u_2$ from Eq. (44), ${\dot{V}}<0$ if

$$\begin{aligned} k'|{\dot{\sigma }}_2|>2.018\left| -\,{k_3}{\left| \sigma _2 \right| ^{0.5}}sgn(\sigma _2)-{k_4}\int _{0}^{t}{sgn}(\sigma _2 )d\tau \right| . \end{aligned}$$

As per STA,

$$\begin{aligned} {\dot{\sigma }}_2=-\,{k_3}{\left| \sigma _2 \right| ^{0.5}}sgn(\sigma _2)-{k_4}\int _{0}^{t}{sgn}(\sigma _2 )d\tau +\rho _l. \end{aligned}$$

Therefore for ${\dot{V}}<0$; $k'|{\dot{\sigma }}_2| >2.018|({\dot{\sigma }}_2-\rho _l)|$.

If $k'|{\dot{\sigma }}_2| >2.018|{\dot{\sigma }}_2|$ then $k'|{\dot{\sigma }}_2| >2.018|{\dot{\sigma }}_2|-2.018|\rho _l|_{max}$.

Therefore for ${\dot{V}}<0$; $k'|{\dot{\sigma }}_2| >2.018|{\dot{\sigma }}_2|$, which implies that if $k'>2.018$ then stability is assured.

Hence with $k'> 2.018$, controller in Eq. (44) ensures convergence of all states.

Without loss of generality, $k'$ can be chosen greater than 2.018. Thus all controllers in Eqs. (38), (42) and (44) are stabilizing controllers. $\square$

6 Simulation results

Fig. 6

Controller performance in simulation. a Evolution of load displacement and b control input

To test performance of controllers in Eqs. (42) and (44), the system in (22) and controllers were simulated in Matlab. $k_1 = 4.7$, $k_2 = 0.01$, $k_3 =10$, $k_4= 0.008$ and $\beta _1=1$ are simulation parameters. These parameters were so tuned to yield the almost same response in terms of output error stabilization. Since STA was used, control gains had to satisfy conditions that are essential for the existence of sliding. Gains $k_1, k_2$ of the controller in Eq. (42) and $k_3, k_4$ of Eq. (44) were so tuned to ensure the existence of sliding and almost same settling time of output. Step command of 0.1 was applied as the reference input. To check disturbance rejection capability sinusoidal varying external disturbance $0.1sin(4 \pi t)$ was added in the input channel. Figure 6a, b shows performance with the disturbance in input channel. It is evident that performance of both controllers is robust. Also, control is smooth. Both yields load to reach at the desired position in about 17 s.

7 Experimental set up

An experimental set up has been designed and developed to validate proposed method as shown in Fig. 7. It consists of hydraulic power pack, inline filter, single rod asymmetrical double acting cylinder driven by 4/3 position proportional valve Atos DHZO-AE-071-L1, oil temperature indicator, linear position transmitter, 10 kg load with pulley arrangement, dSPACE RTC 1104. Hydraulic actuators include hydraulic cylinder of dimension 40/18/300 mm and 230 V, 750 W, 1 H.P., 1425 RPM hydraulic motor.

Fig. 7

Experimental set up of electro-hydraulic servo system

8 Experimental results

Controllers developed in Eqs. (42) and (44) were implemented using dSPACE DS1104 real time interface. The necessary commands were given using Control Desk. Experiments were carried out on real time platform. The real-time control system was programmed using MATLAB/Simulink and gets transferred to the dSPACE board through the Real-Time Workshop. Figure 8a, b illustrate the experimental performance of controllers $u_1$, $u_2$ with external disturbance. The controller gains $k_1 =2.5$, $k_2 = 0.04$, $k_3 =4.7$ and $k_4 = 0.056$ were chosen in experiment to get same performance in terms of settling time i.e. 17 s. The following Tables 2 and 3 illustrate quantitative comparison.

Fig. 8

Controller performance in experimentation. a Evolution of load displacement in experiment and b control input

Table 2 Quantitative comparison of proposed controller without and with estimation

Table 3 Quantitative comparison of two controllers with external disturbance

It is evident that the proposed controller with disturbance estimation shows better control quality at the cost of less control efforts. The proposed finite time output feedback controller is superior to finite time controller using non-singular terminal sliding surface.

9 Conclusions

Relative degree one sliding surface has been proposed for devising STA controller for finite time positioning of the complex electro hydraulic servo system. Disturbance estimation and compensation has been used. Following are concluding remarks:

• 1. The proposed controller with disturbance compensation ensures desired robust performance.

• 2. The controller yields finite positioning of the load to the desired position in 17 s.

• 3. The proposed controller is output feedback controller. It requires information of load position. On the other hand the controller using non-singular terminal sliding surface needs information of load position and velocity.

• 4. The proposed controller with disturbance estimation needs control efforts $8\%$ less than the one without estimation

• 5. More accuracy is observed with proposed controller.

• 6. Thus proposed control approach outperforms the other in terms of control quality and control energy.