1 Introduction

Flatness is an important geometrical feature of cold-rolled strips. Many severe defects and quality problems can appear [1, 2]. Strips with poor flatness are more likely to be broken with quality issues during later manufacturing phases.

In the flatness control system, the flatness effect of force applied by any actuators can be quantified to be the efficiency factors of flatness actuators. Based on the efficiency factors of flatness actuators, the adjustment values can be calculated, and the flatness deviation can be eliminated. Therefore, the flatness actuator efficiency is the basis of the flatness closed-loop control. There are two methods used to obtain the flatness actuator efficiency at present. One is from rolling experiments, and the other one is by finite element simulation [3]. It should be emphasized that the rolling experiments have suffered from some limits, since they can only test a few rolling conditions and the cost is high. The finite element method (FEM) has been applied in a variety of metal forming processes. The 3D elastic–plastic FEM was used to simulate a cold strip rolling process in a 6-high continuously variable crown (CVC) rolling mill to study the effect of the flatness actuator on the strip crown and edge [4]. According to Wang et al. [5], the efficiency factors of flatness actuators for a universal crown control (UCM) mill were obtained using an elastic–plastic FEM. However, the process of finite element simulation is complicated and the calculation time is long, which leads to difficulties of analysis and calculation in real time. In order to overcome these problems, new methods and more attempts should be proposed to obtain the efficiency factor of flatness actuators.

In the past, in order to achieve the setpoints of flatness actuators, static load distribution or dynamic load distribution was used to optimize the rolling schedule. At present, two types of flatness closed-loop control methods are used: One is the pattern recognition method, and the other is the multivariable optimization method [6]. With the development of flatness control technology, the advanced multivariable control techniques, such as singular value decomposition and model predictive control, have been successfully applied in commercially available real-time flatness control systems [2, 7]. These approaches provide new potentials to improve closed-loop control performance and enhance stability. Even though all the above methods are accepted and widely used, certain interests are focused on the incorporation of improved nonlinear techniques applicable in the flatness control problem. To accommodate the presence of modeling uncertainties and unmodeled nonlinearities, the adaptive techniques and online parameter identification coupled with self-tuning regulation are urgently needed. The data-driven model, due to its nonlinearity and capability of adaptive information processing, will be widely used to improve the precision of the flatness control [8, 9].

In the flatness control system, the conventional mathematical model and self-learning are used to control flatness based on the single parameter or stand. The data-driven method as the multivariable optimization method is an efficient alternative. The necessary process information can be extracted directly from huge amounts of the recorded process data in this method [10, 11]. The multivariate regression algorithms, such as principal component analysis (PCA), partial least square (PLS), kernel partial least square (KPLS), and their modified algorithms, can effectively establish models with the high-dimension and coupling data [12]. In PCA, all input variables are given the same weight in the process of normalization. The relationship between input and output variables is not considered. To solve this problem, the PLS algorithm is proposed as a powerful method that can detect the input variables mostly related to the output variables [13]. By orthogonal transformation, PLS can preserve a set of linearly irrelevant principal components and establish a linear model. However, the process data are usually high-dimensional and contain noise. To reduce the negative effect of variable coupling and noise, OSC (orthogonal signal correction)–PLS that combines OSC and PLS together is proposed [14, 15]. KPLS is an effective algorithm that can model collinear and nonlinear data. The basic ideas of KPLS are to map the data points into a feature space with a nonlinear map function and carry out a linear PLS in the feature space [16]. Artificial neural network (ANN) is a family of statistical learning algorithms inspired by biological neural networks, which is used to estimate any nonlinear functions without the need for prior transformations [17, 18]. The prediction error of the KPLS model with indeterminate parameters can be compensated by the ANN algorithm. KPLS combined with ANN is established to predict the flatness values. Furthermore, a coordination optimization algorithm between the flatness and the parameters of stands is presented based on the KPLS–ANN model. The optimization process can effectively modify the setting parameters of work roll bending (WRB), intermediate roll bending (IRB) and roll tilting (RT) of all actuators based on the actual values in rolling process and reduce the flatness. The optimization model has the excellent flatness control capability, and it can meet the demands of online application.

In this paper, the data are collected from 1450 mm UCM cold rolling production lines. By OSC–PLS, the flatness actuator efficiency is obtained. Meanwhile, the KPLS–ANN flatness prediction model is established, and the flatness is optimized based on the model.

2 Structure of 6-high UCM cold mill

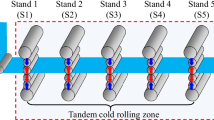
The tandem cold rolling line consists of five UCM cold mills, and each of them influences the flatness. The mills are composed of the back-up rolls, the intermediate rolls and the work rolls. In cold rolling process, the flatness actuators mainly include a WRB device, an IRB device, a RT device, and an intermediate roll shifting (IRS) device. The cold rolling mill can change the flatness and correct the flatness defects by using the flatness actuators.

Here is a brief description of WRB, IRB, RT, and IRS: (1) WRB can make the work roll crown change rapidly within a certain range by acting bending force on roll necks. (2) IRB is similar to the WRB, but the difference is that the IRB acts on the intermediate roll. (3) RT increases the rolling force on one side of the strip while reduces the rolling force on the other side. (4) IRS eliminates the contact between the work roll and the intermediate roll outside strip width, and thus, the flatness control ability is obviously enhanced.

WRB, IRB, and RT can be adjusted offline or in the closed-loop control [2]. In fact, the actuators in the last stand can influence the flatness directly. This paper explores the efficiency factors of WRB, IRB and RT in the last stand. The flatness control will be optimized with the consideration of WRB, IRB and RT in all stands.

In the flatness closed-loop control system, the flatness actuator efficiency can be used to analyze and calculate the flatness from the view of measured plate stress distribution. Therefore, it can realize the comprehensive utilization of flatness measurement information and improve the ability of flatness control. The efficiency factor is defined as the change of flatness caused by unit actuator adjustment, which can be expressed as

$$ {\varvec{E}}_{ij} = \Delta {\varvec{Y}}_{i} (1 /\Delta {\varvec{X}}_{j} ) $$
(1)

where Eij is the element of the efficiency factor matrix E; ΔXj is the adjustment of the jth actuator; and ΔYi is the change of flatness caused by actuators adjustment in the ith flatness measured position.

3 Flatness actuator efficiency achievement

3.1 Flatness actuator efficiency obtained by OSC–PLS

The data of the cold rolling process have large noise and characteristics of multivariable coupling. The central idea of PCA is to reduce the number of dimensions of the data while preserving as many as possible of the variations in the original dataset. Compared with PCA, PLS can not only reduce the dimensionality of high-dimensional data and eliminate noise, but also analyze the relationship between input variables and output variables. OSC is a method of processing data that can remove the orthogonal part of the input variable and the output variable. For the purpose of reducing the number of required latent variables and the random disturbance in the data, this method is used in Refs. [19,20,21]. In order to reduce the effect of variable coupling, the OSC–PLS that combines OSC and PLS was adopted in this paper.

The main steps to obtain the flatness actuator efficiency are as follows.

Step 1 Preprocess the data, including time synchronization process, the incremental computation of flatness and parameters in unit time, and data standardization.

Step 2 Process the data using OSC as outlined in Table 1.

Table 1 Step of OSC algorithm
Full size table

Step 3 Establish the PLS model with the flatness increment and actuator value increment.

Step 4 Obtain the efficiency factor matrix from the OSC–PLS model.

The parameter increments are the input variable matrix X (n × p), and the flatness increments are the output variable matrix Y (n × q).

In order to summarize the variable information of X and Y, the PLS algorithm extracts the principal components t and u from X and Y. Therefore, the PLS model established with t and u can reduce the effect of errors and variable coupling. A linear model of X and Y can be indirectly established with the PLS algorithm [22].

According to Kim et al. [15] and Sampson et al. [23], a PLS model can be established. The steps of PLS algorithm are shown in Table 2. The OSC–PLS model of flatness is given as follows:

$$ {\varvec{Y = XB + C}} $$
(2)
$$ {\varvec{B}} = {\varvec{X}}^{\text{T}} {\varvec{U}}({\varvec{T}}^{\text{T}} {\varvec{XX}}^{\text{T}} {\varvec{U}})^{ - 1} {\varvec{T}}^{\text{T}} {\varvec{Y}} $$
(3)

where T (n × h) is the matrix composed of p principal components t; U (n × h) is the matrix composed of q principal components u; C (n × q) is the residual matrix; and h is the number of the principal components. X has been processed with OSC.

Table 2 Step of PLS and PCA algorithms
Full size table

The PCA algorithm is shown in Table 2. According to Gertler and Cao [24], X can be described by PCA as follows:

$$ {\varvec{X}} = {\varvec{T}}_{ 1} {\varvec{L}}^{\text{T}} $$
(4)

and thus, the PCA model of flatness can be established as

$$ {\varvec{Y}} = {\varvec{XB}}_{2} + {\varvec{C}}_{2} $$
(5)
$$ {\varvec{B}}_{2} = \left( {{\varvec{L}}^{\text{T}} } \right)^{ - 1} ({\varvec{T}}_{1}^{\text{T}} {\varvec{T}}_{1} )^{ - 1} {\varvec{T}}_{1}^{\text{T}} {\varvec{Y}} $$
(6)

where T1 (n × h1) is the score matrix of X; L (p × h1) is the loading matrix; and C2 (n × q) is the residual matrix.

Since the number of the principal components has a great influence on the results of the PLS model, the fivefold cross validation method has been used to determine the number of the principal components. As shown in Fig. 1, prediction error sum of squares (PRESS) of the different principal components is calculated by fivefold cross validation, and the number of the principal components is the best when the PRESS is minimum.

Fig. 1
figure 1

Fivefold cross validation method

Full size image

According to the definition, the efficiency factors are actually the linear regression coefficients of the actuator value changes and the flatness change.

Get flatness actuator increment matrix X2 from cold rolling process parameter increment matrix X

$$ {\varvec{X}} = \left[ {\begin{array}{*{20}c} {{\varvec{X}}_{1} } & {{\varvec{X}}_{2} } \\ \end{array} } \right] $$
(7)

where X1 is the matrix of other process parameter increments.

Therefore, get E from B

$$ {\varvec{Y = XB = X}}_{ 1} {\varvec{B}}_{1} {\varvec{ + X}}_{ 2} {\varvec{E}} $$
(8)
$$ {\varvec{B}} = \left[ {\begin{array}{*{20}c} {{\varvec{B}}_{1} } \\ {\varvec{E}} \\ \end{array} } \right] $$
(9)

where B1 is the linear regression coefficient of X1.

Because the data are standardized

$$ {\varvec{E}} = {\varvec{D}}_{x}^{ - 1} {\varvec{ED}}_{y} $$
(10)

where Dx is the diagonal matrix composed of the standard deviation of the input variables; and Dy is the diagonal matrix composed of the standard deviation of the output variables.

In a similar method, the flatness actuator efficiency factor can be calculated by the PCA model.

1247 sample points were selected at a time interval of 0.2 s for the calculation of the flatness actuator efficiency factors at the last stand. The data mainly include variables such as the flatness values from 16 flatness measured points, rolling speed, rolling force, RT, WRB force and IRB force. The number of the OSC components is 1. According to the fivefold cross validation method, the optimal number of PLS components is 3. The efficiency factors calculated by OSC–PLS, PCA and experiential methods are shown in Fig. 2.

Fig. 2
figure 2

Efficiency factors of RT (a), WRB (b) and IRB (c) calculated by OSC–PLS, PCA, and experiential methods

Full size image

3.2 Validation of flatness actuator efficiency

The flatness changes can be calculated by the change of the actuator values and the efficiency factors. Therefore, the flatness change error reflects the error of the efficiency factors. To validate the flatness actuator efficiency, the flatness changes are calculated and compared with the actual flatness changes. The flatness changes can be calculated as follows:

$$ {\varvec{Y}}_{\text{c}} {\varvec{ = X}}_{ 2} {\varvec{E}} $$
(11)

where Yc (n × q) is the flatness change value matrix.

If the error between the flatness changes and the actual flatness changes is small, the efficiency factors are accurate. To validate the predictive abilities of the models, root mean square error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE) will be used to evaluate the model.

$$ \begin{aligned} {\text{RMSE}} & = \sqrt {\frac{1}{m}\sum\limits_{i = 1}^{m} {(y - y_{c} )^{2} } } \\ {\text{MAE}} & = \frac{1}{m}\sum\limits_{i = 1}^{m} {\left| {y - y_{c} } \right|} \\ {\text{MAPE}} & = \frac{1}{m}\sum\limits_{i = 1}^{m} {\left| {(y - y_{c} ) /y} \right|} \\ \end{aligned} $$
(12)

where y is the actual value; yc is the prediction value; and m is the number of data points.

The flatness changes are calculated based on other data, and compared with the actual flatness changes. According to Fig. 3, the flatness change error based on the OSC–PLS method is less than that based on the PCA method or the experiential method. The OSC–PLS method accurately describes the changes of the flatness, and the flatness actuator efficiency factors at the last stand obtained by OSC–PLS method are the most accurate, which has the minimal RMSE of 1.28 IU and MAE of 1.01 IU.

Fig. 3
figure 3

Flatness change error based on flatness actuator efficiency factors at last stand obtained by experiential method (a), PCA method (b), and OSC–PLS method (c)

Full size image

4 Flatness prediction and optimization

4.1 Flatness prediction based on KPLS–ANN model

KPLS is an effective nonlinear regression algorithm. KPLS with different kernel functions can solve different problems by analyzing the relationship between principal components and generating the regression model in the feature space.

Consider a nonlinear transformation of the input variables xi, i = 1, 2, …, n into feature space F:

$$ x_{i} \in {\varvec{R}}^{a} \to {\user2{\varPhi}}(x_{i} ) \in F $$
(13)

where xi is the vector of the ith row of X (n × p); and Φ(xi) is the vector of the ith row of matrix Φ (n × m) in an m-dimensional feature space F.

Applying the kernel trick, ΦΦT can represent the (n × n) kernel matrix K of the cross dot products between all mapped input data points Φ(xi), i = 1, 2, …, n

$$ {\varvec{K}} = {\user2{\varPhi \varPhi }}^{\text{T}} $$
(14)

where \( {\varvec{K}}(i,j) = {\user2{\varPhi}}(x_{i} ){\user2{\varPhi}}(x_{j} )^{\text{T}} \).

When the Gaussian kernel function is used, \( {\varvec{K}}(i,j) = \exp \left( {\left\| {x_{i} - x_{j} } \right\|^{2} /\sigma^{2} } \right) \) where σ is the kernel parameter.

K should be centered as follows:

$$ {\varvec{K}} = ({\user2{\varPhi}} - {\bar{\user2{\varPhi }}})({\user2{\varPhi}} - {\bar{\user2{\varPhi }}})^{\text{T}} = ({\varvec{I}} - {\varvec{I}}_{\text{N}} ){\user2{\varPhi \varPhi }}^{\text{T}} ({\varvec{I}} - {\varvec{I}}_{\text{N}} )^{\text{T}} $$
(15)

where IN is an (n × n) matrix with all its entries equal to 1/n; and \( {\bar{\user2{\varPhi }}} = {\varvec{I}}_{\text{N}} {\user2{\varPhi}} \).

The KPLS algorithm is outlined in Table 3.

Table 3 Step of KPLS algorithm
Full size table

According to Kim et al. [15], a KPLS model can be described as

$$ {\hat{\varvec{Y}}} = {\user2{\varPhi}}{\varvec{B}}_{\text{KPLS}} $$
(16)
$$ {\varvec{B}}_{\text{KPLS}} = {\user2{\varPhi}}^{\text{T}} {\varvec{U}}({\varvec{T}}^{\text{T}} {\varvec{KU}})^{ - 1} {\varvec{T}}^{\text{T}} {\varvec{Y}} $$
(17)

where \( {\hat{\varvec{Y}}} \) is the prediction of Y; and BKPLS is the regression coefficient.

To establish the nonlinear model, the nonlinear relation between the flatness influence factor and the flatness can be considered in KPLS. However, the number of principal components selected from KPLS may be inaccurate because KPLS extracts the principal components from the infinite high-dimensional feature space. The prediction error of the KPLS model can be compensated by the ANN algorithm, which will overcome the parameter problem in the KPLS model and reduce the prediction error of the model.

The prediction error of the KPLS model is as follows:

$$ \varvec{R = Y} - {\hat{\varvec{Y}}} = \varvec{Y} - {\user2{\varPhi}}{\varvec{B}}_{\text{KPLS}} $$
(18)

To improve the prediction precision of the flatness, the ANN model with single hidden layer is established with R and X. The ANN model is trained by minimizing the square error of the output. The structure of ANN consists of 74 neurons in the input layer and 20 neurons in the output layer. According to Yu et al. [17], the output of the ANN model is as follows:

$$ {\hat{\varvec{R}}} = {\varvec{g}}({\varvec{X}}) = \varvec{R} - {\varvec{R^{\prime}}} $$
(19)

where \( {\hat{\varvec{R}}} \) is the output of the ANN model; g(X) is the ANN model of the residual matrix; and \( {\varvec{R^{\prime}}} \) is the residual matrix of the ANN model.

As shown in Fig. 4, the KPLS–ANN model can be expressed as

$$ \varvec{Y}_{\text{p}} = {\user2{\varPhi}}\varvec{B}_{\text{KPLS}} + \varvec{g}(\varvec{X}) $$
(20)

where Yp is the output of the KPLS–ANN model.

Fig. 4
figure 4

Structure of KPLS–ANN model

Full size image

Since the KPLS–ANN model can find the inherent law of multiple variables in the kernel feature space and the primal space, the KPLS–ANN model can accurately predict the flatness values.

In the cold rolling process, the flatness is affected by many factors and is difficult to be predicted using the linear model. The flatness can be influenced by various factors including the flatness actuators, rolling force, thickness and tension directly or indirectly. In order to achieve the accurate flatness prediction, KPLS and ANN are combined to establish the KPLS–ANN model.

4.2 Flatness optimization based on KPLS–ANN model

The actual rolling process is complicated and variable, and it is difficult to consider a large number of variables that change in real time. The data-driven method can comprehensively analyze the relevant factors affecting the flatness during the rolling process and establish a model of the flatness.

The parameters of each stand have an influence on the final flatness. Considering the influence relation of these parameters to the final flatness, the flatness prediction model is established. Based on the KPLS–ANN flatness prediction model, the gradient descent method is used to optimize setpoints of actuators. The optimization process can effectively modify the initial setting parameters of WRB, IRB and RT in all stands and reduce the flatness. In order to ensure the rationality and feasibility of setpoints, it is necessary to consider reasonable constraints during the optimization algorithm. If there is historical production data of similar products, the initial setpoints should be set according to the production data to avoid the local optimum. The adjustment ranges of RT, WRB and IRB are − 1 to 1 mm, − 840 to 1840 kN, and 0 to 2200 kN, respectively. In every 100 ms, the adjustment amount of RT is less than 0.05 mm and those of WRB and IRB cannot be greater than 50 kN.

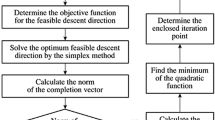
The steps of optimizing the setpoints of flatness actuators are as follows.

Step 1 According to the initial setpoints of flatness actuators and other influencing factors of the flatness including rolling force, thickness, tension and rolling speed, the flatness values can be predicted by the KPLS–ANN model.

Step 2 Calculate the square of the flatness and the gradient approximation of the square (The difference method is used to calculate the approximate value of the gradient due to the complication of gradient of the KPLS–ANN model).

Step 3 Set the square of the flatness as the destination function, and adjust the actuator setpoints with the gradient descent method. The adjustments of actuator setpoints are limited by the mechanical constraints.

Step 4 Predict the new flatness by the KPLS–ANN model.

Step 5 If the gradient approximation of the destination function is equal to zero or steps 2–4 have repeated more than 20 times, continue to step 6; otherwise, return to step 2.

Step 6 Get the optimized setpoints of flatness actuators.

4.3 Results of flatness prediction and optimization

In the cold rolling process, 1942 discrete data points are obtained from different steel strips. The number of measured points of steel strips with various widths is different. In order to process the data conveniently, all the measured points are unified to 20 points by interpolating. The data used for flatness prediction and optimization calculation include 20 flatness values and 74 process variables of 5 stands including rolling speed, rolling force, RT, WRB force, IRB force and so on. 1553 data points are set as training set, and the remaining 389 data points are set as testing set. The KPLS–ANN predictive model is shown in Fig. 5.

Fig. 5
figure 5

Flatness prediction process

Full size image

A part of input variables are given in Table 4.

Table 4 Part of input variables for flatness prediction and optimization
Full size table

The prediction results of the KPLS, ANN, and KPLS–ANN models are shown in Fig. 6. Comparison between the predicted flatness and the actual flatness shows that KPLS, ANN, and KPLS–ANN methods all have good predictive ability. This is because these methods can establish the nonlinear model to analyze the nonlinear relationship between the flatness and the influence factors. The flatness predicted by KPLS–ANN is closer to the actual flatness than those by the other models.

Fig. 6
figure 6

Flatness prediction results by KPLS, ANN, and KPLS–ANN. a Actual flatness; b flatness predicted by KPLS; c flatness predicted by ANN; d flatness predicted by KPLS–ANN

Full size image

As shown in Fig. 7, compared with KPLS and ANN, KPLS–ANN shows the best predictive effect and the lowest RMSE of 0.51 IU, MAE of 0.34 IU, and MAPE of 0.09. It shows that the correlation between the rolling process data and the flatness can be represented by the KPLS–ANN model, and the model can predict the flatness values accurately.

Fig. 7
figure 7

RMSE, MAE, and MAPE of flatness standard deviations

Full size image

Based on the KPLS–ANN model, the flatness can be optimized by the gradient descent method. The capacity of the equipment is limited, and each control parameter also has upper and lower limits. If the flatness corresponding to the setpoints does not reach the target flatness, it is adjusted according to the gradient descent method. When the target has been reached or the adjustment amount has reached the limit, the adjustment is stopped. Figure 8 shows the flatness values optimized by the KPLS and KPLS–ANN models. Whether the KPLS model or the KPLS–ANN model is used, the effect of optimizing all stands is better than that of only optimizing the last stand.

Fig. 8
figure 8

Optimized flatness control results. a Optimized setpoints of last stand by KPLS; b optimized setpoints of last stand by KPLS–ANN; c optimized setpoints of all stands by KPLS; d optimized setpoints of all stands by KPLS–ANN

Full size image

The standard deviations of the flatness values are compared in Fig. 9, while Fig. 10 shows the standard deviations of initial flatness values and the optimized flatness values in box plot. Compared with the optimization by the KPLS model, the optimization by the KPLS–ANN model can reduce the flatness standard deviations more effectively.

Fig. 9
figure 9

Comparison of initial flatness and flatness optimized by KPLS and KPLS–ANN. a Flatness of last stand optimized; b flatness of all stands optimized

Full size image
Fig. 10
figure 10

Standard deviations of initial and optimized flatness values. a Flatness of last stand optimized; b flatness of all stands optimized

Full size image

Only optimizing WRB, IRB and RT in the last stand is not able to obviously reduce the flatness. However, when optimizing WRB, IRB, and RT in all stands, the flatness can be obviously reduced. In the last mill optimized, KPLS–ANN has a better optimization ability that gets the average of flatness standard deviation of 3.49 IU. For all stands optimized, the average of standard deviation is 2.22 IU. Compared to the initial average of standard deviation of 4.10 IU, the optimization is remarkable. The flatness has been significantly optimized by the KPLS–ANN model.

Because of strong self-adapting and self-learning ability of the KPLS–ANN method, it is able to get better accuracy of prediction than traditional models under various complicated working conditions. The results show that the optimization model based on the KPLS–ANN has the excellent flatness control capability. Meanwhile, the flatness optimized by comprehensive adjustment of all stands obtains a better effect than that by adjustment of the last stand.

5 Conclusions

  1. 1.

    The accurate flatness actuator efficiency is obtained. The OSC–PLS method is proposed to obtain the flatness actuator efficiency at the last stand, and the efficiency factors are validated by rolling process data.

  2. 2.

    KPLS–ANN has a high flatness predictive ability. Compared with KPLS and ANN, KPLS–ANN shows the best predictive ability, with lower RMSE, MAE, and MAPE of 0.51 IU, 0.34 IU, and 0.09, respectively.

  3. 3.

    The flatness can be significantly optimized by the KPLS–ANN model. With the setpoints of flatness actuators optimized, the average of flatness standard deviation is 2.22 IU. Compared to the average of initial standard deviation of 4.10 IU, the optimization is effective.