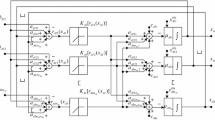
Calculation of the amount of adjustment of an actuator is an important step in flatness control during the cold rolling process. It has a direct effect on the precision with which flatness of strip is controlled. In this paper, an optimal evaluation function for evaluating actuator adjustment is defined based on the efficiency of the actuator and is solved by using a feasible-directions algorithm. This approach can not only determine the amount of adjustment that is optimal but also eliminates the problems associated with irreversible iteration in the traditional method. The software package Visual Studio is used to perform graphical modeling and a function block generator is used to create an optimum function block. The proposed model has been tested on a five-stand tandem cold-rolling mill. The results show that the flatness control deviation is reduced from 9% to 5%, which demonstrates that the model is highly effective.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
The increasingly demanding requirements on the quality of cold-rolled strip has made its flatness rating one of the most important quantitative indices of its properties [1]. Thus, creating a suitable model to determine the amount of adjustment of the actuator is an effective method of producing high-quality strip [2].
It is known that flatness depends on many factors: the entry crown, rolling force, and rolling speed [3]. For strip that is subjected to cold rolling, flatness can be more accurately determined on the basis of the difference between the internal stresses across the material [4, 5]. Thus, flatness is a descriptive attribute that characterizes the extent to which the geometry of the metal strip deviates from the reference plane [6, 7]. Several methods based on general laws have traditionally been used to regulate flatness. These methods only provide a local optimal solution, however, which is inadequate for checking the flatness of rolled strip [8, 9]. The common method of determining non-planarity during the rolling operation by using an inverse matrix is also inadequate, since the inverse matrix does not exist in most cases. Thus, an extension of the traditional flatness algorithm is presented here in order to improve the flatness model.
The function used in this investigation to optimize the estimate of flatness performs the optimization by analyzing the change in flatness in relation to the roll gap. The change in flatness is evaluated based on the amount of sub-block adjustment of the actuator across the width of the strip. The use of a feasible-directions algorithm which has been optimized by the simplex method makes it possible to obtain the optimum estimate. This circumvents the problem of not being able to optimize the estimate because of the appearance of an irreversible iterative matrix. It must be emphasized that the optimum solution which is obtained by this method ensures that the deviation of the strip from planarity will remain with the limits that are specified. This model was tested on a five-stand 1450 tandem cold-rolling mill under factory conditions and showed itself to be highly effective.
The optimum evaluation function is based on a constrained optimization method that is used to calculate adjustments to actuators [10]. Deviations from planarity are eliminated by each actuator with allowance for its efficiency and amount by which it is adjusted. Then values for the total deviation from planarity and the excluded deviation are used to determine the residual deviation. The optimum evaluation function is the sum of the squares of the residual deviations from planarity. The smaller the value of this function, the closer the measured value is to the required flatness. We obtain the following expression to determine the optimum evaluation function J:
where m is the number of measurement segments; n is the number of actuators; g i is the weight factor in the direction of the width of the strip; Δu j is the amount of adjustment of the actuator; Eff ij is efficiency; and mes i and ref i are the measured flatness and the target (required) flatness.
Constraint condition. The working range of the actuator should be taken into account in order to obtain the optimum solution to the problem of determining the amount by which it should be adjusted Δu j . The optimum solution for the rolling operation can be found if the following constraints are observed:
where Δu is the amount of adjustment of the actuator, the components of which are Δu 1, Δu 2, …, Δu n ; A is a constrained matrix in the form of an inequality; b is the constraint vector in the form of an inequality [11, 12].
Model for determining the amount of adjustment. One feature of the model is that it is possible to calculate the optimum point with a constraint by using a series of minimum points without constraints [13]. In this case, the standard strategy is as follows: begin with an allowable point, search for feasible descent directions, and determine a new allowable point [14]. The value of the optimum evaluation function decreases with the transition to a new allowable point [15]. Linear programming is used to find feasible descent directions, which reduces the size of this function as much as possible [16].
Determination of a feasible descent direction for the amount of actuator adjustment. Let us transform the column vector A and the component b in a way that does not change the expressions for A and b. We represent them in the form \( A=\left[\begin{array}{c}\hfill {A}^{\prime}\hfill \\ {}\hfill {A}^{{\prime\prime}}\hfill \end{array}\right] \) and \( b=\left[\begin{array}{c}\hfill {b}^{\prime}\hfill \\ {}\hfill {b}^{{\prime\prime}}\hfill \end{array}\right]. \) We obtain A′∆u = b′ and A″∆u = b″. Thus, the following is the necessary and sufficient condition for the vector that gives the feasible descent direction p
In addition, it must satisfy following conditions in order to be able to be determined:
where e = [1,1, …, 1]T is an n-dimensional unit vector. If the optimum value is negative, then the optimum solution p * is the feasible descent direction vector for determining the amount of adjustment of the actuator.
The simplex method is used to optimize the feasible descent direction. First, a compatible pattern which corresponds to the simplex method is obtained by the method of linear programming in order to ultimately determine the actuator adjustment.
We designate p i = p d 2i–1 − p d 2i . Here, each component p 1 d, p 2 d, …, p d 2n is non-negative. The column A′ is w, i.e., A′ = [a 1′T, a 2′T, …, a w ′T, ]T. We convert the inequality a 1′p ≥ 0, a 2′p ≥ 0, …, a w ′p ≥ 0 into a 1′p – p d 2n+1 = 0, a 2′p – p d 2n+2 = 0, …, a w ′p – p d 2n+w = 0. For p ≤ e, that is for p 1 ≤ 1, p 2 ≤ 1, …, p n ≤ 1, we convert these inequalities into the expressions p 1 + p d 2n+w+1 = 1, p 2 + p d 2n+w+2 = 1, …, p n + p d 2n+w+n = 1. For p ≥ −e (p 1 ≥ −1, p 2 ≥ −1, …, p n ≥ −1), we convert these inequalities into –p n + p d 2n+w+n+1 = 1, −p 2 + p d 2n+w+n+2 = 1, …, −p n + p d 2n+w+n+n = 1. Thus, the linear programming solution for the feasible descent direction is transformed as follows:
The rank of the matrix A d is equal to w + 2n. The solution for the equation A d h d = b d is p 0 d. B is a linearly independent column vector of matrix A d with the dimensions w + 2n, which for p 0 d corresponds to elements B. The remaining components are equal to zero. The inequality p 0 d ≥ is correct. Thus, B is the feasible basis. Let A d = [B, N]. Accordingly, the decompositions of the vectors p d and c appear as follows:
The process of linear programming that is carried out to determine the feasible descent direction vector for the actuator adjustment undergoes a change to the following form
Let p N = 0. We remove p B = B −1 b d from the constraints of the equality. Thus, the main feasible solution for B
The value of the objective function z = c T B B −1 b d.. It corresponds to the main feasible solution. Now let us examine the arbitrary feasible solution p d = [p T B, p T N ]T. For this solution, the value of the objective function
We remove pB = B −1 b d − B −1 Np N from the constraints of the equality Bp B + Np N = b d. After inserting it into the formula we obtain the equality
Let σ T N = (c T B B − 1 N − c T N ), then
Since p d is a feasible solution, we can take p N ≥ 0. Thus, if σ N ≤ 0 is correct, then z ≥ z is also correct. The main solution for B is optimal. The following is a sufficient condition for the main feasible solution to be the optimal solution:
Having made the substitution N = [a w+2n+1, …, a w+4n ]σ N , we obtain the equality
We will refer to this as the numerical value of the criterion p j d for the basis B. The vector σT = c B T B −1 A d − c T is the criterion for p d and σT N = c B T B −1 N − c N T is the criterion for p N . The vector of the criterion for p B
Thus, the numerical value of the criterion is equal to zero for the entire basis.
Linear search for a new actuator adjustment. To determine the new iteration point for the amount of adjustment of the actuator Δu, we perform a linear search along the feasible descent direction p * and from the iteration point for the actuator adjustment Δu
Since the iteration point for the adjustment should be a feasible point, the optimum step multiplier t * should be constrained by Eq. (2). Thus, the linear search becomes a minimization of one variation of a function with a constraint
If the equality A′Δu = b′ and the inequality A′p * ≥ 0 are true for any t ≥ 0, then A′(Δu + tp *) = A′Δu = tA′ and p * ≥ b' are always true. It thus becomes clear that the first constraint of formula (16) is superfluous. Accordingly, this formula can be simplified as follows:
We will assume that A″∆u – b″ = u = [u 1, u 2, …, u τ]T and A″p * = v = [v 1, v 2, …, v τ]T. Then the first constraint of formula (17) changes to the form:
Also, the optimum step multiplier t * can be transformed as follows by minimizing one variable of a function with a constraint:
Thus, we have created an integral model for calculating the amount of adjustment of an actuator (Fig 1).
Developing and testing a graphical model. To substantiate the method proposed above for eliminating deviations from planarity, we developed a modeling program with the use of the software package Visual Studio and the language C. Figure 2 shows the algorithm on which the operation of the program is based. The modeling is done by retrieving a subfunction through the main function in accordance with a prescribed sequence. There are three types of subfunctions. Panduan_1, a subfunction of the first type (critical), determines whether or not all of the numerical values of the criteria are equal to zero. Subfunction Panduan_2 determines whether or not the product of the optimum evaluation function and the feasible descent vector is less than the value specified for the accuracy of the result. A function of the second type calculates the optimum feasible descent direction. Danchunxig_0 subfunctions include artificial variables; Danchunxing_1 monitors the column with the numerical value of the vectorial minimum criterion and chooses a column with the number q; Danchunxig_2 chooses an element from column q and chooses a row with the number p; Danchunxing_3 normalizes the element in column q and row p and performs a basis transformation; Danchunxing_4 selects the finished table at the end of the first stage. A function of the third type finds the optimum solution: subfunction Rongxv_1 subdivides the constrained matrix and the vector; Rongxv_2 transforms the constraints of the inequality. Rongxv_3 calculates the upper limit of the search interval.
To simplify the analysis, it was assumed that there are only two actuators: an actuator for the bending of the work roll and an actuator for the bending of the intermediate roll. We will designate the amount of the adjustment made for the bending of the work roll as x 1 and the amount of the adjustment made for the bending of the intermediate roll as x 2. The constraint for the two actuators consists of following conditions: −0.6 ≤ x 1 ≤ 1, 0.04 ≤ x 2 ≤ 1. Since the variable should be a non-negative quantity in accordance with the model, the amount of adjustment for bending of the intermediate roll is determined as the difference between two non-negative variables: x 1 = x 3 − x 4. Then the overall constraints have the form:
Thus, the main constraint matrix in the program has the form:
The correct element is as follows:
The result of the modeling is shown in Fig. 3. It is apparent from Fig. 3a that with an increase in the number of iterations the sum of the squares of the deviations from planarity decreases after normalization. The model is capable of quickly and continuously eliminating deviations from flatness. It is evident from Fig. 3b that an increase in the number of iterations is accompanied by a decrease in the distance from the iteration point to the optimum point. This shows that the model is sufficiently rigorous. It was determined that the optimum adjustment for bending is 0.3842 for the work roll and 0.1635 for the intermediate roll.
To check the utility of the model, tests were conducted on a five-stand 1450 tandem cold-rolling mill equipped with a profilometer from the Swiss company ABB. The range of strip thickness at the inlet was 1.8–4.0 mm, the width range was 750–1300 mm, and the range of the strip's final thickness was 0.18–1.8 mm. The mill was a six-roll UCM mill. The flatness-monitoring system was built on the basis of TDC controllers and has a CPU551 central processor, an SM500 input/output module, and a CP50MO communications module. The sequence of steps carried out in the operation of the system is as follows:
-
1)
interrupt routine I1 triggers an interrupt from the profilometer;
-
2)
interrupt routine I2 measures flatness;
-
3)
cyclic routine T1 reports data to operating personnel;
-
4)
cyclic routine T2 is a predictive control system that also employs feedback;
-
5)
cyclic routine T4 is data transmission.
With the help a function block generator based on a TDC controller, the model's program, in the C language, is employed to create user-defined function blocks in a certain sequence:
-
1)
the input–output file and the function-block file create a .mask file;
-
2)
the source code file creates a .a file;
-
3)
the .a file and the .mask file create a modular set;
-
4)
when the modular set is imported, a function block developed in accordance with a certain function can be used in the TDC controller.
Figure 4 shows a user-defined function block that was created.
User-defined function block to determine the optimum amount of adjustment: WLO, WUP) lower and upper limits of work-roll bending; ILO, IUP) lower and upper limits of intermediate-roll bending; EWC) “permit calculation of work-roll bending”; EIC) “permit calculation of intermediate-roll bending”; F) deviation from flatness; OTW) optimum result from work-roll bending; OTI) optimum result from intermediate-roll bending.
The distance from the roll gap to the profilometer is 2.97 m. The speed limit for automatic frequency adjustment is 70 m/min. The adjustment for bending takes 1 sec for the work roll and 0.1 sec for the intermediate roll. The dynamic coefficient of the integration regime is 0.4 for bending of the work roll and 0.5 for bending of the intermediate roll. One step in the cycle for bending is 10% for both the work roll and the intermediate roll.
To check the accuracy of the information that was obtained, we analyzed experimental data from 200 sampling points during the rolling of strip (initial thickness was 2.5 mm and final thickness was 0.43 mm; initial width was 1015 mm and final thickness was 1000 mm).
Figure 5 shows the results of experimental studies performed with and without the use of the optimized feasible direction method. It can be seen that the deviation from planarity is 9% if this method is not used and 5% if it is used. Figure 6 presents a comparative analysis of these mathematical models for the case when the iteration matrix is irreversible.
Figure 7 shows a 3D diagram of the deviations from flatness. The fluctuations in these deviations are negligible (Fig. 7a ) when the optimized method of feasible directions is employed and flatness is characterized as corresponding to the prescribed requirements. When the model is used without the optimized method, the fluctuations of the deviation from flatness are substantial (Fig. 7b ) and flatness is characterized as not meeting the requirements.
Conclusions
-
1.
A new model for determining the amount of adjustment of actuators with use of an optimized method of feasible directions has been developed for systems designed to control flatness. Use of the model makes it possible to improve the accuracy of flatness control. In this case, the magnitude of the deviations from flatness decreases from 9% to 5%.
-
2.
An optimized feasible descent directions method based on the simplex method is used to ensure that the optimum actuator adjustment satisfies the necessary conditions. The optimization algorithm obviates the need for matrix inversion and thus eliminates the possibility of obtaining an incorrect solution.
-
3.
Comparison of the optimized feasible direction method and the simplex method makes it possible to speed up the iteration process and improves flatness. The number of iterations is reduced, which can significantly shorten the time required to compute the optimum adjustment and lead to an increase product output.
References
Liu Hong-min, Shan Xiu-ying, and Jia Chun-yu, “Theory-intelligent dynamic matrix model of flatness control for cold rolled strips,” J. Iron & Steel Res. Int., 20, No. 8, 1–7 (2013).
S. Abdelkhalek, P. Montmitonnet, N. Legrand, and P. Buessler, “Coupled approach for flatness prediction in cold rolling of thin strip,” Int. J. Mech. Sci., 53, No. 9, 661–675 (2011).
Jia Chun-yu, Bai Tao, Shan Xiu-ying, et al., “Cloud neural fuzzy PID hybrid integrated algorithm of flatness control,” J. Iron & Steel Res. Int., 21, No. 6, 559–564 (2014).
A. Bemporad, D. Bernardini, F. A. Cuzzola, and A. Spinelli, “Optimization-based automatic flatness control in cold tandem rolling,” J. Proc. Control, 20, No. 4, 396–407 (2010).
V. A. Agureev, E. A. Kalmanovich, A. V. Kuryakin, and S. V. Trusillo, “Use of gage IP-4 to measure the flatness of sheet on cold-rolling mills,” Metallurgist, 51, Nos. 5/6, 316–323 (2007).
R. Nandan, R. Rai, R. Jayakanth, et al., “Regulating crown and flatness during hot rolling. A multiobjective optimization study using genetic algorithms,” Mater. Manuf. Proc., 20, No. 3, 459–478 (2005).
J. Boerchers and A. Gromov, “Topometric measurement of the flatness of rolled products – the system TopPlan,” Metallurgist, 52, Nos. 3/4, 247–252 (2008).
G. Pin, V. Francesconi, F. A. Cuzzola, and T. Parisini, “Adaptive task-space metal strip-flatness control in cold multi-roll mill stands,” J. Proc. Control, 23, No. 2, 108–119 (2013).
S. V. Trusillo, V. A. Agureev, V. Yu. Arashenskii, et al., “Introduction of flatness gage IP-4 on the continuous Wean-Damiron heat-treatment line at the Samara Metallurgical Plant,” Metallurgist, 52, Nos. 9/10, 504–510 (2008).
Liu Hong-min, He Haitao, Shan Xiu-Ying, and Jiang Guang-biao, “Theory-intelligent dynamic matrix model of flatness control for cold rolled strips,” Chin. J. Mech. Eng., 22, No. 2, 01–07 (2009).
Cui Gui-mei and Zhao Yu-xing, “Research of the strip shape control system on cold strip mill,” Adv. Electr. Electron. Eng., 87, 465–470 (2011).
Zhao Yun-bin, “Alternative theorems and sufficient conditions of global convergence for a class of feasible direction algorithms,” J. Syst. Sci. Syst. Eng., 2, No. 3, 266–272 (1993).
He Guang-yu, Lu Qiang, and Chen Chun-xue, “Feasible direction algorithm for solving nonlinear optimization problems,” J. Tsinghua Univ. (Sci. & Technol.), 44, No. 10, 1310–1312 (2004).
Jiang You-bao, Feng Jian, and Meng Shao-ping, “Linear feasible direction algorithm for calculation of reliability index of structure,” J. Southeast Univ. (Nat. Sci. Ed.), 36, No. 2, 312–315 (2006).
Tong Shi-kuan and Xiao Xin-ping, “A feasible descent direction algorithm in trust region for quadratic programming,” J. Wuhan Univ. Technol., 28, No. 5, 732–735 (2004).
Qin Zhi-lin, “A feasible direction interactive algorithm for multi-objective group decision-making problems,” Math. in Econ., 19, No. 4, 20–29 (2002).
This study was conducted with the support of the National Science Foundation of China as part of natural sciences project 51074051. It also received financial support from the Fundamental Research Fund for the Central Universities as part of project N110307001.
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Metallurg, No. 9, pp. 55–61, September, 2015.
Rights and permissions
About this article
Cite this article
Zhu-wen, Y., He-nan, B. & Dian-hua, Z. Optimization and Innovative Modification of a Model Used to Determine the Amount of Adjustment of an Actuator for Flatness Control. Metallurgist 59, 795–804 (2016). https://doi.org/10.1007/s11015-016-0175-0
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11015-016-0175-0