1 Introduction

State and parameter estimations are fundamental problems in vehicle engineering fields, such as system identification, signal processing, and process control of various vehicle systems. A breakthrough milestone for optimal estimation/filter theory is the development of Kalman filter and its successful application in aerospace projects [1,2,3]. Various Kalman series filters have also been implemented in other areas, and alternative filters have been proposed thereafter [4, 5].

The reported state estimators/filters are generally designed to optimize the expected mean squared error, posterior distribution or likelihood of the target states, in an iterative online updating manner [3]. The optimal filter can recursively update the distribution of the system states based on the Bayes’ rule, and a model-based prediction step is generally used to propagate the current system state distribution using the available state observations [6]. While for high-dimensional and nonlinear estimation problems, this might require considerable computing resources to calculate the optimal filter gain at each iteration time step.

The optimal filter gain could also be obtained offline in order to reduce the online calculation complexity, such as the steady-state Kalman filter for time-invariant linear system with some mild conditions [7, 8]. The optimal filter gain can thus be calculated offline and directly applied online with improved calculation efficiency, which contributes to the real time implementation of Kalman filter. While this might enable multiple local linearization of the nonlinear systems, which would possibly yield estimation divergence with unexpected noise distribution or considerable model error.

The computation of steady-state Kalman gain generally requires solving the algebraic Riccati equation with an abstraction of first-order optimality condition. Analytical solution can be obtained for simple low-scale problems with known system model. However, the middle-scale and large-scale problems usually have to be solved via numerical methods, such as Schur vector, symplectic SR algorithm [8], and doubling method [9]. Schur vector approach is a variant of the classical eigenvector approach for Riccati equations, which uses Schur vectors to get a basis for a certain subspace. Symplectic SR algorithm is a QR-like method based on the SR decomposition. The doubling method exploits the Hamiltonian structure to change full matrix inversions into symmetric matrix inversions. These methods generally have the time complexity of \(O\left( {n^{3} } \right)\) and space complexity of \(O\left( {n^{2} } \right)\), which is intractable in high-dimensional estimation problems.

However, various methods are available to solve high-dimensional nonlinear control problems, especially the increasingly populated deep learning and reinforcement learning method [10]. Attributing to the estimation-control duality [1, 11] as introduced by Kalman, e.g., the duality between the Kalman filter and the linear-quadratic regulator, the method for solving optimal control problem could be potentially applied to the optimal estimation problem.

Several deep learning approaches have been attempted for the vehicle system state estimation, and the estimator is represented with deep neural network (NN) [12]. Spiller et al. [13] developed an estimation error model, and proposed a filter learning strategy to minimize the mean squared estimation error with filter gain weighting. The proposed learning filter was able to tune itself according to the uncertainties of the process model, and the boundedness of estimation error h was proved. The filter gain was learned via deep learning, while this method required the measurements of all the states. Korayem et al. [14] and Bonfitto et al. [15] implemented the deep learning techniques to estimate the vehicle slip angle as well as the road angle. The trained neural network could perform accurate estimates at different terrain conditions. Tian et al. [16] proposed a framework for estimating model parameters on the basis of Actor-Critic reinforcement learning (RL). This method was demonstrated and compared using different nonlinear models. The experimental results were also evaluated, and it outperforms the traditional methods in terms of speed, robustness and accuracy.

RL is therefore an alternative method for high-dimensional state estimation problems. RL has been previously applied and achieved superior performances for various challenging domains, such as autonomous driving [17, 18], Atari games [19], and Go [20,21,22]. As stated in Li’s book [10], reinforcement learning is an effective iterative framework widely used in optimal decision-making and control. It generally contains two revolving iteration procedures, namely policy evaluation (PEV) and policy improvement (PIM). The former computes the value function for a fixed policy, and the latter improves the policy by selecting the action that maximizes the inferred value function. Reinforcement learning was shown to be able to handle high-dimensional problems when employing high-capacity approximate functions such as neural networks as its policy and value functions [20, 23].

In this paper, an approximate optimal filter (AOF) framework is proposed by considering accumulated estimation error, which is designed and solved via reinforcement learning. The contributions are: (1) theoretically prove the equivalence between the optimal filter and the AOF in linear systems with Gaussian noise; (2) develop an optimal filtering framework for solving the optimal filter gain by Actor-Critic reinforcement learning.

The rest of the paper is organized as follows. Section 2 describes the problem formulation. In Section 3, the AOF framework is introduced. In Section 4, the estimation-control duality and equivalence are discussed. Section 5 introduces the Actor-Critic reinforcement learning algorithm in order to solve the optimal filter gain. Section 6 provides the simulation example. Section 7 concludes this paper.

2 Problem Definition

2.1 Stochastic System

This study considers a stochastic closed-loop control system with linear time-invariant characteristics and its state estimation as a demonstration, in the form of:

$$\left\{ {\begin{array}{*{20}c} {\varvec{x}_{t + 1} = {\varvec{A}}\varvec{x}_{t} + {\varvec{B}}u_{t} + {\varvec{E}}\xi_{t} } \\ {\varvec{y}_{t} = {\varvec{C}}\varvec{x}_{t} + {\varvec{D}}u_{t} + \zeta_{t} } \\ \end{array} } \right.$$
(1)

where \(t\) is the discrete time step, \(\varvec{x}_{t} \in \varvec{\mathbb{R}}^{n}\) is system state, \(u_{t} \in \varvec{\mathbb{R}}^{m}\) is control input, \(\varvec{y}_{t} \in \varvec{\mathbb{R}}^{r}\) is the available measurement, \(\varvec{\xi}_{t} \in \varvec{\mathbb{R}}^{n}\) is the process noise, and \(\zeta_{t} \in \varvec{\mathbb{R}}^{r}\) is the measurement noise, \({\varvec{A}},\;{\varvec{B}},\;{\varvec{C}},\;{\varvec{D}}\) and \({\varvec{E}}\) are the system characteristic matrices with compatible dimensions.

The process noise \(\varvec{\xi}_{t}\), measurement noise \(\zeta_{t}\), and initial state \(\varvec{x}_{0}\) are assumed as: (1) \(\varvec{\xi}_{t}\) and \(\zeta_{t}\) are individually zero mean, Gaussian white noise with known covariance; (2) \(\varvec{\xi}_{t}\) and \(\zeta_{t}\) are independent, and independent of the initial state \(\varvec{x}_{0}\); and (3) initial state \(\varvec{x}_{0} \sim {\mathcal{N}}\left( {\varvec{\overline{x}_{0}} ,\Sigma_{0}^{2} } \right)\), where \({\varvec{\overline{x}_{0}}}_{0}\) and \({\Sigma }_{0}^{2}\) is the mean and covariance of initial state, respectively. These assumptions can also be represented as:

$$\begin{gathered} \varvec{\mathbb{E}}\left\{ {\xi_{k} } \right\} = 0,\varvec{\mathbb{E}}\left\{ {\zeta_{k} } \right\} = 0,\varvec{\mathbb{E}}\left\{ {\varvec{\xi}_{k} \zeta_{l}^\text{T} } \right\} = 0 \hfill \\ \varvec{\mathbb{E}}\left\{ {\varvec{\xi}_{k} \varvec{\xi}_{l}^\text{T} } \right\} = {\varvec{Q}}\delta_{k,l} ,\varvec{\mathbb{E}}\left\{ {\zeta_{k} \zeta_{l}^\text{T} } \right\} = {\varvec{R}}\delta_{k,l} \hfill \\ \end{gathered}$$
(2)

where \(\delta_{k,l}\) is Kronecker delta function for all time step \(k\) and \(l\), \({\varvec{Q}}\) and \({\varvec{R}}\) are the covariance of process noise and measurement noise, respectively.

2.2 Optimal State Estimation Criterion

The generally used optimal estimation criterion in the literature is to minimize the expected mean square error (MSE) between the estimate and true state [3], given the history information \(\varvec{y}\):

$$\min \varvec{\mathbb{E}}\left\{ {\left\| {\varvec{x}_{t} - \varvec{\hat{x}}_{t} } \right\|_{2}^{2} \left| \varvec{y} \right.} \right\}$$
(3)

where \(\varvec{\hat{x}}_{t} \in \varvec{\mathbb{R}}^{n}\) is the estimated state and \(\varvec{y}\) represents the history information \(\left( {\varvec{\hat{x}}_{0} ,\varvec{y}_{0:t} } \right)\) up to the current time \(t\), containing the necessary initial estimation value and historical measurements data. Note that \({\varvec{\hat{x}}}_{0}\) is the initial estimate and \(\varvec{y}_{0:t}\) denotes the measurement from time step 0 to \(t\). Similar to Kalman filter, the optimal state estimation at time step \(t\), \({\varvec{\hat{x}}}_{t}\), in this study is assumed to have a linear structure in the form of:

$${\varvec{\hat{x}}}_{t} = {\varvec{A}}{\varvec{\hat{x}}}_{t - 1} + {\varvec{B}}u_{t - 1} + {\varvec{L}}_{t - 1} \left( {\varvec{y}_{t} - \varvec{\hat{x}}_{t} } \right)$$
(4)

where \(L_{t - 1} \in \varvec{\mathbb{R}}^{n \times r}\) is the filter gain for the measurement innovation, \(\varvec{\hat{x}}_{t} = {\varvec{C}}\left( {{\varvec{A}}{\varvec{\hat{x}}}_{t - 1} + {\varvec{B}}u_{t - 1} } \right) + {\varvec{D}}u_{t}\) is the predicted measurement at time step \(t\). It should be noted that \({\varvec{L}}_{t - 1}\) is usually denoted as \({\varvec{L}}_{t}\) for traditional filtering problem, while it is regarded as the control input calculated for time step \(t\) and denoted as \({\varvec{L}}_{t - 1}\) for the convenience of subsequent RL setup.

The optimal estimation problem is to find an optimal filter gain \({\varvec{L}}^{*} \in \varvec{\mathbb{R}}^{n \times r}\) which can minimize the expected MSE of estimation error in Eq. (3). For simplicity, this paper defines the estimation error as \(\varvec{\tilde{x}}_{t}\)≝\(\varvec{x}_{t} - {\varvec{\hat{x}}_{t}}\), and the stochastic dynamics of the estimation error can be derived, given the history information up to the current time \(t\), as:

$$\varvec{\tilde{x}}_{t} = \left( {{\varvec{I}} - {\varvec{L}}_{t - 1} {\varvec{C}}} \right)\left( {{\varvec{A}}\varvec{\tilde{x}}_{t - 1} + {\varvec{E}}\varvec{\xi}_{t - 1} } \right) - {\varvec{L}}_{t - 1} \zeta_{t}$$
(5)

Since the optimal state estimate in the previous step has been proved to contain all the previous information for linear systems [3]. The conditional expectation can thus be transformed into an unconditional expectation, and the optimal state estimation problem expressed in Eqs. (3) and (4) can be transformed into the optimal criterion in the form of:

$$\mathop {\min }\limits_{{L_{t - 1} }} \varvec{\mathbb{E}}_{{\varvec{\tilde{x}}_{t} }} \left\{ {\varvec{\tilde{x}}_{t}^\text{T} \varvec{\tilde{x}}_{t} } \right\}$$
(6)

3 Approximate Optimal Filter

On the basis of the estimation-control duality and for the purpose of a more stable filter gain, the considered estimation problem is transformed into a corresponding dual optimal control problem, using the estimation error \(\varvec{\widetilde{x}}_{t}\) as the surrogate system state and the filter gain \({L}_{t-1}\) as the control action. The optimal criterion is generalized into an infinite horizon optimal criterion. An equivalent AOF problem is therefore established and can be solved by RL method considering various initial and predictive information, in order to obtain the optimal filter gain. The detailed AOF problem formulation and reinforcement learning setup are presented as below.

For the considered AOF problem, the RL environment dynamics is derived using Eqs. (1), (4) and (5), via state transition to the next time step \(t + 1\), in the form of:

$$\varvec{\tilde{x}}_{t + 1} = f\left( {\varvec{\tilde{x}}_{t} ,{\varvec{L}}_{t} } \right) = \left( {{\varvec{I}} - {\varvec{L}}_{t} {\varvec{C}}} \right)\left( {{\varvec{A}}\varvec{\tilde{x}}_{t} + {\varvec{E}}\varvec{\xi}_{t} } \right) - {\varvec{L}}_{t} \zeta_{t + 1}$$
(7)

A deterministic filter gain policy \(\pi \left( \cdot \right)\) is selected to represent the mapping from estimate error \(\varvec{\tilde{x}}_{t}\) to filter gain \(L_{t} ,\) i.e.

$${\varvec{L}}_{t} = \pi \left( {\varvec{\tilde{x}}_{t} } \right)$$
(8)

In order to solve this AOF problem using reinforcement learning which can account for various initial and predictive information, a reward signal \(r_{t}\) at time step \(t\), as function of estimation error is formulated by:

$$r_{t} = - \varvec{\tilde{x}}_{t}^{{\text{T}}} \varvec{\tilde{x}}_{t} = - {\text{tr}}\left( {\varvec{\tilde{x}}_{t}^{{\text{T}}} \varvec{\tilde{x}}_{t} } \right)$$
(9)

where \(\text{tr}\left( \cdot \right)\) denotes the matrix trace.

The target of AOF problem is then designed to minimize the discounted accumulative reward signals in the infinite time horizon, under the conditions of initial state distribution \(d_{0}\), environment dynamics \(f\left( \cdot \right)\) and filter gain policy \(\pi \left( \cdot \right)\), as:

$$J\left( \pi \right) = \varvec{\mathbb{E}}_{{\varvec{\tilde{x}}_{0} \sim d_{0} ,\varvec{\tilde{x}}_{t} \sim f }} \left\{ {\mathop \sum \limits_{t = 1}^{\infty } \gamma^{t - 1} r_{t} } \right\} = \varvec{\mathbb{E}}_{\pi } \left\{ {\mathop \sum \limits_{t = 1}^{\infty } \gamma^{t - 1} r_{t} } \right\}$$
(10)

where \(\gamma\) is the discount factor. \(\varvec{\mathbb{E}}_{\pi } \left\{ \cdot \right\}\) denotes the expectation of a random variable relative to the trajectory distribution induced both policy \(\pi\) and initial state \(\varvec{\tilde{x}}_{0}\). The discounting factor is in the range of \(0 \le \gamma < 1\). While \(\gamma = 0\), the AOF is "myopic”, which only maximizes the expected immediate rewards, otherwise the estimator is the expected future accumulated reward.

In order to solve AOF via the RL method, the state-value function \(v^{\pi } \left( {\varvec{\tilde{x}}} \right)\) is defined as the expected future accumulate reward from the state \(\varvec{\tilde{x}}\) induced by policy \(\pi\), as:

$$v^{\pi } \left( {\varvec{\tilde{x}}} \right) = \varvec{\mathbb{E}}_{\pi } \left\{ {\left. {\mathop \sum \limits_{t = 1}^{\infty } \gamma^{t - 1} r_{t} } \right|\varvec{\tilde{x}}_{0} = \varvec{\tilde{x}}} \right\}$$
(11)

The action-value \(q^{\pi } \left( {\varvec{\tilde{x}},\;\;L} \right)\) is the expected future accumulated reward induced by policy \(\pi\) after conducting action \({\varvec{L}}\) from the state \(\varvec{\tilde{x}},\) as shown in Eq. (12)

$$q^{\pi } \left( {\varvec{\tilde{x}},L} \right) = \varvec{\mathbb{E}}_{\pi } \left\{ {\left. {\mathop \sum \limits_{t = 1}^{\infty } \gamma^{t - 1} r_{t} } \right|\varvec{\tilde{x}}_{0} = \varvec{\tilde{x}},L_{0} = L} \right\}$$
(12)

Therefore, the AOF problem can be summarized as:

$$\mathop {\max }\limits_{\pi } J\left( \pi \right){\text{ }} = \varvec{\mathbb{E}}_{\pi } \left\{ { - \sum\limits_{{t = 1}}^{\infty } {\gamma ^{{t - 1}} } \varvec{\tilde{x}}_{t}^\text{T} \varvec{\tilde{x}}_{t} } \right\}$$
(13)

s.t \(\varvec{\tilde{x}}_{{t + 1}} {\text{ }} = \left( {\user2{I} - \pi \left( {\varvec{\tilde{x}}_{t} } \right)\user2{C}} \right)\left( {\user2{A}\varvec{\tilde{x}}_{t} + \varvec{\xi} _{t} } \right) - \pi \left( {\varvec{\tilde{x}}_{t} } \right)\zeta _{{t + 1}} {\text{ }}\)

It can be noticed that the objective function in Eq. (13) is equal to \(\varvec{\mathbb{E}}_{{\varvec{\tilde{x}}_{0} }} \left\{ {v^{\pi } \left( {\varvec{\tilde{x}}_{0} } \right)} \right\}\) and \(\varvec{\mathbb{E}}_{{\varvec{\tilde{x}}_{0} }} \left\{ {q^{\pi } \left( {\varvec{\tilde{x}}_{0} ,\pi \left( {\varvec{\tilde{x}}_{0} } \right)} \right)} \right\}\) using Eqs. (11) and (12), respectively. The optimal policy \(\pi^{*}\), i.e., optimal filter gain which maximize the state-value and can be defined as:

$$\pi^{*} = \mathop {{\text{argmax}}}\limits_{\pi } v^{\pi } \left( {\varvec{\tilde{x}}} \right)$$
(14)

The AOF framework thus formulates a dual optimal control problem from optimal filtering problem, which could be solved by RL algorithms. Section 4 will prove that both the Kalman gain and the steady-state Kalman gain are the optimal solution of the AOF problem in particular cases, i.e., the AOF problem is equivalent to the optimal filtering problem given certain conditions.

4 Equivalence of Optimal Filtering and Approximate Optimal Filter Problem

This section will take the general linear system with Gaussian noise as an example, and prove that transforming the optimal filtering (OF) problem into a dual infinite horizon optimal control problem does not change the optimal filter gain.

4.1 OF Problem in Linear System

4.1.1 The Optimal Solution to the OF Problem

The following Lemma gives the form of Kalman gain, which is the optimal solution to the OF problem.

Lemma 1: Kalman Filter's Recursion [3]

Kalman filter is usually recursion in 2 steps. In what follows, \({\widehat{\Sigma }}_{{n}|{m}}\) and \({\widehat{{x}}}_{{n}|{m}}\) denotes using information up to time \(\mathrm{m}\) to estimated covariance and state, respectively, in time \(n\). For \(t = 0\), initialize predict error covariance \(\hat{\Sigma }_{0| - 1} = \Sigma_{0}^{2}\) and \(\varvec{\hat{x}}_{0| - 1} = \varvec{\overline{x}}_{0}\). For \(t \ge 1\), recurse in the following two steps:

Time update:

Predict state estimate: \(\varvec{\hat{x}}_{t|t - 1} = {\varvec{A}}\varvec{\hat{x}}_{t - 1|t - 1} + {\varvec{B}}u_{t - 1}\).

Predict error covariance:

$$\hat{\Sigma }_{t|t - 1} = {\varvec{A}}\hat{\Sigma }_{t - 1|t - 1} {\varvec{A}}^\text{T} + {\varvec{EQE}}^\text{T}$$
(15)

where \(\varvec{E}\) is the characteristic matrix of the process noise \(\varvec{\xi}\), as termed in Eq. (1).

Measurement update:

The Kalman gain:

$${\varvec{K}}_{t} = \hat{\Sigma }_{t|t - 1} {\varvec{C}}^\text{T} \left( {{\varvec{C}}\hat{\Sigma }_{t|t - 1} {\varvec{C}}^\text{T} + {\varvec{R}}} \right)^{ - 1}$$
(16)

Update state estimate: \(\varvec{\hat{x}}_{t|t} = \varvec{\hat{x}}_{t|t - 1} + {\varvec{K}}_{t} \left( {\varvec{y}_{t} - \varvec{\hat{x}}_{t|t - 1} } \right)\).

Update error covariance: \(\hat{\Sigma }_{t|t} = {\varvec{A}}\hat{\Sigma }_{t|t - 1} {\varvec{A}}^{{\text{T}}} + {\varvec{EQE}}^{{\text{T}}}\).

4.1.2 The Optimal Solution in AOF

It can be noticed that the Kalman gain \({K}_{t}\), before the calculation of state estimation \(\varvec{\widehat{x}}_{t}\), should be subscript \(t-1\) so as to explain the time sequence and for the convenience of the formulated dual optimal control problem. In order to prove the equivalence of AOF problem and the OF problem in linear Gaussian system, the optimal criterion defined in Eq. (3) is used. If all the previous estimates are optimal, only one step in the linear Gaussian case needs to be considered, and the one-step optimal criterion in Eq. (6) is applied. The optimization problem is in the form of:

$$\begin{gathered} \mathop {\min }\limits_{{L_{{t - 1}} }} J = \varvec{\mathbb{E}}_{{\varvec{\hat{x}}_{t} }} \left\{ {\left( {\varvec{x}_{t} - \varvec{\hat{x}}_{t} } \right)^\text{T} \left( {\varvec{x}_{t} - \varvec{\hat{x}}_{t} } \right)\left| {\varvec{\hat{x}}_{{t - 1}}^{*} ,\varvec{y}_{t} } \right.} \right\} = \varvec{\mathbb{E}}_{{\varvec{\tilde{x}}_{t} }} \left\{ {\varvec{\tilde{x}}_{t}^\text{T} \varvec{\tilde{x}}_{t} } \right\} \hfill \\ {\text{s}}.{\text{t}}.\;\;\;\varvec{\tilde{x}}_{{t + 1}} = \left( {\user2{I} - \user2{L}_{t} \user2{C}} \right)\left( {\user2{A}\varvec{\tilde{x}}_{t} + \varvec{\xi} _{t} } \right) - \mathbf{L}_{t} \zeta _{{t + 1}}, \;\;\;\varvec{\tilde{x}}_{{t - 1}}^{*} \sim d_{{\varvec{\tilde{x}}^{*} ,\;t - 1}} \hfill \\ \end{gathered}$$
(17)

where \(\varvec{\tilde{x}}_{t-1}^{*}\) denotes the previous optimal estimation error, which is a random variable that follows a distribution \({d}_{\varvec{\tilde{x}}}^{*},t-1\).

Proposition 1

OF problem in time-invariant linear Gaussian system in Eq. (17) could be solved by AOF framework in Eq. (13) by setting the initial state distribution\({\mathrm{d}}_{0}={\mathrm{d}}_{\varvec{\widetilde{x}}}^{*},\mathrm{t}-1\). The Kalman gain is the optimal action of action value function weighted by distribution \({\text{d}}_{\varvec{\tilde{x}}^{*} ,{\text{t}} - 1}\), i.e.,

$${\varvec{K}}_{t} = \mathop {{\text{argmax}}}\limits_{{{\varvec{L}}_{t - 1} }} \varvec{\mathbb{E}}_{{\varvec{\tilde{x}}_{0} }} \left\{ {q^{{\pi^{*} }} \left( {\varvec{\tilde{x}}_{0} ,{\varvec{L}}_{t - 1} } \right)} \right\},\varvec{\tilde{x}}_{0} \sim d_{{\varvec{\tilde{x}}^{*} ,t - 1}}$$
(18)

Proof: Since action-value considers infinite time horizon. It should be proved that the optimal action does not change by considering \(n\) steps, \(n \ge 1\). First, consider the RL environment dynamics and one step objective function \({J}_{1}\) as:

$$\begin{aligned} J_{1} = & \varvec{\mathbb{E}}_{{\varvec{\tilde{x}}_{0} ,\varvec{\xi}_{0} ,\zeta_{1} }} \left\{ { - \varvec{\tilde{x}}_{1}^{{\text{T}}} \varvec{\tilde{x}}_{1} } \right\} = \varvec{\mathbb{E}}_{{\varvec{\tilde{x}}_{0} ,\varvec{\xi}_{0} ,\zeta_{1} }} \left\{ {{\text{tr}}\left[ { - \varvec{\tilde{x}}_{1} \varvec{\tilde{x}}_{1}^{{\text{T}}} } \right]} \right\} \\ & = - {\text{tr}}[\left( {{\varvec{I}} - {\varvec{L}}_{0} {\varvec{C}}} \right){\varvec{A}}\varvec{\mathbb{E}}_{{\varvec{\tilde{x}}_{0} }} \left\{ {\varvec{\tilde{x}}_{0} \varvec{\tilde{x}}_{0}^{{\text{T}}} } \right\}{\varvec{A}}^{{\text{T}}} \left( {{\varvec{I}} - {\varvec{L}}_{0} {\varvec{C}}} \right)^{{\text{T}}} \\ & + \left( {{\varvec{I}} - {\varvec{L}}_{0} {\varvec{C}}} \right){\varvec{Q}}\left( {{\varvec{I}} - {\varvec{L}}_{0} {\varvec{C}}} \right)^{{\text{T}}} + {\varvec{L}}_{0} {\varvec{RL}}_{0}^{{\text{T}}} ] \\ \end{aligned}$$
(19)

Denote \(\varvec{\mathbb{E}}_{{\varvec{\tilde{x}}_{0} }} \left\{ {\varvec{\tilde{x}}_{0} \varvec{\tilde{x}}_{0}^{T} } \right\}\) as \(P_{0}\). The saddle point only happens when \(\frac{{\partial J_{1} }}{{\partial L_{0} }} = 0\) yield:

$$\begin{aligned} \frac{{\partial J_{1} }}{{\partial {\varvec{L}}_{0} }} = & 2\left( {{\varvec{CA}}P_{0} {\varvec{A}}^{{\text{T}}} + {\varvec{CQ}}} \right)^{{\text{T}}} \\ & - 2{\varvec{L}}_{0} \left( {{\varvec{CA}}P_{0} {\varvec{A}}^{{\text{T}}} {\varvec{C}}^{{\text{T}}} + {\varvec{CQC}}^{{\text{T}}} + {\varvec{R}}} \right){ = 0 } \\ \end{aligned}$$
(20)

i.e.

$${\varvec{L}}_{0}^{*} = \left( {{\varvec{CA}}P_{0} {\varvec{A}}^{{\text{T}}} + {\varvec{CQ}}} \right)^{{\text{T}}} \left( {{\varvec{CA}}P_{0} {\varvec{A}}^{{\text{T}}} {\varvec{C}}^{{\text{T}}} + {\varvec{CQC}}^{{\text{T}}} + {\varvec{R}}} \right)^{ - 1} { }$$
(21)

For any time step \(t \ge 1\), denote that

$$\begin{aligned} P_{t} \left( {{\varvec{L}}_{t - 1} } \right) = & \left( {{\varvec{I}} - {\varvec{L}}_{t - 1} {\varvec{C}}} \right){\varvec{A}}P_{t - 1} {\varvec{A}}^{{\text{T}}} \left( {{\varvec{I}} - {\varvec{L}}_{t - 1} {\varvec{C}}} \right)^{{\text{T}}} { } \\ & + \left( {{\varvec{I}} - {\varvec{L}}_{t - 1} {\varvec{C}}} \right){\varvec{AQA}}^{{\text{T}}} \left( {{\varvec{I}} - {\varvec{L}}_{t - 1} {\varvec{C}}} \right)^{{\text{T}}} { } + {\varvec{G}}_{t - 1} {\varvec{LG}}_{t - 1}^{{\text{T}}} \\ \end{aligned}$$
(22)

Next, consider the two-step objective function \(J_{2}\),

$$\begin{aligned} J_{2} = & \varvec{\mathbb{E}}_{{\varvec{\tilde{x}}_{0} ,\varvec{\xi}_{0} ,\zeta_{1} ,\varvec{\tilde{x}}_{1} ,\varvec{\xi}_{1} ,\zeta_{2} }} \left\{ { - \varvec{\tilde{x}}_{1}^{{\text{T}}} \varvec{\tilde{x}}_{1} - \gamma \varvec{\tilde{x}}_{2}^{{\text{T}}} \tilde{x}_{2} } \right\}{ } \\ & = \varvec{\mathbb{E}}_{{\varvec{\tilde{x}}_{0} ,\varvec{\xi}_{0} ,\zeta_{1} ,\varvec{\tilde{x}}_{1} ,\varvec{\xi}_{1} ,\zeta_{2} }} \left\{ { - {\text{tr}}\left[ {\varvec{\tilde{x}}_{1} \varvec{\tilde{x}}_{1}^{{\text{T}}} } \right] - \gamma {\text{tr}}\left[ {\varvec{\tilde{x}}_{2} \varvec{\tilde{x}}_{2}^{{\text{T}}} } \right]} \right\} \\ & = - {\text{tr}}[P_{1} \left( {{\varvec{L}}_{0} } \right){ } + \gamma \left( {{\varvec{I}} - {\varvec{L}}_{1} {\varvec{C}}} \right){\varvec{A}}P_{1} \left( {{\varvec{L}}_{0} } \right){\varvec{A}}^{{\text{T}}} \left( {{\varvec{I}} - {\varvec{L}}_{1} {\varvec{C}}} \right)^{{\text{T}}} \\ { } & + \left( {{\varvec{I}} - {\varvec{L}}_{1} {\varvec{C}}} \right){\varvec{Q}}\left( {{\varvec{I}} - {\varvec{L}}_{1} {\varvec{C}}} \right)^{{\text{T}}} + {\varvec{L}}_{1} {\varvec{RL}}_{1}^{{\text{T}}} ] \\ \end{aligned}$$
(23)

The saddle point only happens when \(\frac{{\partial J_{2} }}{{\partial L_{0} }} = 0\) and \(\frac{{\partial J_{2} }}{{\partial L_{1} }} = 0\) yield

$$\begin{gathered} \frac{{\partial J_{2} }}{{\partial \user2{L}_{0} }} = 2\left( {\user2{CA}P_{0} \user2{A}^\text{T} + \user2{CQ}} \right)^\text{T} \hfill \\ \quad \quad \quad - 2\user2{L}_{0} \left( {\user2{CA}P_{0} \user2{A}^\text{T} \user2{C}^\text{T} + \user2{CQC}^\text{T} + \user2{R}} \right) \hfill \\ \quad \quad \quad - \gamma \left\{ {\user2{A}^\text{T} \left( {\user2{I} - L_{1} \user2{C}} \right)^\text{T} \left( {\user2{I} - \user2{L}_{1} \user2{C}} \right)\user2{A}} \right. \hfill \\ \quad \quad \quad \left[ { - 2\left( {\user2{CA}P_{0} \user2{A}^\text{T} + \user2{CQ}} \right)^\text{T} } \right. \hfill \\ \quad \quad \quad \left. {\left. { + 2\user2{L}_{0} \left( {\user2{CA}P_{0} \user2{A}^\text{T} \user2{C}^\text{T} + \user2{CQC}^\text{T} + \user2{R}} \right)} \right]} \right\}^\text{T} = 0 \hfill \\ \end{gathered}$$
(24)
$$\begin{aligned} \frac{{\partial J_{2} }}{{\partial {\varvec{L}}_{1} }} = & 2\gamma \left( {{\varvec{CA}}P_{1} \left( {{\varvec{L}}_{0} } \right){\varvec{A}}^\text{T} + {\varvec{CQ}}} \right)^\text{T} { } \\ & - 2\gamma {\varvec{L}}_{1} \left( {{\varvec{CA}}P_{1} \left( {{\varvec{L}}_{0} } \right){\varvec{A}}^\text{T} {\varvec{C}}^\text{T} + {\varvec{CQ}}C^\text{T} + {\varvec{R}}} \right) = 0 \\ \end{aligned}$$
(25)
$$\begin{gathered} \user2{L}_{0}^{*} = \left( {\user2{CA}P_{0} \user2{A}^\text{T} + \user2{CQ}} \right)^\text{T} \hfill \\ \quad\,\quad \left( {\user2{CA}P_{0} \user2{A}^\text{T} \user2{C}^\text{T} + \user2{CQC}^\text{T} + R} \right)^{{ - 1}} \hfill \\ \user2{L}_{1}^{*} = \left( {\user2{CA}P_{1}^{*} \user2{A}^\text{T} + \user2{CQ}} \right)^\text{T} \hfill \\ \quad \,\quad\left( {\user2{CA}P_{1}^{*} \user2{A}^\text{T} \user2{C}^\text{T} + \user2{CQC}^\text{T} + \user2{R}} \right)^{{ - 1}} \hfill \\ \end{gathered}$$
(26)

The optimal \({\varvec{L}}_{0}^{*}\) is the same as \(J_{1}\). where \(P_{1}^{*}\) is \(P_{1} \left( {{\varvec{L}}_{0}^{*} } \right)\). It is proved by mathematical induction that the optimal solution for \(n\) steps is given by:

$$\begin{gathered} {\varvec{L}}_{0}^{*} = \left( {{\varvec{CA}}P_{0} {\varvec{A}}^\text{T} + {\varvec{CQ}}} \right)^\text{T} { }\left( {{\varvec{CA}}P_{0} {\varvec{A}}^\text{T} {\varvec{C}}^\text{T} + {\varvec{CQ}}C^\text{T} + {\varvec{R}}} \right)^{ - 1} \hfill \\ {\varvec{L}}_{n}^{*} = \left( {{\varvec{CA}}P_{n}^{*} {\varvec{A}}^\text{T} + {\varvec{CQ}}} \right)^\text{T} { }\left( {{\varvec{CA}}P_{n}^{*} {\varvec{A}}^\text{T} {\varvec{C}}^\text{T} + {\varvec{CQC}}^\text{T} + {\varvec{R}}} \right)^{ - 1} \hfill \\ \end{gathered}$$
(27)

where \(P_{n}^{*} = { }P_{n} \left( {{\varvec{L}}_{0}^{*} ,{\varvec{L}}_{1}^{*} , \ldots ,{\varvec{L}}_{n - 1}^{*} } \right)\). This solution is similar to Kalman filter's recursion, which is not affected by the discount factor \(\gamma\).

If \(\varvec{\tilde{x}}_{0} \sim d_{{\varvec{\tilde{x}}^{*} ,t - 1}}\)

$$\begin{aligned} {\varvec{K}}_{t} = & \mathop {{\text{argmax}}}\limits_{{L_{t - 1} }} \varvec{\mathbb{E}}_{{\varvec{\tilde{x}}_{0} }} \left\{ {q^{{\pi^{*} }} \left( {\varvec{\tilde{x}}_{0} ,{\varvec{L}}_{t - 1} } \right)} \right\} \\ & = \left( {{\varvec{CA}}P_{{\varvec{\tilde{x}}^{*} ,t - 1}} {\varvec{A}}^\text{T} + {\varvec{CQ}}} \right)^\text{T} \left( {{\varvec{CA}}P_{{\varvec{\tilde{x}}^{*} ,t - 1}} {\varvec{A}}^\text{T} {\varvec{C}}^\text{T} + {\varvec{CQC}}^\text{T} + {\varvec{R}}} \right)^{ - 1} { } \\ \end{aligned}$$
(28)

where \(P_{{\varvec{\tilde{x}}^{*} ,\;\;t - 1}} = {\mathbb{E}}_{{\varvec{\tilde{x}}_{t - 1}^{*} }} \left\{ {\varvec{\tilde{x}}_{t - 1}^{*} \;\;\;\varvec{\tilde{x}}_{t - 1}^{*{\text{T}}} } \right\}\). The statement is then proved.

4.2 Optimal Filtering Problem in Steady-State in Linear Gaussian System

4.2.1 The Optimal Solution to the OF Problem

Lemma 2: Steady-state Kalman Gain

The steady-state Kalman gain is pre-calculable if the following statements are fulfilled: If \(\left({\varvec{A}},{\varvec{C}}\right)\) is completely observable and \(\left({\varvec{A}},{\varvec{E}}\right)\) is completely controllable, the predicted error covariance matrix \({\widehat{\Sigma }}_{t|t-1}\) would converge to \(\widehat{\Sigma }\) under the Kalman filter recursion. Thus, the steady-state Kalman gain \({K}_{\infty }\) could be calculated before any observation is made. \(\widehat{\Sigma }\) satisfies discrete-time algebraic Riccati equation as:

$$\hat{\Sigma } = {\varvec{A}}\hat{\Sigma }{\varvec{A}}^\text{T} - {\varvec{A}}\hat{\Sigma }{\varvec{C}}^\text{T} \left( {{\varvec{C}}\hat{\Sigma }{\varvec{C}}^\text{T} + {\varvec{R}}} \right)^{ - 1} {\varvec{C}}\hat{\Sigma }{\varvec{A}}^\text{T}$$
(29)

Steady-state Kalman gain \({\varvec{K}}_{\infty }\) is:

$${\varvec{K}}_{\infty } = \hat{\Sigma }{\varvec{C}}^\text{T} \left( {{\varvec{C}}\hat{\Sigma }{\varvec{C}}^\text{T} + {\varvec{R}}} \right)^{ - 1}$$
(30)

Steady-state Kalman filter output estimate by:

$$\varvec{\hat{x}}_{t} = {\varvec{A}}\varvec{\hat{x}}_{t - 1} + {\varvec{B}}u_{t - 1} + {\varvec{K}}_{\infty } \left( {\varvec{y}_{t} - \varvec{\hat{x}}_{t|t - 1} } \right)$$
(31)

The Kalman gain converges when the estimation error becomes a stationary distribution. In other words, the estimation error is considered steady under a time-invariant gain.

4.2.2 The Optimal Solution in AOF

Proposition 2

The AOF framework could solve the OF problem in steady-state in linear system by setting AOF's initial state as steady-state distribution and using a state-independent time-invariant matrix as the policy directly.

Proof: When the terminal time \(T\) is sufficiently large, the estimation error distribution becomes stationary distribution \({d}_{\varvec{\tilde{x}},\mathrm{ steady}}\) under \({{\varvec{L}}}_{t-1}\) which makes spectral radius \(\rho \left[ {\left( {{\varvec{I}} - {\varvec{L}}_{t - 1} {\varvec{C}}} \right)A} \right] = \mathop {\max }\limits_{1 \le t \le n} \left| {\lambda_{t} } \right| < 1\). Following this, the OF problem in steady-state is derived as:

$$\begin{aligned} \mathop {\min }\limits_{{L_{t - 1} }} J & = \varvec{\mathbb{E}}_{{\varvec{\tilde{x}}_{t} }} \left\{ {\varvec{\tilde{x}}_{t}^{{\text{T}}} \varvec{\tilde{x}}_{t} } \right\} \cong \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\mathop \sum \limits_{t}^{t + T} \varvec{\tilde{x}}_{t}^{{\text{T}}} \varvec{\tilde{x}}_{t} \\{\text{s}}.{\text{t}}.{ }\varvec{\tilde{x}}_{t + 1} & = \left( {{\varvec{I}} - {\varvec{L}}_{t} {\varvec{C}}} \right)\left( {{\varvec{A}}\varvec{\tilde{x}}_{t} + \varvec{\xi}_{t} } \right) - {\varvec{L}}_{t} \zeta_{t + 1} \varvec{\tilde{x}}_{t - 1}^{*} \sim d_{{\varvec{\tilde{x}}^{*} ,{\text{ steady}}}} \\ \end{aligned}$$
(32)

where previous optimal estimation error \(\varvec{\tilde{x}}_{t - 1}^{*}\) is in steady-state and \(d_{{\varvec{\tilde{x}}^{*} , \;stead\varvec{A}}}\) is its distribution. AOF framework could extend to Eq. (32) by setting the filter gain given by policy \(\pi\) and the initial state \(\varvec{\tilde{x}}_{0} = \varvec{\tilde{x}}_{t - 1}^{*} ,d_{0} = d_{{\varvec{\tilde{x}}^{*} ,{\text{steady}}}}\). Optimization object could be extended to average reward or discounted reward [10] in the form of:

$$\begin{aligned} \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\mathop \sum \limits_{t = 1}^{t + T} \varvec{\tilde{x}}_{t}^\text{T} \varvec{\tilde{x}}_{t} & = \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\mathop \sum \limits_{t = 1}^{t + T} \varvec{\mathbb{E}}_{\pi } \left\{ {\varvec{\tilde{x}}_{t}^\text{T} \varvec{\tilde{x}}_{t} } \right\} \\ & = \frac{1}{1 - \gamma }\mathop \sum \limits_{t = 1}^{\infty } \varvec{\mathbb{E}}_{\pi } \left\{ { - \gamma^{t - 1} r_{t} } \right\} \\ \end{aligned}$$
(33)

From Eqs. (32) and (33), a particular AOF problem is formulated as:

$$\begin{aligned} \mathop {\max }\limits_{\pi } J\left( \pi \right) & = \varvec{\mathbb{E}}_{\pi } \left\{ {\mathop \sum \limits_{t = 1}^{\infty } \gamma^{t - 1} r_{t} } \right\}{\text{s}}.{\text{t}}.{ }\varvec{\tilde{x}}_{t + 1} \\ & = \left( {{\varvec{I}} - {\varvec{L}}_{t} {\varvec{C}}} \right)\left( {{\varvec{A}}\varvec{\tilde{x}}_{t} + \varvec{\xi}_{t} } \right) - {\varvec{L}}_{t} \zeta_{t + 1}, \varvec{\tilde{x}}_{0} \sim d_{{\varvec{\tilde{x}}^{*} ,{\text{ steady}}}} \\ \end{aligned}$$
(34)

which is an AOF problem in Eq. (13) when the initial state is steady. If the policy is restricted to a state-independent time-invariant matrix, i.e., \(\pi = L\). Then the optimal policy \({\pi }^{*}\) is steady-state Kalman gain. This result will be verified by numerical experiments.

In this Section, it is proved that no matter what initial state distribution \(d_{0}\) is, the optimal action of AOF is the same as Kalman gain. Therefore, the optimality is preserved, and the steady-state Kalman gain is optimal AOF action while initial state is steady.

5 Reinforcement Learning Algorithm

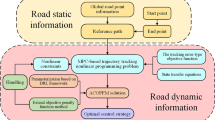
On the basis of the established AOF problem, a reinforcement learning (RL) algorithm as described in Ref. [23] is implemented, in order to solve the AOF problem in infinite horizon and obtain an optimal policy of Eq. (34). The process of selected Actor-Critic RL algorithm is illustrated in Fig. 1, including iterative Policy Evaluation (PEV) and Policy Improvement (PIM) after the initialization.

Fig. 1
figure 1

The process of the Actor-Critic RL algorithm

Full size image

For presentation simplicity, \({\varvec{\widetilde{x}}}^{^{\prime}}\) denotes the state at the next time step of \(\varvec{\widetilde{x}}\), and \(k\) is the iteration step of RL. The RL algorithm involves a parameterized critic function \(V\left(\varvec{\widetilde{x}};w\right)\) (Critic) for value approximation and a parameterized actor function \(\pi \left(\varvec{\widetilde{x}}; \theta \right)\) (Actor), for policy approximation, which optimizes the state trajectory starting from an initial state distribution.

The RL environment model is represented in Eq. (7), and an initial state sampler is applied to obtain the initial state. The filter gain policy \(\pi\) is parameterized as:

$$\pi \left( {\varvec{\tilde{x}};\;\theta } \right) = {\varvec{L}}$$
(35)

where \(\theta\) is the parameter matrix of policy \(\pi \in \varvec{\mathbb{R}}^{n\times r}\). The state-value is approximated as \(V\left(\varvec{\widetilde{x}}; w\right)\) which is a mapping from \(\mathcal{S}\to \varvec{\mathbb{R}}^{-}\) and \(w\) is the function parameter. Detailed initialization, policy evaluation and policy improvement process are explained below.

5.1 Sample Initial State

As described in the previous section, the AOF problem is solved with the initial state following the distribution \({d}_{\varvec{\widetilde{x}},steady}\), i.e., \({\varvec{\widetilde{x}}}_{0}\sim {d}_{\varvec{\widetilde{x}}, steady}\). At the beginning of the Actor-Critic RL algorithm, a batch of initial states in \({d}_{\varvec{\widetilde{x}}, steady}\) need to be sampled, as:

$${\mathcal{B}} = \left\{ {\varvec{\tilde{x}}^{\left( 0 \right)} ,\varvec{\tilde{x}}^{\left( 1 \right)} , \ldots ,\varvec{\tilde{x}}^{\left( j \right)} , \ldots ,\varvec{\tilde{x}}^{{\left( {M - 1} \right)}} } \right\}$$
(36)

where M is the batch size.

5.2 Policy Evaluation (PEV)

In order to converge to an optimal state value, as expressed in Eq. (11), the immediate reward signal \(r\left(\varvec{\widetilde{x}},\pi \left(\varvec{\widetilde{x}};\theta \right)\right)\) is used to update the Critic function \(V\left(\varvec{\widetilde{x}};w\right)\). The time-differential loss function of Critic, \({J}_{\mathrm{critic}}\), is defined as:

$$J_{{{\text{critic}}}} = \varvec{\mathbb{E}}_{{\varvec{\tilde{x}}\sim {\mathcal{B}}}} \left\{ {\frac{1}{2}\left( {r\left( {\varvec{\tilde{x}},\pi \left( {\varvec{\tilde{x}};\theta } \right)} \right) + \gamma V\left( {\varvec{\tilde{x}}^{^{\prime}} ;w} \right) - V\left( {\varvec{\tilde{x}};w} \right)} \right)^{2} } \right\}$$
(37)

where \(V\left(\varvec{\widetilde{x}};w\right)\) and \(V\left({\varvec{\widetilde{x}}}^{^{\prime}};w\right)\) are the approximate state value at current and next time step, respectively, with function parameters of \(w\); \(r\left(\varvec{\widetilde{x}},\pi \left(\varvec{\widetilde{x}};\theta \right)\right)\) is the immediate reward; \(\gamma\) is the discount factor. For the RL updates at current time, the state at the next time step \({\varvec{\widetilde{x}}}^{^{\prime}}\) is calculated using the model derived in Eq. (7).

In Eq. (37), the state \(\varvec{\widetilde{x}}\) follows the distribution of batch \(\mathcal{B}\). The predefined environment model and reward function are used to acquire the next state and reward given action \(\pi \left(\varvec{\widetilde{x}};\theta \right)\). The semi-gradient of the Critic loss is used in order to optimize the Critic function \(V\left(\varvec{\widetilde{x}};w\right)\), which is derived as:

$$\frac{{\partial J_\text{critic} }}{\partial w} = \varvec{\mathbb{E}}_{{\varvec{\tilde{x}}\sim {\mathcal{B}}}} \left\{ {\left( {r\left( {\varvec{\tilde{x}},\pi \left( {\varvec{\tilde{x}};\theta } \right)} \right) + \gamma V\left( {\varvec{\tilde{x}}^{^{\prime}} ;w} \right) - V\left( {\varvec{\tilde{x}};w} \right)} \right)\left( { - \frac{{\partial V\left( {\varvec{\tilde{x}};w} \right)}}{\partial w}} \right)} \right\}$$
(38)

The parameters of Critic function \(w\) are then updated via gradient descend method, as:

$$w_{k + 1} = w_{k} - \alpha \frac{{\partial J_{{{\text{critic}}}} }}{\partial w}$$
(39)

where \({w}_{k}\) and \({w}_{k+1}\) are the parameters at iteration \(k\) and \(k+1\), respectively, and \({\alpha }\) is the learning rate of the Critic function.

5.3 Policy Improvement (PIM)

In the PIM process, the purpose is to update the Actor function \(\pi \left(\varvec{\widetilde{x}};\theta \right)\) using the updated Critic function \({V}^{k}\left(\varvec{\varvec{\widetilde{x}}};w\right)\). The Actor loss function is defined as:

$$J_\text{actor} = \varvec{\mathbb{E}}_{{\varvec{\tilde{x}}\sim {\mathcal{B}}}} \left\{ {r\left( {\varvec{\tilde{x}},\pi \left( {\varvec{\tilde{x}};\theta } \right)} \right) + \gamma V\left( {\varvec{\tilde{x}}^{^{\prime}} ;w} \right)} \right\}$$
(40)

The gradient of Actor's loss function is:

$$\frac{{\partial J_\text{actor} }}{\partial \theta } = \frac{{\partial \varvec{\mathbb{E}}_{{\varvec{\tilde{x}}\sim {\mathcal{B}}}} \left\{ {r\left( {\varvec{\tilde{x}},\pi \left( {\varvec{\tilde{x}};\theta } \right)} \right) + \gamma V\left( {\varvec{\tilde{x}}^{^{\prime}} ;w} \right)} \right\}}}{\partial \theta }$$
(41)

The Actor is updated by gradient ascend method, as:

$$\theta_{k + 1} = \theta_{k} + \beta \frac{{\partial J_\text{actor} }}{\partial \theta }$$
(42)

where \({\theta }_{k}\) and \({\theta }_{k+1}\) are the parameters at iteration \(k\) and \(k+1\), respectively, and \(\beta\) is the learning rate of the Actor function.

5.4 RL Algorithm Design

The pseudo-code for filter gain policy training using Actor-Critic RL is shown as follows:

figure g

Algorithm 1 is trained offline until converges, and the optimal Actor and Critic functions are obtained. Then the optimal gain \({{\varvec{L}}}^{*}\) could be calculated online using the optimal Actor filter gain policy \({\pi }^{*}\).

6 Simulation Results

In this section, the Actor-Critic RL algorithm designed in Sect. 5 is used to solve the AOF problem of automobiles, which will be compared with the steady-state Kalman Filter. The selected simulation example is a typical vehicle sideslip angle estimation problem with noisy lateral acceleration and yaw rate measurements.

6.1 RL Environment Setup

A 2-degrees of freedom (DOF) yaw-plane vehicle model is demonstrated, which has the analytical solutions and facilities method verification. The continuous process model and measurement model are expressed as:

$$\left\{ {\begin{array}{*{20}c} {\varvec{\dot{x}} = \left[ {\begin{array}{*{20}c} {\dot{\beta }_\text{s} } \\ {\dot{\omega }_\text{r} } \\ \end{array} } \right] = \varvec{A}x + \varvec{B}u} \\ {\varvec{y} = \left[ {\begin{array}{*{20}c} {a_{y} } \\ {\omega_\text{r} } \\ \end{array} } \right] = \varvec{C}x + \varvec{D}u} \\ \end{array} } \right.$$
(43)

where

$$\begin{gathered} {\varvec{A}} = \left[ {\begin{array}{*{20}c} {\frac{{\left( {C_\text{f} + C_{r} } \right)}}{{mv_{x} }}} & {\frac{{\left( {aC_\text{f} - bC_\text{r} } \right)}}{{mv_{x}^{2} }} - 1} \\ {\frac{{\left( {aC_\text{f} - bC_\text{r} } \right)}}{{I_{zz} }}} & {\frac{{\left( {a^{2} C_\text{f} + b^{2} C_\text{r} } \right)}}{{v_{x} I_{zz} }}} \\ \end{array} } \right],{\varvec{B}} = \left[ {\begin{array}{*{20}c} { - \frac{{C_\text{f} }}{{mv_{x} }}} \\ { - \frac{{aC_\text{f} }}{{I_{zz} }}} \\ \end{array} } \right] \hfill \\ {\varvec{C}} = \left[ {\begin{array}{*{20}c} {\frac{{\left( {C_\text{f} + C_{r} } \right)}}{m}} & {\frac{{\left( {aC_\text{f} - bC_\text{r} } \right)}}{{mv_{x} }}} \\ 0 & 1 \\ \end{array} } \right],{\varvec{D}} = \left[ {\begin{array}{*{20}c} { - \frac{{C_\text{f} }}{m}} \\ 0 \\ \end{array} } \right] \hfill \\ \end{gathered}$$

In Eq. (43), \(\varvec{x}={\left[\begin{array}{cc}{\beta }_{\mathrm{s}}& {\omega }_{\mathrm{r}}\end{array}\right]}^{\mathrm{T}}\) is the vehicle system state, \({\beta }_{\mathrm{s}}\) is sideslip angle, and \({\omega }_{\mathrm{r}}\) is the yaw rate. The control input is \(u=\delta ,\) which is the front-wheel steer angle. The measurement \(\varvec{y}={\left[\begin{array}{cc}{a}_{y}& {\omega }_{\mathrm{r}}\end{array}\right]}^\text{T}\) includes lateral acceleration and yaw rate of the vehicle. Other parameters are explained and listed in Tables 1 and 2.

Table 1 Parameters of vehicle system dynamics
Full size table
Table 2 Parameters of performance evaluation
Full size table

The discretized model with sample time \(\Delta t\)=0.01 s is applied. The process noise \({\varvec{\xi} }_{1}\) and \({\varvec{\xi} }_{2}\) introduced by side-slope of the road and side wind are considered, along with noise input matrix \({\varvec{E}}\), as expressed in Eq. (44).

$$\varvec{\xi}_{t} = \left[ {\begin{array}{*{20}c} {\varvec{\xi}_{1,t} } \\ {\varvec{\xi}_{2,t} } \\ \end{array} } \right],{ }{\varvec{E}} = \left[ {\begin{array}{*{20}c} {\frac{1}{{mv_{x} }}} & {\frac{1}{{mv_{x} }}} \\ 0 & {\frac{{l_{{\text{a}}} }}{{I_{zz} }}} \\ \end{array} } \right],\varvec{\xi}_{1,t} \sim {\mathcal{N}}\left( {0,\sigma_{{\text{s}}}^{2} } \right),\varvec{\xi}_{2,t} \sim {\mathcal{N}}\left( {0,\sigma_{{\text{w}}}^{2} } \right)$$
(44)

where \({l}_{\mathrm{a}}\) is the length of equivalent moment arm of the side wind, and \({\sigma }_{\bullet }^{2}\) is the respective variance.

The measurement noise is characterized from the Bosch SMI700 datasheet. \({\zeta }_{1}\) and \({\zeta }_{2}\) are measurement noises of vehicle lateral acceleration and yaw rate, respectively, which can be expressed as:

$$\varvec{\zeta }_{t} = \left[ {\begin{array}{*{20}c} {\zeta_{1,t} } \\ {\zeta_{2,t} } \\ \end{array} } \right],\;\;\varvec{\zeta }_{1,t} \sim {\mathcal{N}}\left( {0,\sigma_{y}^{2} } \right),\varvec{\zeta }_{2,t} \sim {\mathcal{N}}\left( {0,\sigma_{r}^{2} } \right)$$
(45)

6.2 Performance Evaluation

In order to reduce the random bias of the simulation, 10,000 estimation trails are averaged for the performance evaluation. Each trajectory has 1000 time steps starting from different initial states. The transient and steady-state performances are investigated by dividing the state trajectories into transient and steady-state period. The critical time \(\widetilde{t}\) is defined as the time when the transient state becomes steady, which is indicated by the log of MSE of SSKF. The average loss in the transient-state is defined as:

$$Loss_\text{tran} = \frac{1}{N}\mathop \sum \limits_{\text{test}} \frac{{\mathop \sum \nolimits_{1}^{{\tilde{t}}} \left( {x_{t} - \hat{x}_{t} } \right)^\text{T} \left( {x_{t} - \varvec{\hat{x}}_{t} } \right)}}{{\tilde{t}}}$$
(46)

where \(\widetilde{t}\) is the critical time. The state after critical time is regarded as steady-state.

The average steady-state loss is in the form of:

$$Loss_\text{ss} = \frac{1}{N}\mathop \sum \limits_\text{test} \frac{{\mathop \sum \nolimits_{{ \tilde{t} + 1}}^{{T_\text{test} }} \left( {\varvec{{x}}_{t} - \varvec{\hat{x}}_{t} } \right)^\text{T} \left( {\varvec{{x}}_{t} - \varvec{\hat{x}}_{t} } \right)}}{{T_\text{test} - \tilde{t}}}$$
(47)

The average loss of full trajectory is:

$$Loss_\text{full} = \frac{1}{N}\mathop \sum \limits_\text{test} \frac{{\mathop \sum \nolimits_{1}^{{T_\text{test} }} \left( {\varvec{{x}}_{t} - \varvec{\hat{x}}_{t} } \right)^\text{T} \left( {\varvec{{x}}_{t} - \varvec{\hat{x}}_{t} } \right)}}{{T_\text{test} }}$$
(48)

As illustrated at the dash line in Fig. 2, critical time \(\tilde{t}\) is 195 steps. The control input \(u\left( t \right)\) is considered as a typical combined sinusoidal steering scenario, in the form of:

$$u\left( t \right) = \frac{{\uppi} }{60}\left[ {\sin \left( {0.2{{\uppi} } t} \right) + \sin \left( {0.5{{\uppi} } t} \right) + \sin \left( {1.5{{\uppi} } t} \right)} \right]$$
(49)
Fig. 2
figure 2

Mean square error of steady-state Kalman Filter

Full size image

Since the filter gain for the considered vehicle sideslip angle estimation is a 2-by-2 matrix and contains 4 elements, the following performance indexes are defined in order to compare the obtained filter gain \({\varvec{L}}\) and the steady-state Kalman gain \({{\varvec{K}}}_{\infty }\):

$${\varvec{D}}_{i,j} = \left| {{\varvec{L}}_{i,j} - {\varvec{K}}_{{\infty { }i,j}} } \right|$$
(50)

The accuracy is defined by:

$${\mathcal{E}}_{i,j} { } = \frac{{{\varvec{D}}_{i,j} }}{{\left| {{\varvec{K}}_{{\infty { }i,j}} } \right|}} \times 100{\text{\% }}$$
(51)

where \({\#}_{i,j}\) indicates the element in row \(i \in \left[ {1,2} \right]\), column \({ }j \in \left[ {1,2} \right]\) of matrix \(\#\) and \(\left| \cdot \right|\) denotes the absolute value. \({\varvec{K}}_{{\infty { }i,j}}\) is the pertinent element in steady-state Kalman gain \(K_{\infty }\). The analytical \({{\varvec{K}}}_{\infty }\) is calculated from Eq. (30).

6.3 Solving via AOF

Since the true state value function \(v^{\pi } \left( {\varvec{\tilde{x}}} \right):{\mathcal{S}} \to \varvec{\mathbb{R}}^{ - }\) is a mapping from state space to negative real number, the approximate state-value function \(V\left( {\varvec{\tilde{x}};w} \right)\) is designed as a negative quadratic function of \(\varvec{\widetilde{x}}\):

$$V\left( {\varvec{\tilde{x}};w} \right) = - \varvec{\tilde{x}}^\text{T} w\varvec{\tilde{x}}$$
(52)

where \(w\) is a positive-symmetric parameter matrix updated in PEV, and \(w\) is initialized as an identity matrix. Meanwhile, a matrix gain is utilized and it is initialized as a zero matrix.

$$\pi \left( {\varvec{\tilde{x}};\theta } \right) = {\varvec{L}} = \left[ {\begin{array}{*{20}c} {\theta_{11} } & {\theta_{12} } \\ {\theta_{21} } & {\theta_{22} } \\ \end{array} } \right]$$
(53)

The initial state \({\mathcal{B}}\) is sampled from running the environment model, with the given initial uniform estimation error \(\varvec{\tilde{x}}_{0} = \left[ {\begin{array}{*{20}c} {E_{1} } & {E_{2} } \\ \end{array} } \right]^{{\text{T}}}\), which is defined as:

$$\begin{gathered} E_{1} \sim {\mathcal{U}}\left[ {\begin{array}{*{20}c} { - \frac{5}{180}{{\uppi}} } & {\frac{5}{180}{{\uppi}} } \\ \end{array} } \right] \hfill \\ E_{2} \sim {\mathcal{U}}\left[ {\begin{array}{*{20}c} { - \frac{10}{{180}}{{\uppi}} } & {\frac{10}{{180}}{{\uppi}} } \\ \end{array} } \right] \hfill \\ \end{gathered}$$
(54)

During the offline training process, the batch size is set as 512, the learning rate of Actor is 0.0001, and the learning rate of Critic is 0.0001. Adam optimization method is implemented to update the parameters of Critic and Actor. The discount factor is set to 0.9999. As illustrated in Fig. 3, the 4 elements in the gain matrix can converge after training, which means the RL policy \(\pi\) converge to steady-state Kalman gain \({\varvec{K}}_{\infty }\). Elements in gain \({\varvec{L}}\) are, respectively, shown in Table 3. The result shows that the differences are less than 1%, which implies the effectiveness of AOF problem formulation and RL algorithm. The obtained yaw rate and slip angle are compared in Fig. 4, demonstrating 20 seconds. It is shown that the filtered sideslip angle could well represent the modeled sideslip angle, even with obvious model uncertainty and noisy measurement of lateral acceleration and yaw rate.

Fig. 3
figure 3

Training process of the 4 gain elements of AOF

Full size image
Table 3 Comparison of the obtained filter gain
Full size table
Fig. 4
figure 4

Comparisons of (a) yaw rate and (b) slip angle

Full size image

6.4 Effects of Discount Factor

In order to further analyze the effect of different discount factors, different filter gain policies learned with different discount factors are compared. Setting remain unchanged compared with previous protocols. The selected discount factors are \(\gamma = \left\{ {0.01,{ }0.25,{ }0.5,{ }0.75,{ }0.99} \right\}\). After averaged over 10 runs for each discount factor, 4 elements in the gain \({\varvec{L}}\) are close to the optimal solution of steady-state Kalman gain \({\varvec{K}}_{\infty }\). Gains learned from different discount factors are shown in Table 4. The accuracy of each element is shown in Table 5, which is less than 5%. Their corresponding performances are shown in Table 6, and the average losses are close to steady-state Kalman gain \({\varvec{K}}_{\infty }\).

Table 4 Filter gain with different discount factor
Full size table
Table 5 Accuracy with different discount factor
Full size table
Table 6 Performance with different discount factor
Full size table

Different discount factors in general reinforcement learning setting lead to different policies, where a larger discount factor makes agents more farsighted to the future reward. However, in Table 4, the policies show negligible effects of choosing different discount factors. This might attribute to the fact that the initial state distribution is assumed to be steady.

7 Conclusions

An approximate optimal filter (AOF) framework is proposed to solve the optimal filter gain, transforms the optimal filtering (OF) problem with minimum expected MSE into an equivalent infinite-horizon optimal control problem. The equivalence between the AOF problem and the OF problem is proved in particular parameter settings. The solutions to the AOF problem are equal to the Kalman gain and the steady-state Kalman gain for a linear Gaussian problem, when the initial state distribution and the policy format are properly designed. The Actor-Critic RL algorithm is designed to solve the established AOF problem in steady state. Simulation results of a vehicle sideslip angle estimation problem, on the basis of measured lateral acceleration and yaw rate, have shown that the RL policy can converge to the optimal steady-state Kalman gain with negligible error. The results demonstrate the effectiveness of the proposed AOF framework, which is promising for high-dimensional nonlinear systems.

Further practical applications of the proposed method and for nonlinear systems will be addressed in the next stage.