Introduction

Functionally graded materials (FGMs) are heterogeneous composites typically made from a mixture of metals and ceramics. The most distinct characteristics of FGMs are their non-uniform microstructures with spatially graduated macro-properties. These materials are designed to improve and optimize the thermo-mechanical characteristics of structures at different scales. Most FGM families are gradually composed of a refractory ceramic to metal. Typically, FGMs are constructed from a mixture of ceramic and metal or a combination of different materials.

The ceramic in the FGM provides a barrier against thermal effects and protects the metal against corrosion and oxidation, as the FGM is hard and reinforced by the metal composition. These materials have received significant attention recently because of their advantages that include decreasing the disparity in material properties and reducing thermal stresses, as well as their use and growth in the fields of aeronautics and aerospace, where they can serve as thermal barriers due to their rich ceramic compositions. FGMs are used in a wide range of applications, including in medicine, the automotive industry, military equipment, electricity, nuclear power, and so on. FGMs are also currently being developed for general use as structural members in extremely high-temperature environments and applications.

Due to the large number of applications of FGMs, several studies have been carried out on the mechanical and thermal behavior of FGMs, in-depth theoretical and experimental studies have been carried out and published on fracture mechanics, the distribution of thermal stresses and the treatment of cracks in FGM structures. Among FGM structures are the beams that represent a major focus for researchers due to their applications.

Many approaches, including shear strain beam theory, the energy method and the finite element method, have been used. Most of these approaches are based on simplifying assumptions.

Li et al. (2010) studied the static bending and the dynamic response of FGM beams using the higher-order shear deformation theory “HSDT”. A finite element model (FEM) and Navier solutions are developed by Vo et al. (2015) and they also used the quasi-3D theory to determine the displacement and stresses of FG sandwich beams for various power-law index, skin–core–skin thickness ratios and boundary conditions.

A new 2-node beam element based on Quasi-3D beam theory and mixed formulation is developed by Nguyen et al. (2019) for static bending of functionally graded (FG) beams, the transverse shear strains and stresses of the proposed beam element are parabolic distributions through the thickness of the beam and the transverse shear stresses disappear on the top and bottom surfaces of the beam. The proposed beam element is free of shear without selective or reduced integration.

Chikh (2019) developed various theories of higher-order with hyperbolic shear deformation beams for bending of FG beams. These theories are developed as a function of the assumption of constant transverse displacement and variation in axial displacement of the higher-order through the thickness of the beam, these theories satisfy the zero stress on the top and bottom surfaces of the beam, so that a shear adjustment factor is not necessary.

Recently, Khebizi et al., (2019a, 2019b) studied the mechanical behavior of FGM beams by a three-dimensional modeling method based on the exact theory of Saint Venant, in which the deformation of the section of the FGM beam is taken into account. Beams made of a single FGM layer as well as a sandwich configuration have been studied by Bhandari and Sharma (2020) where thin and thick beams have been investigated in terms of temperature, displacements and stresses, using a unified formulation, they offered many one-dimensional displacements-based beam models that could be easily translated into higher-order theories, classical Euler–Bernoulli and Timoshenko models. The thermo-mechanical problems studied, although they offer a global bending deformation are governed by three-dimensional stress fields that call for very accurate models. Althoey and Ali (2021) provided a simplified method and solution for FGM beam, normal and shear stress are analyzed and using two material functions, power-law (P-FGM) and exponential (E-FGM). Also, the influence of material functions on FGM beam deflection has been investigated through analytical solution considering simply supported and cantilever FGM beams which exhibited a smaller deformation compared with homogenous steel beams of the same size and similar loadings. They concluded from their results that the non-dimensional normal stress and shear stress are independent of the elastic modulus values of the constituent materials, but rather depend on both the ratio of the elastic modulus and the location across the beam thickness in the E-FGM material function model. Large deflection analysis of functionally graded beams based on geometrically exact three-dimensional beam theory and isogeometric analysis was employed by Nguyen et al. (2022) to model the spatial behavior of the beams under different loading conditions. Five standard benchmark test cases were conducted to validate the accuracy and efficiency of the proposed approach.

In this study, we present a three-dimensional modeling of the static and cyclic response of FGM beams using the finite element method, in which the FGM beams are modeled by hexahedral elements type C3D20R (see Fig. 3).

Distribution of mechanical properties of FGM beams

FGMs consist of a combination of two or more materials with different structural and functional properties, in which the mechanical properties are distributed among these materials in an ideal way to improve the performance of their general structure. Generally, FGMs are made of a mixture of ceramic and metal (see Fig. 1). The ceramic constituent offers high-temperature resistance due to its low thermal conductivity. In contrast, the ductile metal component prevents fracture caused by stresses due to a high-temperature gradient in a very short period of time.

Fig. 1
figure 1

FGM beam

Full size image

The most distinct characteristics of FGMs are their non-uniform microstructures with macro-properties that graduate in space. Consequently, their mechanical properties vary gradually and continuously from one surface to another through the thickness and can be defined by the variation of the fractions of volume.

Figure 1 shows that the properties of materials, such as Young's modulus (E) and Poisson's ratio (ν), at the top and bottom beam surfaces vary continuously through the thickness (z axis), whereas E = E(z) and ν = ν(z).

Poisson's ratio has a very small impact on strain when compared to Young's modulus. Therefore, Poisson's ratio can be assumed to be constant (2019b; Ben-oumrane et al., 2009; Delale & Erdogan, 1983; Guenfoud et al., 2016; Hadj et al., 2016; Khebizi et al., 2019a). However, Young's modulus varies through the thickness of the FGM beam according to the power-law (P-FGM), exponential, Mori Tanaka or sigmoid distribution.

The distribution methods of the mechanical properties of FGM beams are presented in detail in the work of Khebizi et al., (2019a, 2019b).

In the present work, we considered that the Young's modulus varies according to the power-law as following:

$$E (\mathrm{z}) = {E}_{\mathrm{b}}+({E}_{\mathrm{t}} - {E}_{\mathrm{b}})\times {\left(\frac{z}{h}+\frac{1}{2}\right)}^{p}$$
(1)

where P is the power-law exponent, Et and Eb denote Young’s modulus at the top and bottom beam surfaces, respectively.

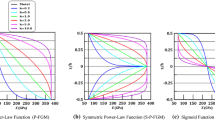
Figure 2 clearly shows that Young's modulus changes rapidly near the bottom surface for p < 1 and increases rapidly near the top surface for p > 1.

Fig. 2
figure 2

Variation of Young's modulus through the thickness of P-FGM beam

Full size image

Formulation of C3D20R finite element

In this study, the twenty-node brick element (C3D20R) with reduced integration points (3 × 3 × 3) is employed (Fig. 3). This element behaves very well in bending and rarely exhibits hour-glassing despite the reduced integration. The displacement of each element is a continuous function of the nodal displacement using the shape functions of displacement and geometry (iso-parametric formulation) according to Dhondt (2004).

Fig. 3
figure 3

hexahedral C3D20R element

Full size image

In classical finite element formulations, a predetermined set of material properties is used for each element so that the property field is constant within an individual element. To model a continuously non-homogeneous material, the property function of the material must be discretized according to the mesh size of the elements. This approximation can provide large discontinuities according to the formulation set by Smith (2011). Since in the elastic analysis of FGMs, each Gaussian point of the element has its own stress–strain curve, the assumption of constant properties for each element may lead to invalid results. Therefore, the graded finite element is highly preferable for modeling problems dealing with non-homogeneous materials. Zafarmand and Kadkhodayan (2019) recommended that in the case of 3D elastic analysis, the second-order three-dimensional continuum (solid) elements should be considered. These elements provide higher accuracy than the first-order ones for smooth problems that do not involve severe element distortions and are very effective in bending dominated problems. The domain in local coordinates for a hexahedral C3D20R element is a cube extending from − 1 to + 1 (− 1 ≤ g, h, r ≤ 1) along each coordinate axis. This element contains 20 nodes, they are located at the vertices and in the middle of the edges as shown in Fig. 3. The node numbering convention used in Abaqus for this element is presented by Smith (2011), where the corner nodes are numbered first, followed by the mid-side nodes for second-order elements is also shown in Fig. 3. Furthermore, Liew and Rajendran (2002) have shown that the reduced integration points are the so-called superconvergent points, in which the stress is one order more accurate than in any other point. However, because of reduced integration, so-called zero-energy modes can arise, leading to hour-glassing.

According to Smith (2011), the interpolation function is given as below:

$$\begin{array}{c}u=-1/8\left(1-g\right)\left(1-h\right)\left(1-r\right)\left(2+g+h+r\right){u}_{1}\\ -1/8(1+g)(1-h)(1-r)(2-g+h+r){u}_{2}\\ -1/8\left(1+g\right)\left(1+h\right)\left(1-r\right)\left(2-g-h+r\right){u}_{3}\\ -1/8(1-g)(1+h)(1-r)(2+g-h+r){u}_{4}\\ -1/8\left(1-g\right)\left(1-h\right)\left(1+r\right)\left(2+g+h-r\right){u}_{5}\\ -1/8(1+g)(1-h)(1+r)(2-g+h-r){u}_{6}\\ -1/8\left(1+g\right)\left(1+h\right)\left(1+r\right)\left(2-g-h-r\right){u}_{7}\\ -1/8(1-g)(1+h)(1+r)(2+g-h-r){u}_{8}\\ +1/4\left(1-g\right)\left(1+g\right)\left(1-h\right)\left(1-r\right){u}_{9}\\ +1/4(1-h)(1+h)(1+g)(1-r){u}_{10}\\ +1/4\left(1-g\right)\left(1+g\right)\left(1+h\right)\left(1-r\right){u}_{11}\\ +1/4(1-h)(1+h)(1-g)(1-r){u}_{12}\\ +1/4\left(1-g\right)\left(1+g\right)\left(1-h\right)\left(1+r\right){u}_{13}\\ +1/4(1-h)(1+h)(1+g)(1+r){u}_{14}\\ +1/4\left(1-g\right)\left(1+g\right)\left(1+h\right)\left(1+r\right){u}_{15}\\ +1/4(1-h)(1+h)(1-g)(1+r){u}_{16}\\ +1/4\left(1-r\right)\left(1+r\right)\left(1-g\right)\left(1-h\right){u}_{17}\\ +1/4(1-r)(1+r)(1+g)(1-h){u}_{18}\\ +1/4\left(1-r\right)\left(1+r\right)\left(1+g\right)\left(1+h\right){u}_{19}\\ +1/4(1-r)(1+r)(1-g)(1+h){u}_{20}\end{array}$$
(2)

All the iso-parametric solid elements are integrated numerically by reduced integration. For the second-order elements, Gauss integration is used because it is efficient and especially adequate to the polynomial product interpolations used in these elements. For the 20-node brick elements, the interpolation function given in Eq. (2) can be rewritten as:

$$\mathbf{u}={N}^{I}(g,h,r){\mathbf{u}}^{I}\text{ sum on }I$$
(3)

The isoparametric shape functions \({N}^{I}\) can be written as (Smith, 2011):

$${N}^{I}(g,h,r)=1/8{\Sigma }^{I}+1/4g{\Lambda }_{1}^{I}+1/4h{\Lambda }_{2}^{I}+1/4r{\Lambda }_{3}^{I}+1/2hr{\Gamma }_{1}^{I}+1/2gr{\Gamma }_{2}^{I}+1/2gh{\Gamma }_{3}^{I}+1/2ghr{\Gamma }_{4}^{I}$$
(4)

where

$$\begin{array}{c}{\Sigma }^{I}=\left[+1,+1,+1,+1,+1,+1,+1,+1\right],\\ {\Lambda }_{1}^{I}=\left[-1,+1,+1,-1,-1,+1,+1,-1\right],\\ {\Lambda }_{2}^{I}=\left[-1,-1,+1,+1,-1,-1,+1,+1\right],\\ {\Lambda }_{3}^{I}=\left[-1,-1,-1,-1,+1,+1,+1,+1\right],\\ {\Gamma }_{1}^{I}=\left[+1,+1,-1,-1,-1,-1,+1,+1\right],\\ {\Gamma }_{2}^{I}=\left[+1,-1,-1,+1,-1,+1,+1,-1\right],\\ {\Gamma }_{3}^{I}=\left[+1,-1,+1,-1,+1,-1,+1,-1\right],\\ {\Gamma }_{4}^{I}=\left[-1,+1,-1,+1,+1,-1,+1,-1\right],\end{array}$$
(5)

and the superscript \(\mathrm{I}\) denotes the node of the element. The last four vectors \({\Gamma }_{\alpha }^{I}\), (\(\alpha\) has a range of four), are the hourglass base vectors, which are the deformation modes associated with noenergy in the 1-point integration element but resulting in a non-constant strain field in the element.

In the uniform strain formulation, the gradient matrix \({B}^{I}\) is defined by integrating over the element as (Smith, 2011):

$${\mathbf{B}}^{I}=\frac{1}{{V}_{\mathrm{el}}}{\int }_{{V}_{\mathrm{el}}}{N}_{i}^{I}(g,h,r){\mathrm{d}V}_{\mathrm{el}}$$
(6)
$${N}_{i}^{I}\left(g,h,r\right)=\frac{\partial {N}^{I}}{\partial {x}_{i}}$$
(7)

where \({V}_{\mathrm{el}}\) is the element volume and I has a range of three.

In the centroidal strain formulation the gradient matrix is \({B}^{I}\) simply given as:

$${B}_{i}^{I}={N}_{i}^{I}\left(\mathrm{0,0},0\right)$$
(8)

which has the following antisymmetric property:

$${B}_{i}^{1}={B}_{i}^{7}$$
$${B}_{i}^{3}={B}_{i}^{5}$$
$${B}_{i}^{2}={B}_{i}^{8}$$
$${B}_{i}^{4}={B}_{i}^{6}$$
(9)

It can be seen from the Eqs. (2)–(9) that the centroidal strain formulation reduces the amount of effort required to compute the gradient matrix. This cost saving also extends to strain and element nodal force calculations because of the antisymmetric property of the gradient matrix. However, the centroidal strain formulation is less accurate when the elements are skewed. For hexahedron elements in a parallelepiped configuration, the uniform strain approach is identical to the centroidal strain approach according to Smith (2011).

Numerical applications and discussion

Simply supported P-FGM beam subjected to static loading

In this section, we study a simply supported FGM beam (Fig. 4), for which the ratio between its length and height (L/h) is equal to 5. The bottom surface of the beam is assumed to be aluminum (Al), while its top surface is assumed to be pure alumina (Al2O3). The distribution of material properties through the thickness of the FGM beam is achieved by the power-law (P-FGM). The mechanical properties of aluminum are \(E_{{\text{m}}} = 70{\text{ GPa}}\) and \(\nu_{{\text{m}}} = 0.3\), while the same properties for alumina are \(E_{{\text{c}}} = 380{\text{ GPa}}\) and \(\nu_{{\text{c}}} = 0.3\). This beam is subjected to a uniformly distributed load of q = 10 N/m (Fig. 4).

Fig. 4
figure 4

Simply supported FGM beam subjected to a uniformly distributed load

Full size image

The P-FGM beam is modeled in this work using Abaqus software. Figure 5 shows the mesh of the beam consisting by hexahedral elements type C3D20R characterized by 20 nodes with 27 integration points.

Fig. 5
figure 5

Mesh of P-FGM beam consisting by 80,000 C3D20R elements

Full size image

The three-dimensional field of vertical displacement and normal stresses field \({\sigma }_{xx}\) of the FGM beam are shown in Figs. 6 and 7, respectively.

Fig. 6
figure 6

Three-dimensional vertical displacement field of FGM beam obtained by Abaqus software for different values of P

Full size image
Fig. 7
figure 7

Three-dimensional normal stress field \({\upsigma }_{\mathrm{xx}}\) of FGM beam obtained by finite element method using Abaqus software for different values of P

Full size image

The results of deflection along the length of the mean-line of the beam (W), the normal stresses σxx at mid-span of the FGM beam (x = L/2) and the shear stresses \({\sigma }_{xz}\) at the level of the support (x = 0), obtained by the finite element method, are shown in Figs. 8 and 9, respectively.

Fig. 8
figure 8

Deflection along the length of the midline FGM beam

Full size image
Fig. 9
figure 9

Distribution of normal stresses \({\sigma }_{xx}\) at mid-span (x = L/2) and shear stresses \({\sigma }_{xz}\) at the level of the support (x = 0) through the thickness of P-FGM beam

Full size image

Discussion

From Fig. 8, we can clearly see that the vertical displacement increases with increasing P of the FGM beam. This is due to the influence of Young’s modulus, which is high for the ceramic (P = 0) compared to that of the metal (P = + ∞).

Figure 9 shows that the variation of normal stresses \({\sigma }_{xx}\) through the thickness of the FGM beam is not linear. In contrast, for the isotropic beams (pure ceramic or pure metal), the variation of the normal stress is linear. It can also be seen that the distribution of the shear stresses, \({\sigma }_{xz}\), through the thickness of the FGM beam is parabolic and asymmetric. The maximum value of the shear stress is located at a point above the mid-plane of the FGM beam. For the reason of simplicity, we present the numerical results in terms of non-dimensional quantities.

$$\mathrm{Displacement }\overline{w }\left(x=\frac{L}{2}\right)=100 \frac{{E}_{\mathrm{m}}\mathrm{b}{h}^{3}}{q{L}^{4}} w$$
(10)
$$\mathrm{Normal stress }{\overline{\sigma }}_{xx}\left(x=\frac{L}{2},y=\frac{h}{2}\right)=\frac{bh}{qL}{\sigma }_{xx}$$
(11)
$$\mathrm{Shear stress}{ \overline{\sigma }}_{xz}\left(x=0,y=0\right)=\frac{bh}{qL}{\sigma }_{xz}$$
(12)

The various non-dimensional parameters used are:

Tables 1, 2 and 3 present the non-dimensional deflections, normal stresses and shear stresses of the FGM beam, respectively.

Table 1 Maximum non-dimensional deflection of the midline of P-FGM beam
Full size table
Table 2 Non-dimensional normal stress \({\overline{\sigma }}_{xx}\) (x = L/2, z = h/2) of P-FGM beam
Full size table
Table 3 Non-dimensional shear stress \({\overline{\sigma }}_{xz}\) (x = 0, y = 0) of P-FGM beam
Full size table

Table 1 shows the maximum non-dimensional deflection of the P-FGM beam, where we note an excellent agreement between the results obtained by our model and those obtained by other authors (Li et al., 2010, Vo et al., 2015, Nguyen et al., 2019 and Chikh, 2019). Table 2 and Fig. 10 also show good convergence of the results of non-dimensional normal stresses of the P-FGM beam obtained by the various models.

Fig. 10
figure 10

Non-dimensional normal stress \({\overline{\sigma }}_{xx}\) (x = L/2) through the thickness of P-FGM beam, comparison between different models

Full size image

Table 3 and Fig. 11 show that the non-dimensional shear stress obtained by our investigation with the finite element method is close to that obtained by other models in the literature.

Fig. 11
figure 11

Non-dimensional shear stress \({\overline{\sigma }}_{xz}\) (at x = 0) through the thickness of P-FGM beam, comparison between different models

Full size image

Generally, we observe that the numerical values obtained by our model are in good agreement with the analytical results given by Li et al. (2010) and Vo et al. (2015) with Navier’s theory, Vo et al. (2015) with a finite element model, quasi-3D theory (Nguyen et al., 2019) and hyperbolic shear deformation theories (Chikh, 2019).

For illustrating the effect of the index P on the deflection of the FGM beam under a uniformly distributed static load, the non-dimensional deflection, the non-dimensional normal stress, and non-dimensional shear stress are shown in Figs. 12, 13 and 14, respectively. We note that increasing the index parameter of the material P reduces the stiffness of the FGM beam and therefore leads to an increase in deflections and normal stresses. This is due to the fact that the higher values of P correspond to a high portion of metal compared to the ceramic part, which makes this FGM beam more flexible.

Fig. 12
figure 12

Variation of non-dimensional deflection \(\overline{\mathrm{w} }\) in function of index parameter P of FGM beam

Full size image
Fig. 13
figure 13

Variation of non-dimensional normal stress \({\overline{\upsigma }}_{\mathrm{xx}}\) in function of index parameter P of FGM beam

Full size image
Fig. 14
figure 14

Variation of non-dimensional shear stress \({\overline{\sigma }}_{xz}\) in function of index parameter P of FGM beam

Full size image

The evolution of the non-dimensional shear stresses through the thickness of the P-FGM beam for various parameters of the material P is shown in Fig. 14. The influence of the index P is unlimited and its increase leads to a decrease in the shear stress.

Simply supported P-FGM beam subjected to cyclic loading

In this section, we study the behavior of an FGM beam (Fig. 15) simply supported (L = 2.5 m, h = 0.5 m and b = 1.0 m) and subjected to a cyclic load with a maximum value of 100 Kn. This cyclic load is applied at the mid-span of the beam (Fig. 15). The history of cyclic loading is shown in Fig. 16.

Fig. 15
figure 15

Simply supported FGM beam subjected to a cyclic load

Full size image
Fig. 16
figure 16

Cyclic loading history

Full size image

The bottom surface of the beam is assumed to be aluminum (Al), while its top surface is assumed to be pure alumina (Al2O3). The mechanical properties are varied through the thickness of FGM beam according to the power-law distribution method (P-FGM). The mechanical properties of aluminum are \(E_{{\text{m}}} = 70\;{\text{GPa}}\), \(\nu_{{\text{m}}} = 0.3\), and those of alumina are \(E_{{\text{c}}} = 380{\text{ GPa}}\), \(\nu_{{\text{c}}} = 0.3\).

In this work, we model the P-FGM beam using Abaqus software based on the finite element method. Figure 17 shows the mesh of the beam consisting of hexahedral C3D20R elements.

Fig. 17
figure 17

Mesh of FGM beam

Full size image

The results obtained are shown in the following figures.

Discussion

From Fig. 18, we can clearly see that the vertical displacement at point G (x = L/2, y = 0 and z = 0) changes alternately. This is due to the nature of the load (cyclic inverted) applied to the FGM beam, with the maximum displacement corresponding to the maximum loading for each type of FGM beam. The value of the displacement at point G increases with increasing material parameter P of the FGM beam from P = 0 (pure ceramic) to P = + ∞ (pure metal).

Fig. 18
figure 18

Vertical displacement at point G (x = L/2, y = 0 and z = 0)

Full size image

It is noteworthy that in Figs. 19 and 20, relating to the normal stresses at points A and B, respectively, the values of these stresses are also evolved in an alternating manner according to the nature of the load applied on the FGM beam. This load results in simultaneous positive and negative normal stresses and alternating between points A and B. However, the value of the normal stresses engendered on the upper surface (compressive stresses) at point A is greater compared to the normal stresses engendered on the lower surface (tensile stresses) at point B. This is due to the graduation of the value of the material parameter P from the upper surface to the lower surface of the FGM beam.

Fig. 19
figure 19

Normal stress at point A (x = L/2, y = 0, z = + h/2)

Full size image
Fig. 20
figure 20

Normal stress at point B (x = L/2, y = 0, z = − h/2)

Full size image

Figure 21 illustrates the change in the resulting shear stresses in the FGM beam at point O. We also note that these stresses change alternately and inversely with the change in the values and direction of the load applied on the FGM beam. The results of these stresses are equal values between them regardless of the change of the value in the material parameter P.

Fig. 21
figure 21

Shear stress at point C (x = 0, y = 0, z = 0)

Full size image

The force–displacement curve at point G of the P-FGM beam shown in Fig. 22 shows that there is a linear relationship between the applied force and the resulting displacement. The presence of two positive and negative limit values indicates that there is a change in the direction of the load applied to the FGM beam.

Fig. 22
figure 22

Load–deflection curve at point G (x = L/2, y = 0, z = 0)

Full size image

It can clearly be seen that the stress–strain curves at points A and B on the P-FGM beam shown in Figs. 23 and 24, respectively, are line diagrams.

Fig. 23
figure 23

Normal stress–strain curve at point A (x = L/2, y = 0 and z = + h/2)

Full size image
Fig. 24
figure 24

Normal stress–strain curve at point B (x = L/2, y = 0 and z = − h/2)

Full size image

Figure 25 presents the curve of the evolution of the shear stresses at point O as a function of the strain at the same point of the P-FGM beam. We also note the existence of a linear relation between the shear stresses and the strain, where we recorded the lowest strain rate for the all-ceramic and all-metal beams, respectively.

Fig. 25
figure 25

shear stress–strain curve at point O (x = 0, y = 0 and z = 0)

Full size image

Conclusion

In this study, a hexahedral finite element type C3D20R “quadratic brick element” characterized by 20 nodes with 27 integration points (3 × 3 × 3) was utilized for the numerical analysis of the static and cyclic behavior of simply supported P-FGM beams.

The performance, reliability and versatility of the C3D20R element have been evaluated through numerical bending applications of FGM beams. The results obtained from the static study were compared with analytical solutions from the literature. These comparisons have shown that the arrows and the stresses obtained are identical and also that the results obtained by studying the P-FGM beams subjected to a cyclic load are very acceptable.

Therefore, our three-dimensional modeling based on hexahedral finite elements of the C3D20R type implanted in the Abaqus calculation code was able to simulate and describe the static and cyclic behavior of FGM beams.