Keywords

1 Introduction

Laminated composite /sandwich materials are being increasingly used in the aeronautical and aerospace industry due to their lightweight and tailor made characteristic. However, the main disadvantage of layered material is the weakness at interfaces. In the absence of any graded material at the interface, there is every chance of delamination to occur. To overcome of interface problem associated with layered materials, a new class of materials named functionally graded material (FGM) has been proposed whose physical properties vary through the thickness in a continuous manner and are therefore free from interface weaknesses. These advanced composite materials were first introduced by a group of scientists in Sendai (Japan) in 1984 [7, 14].

Three dimensional (3D) elasticity solutions based on the solution of partial differential equations (PDEs) with appropriate boundary conditions are valuable because they represent a more realistic and closer approximation to the actual behavior of the structures. Sankar [9] has presented a 2D elasticity solution under plane stress condition for functionally graded (FG) beams subjected to sinusoidal loads by assuming Young’s modulus to vary exponentially through the thickness of beam. Further, Sankar and Tzeng [10] extended the same elasticity solutions for a FG beams subjected to thermal loads.

Bian et al. [1] extended the Soldatos and Liu [12] plate theory for stress analysis of FG plate under cylindrical bending. Transfer matrix method (TMM) proposed by Thomson [13] is used to derive the shape functions. TMM approach helps to improve the computational efficiency as compared to original model developed by Soldatos and Liu [12]. The shear stiffness and shear correction coefficients associated with first-order shear deformation theory were calculated by Nguyen et al. [8] for FG simply supported plates under cylindrical bending.

A finite element (FE) model based on first-order shear deformation theory (FOST) is developed by Chakraborty and Gopalakrishnan [2] to study the thermoelastic behavior of FG beam structures. The exact solution of static part of the governing differential equations is used in the formulation to construct interpolating polynomials, which results in stiffness matrix having super-convergent property. Extension of the formulation to capture wave propagation behavior in a FG beam with high frequency impulse loading is also given by Chakraborty and Gopalakrishnan [3].

The meshless local Petrov-Galerkin (MLPG) method is a novel numerical approach. MLPG method allows the construction of the shape functions and domain discretization without defining elements. The use of MLPG approach to study transient thermoelastic response of FG composites heated by Gayssial laser beam is demonstrated by Ching and Chen [4]. Extensive parametric studies for transient and steady-state thermomechanical responses with respect to spatial distribution, volume fraction of material constituents, rate of laser power and radius of laser beam have been presented. Further, Sladek et al. [11] has proposed MLPG approach for crack analysis in anisotropic FG materials for quasi-static and transient elastodynamic problems.

An effort is put in this paper to reformulate the semi analytical model developed by Kant et al. [6] for stress analysis of simply (diaphragm) supported FG pate under cylindrical bending. 2D elasticity solution presented by Sankar [9] is used for the comparison.

2 Semi-analytical Formulation

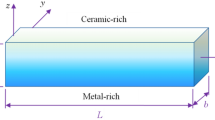
A FG beam (Fig. 1) supported on two opposite edges, x = 0 and L, is considered. The length of beam is L and thickness is h. The beam is assumed to be in a state of 2D plane stress in x-z plane and width in the y direction is considered as unity. The top surface of the beam is subjected to only transverse loading, which can be expressed as,

Fig. 1
figure 1

FG Beam subjected to transverse loading

Full size image
$$ p(x) = \sum\limits_{m} {p_{0m} \sin \frac{m\pi x}{L}} ,\quad {\text{where}}\;m = 1,3,5, \ldots $$
(1)

The bottom surface is completely free of any stresses. In Eq. (1), m is assumed to be odd. The loading is symmetric about the center of beam and any arbitrary normal loading can be expressed with the help of Fourier series involving the terms of the type \( p_{0m} \sin \frac{m\pi x}{L} \).

The 2D equations of equilibrium are,

$$ \frac{{\partial \sigma_{x} }}{\partial x} + \frac{{\partial \tau_{xz} }}{\partial z} + B_{x} = 0\quad \quad \frac{{\partial \tau_{zx} }}{\partial x} + \frac{{\partial \sigma_{z} }}{\partial z} + B_{z} = 0 $$
(2)

where, B x and B z are the body forces per unit volume in x and z directions, respectively and from the linear theory of elasticity, the strain-displacement relations in 2D are,

$$ \varepsilon_{x} = \frac{\partial u}{\partial x} ;\quad \varepsilon_{z} = \frac{\partial w}{\partial z}\quad {\text{and}}\quad \gamma_{xz} = \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} .$$
(3)

It is assumed here that the FG material is isotropic at every point. Further, it is assumed that the Poisson’s ratio is constant through the thickness of the beam. The variation of the modulus of elasticity through the thickness of beam is given by \( E(z) = E_{o} e^{\lambda z} \). Therefore, the material constitutive relations for FG beam under plane stress condition can be written as,

$$ \left\{ \begin{gathered} \sigma_{x} \hfill \\ \sigma_{z} \hfill \\ \tau_{xz} \hfill \\ \end{gathered} \right\} = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & 0 \\ {C_{21} } & {C_{22} } & 0 \\ 0 & 0 & {C_{33} } \\ \end{array} } \right]\left\{ \begin{gathered} \varepsilon_{x} \hfill \\ \varepsilon_{z} \hfill \\ \gamma_{xz} \hfill \\ \end{gathered} \right\} $$
(4)

The reduced material coefficients, C ij for a FG beam are,

$$ C_{11} = C_{22} = \frac{{E_{o} e^{\lambda z} }}{{\left( {1 - \upsilon^{2} } \right)}}\quad C_{12} = C_{21} = \frac{{\upsilon E_{o} e^{\lambda z} }}{{\left( {1 - \upsilon^{2} } \right)}}\quad \text{and}\quad C_{33} = \frac{{E_{o} e^{\lambda z} }}{{2\left( {1 + \upsilon } \right)}} \, $$
(5)

where

\( \lambda = - \ln \frac{{E_{o} }}{{E_{h} }} \) :

Gradation factor

E o :

Young’s modulus at the bottom of the beam

E h :

Young’s modulus at the top of the beam

\( \upsilon \) :

Poisson’s ratio

The Eqs. (2)–(4) have a total of eight unknowns \( u,w,\varepsilon_{x} ,\varepsilon_{z} ,\gamma_{xz} ,\sigma_{x} ,\sigma_{z} ,\tau_{xz} \) in eight equations. After a simple algebraic manipulation of the above sets of equations, a set of PDEs involving only four primary dependent variables \( u,w,\tau_{zx} \;{\text{and}}\;\sigma_{z} \) are obtained as follows,

$$ \begin{aligned} \frac{\partial u}{\partial z} & = \frac{{\tau_{xz} }}{{C_{33} }} - \frac{\partial w}{\partial x} \\ \frac{\partial w}{\partial z} & = \frac{1}{{C_{22} }}\left( {\sigma_{z} - C_{21} \frac{\partial u}{\partial x}} \right) \\ \frac{{\partial \tau_{xz} }}{\partial z} & = \left( { - C_{11} + \frac{{C_{12} C_{21} }}{{C_{22} }}} \right)\frac{{\partial^{2} u}}{{\partial x^{2} }} - \frac{{C_{12} }}{{C_{22} }}\frac{{\partial \sigma_{z} }}{\partial x} - B_{x} \\ \frac{{\partial \sigma_{z} }}{\partial z} & = - \frac{{\partial \tau_{xz} }}{\partial x} - B_{z} \\ \end{aligned} $$
(6)

A secondary dependent variable, \( \sigma_{x} \) can be expressed as a function of the primary dependent variables as follows,

$$ \sigma_{x} = C_{11} \frac{\partial u}{\partial x} + C_{12} \frac{\partial w}{\partial z} $$
(7)

The above PDEs defined by Eq. (6) can be reduced to a coupled first-order ODEs by using Fourier trigonometric series expansion for primary dependent variables satisfying the simple (diaphragm) support end conditions at x = 0, L, as follows,

$$ \begin{aligned} u(x,z) & = \sum\limits_{m} {u_{m} (z)\cos \frac{m\pi x}{L}} \\ w(x,z) & = \sum\limits_{m} {w_{m} (z)\sin \frac{m\pi x}{L}} \\ \end{aligned} $$
(8)

From the basic relations of theory of elasticity, it can be shown that,

$$ \begin{aligned} \tau_{xz} (x,z) & = \sum\limits_{m} {\tau_{xzm} (z)\cos \frac{m\pi x}{L}} \\ \sigma_{z} (x,z) & = \sum\limits_{m} {\sigma_{zm} (z)\sin \frac{m\pi x}{L}} \\ \end{aligned} $$
(9)

Substituting Eqs. (7)–(8) into Eq. (6) and using orthogonality conditions of trigonometric functions, the following ODEs are obtained,

$$ \begin{aligned} \frac{{du_{m} (z)}}{dz} & = - \frac{m\pi }{L}w_{m} (z) + \frac{1}{{C_{33} }}\tau_{xzm} (z) \\ \frac{{dw_{m} (z)}}{dz} & = \frac{{C_{21} }}{{C_{22} }}\frac{m\pi }{L}u_{m} (z) + \frac{1}{{C_{22} }}\sigma_{zm} (z) \\ \frac{{d\tau_{xzm} (z)}}{dz} & = \left( {C_{11} - \frac{{C_{12} C_{21} }}{{C_{22} }}} \right)\frac{{m^{2} \pi^{2} }}{{L^{2} }}u_{m} (z) - \frac{{C_{12} }}{{C_{22} }}\frac{m\pi }{L}\sigma_{zm} (z) - B_{x} (x,z) \\ \frac{{d\sigma_{zm} (z)}}{dz} & = \frac{m\pi }{L}\tau_{xzm} (z) - B_{z} (x,z) \\ \end{aligned} $$
(10)

Equation (10) represents the governing two-point BVP in ODEs in the domain 0 < z < h with stress components known at the top and bottom surfaces (boundary conditions) of the beam. The basic approach to the numerical integration of the BVP defined in Eq. (10) is to transform the given BVP into a set of initial value problems (IVPs)—one non-homogeneous and n/2 homogeneous. The solution of BVP defined by Eq. (10) is obtained by forming a linear combination of one non-homogeneous and n/2 homogeneous solutions so as to satisfy the boundary conditions at z = 0 and h [5]. This gives rise to a system of n/2 linear algebraic equations, the solution of which determines the unknown components at the starting edge \( z = 0 \). Then a final numerical integration of Eq. (10) produces the desired results.

3 Numerical Study

Numerical investigations on simply supported narrow beam with plane stress condition are performed to establish the accuracy of the formulation presented in the preceding sections of the paper. The elasticity solution presented by Sankar [9] is considered as benchmark solution for comparison. Elasticity modulus at the bottom of beam is 1.0 GPa and Poisson’s ratio is 0.3. The ratio of elasticity modulus at top and bottom are 5, 10, 20, and 40. Following normalizations are used here for the uniform comparison of the results.

$$ \begin{aligned} \overline{u} & = \frac{{E_{h} u(0,z)}}{{p_{0} h}};\quad \overline{w} = \frac{{100E_{h} h^{3} w(L/2,z)}}{{p_{0} L^{4} }} \\ \overline{{\sigma_{x} }} & = \frac{{\sigma_{x} (L/2,z)}}{{p_{0} L^{2} }};\quad \overline{{\tau_{xz} }} = \frac{{\tau_{xz} (0,z)}}{{p_{0} L}};\quad \overline{{\sigma_{z} }} = \frac{{\sigma_{z} }}{{p_{0} }} \\ \end{aligned} $$

The normalized inplane normal stress (\( \overline{{\sigma_{x} }} \)), transverse shear stress (\( \overline{{\tau_{xz} }} \)) and transverse displacement (\( \overline{w} \)) for different aspect ratios and different gradation factors (\( \lambda \) = 5, 10, 20 and 40) are detailed in Table 1. Through thickness variations of inplane displacement (\( \overline{u} \)), transverse displacements (\( \overline{w} \)), inplane normal stress (\( \overline{{\sigma_{x} }} \)) and transverse shear stress (\( \overline{{\tau_{xz} }} \)) for an aspect ratio of 5 are shown in Fig. 2. It can be concluded from the results presented in Table 1 that the present semi analytical formulation works well for any variation of Young’s modulus and for any aspect ratio and therefore, it is very well proved about the stability, consistency, reliability and accuracy of semi analytical formulation.

Table 1 Normalized inplane normal stresses (\( \overline{{\sigma_{x} }} \)), transverse shear stresses (\( \overline{{\tau_{xz} }} \)) and transverse displacement (\( \overline{w} \)) of FG beam under sinusoidal transverse load with different gradation factors
Full size table
Fig. 2
figure 2

Through thickness variation of a inplane displacement \( \overline{u} \), b inplane normal stress \( \overline{{\sigma_{x} }} \) and c transverse shear stress \( \overline{{\tau_{xz} }} \) for simply supported FG beam under sinusoidal load

Full size image

4 Concluding Remarks

A simple semi analytical formulation presented here for 2D stress analysis of FG beam under plane stress condition of elasticity. A two-point BVP governed by a set of coupled first-order ODEs is formed by assuming a chosen set of primary variables in the form of trigonometric functions along the longitudinal direction of the beam which satisfy the simply (diaphragm) supported end conditions exactly. No simplifying assumptions through the thickness of the beam are introduced. Exact 2D elasticity solution is used for comparison and to show the effectiveness and simplicity of the semi analytical formulation. The present mixed semi analytical model is relatively simple in mathematical complexity and computational efforts.