1 Introduction

Once the structural construction is completed, monitoring, maintenance and repair start during the operative phase. This process is very important for large-scale structures such as bridges, industrial and offshore structures, and if it is not done properly, the probability of suffering massive financial and human losses becomes very high. The most important phase of the process is appropriate monitoring and assessment of the structural condition. Proper performance in this phase provides sufficient time to adopt a suitable strategy to repair the damaged elements. The principal purpose of monitoring is the detection of the non-expected structural behaviors. Any unusual and uncommon changes in structural response that happen during the usage of a structure are called damage. Hence, damage detection is considered as the most important phase of the assessment of structural condition.

Damage assessment includes identifying location and severity of the damage. The problem is an inverse optimization problem, and there are different methods for the solution of this problem. Damage results in changes in structural properties including stiffness and mass of the structure (Perera et al. 2009). Therefore, dynamic modal features, natural frequencies and mode shapes are changed. The dynamic features are obtained by finite element formulation for different states of damage. The dynamic methods are divided into two categories: modal based and signal based (Boonlong 2014; Fan and Qiao 2009; Masoumi and Jamshidi 2015; Rucka 2011). The modal-based methods can be implemented in two steps. The two-step damage assessment methods locate the damage in the first step and quantify its severity in the second step (Seyedpoor 2012; Seyedpoor and Montazer 2016; Vo-Duy et al. 2016; Xiang and Liang 2012), while the one-step damage detection methods detect the damage and quantify its severity, simultaneously.

One of the common one-step damage assessment methods is comparison of structural dynamic characteristics between the actual and computed damage states. The method can be performed using optimization algorithms and formulation of an objective function based on modal parameters. In this method, the objective function is often based on the difference of natural frequencies and mode shapes between the actual and computed damage states. Different damage assessment methods have been presented by many researchers (Doebling et al. 1996; Doebling et al. 1998; Farrar and Worden 2007; Salawu 1997; Sohn et al. 2003; Tributsch and Adam 2014, 2018).

As mentioned, in most of the studies on damage detection literature, the objective function is formulated based on structure’s dynamic features. Perera and Torres (2006) proposed a genetic algorithm (GA) to detect the damage of a beam structure using an objective function on the same basis. Villalba and Laier (2012) solved damage identification problem of several truss structures through GA algorithm and a methodology based on natural frequencies and mode shapes. To assess damage of truss structures, Majumdar et al. (2012) presented a method based on ant colony optimization (ACO) algorithm and changes in natural frequencies. Zhu et al. (2017) applied the bird mating optimizer for solving damage detection problems of several structures. Additionally, to assess damage in skeletal structures, an improved hybrid stochastic/deterministic Pincus–Nelder–Mead optimization algorithm was utilized by Nhamage et al. (2016). Kaveh et al. (2016) studied four different truss structures to demonstrate the ability of simplified dolphin echolocation (SDE) algorithm to detect damages. They examined different damage scenarios in the presence of two different levels of with/without noise. Also, they presented a significant mutation based on the fact that most of the elements are often undamaged in the structure. According to this mutation, there is a 30% probability that every element is undamaged. Therefore, using this mutation increases the opportunity of the algorithm to obtain the exact solution.

In most of the above-mentioned studies, the objective function has been formulated based on natural frequencies and mode shapes. Kaveh and Zolghadr (2015) investigated two different objective functions using ECSS algorithm to detect damage of the steel truss structures. In addition to using an objective function based on natural frequencies and mode shapes which aimed to find exact locations and severity of damages, they examined another objective function which was only based on natural frequencies; the purpose of examining the objective function was to find solutions whose frequencies are equal to frequencies of actual damage state (experimental scenario). As an example, the objective function finds multiple probable solutions (global optimal solutions) for every experimental scenario in symmetric structures.

One of the effective methods for solving many optimization problems is the use of metaheuristic algorithms (Kazemzadeh Azad 2018; Tejani et al. 2018a). Metaheuristic algorithms are widely used as effective tools for structural optimization (Hasançebi and Azad 2015; Kaveh 2017a, b; Kazemzadeh Azad 2017). Many of these algorithms, after being introduced and presented, are modified by other researchers, and their improved versions are presented (Kaveh et al. 2017, 2018; Tejani et al. 2018a, b). One of the metaheuristic algorithms that is presented recently by Kaveh and Bakhshpoori (2016b) is the water evaporation optimization (WEO) algorithm. Also, they enhanced the convergence rate of the WEO and introduced the accelerated water evaporation optimization (Kaveh and Bakhshpoori 2016a). The WEO algorithm has been proposed based on the evaporation of water molecules at the nano-scale. The evaporation has been presented by Wang et al. (2012) in order to simulate molecular dynamics on the evaporation of nanoscale water aggregation on a solid substrate with different surface wettabilities.

In this study, a new objective function is presented based on the natural frequencies and mode shapes of the structures. Several skeletal structures are tested to demonstrate the effectiveness of the proposed objective function. This objective function is a two-phase process. In the first phase, the only difference of the natural frequencies between experimental scenario and computed solution is studied. If the difference becomes zero, computed solution is detected as a probable solution. In the second phase, the differences of the natural frequencies and mode shapes between actual damage scenario and computed solution are studied. This phase is performed if the computed solution obtained from the first phase is detected as a probable solution. The purpose of defining such an objective function is to reduce the burden of the calculations and increase the rate of the convergence of the algorithm running in every iteration. In order to demonstrate the efficiency of the proposed method, accelerated WEO algorithm with mutation is employed.

The remainder of this paper is organized as follows: Damage assessment approach is provided in Sect. 2. In Sect. 3, the optimization algorithms are presented. Numerical examples are examined in Sect. 4. Finally, conclusions are provided in Sect. 5.

2 Method for Damage Assessment

In this section, the inverse problem of structural damage detection using changes in dynamic parameters is described. The process of the problem solving is shown in Fig. 1.

Fig. 1
figure 1

Damage assessment approach

Full size image

2.1 Finite Element Model of a Structure

To model a structure for finite element method and to calculate its natural frequencies and mode shapes, first, stiffness and mass matrices of the elements are computed using Eqs. (1) and (2). Then, the stiffness and mass matrices of the structure for undamaged state are assembled by Eqs. (3) and (4).

$$ \left[ {k^{e} } \right] = \left[ L \right]^{T} \left[ {k^{e'} } \right]\left[ L \right] $$
(1)
$$ \left[ {m^{e} } \right] = \left[ L \right]^{T} \left[ {m^{e'} } \right]\left[ L \right] $$
(2)
$$ \left[ K \right] = \sum\limits_{i = 1}^{\text{ne}} {\left[ {k_{i}^{e} } \right]} $$
(3)
$$ \left[ M \right] = \sum\limits_{i = 1}^{\text{ne}} {\left[ {m_{i}^{e} } \right]} $$
(4)

where [k e i ] and [m e i ] are the stiffness and mass matrices of the ith element, respectively. Also, [K] and [M] are the stiffness and mass matrices of the structure, respectively. Here, ne is the number of structural elements.

Modal parameters are calculated using the following eigenvalue equation:

$$ \left( {\left[ K \right] - \omega_{j}^{2} \left[ M \right]} \right)\left\{ {\phi_{j} } \right\} = 0 $$
(5)

Where ωj and {ϕj} are the jth natural frequency and mode shape of the structure.

2.2 Simulation of Structural Damage Using the β Vector

In modeling the structure using finite element formulations, reduction in structural properties such as elasticity modulus and cross-sectional area are used to simulate damage. The elasticity modulus of damaged element, Eid, is considered as:

$$ E_{id} = \left( {1 - \beta_{i} } \right)E_{i} $$
(6)

where βi and Ei are damage severity and elastic modulus of the ith element, respectively; βi is between 0, for completely healthy element, and 1, for a completely damaged element.

The β vector is a vector of dimension ne× 1, and the numerical value of the ith array of this vector is the damage severity corresponding to the ith structural element. Different damage scenarios can be defined using the β vector.

2.3 Estimating Natural Frequencies and Mode Shapes of a Damage Scenario

In order to model the damage state, one damage scenario is defined and shown by β vector. By applying β vector to structural elasticity modulus, the stiffness matrix of structure corresponding to the damage scenario,[Kd], is equal to:

$$ \left[ {K_{d} } \right] = \sum\limits_{i = 1}^{\text{NE}} {\left( {1 - \beta_{i} } \right)\left[ {k_{i}^{e} } \right]} $$
(7)

Thus, natural frequencies and mode shapes of the damage scenario are obtained by the following equation:

$$ \left( {\left[ {K_{d} } \right] - \omega_{d,j}^{2} \left[ M \right]} \right)\left\{ {\phi_{d,j} } \right\} = 0 $$
(8)

where {ϕd,j} and ωd,j are the mode shape and natural frequency of the jth mode corresponding to the damage scenario, respectively.

2.4 Formulation of the Method

As it was previously mentioned, the present method has two phases:

Phase 1 In this phase, only the difference of natural frequencies between experimental scenario and computed damage solution is checked as follows:

$$ F_{1} = \sum\limits_{j = 1}^{\text{nm}} {\left( {\left| {\frac{{\omega_{d,j}^{\text{AWEO}} - \omega_{d,j}^{\text{real}} }}{{\omega_{d,j}^{\text{real}} }}} \right|} \right)} $$
(9)

where ω AWEO d, j and ω real d, j are the natural frequency of the jth mode corresponding to the damage solution computed by the accelerated WEO algorithm and the experimental scenario, respectively.

Phase 2 In this phase, only the difference of mode shapes between actual and computed damage solution is checked as follows:

$$ F_{2} = \sum\limits_{j = 1}^{\text{nm}} {\sum\limits_{i = 1}^{\text{ndof}} {\left( {\left| {\frac{{\phi_{d,ij}^{\text{AWEO}} - \phi_{d,ij}^{\text{real}} }}{{\phi_{d,ij}^{\text{real}} }}} \right|} \right)} } $$
(10)

where ϕ AWEO d, ij and ϕ real d, ij are the jth mode shape of the ith degree of freedom corresponding to the computed and actual the damage scenario, respectively; and ndof is the number of structural degrees of freedom.

In most of the studies on damage assessment, differences of natural frequencies and mode shapes between actual and computed damage states are simultaneously formulated, i.e., their defined objective function, F, is expressed as:

$$ F = F_{1} + F_{2} $$
(11)

When the values of F1 and F2 become zero, the actual and computed damage scenarios become identical. According to the number of calculating fractions in F1 and F2, the burden of calculations corresponding to F1 is much less than F2. Therefore, instead of simultaneous use of F1 and F2, first the F1 is checked. If the value is equal to zero, then the F2 is checked. In this way, the total load of calculations is greatly reduced. As the algorithm minimizes the F1, when F1 is equal to zero and F2 is not, this scenario can be excluded from search space and the algorithm should be run again.

2.5 Application of the Objective Function to the Algorithm

This process is illustrated in Fig. 2. The parameter i indicates the number of total iterations, and j is the number of consecutive iterations, where the F1 value is not equal to zero corresponding to the best computed solution in each iteration. Also, tmax is the maximum number of iterations in which the algorithm has the opportunity to find one scenario whose value of F1 is equal to zero.

Fig. 2
figure 2

Application of the objective function to the algorithm

Full size image

The first and second phases of the objective function, as shown in Fig. 2, include the following steps 1–4 and the steps 6–7, 9–11, respectively.

  • Step 1 Different damage solutions are randomly generated and evaluated by F1. Then, the generated solution with the less value of F1 is saved as the best solution.

  • Step 2 Different damage solutions of the ith iteration are generated based on accelerated WEO algorithm formulation, and their F1 values are obtained.

  • Step 3 The best solution in F1 value terms is updated.

  • Step 4 The F1 value of the best solution is checked. If this value is equal to zero, then steps 8–9 are run; otherwise, step 5 is executed.

  • Step 5 The value of j is checked. If it is less than tmax, i and j are equated to i + 1 and j + 1, respectively, and steps 2–4 are executed again. Otherwise, the algorithm’s opportunity to find a solution with the value of F1 being equal to zero is finished, and steps 6–7 are run.

  • Step 6 The values of F2 corresponding to the best solution and every symmetric scenario (if the considered structure is symmetric) are calculated.

  • Step 7 The best answer based on the values of F2 is updated.

  • Step 8 The best computed solution is saved as the probable solution.

  • Step 9 The value of F2 corresponding to the best solution is checked. If this value is equal to zero, the best computed solution is equal to the experimental scenario and step 12 is executed.

  • Step 10 If the considered structure is symmetric, the symmetric scenarios of the best computed solution are obtained and saved as the probable damage solutions.

  • Step 11 The F2 value of every symmetric scenario is obtained. If this value is equal to zero in one of the scenarios, the scenario is equal to experimental scenario and step 12 is run. Otherwise, the j value is one, i value is increased to i + 1, and steps after step 1 are performed again.

  • Step 12 The process of finding actual damage scenario is finished, and the best computed solution is saved as solution found by this approach.

2.6 Reporting the Best Computed Solution

In the last step, the best computed damage solution shown by β vector is reported.

3 Optimization Algorithms

Water evaporation optimization (WEO) is a physics-based metaheuristic algorithm, introduced by Kaveh and Bakhshpoori (2016b). Also, accelerated water evaporation optimization (Kaveh and Bakhshpoori 2016a) is a version of WEO and has been developed to solve engineering and multidisciplinary optimization problems.

3.1 Water Evaporation Optimization

WEO is proposed based on inspiration of evaporation of water molecules on the surface of solid materials. Steps of the WEO implementation are as follows:

3.1.1 Initializing Algorithm Parameters

In the first step, algorithm parameters such as number of iteration (tmax), number of water molecules (nWM), minimum and maximum values of monolayer evaporation probability (MEPmin = 0.03 and MEPmax = 0.6), and minimum and maximum values of droplet evaporation probability (DEPmin= 0.6 and DEPmax = 1) are determined. These evaporation probability parameters have been defined based on molecular dynamics (MD) simulations presented by Wang et al. (2012). Also, the positions of all water molecules are randomly initialized in an n-dimensional search space (WM(0)) as follows:

$$ {\text{WM}}_{i,j}^{(0)} = {\text{Round}}(x_{j,\hbox{min} } + {\text{rand}}_{i,j} \, . { (}x_{j,\hbox{max} } - x_{j,\hbox{min} } )) $$
(12)

in which, WM (0) i, j are the initial values of the jth variable corresponding to the ith water molecule; randi,j is a random number in the range (0,1); xj,min and xj,max are the minimum and maximum permissible values for the jth variable.

3.1.2 Generating Water Evaporation Matrix

WEO has two independent sequential phases including monolayer and droplet evaporation phases, and molecules are updated globally and locally, respectively, in these phases. Variations of charge value (q) are q > 0.4e and q < 0.4e in the monolayer and droplet evaporation phases, respectively.

In the monolayer evaporation phase (t ≤ tmax/2), the objective function value of the individuals (Fit t i ) is scaled to the range [− 3.5, − 0.5]. Then, the corresponding substrate energy vector (Esub(i)) is generated as follows:

$$ E_{\text{sub}} (i)^{t} = \frac{{(E_{\hbox{max} } - E_{\hbox{min} } ) \times ({\text{Fit}}_{i}^{t} - {\text{Min}}({\text{Fit}}))}}{{({\text{Max}}({\text{Fit}}) - {\text{Min(Fit}}))}} + E_{\hbox{min} } $$
(13)

in which, Emax and Emin are equal to − 0.5 and − 3.5, respectively; Max and Min are the maximum and minimum functions, respectively. Then, the monolayer evaporation probability (MEP) is constructed as follows:

$$ {\text{MEP}}_{ij}^{t} = \left\{ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right. \, \begin{array}{*{20}c} {\text{if}} \\ {i{\text{f}}} \\ \end{array} \, \begin{array}{*{20}c} {{\text{rand}}_{ij} < \exp (E_{\text{sub}} (i)^{t} )} \\ {{\text{rand}}_{ij} \ge \exp (E_{\text{sub}} (i)^{t} )} \\ \end{array} $$
(14)

where MEP t ij is the updating probability for the jth variable of the ith water molecule at the tth iteration.

In the droplet evaporation phase (t > tmax/2), the objective function value of individuals (Fit t i ) is scaled to the range [− 50°, − 20°] by using contact angle (θ(i)t):

$$ \theta (i)^{t} = \frac{{(\theta_{\hbox{max} } - \theta_{\hbox{min} } ) \times ({\text{Fit}}_{i}^{t} - {\text{Min(Fit}}))}}{{({\text{Max(Fit)}} - {\text{Min(Fit}}))}} + \theta_{\hbox{min} } $$
(15)

Then, the droplet evaporation probability (DEP) is constructed as follows:

$$ \begin{aligned} {\text{DEP}}_{ij}^{t} &= \left\{ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right. \, \begin{array}{*{20}c} {\text{if}} \\ {\text{if}} \\ \end{array} \, \begin{array}{*{20}c} {{\text{rand}}_{ij} < J(\theta_{i}^{(t)} )} \\ {{\text{rand}}_{ij} \ge J(\theta_{i}^{(t)} )} \\ \end{array} \\ J(\theta ) &= J_{0} P_{0} \left( {\frac{2}{3} + \frac{{\cos^{3} \theta }}{3} - \cos \theta } \right)^{ - 2/3} (1 - \cos \theta ),\quad J_{0} P_{0} = \frac{1}{24} \\ \end{aligned} $$
(16)

in which, MEP t ij is the updating probability for the jth variable of the ith water molecule at the tth iteration; J is evaporation flux, and maximum and minimum value of it is 1 and 0.6, respectively; J0 and P0 are constant values.

3.1.3 Generating Random Permutation-Based Step Size Matrix

In this step, a random permutation-based step size matrix is calculated as follows:

$$ S = {\text{rand}} \cdot ({\text{WM}}^{(t)} \left[ {permute1(i)(j)} \right] - {\text{WM}}^{(t)} \left[ {permute2(i)(j)} \right]) $$
(17)

in which, permute1 and permute2 are different rows permutation functions; i and j are the number of water molecules and design variables of the problem, respectively; WM is the evaporated set of water molecules.

3.1.4 Generation of the Evaporated Water Molecules and Updating the Matrix of Water Molecules

After calculating step size matrix, the evaporated set of water molecules (WM(t+1)) is generated according to the matrix and evaporation probability matrix to the current set of molecules (WM(t)):

$$ {\text{WM}}^{(t + 1)} = {\text{Round}}\left( {{\text{WM}}^{(t)} + S \times \left\{ {\begin{array}{*{20}c} {{\text{MEP}}^{(t)} } \\ {{\text{DEP}}^{{ ( {\text{t)}}}} } \\ \end{array} } \right. \, \begin{array}{*{20}c} {t \le t_{\hbox{max} } /2} \\ {t > t_{\hbox{max} } /2} \\ \end{array} } \right) $$
(18)

The rounding function rounds the values of design variables to the nearest discrete available value. In other words, the function is used for discrete optimization problems. The best water molecule is returned after evaluating the molecules based on the objective function.

3.1.5 Terminating Condition Check

Steps 2–4 are repeated until the termination condition, number of iterations (t), is satisfied.

3.2 Accelerated Water Evaporation Optimization (Accelerated WEO)

As it was previously mentioned, in WEO algorithm, molecules are updated in two independent sequential phases including monolayer and droplet evaporation, while the process is performed by the simultaneous use of both phases in accelerated WEO.

Steps of the accelerated WEO implementation are as follows:

3.2.1 Initializing Algorithm Parameters

In this step, in addition to the details described in the WEO, the worst water molecule (worst-WM) in objective function value terms is monitored.

3.2.2 Generating Water Evaporation Matrix

The distance vector between all water molecules and the worst current one (dist) is first calculated by using:

$$ {\text{dist}}_{i} = \left| {{\text{worstWM}} - {\text{WM}}_{\text{i}} } \right|,\quad i = 1,2, \ldots ,{\text{ nWM}} $$
(19)

The molecules are sorted based on their distance values in ascending order. Then, the DEP and MEP matrices are generated for updating the first and second half of the molecules, respectively, using Eqs. (3) and (5). It should be noted that the droplet and evaporation probability matrices and their corresponding details, substrate energy and contact angle vectors, include nWM/2 rows. Then, mixed evaporation matrix (MDEP) is assembled from MEP and DEP matrices using the pseudocode shown in Fig. 3.

Fig. 3
figure 3

Pseudocode for constructing the MDEP matrix

Full size image

3.2.3 Generating Random Permutation-Based Step Size Matrix

In this step, similar to the one described in WEO, a random permutation-based step size matrix is calculated using Eq. (17).

3.2.4 Generate Evaporated Water Molecules and Update the Matrix of Water Molecules

The evaporated set of water molecules (WM(t+1)) is generated according to the step size matrix and mixed evaporation probability matrix (MDEP) to the current set of molecules (WM(t)):

$$ {\text{WM}}^{(t + 1)} = {\text{Round}}({\text{WM}}^{(t)} + S \times {\text{MDEP}}^{{ ( {\text{t)}}}} ) $$
(20)

Then, the best water molecule is returned after evaluating the molecules based on the objective function.

3.2.5 Terminating Condition Check

Steps 2–4 are repeated until termination condition, number of iteration of the algorithm (t), is satisfied.

4 Numerical Examples

In this section, three numerical examples consisting of a two-span beam, a two-bay three-story frame and a 72-bar spatial truss have been examined. To show the performance of the proposed objective function, every numerical example has been studied using three different damage scenarios and their results have been reported. A number of modes and degrees of freedom (DOF) are considered as input data that have an effect on the process of problem solving. The more number of these used, the easier it is to obtain a better solution; however, the number of calculated fractions during every evaluation of the objective function will be increased. Therefore, the number of modes and DOF must be chosen carefully. The number of modes considered for every structure has been mentioned in the corresponding part of the example. Additionally, the number of degrees of freedom in each example is the total number of structural degrees of freedom. All of the scenarios have been run 30 times independently. Also, tmax and the population sizes are considered as 1000 and 30, respectively.

To evaluate the performance of this method with other metaheuristic algorithms, CBO and ECBO algorithms are used. It should be noted CBO and ECBO algorithms are applied to only one scenario for each problem.

4.1 A Two-Span Beam

The first example is a two-span beam as shown in Fig. 4. The material and section properties of the elements of the beam are given in Table 1. This beam has 63 degrees of freedom, and the ten first modes are considered for all of the scenarios. This beam is symmetric; therefore, there is one other scenario whose natural frequencies are equal to the natural frequencies of the considered one. The damage scenarios of this example are provided in Table 2.

Fig. 4
figure 4

Schematic of the two-span beam

Full size image
Table 1 Material and section properties of the two-span beam
Full size table
Table 2 Damage scenarios of the two-span beam
Full size table

In Table 3, the number of successful runs for every scenario of this example is reported. Successful run is a run in which the considered scenario is found. Table 4 presents the results of the selected run for each scenario at the end of two phases. For each scenario, two successful runs have been chosen to report. Results are presented in two cases: Case I a symmetric successful run in which the algorithm has found one symmetric solution in the first phase and considered scenario is found in the second phase. Case II a successful run in which the algorithm has found considered scenario in the first phase and this solution is not changed in the second phase.

Table 3 Number of successful runs for the two-span beam
Full size table
Table 4 Results of the two-span beam
Full size table

Figures 5 and 6 show the evolutionary processes of damage severities of the damaged elements in the first phase corresponding to two successful runs of Scenario 1 and their symmetric solutions. Figures 7 and 8 show the variation of F1 with the number of iterations corresponding to these successful runs.

Fig. 5
figure 5

Evolutionary processes of damage severities in the first phase for the two-span beam corresponding to Scenario 1

Full size image
Fig. 6
figure 6

Evolutionary processes of damage severities in the first phase for the two-span beam corresponding to Scenario 1

Full size image
Fig. 7
figure 7

Variation of the F1 with the number of iterations for the two-span beam using the accelerated WEO (Scenario 1)

Full size image
Fig. 8
figure 8

Variation of the F1 with the number of iterations for the two-span beam using the accelerated WEO (Scenario 1)

Full size image

4.1.1 Noise for the Two-Span Beam

In real dynamic tests, avoiding the noise is impossible. Considering the noise causes a small deviation in the modal data; therefore, the value of objective function F1 will not reach to zero anymore. Hence, calculation is continued until the last iteration, and at the end, the second phase is performed. In the second phase, the value of F2 for the computed solution and the symmetric scenarios of the computed solution are calculated. Then, the best answer is considered as the solution found by this approach.

Producing small deviation in the experimental dynamic parameters is measured as:

$$ \omega_{{{\text{noise}},j}} = \omega_{d,j}^{\text{real}} \times (1 + {\text{random}}\left( { - 1,1} \right) \times {\text{Noise}}_{f} ) $$
(21)
$$ \varphi_{{{\text{noise}},ij}} = \phi_{d,ij}^{\text{real}} \times (1 + {\text{random}}\left( { - 1,1} \right) \times {\text{Noise}}_{\varphi } ) $$
(22)

where noise implies a noisy value; Noisef and Noiseφ are the deviations of the natural frequencies and mode shapes which are 1 and 3%, respectively (Kaveh et al. 2016).

Table 5 shows the results of the scenarios by considering noise for this example. Figure 9 illustrates the results of the two-span beam corresponding to Scenario 2. Figure 10 shows the evolutionary processes of damage severities of the damaged elements in the first phase corresponding to Scenario 2 and their symmetric solutions. Also, Fig. 11 shows the variation of F1 with the number of iterations.

Table 5 Results of the two-span beam by considering noise
Full size table
Fig. 9
figure 9

Result of applying noise to the two-span beam corresponding to Scenario 2

Full size image
Fig. 10
figure 10

Evolutionary processes of damage severities in the first phase for the two-span beam corresponding to Scenario 2 by considering noise

Full size image
Fig. 11
figure 11

Variation of the F1 with the number of iterations for the two-span beam using the accelerated WEO (Scenario 2 by considering noise)

Full size image

4.2 A Two-Bay Three-Story Frame

The second example is the two-bay three-story frame, shown in Fig. 12. As observed in Fig. 12, the beams and columns of the frame are modeled using 3 and 2 identical finite elements, respectively. The material section properties of the beams and columns are given in Table 6. This frame has 99 degrees of freedom, and the fifteen first modes are considered for all of the scenarios. The damage scenarios of this example are shown in Table 7.

Fig. 12
figure 12

Schematic of the two-bay three-story frame

Full size image
Table 6 Material and section properties of the two-bay three-story frame
Full size table
Table 7 Damage scenarios of the two-bay three-story frame
Full size table

In Table 8, the number of successful runs for all the scenarios of this example is reported. Table 9 presents the results of the selected run for each scenario at the end of two phases. For each scenario, one successful run has been chosen to report.

Table 8 Number of successful runs for the two-bay three-story frame
Full size table
Table 9 Results of the two-bay three-story frame
Full size table

Figure 13 shows the evolutionary processes of the damage severities of the damaged elements in the first phase corresponding to one of the successful runs of Scenario 2. Additionally, Fig. 14 shows the variation of F1 with the number of iterations corresponding to the successful run for accelerated WEO, CBO and ECBO algorithms.

Fig. 13
figure 13

Evolutionary processes of damage severities in the first phase for the two-span three-story frame corresponding to Scenario 2

Full size image
Fig. 14
figure 14

Variation of the F1 with the number of iterations for the two-span three-story frame using the accelerated WEO, CBO and ECBO (Scenario 2)

Full size image

4.3 A 72-Bar Spatial Truss

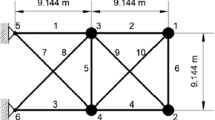
The third example, shown in Fig. 15, is a 72-bar spatial truss. This truss is a benchmark in field of optimization and damage detection and has been studied by many researchers (Sedaghati 2005; Kaveh et al. 2016; Tejani et al. 2016). The properties of this example are represented in Table 10. Four non-structural masses of 2270.0 kg are added to the four first nodes. This truss has 48 degrees of freedom, and the sixteen first modes are considered for all of the damage scenarios. This structure is symmetric, and for every considered scenario, there may be three or seven other scenarios whose natural frequencies are equal to the natural frequencies of the considered one. The damage scenarios of this example are shown in Table 11.

Fig. 15
figure 15

Schematic of the 72-bar spatial truss

Full size image
Table 10 Properties of the 72-bar spatial truss
Full size table
Table 11 Damage scenarios of the 72-bar spatial truss
Full size table

In Table 12, the number of successful runs for each scenario of this example is reported. Table 13 presents the results of the selected run for each scenario at the end of two phases. In this example, for each scenario, two successful runs have been chosen to report. Results are presented in two cases: Case I a symmetric successful run in which the algorithm has found one symmetric solution in the first phase and the considered scenario is found in the second phase. Case II a successful run in which the algorithm has found the considered scenario in the first phase and this solution has not changed in the second phase.

Table 12 Number of successful runs for the 72-bar spatial truss
Full size table
Table 13 Results of the 72-bar spatial truss
Full size table

Figures 16 and 17 show evolutionary processes of damage severities of the damaged elements in the first phase corresponding to successful runs of Scenario 3 and their symmetric solutions. Also, Figs. 18 and 19 show the variation of F1 with the number of iterations corresponding to these successful runs.

Fig. 16
figure 16

Evolutionary processes of damage severities in the first phase for the 72-bar spatial truss corresponding to Scenario 3

Full size image
Fig. 17
figure 17

Evolutionary processes of damage severities in the first phase for the 72-bar spatial truss corresponding to Scenario 3

Full size image
Fig. 18
figure 18

Variation of the F1 with the number of iterations for the 72-bar spatial truss using the accelerated WEO (Scenario 3)

Full size image
Fig. 19
figure 19

Variation of the F1 with the number of iterations for the 72-bar spatial truss using the accelerated WEO (Scenario 3)

Full size image

According to population size of the algorithm and the number of freedom degrees and modes considered in the first example, 192,000 fractions must be calculated in each iteration of algorithm if natural frequencies and mode shapes are evaluated simultaneously. While utilizing the two-phase method reduces this value to one of 300, 930 and 1560 fractions corresponding to the best scenario found in that iteration in the first example. Also, these values are reduced from 45,000 to one of 450 and 1935 for the second example and from 23,520 to one of 480, 1248 and 6624 for the third example.

5 Conclusions

In this paper, a two-phase method based on the structural dynamic characteristics for damage detection of skeletal structures is presented. The use of a two-phase approach greatly decreases the number of comparisons between modes for experimental and computed solutions. Therefore, the rate of number of calculated fractions in each run of the algorithm with this method is greatly reduced compared to objective function in which the frequencies and mode shapes are evaluated simultaneously. (The rate of number of calculated fractions in each iteration for examples 1, 2 and 3 is reduced about 91, 95 and 75%, respectively.) The effectiveness of the proposed approach is evaluated by examining three different numerical examples consisting of a two-span beam, a two-span three-story frame and a 72-bar spatial truss using the accelerated WEO algorithm with significant mutation, and their results are reported. Comparison of the number of the calculated fractions in each run of the algorithm for the single-phase method and the two-phase approach, is presented. This comparison shows that the use of the two-phase method greatly decreases the burden of the calculation. Also, by utilizing the presented objective function suitable results are obtained. Investigating the effect of noise in the two-span beam example showed that the proposed method is capable of finding suitable results despite the existence of deviation in the modal data.

The results show other metaheuristic algorithms such as CBO and ECBO also act successfully, although these two algorithms have less number of successful runs compared to the accelerated WEO algorithm.

Finally, it is suggested that this approach should be used for detecting the damage of symmetric large-scale structures, such as dome and tower trusses, and to compare the results with the results of the traditional single objective method in order to better evaluate the effectiveness of the presented approach. For additional efficiency, it is also advised to combine the presented approach with other methods of damage detection.