PeriFast/Dynamics: A MATLAB Code for Explicit Fast Convolution-based Peridynamic Analysis of Deformation and Fracture

Abstract

We present PeriFast/Dynamics, a compact and user-friendly MATLAB code for fast peridynamic (PD) simulations for deformation and fracture. PeriFast/Dynamics uses the fast convolution-based method (FCBM) for spatial discretization and an explicit time marching scheme to solve large-scale dynamic fracture problems. Different from existing PD solvers, PeriFast/Dynamics does not require neighbor search and storage, due to the use of the Fast-Fourier transform and its inverse to compute the integral operator. Run-times and memory allocation are independent of the number of neighbors inside the PD horizon, leading to faster computations and lower storage requirements. The governing equations and discretization method are briefly reviewed, the code structure explained, and individual modules described in detail. A demonstrative example on dynamic brittle fracture in 3D, with multiple crack branching events, is solved using three different constitutive models: a bond-based, an ordinary state-based, and a correspondence model. The small differences between results with the three different constitutive models are explained. Users are provided with a step-by-step description of the problem setup and execution of the code. PeriFast/Dynamics is a branch of the PeriFast suite of codes, and is available for download at the GitHub link provided in reference [1].

1 Introduction

Computational modeling of damage and fracture has been one of the most challenging areas in computational mechanics. Classical theories with the governing equations expressed in terms of partial differential equations (PDEs) are not fully capable of describing fracture since cracks are, in fact, evolving discontinuities in the continuum, and spatial derivatives at discontinuities in the displacement field are not defined. Peridynamic formulations for mechanics [2] offer alternative nonlocal approaches in which spatial derivatives are replaced with volume integrals of the primary unknowns over a certain finite region around each point, hence, allowing discontinuities (in the unknown field) to emerge and evolve in a mathematical consistent way since integration is not affected by discontinuities. PD makes seamless modeling of fracture and damage possible. In PD, cracks can naturally emerge, propagate, branch, and coalesce without the need of external, ad-hoc rules and conditions (e.g., see [3,4,5]). Significant interest on modeling fracture with PD has been observed [6,7,8].

The most common, straightforward and functional discretization for PD equations is the so-called meshfree method. In this, one approximates the integral over the nonlocal region (the PD horizon region) with a Riemann-type sum, normally using the one-point Gaussian integration, or a slight modification of that to account for nodal volumes (usually cubes) that are only partially covered by the PD horizon region [9]. Note that the commercially available computer-aided engineering (CAE) software is mostly based on the finite element method (FEM) and classical PDEs. Consequently, they are inherently different from meshfree PD in terms of data structures for geometry (elements and quadrature nodes in FEM, versus nodes in meshfree PD), and in terms of solvers used, since they are based on different numerical approximation methods. There have been several attempts to manipulate commercial FEM packages to perform PD analyses (e.g., see [10, 11]). Some commercial codes, e.g., LS-Dyna, have added PD capabilities as separate modules in their platform. In LS-Dyna, for example, the Discontinuous Galerkin method is used to approximate solutions to PD models ([12, 13]). U.S. National labs like Sandia and Oak Ridge National Laboratories, and research groups in academia and research labs in industry developed in-house codes for PD. Peridigm [14] is one of the few open-source PD software available from Sandia. The MOOSE-based PD code for implicit thermomechanical analysis by Idaho National Laboratory [15] is another example.

Because of its versatility in solving problems in fracture and damage, the meshfree method with direct summation for the quadrature is adopted by most existing PD in-house codes. In this approach, at every node, a loop is performed over all nodes in its “family” (neighboring nodes positioned within a finite size distance from the current node). If $N$ is the total number of nodes and $M$ is the number of nodes in the family of an arbitrary node, the nested loops result in solvers with the computational complexity of, at best, $O(NM)$. In 3D PD simulations with coarsest grids, $M$ is at least in order of hundreds, which make PD simulations costly when compared with, for example, FEM solvers for corresponding local models. Using FEM solvers for PD is, obviously, an option but the complexity would be the same; in addition, FEM solvers are not practical for solving problems with discontinuities. That is where the advantage of the meshfree method comes in. These observations show the need for faster solvers for PD models, especially for problems involving discontinuities, like fracture and damage.

Various attempts have been made to reduce the cost of PD simulations. One popular approach is the local-nonlocal coupling where only areas around cracks are modeled by PD, while the rest of the body is modeled using the local theory, discretized by FEM or by an efficient meshfree method [16,17,18]. Another way pursued for addressing PD high computational cost is grid refinement where necessary (mostly areas with damage) [19, 20]. These approaches, however, require prior knowledge of where fracture is likely to occur, or they need to employ smart adaptive schemes for determining those zones, which adds challenges and coding complexities. Moreover, for cases in which the damaged and fragmented region comprises most of the body, these coupling/adaptive approaches lose their advantage relative to a full PD model.

Recently, the fast convolution-based method (FCBM) for PD was introduced [21,22,23]. In this method, nodal quadrature is expressed in terms of convolution sums, which are evaluated efficiently via fast Fourier transform operations. Since the quadrature is evaluated by multiplication of the Fourier modes of the convolving functions, looping over the family of neighbors is not performed. The major cost is associated with the FFT operations, which leads to an $O\left(N{\mathrm{log}}_{2}N\right)$ complexity. No neighbor search and storage are required in FCBM, resulting in fast initialization and low memory requirements. The studies mentioned above have shown speedups as high as thousands compared with the direct quadrature PD solver. Certain variations of FCBM have been proposed and used in [24,25,26,27].

In the original meshfree method with direct summation quadrature, for a fixed horizon size, $M$ scales with $O(N)$ in an m-convergence test [28], leading to $O\left({N}^{2}\right)$ complexity. For a $\delta$-convergence calculation [28], in which $M$ is kept fixed while reducing the horizon size (thus increasing $N$), the direct summation quadrature would scale as $O\left(NM\right)$ which, at first glance, looks better than $O\left(N{\mathrm{log}}_{2}N\right)$. However, based on the performance comparison between direct quadrature and FCBM, for an m-factor (ratio of horizon size to grid spacing) of 3 in a 3D computation, the direct summation quadrature outperforms FCBM only when $N$ becomes larger than $7\times {10}^{58}$.

Another advantage of the FCBM-PD is its low barrier for utilizing HPC. One can simply call parallel or GPU-based FFT libraries instead of the serial ones to benefit from parallel computing at no additional programming effort. An FCBM for PD diffusion code has been published as supplementary material in a previous study [22]. That code, however, was designed for a limited class of diffusion problems.

Here, we introduce PeriFast/Dynamics, an FCBM-based code written in MATLAB for modeling deformation and fracture using peridynamics. PeriFast/Dynamics is simple, compact, and easy to use and expand to a variety of other problems. After brief reviews of PD formulations for deformations/fracture/damage and the main steps in the FCBM for discretizing such formulations, we provide the overall description of the PeriFast/Dynamics code structure with detailed explanations for each of its modules (m-files). In addition, we present an example showing how the code can be used, and how one can extend it to other material models and applications. Full details of the PD theory and FCBM discretization can be found in the following references, for example: [22, 23, 29, 30].

The paper is organized as follows: governing equations for the initial boundary value problems for deformations and damage are discussed in Section 2; in Section 3, the FCBM discretization is briefly reviewed; data structures used in PeriFast/Dynamics are shown in Section 4; the code’s general structure and details of each of its modules are presented in Section 5; in Section 6, a demonstrative example is provided with step-by-step instructions for a user to perform a 3D peridynamic analysis of dynamic brittle fracture using the freely-available code.

2 The Peridynamic Initial-Value Volume-Constrained Problem for Dynamic Fracture

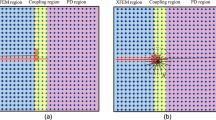
PeriFast/Dynamics analysis aims to solve PD equations of dynamic deformation and damage subjected to initial conditions (IC) and volume constraints (VC), a.k.a. nonlocal boundary conditions. Consider a 3D peridynamic body ($\mathrm{B}$), with constrained volumes ${\Gamma }_{1},{\Gamma }_{2},$ and ${\Gamma }_{3}$ on which the displacement field components ${u}_{1},{u}_{2},$ and ${u}_{3}$ are respectively prescribed. The constrained volumes usually coincide with one another, but they do not have to. Figure 1 shows a generic 2D PD body with constrained volumes.

Fig. 1

Schematic of a 2D peridynamic body ($B$), consisting of the domains ${\Omega }_{1}$ and ${\Omega }_{2}$, where displacement components ${u}_{1}$ and ${u}_{2}$ are unknown, respectively, and the constrained volumes (${\Gamma }_{1}$ and ${\Gamma }_{2}$) where ${u}_{1}$ and ${u}_{2}$ are independently prescribed. (Figure adopted from [23])

Let ${\varvec{x}}(t)=\left\{{x}_{1}(t),{x}_{2}(t),{x}_{3}(t)\right\}$ be the position vector of a material point at time $t$, with $i=\mathrm{1,2},3$ corresponding to the three Cartesian coordinate directions in 3D. The PD initial-value volume-constrained (IVVC) problem for dynamics is [31]

$$\left\{\begin{array}{ll}\rho \frac{{\partial }^{2}{u}_{i}({\varvec{x}},t)}{\partial {t}^{2}}={L}_{i}\left({\varvec{x}},t\right)+{b}_{i}\left({\varvec{x}},t\right) & {\varvec{x}}\in {\Omega }_{i},\;t>0 \\ {u}_{i}\left({\varvec{x}},0\right)={u}_{i}^{0};\; {v}_{i}\left({\varvec{x}},0\right)={v}_{i}^{0} \left(\mathrm{I}.\mathrm{C}.\right) & {\varvec{x}}\in {\Omega }_{i} \\ {u}_{i}\left({\varvec{x}},t\right)={g}_{i}\left({\varvec{x}},t\right) \left(\mathrm{V}.\mathrm{C}.\right) & {\varvec{x}}\in {\Gamma }_{i},\;t\ge 0\end{array}\right.;\;i=\mathrm{1,2},3$$

(1)

where ${u}_{i}$ is the displacement in the $i$-direction, ${v}_{i}$(velocity) is the time-derivative of ${u}_{i}$, ${g}_{i}$ is a given volume constraints on ${\Gamma }_{i}$, and ${b}_{i}$ is the body/external force density in the $i$-direction. ${L}_{i}$ denotes the internal force density in $i$-direction and is defined as

$${L}_{i}\left({\varvec{x}},t\right)={\int }_{{\mathcal{H}}_{x}}\mu \left({\varvec{x}}{,{\varvec{x}}}^{\boldsymbol{^{\prime}}}, t\right){f}_{i}\left({\varvec{x}},{{\varvec{x}}}^{\boldsymbol{^{\prime}}},t\right) \mathrm{d}{\varvec{x}}\boldsymbol{^{\prime}}; \; i=\mathrm{1,2},3$$

(2)

where ${\mathcal{H}}_{x}$ is the finite size neighborhood of ${\varvec{x}}$ where the nonlocal interactions pertaining to ${\varvec{x}}$ occur. ${\mathcal{H}}_{x}$ is known as the family or the horizon region of point ${\varvec{x}}$ and is usually a sphere in 3D, centered at ${\varvec{x}}$ with the radius $\delta$ referred to as the horizon size. ${{\varvec{x}}}^{\boldsymbol{{\prime}}}$ denotes the position vector for family nodes in ${\mathcal{H}}_{x}$. ${f}_{i}\left({\varvec{x}},{{\varvec{x}}}^{\boldsymbol{{\prime}}},t\right)$ is the dual force density: the net force between the material volume at ${\varvec{x}}$ and the material volume at ${\varvec{x}}\boldsymbol{^{\prime}}$, and is determined by a PD constitutive model. PD material models, which define the expression for ${f}_{i}\left({\varvec{x}},{{\varvec{x}}}^{\boldsymbol{{\prime}}},t\right)$ in Eq. (2), can be of two types: bond-based (BB) and state-based (SB). In BB-PD, the dual force density for each pair of nodes depends on the displacement of those nodes only, whereas in the more general SB-PD, the dual force density for each pair of nodes can depend on the deformation of the entire families of ${\varvec{x}}$ and ${{\varvec{x}}}^{\boldsymbol{{\prime}}}$. In SB-PD, PD states are introduced as general nonlinear mappings, generalizations of tensors, which are linear mappings, in the classical continuum mechanics theory [32]. The constitutive relationships define the PD “force-state” as a function of the PD “deformation-state” and other quantities. ${f}_{i}$ in Eq. (2) is defined based on the force-states at ${\varvec{x}}$ and ${{\varvec{x}}}^{\boldsymbol{{\prime}}}$ [32]. The relationship between PD force and deformation states can either be directly constructed/obtained in the nonlocal setting (the “native PD approach”), or it can be derived by a conversion (or “translation”) method from a classical (local) constitutive model. The latter is known as the PD correspondence approach, which usually leads to non-ordinary state-based (NOSB) PD models. In ordinary state-based (OSB) PD models, the force vector between ${\varvec{x}}$ and ${{\varvec{x}}}^{\boldsymbol{^{\prime}}}$ is collinear to the bond vector connecting the two points, while NOSB-PD models this does not necessarily happen [32]. Correspondence models are convenient since they can use existing constitutive local models, but can suffer from numerical instabilities (zero energy modes, see [33,34,35]), and tend to have a higher computational cost than corresponding OSB ones. The constitutive model formulas used in this work are given in Appendix.

The function $\mu$ in Eq. (2) is a history-dependent bond-level damage function with the following binary definition normally used for brittle-type damage:

$$\mu ({\varvec{x}}{,{\varvec{x}}}^{\boldsymbol{{\prime}}}, t)=\left\{\begin{array}{cc}1 & {{\varvec{xx}}}^{\boldsymbol{{\prime}}} \;\mathrm{bond\;is\;intact}\;(\mathrm{carries\;force})\;\mathrm{at\;time}\;t \\ 0 & {{\varvec{xx}}}^{\boldsymbol{{\prime}}}\;\mathrm{bond\;is\;broken}\;(\mathrm{does\;not\;carry\;a\;force})\;\mathrm{at\;time}\;t\end{array}\right.$$

(3)

Note that PD bonds refer to pairs of family points. A broken bond means that the interaction between the two family points that the bond connects no longer exists. In PeriFast/Dynamics, we use the energy-based damage model proposed in [23], which is consistent with the FCBM discretization. In this model, once the strain energy density ($W$) at a point reaches a critical strain energy density (${W}_{c}$), that point loses all of its bonds irreversibly, i.e., it is completely detached from the body. The definition for $\mu$ in this approach can be expressed as

$$\mu \left({\varvec{x}},{{\varvec{x}}}^{{\prime}},t\right)=\lambda \left({\varvec{x}},t\right)\lambda \left({{\varvec{x}}}^{{\prime}},t\right)=\lambda \lambda {^{\prime}}$$

(4)

where

$$\lambda ({\varvec{x}},t)=\left\{\begin{array}{cc}1 & \mathrm{if}\;W\left({\varvec{x}},t\right) \le {W}_{\mathrm{c}} \\ \; 0 & \quad \mathrm{if}\;W\left({\varvec{x}},t\right) >{W}_{{\varvec{c}}}\end{array}\right.$$

(5)

The definition of $W\left({\varvec{x}},t\right)$ depends on the constitutive model. For the material models implemented in PeriFast, $W$ is provided in Appendix. The threshold ${W}_{\mathrm{c}}$ is calibrated to the critical fracture energy ${G}_{0}:$

$${W}_{{\varvec{c}}}=\frac{{G}_{0}}{2\delta }$$

(6)

The details of calibration can be found in [23]. Note that the calibrated formula shown in reference [23] does not include the 2 in the denominator. There, the 2 was incorporated into formula for $W$, leading to equivalent results as here. We prefer the current formula for clarity.

Most engineering measurements are taken on surfaces of the domain, leading to mathematical descriptions in terms of (classical) Dirichlet, Neumann, or mixed boundary conditions. In order to approximate a (classical) Dirichlet boundary condition in the PD nonlocal settings described by Eq. (1), one can impose displacements on a $\delta$-thick volumetric layer at the boundary: this is known as the “naïve approach” [36]. For more accurate enforcement of local boundary conditions in PD models, please see, e.g., [36,37,38,39,40]. In the current version of PeriFast/Dynamics, we use the naïve approach. The mirror-based fictitious nodes method (FNM) [36] is also compatible with FCBM and has been implemented in the PeriFast/Corrosion branch [41].

Traction boundary conditions (Neumann type) are usually implemented as body force densities applied on a $\delta$-thick layer at the corresponding boundary. Other options can be used, for example, one can specify a certain profile for ${g}_{i}$ in Eq. (1), that approximates, for example, the desired Dirichlet and Neumann boundary conditions, see [22, 36]. The body force approach is implemented here in PeriFast/Dynamics.

In order to be able to use the FCBM-PD, a constitutive model needs to be setup in convolutional form. For the PeriFast/Dynamics code, the linearized BB, linearized native OSB-PD model, and PD correspondence model are implemented based on the formulations presented in [23, 42], where the convolutional forms for each of these constitutive models, including brittle fracture, have been derived.

While for linearized PD models and PD correspondence models of the form shown in [32], convolutional structures are easy to obtain (see [42,43,44]), a case-by-case investigation is needed for general nonlinear models to find a convolutional form to which FCBM can be applied. One example for a nonlinear bond-based model is provided in [23], while references [43, 44] show the procedure for obtaining the convolution form in the case of elasto-plasticity and ductile failure.

3 Review of the Fast Convolution-Based Discretization Method (FCBM)

PeriFast/Dynamics uses the fast convolution-based method (FCBM) to solve the PD-IVVC problem in Eq. (1). In FCBM, the convolution theorem and efficient FFT algorithms are employed to evaluate the mid-point quadrature at significantly lower costs compared to the direct summation that is traditionally used. Details of the method are given in [23] and briefly summarized below. Identification and looping over neighbors of a given node are no longer needed in FCBM, making the method independent of the neighbor numbers. The initial family search is eliminated, and memory allocation is significantly reduced, since neighbor information does not need to be stored. We aim to approximate the integral over the horizon region in Eq. (1) using mid-point integration (one-point Gaussian quadrature) but evaluated using the Fast Fourier Transform (FFT) and its inverse, instead of the regular direct summation through a nested loop over the horizon region. For FFT to be applicable in computing the convolution sums, the problem needs to be extended by periodicity to the entire space. This is done by first embedding the PD domain in a rectangular box (with a buffer of at least $\delta$ between the surface of the domain and the edge of the box), which is then extended by periodicity to the entire space.

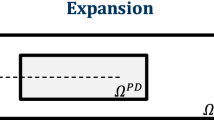
Figure 2 shows the box (delineated by the dashed line) with the actual domain contained in it, extended by periodicity as depicted in Fig. 1. Note that the box edges should be at least one horizon ($\delta$) away from the boundary of the body $\mathrm{B}$. This will ensure that there will be no wrap-around effect in the circular convolution discussed below.

Fig. 2

Extension of a generic peridynamic body to a periodic box in 2D. (Figure adopted from [23])

After extension of the body to ${\mathbb{T}}$, the following characteristic functions, are defined for distinguishing various subdomains (partitioning ${\mathbb{T}}$ in a way):

$${\chi }_{\mathrm{B}}\left({\varvec{x}}\right)=\left\{\begin{array}{cc}1& {\varvec{x}}\in \mathrm{B }\\ 0& {\varvec{x}}\in {\mathbb{T}}\backslash \mathrm{B}=\Lambda \end{array}\right.$$

(7)

$${\chi }_{{\Omega }_{i}}\left({\varvec{x}}\right)=\left\{\begin{array}{ll}1& {\varvec{x}}\in {\Omega }_{i} \\ 0& {\varvec{x}}\in {\mathbb{T}}\backslash {\Omega }_{i}={\Gamma }_{i}\cup\Lambda \end{array}\right.;\;\mathrm{and}\;{\chi }_{{\Gamma }_{i}}\left({\varvec{x}}\right)={\chi }_{\mathrm{B}}\left({\varvec{x}}\right)-{\chi }_{{\Omega }_{i}}\left({\varvec{x}}\right)$$

(8)

${\chi }_{\mathrm{B}}$ is defined for eliminating any interaction between the PD body and the rest of the box and ${\chi }_{{\Omega }_{i}}$ is for applying the BCs.

Using ${\chi }_{\mathrm{B}}$ and ${\chi }_{{\Omega }_{i}}$, the PD IVVC problem in Eq. (1) is modified as follows:

$$\left\{\begin{array}{ll}\rho \frac{{\partial }^{2}{u}_{i}}{\partial {t}^{2}}={\chi }_{{\Omega }_{i}}\left({\int }_{\mathbb{T}}{\chi }_{\mathrm{B}}{\chi }_{\mathrm{B}}^{^{\prime}}\mu {f}_{i}\mathrm{d}{V}_{{{\varvec{x}}}^{\boldsymbol{^{\prime}}}}+{b}_{i}\right)+\left(1-{\chi }_{{\Omega }_{i}}\right)\rho \frac{{\partial }^{2}{w}_{i}}{\partial {t}^{2}}& {\varvec{x}}\in {\mathbb{T}},\;t>0\\ {u}_{i}\left({\varvec{x}},0\right)={\chi }_{{\Omega }_{i}}{u}_{i}^{0}+\left(1-{\chi }_{{\Omega }_{i}}\right){w}_{i}\left({\varvec{x}},0\right) & {\varvec{x}}\in {\mathbb{T}} \\ {v}_{i}\left({\varvec{x}},0\right)={\chi }_{{\Omega }_{i}}{v}_{i}^{0}+\left(1-{\chi }_{{\Omega }_{i}}\right)\frac{\partial {w}_{i}\left({\varvec{x}},0\right)}{\partial t} & {\varvec{x}}\in {\mathbb{T}}\end{array}\right.$$

(9)

where ${w}_{i}\left({\varvec{x}},t\right)$ is known from the given data:

$${w}_{i}\left({\varvec{x}},t\right)=\left\{\begin{array}{cc}{g}_{i}\left({\varvec{x}},t\right)& {\varvec{x}}\in {\Gamma }_{i}\\ 0& {\varvec{x}}\in {\mathbb{T}}\backslash {\Gamma }_{i}\end{array}\right.$$

(10)

Changing the domain of integration from ${\mathcal{H}}_{x}$ in Eq. (2) to ${\mathbb{T}}$ in Eq. (10) does not alter the integral because ${f}_{i}$ is zero outside of the horizon region.

The solution to Eq. (10) on ${\Omega }_{i}$ is the same as the solution to Eq. (1). Equation (10), however, is defined over a periodic domain (${\mathbb{T}}$) which allows for utilizing FFT for fast evaluation of the circular convolutions arising from discretization of PD integrals.

PeriFast/Dynamics uses uniform grid spacing for spatial discretization at this stage. The discrete coordinates are defined:

$$\begin{array}{l}{{\varvec{x}}}_{nmp}=\left\{\left(n-1\right)\Delta {x}_{1},\left(m-1\right)\Delta {x}_{2},\left(p-1\right)\Delta {x}_{3}\right\},\;\mathrm{ where\;}\Delta{x}_{1}=\frac{{L}_{1}}{{N}_{1}};\;\Delta {x}_{2}=\frac{{L}_{2}}{{N}_{2}};\Delta {x}_{3}=\frac{{L}_{3}}{{N}_{3}}\\\mathrm{and}\;n=\left\{\mathrm{1,2},\dots ,{N}_{1}\right\};\;m=\left\{\mathrm{1,2},\dots ,{N}_{2}\right\} ;p=\left\{\mathrm{1,2},\dots ,{N}_{3}\right\}\end{array}$$

(11)

${L}_{1}, {L}_{2}$ and ${L}_{3}$ are the dimensions of the box ${\mathbb{T}}$ in 3D, and ${N}_{1},{N}_{2}$, and ${N}_{3}$ are number of nodes in each coordinate direction. Note that FCBM might be compatible with nonuniform discretizations if the nonuniform FFT is employed, but this is an area for future research.

Using mid-point quadrature for the integral in Eq. (9). One gets

$${L}_{i}^{nmp,t}=\sum_{q,s,r=1}^{{N}_{3},{N}_{2},{N}_{1}}{\chi }_{\mathrm{B}}^{nmp}{\chi }_{\mathrm{B}}^{rsq}\mu \left({{\varvec{x}}}_{rsq},{{\varvec{x}}}_{nmp},t\right){f}_{i}\left({{\varvec{x}}}_{rsq},{{\varvec{x}}}_{nmp},t\right) {V}^{rsq}$$

(12)

where $\sum_{q,s,r=1}^{{N}_{3},{N}_{2},{N}_{1}}=\sum_{q=1}^{{N}_{3}}\sum_{s=1}^{{N}_{2}}\sum_{r=1}^{{N}_{1}} .$ Note that to compute PD integrals more accurately, one can use the partial-volume correction algorithms [45, 46]. These algorithms can be easily incorporated to the FCBM framework by introducing a volume correction function to Eq. (12). The correction functions can be defined similar to the one defined in [45]. This is not done here because we will tend to use relatively large m-values (m is the ratio of horizon size to grid spacing), reducing the error in that way. An analysis of the influence of partial-volume algorithms on FBCM results is planned in the future.

The key step in FCBM is to express the summation in the equation above in terms of linear combinations of convolutions, in the following general form:

$$\begin{aligned}{L}_{i}^{nmp,t}&=\sum_{l=1}^{{N}_{c}}\left[{a}_{l}\left({{\varvec{x}}}_{nmp},t\right)\sum_{q,s,r=1}^{{N}_{3},{N}_{2},{N}_{1}}{b}_{l}\left({{\varvec{x}}}_{rsq},t\right){c}_{l}\left({{\varvec{x}}}_{nmp}-{{\varvec{x}}}_{rsq},t\right)\right]\\&=\sum_{l=1}^{{N}_{c}}{a}_{l}^{nmp,t}{\left[{b}_{l}*{c}_{l}\right]}^{nmp,t}\end{aligned}$$

(13)

where ${N}_{c}$ is a positive integer that denotes the number of convolutions, and for each $l=1,\dots ,{N}_{c}$: ${a}_{l}$ is a function of point ${\varvec{x}},{b}_{l}$ is function of ${\varvec{x}}\boldsymbol{^{\prime}},$ and ${c}_{l}$ is a function of $({\varvec{x}}-{\varvec{x}}\boldsymbol{^{\prime}})$. Here ${c}_{l}$ functions are referred to as the kernel functions. Note that different constitutive models lead to different ${a}_{l}$, ${b}_{l}$, and ${c}_{l}$ functions that need to be defined in the code. Convolutional forms for the linearized bond-based, linearized native state-based, and PD correspondence models used in this work are provided in Appendix. Generally, a convolutional structure is natural for the integral operator in linear PD formulations [23, 47]. For nonlinear PD models, one needs to either linearize them or investigate on a case-by-case basis to see if such a structure can be found. In our previous publication [23] (see also Eq. (13) in the present manuscript) we showed how to obtain the convolutional structure for a large class of nonlinear PD problems. For problems that do not fall directly into this general setting, like the PD model with critical bond-strain damage criterion, we had to introduce a modified damage criterion (based on critical nodal strain energy density, instead of critical bond-strain) which allowed us to recast the formulation into that general setting and easily obtain the convolutional structure needed. Several examples for constructing convolution-based discretizations for nonlinear PD problems have been shown for nonlinear diffusion [22], and nonlinear elasticity (bond-based) with brittle fracture [23]. Notably, PD correspondence models of the form presented in [38] also fall into the general setting mentioned above and, therefore, it is easy to derive their convolutional structure (see [42,43,44]).

Using the discrete convolution theorem, Eq. (13) can be computed as

$${L}_{i}^{nmp,t}=\sum\limits_{l=1}^{{N}_{c}}{a}_{l}^{nmp,t}{\left\{{\mathbf{F}}^{-1}\left[\mathbf{F}\left({b}_{l}\right)\mathbf{F}\left({c}_{l}^{s}\right) \right]\right\}}^{nmp,t}$$

(14)

where $\mathbf{F}$ and ${\mathbf{F}}^{-1}$ denote the FFT and inverse FFT operations, and ${c}_{l}^{s}$ is the shifted kernel with respect to the box coordinates. ${c}_{l}^{s}$ is the periodic version of ${c}_{l}$ function over ${\mathbb{T}}$, where the origin of ${c}_{l}$ is shifted to coincide with the corners of ${\mathbb{T}}$. This is necessary for the circular convolution operation to represent the PD convolution integrals. Figure 3 shows the original and the shifted version of a generic 2D radial kernel.

Fig. 3

On the left: a 2D generic kernel function in its original form centered at zero (${c}_{l}$). On the right: the periodic shifted version (${c}_{l}^{s}$) used in the fast convolution on ${\mathbb{T}}=[{x}_{\mathrm{min}} {x}_{\mathrm{max}}]\times [{y}_{\mathrm{min}} {y}_{\mathrm{max}}]$. The colored disk denotes the non-zero part of the kernel function

In Section 4.6 the operation of generating the shifted kernel from the given kernel function in PeriFast is described.

By comparing Eqs. (13) and (15), we can see that the summation over the neighbors of ${{\varvec{x}}}_{nmp}$ no longer appears in the fast convolution computation, and therefore FCBM is independent of the number of neighbors of a given node. As a consequence, there is no need to search, identify, and store neighbor information, leading to important CPU and storage savings.

The displacement and velocity fields at each time step $\Delta t$ are updated explicitly via the velocity-Verlet algorithm (see [4] for details):

$${u}_{i}^{nmp,t+\Delta t}={\chi }_{{\Omega }_{i}}^{nmp}\left\{{u}_{i}^{nmp,t}+\Delta t\left[{v}_{i}^{nmp,t}+\frac{\Delta t}{2\rho }\left({L}_{i}^{nmp,t}+{b}_{i}^{nmp,t}\right)\right]\right\}+\left(1-{\chi }_{{\Omega }_{i}}^{nmp}\right){w}_{i}^{nmp,t+\Delta t}$$

(15)

$${v}_{i}^{nmp,t+\Delta t}={\chi }_{{\Omega }_{i}}^{nmp}\left\{{v}_{i}^{nmp,t}+\frac{\Delta t}{2\rho }\left[\left({L}_{i}^{nmp,t}+{b}_{i}^{nmp,t}\right)+\left({L}_{i}^{nmp,t+\Delta t}+{b}_{i}^{nmp,t+\Delta t}\right)\right]\right\}$$

(16)

Remark: in addition to the internal force density, all other PD integrals, if used (e.g., PD strain energy density), need to be expressed in the form of Eq. (13), in order to be computed using the FCBM.

Remark: in order to impose periodic BC in FCBM, one takes ${\chi }_{\mathrm{B}}({\varvec{x}})={\chi }_{{\Omega }_{i}}({\varvec{x}})=1$ for all ${\varvec{x}}$. This implies that the body becomes a torus/periodic box: ${\chi }_{\mathrm{B}}\equiv {\chi }_{{\Omega }_{i}}\equiv {\mathbb{T}}$. In this case, the Fourier basis functions employed in the FFT operations naturally capture the “wrap-around” effect expected in a periodic setting. This is in contrast with other discretization methods such as FEM or other meshfree methods where the periodic/wrap-around condition needs to be explicitly enforced on the boundary nodes. In the case of Fourier-based discretizations, like Fourier spectral methods and FCBM, periodic BCs are naturally captured and there is no need to explicitly enforce any type of conditions or constrains. The characteristic function introduced in our FCBM approach allows the extension of this Fourier-based method to bounded domains with non-periodic BCs.

Remark: convergence studies for FCBM have shown a quadratic rate for diffusion problems in 1D and 2D [21, 22] and a super linear rate in a 3D elasticity example [23]. For fracture problems, an m-convergence study in 2D was reported in [23], and a $\delta$-convergence study can be found in [43, 44]. Convergence studies for certain variations of FCBM can also be found in [24,25,26].

4 PeriFast/Dynamics Code Description

In this section, we describe the data structures used in the discretization in PeriFast/Dynamics, discuss the overall structure of the code and provide details of each of its modules (m-files).

4.1 Data Structure for PD Nodes

PeriFast/Dynamics stores the PD nodal positions and nodal values for different quantities in a consistent way with MATLAB’s multi-dimensional FFT operations.

Let ${\mathbb{T}}=[{x}_{\mathrm{min}} {x}_{\mathrm{max}}]\times [{y}_{\mathrm{min}} {y}_{\mathrm{max}}]\times [{z}_{\mathrm{min}} {z}_{\mathrm{max}}]$ denote a periodic box in 3D, with the uniform discretization given below:

$$\begin{array}{l}{{\varvec{x}}}_{ijk}=\left\{\begin{array}{c}{x}_{i}\\ {y}_{j}\\ {z}_{k}\end{array}\right\}=\left\{\begin{array}{c}{x}_{\mathrm{min}}+\left(i-1\right)\Delta x\\ {y}_{\mathrm{min}}+\left(\,j-1\right)\Delta y\\ {z}_{\mathrm{min}}+\left(k-1\right)\mathrm{\Delta z}\end{array}\right\};\;\Delta x=\frac{{L}_{1}}{{N}_{1}},\Delta y=\frac{{L}_{2}}{{N}_{2}};\;\mathrm{\Delta z}=\frac{{L}_{3}}{{N}_{3}};\\\mathrm{and}\;i=\mathrm{1,2},\dots ,{N}_{1} j=\mathrm{1,2},\dots ,{N}_{2} k=\mathrm{1,2},\dots ,{N}_{3} ,\\{L}_{1}={x}_{max}-{x}_{min},{L}_{2}={y}_{max}-{y}_{min},{L}_{3}={z}_{max}-{z}_{min}\end{array}$$

(17)

In PeriFast/Dynamics the $x$, $y$, and $z$-coordinates of all nodes are stored in three distinct 3D arrays of size ${N}_{2}\times {N}_{1}\times {N}_{3}$:

$$\begin{array}{l}\mathbf{X}\boldsymbol{ }={\left[{X}_{jik}\right]}_{{N}_{2}\times {N}_{1}\times {N}_{3}},\mathbf{Y}\boldsymbol{ }={\left[{Y}_{jik}\right]}_{{N}_{2}\times {N}_{1}\times {N}_{3}}, \mathbf{Z}\boldsymbol{ }={\left[{Z}_{jik}\right]}_{{N}_{2}\times {N}_{1}\times {N}_{3}}\\i=\mathrm{1,2},\dots ,{N}_{1} j=\mathrm{1,2},\dots ,{N}_{2} k=\mathrm{1,2},\dots ,{N}_{3}\end{array}$$

(18)

where ${X}_{jik}$, ${Y}_{jik}$, and ${Z}_{jik}$ respectively denote the $x,y,$ and $z$-coordinates of node ${{\varvec{x}}}_{ijk}$. Note that the index in y-direction precedes the x-direction index, due to the way MATLAB’s meshgrid function generates 3D arrays. While in traditional solvers all nodal data are usually vectorized regardless of the spatial dimension, in FCBM it is necessary to work with multi-dimensional arrays, because of using multi-dimensional FFT operations.

In PeriFast/Dynamics, functions of space and time are defined as functions of $\mathbf{X}$,$\mathbf{Y},\mathbf{Z},$ and $t$, and return outputs in the form of 3D ${N}_{2}\times {N}_{1}\times {N}_{3}$ arrays containing their nodal values.

For example, let ${\varvec{C}}\left({\varvec{x}}\right)$ be a $3\times 3$ tensor-valued function defined in 3D. The discrete version of this function in PeriFast/Dynamics is

$${{\varvec{C}}}_{pq}\boldsymbol{ }\left({\varvec{X}},{\varvec{Y}},{\varvec{Z}}\right)={\left[{\left({C}_{pq}\right)}_{jik}\right]}_{{N}_{2}\times {N}_{1}\times {N}_{3}};\;\mathrm{for\;each}\;p,q=\mathrm{1,2},3$$

(19)

For each $p$ and $q$ (each component of the tensor ${\varvec{C}}$), ${\mathbf{C}}_{pq}$ is a 3D ${N}_{2}\times {N}_{1}\times {N}_{3}$ array returned by a function of $\mathbf{X}$,$\mathbf{Y},$ and $\mathbf{Z}$. See PeriFast’s nodes_and_sets.m module for examples of such definitions.

4.2 The Overall Code Structure

The current version of PeriFast/Dynamics consists of 14 MATLAB m-files: main.m, inputs.m, nodes_and_sets.m, pre_constitutive.m, constitutive.m, update_tractions.m, update_VC.m, initial_gpu_arrays.m, dump_output.m, visualization.m, open_Matlab_video.m, create_matlab_video.m close_Matlab_video.m and postprocess.m.main.m is the script that executes the program. inputs.m contains certain input data including material properties, simulation time, time steps, initial and boundary conditions, visualization parameters. nodes_and_sets.m contains the PD horizon and discrete geometrical data including nodal coordinates and discrete characteristic functions that define various subdomains: the original body, constrained volumes, pre-damaged regions, and subregions where tractions are applied as a body force. Pre_constitutive.m, and constitutive.m contain the material model information (available in the form of Eq. (13)). Functions that are independent of the field variables and time, i.e., are not changing during the simulations, are defined in pre_constitutive.m. The kernel functions are usually of this type and are defined in this module. The precomputed functions in pre_constitutive.m as well as the displacement field and other inputs are passed onto the module constitutive.m, where the internal force density, strain energy density, and damage are computed. constitutive.m is the module that is called in each time step to update the material response. Files update_tractions.m, and update_VC.m are modules called when traction and displacement boundary conditions need to be updated, respectively. initial_gpu_arrays.m, converts variables involved in the convolution operations to MATLAB’s “gpuarray” type to use GPU-based computations. Dump_output.m script is called every several time steps (frequency defined by the user in inputs.m) to record output data into a Matlab variable and into a Tecplot 360 [48] file (user can determine in inputs.m if Tecplot file is desired). If visualization is requested by the user (in inputs.m), visualization.m is called as well to plot results in Matlab at every snapshot during the analysis (number of data dump and visualization frames can be set by the user in inputs.m).

Naturally, performing the visualization during the analysis slows down the run time. For speed tests, or if solving a larger problem, it is recommended to turn off visualization_during_analysis (in inputs.m). One can postprocess the recorded output data once the simulation is completed. The option to generate a Tecplot output (tecplot_output in inputs.m) file may also affect the speed of the analysis.

For a given problem, the user needs to specify input data in inputs.m and geometrical data in nodes_and_sets.m. Currently, the geometry data (the characteristic function, the boundary regions, the box domain coordinates) is setup manually, on a case by case basis. The users are invited to contribute functions to the code that would automate this step, for example, to directly import various CAD systems representations of the geometry data.

In this version, three material models have been implemented in PeriFast/Dynamics: (1) linearized bond-based isotropic elastic; (2) linearized state-based isotropic elastic; and (3) PD correspondence model for a hyperelastic material. We model brittle damage in all of the three cases (see Section 2 and Appendix for the damage models). New material models can be added to PeriFast/Dynamics by defining additional material types in pre_constitutive.m and constitutive.m. The user can also easily specify additional variables to output in dump_output.m (e.g., internal variables in history dependent material models) and customize visualization.m, open_Matlab_video.m, create_matlab_video.m and close_Matlab_video.m as desired.

In the following, we take a closer look at each m-file.

4.3 Description of main.m

Box 1 shows the structure of main.m as the executable main file of the program. The file consists of three stages: reading input information, initialization, and the time computation loop. After the time loop a outputs are saved in a file named: results.mat.

Box 1 Structure of the main program file: main.m

4.4 Description of inputs.m

In the inputs.m file, user-prescribed data are assigned to variables and passed onto the main program. The user needs to directly insert the input data in this file.

Box 2 Structure of inputs.m

The terms in the parentheses denote the MATLAB variable names used in the code. Props is a 1D array, while Fb, IC_u and IC_v are structure arrays-type variables, each containing three functions corresponding to each vector component. The function of the body force’s x-component for example is Fb(1).func. The variables used for traction and displacement boundary conditions are also of struct type. For BCs, however, each coordinate direction has a distinct variable associated with it, containing the number of the prescribed BCs in that direction and the corresponding functions. For example, if one needs to enforce two traction BCs in y direction, one sets trac_y.No = 2, and then define the two functions trac_y(1).func and trac_y(2).func.

The desired number of data dumps and frames for visualization is selected by the user through variables number_of_data_dump and number_of_visualization_frames.

Variable tecplot_output can be either 1 or 0. Choosing value 1 leads to the selected outputs being saved as a Tecplot file during the analysis (in the current version of the code we choose damage index as an output to be saved in a Tecplot file as an example; users can select any desired outputs). Using value 0 cancels the Tecplot output.

Variable visualization_during_analysisis either 0 or 1, with 1 requesting Matlab visualization during the analysis phase, and 0 leaving out run-time visualization. Note that plots/animations can be obtained by postprocessing the output saved in Results.mat file. The variable visualization_during_analysis can be set to 0 so that the results can be plotted/animated by running postprocess.m after saving Results.mat. This is, in fact, the recommended option when solving larger problems since plotting during analysis slows down the solver. In this version of the code the default option sets the visualization_during_analysisis variable to 0.

The user can choose the desired outputs among dumped outputs (dump_output.m) to be plotted/animated by defining a vector of integers, outputs_var_for_visualization in inputs.m. A number is assigned for each output and used for defining outputs_var_for_visualization in inputs.m. In the current version of PeriFast/Dynamic code, u₁,u₂,u₃,u_mag,v₁,v₂,v₃, v_mag, W, d (i.e., displacement vector components, displacement magnitude, velocity vector components, velocity magnitude, strain energy density, damage index) and lambda are dumped as outputs and the assigned number for them is 1 through 11, respectively. For example, if users want to visualize u₁, u₂, and d among these dumped outputs, they need to set outputs_var_for_visualization = [1, 2, 10]. Note that in order to add any other outputs for visualization which is not defined in the current version of dump.output.m, users first need to add it to dump.output.m and then modify visualization.m, open_Matlab_video.m, create_Matlab_video.m and close_Matlab_video.m to visualize that as well.

4.5 Description of nodes_and_sets.m

nodes_and_sets.m contains nodal coordinates and the geometrical information of the problem. Before describing its details, we first point out how the domain extension required by FCBM (see Fig. 2) is implemented in PeriFast/Dynamics. Given a PD body ($\mathrm{B}$) defined by the original PD-IVVC problem, it is first assumed that the body is enclosed in a rectangular box, as tight as possible to the body. This enclosing box is shown in Fig. 4 for the 2D case with dash-line. Note that this is different from the box that is repeated by periodicity. Assuming a coordinate origin, we define the coordinates of the enclosing box vertices. To construct the periodic box ${\mathbb{T}}$, the enclosing box is extended along each direction/axis with an extension at least as large as the horizon size to avoid the “wrap-around” effect in the circular convolution. Figure 4 shows a PD body, the enclosing box (the dash-line), and the extended periodic box ${\mathbb{T}}$ in 2D. ${l}_{e}$ denotes the extension length (which should be selected larger than $\delta$).

Fig. 4

A 2D generic PD body ($\mathrm{B}$), the enclosing box (shown by the dash-line), and one possible extension to the periodic box ${\mathbb{T}}$

Note that the best choice of the enclosing box (and the coordinate system directions) is the one that leads to the least extra space between the body and the box. Considering a fixed nodal spacing, less gap results in less excess degrees of freedom in FCBM. If the body itself is a rectangular box, then the enclosing box would be the body itself.

Box 3 shows the structure of nodes_and_sets.m.

Box 3 Structure of nodes_and_sets.m

In nodes_and_sets.m, the user first defines the horizon size ($\delta$), the enclosing box dimensions, the extension length (${l}_{e}$ in Fig. 4), and the number of nodes in each direction. The program then extends the enclosed box to find ${\mathbb{T}}$, and then create nodes according to Eqs. (14) and (15). Next, the various characteristic functions/node sets are defined by the user to describe different subdomains corresponding to the original body, traction forces, volume constraints, and pre-damage. At the end, node sets representing displacement BCs in the same directions are merged to form three distinct node sets ${\chi }_{{\Gamma }_{1}}, {\chi }_{{\Gamma }_{2}}, {\chi }_{{\Gamma }_{3}}$. Then ${\chi }_{{\Omega }_{1}},$ ${\chi }_{{\Omega }_{2}}$,${\chi }_{{\Omega }_{3}}$ are obtained by Eq. (5). The horizon, box ${\mathbb{T}}$ info, nodal coordinates, and the characteristic functions are passed onto main.m to be used in the analysis.chit_x, chit_y, chit_z, and chiG_x, chiG_y, chiG_z are all struct type variables and include the number of BCs in their specific direction, as well as the node sets for each of those. For example, if there are two traction BCs given in the y direction, one needs to set chit_y.No = 2, and define chit_y(1).set and chit_y(2).set, where each of these sets are 3D ${N}_{2}\times {N}_{1}\times {N}_{3}$ arrays with value 1 for nodes in the node set and zero elsewhere.

Remark: the number of node sets in chit_x, chit_y, chit_z, and chiG_x, chiG_y, chiG_z, should be consistent with number of tractions and displacement BCs given by trac_x, trac_y, trac_z, and dispBC_x, dispBC_y, dispBC_z, in inputs.m respectively.

4.6 Description of pre_constitutive.m

This m-file contains the time-invariant functions needed for evaluation of the PD constitutive terms such as the internal force, strain energy, etc., available in the form of form of Eqs. (10) and (11). For most well-known material models, kernel functions (${c}_{l}$ is Eq. (10)) are invariant in time and should be defined in this module. Note that this module returns the FFT of the kernel functions in their shifted forms (${c}_{l}^{s}$) described in previous section (see Fig. 3).

Box 4 gives the structure of pre_constitutive.m.

Box 4 Structure of pre_constitutive.m

Here is how the “shift operation” shown in Fig. 4 is carried out in PeriFast/Dynamics: for obtaining ${c}_{l}^{s}$, first, ${c}_{l}$ is translated such that its origin coincides with the center of the box: ${c}_{l}\left(\mathbf{X}-{x}_{c},\mathbf{Y}-{y}_{c},\mathbf{Z}-{z}_{c}\right)$. Then the fftshift MATLAB function is used on the translated ${c}_{l}$. The fftshift command breaks down the array from mid-planes of the box and swap the partitions, resulting in the desired shifted form: ${c}_{l}^{s}$. More information on fftshift is provided in the MATLAB documentation.

The coded PD correspondence model for the hyperelastic material (material ID = 2) uses St. Venant–Kirchhoff classical model for finite deformation elasticity. The implemented correspondence model includes the stability term introduced in [33] to suppresses zero energy modes and stabilizing the PD correspondence solutions.

4.7 Description of constitutive.m

This module takes the displacement field, history-dependent variables such as the old damage parameter, material properties (defined in inputs.m), discretization info (defined in nodes_and_sets.m), and the invariant parameters in the constitutive response (from pre_constitutive.m) as inputs, and returns the internal force density, strain energy density, and updated history-dependent variables (e.g. damage) as outputs. Box 5 presents the structure of this module.

Box 5 Structure of constitutive.m

Note that user-defined material models are allowed in PeriFast/Dynamics and can be introduced by defining appropriate functions in pre_constitutive.m and constitutive.m, with additional material IDs, in the If-statements.

While PeriFast/Dynamics can adopt different user-defined damage models along with the user-defined constitutive laws, in the current version, for the three included constitutive models, we used the same energy-based pointwise damage model introduced in [23]. In this damage model, the parameter that store damage information is a binary variable denoted by lambda which is 0 for a damaged node and 1 otherwise. A damaged node is a node for which its strain energy density exceeds a threshold calibrated to the critical fracture energy of the material. The damage index (here tracked by the variable named damage) varies between 0 and 1 and it is computed from lambda using the following relation [23]:

$$d\left({\varvec{x}},t\right)=1- \frac{{\int }_{{\mathcal{H}}_{x}}{\chi }_{\mathrm{B}}{\chi }_{B}^{{\prime}}\mu \mathrm{d}{V}_{{x}^{{\prime}}}}{{\int }_{{\mathcal{H}}_{x}}{\chi }_{\mathrm{B}}{\chi }_{B}^{{\prime}}\mathrm{d}{V}_{{x}^{^{\prime}}}}=1-\frac{{\int }_{{\mathcal{H}}_{x}}{\chi }_{\mathrm{B}}{\chi }_{B}^{{\prime}}\mathrm{\lambda \lambda ^{{\prime}}}\omega \left(\left|{\varvec{\xi}}\right|\right)\mathrm{d}{V}_{{x}^{{\prime}}}}{{\int }_{{\mathcal{H}}_{x}}{\chi }_{\mathrm{B}}{\chi }_{B}^{{\prime}}\omega \left(\left|{\varvec{\xi}}\right|\right)\mathrm{d}{V}_{{x}^{{\prime}}}}$$

(20)

In Eq. (20), $\omega$ is the influence function and ${\varvec{\xi}}={{\varvec{x}}}^{\boldsymbol{{\prime}}}-{\varvec{x}}$ denotes the bond vector. The influence function $\omega \left(\left|{\varvec{\xi}}\right|\right)=\frac{1}{\left|{\varvec{\xi}}\right|}$ is used in this work.

Lambda, damage, and any other history-dependent quantities, are defined in a structure-type variable named history_var.

Remark: if one intends to study stress waves only (i.e., deformation without damage/fracture), one can either comment out the commands corresponding to updating damage, or just prescribe a very large fracture energy value in inputs.m.

4.8 Description of update_VC.m

This module takes the displacement BCs as functions of space and time (from inputs.m), and also their corresponding node sets (from nodes_and_sets.m), and returns the nodal values for functions ${w}_{i}$ ($i=\mathrm{1,2},3$) in Eq. (15) as outputs. Box 6 shows the structure of update_VC.m.

Box 6 Structure of update_VC.m

4.9 Description of update_tractions.m

In PeriFast/Dynamics, traction BCs are enforced as body forces applied uniformly on a $\delta$-thick layer of the body at the boundary (distributed uniformly through the thickness of the layer). The body force nodal value is obtained by dividing the traction force at a point by $\delta$. The structure of update_tractions.m is very similar to update_VC.m.

Box 7 Structure of update_tractions.m

4.10 Description of initial_gpu_array.m

To accelerate computations using GPUs, one needs to convert variables involved in the convolution operations to MATLAB’s “gpuarray” type using the file initial_gpu_array.m. Then, calls to MATLAB’s FFT and inverse FFT functions will automatically use the GPU for these operations. Note that the Parallel Computing Toolbox needs to be installed to enable GPU computing in MATLAB.

4.11 Description of dump_output.m

This module gets the snapshot number (ks), displacements and velocities in x, y, and z directions, strain energy density, damage index, and lambda as inputs. These variables along with other post-processed quantities such as displacement magnitude, are stored in a single structure-type MATLAB variable named Output. If the visualization switch is on (if visualization_during_analysis =  = 1) this variable is passed onto the visualization module for creating MATLAB plots during the analysis. The frequency of visualization of outputs is dependent on the number _of _visualization_frames defined in inputs.m. Also, if the Tecplot switch is ON in inputs.m file, the desired output is saved as a Tecplot file (.plt). Results stored in Output can be used for any desired post-processing operation. dump_output.m module can be easily modified by the user to store other user-defined outputs.

4.12 Description of visualization.m and postprocess.m

This module takes the outputs from dump_output.m, the snapshot number, nodal coordinates, and the body node set, and uses them to visualize the results. This module, too, can be easily modified by the user to plot the desired figures and/or record animations (user can select the desired output for visualization in inputs.m), and to export files in user-defined formats for further processing in external software. In order to record Matlab videos from the snapshots, create_Matlab_video.m is used. There is an option in input.m to select whether the user desires to visualize the results during the analysis or after. The default is to perform the visualization after the analysis by running postprocess.m and using the data saved in the Results.mat file.

4.13 Description of open_Matlab_video.m, create_Matlab_video.m and close_Matlab_video.m

These modules are used for creating Matlab videos from the outputs. For every desired output to be animated, first, a video file needs to be opened using open_Matlab_video.m. Next, by calling create_Matlab_video.m, the sequence of frames from the desired output is written to the video file. Finally, the video file needs to be closed by using close_Matlab_video.m. In the current version of PeriFast/Dynamics, a video file for damage evolution is created. Users can easily add any other desired output for creating a video by modifying outputs_var_for_visualization in inputs.m. For example, for the nodal velocity vector components and the strain energy density, one can define outputs_var_for_visualization = [5,6,7, 9], where v₁, v₂, v₃, and W are assigned the indices 5, 6, 7, and 9 in this version of code.

5 Example of Running PeriFast/Dynamics: 3D Dynamic Analysis of Brittle Fracture in a Glass Plate

In this section, we show how a particular problem on dynamic fracture in glass is setup and run with PeriFast/Dynamics. The physical problem is an example of dynamic brittle fracture in which crack branching takes place, when the applied loading is sufficiently high. For the crack to grow straight, one needs to lower the applied stress, see below. These type of problems, until the advent of PD, have been especially difficult to correctly simulate [12, 49].

5.1 Problem Setup

We consider a thin single-edge glass plate of size $0.1\times 0.04\times 0.002\;{m}^{3}$ with a pre-crack, subjected to sudden uniaxial tensile stress of ${\sigma }_{0}=4\;\mathrm{MPa}$ on its top and bottom edges (see Fig. 5). These types of boundary conditions are not easily replicated in experiments, with crack surface ramped-up loadings being a more realizable scenario [50]. However, these boundary conditions are the most employed in numerical simulations of crack branching, and this is the reason for using them here. See [49] for comparison of different types of dynamic loading that induce crack branching in glass samples of this type.

Fig. 5

Problem description for the 3D numerical example of dynamic brittle fracture. The thickness of the sample along the z-direction is exaggerated for visibility

The material properties are selected the same as in [49]: density $\rho =2440\;kg.{m}^{-3}$, Young modulus$E=72\;\mathrm{GPa}$, Poisson ratio $\nu =0.25$, and fracture energy ${G}_{0}=3.8\;J.{m}^{-2}$. Since $\nu$ is restricted to be $0.25$ for the bond-based model, the choice of 0.25 with the state-based models, allows for the comparison of the simulation results against each other. The horizon size $\delta =$ 1.02e-3 m, and the grid spacing is chosen to be $\Delta x=\Delta y=\Delta z=$ 2e-4 m. The addition of 0.02e-3 to 1e-3 for the horizon size is to avoid numerical sensitivity when the horizon size $\delta$ is an exact multiple of the grid spacing.

5.2 Defining the Code Input Data

The following input data is used to solve the problem define above with PeriFast/Dynamics:

5.2.1 In inputs.m

• 1. Material properties are entries in the props variable in the following order: material ID, $\rho$, ${G}_{0}$, $E$, $\nu$. Set:

  props = [0; 2440; 3.8; 72e9; 0.24];

  0, 1, or 2 for the material ID determines if which material model is employed. If material ID = 0, then the bond-based model is used, and the value defined for $\nu$ is disregarded.

• 2. Define the simulation time, time step, run in gpu switch, snapshot frequency, visualization, and Tecplot output switches as

  t_max = 33e-6;

  dt = 5e-8;

  number_of_data_dump= 100;

  number_of_visualization_frames = 30;

  run_in_gpu = 0;

  tecplot_output= 0;

  visualization_during_analysis= 0;

  outputs_var_for_visualization = [10];

• 3. Set all the functions for the body force components and the initial displacements and velocities to zero (this is the default case).

• 4. Define the traction BCs by setting

  trac_y.No = 2;

  trac_y(1).func = @(x,y,z,t) 4e6;

  trac_y(2).func = @(x,y,z,t) -4e6;

5.2.2 In nodes_and_sets.m:

• 1. Define the PD horizon size: delta = 1.02e-3;

• 2. Define the enclosing box by providing the minimum and the maximum of the box dimension along each coordinate direction in

  x_min = 0; x_max = 0.1;

  y_min = 0; y_max = 0.04;

  z_min = 0; z_max = 0.002;

• 3. Define the extension length to form the periodic box: extension = 2e-3;

• 4. As noted earlier, this should be larger than the horizon size.

  Define the resolution in each direction

  Nx = 510;

  Ny = 210;

  Nz = 20;

  which results in over 2 million nodes. These values are calculated from the dimension of the extended box and the grid spacing of $\Delta x=\Delta y=\Delta z=$ 2.5e-4.

• 5. Define ${\chi }_{\mathrm{B}}$ (body node set) with value 1 for nodes inside the body and 0 otherwise. For our example, we set

  chiB = ones (Ny, Nx, Nz);

  chiB (Z < z_min | Z > z_max ) = 0;

  chiB (Y < y_min | Y > y_max ) = 0;

  chiB (X < x_min | X > x_max ) = 0;

• 6. Define the node sets for the traction BCs

  chit_y.No = 2;

  chit_y(1).set = double(chiB == 1 & Y > y_max - delta + dy/2 & Y < y_max + dy/2);

  chit_y(2).set = double(chiB == 1 & Y > y_min - dy/2 & Y < y_min + delta - dy/2);

  The “double” command converts the logical arrays in the arguments to double arrays for computation.

• 7. Define the node set representing the pre-crack (the notch region)

  chi_predam = double(chiB == 1 & abs(Y - y_min - Ldy/2)<= (delta/2) & X < x_min + Ldx/2);

5.3 Selection of Outputs

Components of the displacement and the velocity vectors as well as their magnitude, strain energy density, damage index, and lambda are selected as the output variables by defining the following commands in dump_output.m file:

• Output(ks).u1 = u1;

• Output(ks).u2 = u2;

• Output(ks).u3 = u3;

• Output(ks).u_mag = sqrt(u1.^2 + u2.^2 + u3.^2);

• Output(ks).v1 = v1;

• Output(ks).v2 = v2;

• Output(ks).v3 = v3;

• Output(ks).v_mag = sqrt(v1.^2 + v2.^2 + v3.^2);

• Output(ks).W = W;

• Output(ks).d = damage;

• Output(ks).lambda = lambda;

5.4 Execution of the Program

For faster computations, one can use the Matlab’s capabilities for parallel, multi-threading, and GPU-based computations. In the current version of PeriFast/Dynamics, multithreading is immediately accessed by simply changing the maximum number of threads used in the run: LASTN = maxNumCompThreads (p), at the beginning of main.m, where p is the max number of threads desired. The default option is for serial computations, using p = 1. GPU-based computation is explained in Section 4.2.

LASTN = maxNumCompThreads(1);

To execute the code, we run the main.m file.

5.5 Visualization of Results

Figure 6 shows the damage index 3D MATLAB profiles obtained by the bond-based and the state- models (native and correspondence). Evolution of velocity fields, as well as strain energy density and damage index during fracture are provided in Videos 1, 2, and 3 for these PD models, respectively.

Fig. 6

Damage index profiles in glass obtained from PeriFast 3D analysis with a the bond-based, b the linearized state-based, and c the correspondence models

5.6 Explanations of Differences Between Models

The results shown in Fig. 6a for the bond-based model are similar to those obtained with a 2D plane stress simulation in [49]. This is a good verification of the PeriFast/Dynamics’ implementation. The slight differences between damage patterns (branching near the edge) from the three FCBM-based models stem from the small actual difference between the PD constitutive models.

Although the force density in the state-based and the bond-based models in Eqs. (A-1 and A-5) are different in general, for the linearized versions in Eqs. (A-1 and A-6, if the Poisson ratio is chosen as ¼ in the state-based model, the first term in Eq. (A-6) vanishes and the bond-based formula is recovered, for points in the bulk. These models, however, even for the one-quarter Poisson ratio value, are slightly different near surfaces. The root cause for this difference is in the different PD elastic micro-moduli computed in these two models. In the bond-based formulation (see [47]) the micro-modulus is computed based on a calibration for points in the bulk, and, assuming no surface correction is used for points near boundaries, has the value equal to $\frac{12E}{\pi {\delta }^{4}}$ in 3D. In the state-based formulation, the bond-level elasticity constant, $\frac{30\mu }{m}$, depends on the weighted volume at a node, denoted by $m$. The weighted volume in our model is obtained numerically by approximating the following integral over the horizon (see [47]):

$$m={\int }_{{\mathcal{H}}_{x}}\omega \left(\left|{\varvec{\xi}}\right|\right){\left|{\varvec{\xi}}\right|}^{2} {\mathrm{dV}}_{{\varvec{x}}\boldsymbol{^{\prime}}}$$

(21)

We can easily show the equivalency of the elastic constants in the native state-based model ($\frac{30\mu }{m}$) to the bond based micromoduli at the continuum level for points in the bulk by computing $m$ for nodes in the bulk (over a full spherical neighborhood) and using the following influence function $\omega \left(\left|{\varvec{\xi}}\right|\right)=\frac{1}{\left|{\varvec{\xi}}\right|}$(used in this work):

$$\frac{30\mu }{m}=\frac{30\mu }{\int_0^{\pi}\int_0^{2\pi}\int_0^{\delta}{r}^{3}sin\phi\;dr\;d\phi d\theta }=\frac{30\mu }{\pi {\delta }^{4}}=\frac{12E}{\pi {\delta }^{4}}$$

(22)

The domain of integration in computing $m$, i.e., neighborhood ${\mathcal{H}}_{x}$, varies, however, for nodes near surfaces, including original domain boundaries and growing crack surfaces, compared to the nodes in the bulk, leading to automatically modified bond-level elastic properties near the surfaces for the native state-based models. In other words, for points near the boundary, the function $m$, according to Eq. (21) in the state-based model, changes value, while in bond-based models, unless PD surface correction algorithms (e.g., see [37]) are enforced, the bulk parameters are used everywhere.

We tested a state-based model, to compare with the results from the bond-based shown in Fig. 6a, by setting $\nu =0.25$ and $m=\pi {\delta }^{4}$ at all points in the domain (independent on whether they are near a boundary or not). We obtained results identical to the bond-based model.

While the bond-based and native state-based models differ mostly near surfaces as described above, the correspondence model is intrinsically different from the other two, making use of a “translation” between PD concepts (force and displacements maps) and classical continuum mechanics quantities (stresses and strains tensors) and employing, a local constitutive model for defining the stress–strain relationship.

As the horizon goes to zero, one expects the bond-based and native state-based models approach identical solutions since their near-the-surface differences vanish. The correspondence model, in the limit of $\delta$-convergence, and for well-behaved problems, also converges to the classical solution of the corresponding problem. For problems with damage/fracture, this statement needs further investigation, which is outside the scope of the current work.

The 3D PD dynamic brittle fracture analyses, using a single processor, with over 2 × 10⁶ nodes and over 660 time steps took about 1.15, 1.67, and 2.87 h to complete, with the bond-based, native state-based, and the correspondence models, respectively. When employing GPU-based calculations, the computational time is around 5 min, 6 min, and 11 min, for the three different constitutive models, respectively. Computations were performed on a Dell-Precision T7910 workstation PC, Intel(R) Xeon(R) CPU E5-2643 W v4 @3.40 GHz logical processors, and 128 GB of installed memory and NVIDIA Quadro M4000 GPU with 8 GB memory.

6 Summary and Possible Extensions of PeriFast/Dynamics

We introduced a compact Matlab-based code, PeriFast/Dynamics, which is an implementation of the Fast Convolution-Based Method (FCBM) for dynamic deformations and fracture problems in 3D. The current version of the code uses explicit time integration and offers three different options in terms of peridynamic (PD) material models: the linearized bond-based and ordinary state-based models for isotropic elastic materials, and the PD correspondence model for isotropic hyperelastic materials. Each of these comes with a model for brittle damage based on nodal strain energy density. The code is modularized with the explicit purpose to make it user-friendly and easier to adapt, modify, and extend to other problems. As long as the PD formulation for a particular problem can be setup to exhibit a convolutional structure, one can simply update/modify the MATLAB files defining the constitutive model for that particular problem. For example, elasto-plastic and ductile failure problems can easily be implemented with the structure of our code. The code could also be extended to include a pre-processor step that reads CAD-generated sample geometries and boundary conditions and automatically determines the characteristic functions that identify the domain and boundary regions in the computational box.

Because of the FCBM used to discretize the PD formulations, PeriFast/Dynamics’ simulation run-times and memory requirements are independent of the number of neighbors of a node. Previous studies showed that the FCBM leads to speedups of tens to thousands compared against the traditional meshfree method, depending on the number of neighbors used.

We have briefly reviewed the PD governing equations for dynamic brittle fracture and the FCBM discretization, followed by describing the data structures used in the code. The general structure of PeriFast/Dynamics and detailed descriptions of each of the m-files contained in the code have been given. A demonstrative example of dynamic brittle fracture in glass in 3D, solved using three different constitutive models, has been provided, with step-by-step descriptions for input data and choices of outputs.

6.1 Possible Extensions

Note that the current version uses damage models with a single parameter, which can be calibrated to the critical fracture energy (material fracture toughness). These models work well in problems with pre-cracks, but when applied to problems with no pre-cracks, a higher and higher effective strength is found if one uses smaller and smaller horizon sizes (for a discussion of how to select a “proper” horizon size please see [51, 52]). For quasi-brittle fracture problems in bodies without pre-cracks we recommend using (and implementing), for example, the two-parameter bond-failure model (see [53]). Such an extension is immediate by defining lambda in constitutive.m as a non-binary variable with a gradual transition from 1 to 0, capturing a softening behavior at the microscale.

To implement ductile failure models, one can use, for example, the new PD correspondence model introduced and verified in [43, 44]. The PeriFast version presented here uses an explicit time integration scheme (velocity Verlet) and solves dynamic problems. Implicit solvers using iterative methods such as the nonlinear conjugate gradient method have been used with FCBM before (see [23]) and can be easily added to the code to perform static and quasi-static analyses.

PeriFast/Corrosion is one branch of the PeriFast suite of Matlab-based codes that implement the FCBM for PD models. The PeriFast/Corrosion branch solves corrosion damage problems (pitting corrosion, including with formation of lacy covers) and is described in [41]. By coupling the/Corrosion and/Dynamics code branches of PeriFast, one can solve, for example, stress-corrosion cracking problems like those in [5]. Because the code is fast and memory requirements are relatively low, one can solve such problems for samples at engineering-relevant scales.

Another possible extension of the code presented here is to model thermomechanical fracture and damage. Using the diffusion-type solver structure implemented in the/Corrosion branch of PeriFast, one can easily write a similar solver for transient thermal transport and couple it with the mechanics code/Dynamics to simulate thermomechanical fracture.

While not immediate, other interesting extensions may be possible: (1) fracture in heterogeneous materials (these could use, for example, the masking functions used in [41] to generate a polycrystalline microstructure); (2) impact and fragmentation (contact detection algorithms would be required for such models).

Appendix. Constitutive models included in PeriFast/Dynamics

• 1. Linearized bond-based elastic material model

This model is basically the linearized version of the micro-elastic solid (see [47]). The internal force density for this material is

$${\varvec{L}}\left({\varvec{x}},t\right)= {\int }_{{\mathcal{H}}_{x}}{\chi }_{\mathrm{B}}{\chi }_{B}^{{\prime}}\mu {\varvec{f}}\left({\varvec{x}},{{\varvec{x}}}^{\boldsymbol{{\prime}}},t\right)d{V}_{x{^{\prime}}}={\int }_{{\mathcal{H}}_{x}}{\chi }_{\mathrm{B}}{\chi }_{B}^{{\prime}} \lambda {\lambda }^{{\prime}}\mathbf{C}\left({\varvec{\xi}}\right){\varvec{\eta}}d{V}_{x{^{\prime}}}$$

(A-1)

where ${\varvec{\xi}}$ Is the bond vector, ${\varvec{\eta}}$ is the relative displacement and $\mathbf{C}\left(\xi \right)=\alpha \omega \left(\left|{\varvec{\xi}}\right|\right)\frac{{\varvec{\xi}}\otimes{\varvec{\xi}}}{{\left|{\varvec{\xi}}\right|}^{2}}$ with $\alpha = \frac{12E}{\pi {\delta }^{4}}$ and $\left(\left|{\varvec{\xi}}\right|\right)=\frac{1}{\left|{\varvec{\xi}}\right|}$.

And the strain energy density is

$$W\left({\varvec{x}},t\right)=\frac{1}{2}{\int }_{{\mathcal{H}}_{x{^{\prime}}}}{\chi }_{\mathrm{B}}{\chi }_{B}^{^{\prime}} \lambda {\lambda }^{^{\prime}}{\varvec{\eta}}.\left(\frac{1}{2}\mathbf{C}\left({\varvec{\xi}}\right){\varvec{\eta}}\right)d{V}_{x{^{\prime}}}$$

(A-2)

The convolutional form of the internal force density and strain energy density for linearized bond-based models (Eqs. (A-1) and (A-2)) used in this work are [23]

$${L}_{i}={\int }_{{\mathcal{H}}_{x}}{\chi }_{\mathrm{B}}{\chi }_{B}^{^{\prime}} \lambda {\lambda }^{^{\prime}}{\mathrm{C}}_{ij}{\eta }_{j}d{V}_{x{^{\prime}}}= {\int }_{{\mathcal{H}}_{x}}{\chi }_{\mathrm{B}}{\chi }_{B}^{^{\prime}} \lambda {\lambda }^{^{\prime}}{\mathrm{C}}_{ij}\left({u}_{j}^{^{\prime}}-{u}_{j}\right)d{V}_{{x}^{^{\prime}}}={\chi }_{\mathrm{B}}\lambda \left\{\left[{\mathrm{C}}_{\mathrm{ij}}*({\chi }_{\mathrm{B}}\lambda {u}_{j})\right]-[{\mathrm{C}}_{\mathrm{ij}}*{\chi }_{\mathrm{B}}\lambda ]{u}_{j}\right\}$$

(A-3)

$$W\left({\varvec{x}},t\right)=\frac{1}{2}{\int }_{{\mathcal{H}}_{x{^{\prime}}}}{\chi }_{\mathrm{B}}{\chi }_{B}^{^{\prime}} \lambda {\lambda }^{^{\prime}}{\eta }_{i}\left(\frac{1}{2}{\mathrm{C}}_{\mathrm{ij}}{\eta }_{j}\right)d{V}_{x{^{\prime}}}=\frac{1}{4} {\chi }_{\mathrm{B}}\lambda \left(\left[{\mathrm{C}}_{ij}*{\chi }_{\mathrm{B}}\lambda {u}_{i}{u}_{j}\right]-2\left[{\mathrm{C}}_{ij}*{\chi }_{\mathrm{B}}\lambda {u}_{i}\right]{u}_{j}+\left[{\mathrm{C}}_{ij}*{\chi }_{\mathrm{B}}\lambda \right]{u}_{i}{u}_{j}\right)$$

(A-4)

• 2. Linearized state-based elastic material model

This model is the linearized version of the native state-based linear elastic solid (see [47]). The internal force density for this material is

$${\varvec{L}}\left({\varvec{x}},t\right)= {\int}_{{\mathcal{H}}_{x}}{\chi }_{\mathrm{B}}{\chi }_{B}^{^{\prime}}\mu {\varvec{f}}\left({\varvec{x}},{{\varvec{x}}}^{\boldsymbol{^{\prime}}},t\right)d{V}_{x{^{\prime}}}={\int}_{{\mathcal{H}}_{x}}{\chi }_{\mathrm{B}}{\chi }_{B}^{^{\prime}}\mu (\underset{\_}{\mathbf{T}}\left[{\varvec{x}},t\right]\langle {\varvec{\xi}}\rangle -\underset{\_}{\mathbf{T}}\left[{\varvec{x}}\boldsymbol{^{\prime}},t\right]\langle -{\varvec{\xi}}\rangle )d{V}_{x{^{\prime}}}$$

(A-5)

where

$$\underset{\_}{\mathbf{T}}\langle {\varvec{\xi}}\rangle =\left(\frac{3k-5G}{m}\right)\omega \left(\left|{\varvec{\xi}}\right|\right)\vartheta{\varvec{\xi}}+\frac{15G}{m}\omega \left(\left|{\varvec{\xi}}\right|\right)\frac{{\varvec{\xi}}\otimes{\varvec{\xi}}}{{\left|{\varvec{\xi}}\right|}^{2}}{\varvec{\eta}}$$

(A-6)

where $k$ and $G$ here are the bulk and shear moduli, respectively, and $\vartheta$ is the a nonlocal dilation [47].

The strain energy density for this linearized state-base material model is [47]

$$W\left({\varvec{x}},t\right)=\frac{1}{2}\left(\left(k-\frac{\alpha m}{9}\right){\vartheta }^{2}+\alpha {\int}_{{\mathcal{H}}_{x}}\mu \omega \left(\left|{\varvec{\xi}}\right|\right){\varvec{\eta}}.\frac{{\varvec{\xi}}\otimes{\varvec{\xi}}}{{\left|{\varvec{\xi}}\right|}^{2}}{\varvec{\eta}}d{V}_{{x}^{^{\prime}}} \right),\alpha =\frac{15G}{m}$$

(A-7)

Note: by adopting a Poisson ratio of one-quarter, the first terms on the right-hand side of Eq. (A-6) and (A-7) vanish and the linearized bond-based model presented by Eq. (A-1) and (A-2) is recovered for the points in the bulk as explained in Section 5.6.

The convolution structures for $\vartheta$ and $m$ are derived in [23]. Let $\mathbf{C}\left({\varvec{\xi}}\right)=30G \omega \left(\left|{\varvec{\xi}}\right|\right)\frac{{\varvec{\xi}}\otimes{\varvec{\xi}}}{{\left|{\varvec{\xi}}\right|}^{2}}$ and ${\varvec{a}}\left({\varvec{\xi}}\right)=\omega \left(\left|{\varvec{\xi}}\right|\right){\varvec{\xi}}$ with $\left(\left|{\varvec{\xi}}\right|\right)=\frac{1}{\left|{\varvec{\xi}}\right|}$, the convolution structure for internal force density and strain energy density (Eqs. (A-6) and (A-7)) obtained as [23].

$${L}_{i}={\chi }_{\mathrm{B}}\lambda \left(\left(\frac{3k-5G}{m}\right)\left(-\vartheta \left[{a}_{i}* {\chi }_{\mathrm{B}}\lambda \right]-\left[{a}_{i}*{\chi }_{\mathrm{B}}\lambda \vartheta \right]\right)+\frac{1}{m} \left({[\mathrm{C}}_{ij}*{\chi }_{\mathrm{B}}\lambda {u}_{j}]-[{\mathrm{C}}_{ij}*{\chi }_{\mathrm{B}}\lambda ]{u}_{j}\right)\right)$$

(A-8)

$$\begin{aligned}W\left({\varvec{x}},t\right)&=\frac{1}{2}\left(\left(k-\frac{\alpha m}{9}\right){\vartheta }^{2}+\frac{1}{2m}{\int}_{{\mathcal{H}}_{x}}{\chi }_{\mathrm{B}}{\chi }_{B}^{^{\prime}}\lambda {\lambda }^{^{\prime}}{\eta }_{i}{\mathrm{C}}_{ij}{\eta }_{j} d{V}_{{x}^{^{\prime}}} \right)\\&=\frac{1}{2}\left(\left(k-\frac{\alpha m}{9}\right){\vartheta }^{2}+\frac{1}{2m}{\int}_{{\mathcal{H}}_{x}}{\chi }_{\mathrm{B}}{\chi }_{B}^{^{\prime}}\lambda {\lambda }^{^{\prime}}{\mathrm{C}}_{ij}({u}_{i}^{^{\prime}}{u}_{j}^{^{\prime}}-{u}_{i}^{^{\prime}}{u}_{j}-{u}_{i}{u}_{j}^{^{\prime}}+{u}_{i}{u}_{j}) d{V}_{{x}^{^{\prime}}} \right)\\&= \frac{1}{2}\left(\left(k-\frac{\alpha m}{9}\right){\vartheta }^{2}+\frac{1}{2m}{\chi }_{\mathrm{B}}\lambda \left\{\left[{\mathrm{C}}_{ij}*{\chi }_{\mathrm{B}}\lambda {u}_{i}{u}_{j}\right]-{u}_{j}\left[{\mathrm{C}}_{ij}*{\chi }_{\mathrm{B}}\lambda {u}_{i}\right]-{u}_{i}\left[{\mathrm{C}}_{ij}*{\chi }_{\mathrm{B}}\lambda {u}_{j}\right]+{u}_{i}{u}_{j}[{\mathrm{C}}_{ij}*{\chi }_{\mathrm{B}}\lambda ]\right\}\right)\end{aligned}$$

(A-9)

The details on deriving the convolutional structure for linearized bond-based and state-based models are provided in [23].

• 3. PD correspondence hyperelastic material model

This model uses the correspondence formulation introduced in [32], and uses the classical Saint–Venant-Kirchhoff hyperelastic constitutive law. The internal force density for this material is

$${\varvec{L}}({\varvec{x}},t) ={\int}_{\mathcal{H}}{\chi }_{\mathrm{B}}{\chi }_{B}^{^{\prime}}\mu \left(\underset{\_}{\mathbf{T}}\langle {\varvec{\xi}}\rangle -\underset{\_}{\mathbf{T}\mathbf{^{\prime}}}\langle -{\varvec{\xi}}\rangle \right) \mathrm{d}{V}_{x{^{\prime}}}$$

(A-10)

where

$$\underset{\_}{\mathbf{T}}\langle {\varvec{\xi}}\rangle = \omega \left(\left|{\varvec{\xi}}\right|\right){\varvec{\sigma}}\left(\overline{\mathbf{F} }\right){\mathbf{K}}^{-1}{\varvec{\xi}}$$

(A-11)

$\mathbf{K}$ is the shape tensor and ${\varvec{\sigma}}$ is the first Piola–Kirchhoff (P-K) stress tensor which is in terms of $\overline{\mathbf{F} }$,the PD deformation gradient and defined based on the classical constitutive model that we use (for details on the correspondence formulation please see [32]). One issue encountered when using a PD correspondence model for problems with cracks is material instabilities in the form of zero energy modes. A number of solutions have been proposed to reduce/eliminate these zero energy modes. For a review of various strategies for stabilizing PD correspondence models please see [54]. In this work we use the method introduced in [33] in which a stabilizing term ($\underset{\_}{{\mathbf{T}}^{\mathbf{s}}}\langle {\varvec{\xi}}\rangle$) is added to the force state formulation $\underset{\_}{{\mathbf{T}}^{\mathbf{c}}}\langle {\varvec{\xi}}\rangle$ as follows:

$$\begin{array}{l}\underline{\mathbf{T}}\langle {\varvec{\xi}}\rangle =\underline{{\mathbf{T}}^{\mathbf{c}}}\langle {\varvec{\xi}}\rangle + \underline{{\mathbf{T}}^{\mathbf{s}}}\langle {\varvec{\xi}}\rangle = \omega \left(\left|{\varvec{\xi}}\right|\right) \left({\varvec{\sigma}}\left(\overline{\mathbf{F}}\right){\mathbf{K}}^{-1}{\varvec{\xi}}+\boldsymbol{ }\frac{GC}{{\omega }_{0}}\underline{\mathbf{z}}\langle {\varvec{\xi}}\rangle \right) ,\;\underline{\mathbf{z}}\langle {\varvec{\xi}}\rangle =\underline{\mathbf{Y}}\langle {\varvec{\xi}}\rangle -\overline{\mathbf{F}}{\varvec{\xi}},\\{\omega }_{0}={\int}_{\mathcal{H}}\omega (\left|{\varvec{\xi}}\right|)\mathrm{d}{V}_{{\varvec{\xi}}} ,\;C=18k/\pi {\delta }^{5}\end{array}$$

(A-12)

For the Saint–Venant Kirchhoff model used in this study we have

$$\mathbf{S}=\lambda tr\left(\mathbf{E}\right)\mathbf{I}+2G\mathbf{E}$$

(A-13)

where $\mathbf{S}$ is the second P-K stress tensor and needed to be converted to the first P-K (${\varvec{\sigma}}$)stress tensor to be used in Eq. (A-11). $\mathbf{E}$ is the Lagrangian Green strain tensor, and $\lambda$ and $G$ are the Lamé constant and shear modulus of the material. $\mathbf{I}$ is the identity tensor.

For the PD correspondence model, we use the classical formulation to compute the strain energy density as $W\left(x,t\right)=\frac{1}{2}\mathbf{S}\left({\varvec{x}},t\right):\mathbf{E}({\varvec{x}},t)$.

Let ${\varvec{a}}\left({\varvec{\xi}}\right)=\omega \left(\left|{\varvec{\xi}}\right|\right){\varvec{\xi}}$, $\omega \left(\left|{\varvec{\xi}}\right|\right)=\frac{1}{\left|{\varvec{\xi}}\right|}$ and$\beta = \frac{GC}{{\omega }_{0}}$, then the convolutional form for the internal force density in the PD correspondence model (Eq. A-10)) is

$$\begin{aligned}{L}_{i}&= {-\chi }_{\mathrm{B}}\lambda \left({\sigma }_{ij}{\mathrm{K}}_{\mathrm{jp}}^{-1}\left[{a}_{p}*{\chi }_{\mathrm{B}}\lambda \right]+\left[{\sigma }_{ij}{\mathrm{K}}_{\mathrm{jp}}^{-1}{*\chi }_{\mathrm{B}}\lambda {a}_{p}\right]\right.\\&\quad\left.-\beta \left(-2\left[{\chi }_{\mathrm{B}}\lambda *{a}_{i}\right]-2\left[{\chi }_{\mathrm{B}}\lambda *\omega \right]{u}_{i}+2\left[{\chi }_{\mathrm{B}}\lambda {u}_{i}*\omega \right]+{\overline{\mathrm{F}} }_{ij}\left[{a}_{j}{*\chi }_{\mathrm{B}}\lambda \right]+[{\chi }_{\mathrm{B}}\lambda {\overline{\mathrm{F}} }_{ij}*{a}_{j}]\right)\right)\end{aligned}$$

(A-14)

The detailed derivation of the convolutional form of the PD-correspondence model is given in [42] (see Section 10.3.4 there), and [43, 44].