1 Introduction

Peridynamics (PD) [1] based on a non-local theory uses integro-differential equations rather than differential equations to describe the governing equations of motion. This facilitates easy modelling of problems involving discontinuous and/or singular solutions without any additional pre- and post-processing techniques. This is in contrast to conventional approaches that require conforming mesh with special elements, viz., singular elements or enrichment techniques to capture the necessary physics of the problem. Further, the conventional approaches require additional post-processing techniques to estimate the fracture parameters and a fracture criteria for the discontinuous surface to evolve.

Since its inception, the PD theory has been applied to wider variety of problems in science and engineering [2,3,4,5,6,7,8,9]. As with any other numerical method, the PD theory has its share of difficulties. The biggest disadvantage of the PD is the low computational efficiency, which limits the engineering application of this method. Hence, improving the computational efficiency of PD has been concerning in the scientific community and the recent focus amongst the researchers is on improving the computational efficiency of the framework [10,11,12,13,14].

The local theory-based numerical methods (e.g. the finite element method (FEM), extended FEM (XFEM), boundary element method (BEM), isogeometric analysis (IGA), meshfree method, etc.) have high computational efficiency. The coupling of PD and the local theory-based numerical method becomes an effective technique to enhance the computational efficiency of PD. PD has been coupled with FEM [15,16,17,18,19], BEM [20,21,22], IGA [23,24,25], and XFEM [26,27,28,29], to name a few.

Amongst aforementioned approaches, coupling with the XFEM has gained attention. This is because the XFEM does not require the discontinuities to conform to the background discretization, but requires a fracture criteria for modelling crack propagation. So a combination of the PD theory with the XFEM is an ideal choice, especially for three-dimensional problems with complex crack patters and morphologies. The coupling of the PD with the XFEM yields a framework that shares the advantages of both the methods, thus facilitating simulation of fracture process of large-scale engineering structures.

Recently, the present authors developed a coupling approach that combines the PD with the XFEM for three-dimensional crack propagation fulfilling both the quasi-static and dynamic loadings [30]. In our previous study, the bond-based PD [31] was used, and so Poisson’s ratio is limited to \(\frac{1}{4}\) under plane strain and 3D conditions and \(\frac{1}{3}\) under plane stress condition. Existing coupling approaches between the PD and the XFEM are all based on the bond-based PD [26,27,28,29]. To improve the modelling capability and to relax the constraint on Poisson’s ration, Silling [32] proposed a state-based peridynamics theory (SBPD) that is suitable for any material. Hence, the primary objective of this work is to develop a coupling strategy between the SBPD and the XFEM method. To facilitate easy discussion, we have restricted the focus to two-dimensional crack propagation problems under quasi-static and dynamic loading conditions. This is accomplished by dividing the domain into two regions, namely, SBPD region, which is used in the crack tip and the potential crack growth domain, thus the fracture criteria for crack growth is not required, and the XFEM region, which is applied in the rest of the computational domain to reduce the computational cost and improve the computational efficiency. The accuracy and efficiency of the proposed coupled framework are demonstrated through a few standard problems involving quasi-static crack propagation and dynamic crack branching. The coupling approach based on the state-based PD with the XFEM method has not been found in the literature, and this study is an extension of our previous work, i.e. relaxing the constraint on Poisson’s ration.

The manuscript is organized as follows. The coupling scheme between the state-based PD and the XFEM is presented in Sect. 2, and its accuracy verification is discussed in Sect. 3. Several 2D crack propagation and dynamic crack branching simulations are discussed in Sect. 4. Some major conclusions are given in Sect. 5.

2 Formulation for coupling SBPD and XFEM

The main idea of coupling the SBPD and the XFEM is to capture the physics in the vicinity of the crack tip and potential crack propagation regions using the PD, and the rest of the computational domain is modelled using the XFEM.

The coupled method possess the advantages of the SBPD for the crack propagation and the XFEM for describing the discontinuous displacements independent of the underlying background discretization. Thus, the coupled method enhances the computation efficiency in comparison with the conventional SBPD and avoids the need for a fracture criteria for crack propagation. A coupling scheme between the SBPD and the XFEM is presented in this section.

2.1 The state-based peridynamics

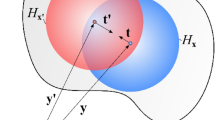
In PD, a solid consists of some material points, and \(\varvec{x}\), the material point, interacts with other material points within its horizon \(H_{\varvec{x}}\) with horizon radius \(\delta \). Under the external loading condition, the displacements of the material points \(\varvec{x}_i\) and \(\varvec{x}_j\) in the initial configuration are \(\varvec{u}(\varvec{x}_i)\) and \(\varvec{u}(\varvec{x}_j)\), and the locations in the deformed configuration are \(\varvec{y}_i\) and \(\varvec{y}_j\), respectively. In the SBPD, the force density vectors have unequal magnitudes and are parallel to the relative position vector in the deformed state, and the balance of angular momentum can be satisfied. Assuming small deformation, the equations of motion in discrete form for a material point \(\varvec{x}_i\) at time t is expressed as [33]:

$$\begin{aligned} \begin{aligned}&\sum _{j=1}^{N} \psi _{i j}\left( \frac{4 b \delta V_{j} V_{i}}{\left\| \varvec{x}_{j}-\varvec{x}_{i}\right\| }\left( \varvec{u}_{i}-\varvec{u}_{j}\right) +\sum _{m=1}^{N} \psi _{i m} \frac{2 a d^{2} \delta ^{2} V_{m} V_{j} V_{i}}{\left\| \varvec{x}_{j}-\varvec{x}_{i}\right\| \left\| \varvec{x}_{m}-\varvec{x}_{i}\right\| }\left( \varvec{u}_{i}-\varvec{u}_{m}\right) \right. \\&\left. \quad +\sum _{n=1}^{N} \psi _{j n} \frac{2 a d^{2} \delta ^{2} V_{n} V_{j} V_{i}}{\left\| \varvec{x}_{j}-\varvec{x}_{i}\right\| \left\| \varvec{x}_{n}-\varvec{x}_{j}\right\| }\left( \varvec{u}_{j}-\varvec{u}_{\varvec{n}}\right) \right) +\rho \varvec{\ddot{ u }} _ { i }V_{i} = \varvec{b}\left( \varvec{x}_{i}\right) V_{i} \end{aligned} \end{aligned}$$
(1)

where N is the number of material points within the horizon of \(\varvec{x}_i\) and \(\rho \) denotes the mass density. \(\varvec{\ddot{u}}_i\), \(V_{i}\) and \(\varvec{b}(\varvec{x}_i)\) are the acceleration vector, the volume and the body force density of a material point \(\varvec{x}_i\), respectively. \(\psi _{ij}\) is the status function and a,  b and d are the PD parameters. For 2D problem, the PD parameters are defined as [34]:

$$\begin{aligned} a=\frac{1}{2}(k-2\mu ),\quad b=\frac{6\mu }{\pi h \delta ^4}, \quad d=\frac{2}{\pi h \delta ^3} \end{aligned}$$
(2)

where h is the thickness, k is \(\frac{E}{2(1-\nu )}\) for plane stress and \(\frac{E}{2(1+\nu )(1-2\nu )}\) for plane strain, \(\mu =\frac{E}{2(1+\nu )}\), E and \(\nu \) are Young’s modulus and Poisson’s ratio.

It is assumed that two material points \(\varvec{x}_i\) and \(\varvec{x}_j\) are connected by a bond and the stretch \(s_{ij}\) is computed by:

$$\begin{aligned} s_{ij}=\frac{{\left\| {{\varvec{y_j-y_i}}} \right\| - \left\| {\varvec{x_j-x_i }} \right\| }}{{\left\| {\varvec{x_j-x_i }} \right\| }} \end{aligned}$$
(3)

where, \(\psi _{ij}=1\) for \(s_{ij}<s_c\), 0 for \(s_{ij} \ge s_c\), \(s_c\) is the critical bond stretch. For 2D problem, the critical bond stretch is defined as [34]:

$$\begin{aligned} s_c=\sqrt{\frac{G_c}{(\frac{6}{\pi }\mu +\frac{16}{9\pi ^2}(k-2\mu ))\delta }} \end{aligned}$$
(4)

where \(G_c\) is the macroscopic critical energy release rate.

Equation (1) can be written in matrix form as follows:

$$\begin{aligned} \begin{aligned}&\sum _{j=1}^{N} \psi _{ij}\left( \textbf{k}_{ij}^{11} \textbf{u}_{i}+\textbf{k}_{i j}^{12} \textbf{u}_{j}+\sum _{m}^{N} \psi _{im}\left( \overline{\textbf{k}}_{i m}^{11} \textbf{u}_{k}+\overline{\textbf{k}}_{i m}^{12} \textbf{u}_{i}\right) \right. \\&\left. \quad +\sum _{n}^{N} \psi _{j n}\left( \overline{\textbf{k}}_{i n}^{11} \textbf{u}_{n}+\overline{\textbf{k}}_{ij}^{12} \textbf{u}_{j}\right) \right) +\textbf{m}_{i}^{P D}\ddot{u}_{i}=\textbf{R}_{i}^{P D} \end{aligned} \end{aligned}$$
(5)

with

$$\begin{aligned} \varvec{k}_{i j}^{P D}= & {} \frac{4 \delta b V_{i} V_{j}}{{\left\| {{{\varvec{x}}_j} - {{\varvec{x}}_i}} \right\| }}\left[ \begin{array}{cccc} l^{2} &{}\quad lm &{}\quad -l^{2} &{}\quad -lm \\ lm &{}\quad m^{2} &{}\quad -lm &{}\quad -m^{2} \\ -l^{2} &{}\quad -lm &{}\quad l^{2} &{}\quad lm \\ -lm &{}\quad -m^{2} &{}\quad lm &{}\quad m^{2} \end{array}\right] =\left[ \begin{array}{cc} \varvec{k}_{i j}^{11} &{}\quad \varvec{k}_{i j}^{12} \\ \varvec{k}_{i j}^{21} &{}\quad \varvec{k}_{i j}^{22} \end{array}\right] \end{aligned}$$
(6)
$$\begin{aligned} \overline{\varvec{k}}_{i m}^{P D}= & {} \frac{2 \delta ^{2} d^{2} a}{\left\| \varvec{x}_{m}-\varvec{x}_{k}\right\| } \frac{V_{i} V_{j} V_{m}}{{\left\| {{{\varvec{x}}_j} - {{\varvec{x}}_i}} \right\| }}\left[ \begin{array}{cccc} l^{2} &{}\quad lm &{}\quad -l^{2} &{}\quad -lm \\ lm &{} \quad m^{2} &{}\quad -lm &{}\quad -m^{2} \\ -l^{2} &{} \quad -lm &{}\quad l^{2} &{}\quad lm \\ -lm &{}\quad -m^{2} &{}\quad lm &{}\quad m^{2} \end{array}\right] =\left[ \begin{array}{cc} \overline{\varvec{k}}_{i m}^{11} &{}\quad \overline{\varvec{k}}_{i m}^{12} \\ \overline{\varvec{k}}_{i m}^{21} &{}\quad \overline{\varvec{k}}_{im}^{22} \end{array}\right] \end{aligned}$$
(7)
$$\begin{aligned} \overline{\varvec{k}}_{j n}^{P D}= & {} \frac{2 \delta ^{2} d^{2} a}{\left| \varvec{x}_{n}-\varvec{x}_{j}\right| } \frac{V_{i} V_{j} V_{n}}{{\left\| {{{\varvec{x}}_j} - {{\varvec{x}}_i}} \right\| }}\left[ \begin{array}{cccc} l^{2} &{}\quad lm &{}\quad -l^{2} &{}\quad -lm \\ lm &{}\quad m^{2} &{}\quad -lm &{} \quad -m^{2} \\ -l^{2} &{}\quad -lm &{} \quad l^{2} &{}\quad lm \\ -lm &{}\quad -m^{2} &{}\quad lm &{}\quad m^{2} \end{array}\right] =\left[ \begin{array}{cc} \overline{\varvec{k}}_{i n}^{11} &{}\quad \overline{\varvec{k}}_{i j}^{12} \\ \overline{\varvec{k}}_{i n}^{21} &{}\quad \overline{\varvec{k}}_{i j}^{22} \end{array}\right] \end{aligned}$$
(8)

where \(\textbf{R}_{i}^{P D}=\varvec{b}\left( \varvec{x}_{i}\right) V_{i}\), \(\textbf{m}_{i}^{P D}=\rho V_{i}\), \(l = \frac{ x _ { j } - x _ { i } }{ \Vert \varvec{ x_j-x_i}\Vert }\) and \( m = \frac{ y _ { j } - y _ { i } }{ \Vert \varvec{ x_j-x_i}\Vert }\).

2.2 The extended finite element method

In XFEM setting, the standard finite element approximation is augmented by some special functions based on the partition of unity. This process is commonly referred to as enrichment strategy. This facilitates the representation of the discontinuities independent of the underlying background mesh. For a domain with a discontinuous surface, the enriched displacements approximation is expressed as [35]

$$\begin{aligned} \varvec{u} = \sum _{ i\in \varvec{N}^{a} } N _{i } ( \varvec{x} ) \varvec{u} _ { i } + \sum _ { m \in \varvec{N}^{s}}{N}_{m}(\varvec{x})[\phi (\varvec{x})-\phi (\varvec{x}_{m} )] \varvec{a} _{m} \end{aligned}$$
(9)

where \(\varvec{u}_{i}\) and \(\varvec{a}_{m}\) are the nodal displacements and enriched variables, respectively. \(\varvec{N}^{a}\) is the set of all nodes in the considered domain, while \(N ^{s}\) is the set of enriched nodes. \(N_{i}(\varvec{x})\) and \(N_{m}(\varvec{x})\) denote the standard finite element shape functions. In this work, the enrichment function \(\phi \) is +1 on one side of the crack and -1 on the other side. The corresponding weak form and discretized form are obtained by employing the standard Bubnov-Galerkin method. For additional details, interested readers are referred to  [36] and references therein.

2.3 The coupling approach between SBPD and XFEM

A schematic of the computational domain partitioned into regions, viz., SPBD region, XFEM region and an overlapping region is shown in Fig. 1. The original crack without the crack tip is considered as a part of the XFEM region. The crack tip and the potential crack propagation region are included in the SBPD region and in the overlapping region, both the descriptions coexist. An overlapping region is required because the XFEM region is modelled using the local theory and the PD region is modelled using the non-local theory. In Fig. 1, ‘blue’ square and ‘red’ diamond represent the standard and the enriched nodes in XFEM region, while the ‘blue’ circle represents the standard PD nodes, and the ‘green’ circle denotes the coupled nodes.

Fig. 1
figure 1

Region divisions, a coupling elements, and b coupling bonds

Full size image

In the coupling region, the XFEM element contains PD material points to form a coupling element, and the PD material points in the coupling region also interacts with the XFEM nodes in the horizon to form a coupling bond. In the coupling element, all nodes (including PD material points and XFEM nodes) only exert force on the XFEM nodes. In the coupling bond, all nodes (including PD material points and XFEM nodes) only exert force on PD material points. Aforementioned definition of coupling element and bond ensures that the information between the XFEM region and the PD region is transferred seamlessly and smoothly.

In the coupling region, XFEM nodes in the coupling element interact with all surrounding nodes (including nodes that belong to the XFEM region and material points of PD region). Using the above coupling element treatment scheme, the relevant terms of PD material points in the stiffness and mass matrices of the coupling element are zero. To present the displacement of the XFEM accurately, the terms corresponding to the enriched variables (including XFEM nodes and PD material points) in the stiffness and mass matrices of the coupling element are retained. A material point in the coupling region interacts with all nodes in its horizon (including XFEM nodes and PD material points). According to the processing method of coupling bond, the material points are set to zero for the term corresponding to XFEM nodes in the stiffness and mass matrices.

With \(\varvec{\delta }\) denoting the global nodal variable vector and \(\varvec{F}\) being the global external nodal force vector, the governing equation of the coupling XFEM-PD is obtained as follows:

$$\begin{aligned} \varvec{M}\ddot{ \varvec{\delta } } + \varvec{K} \varvec{\delta } = \varvec{F} \end{aligned}$$
(10)

where \(\varvec{K}\) and \(\varvec{M}\) are the global stiffness and mass matrices, respectively. Through the assembly of stiffness and mass matrices of all XFEM elements and PD nodes, the global stiffness and mass matrices are thus obtained.

In this study, PD region denotes the vicinity of crack tips and potential region where the crack is likely to propagate, and XFEM region is the area behind the crack tip and the rest of the body. Thus PD theory is not used in the whole computational domain, so the role of XFEM is to reduce the computational cost and improve the computational efficiency. In order to simplify the problem, the PD region remains unchanged in this study, in fact a variable PD region can further save time. It is noted that the coupling region can be a free-shape zone. The coupling scheme and numerical implementation are the same as those given in Ref. [30].

In the coupled SBPD and FEM, the computational domain is also divided two regions, namely, SBPD region and FEM region. The FEM region in the coupled SBPD and FEM is the XFEM region in the coupled SBPD and XFEM. In addition, the FEM region contains cracks. In the FEM, element edges should be aligned with crack faces, while meshes are independent of the internal geometry and physical interfaces (such as cracks) in the XFEM, as shown in Fig. 1. It is obvious that the XFEM is more convenient than the FEM for modelling cracks. Hence, the XFEM is adopted instead of the ordinary FEM in the cracked domain in this study, i.e. the coupled SBPD and XFEM is used instead of the coupled SBPD and FEM.

3 Accuracy verification

To verify the accuracy of the proposed framework, a cantilever beam with an edge crack under a uniformly distributed shearing force is considered, as shown in Fig. 2. The length D of the cantilever beam is 50 mm, the height L is 20 mm, the crack length \(\mathrm d_1\) is 5 mm, and \(\mathrm d_2\) is 2.5 mm. The shear force on the right end is \(\mathrm P=-1\) KN/m. Following material properties are considered for this study: Young’s modulus \(E = \)1 GPa, Poisson’s ratio \(\nu =\) 0.2. A state of plane stress condition is assumed. In order to investigate the influence of region division on the accuracy, two different region division schemes are adopted, as shown in Fig. 3. In Fig. 3, \(\mathrm L_1 = 3.5 \) mm, \(\mathrm L_2 = 1.5 \) mm, \(\mathrm L_3=15\) mm, \(\mathrm L_4 = 20 \) mm, \(\mathrm L_5 = 1.5\) mm, \(\mathrm L_6= 15\) mm, and \(\mathrm L_7 = 13.5\) mm. The grid is evenly divided with a spacing of \(\Delta x = \)0.5 mm. In the PD region, the size of horizon \(\delta = 3\Delta x \) is used.

The horizontal displacements on \( y=\frac{L}{2}\) and the vertical displacements on \(x=\frac{D}{2}\), respectively, and the results obtained with XFEM are also given in Figs. 4 and 5 for comparison. From Figs. 4 and 5, it is found that (1) the displacements obtained by the coupling model with the two region division schemes match well with the results obtained by XFEM, which shows that the coupling model has good solution accuracy, and (2) the results of the coupling model with the two region division schemes are almost the same, which show that the influence of region division is small.

Fig. 2
figure 2

Schematic illustration of the cantilever beam with an edge crack

Full size image
Fig. 3
figure 3

Two region division schemes of the cantilever beam, a coupling model 1, and b coupling model 2

Full size image
Fig. 4
figure 4

Comparison on horizontal displacements on \( x=\frac{D}{2}\)

Full size image
Fig. 5
figure 5

Comparison on vertical displacements \( y=\frac{L}{2}\)

Full size image

4 Numerical examples

To show the performance of the present framework for 2D crack propagation problem, four numerical examples, viz., two for quasi-static boundary conditions and two for dynamic loading, are considered. For all the numerical examples, a state of plane stress condition is assumed unless mentioned otherwise. A structured 4-node quadrilateral element is used.

4.1 Quasi-static analysis: Mode-I crack propagation in an edge-cracked plate

The first example deals with a square plate with an edge crack under uniaxial tension as depicted in Fig. 6. The plate length is \(\mathrm L=0.1\) m, the thickness is \(\mathrm t=1\) mm, and the crack length is 50 mm. The top and the bottom edges of the plate are subjected to Dirichlet boundary conditions. The material properties considered for this example include: Young’s modulus is \(E=\) 35,770 MPa, Poisson’s ratio is \(\nu = \) 0.38, and critical energy release rate is \(G_ {IC}=\) 9.8 N/m. The computational domain is disctretized with a uniform grid size of \(\Delta x=1\) mm. In the PD region, the size of horizon is \(\delta = 3 \Delta x \).

The region division is shown in Fig. 7, \(\mathrm L_1=53\) mm, \(\mathrm L_2 = 20\) mm, \(\mathrm L_3=3\) mm and \(\mathrm L_4=34\) mm. The Dirichlet boundary conditions are imposed incrementally with \(\Delta u_y=\) 5\(\times \)10\(^{-5}\) mm before fracture. Once the bond is broken, the displacement increment is reduced to \(\Delta u_{y}=5\times 10^{-6}\) m, until crack propagation is completed. The crack growth process is shown in Fig. 8, in which Fig. 8a–c are the crack propagation processes obtained by the coupling method and Fig. 8d–f are the crack propagation processes simulated by the pure PD. It can be found that the crack path simulated by the two methods are consistent, and conform to the mode-I crack propagation path. When the displacement increment reaches 0.0041 mm, the crack starts propagation, and the plate is snapped when the displacement increment reaches 0.005 mm. The calculation time estimated for the coupling method and the pure PD is 2543 s and 3564 s, respectively, and this means that the coupling method has much higher efficiency than the pure PD.

Fig. 6
figure 6

Schematic illustration of the square plate with an edge crack

Full size image
Fig. 7
figure 7

Schematic representation of sub-division of the computational domain into three regions

Full size image
Fig. 8
figure 8

Crack propagation paths, a–c for the coupling method, and d–f for the pure PD

Full size image

4.2 Quasi-static analysis: mixed-mode crack propagation in a central-cracked-square plate

Mixed-mode crack propagation in a square plate with a central crack as shown in Fig. 9 is considered. The side length of the plate is \(\mathrm 2W =\) 150 mm, the plate thickness is \(\mathrm t=\) 5 mm, the crack length is \(2a = \) 45 mm, and the inclined angle of the crack is \(\alpha \). There are two loading circular holes on the upper and lower corners, \(r=\) 4 mm, and \(d=\) 25 mm. The material parameters are: Young’s modulus \(E=\) 2940 MPa, Poisson’s ratio \(\nu =\) 0.38, and average fracture toughness \(K_{IC}=\) 1.33 MPa\(\sqrt{\textrm{m}}\). The conversion relationship between energy release rate \(G_{IC}\) and average fracture toughness \(K_{IC}\) is \(G_{IC}=\frac{K_{IC}^2}{E}\). The displacement loading is adopted, it is loaded step by step, and the increment of each loading is \(\Delta u_{y}=1\times 10^{-7}\) m. The computational domain is evenly divided, and the grid spacing is \(\Delta x=\) 1 mm. In the PD region, \(\delta = 3\Delta x \). The region division is shown in Fig. 10, \(\mathrm L_1=\) 49 mm, \(\mathrm L_2=\) 85 mm, \(\mathrm L_3=\) 3 mm, \(\mathrm L_4=\) 46 mm, and \(\mathrm L_5=\) 82 mm.

Fig. 9
figure 9

Schematic illustration of the plate with a central crack

Full size image
Fig. 10
figure 10

Region division of the plate with a central crack

Full size image

Two crack angles are considered, i.e. 45\(^\circ \) and 62.5\(^\circ \). The ultimate load can be obtained by calculating the sum of the nodal forces in the loaded circular hole. When the crack angle is 45\(^\circ \), the plate begins to damage when the load is about 2050 N. The ultimate failure load is about 2350 N, and the final crack paths are shown in Fig. 11a, which matches well with the experimental crack paths shown in Fig. 11b. For the crack with 62.5\(^\circ \) inclined angle, the crack grows when the load is about 2350 N, and the ultimate failure load is about 2900 N. The crack paths are shown in Fig. 12a, which agrees well will with the path predicted in the experiment  [37] shown in Fig. 12b. It is noted that the computed figures are rotated by \(90^\circ \) counterclockwise for comparing with the experimental results.

Fig. 11
figure 11

Comparison on the crack propagation paths for \(45^\circ \) crack between the present study (a) and the experimental data (b)

Full size image
Fig. 12
figure 12

Comparison on the crack propagation paths for \(62.5^\circ \) crack between the present study (a) and the experimental data (b)

Full size image

The ultimate failure loads obtained with the coupling method for the 45\(^\circ \) crack and 62.5\(^\circ \) crack are 2200 N and 2950 N, respectively. The average ultimate failure loads obtained with the experiment for the 45\(^\circ \) crack and 62.5\(^\circ \) crack are 2330 N and 3197.5 N [37], respectively. It is found that the ultimate failure loads obtained by the coupling method almost match with the experimental values.

The computational time is 38,333 s for the 45\(^\circ \) crack and 45,973 s for the 62.5\(^\circ \) crack using the coupling method. The computational time is 52,439 s for the 45\(^\circ \) crack and 63,264 s for the 62.5\(^\circ \) crack using the pure PD. This shows that the proposed framework can significantly improve the calculation efficiency compared with the pure PD.

4.3 Dynamic crack propagation and branching in an edge-cracked plate

An edge-cracked plate subjected to uniaxial tension, as shown in Fig. 13, is simulated to verify the performance of the proposed framework for dynamic crack propagation problem. The plate length is \(\mathrm L=\) 0.4 m, the plate width is \(\mathrm D=\) 0.1 m, and the plate thickness is \(\mathrm t = \)0.001 m. Young’s modulus is \(\mathrm E = \) 65 GPa, Poisson’s ratio is \(\nu = \) 0.2, material density is \(\rho \)= 2235 kg/m\(^3\), and critical energy release rate is \(\mathrm G_ {IC}=\) 204 N/m. The top and the bottom face is subjected to uniform pressure of \(\mathrm P=\) 14 MPa. The time integration step is \(\Delta t=\) 25 ns, and the total computational time is 40 \(\mathrm{{\mu }} \textrm{s}\).

Fig. 13
figure 13

Geometry model of the rectangle plate with an edge crack

Full size image

The domain is divided into uniform grid, and two different spacing division methods are adopted, i.e. \(\Delta x=\) 1 mm and \(\Delta x=\) 0.5 mm. In the PD region, \(\delta = 3\Delta x \). Figure 14 presents the schematic of the division of the computational domain into three regions. For \(\Delta x=1\) mm, \(\mathrm L_1=\) 47 mm, \(\mathrm L_2=\) 3 mm, and \(\mathrm L_3=\) 50 mm. For \(\Delta x=\) 0.5 mm, \(\mathrm L_1=\) 48.5 mm, \(\mathrm L_2=\) 1.5 mm, and \(\mathrm L_3=\) 50 mm. In order to prevent the loading boundary from being damaged first in the calculation process, the material points less than \(\delta \) from the upper and lower boundaries are set as non-destructive areas.

Fig. 14
figure 14

Region division of the plate with an edge crack

Full size image

The crack paths obtained by the coupling method under two different discrete schemes and the pure PD [38] are represented in Fig. 15. It is found that the crack propagation and branching paths simulated by the proposed framework are almost consistent with crack paths obtained by the pure PD, but the crack paths for the coupling method with \(\Delta x=0.5\) mm is more consistent with the results obtained by the pure PD. This shows that the coupling method has good convergence in solving the dynamic crack propagation problem.

Fig. 15
figure 15

Crack propagation and branching paths, a coupling model for \(\Delta x=1\) mm, b coupling model for \(\Delta x=0.5\) mm, and c PD model

Full size image

The crack propagation velocity is also an important index to measure the dynamic crack propagation. The fixed time interval \(\Delta t=2\,\mathrm{\mu }\)s is adopted. Figure 16 shows the comparison of crack growth speeds of the coupled method under two different discrete schemes. It is obvious that the fluctuation of crack propagation speed decreases with the mesh refinement. In addition, the crack growth speeds obtained by the coupled method with \(\Delta x=0.5\) mm are compared with those simulated by the PD, as shown in Fig. 17. The crack propagation speed curve of the coupling method is almost consistent with the results calculated by the PD, the maximum velocities of the crack propagation obtained from the coupling method, the PD and the experiment [38] are 1721 m/s, 1681 m/s and 1580 m/s, respectively. The Rayleigh wave velocity is about 3244 m/s, and the maximum crack growth velocity calculated by the coupling method is far less than the Rayleigh wave velocity, so the coupling method can also have high accuracy in the simulation of crack growth velocity.

Fig. 16
figure 16

Comparison on crack propagation velocities for the coupling method with different discrete schemes

Full size image
Fig. 17
figure 17

Comparison on crack propagation velocities for different methods

Full size image

4.4 Simulation of Kalthoff–Winkler experiment

The last numerical example is devoted to simulation of dynamic crack growth for the Kalthoff–Winkler experimenting test. The details of geometry and boundary conditions of the Kalthoff–Winkler test are then shown in Fig. 18a. The impactor velocity is \(\mathrm v_0=16.5\) m/s. Due to the geometric symmetry, only the upper part of the plate as shown in Fig. 18b is used for simulation. Young’s modulus \(E= \) 190 Gpa, Poisson’s ratio \(\nu =\) 0.3, material density \(\rho \)= 8000 kg/m\(^3\), and critical energy release rate \(\mathrm G_ {IC}=\) 22170 N/m are adopted. The time integration step is \(\Delta t=\) 50 ns, and the total computational time is 80 \(\mathrm{\mu } \textrm{s}\).

Fig. 18
figure 18

Geometry model of the rectangular plate, a the whole geometry model, and b the computational model

Full size image

The grid is evenly divided, and the grid spacing is \(\Delta x =\) 1 mm. In the PD region, \(\delta = 3\Delta x \). Figure 19 represents the region division, \(L_1 =\) 0.047 m, \(L_2=\) 0.003 m and \(L_3=\) 0.05 m.

Fig. 19
figure 19

Region division of the rectangle plate

Full size image

The crack paths obtained by the proposed framework are plotted in Fig. 20. The crack path results from the present approach are then compared with the reference crack paths derived from the XFEM. The crack path obtained by the coupling method extends linearly along the direction of 65\(^\circ \), which is consistent with the value of 67.5\(^\circ \) given in Ref. [39]. It shows that the proposed framework has good accuracy for simulating dynamic crack propagation problem.

Fig. 20
figure 20

Comparison on the crack propagation paths between the coupling method (a) and the XFEM (b)

Full size image

The crack growth velocity is also investigated. The fixed time interval \(\Delta t=2.5 \mathrm{\mu } \textrm{s}\) is adopted. The Rayleigh wave velocity is \(CR = 2799.2 \) m/s. In this analysis, the relative crack propagation velocity is defined as \(\frac{V}{CR}\). Figure 21 shows the relative crack propagation velocity obtained by the coupling method, which is compared with the results obtained by the NOSB-PD [40], discrete method (DM) [41], 2D XFEM-PD [29] and discrete element method (DEM) [42]. In the coupling method, the crack growth starts at 22.5 \(\mathrm{\mu } \textrm{s}\), and the propagation velocity is always much lower than that of Rayleigh wave speed. The results from the coupling method match well with those obtained by other numerical methods.

Fig. 21
figure 21

Comparison on the crack growth speeds amongst different methods

Full size image

5 Conclusions

In this work, we have presented an efficient coupling approach between the XFEM and the state-based PD for two-dimensional crack propagation problems. Numerical simulations are accounted for fulfilling both the quasi-static and time-dependent dynamic boundary conditions. The SBPD is used in the vicinity of the crack tips and along the potential crack propagation regions, while the XFEM is adopted in the other regions. The coupling method has the advantages of the state-based PD and the XFEM, and can overcome the disadvantages of the two methods, so it can effectively simulate the crack propagation. The PD region remains unchanged in this study, and the potential crack propagation region is known in advance. A variable PD region can further save time, and this is a topic for future communication. The current development is flexible and has no limitation to solve other more complex problems such as fracture in three dimensions.