Accelerated Peridynamic Computation on GPU for Quasi-static Fracture Simulations

Abstract

Due to the adoption of integral equations instead of partial differential equations to describe the deformations of materials, the peridynamics has advantages in dealing with fracture problems. However, the non-local effect of peridynamics brings too much computation cost to make large-scale engineering applications challenging. In this paper, a parallel algorithm in the Compute Unified Device Architecture (CUDA) framework is presented to speed up the computational process of a peridynamic model for quasistatic fracture simulations on GPU, in which the peridynamic model is numerically implemented by the peridynamics-based finite element method (PeriFEM) [1]. The parallel algorithm makes crack simulations by the pure peridynamics with millions of degrees of freedom possible with one GPU. To validate the accuracy and efficiency of the parallel algorithm based on PeriFEM, several numerical benchmarks are performed, and the results are compared with those obtained by the finite element method (FEM) and the serial algorithm. The results of the comparison show that the presented parallel algorithm is effective and efficient.

1 Introduction

Due to the classical continuum mechanics (CCM) uses partial differential equations to describe the deformations of solid materials and structures, it is difficult to simulate crack growth by numerical methods that rely on the CCM theory for a long time. Although there are many methods to simulate cracks in the framework of CCM, such as meshfree techniques and extended finite element methods (XFEM), it is needed to add supplementary conditions to approximate discontinuous displacement fields [2, 3]. Moreover, they cannot be used to spontaneously simulate the deformation process of material from loading to failure. In this background, Silling firstly proposed the peridynamic theory which uses integral equations to describe the motion of material points [4, 5]. The integrand in the peridynamic (PD) equation of motion is free of spatial derivatives of the displacement field. Thus, it is applicable in the presence of discontinuities in the displacement field, such as crack initiation and propagation.

On the other hand, PD assumes that one material point can interact with others in its horizon by bonds which can be seen as springs. This leads to expensive computation and memory costs compared with FEM, which limits the application of PD in engineering. To solve this problem, many researchers have proposed plenty of schemes to couple CCM and PD, and PD is only applied in the area where damage occurs [6,7,8,9,10,11]. The coupling methods are divided into two types that one is force-based schemes and the other energy-based schemes. However, the force-based schemes possibly lead to the inconsistency of the strain energy density function under the affine deformation, while the energy-based schemes may bring the ghost force to the coupling boundary. Furthermore, the coupling methods extremely reduce the computation consumption, but it is hard to implement in parallel due to the complex algorithm.

For accurate and fast simulations, parallel computing is another option. There are many computing techniques such as Message Passing Interface (MPI), Open Multi-Processing (OpenMP), CUDA, and Open Computing Language (OpenCL). MPI is a standard for developing high-performance computing (HPC) applications on distributed memory architecture. But due to the massive communications between the master and slave processors in MPI programming, the master processor may become the bottleneck of system performance [12]. MPI is suitable for large-scale problems which should be executed in clusters. OpenMP is a kind of application programming interface (API) with shared memory architecture, and it provides a multithreaded capacity [13]. So OpenMP can be easily implemented to achieve thread-level parallel computing. However, due to hardware limitations, OpenMP can only start a very small number of threads.

With the rising computational power and the increasingly low price, a graphics processing unit (GPU) is ubiquitous in HPC [14]. GPU has evolved into a highly parallel, multithreaded, multi-core processor with tremendous computational power and super high memory bandwidth compared with the central processing unit (CPU). At the same time, the popularity of general-purpose graphics processing units (GPGPU) makes it a trend to use GPU for computing. CUDA and OpenCL are two major GPGPU frameworks at present. CUDA launched by NVIDIA corporation is a general-purpose parallel computing platform and programming model that allows users to directly utilize NVIDIA GPU for parallel computing [15]. OpenCL was first developed by Apple corporation in 2008 as a standard designed to achieve portability and efficiency for parallel computing [16]. CUDA is a general-purpose parallel computing architecture developed by NVIDIA, which enables GPUs to solve complex computing problems. Compared with OpenCL, programs written by the GPU can run on CUDA-enabled processors with ultra-high performance.

Currently, PD-based parallel algorithms and codes with great potential for engineering applications are limited. There are some open-source codes that can be used for PD simulations, such as PDLammps, Peridigm, PeriPy, and PeriHPX. PDLammps is an add-on module to Sandia’s Lammps molecular dynamics package and can implement a simplified PD model [17]. Peridigm is an open-source computational PD code. It is a massively parallel code for implicit and explicit multi-physics simulations centering on solid mechanics and material failure [18]. The state-based PD is successfully applied to Peridigm [19]. OpenMP can be used for CPU parallelism. For example, CPU acceleration is used to accelerate PD-SPH simulations [20]. PeriPy is an open-source and high-performance python package for solving PD problems in solid mechanics [21]. PeriHPX implements a PD model of fracture using meshfree and finite element discretizations with an open-source C++ standard library HPX for parallelism and concurrency [22]. There are also some researches that pay attention to accelerating part of calculations, such as assembling total stiffness matrix by making most of the shared memory on OpenMP or GPU and creating neighbor lists [23,24,25,26,27]. But parallel computation of the whole process is still needed. On the other hand, most parallel computations for PD models adopt explicit numerical methods to get solutions, while some bond-based PD models of composites are solved by implicit algorithms before failure occurs [28, 29].

This paper presents a parallel computing algorithm of bond-based PD for quasi-static fracture simulations based on the CUDA framework, which expects to apply PD to engineering without high-performance computers. We compare the calculation speed of PeriFEM with that of FEM for structures that have millions of degrees of freedom (DOFs) in the CUDA framework and study the relationship between DOFs and the calculation time of each part. The results show that the calculation speed of PeriFEM can be close to that of FEM in the CUDA framework.

The remainder of this paper is organized as follows. Section 2 briefly introduces the bond-based PD theory and describes PeriFEM. Section 3 describes the quasi-static implicit solution method and the parallel computing algorithm. The numerical benchmarks and the analysis of the results are provided in Sect. 4. Concluding remarks are given in Sect. 5.

2 A Quick Overview on the Bond-Based Peridynamics

In this section, we will briefly introduce the bond-based PD and PeriFEM.

2.1 Bond-Based Peridynamics

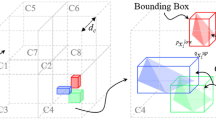
The bond-based peridynamic model is proposed by Silling [4], which assumes that a point $\varvec{x}$ in a complete domain $\Omega$ interacts with all points in its neighborhood, $\mathcal {H}_{\delta }(\varvec{x})=\left\{ \varvec{x^{\prime } }\in \Omega :\left| \varvec{x^{\prime }}-\varvec{x}\right| \le \delta \right\}$, where $\delta$ is referred to as the peridynamic horizon that denotes the cut-off radius of the action scope of $\varvec{x}$, as shown in Fig. 1.

Fig. 1

Continuum body $\Omega$ and neighborhood of $\varvec{x}$, $\mathcal {H}_{\delta }(\varvec{x})$

The bond-based peridynamic equation for a quasi-static problem, which uses a pairwise force function $\varvec{f}$ to describe the interaction between material points, is written as follows

$$\begin{aligned} \int _{H_{\delta (\varvec{x})}} \varvec{f}\left( \varvec{\xi }\right) dV_{\varvec{\xi }}+ \varvec{b}(\varvec{x})=0, \end{aligned}$$

(1)

where $\varvec{b}(\varvec{x})$ is a prescribed body force density, and $\varvec{\xi }=\varvec{x^{\prime }}-\varvec{x}$ is the relative position vector called a bond.

For linear elasticity and small deformations, the vector-valued function $\varvec{f}$ takes the form as follows [4]

$$\begin{aligned} \varvec{f}(\varvec{\xi })=\frac{c(\varvec{x},\varvec{\xi })+c(\varvec{x^{\prime }},\varvec{\xi })}{2}\frac{\varvec{\xi }\otimes \varvec{\xi }}{|\varvec{\xi }|^2}\cdot \varvec{\eta }, \end{aligned}$$

(2)

where $\varvec{\eta }(\varvec{\xi })=\varvec{u}(\varvec{x^{\prime }})-\varvec{u}(\varvec{x})$ is the relative displacement vector with the displacement field $\varvec{u}$, and $c(\varvec{x},\varvec{\xi })$ is the micromodulus function, which is related to the bond stiffness. For the homogeneous materials, $c(\varvec{x},\varvec{\xi })=c(|\varvec{\xi }|), \forall \varvec{x}\in \Omega$.

In PD, the stretch-based criterion proposed by Silling and Askari [5] has been widely used for fracture simulations. When the bond stretch s is larger than a critical value $s_{crit}$, the bond will break in an irreversible manner. The bond stretch s is defined as

$$\begin{aligned} s=\frac{|\varvec{\xi }+\varvec{\eta }|-|\varvec{\xi }|}{|\varvec{\xi }|}. \end{aligned}$$

(3)

This failure law is implemented by introducing a history-dependent scalar-valued function $\mu (\varvec{\xi }, t)$ to describe the status of bonds, which is defined as

$$\begin{aligned} \mu (\varvec{\xi }, t)=\left\{ \begin{array}{ll} 1, &{} \text{ if } s\left( t^{\prime }, \varvec{\xi }\right) <s_{crit} \quad \text{ for } \text{ all }\ 0 \leqslant t^{\prime } \leqslant t, \\ 0, &{} \text{ otherwise }, \end{array}\right. \end{aligned}$$

(4)

where t and $t^{\prime }$ denote the computational steps. Note that the critical bond stretch $s_{crit}$ is considered as an intrinsic material parameter. And the effective damage for each point $\varvec{x}$ is defined as

$$\begin{aligned} \phi (\varvec{x},t)=1-\frac{\int _{H_{\delta (\varvec{x})}} \mu (\varvec{\xi }, t)d V_{\varvec{\xi }}}{\int _{H_{\delta (\varvec{x})}} d V_{\varvec{\xi }}}, \end{aligned}$$

(5)

which can indicate the damage of the structure.

2.2 Peridynamics-Based Finite Element Method (PeriFEM)

PeriFEM is an algorithm framework for numerically implementing the bond-based PD model that is compatible with the traditional algorithm framework of the FEM. So the PD simulation can make use of the existing FEM software platform or high-performance computing architecture, to facilitate the promotion of PD in engineering applications.

From [7], in order to reconstruct the formulation for potential energy, the finite element framework is used to solve the PD problems. The total potential energy can be rewritten as

$$\begin{aligned} \Pi (\varvec{u})=\dfrac{1}{4}\int _{\Omega }\int _{H_{\delta (\varvec{x})}}\varvec{f}(\varvec{\xi })\cdot \varvec{\eta }(\varvec{\xi })dV_{\varvec{\xi }}dV_{\varvec{x}}-\int _{\Omega }\varvec{u}(\varvec{x})\cdot \varvec{b}(\varvec{x})dV_{\varvec{x}}, \end{aligned}$$

(6)

where the first and second terms on the right-hand side are the deformation energy and external work, respectively.

Note that $\varvec{f}(\varvec{\xi })=0$, for $\forall |\varvec{\xi }| > \delta$, i.e., $\forall \varvec{x^{\prime }} \notin H_{\delta (\varvec{x})}$, then the inner integral defined on $H_{\delta (\varvec{x})}$ can be extended to the entire domain $\Omega$. Furthermore, a new type of integral operation is defined as [1]

$$\begin{aligned} \int _{\bar{\Omega }} \bar{\varvec{g}}(\varvec{x^{\prime }}, \varvec{x}) d \bar{V}_{\varvec{x^{\prime }}\varvec{x}}:=\int _{\Omega }\int _{\Omega } \varvec{g}(\varvec{\xi }) d V_{\varvec{\xi }} d V_{\varvec{x}}, \end{aligned}$$

(7)

where $\bar{\Omega }$ is an integral domain generated by two $\Omega$s, and $\bar{\varvec{g}}(\varvec{x^{\prime }}, \varvec{x})$ is a double-parameter function related to $\varvec{g}(\varvec{\xi })$ and is defined on $\bar{\Omega }$. Then, Eq. (6) can be represented in a single integral form

$$\begin{aligned} \Pi (\varvec{u})=\frac{1}{4}\int _{\bar{\Omega }} \bar{\varvec{f}}(\varvec{x^{\prime }}, \varvec{x}) \cdot \bar{\varvec{\eta }}(\varvec{x^{\prime }}, \varvec{x}) d \bar{V}_{\varvec{x^{\prime }}\varvec{x}} - \int _{\Omega } \varvec{u(\varvec{x})} \cdot \varvec{b}(\varvec{x}) d V_{\varvec{x}}. \end{aligned}$$

(8)

A new type of element called the peridynamic element (PE) is introduced in the new integral domain $\bar{\Omega }$ in Eq. (8). These PEs are constructed based on the elements in the classical FEM, which are characterized as sharing nodes between adjacent elements, and are thus called the continuous elements (CEs). Also, there is another situation that each element has its own nodes (nodes are not shared between adjacent elements), which is called the discrete elements (DEs) [30]. Both CE and DE are called local elements. In the following, we will only use CE as a type of local elements for discussion, and DE as another local elements also applies to the discussion below.

In this paper, for domain $\Omega$, we use the method in Han and Li [1] to generate a new integral domain $\bar{\Omega }$ and then discretize the domain $\Omega$ with CEs and the domain $\bar{\Omega }$ with PEs. Now, we have two sets of elements, CEs and PEs. For any CE $e_{i}$, we define the shape function matrix of CE

$$\begin{aligned} \varvec{N}_i(\varvec{x})= \begin{bmatrix} N_{i_{1}}(\varvec{x})&{} 0&{}0&{} N_{i_{2}}(\varvec{x})&{} 0&{}0&{} \cdots &{} N_{i_{n_{i}}}(\varvec{x})&{} 0&{}0\\ 0&{} N_{i_{1}}(\varvec{x})&{}0&{} 0&{} N_{i_{2}}(\varvec{x})&{}0&{} \cdots &{} 0&{} N_{i_{n_{i}}}(\varvec{x})&{}0\\ 0&{}0&{} N_{i_{1}}(\varvec{x})&{}0&{} 0&{} N_{i_{2}}(\varvec{x})&{} \cdots &{} 0&{}0 &{}N_{i_{n_{i}}}(\varvec{x}) \end{bmatrix}, \end{aligned}$$

(9)

and the nodal displacement vector of CE

$$\begin{aligned} \varvec{d}_i= \begin{bmatrix} u_{i_{1}}&v_{i_{1}}&w_{i_{1}}&u_{i_{2}}&v_{i_{2}}&w_{i_{2}}&\cdots&u_{i_{n_{i}}}&v_{i_{n_{i}}}&w_{i_{n_{i}}} \end{bmatrix}^T. \end{aligned}$$

(10)

For any PE $\bar{e}_{k}$, we define the shape function matrix of PE

$$\begin{aligned} \bar{\varvec{N}}_k(\varvec{x'},\varvec{x})= \begin{bmatrix} \varvec{N}_j(\varvec{x'})&{} \varvec{0}\\ \varvec{0}&{} \varvec{N}_i(\varvec{x}) \end{bmatrix}, \end{aligned}$$

(11)

and the nodal displacement vector of PE

$$\begin{aligned} \bar{\varvec{d}}_k= \begin{bmatrix} \varvec{d}_j\\ \varvec{d}_i\\ \end{bmatrix}, \end{aligned}$$

(12)

so the difference matrix for shape function can be written as

$$\begin{aligned} \bar{\varvec{B}}_k(\varvec{x'},\varvec{x})=\bar{\varvec{H}}\bar{\varvec{N}}(\varvec{x'},\varvec{x}), \end{aligned}$$

(13)

where $\bar{\varvec{H}}=[\varvec{I}, \varvec{-I}]$ is the difference operator matrix with $\varvec{I}$ being an identity matrix. In addition, the micromodulus tensor has the matrix form

$$\begin{aligned} \varvec{D}(\varvec{\xi })=\dfrac{c(|\varvec{\xi }|)\mu (\varvec{\xi ,t})}{|\varvec{\xi }|^2} \begin{bmatrix} \xi _1^2&{} \xi _1\xi _2&{}\xi _1\xi _3\\ \xi _2\xi _1&{} \xi _2^2&{}\xi _2\xi _3\\ \xi _3\xi _1&{} \xi _3\xi _2&{}\xi _3^2 \end{bmatrix}. \end{aligned}$$

(14)

Consequently, the total potential energy can be approximated as

$$\begin{aligned} \Pi (\varvec{d})=\frac{1}{4}\varvec{d}^{T}\bar{\varvec{K}}\varvec{d}-\varvec{d}^{T}\varvec{F}, \end{aligned}$$

(15)

where $\varvec{d}$ is the total nodal displacement vector and

$$\begin{aligned} \bar{\varvec{K}}=\sum _{k=1}^{\bar{m}}\bar{\varvec{G}}^T_k\bar{\varvec{K}}_k\bar{\varvec{G}}_k, \quad \varvec{F}=\sum _{i=1}^{m}\varvec{G}^T_i\varvec{F}_i, \end{aligned}$$

(16)

are the total stiffness matrix and total load vector, respectively. $\bar{\varvec{G}}_{k}$ and $\varvec{G}_{i}$ are the transform matrix of the degree of freedom, which satisfies

$$\begin{aligned} \bar{\varvec{d}}_{k}=\bar{\varvec{G}}_k\varvec{d},\quad \varvec{d}_{i}=\varvec{G}_i\varvec{d}, \end{aligned}$$

(17)

respectively. Furthermore,

$$\begin{aligned} \bar{\varvec{K}}_k=\int _{\bar{\Omega }_k}\bar{\varvec{B}}_k^T(\varvec{x'},\varvec{x})\varvec{D}(\varvec{\xi })\bar{\varvec{B}}_k(\varvec{x'},\varvec{x})d\bar{V}_{\varvec{x'x}}, \end{aligned}$$

(18)

$$\begin{aligned} \varvec{F}_i=\int _{\Omega _i}\varvec{N}_i^T(\varvec{x})\varvec{b}(\varvec{x})dV_x, \end{aligned}$$

(19)

are the element stiffness matrix and the element load vector, respectively.

Finally, from Eq. (15), a linear system including the solution of the nodal displacement vector $\varvec{d}$ can be derived as

$$\begin{aligned} \frac{1}{2}\bar{\varvec{K}}\varvec{d}=\varvec{F}. \end{aligned}$$

(20)

Remark 1

A special case: two-node PE. Typically if the 2-node, 4-node, and 8-node local elements (CEs or DEs) are used in 1, 2, and 3-dimensional classical finite element discretization, a PE generated by them is 4-node, 8-node, and 16-node, respectively. Particularly, let us consider a special kind of DE that is only one node in the centroid of the element, and its shape function is constant, which can be regarded as a material point. As a result, Eq. (11) becomes an identity matrix. In this case, the corresponding PE will only have two nodes and the PeriFEM will be reduced to a special form [31], i.e., two-node PE. It should be noted that the two-node PE is suitable to 1-, 2-, and 3-dimensional cases. In addition, a PE composed of a DE and itself is ignored, because its PE stiffness is zero [30].

3 Numerical Implementation of PeriFEM in CUDA

By reviewing PeriFEM in Sect. 2.2, it is worth noting that there is no data exchange among PEs, so this numerical algorithm is naturally suitable for parallel computing in GPU by matching each CE with a thread. The flowchart of the numerical algorithm is provided in Fig. 2. Next, we will introduce in detail the implementation processes of some steps in CUDA.

Fig. 2

Flowchart of the numerical algorithm with N being the number of total progressive increments

3.1 Generating PE Mesh Data by GPU

The PE mesh data is generated from the CE mesh data in PeriFEM. It is known that theoretically, we need to execute the loop $N^2$ times to construct the neighborhood data for N CEs in serial computation. It is acceptable for small-scale problems, but it is hard to implement due to the increasing computational cost for large-scale problems for example with millions of elements.

It is found that the process of creating neighborhood data for different CEs is independent and repetitive, so we can match each CE with a thread in GPU to construct the neighborhood data. The diagram of generating neighborhood data for CEs by multithreads in GPU is shown in Fig. 3.

Fig. 3

Diagram of generating neighborhood data for CEs by multithreads in GPU

During generating neighborhood data for CEs by multithreads at the same time, the PE data is obtained and a list is chosen to store it. As shown in Fig. 4, in the list for the current thread, the first number represents the number of related elements, and the parameter $step\_length$ is directly related to the maximum number of elements in all neighborhoods, for example, we can set $step\_length$ to 30 if choosing $\delta$ to be 3 times the mesh size. Finally, a one-dimensional list with a size of the number of CEs times $step\_length$ is used to store PE data in global memory [27].

Fig. 4

The data format of the list of storing the PE data

After the PE mesh data is obtained, the PE stiffness matrices are calculated in parallel according to Eq. (18) by matching the PEs in a CE’s neighborhood with one thread. Compared with the serial algorithm, it can be seen that parallel computation in GPU is an effective way to improve computational efficiency.

3.2 Assembling and Storing Total Stiffness Matrix by CPU

After getting the PE stiffness matrices, we need to assemble the total stiffness matrix. There exists a security problem called the thread race condition when assembling the total stiffness matrix in GPU, so the step of assembling the total stiffness matrix is executed by the CPU in serial.

It is well known in the PeriFEM that only the interacting elements contribute to the total stiffness matrix; this brings the banded and sparse distribution of the non-zero values in the total stiffness matrix. Therefore, the sparse storage of the total stiffness matrix is an effective way to reduce memory usage. We adopt the method of compressed sparse row (CSR) [32] to save the total stiffness matrix. In order to display how to store a matrix using CSR, we give an example of the mapping relationship between full storage and CSR sparse storage as shown in Fig. 5. The related parameters in CSR such as two indexes row and col are described in Table 1. Thus, we can directly assemble the total stiffness matrix saved in sparse format, which can reduce the memory and time consumption, and then allow us to solve the problems with more degrees of freedom by GPU.

Fig. 5

The example of how a matrix is stored using CSR

Table 1 The related parameters in CSR

3.3 Applying Displacement Boundary Conditions and Solving Linear Equations by GPU

After getting the total stiffness matrix, we need to apply boundary conditions and then obtain the linear equations. For simplicity, we adopt the penalty method of multiplying by a big number [33] to apply boundary conditions. In general, it is easy to apply displacement boundary conditions for a fully stored total stiffness matrix because we just need to find the nodes that should be processed in turn. However, this step is troublesome when the stiffness matrix is compressed into sparse format storage. But, we can use the parallel algorithm with thousands of threads to modify the values in the total stiffness matrix and create the load vector at the same time.

We get the linear Eq. (20) where $\varvec{d}$ is the unknown displacement vector after processing the boundary conditions and creating the load vector. The linear equations are solved by applying the conjugate gradient (CG) method as shown in Algorithm 1. As we know, solving linear equations in FEM is usually the most time-consuming part because of nonlinear iterations. But from the above CG algorithm, it is found that the algorithm contains a lot of vector additions, internal products, and matrix multiplications, which is suitable for parallel calculations to save computational time.

The cuSPARSE library in CUDA is a set of basic linear algebra subroutines for handling sparse matrices, and it can accelerate the calculations of matrices and vectors in GPU [32, 34]. The cuBLAS library is an implementation of Basic Linear Algebra Subprograms (BLAS) at the NVIDIA®CUDA™runtime which allows the user to access the computational resources of NVIDIA GPU [35]. Therefore, the solver used in this paper is written by the cuSPARSE and cuBLAS libraries, which make us get the best efficiency in solving linear equations.

3.4 Updating the Bond State for Every PE by GPU

Before starting the next increment step, we need to update the bond state for every PE. Exactly, it is necessary to judge whether the bond stretch of each bond in every PE exceeds the threshold, and then the contributions of broken bonds are removed from the total stiffness matrix. Because the state of each bond is independent, it is easy to update the state of each bond by the parallel program. One thread in GPU matches one CE to update the states of all bonds in this element as shown in Fig. 6.

Fig. 6

The diagram of how to update the bond states for a PE

4 Numerical Results

In this section, the uniform deformation of a plate is firstly investigated to verify the validity of PeriFEM based on GPU by comparing it with results obtained by FEM in Sect. 4.1. Next, in Sect. 4.2, the damage of a single-edge-notched plate under symmetric stretches is investigated to show the computational efficiency brought by GPU. Finally, the PeriFEM based on GPU is applied to other typical examples in Sect. 4.3. In these examples, Young’s modulus and Poisson’s ratio are fixed as $E=2.06\times 10^{11}$ Pa and $\nu =1/3$ respectively, and the horizon size is chosen as $\delta =3\Delta x$ where $\Delta x$ is the mesh size of CEs. The micromodule coefficient is assumed to be the exponential function [36].

Table 2 gives the information on the hardware configuration of CPU and GPU in the calculation. For the software environment configuration, the 11.4 version of CUDA toolkit is used where the driver is 516.94 and the compiler is nvcc. The two-dimensional grids and blocks are used in all the CUDA computations. The size of block is (32, 32) and the size of grids is $(int(sqrt(NUM / 32.0 / 32.0)) + 1, int(sqrt(NUM / 32.0 / 32.0)) + 1)$ with NUM representing the total number of threads that need to be excuted. In the below simulations, all programs in the CPU framework are run in serial.

Table 2 The information of hardware configuration of CPU and GPU

In addition, the size of the load step should change with the grid size. In order to quantitatively compare the computational efficiency, we choose the following equation to calculate the load step

$$\begin{aligned} load\_step= \frac{displacement}{element\_size/5}. \end{aligned}$$

(21)

4.1 Uniform Deformation of a Plate

Considering the uniform deformation of a square plate, the geometry and boundary conditions of the problem are shown in Fig. 7. The square plate has sides of a length of 1 m. The left and right sides are free sides, the lower side is fixed along the vertical direction, and the upper side bears a vertical displacement of 0.1 m. The plane is discretized into $100\times 100$ quadrilateral CEs, that is, the mesh size is $\Delta x=\Delta y=0.01$ m.

Fig. 7

The geometry and boundary conditions of the problem

The displacement contours calculated by the PeriFEM in CUDA are shown in Fig. 8a, b. The results obtained from FEM in CUDA are shown in Fig. 8c, d. It can be seen that the results from the two methods are in good agreement, except that the horizontal displacement corresponding to the PeriFEM has obvious errors due to the surface effect of PD. There are many techniques to avoid or modify the surface effect of PD [7, 31, 37].

Fig. 8

Displacement contours by (a, b) PeriFEM in CUDA and (c, d) FEM in CUDA

In the CUDA framework, we compare the time cost of PeriFEM simulations with that of FEM simulations with the increase in the number of CEs. The total time consumption is shown in Fig. 9. As we know, these two kinds of simulations consume more time as the number of CEs increases. However, compared with the FEM simulations, the PeriFEM simulations need more time for the same number of CEs, and this happens because generating the PEs from CEs needs to take much time in the PeriFEM simulations.

Fig. 9

The total time consumption of PeriFEM similations and FEM similations with the increase of number of CEs

It is well known that in the CPU framework compared with FEM simulations based on CEs, PeriFEM simulations need to generate a large number of PEs from CEs, which leads to more time cost in calculating PE stiffness matrices. But in the CUDA framework, it can be computed simultaneously, so the time consumption of calculating PE stiffness matrices in PeriFEM simulations is essentially the same as calculating CE stiffness matrices in FEM simulations, although the number of PE is much more than CE. This just reflects the advantages of GPU.

Furthermore, we find an interesting phenomenon in the processes of simulations. When applying the same solver based on the conjugate gradient method to solve linear equations, although the bandwidth of the total stiffness matrix in PeriFEM is wider than that in FEM, the time consumption of solving linear equations in PeriFEM is smaller than that in FEM. In other words, for the same error criterion in the conjugate gradient method, the iteration steps in PeriFEM are fewer than those in FEM. The time consumption of solving linear equations in PeriFEM and FEM simulations with the increase in the number of CEs is displayed in Fig. 10.

Fig. 10

Time consumption of solving linear equations in PeriFEM and FEM simulations with the increase of number of CEs

4.2 Single-Edge-Notched Plate Under Symmetric Stretches

Here, we consider a single-edge-notched square plate under symmetric stretches to compare the computational efficiency between CPU and GPU. The geometry and boundary conditions are shown in Fig. 11a. The plane is discretized into $200\times 200$ quadrilateral CEs, that is, the mesh size is $\Delta x=\Delta y=0.005$ m. The critical stretch in Eq. (4) is set to be $s_{crit}=0.02$.

Fig. 11

(a) The geometry and boundary conditions of the problem. (b) Damage contours of the notched plate predicted by PeriFEM based on CUDA

Figure 11b shows the crack paths predicted by the PeriFEM based on CUDA. It can be seen that the crack paths are along the horizontal direction. The result is the same as in literature [26].

In order to display the computational efficiency of GPU, the PeriFEM based on CPU is also used to predict the crack paths. For the different parts with the increase in the number of CEs, we compare the time consumption based on GPU simulations with that based on CPU simulations, as shown in Fig. 12. It is noted that no matter which part in the calculations, the CPU computation time is much longer than that of the GPU, which demonstrates that the GPU has an incomparable advantage compared to the CPU.

Fig. 12

Time consumption for the different parts based on GPU simulations and CPU simulations with the increase of number of CEs: (a) total time consumption, (b) generating PE mesh data, (c) calculating the PE stiffness matrix, (d) applying boundary conditions, (e) solving linear equations and (f) updating the bond state

Meanwhile, we also compared the time consumption of different parts for GPU simulations when the number of CEs increases. Figure 13 shows the most time-consuming parts in one iteration step, while the most time-consuming parts in the whole simulation are displayed Fig. 14. It is found from Fig. 13 that the steps of assembling the total stiffness matrix and generating PE mesh data are the two most time-consuming parts in one step, but the total stiffness matrix is only assembled once and the PE mesh data is only generated once, so they do not spend much time in the whole simulation as shown in Fig. 14. As we know, the linear equations must be solved repeatedly in the whole simulation, which makes it the most time-consuming step. It is concluded that the speed of the CUDA program mainly depends on the speed of solving linear equations, and the optimization should mainly focus on how to solve linear equations in order to speed up the PeriFEM GPU calculation.

Fig. 13

Time consumption of different parts in one iteration step of GPU simulations with the increase of number of CEs

Fig. 14

Time consumption of different parts in the whole GPU simulations with the increase of number of CEs

4.3 Typical Examples

In the last two subsections, the validity and high efficiency of the PeriFEM based on GPU have been verified. In the following, typical example applications will be considered by using the PeriFEM based on GPU.

4.3.1 Single-Edge-Notched Plate Under Nonsymmetric Stretch

Let us consider a single-edge-notched square plate under nonsymmetric stretch. The geometry and boundary conditions are shown in Fig. 15. The plane is discretized into $200\times 200$ structured quadrilateral CEs, that is, the mesh size is $\Delta x=\Delta y=0.005$ m and the DOFs are 81002. The critical stretch in Eq. (4) is set to be $s_{crit}=0.02$. It takes around 43.4 h to complete the whole simulation.

Fig. 15

The geometry and boundary conditions of the problem

Figure 16 shows the evolution of the effective damage contours predicted by the PeriFEM based on CUDA. First, the damage initiates, i.e., the bond breaks for the first time, at Step 3. Then, the damage develops slowly in the next several steps. After that, the damage propagates suddenly at Step 8, which drops drastically. The predicted crack path is in good agreement with that in literature [38].

Fig. 16

Damage contours of the single-edge-notched plate predicted by the PeriFEM based on CUDA at the different steps: (a) Step 3, (b) Step 6, (c) Step 8 and (d) Step 11. The black dotted line in (d) shows the results in [38]

4.3.2 Double-edge-Notched Plate Under Tension and Shear

In this example, we consider the mixed-mode fracture of a double-edge-notched square plate. The geometry and boundary conditions are shown in Fig. 17. The plane is discretized into 29,944 unstructured quadrilateral CEs, that is, the average size of the CEs is $\Delta x=1.25$ mm and the DOFs are 60,618. The critical stretch in Eq. (4) is set to be $s_{crit}=0.02$. It takes around 19.9 h to complete the whole simulation.

Fig. 17

The geometry and boundary conditions of the problem

The effective damage evolution contours of this test are shown in Fig. 18. The damage appears first at the notched corners at Step 4. In Step 5, the damage is more obvious than in Step 4, and it could be found that the damage of the left notched corner propagates downward, and the damage of the right notched corner propagates upward. Then, the cracks propagate destructively at Step 6. The predicted crack path is similar to the results reported in [39].

Fig. 18

Damage contours of the double-edge-notched plate predicted by the PeriFEM based on CUDA at the different steps: (a) Step 4, (b) Step 5, (c) Step 6 and (d) Step 10. The black dotted line in (d) shows the results in [39]

4.3.3 A Skewly Notched Beam Under Load

In this example, we consider the mixed mode I + III failure of a skew notched beam in three dimensions. The geometry and boundary conditions are shown in Fig. 19. In this case, we choose the two-node PEs (see Remark 1). The beam is discretized into 172,109 nodes with 516,327 DOFs, the average distance of the nodes is $\triangle x=1$ mm and the average volume is 1.195 mm$^3$. Poisson’s ratio is $\nu =1/4$ and the critical stretch in Eq. (4) is set to be $s_{crit}=0.05$. It takes around 57.8 h to complete the whole simulation.

Fig. 19

The geometry and boundary conditions of the problem with a 2-mm cross section

The effective damage path of this test is shown in Fig. 20. The top of the damage profile, at various heights, is shown in Fig. 21 respectively. The crack starts from the $45^{\circ }$ slanted notch and then twists until it aligns with the mid-plane. The twist and rotation, with the final position of the crack surface close to the symmetric plane of the beam, are similar to the [40], which further demonstrates the accuracy of the PeriFEM based on GPU.

Fig. 20

Damage contours of the skew notched beam predicted by the PeriFEM based on CUDA

Fig. 21

Damage contours at various heights (top view): (a) 20.0mm, (b) 22.5mm, (c) 25.0mm, (d) 30.0mm and (e) 35.0mm

5 Conclusions

The PeriFEM based on GPU is proposed to rapidly implement peridynamics simulations in this paper. Five examples were successfully carried out using this parallel algorithm, which demonstrates its validity and high efficiency. Consequently, the parallel algorithm can be easily applied to large-scale engineering problems, especially for fracture peridynamics simulations.

We only consider the situation of one GPU in our algorithm, and for the larger-scale problems, the multi-GPUs simulation is a good choice, which will be the focus of our future work.