A parallel acceleration GPU algorithm for large deformation of thin shell structures based on peridynamics

Abstract

Loaded shell structures may deform, rotate, and crack, leading to fracture. The traditional finite element method describes material internal forces through differential equations, posing challenges in handling discontinuities and complicating fracture problem resolution. Peridynamics (PD), employing integral equations, presents advantages for fracture analysis. However, as a non-local theory, PD requires discretizing materials into nodes and establishing interactions through bonds, leading to reduce computational efficiency. This study introduces a GPU-based parallel PD algorithm for large deformation problems in shell structures within the compute unified device architecture (CUDA) framework. The algorithm incorporates element mapping and bond mapping for high parallelism. The algorithm optimizes data structures and GPU memory usage for efficient parallel computing. The parallel computing capabilities of GPU expedite crack analysis simulations, greatly reducing the time required to address large deformation problems. Experimental tests confirm the algorithm’s accuracy, efficiency, and value for engineering applications, demonstrating its potential to advance fracture analysis in shell structures.

1 Introduction

Shell structures are highly valued for their lightweight nature, streamlined manufacturing processes, and robust compressive strength, rendering them indispensable in various industries such as automotive, marine, and aerospace [1, 2]. However, despite these advantages, real-world applications often expose these structures to failure due to noticeable displacement, significant rotation, and constrained elastic strain behaviors. Consequently, there is an urgent need for reliable numerical simulation methods that can effectively analyze substantial deformations and fractures in thin plate bending. Nevertheless, the computational time required to address large deformation problems in plate and shell structures is excessively long. Therefore, expediting the solution algorithm to efficiently handle such issues holds practical engineering significance.

Numerical simulation studies on large deformations of plate and shell structures have traditionally relied on classical continuous mechanics (CCM). This theory utilizes partial differential equations to represent material deformation, which presents challenges when simulating crack growth through numerical methods based on CCM. Within the finite element method (FEM) framework, material properties are applicable only when the analyzed model exhibits a spatially continuous and twice differentiable displacement domain. Consequently, defining spatial derivatives at discontinuities becomes impossible, necessitating additional techniques for constructing fracture models. Although meshless technology and extended FEM (XFEM) can simulate cracks within the CCM framework, approximating discontinuous displacement domains requires incorporating auxiliary conditions. Furthermore, these approaches still lack automatic simulation of deformation from loading to damage [3, 4].

In this context, Silling introduced the peridynamic (PD) theory [5], a non-local theory. Unlike the FEM, the PD model characterizes the material behavior of a node within the structure through an integral equation that describes the displacement in its surroundings. By avoiding spatial derivatives, PD theory maintains its applicability even across discontinuity surfaces. Consequently, it is well-suited for scenarios involving discontinuities within the displacement domain, such as crack initiation, propagation, and proliferation [6, 7].

According to the PD theory, nodes interact with their adjacent counterparts through bonds [8]. In computational simulations, materials are discretized into nodes that encapsulate information such as coordinates, volume, and density. Moreover, within the PD framework, relationships between nodes and their neighboring counterparts are established [9]. When numerical methods are employed for solving these computations, a smaller incremental step size is often required to ensure numerical stability and precision, resulting in a significant number of iterative steps. Compared to FEMs, PD theory entails higher computational and storage costs, posing challenges for addressing large-scale problems. Simulating large-scale problems using PD requires substantial computing resources. Therefore, minimizing the computational expenses associated with PD models is crucial for promoting their widespread application and further advancement.

Enhancing the efficiency of solving large-scale PD problems has consistently remained a primary focal point for researchers. Greta proposed a hybrid discretization and multi-grid method within the multi-adaptive framework [10], which enables variable-size grid characteristics in PD models by coupling grids of different sizes. Fine grids are exclusively utilized in critical regions and boundaries, while coarser grids are employed for discretization purposes in other areas. This approach allows for tracking critical regions and updating grid coupling schemes based on time evolution, thereby effectively enhancing the efficiency of solving PD models. Arman et al. introduced a hybrid meshless discretization method within an adaptive framework [11]. It adopts a standard scheme with higher computational costs but greater accuracy in local critical regions of PD models, while employing an efficient meshless scheme in other areas. The meshless region is dynamically switched to the standard scheme region according to computational requirements. Consequently, the portion discretized by the standard scheme evolves over time and follows the crack/damage form, ultimately resulting in an efficiently optimized pure PD model that maximizes computing resources.

The autonomous nature of PD element data enables each PD problem to be processed independently by a processing element, eliminating the need for data exchange with other PD elements. According to Amdahl’s law [12], the efficiency of algorithm parallelization increases with a higher proportion of content that can be parallelized in the overall algorithm “f” and a larger number of processing cores “n”. The maximum parallel acceleration ratio can be achieved as the value of “f” approaches 1 and “n” tends to infinity, leading to optimal efficiency in parallel acceleration. When utilized a fixed value for “n” on the same computing device, a larger “f” value will result in enhanced parallel acceleration efficiency. In the context of solving PD problems, PD element calculation serves as the core of the algorithm and demonstrates data independence, rendering it highly suitable for parallel processing. Consequently, when addressing PD problems, efficient parallel solving can be achieved by fully exploiting data independence.

With the rapid advancement of computing technology, significant improvements in central processing unit (CPU) performance have been observed over the past few decades. However, the bottleneck of single-core CPU performance and the emergence of multi-core CPUs, along with powerful parallel computing technologies, have become prominent research focuses. In this context, graphics processing units (GPUs) have garnered considerable attention due to their impressive computational power and high memory bandwidth. The ability of GPUs to process extensive amounts of data and computing tasks simultaneously contributes to enhanced computing efficiency and speed. This parallel computing power arises from hundreds of processing units within GPUs that enable concurrent execution of multiple tasks. Consequently, GPUs have demonstrated exceptional performance in scientific computing. Compute unified device architecture (CUDA), introduced by NVIDIA in 2007, is a parallel computing architecture that empowers developers to harness formidable GPU computing power for general-purpose computation. The availability of CUDA facilitates utilization of parallel computing capabilities leading to substantially improved computational efficiency when tackling complex mathematical models and algorithms.

CUDA has been effectively employed in the field of computational mechanics, demonstrating its practicality and usefulness. Notably, Liu utilized CUDA to simulate fluid dynamic problems in a 2D square column [13]. Furthermore, Wang successfully incorporated CUDA-based parallel computing in the calculation of three-dimensional elastic static boundary elements [14]. These studies illustrate the practical application of CUDA in enhancing computations within the domain of computational mechanics.

Considering the autonomous nature of PD element data and the absence of data exchange requirements, leveraging the parallel computing capabilities of GPUs enables the decomposition of intricate computational tasks into multiple independent subtasks based on elements. The utilization of the abundant processing elements within GPUs facilitates efficient execution of parallel processing. The primary aim of this study is to investigate tailored parallel solutions for addressing large-scale PD deformation problems on the GPU platform.

Considering the distinctive modeling attributes of the PD model, we have developed a parallel computing method within the CUDA framework to effectively handle extensive deformations in PD plate and shell structures. This approach leverages the architectural advantages of GPUs and assigns each element's computation to a separate thread on the GPU, enabling efficient and simultaneous multi-threaded parallel computing. To validate our proposed algorithm, we conducted a comparative analysis against results obtained from a CPU-based algorithm. Furthermore, we evaluated the acceleration performance of our algorithm by comparing its resolution time and acceleration ratio with those achieved by the CPU-based method. The experimental findings unequivocally demonstrate that leveraging parallel resolution on GPU platforms significantly enhances computational efficiency for large-scale PD deformation problems. Consequently, this strategy emerges as a viable solution for conducting extensive PD simulations.

2 A brief overview of peridynamic theory

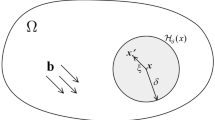
As shown in Fig. 1, the local coordinate system of the microbeam bond is denoted as o-xyz, and node $xi$ and its adjacent node $xj$ are located in the PD domain $H(xi)$ with a radius of δ. The displacements of any node on the bond centerline are defined as $u^{\prime}_{1} (x)$,$u^{\prime}_{2} (x)$, and $u^{\prime}_{3} (x)$.

Fig. 1

PD shell model

The generalized strain vector at any position on the microbeam can be defined as

$${{\varvec{\upvarepsilon}}} = \left[ {\begin{array}{*{20}c} {\varepsilon_{x} } & {\kappa_{y} } & {\kappa_{z} } & {\phi_{x} } \\ \end{array} } \right]^{{\text{T}}} ,$$

(1)

where $\varepsilon_{x}$,$\kappa_{y}$,$\kappa_{z}$ and $\phi_{x}$ represent the axial strain, y and z direction curvature, and torsion angle per element length of the microbeam, respectively.

$$\begin{aligned} \varepsilon_{x}& = \frac{{\partial u^{\prime}_{1} }}{\partial x} + \frac{1}{2}\left( {\frac{{\partial u^{\prime}_{1} }}{\partial x}} \right)^{2} + \frac{1}{2}\left( {\frac{{\partial u^{\prime}_{2} }}{\partial x}} \right)^{2} + \frac{1}{2}\left( {\frac{{\partial u^{\prime}_{3} }}{\partial x}} \right)^{2} , \hfill \\ \kappa_{y}& { = }\frac{{\partial^{2} u^{\prime}_{3} }}{{\partial x^{2} }}{, }\,\kappa_{z} { = }\frac{{\partial^{2} u^{\prime}_{2} }}{{\partial x^{2} }}{, }\,\phi_{x} = \frac{{\partial \theta^{\prime}_{1} }}{\partial x}. \hfill \\ \end{aligned}$$

(2)

The corresponding generalized stress increment can be expressed as

$${\mathbf{S}}_{PD} = \left\{ {\begin{array}{*{20}c} {{{F}}_{x}^{PD} } & {{{M}}_{y}^{PD} } & {{{M}}_{z}^{PD} } & {{{T}}_{x}^{PD} } \\ \end{array} } \right\}^{{\text{T}}} = {\mathbf{D}}_{PD} {{\varvec{\upvarepsilon}}},$$

(3)

where ${{F}}_{x}^{PD}$, ${{M}}_{y}^{PD}$, ${{M}}_{z}^{PD}$, and ${{T}}_{x}^{PD}$ are the axial stress, y-axis and z-axis bending moment, and element length torque of the microbeam key, respectively, and ${\mathbf{D}}_{PD}$ is the micromodulus parameter matrix.

$${\mathbf{D}}_{PD} = \left[ {\begin{array}{*{20}c} {c_{ax} } & 0 & 0 & 0 \\ 0 & {c_{by} } & 0 & 0 \\ 0 & 0 & {c_{bz} } & 0 \\ 0 & 0 & 0 & {c_{tor} } \\ \end{array} } \right].$$

(4)

The above-generalized strain is decomposed into an incremental decomposition, and the displacement component of any node on the microbeam key at the time $t + {{\varDelta}} t$ can be defined as

$$\overline{u^{\prime}}_{1} = u^{\prime}_{1} + {{\varDelta}} u^{\prime}_{1} , \, \overline{u^{\prime}}_{2} = u^{\prime}_{2} + {\varDelta} u^{\prime}_{2} , \, \overline{u^{\prime}}_{3} = u^{\prime}_{3} + {\varDelta} u^{\prime}_{3} , \, \overline{\theta^{\prime}}_{1} = \theta^{\prime}_{1} + {\varDelta} \theta^{\prime}_{1} .$$

(5)

where $u^{\prime}_{1}$,$u^{\prime}_{2}$,$u^{\prime}_{3}$, and $\theta^{\prime}_{1}$ are the displacement components at the time $t$, and ${\varDelta} u^{\prime}_{1}$,${\varDelta} u^{\prime}_{2}$,${\varDelta}u^{\prime}_{3}$, and ${\varDelta} \theta^{\prime}_{1}$ are the incremental displacement components from $t$ to $t + {\varDelta} t$.

The generalized strain at any position on the microbeam bond at the time $t + {\varDelta} t$ is

$${\mathbf{\overline{\varepsilon } = \varepsilon + {\varDelta} \varepsilon }},$$

(6)

where ${{\varvec{\upvarepsilon}}}$ is the generalized strain of the microbeam bond at the time $t$.${\varDelta}\,\varepsilon$ is the increment of generalized strain from $t$ to $t + {\varDelta} t$, which can be defined as

$${\mathbf{{\varDelta} \varepsilon }} = \left[ {\begin{array}{*{20}c} {{\varDelta} \varepsilon_{x} } & {{\varDelta} \kappa_{y} } & {{\varDelta} \kappa_{z} } & {{\varDelta} \phi_{x} } \\ \end{array} } \right]^{{\text{T}}} ,$$

(7)

where ${\varDelta} \varepsilon_{x}$, ${\varDelta}\kappa_{y}$, ${\varDelta} \kappa_{z}$ and ${\varDelta}\phi_{x}$ respectively represent the axial strain, y and z direction curvature, and torsion angle increment per element length of the microbeam bond, respectively.

$$\begin{aligned} {\varDelta} \varepsilon_{x}& = \frac{{\partial {\varDelta} u^{\prime}_{1} }}{\partial x} + \frac{1}{2}\left( {\frac{{\partial {\varDelta} u^{\prime}_{1} }}{\partial x}} \right)^{2} + \frac{1}{2}\left( {\frac{{\partial {\varDelta} u^{\prime}_{2} }}{\partial x}} \right)^{2} + \frac{1}{2}\left( {\frac{{\partial {\varDelta} u^{\prime}_{3} }}{\partial x}} \right)^{2} , \hfill \\ {\varDelta} \kappa_{y} &{ = }\frac{{\partial^{2} {\varDelta} u^{\prime}_{3} }}{{\partial x^{2} }}{, }\,{\varDelta} \kappa_{z} { = }\frac{{\partial^{2} {\varDelta} u^{\prime}_{2} }}{{\partial x^{2} }}{, }\,{\varDelta} \phi_{x} = \frac{{\partial {\varDelta} \theta^{\prime}_{1} }}{\partial x}. \hfill \\ \end{aligned}$$

(8)

The generalized strain increment in the above equation can also be divided into linear and nonlinear strain increments.

$${\mathbf{{\varDelta} \varepsilon }} = {\mathbf{{\varDelta} \varepsilon }}_{L} + {\mathbf{{\varDelta} \varepsilon }}_{N} ,$$

(9)

where

$$\begin{aligned} {\mathbf{{\varDelta} \varepsilon }}_{L}& = \left\{ {\begin{array}{*{20}c} {\frac{{\partial {\varDelta} u^{\prime}_{1} }}{\partial x}} & {\frac{{\partial^{2} {\varDelta} u^{\prime}_{3} }}{{\partial x^{2} }}} & {\frac{{\partial^{2} {\varDelta} u^{\prime}_{2} }}{{\partial x^{2} }}} & {\frac{{\partial {\varDelta} \theta^{\prime}_{1} }}{\partial x}} \\ \end{array} } \right\}^{{\text{T}}} , \hfill \\ {\mathbf{{\varDelta} \varepsilon }}_{N}& = \left\{ {\begin{array}{*{20}c} {\frac{1}{2}\left( {\frac{{\partial {\varDelta} u^{\prime}_{1} }}{\partial x}} \right)^{2} + \frac{1}{2}\left( {\frac{{\partial {\varDelta} u^{\prime}_{2} }}{\partial x}} \right)^{2} + \frac{1}{2}\left( {\frac{{\partial {\varDelta} u^{\prime}_{3} }}{\partial x}} \right)^{2} } & 0 & 0 & 0 \\ \end{array} } \right\}^{{\text{T}}} . \hfill \\ \end{aligned}$$

(10)

The corresponding generalized stress increment can be expressed as

$${\mathbf{{\varDelta} S}}_{{{\text{PD}}}} = \left\{ {\begin{array}{*{20}c} {{\varDelta} F_{x}^{{{\text{PD}}}} } & {{\varDelta} M_{y}^{{{\text{PD}}}} } & {{\varDelta} M_{z}^{{{\text{PD}}}} } & {{\varDelta}T_{x}^{{{\text{PD}}}} } \\ \end{array} } \right\}^{{\text{T}}} = {\mathbf{D}}_{{{\text{PD}}}} {\mathbf{{\varDelta} \varepsilon }},$$

(11)

where ${\varDelta} F_{x}^{{{\text{PD}}}}$, ${\varDelta} M_{y}^{{{\text{PD}}}}$, ${\varDelta} M_{z}^{{{\text{PD}}}}$, and ${\varDelta} T_{x}^{{{\text{PD}}}}$ are the axial stress, bending moment in the y-axis and z-axis directions, and torque increment per element length of the microbeam key, respectively.

In CCM theory, according to the incremental virtual work equation, the increase of virtual strain energy density in a small incremental step is

$$\begin{aligned} {\varDelta} W_{{{\text{CCM}}}}^{L} \left( {x_{i} } \right)& = \frac{1}{t}\delta \left( {{\mathbf{{\varDelta} E}}_{L}^{{\text{T}}} } \right){\mathbf{D}}\left( {{\mathbf{{\varDelta} E}}_{L} } \right), \hfill \\ {\varDelta} W_{{{\text{CCM}}}}^{R} \left( {x_{i} } \right)& = \frac{1}{t}\delta \left( {{\mathbf{{\varDelta} E}}_{L}^{{\text{T}}} } \right){\mathbf{S}} = \frac{1}{t}\delta \left( {{\mathbf{{\varDelta} E}}_{L}^{{\text{T}}} } \right)\sum\limits_{k = 0}^{n} {{\mathbf{D}}\left( {{\mathbf{{\varDelta} E}}} \right)_{k} } , \hfill \\ {\varDelta} W_{{{\text{CCM}}}}^{S} \left( {x_{i} } \right) &= \frac{1}{t}\delta \left( {{\mathbf{{\varDelta} E}}_{N}^{{\text{T}}} } \right){\mathbf{S}} = \frac{1}{t}\delta \left( {{\mathbf{{\varDelta} E}}_{N}^{{\text{T}}} } \right)\sum\limits_{k = 0}^{n} {{\mathbf{D}}\left( {{\mathbf{{\varDelta} E}}} \right)_{k} } , \hfill \\ {\varDelta} W_{{{\text{CCM}}}}^{N} \left( {x_{i} } \right) &= \frac{1}{t}\left\{ \begin{gathered} \delta \left( {{\mathbf{{\varDelta} E}}_{L}^{{\text{T}}} } \right){\mathbf{D}}\left( {{\mathbf{{\varDelta} E}}_{N} } \right) + \delta \left( {{\mathbf{{\varDelta} E}}_{N}^{{\text{T}}} } \right){\mathbf{D}}\left( {{\mathbf{{\varDelta} E}}_{L} } \right) \hfill \\ + \delta \left( {{\mathbf{{\varDelta} E}}_{N}^{{\text{T}}} } \right){\mathbf{D}}\left( {{\mathbf{{\varDelta} E}}_{N} } \right) \hfill \\ \end{gathered} \right\}. \hfill \\ \end{aligned}$$

(12)

where $t$ represents the element thickness.

Similarly, in the framework of PD theory, the increase of virtual strain energy density in the same incremental step is

$$\begin{aligned} {\varDelta} W_{{{\text{PD}}}}^{L} \left( {x_{i} } \right)& = \frac{t}{2}\delta \left( {{\mathbf{{\varDelta} \varepsilon }}_{L}^{{\text{T}}} } \right){\mathbf{D}}_{{{\text{PD}}}} \left( {{\mathbf{{\varDelta}\varepsilon }}_{L} } \right)\int_{0}^{2\pi } {\int_{0}^{\delta } {\int_{0}^{1} {\xi^{2} {\text{d}}\chi {\text{d}}\xi {\text{d}}\alpha } } } , \hfill \\ {\varDelta} W_{{{\text{PD}}}}^{R} \left( {x_{i} } \right)& = \frac{t}{2}\delta \left( {{\mathbf{{\varDelta} \varepsilon }}_{L}^{{\text{T}}} } \right)\sum\limits_{k = 0}^{n} {{\mathbf{D}}_{{{\text{PD}}}} \left( {{\mathbf{{\varDelta} \varepsilon }}} \right)_{k} } \int_{0}^{2\pi } {\int_{0}^{\delta } {\int_{0}^{1} {\xi^{2} {\text{d}}\chi {\text{d}}\xi {\text{d}}\alpha } } } , \hfill \\ {\varDelta}W_{{{\text{PD}}}}^{S} \left( {x_{i} } \right) &= \frac{t}{2}\delta \left( {{\mathbf{{\varDelta} \varepsilon }}_{N}^{{\text{T}}} } \right)\sum\limits_{k = 0}^{n} {{\mathbf{D}}_{{{\text{PD}}}} \left( {{\mathbf{{\varDelta} \varepsilon }}} \right)_{k} } \int_{0}^{2\pi } {\int_{0}^{\delta } {\int_{0}^{1} {\xi^{2} {\text{d}}\chi {\text{d}}\xi {\text{d}}\alpha } } } , \hfill \\ {\varDelta} W_{{{\text{PD}}}}^{N} \left( {x_{i} } \right) &= \frac{t}{2}\left\{ {\begin{array}{*{20}c} {\delta \left( {{\mathbf{{\varDelta} \varepsilon }}_{L}^{{\text{T}}} } \right){\mathbf{D}}_{{{\text{PD}}}} \left( {{\mathbf{{\varDelta} \varepsilon }}_{N} } \right) + } \\ {\delta \left( {{\mathbf{{\varDelta}\varepsilon }}_{N}^{{\text{T}}} } \right){\mathbf{D}}_{{{\text{PD}}}} \left( {{\mathbf{{\varDelta} \varepsilon }}_{L} } \right) + } \\ {\delta \left( {{\mathbf{{\varDelta} \varepsilon }}_{N}^{{\text{T}}} } \right){\mathbf{D}}_{{{\text{PD}}}} \left( {{\mathbf{{\varDelta} \varepsilon }}_{N} } \right)} \\ \end{array} } \right\}\int_{0}^{2\pi } {\int_{0}^{\delta } {\int_{0}^{1} {\xi^{2} {\text{d}}\chi {\text{d}}\xi {\text{d}}\alpha } } } . \hfill \\ \end{aligned}$$

(13)

The factor of ½ in Eq. 13 can be attributed to the fact that each bond endpoint of a bond “owns” only half the energy in the bond [15].

The generalized strain increment transformation matrix ${\mathbf{T}}_{\xi }$ of microbeam keys and nonlinear shell elements is

$${\mathbf{{\varDelta} \varepsilon }} = {\mathbf{T}}_{\xi } {\mathbf{{\varDelta} E}},$$

(14)

where

$$ \begin{gathered} {\mathbf{T}}_{\xi } = \left[ \begin{gathered} {\text{ }}{\mathbf{{T}}_{p1}}\,\,\,\,\,{\text{ }}{\mathbf{0}} \hfill \\ {\text{ }}{\mathbf{0}}{\text{ }}\,\,\,{\text{ }}\,\,\,\,{\mathbf{{T}}_{b1}} \hfill \\ {\text{ }}{\mathbf{{T}}_{p1}}{\text{ }}\,\,\,{\text{ }}\,{\mathbf{0}} \hfill \\ {\text{ }}{\mathbf{0}}{\text{ }}\,\,\,{\text{ }}\,\,\,{\mathbf{{T}}_{b2}} \hfill \\ \end{gathered} \right]. \hfill \\ {\mathbf{{T}}_{p1}} = \left[ {{\text{ }}\left( {\cos \alpha } \right)^{2} {\text{ }}\left( {\sin \alpha } \right)^{2} {\text{ }}\sin \alpha \cos \alpha {\text{ }}} \right] \hfill \\ {\mathbf{{T}}_{b1}} = \left[ {{\text{ }}\left( {\cos \alpha } \right)^{2} {\text{ }}\left( {\sin \alpha } \right)^{2} {\text{ }}\sin \alpha \cos \alpha {\text{ }}} \right] \hfill \\ {\mathbf{{T}}_{p2}} = \frac{{6\left( {1 - 2\chi } \right)}}{\xi }\left[ {{\text{ }} - \sin \alpha \cos \alpha {\text{ }}\sin \alpha \cos \alpha {\text{ }}\left( {\cos \alpha } \right)^{2} - \frac{1}{2}{\text{ }}} \right] \hfill \\ {\mathbf{{T}}_{b2}} = \left[ {{\text{ }} - \sin \alpha \cos \alpha {\text{ }}\sin \alpha \cos \alpha {\text{ }}\left( {\cos \alpha } \right)^{2} - \frac{1}{2}{\text{ }}} \right] \hfill \\ \end{gathered} $$

(15)

where χ is the shape parameter, and α represents the angle between the coordinate system of microbeam keys and that of elements.

Let the virtual strain energy density increment under the PD theory in Eq. (13) be equal to that under the CCM theory in Eq. (12), and the PD micromodulus parameter can be obtained as follows:

$$\begin{aligned} c_{ax} = \frac{6E}{{\pi t\delta^{3} \left( {1 - v} \right)}},\,\,c_{by} = \frac{Et}{{2\pi \delta^{3} \left( {1 - v} \right)}},\,\,c_{bz} = \frac{{E\left( {1 - 3v} \right)}}{{6\pi t\delta \left( {1 - v^{2} } \right)}},\,\,c_{tor} = \frac{{Et\left( {1 - 3v} \right)}}{{2\pi \delta^{3} \left( {1 - v^{2} } \right)}}.\end{aligned}$$

(16)

The adaptive mesh refinement method dynamically adjusts the mesh size based on the solution accuracy requirements, resulting in fewer mesh elements and saving computational resources. This is particularly crucial for large-scale computing problems as it significantly reduces computation time and memory requirements, thereby improving both computational efficiency and solution accuracy [16]. By coupling the flexible meshless method with PD, the proposed method effectively handles non-local effects in complex geometries, large deformations, or dynamic boundary conditions [17]. Lubinea introduced a deformation strategy that combines non-local theory with local continuous medium mechanics to ensure both accuracy and computational efficiency [18]. In this study, we adopt Lubineau’s coupling strategy due to its relative simplicity of implementation while also planning to explore other methods in future research.

As shown in Fig. 2, the PD-CCM coupling model is composed of three subdomains: the pure CCM model $\Omega 1$, the pure PD model $\Omega 2$, and the coupling domain $\Omega m$.

Fig. 2

Coupling model of the PD-CCM shell and coupling scalar function

For any node ${\text{x}}_{i}$ on the shell neutral layer, the virtual strain energy density increment at node ${\text{x}}_{i}$ when it is located in the pure CCM model domain $\Omega_{1}$ is

$$\begin{aligned} {\varDelta}W_{{{\text{CCM}}}} ({\text{x}}_{i} ) &= \frac{1}{2}\delta \left( {{\mathbf{{\varDelta} E}}^{{\text{T}}} } \right){\mathbf{D}}\left( {{\mathbf{{\varDelta} E}}} \right) \\ &= {\varDelta} W_{{{\text{CCM}}}}^{L} ({\text{x}}_{i} ) + {\varDelta} W_{{{\text{CCM}}}}^{R} ({\text{x}}_{i} ) + {\varDelta} W_{{{\text{CCM}}}}^{S} ({\text{x}}_{i} ) + {\varDelta} W_{{{\text{CCM}}}}^{N} ({\text{x}}_{i} ). \\ \end{aligned}$$

(17)

The virtual strain energy density increment at node ${\text{x}}_{i}$ when it is located in the pure PD model domain $\Omega 2$ is

$$\begin{aligned} {\varDelta} W_{{{\text{PD}}}} \left( {{\text{x}}_{i} } \right) &= \frac{t}{4}\int_{{\hbar \left( {{\text{x}}_{i} } \right)}} {\int_{{{\text{x}}_{i} }}^{{{\text{x}}_{j} }} {\delta \left( {{\mathbf{{\varDelta} \varepsilon }}^{{\text{T}}} } \right)} } {\mathbf{D}}_{PD} \left( {{\mathbf{{\varDelta} \varepsilon }}} \right){\text{d}}x{\text{d}}V_{{{\text{x}}_{j} }} \\ &= {\varDelta} W_{{{\text{PD}}}}^{L} ({\text{x}}_{i} ) + {\varDelta} W_{{{\text{PD}}}}^{R} ({\text{x}}_{i} ) + {\varDelta} W_{{{\text{PD}}}}^{S} ({\text{x}}_{i} ) + {\varDelta} W_{{{\text{PD}}}}^{N} ({\text{x}}_{i} ). \\ \end{aligned}$$

(18)

The virtual strain energy density increment at node ${\text{x}}_{i}$ when it is located in the coupling domain $\Omega m$ is

$$\begin{aligned} {\varDelta} W_{{{\text{Hb}}}} \left( {{\text{x}}_{i} } \right)&= \frac{1}{2}\delta \left( {{\mathbf{{\varDelta} E}}^{{\text{T}}} } \right){\mathbf{D}}_{{{\text{Hb}}}} \left( {{\mathbf{{\varDelta} E}}} \right) + \frac{t}{4}\int_{{\hbar \left( {{\text{x}}_{i} } \right)}} {\int_{{{\text{x}}_{i} }}^{{{\text{x}}_{j} }} {\alpha \left( x \right)\delta \left( {{\mathbf{{\varDelta} \varepsilon }}^{{\text{T}}} } \right)} } {\mathbf{D}}_{{{\text{PD}}}} \left( {{\mathbf{{\varDelta} \varepsilon }}} \right){\text{d}}x{\text{d}}V_{{{\text{x}}_{j} }}& \\&= {\varDelta} W_{{{\text{Hb}}}}^{L} \left( {{\text{x}}_{i} } \right) +{\varDelta} W_{{{\text{Hb}}}}^{R} \left( {{\text{x}}_{i} } \right) + {\varDelta} W_{{{\text{Hb}}}}^{S} \left( {{\text{x}}_{i} } \right) + {\varDelta} W_{{{\text{Hb}}}}^{N} \left( {{\text{x}}_{i} } \right).& \\ \end{aligned}$$

(19)

where $\alpha \left( x \right)$ is the coupling scalar function, and ${\varDelta} W_{{{\text{Hb}}}}^{L} \left( {{\text{x}}_{i} } \right)$, ${\varDelta} W_{{{\text{Hb}}}}^{R} \left( {{\text{x}}_{i} } \right)$, ${\varDelta} W_{{{\text{Hb}}}}^{S} \left( {{\text{x}}_{i} } \right)$, and ${\varDelta} W_{{{\text{Hb}}}}^{N} \left( {{\text{x}}_{i} } \right)$ are respectively represented as

$$\begin{aligned}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, {\varDelta} W_{{{\text{Hb}}}}^{L} \left( {{\text{x}}_{i} } \right) =& \frac{1}{t}\delta \left( {{\mathbf{{\varDelta} E}}_{L}^{{\text{T}}} } \right){\mathbf{D}}_{{{\text{Hb}}}} \left( {{\mathbf{{\varDelta} E}}_{L} } \right) + \int_{{\hbar \left( {{\text{x}}_{i} } \right)}} {\frac{1}{2}\int_{{{\text{x}}_{i} }}^{{{\text{x}}_{j} }} {\alpha \left( x \right)\delta \left( {{\mathbf{{\varDelta} \varepsilon }}_{L}^{{\text{T}}} } \right)} {\mathbf{D}}_{{{\text{PD}}}} \left( {{\mathbf{{\varDelta} \varepsilon }}_{L} } \right){\text{d}}x{\text{d}}V_{{{\text{x}}_{j} }} } , \\ {\varDelta} W_{{{\text{Hb}}}}^{R} \left( {{\text{x}}_{i} } \right) =& \frac{1}{t}\delta \left( {{\mathbf{{\varDelta} E}}_{L}^{{\text{T}}} } \right)\sum\limits_{k = 0}^{n} {{\mathbf{D}}_{{{\text{Hb}}}} \left( {{\mathbf{{\varDelta} E}}} \right)_{k} } + \int_{{\hbar \left( {{\text{x}}_{i} } \right)}} {\frac{1}{2}\int_{{{\text{x}}_{i} }}^{{{\text{x}}_{j} }} {\alpha \left( x \right)\delta \left( {{\mathbf{{\varDelta} \varepsilon }}_{L}^{{\text{T}}} } \right){\mathbf{D}}_{{{\text{PD}}}} \sum\limits_{k = 0}^{n} {\left( {{\mathbf{{\varDelta} \varepsilon }}} \right)_{k} {\text{d}}x{\text{d}}V_{{{\text{x}}_{j} }} } } } , \\ {\varDelta} W_{{{\text{Hb}}}}^{S} \left( {{\text{x}}_{i} } \right) =& \frac{1}{t}\delta \left( {{\mathbf{{\varDelta} E}}_{N}^{{\text{T}}} } \right)\sum\limits_{k = 0}^{n} {{\mathbf{D}}_{{{\text{Hb}}}} \left( {{\mathbf{{\varDelta} E}}} \right)_{k} } + \int_{{\hbar \left( {{\text{x}}_{i} } \right)}} {\frac{1}{2}\int_{{{\text{x}}_{i} }}^{{{\text{x}}_{j} }} {\alpha \left( x \right)\delta \left( {{\mathbf{{\varDelta} \varepsilon }}_{N}^{{\text{T}}} } \right){\mathbf{D}}_{{{\text{PD}}}} \sum\limits_{k = 0}^{n} {\left( {{\mathbf{{\varDelta} \varepsilon }}} \right)_{k} } } {\text{d}}x{\text{d}}V_{{{\text{x}}_{j} }} } , \\ {\varDelta} W_{{{\text{Hb}}}}^{N} \left( {{\text{x}}_{i} } \right) =& \frac{1}{t}\left[ \begin{gathered} \delta \left( {{\mathbf{{\varDelta} E}}_{L}^{{\text{T}}} } \right){\mathbf{D}}_{{{\text{Hb}}}} \left( {{\mathbf{{\varDelta}E}}_{N} } \right) + \hfill \\ \delta \left( {{\mathbf{{\varDelta} E}}_{N}^{{\text{T}}} } \right){\mathbf{D}}_{{{\text{Hb}}}} \left( {{\mathbf{{\varDelta}E}}_{L} } \right) + \hfill \\ \delta \left( {{\mathbf{{\varDelta} E}}_{N}^{{\text{T}}} } \right){\mathbf{D}}_{{{\text{Hb}}}} \left( {{\mathbf{{\varDelta} E}}_{N} } \right) \hfill \\ \end{gathered} \right] + \int_{{\hbar \left( {{\text{x}}_{i} } \right)}} {\frac{1}{2}\int_{{{\text{x}}_{i} }}^{{{\text{x}}_{j} }} {\alpha \left( x \right)\left[ \begin{gathered} \delta \left( {{\mathbf{{\varDelta} \varepsilon }}_{L}^{{\text{T}}} } \right){\mathbf{D}}_{{{\text{PD}}}} \left( {{\mathbf{{\varDelta} \varepsilon }}_{N} } \right) + \hfill \\ \delta \left( {{\mathbf{{\varDelta} \varepsilon }}_{N}^{{\text{T}}} } \right){\mathbf{D}}_{{{\text{PD}}}} \left( {{\mathbf{{\varDelta} \varepsilon }}_{L} } \right) + \hfill \\ \delta \left( {{\mathbf{{\varDelta} \varepsilon }}_{N}^{{\text{T}}} } \right){\mathbf{D}}_{{{\text{PD}}}} \left( {{\mathbf{{\varDelta} \varepsilon }}_{N} } \right) \hfill \\ \end{gathered} \right]{\text{d}}} x{\text{d}}} V_{{{\text{x}}_{j} }} . \\ \end{aligned}$$

(20)

Due to the equality of the virtual strain energy density increment at node ${\text{x}}_{i}$,

$${\varDelta} W_{{{\text{CCM}}}} ({\text{x}}_{i} ) = {\varDelta}W_{{{\text{PD}}}} \left( {{\text{x}}_{i} } \right) = {\varDelta} W_{{{\text{Hb}}}} \left( {{\text{x}}_{i} } \right).$$

(21)

Substituting Eq. (12) into Eq. (17), and then substituting Eqs. (17) and (20) into Eq. (21),

$${\mathbf{D}}_{{{\text{Hb}}}} = {\mathbf{D}} - \frac{t}{2}\int_{{\hbar \left( {{\text{x}}_{i} } \right)}} {\int_{{{\text{x}}_{i} }}^{{{\text{x}}_{j} }} {\alpha \left( x \right){\mathbf{T}}_{\xi }^{{\text{T}}} {\mathbf{D}}_{{{\text{PD}}}} {\mathbf{T}}_{\xi } } {\text{d}}} x{\text{d}}V_{{{\text{x}}_{j} }} .$$

(22)

Considering the coupling function $\alpha \left( x \right)$ as a linear scalar function, Eq. (22) can be simplified as

$${\mathbf{D}}_{{{\text{Hb}}}} = {\mathbf{D}} - \frac{t}{2}\int_{{\hbar \left( {{\text{x}}_{i} } \right)}} {\xi \frac{{\alpha \left( {{\text{x}}_{i} } \right) + \alpha \left( {{\text{x}}_{j} } \right)}}{2}} {\mathbf{T}}_{\xi }^{{\text{T}}} {\mathbf{D}}_{{{\text{PD}}}} {\mathbf{T}}_{\xi } {\text{d}}V_{{{\text{x}}_{j} }} .$$

(23)

For the coupling domain $\Omega m$, the material parameters for different regions can be obtained according to the principle of strain energy density conservation. With the material parameters delineated for various regions, the stiffness matrix and structural reaction vector of different regions can be derived. Subsequently, the stiffness matrix and structural reaction vector of the entire structure can be determined. Finally, the global equilibrium equation for each incremental step can be systematically established.

In this study, the fracture criterion based on the idea of strain energy is used to simulate the damage and fracture of shell structures. As shown in Fig. 3, in the 2D case, the fracture energy can be determined by the energy released by all bonds on the fracture surface of the element fracture. The integral equation of the fracture energy $G_{c}$ under the 2D condition can then be defined as

$$G_{c} = 2t\sum\limits_{k = 1}^{n} {\int_{0}^{\delta } {\int_{z}^{\delta } {\int_{0}^{{\cos^{ - 1}\,\, \left( {{z \mathord{\left/ {\vphantom {z \xi }} \right. \kern-0pt} \xi }} \right)}} {{\varDelta} \omega_{c} \xi } {\text{d}}\varphi } {\text{d}}\xi } {\text{d}}z} .$$

(24)

where $t$ is the thickness of the shell,$\Delta \omega_{c}$ is the critical micropotential energy of each microbeam bond in each incremental step, expressed as

$${\varDelta} \omega_{c} = \frac{1}{2}\int_{{x_{i} }}^{{x_{j} }} {{\mathbf{{\varDelta} \varepsilon }}^{{\text{T}}} {\mathbf{D}}_{{{\text{PD}}}} {\mathbf{{\varDelta} \varepsilon }}{\text{d}}x} + \int_{{x_{i} }}^{{x_{j} }} {{\mathbf{{\varDelta} \varepsilon }}^{{\text{T}}} {\mathbf{S}}_{{{\text{PD}}}} {\text{d}}x} ,$$

(25)

Fig. 3

Schematic diagram of the fracture surface

Assuming that uniform deformation occurs in the PD domain of node ${\text{x}}_{i}$, then (25) can be simplified as

$${\varDelta} \omega_{c} = \frac{1}{2}{\mathbf{{\varDelta} \varepsilon }}^{{\text{T}}} {\mathbf{D}}_{{{\text{PD}}}} {\mathbf{{\varDelta} \varepsilon }}\xi + {\mathbf{{\varDelta} \varepsilon }}^{{\text{T}}} {\mathbf{S}}_{{{\text{PD}}}} \xi .$$

(26)

By substituting Eq. (26) into the fracture energy integral Eq. (24), the following can be obtained:

$$G_{c} = \frac{{t\delta^{4} }}{2}\sum\limits_{k = 1}^{n} {\left( {\frac{1}{2}{\mathbf{{\varDelta} \varepsilon }}^{{\text{T}}} {\mathbf{D}}_{{{\text{PD}}}} {\mathbf{{\varDelta} \varepsilon }} + {\mathbf{{\varDelta} \varepsilon }}^{{\text{T}}} {\mathbf{S}}_{{{\text{PD}}}} } \right)} .$$

(27)

Finally, the energy fracture criterion of microbeam bonds [19] can be expressed as

$$\omega_{{{\text{bond}}}} = \sum\limits_{k = 1}^{n} {\left( {\frac{1}{2}{\mathbf{{\varDelta} \varepsilon }}^{{\text{T}}} {\mathbf{D}}_{{{\text{PD}}}} {\mathbf{{\varDelta} \varepsilon }} + {\mathbf{{\varDelta} \varepsilon }}^{{\text{T}}} {\mathbf{S}}_{{{\text{PD}}}} } \right) = \frac{{2G_{c} }}{{t\delta^{4} }}} .$$

(28)

The motion equation of node x can be formulated within the framework of PD theory

$$\rho ({\mathbf{x}}_{i} ){\mathbf{\ddot{u}}}({\mathbf{x}}_{i} ,t) = \int_{{H_{{{\mathbf{x}}_{i} }} }} {[{\mathbf{f}}_{ij} - {\mathbf{f}}_{ji} ]} {\text{d}}V_{{{\mathbf{x}}_{j} }} + {\mathbf{b}}({\mathbf{x}}_{i} ,t),$$

(29)

where $\rho ({\mathbf{x}}_{i} )$ represents the mass density at node ${\mathbf{x}}_{i}$,${\mathbf{\ddot{u}}}({\mathbf{x}}_{i} ,t)$ denotes the acceleration vector at node ${\mathbf{x}}$ during time $t$,$H_{{{\mathbf{x}}_{i} }}$ denotes the neighborhood of node ${\mathbf{x}}_{i}$, which refers to the set comprising all nodes that interact with it.${\mathbf{f}}_{ij}$ and ${\mathbf{f}}_{ji}$ are force density functions governing node interactions dependent on relative displacement and position,${\text{d}}V_{{{\mathbf{x}}_{j} }}$ is the volume integral over all nodes in the neighborhood, and ${\mathbf{b}}({\mathbf{x}}_{i} ,t)$ refers to external force density acting upon node ${\mathbf{x}}_{i}$.

The volume $V_{{{\mathbf{x}}_{i} }}$ of material node ${\mathbf{x}}_{i}$ is multiplied on both sides of Eq. (29),

$${\mathbf{m}}({\mathbf{x}}_{i} ){\mathbf{\ddot{u}}}({\mathbf{x}}_{i} ,t) = {\mathbf{p}}({\mathbf{x}}_{i} ,t) - {\mathbf{r}}({\mathbf{x}}_{i} ,t),$$

(30)

where ${\mathbf{m}}({\mathbf{x}}_{i} )$ is the mass matrix of the material node,${\mathbf{p}}({\mathbf{x}}_{i} ,t)$ and ${\mathbf{r}}({\mathbf{x}}_{i} ,t)$ are the external force and internal force vectors of the material node ${\mathbf{x}}_{i}$ respectively, and there is

$$\begin{aligned} {\mathbf{p}}({\mathbf{x}}_{i} ,t) &= V_{{{\mathbf{x}}_{i} }} {\mathbf{b}}({\mathbf{x}}_{i} ,t), \\ {\mathbf{r}}({\mathbf{x}}_{i} ,t) &= - V_{{{\mathbf{x}}_{i} }} \int_{{H_{{{\mathbf{x}}_{i} }} }} {[{\mathbf{f}}_{ij} - {\mathbf{f}}_{ji} ]} {\text{d}}V_{{{\mathbf{x}}_{j} }} . \\ \end{aligned}$$

(31)

The overall equation of motion for the object can be derived by aggregating the equations of motion for all constituent particles.

$${\mathbf{M\ddot{u}}}(t) = {\mathbf{P}}(t) - {\mathbf{R}}(t),$$

(32)

where ${\mathbf{M}}$ is the overall mass matrix of all material nodes,${\mathbf{\ddot{u}}}(t)$ is the overall acceleration vector of all material nodes at time $t$,${\mathbf{P}}(t)$ and ${\mathbf{R}}(t)$ are the overall external force and internal force vectors at time $t$, respectively.

To solve the total motion Eq. (32) of the object, the time course is discretized into multiple discrete time points, as depicted in Fig. 4. Each pair of consecutive time points is separated by a specific time step, where $t - {\varDelta}t_{n - 1}$,$t$, and $t + {\varDelta}t$ correspond to times $n - 1$,$n$, and $n + 1$, respectively. The time step from $n - 1$ to $n$ is denoted as ${\varDelta}t_{n - 1}$ and referred to as the ‘$n - 1$’ incremental step; similarly, the time step from $n$ to $n + 1$ is denoted as ${\varDelta}t_{n}$ and termed the ‘$n$’ incremental step.

Fig. 4

Time node after discretization

For the static calculation example presented in this paper, we have employed the implicit solving algorithm. By substituting ${\mathbf{\ddot{u}}}(t) = {\mathbf{0}}$ into Eq. (32), we obtain the discretized equation.

$${\mathbf{P}}_{n} - {\mathbf{R}}_{n} = {\mathbf{0}}.$$

(33)

The incremental method, similar to the traditional FEM, is employed for solving the aforementioned nonlinear equation group. The equilibrium equation of the $n^{th}$ incremental step can be derived as follows:

$$\begin{aligned} {\mathbf{K{\varDelta} u}}_{n}& = {\mathbf{P}}_{n + 1} - {\mathbf{R}}_{n} \\ {\mathbf{K}} &= \sum\limits_{e = 1}^{m} {\left( {{\mathbf{A}}^{e} } \right)^{{\text{T}}} } \left( {{\mathbf{T}}^{e} } \right)^{{\text{T}}} ({\mathbf{K}}_{L} + {\mathbf{K}}_{S} + {\mathbf{K}}_{N} ){\mathbf{T}}^{e} {\mathbf{A}}^{e} \\ \end{aligned}$$

(34)

where ${\mathbf{K}}_{L}$,${\mathbf{K}}_{S}$, and ${\mathbf{K}}_{N}$ are respectively derived from the linear stiffness matrix, initial stress matrix, and nonlinear stiffness matrix for the three zones; $m$ represents the total number of elements; ${\mathbf{T}}^{e}$ denotes the conversion matrix between the local coordinate system and global coordinate system of each plate element; and ${\mathbf{A}}^{e}$ is the element selection matrix composed of 0 s and 1 s for efficient mapping of global displacement to element displacement.

The linearization method is commonly employed for iterative solutions of the aforementioned nonlinear equations. In this study, we adopt an incremental iteration approach to achieve linearization solving. Specifically, during each small incremental step, the linearization process can be effectively accomplished by disregarding the influence of geometric nonlinear matrix.

$${\mathbf{K}}_{N} = {\mathbf{0}}$$

(35)

The large displacement stiffness matrix ${\mathbf{K}}_{N}$ should be excluded when solving the nonlinear system (34).

The iterative method is employed to solve (34), which can be expressed in the form of iteration as follows:

$${\mathbf{K}}_{n}^{k} {\mathbf{{\varDelta} \overline{u}}}_{n}^{k} = {\mathbf{P}}_{n}^{k} - {\mathbf{R}}_{n}^{k}$$

(36)

where superscript $k$ denotes the kth iteration step in the current incremental step, and ${\mathbf{{\varDelta} \overline{u}}}_{n}^{k}$ denotes the incremental displacement of the kth iteration step in the current incremental step. If the increment of external force in the nth incremental step is ${\varDelta} {\mathbf{P}}_{n}$ and remains unchanged in the iteration solution of the incremental step, then:

$${\mathbf{P}}_{n}^{k} = {\mathbf{P}}_{n + 1} = {\mathbf{P}}_{n} + {\mathbf{{\varDelta} P}}_{n}$$

(37)

When the nth incremental step starts to iterate, the initial value is defined as

$${\mathbf{S}}_{0} {\mathbf{ = 0,}}\;{\mathbf{{\varDelta} S}}_{n} {\mathbf{ = 0,}}\;{\mathbf{{\varDelta} u}}_{n}^{0} {\mathbf{ = 0,}}\;{\mathbf{S}}_{n}^{0} {\mathbf{ = S}}_{n} {\mathbf{,}}\;{\mathbf{P}}_{n}^{0} {\mathbf{ = P}}_{n + 1} {\mathbf{,}}\;{\mathbf{R}}_{n}^{0} {\mathbf{ = R}}_{n} .$$

(38)

The structural reaction vector, linear stiffness matrix and initial stress matrix after $k$ iterations are as follows:

$$ \begin{gathered} ({\mathbf{R}})_{n}^{k} = \sum\limits_{e = 1}^{m} {\left( {{\mathbf{A}}^{e} } \right)^{{\text{T}}} } \left( {{\mathbf{T}}^{e} } \right)^{{\text{T}}} \left( {\int_{a} {{\mathbf{B}}_{L}^{T} } {\mathbf{S}}_{n}^{k - 1} {\text{d}}a} \right)^{e} {\mathbf{A}}^{e} , \hfill \\ ({\mathbf{K}}_{L} )_{n}^{k} = \sum\limits_{e = 1}^{m} {\left( {{\mathbf{A}}^{e} } \right)^{{\text{T}}} } \left( {{\mathbf{T}}^{e} } \right)^{{\text{T}}} \left( {\int_{a} {{\mathbf{B}}_{L}^{T} {\mathbf{D}}} {\mathbf{B}}_{L} {\text{d}}a} \right)^{e} {\mathbf{T}}^{e} {\mathbf{A}}^{e} , \hfill \\ ({\mathbf{K}}_{S} )_{n}^{k} = \sum\limits_{e = 1}^{m} {\left( {{\mathbf{A}}^{e} } \right)^{{\text{T}}} } \left( {{\mathbf{T}}^{e} } \right)^{{\text{T}}} \left( {\int_{a} {{\mathbf{G}}^{T} {\mathbf{Q}}_{n}^{k - 1} } {\mathbf{G}}{\text{d}}a} \right)^{e} {\mathbf{T}}^{e} {\mathbf{A}}^{e} . \hfill \\ \end{gathered} $$

(39)

where ${\mathbf{B}}_{L}$ is the shape matrix, describing the relationship between ${\mathbf{{\varDelta} \varepsilon }}_{L}$ and ${\mathbf{{\varDelta} \overline{u}}}_{n}^{k}$,${\mathbf{D}}$ is the material parameter matrix,$a$ is the element area,${\mathbf{Q}}n$ is the stress-related matrix, and ${\mathbf{G}}$ is the shape matrix related to nonlinear terms.

By substituting Eqs. (37) and (39) into Eq. (36), the incremental displacement can be determined at the current iteration step:

$$\begin{aligned} {\mathbf{{\varDelta} \overline{u}}}_{n}^{k} &= \left( {{\mathbf{K}}_{n}^{k} } \right)^{ - 1} ({\mathbf{P}}_{n}^{k} - {\mathbf{R}}_{n}^{k} ) \hfill \\ {\mathbf{{\varDelta} u}}_{n}^{k}& = {\mathbf{{\varDelta} u}}_{n}^{k - 1} + {\mathbf{{\varDelta} \overline{u}}}_{n}^{k} \hfill \\ \end{aligned}$$

(40)

The increments of generalized strain and generalized stress at any position within the element are as follows:

$$\begin{aligned} {\mathbf{{\varDelta} E}}_{n}^{k}& = ({\mathbf{B}}_{L} + {\mathbf{B}}_{N} )({\mathbf{{\varDelta} u}}_{n}^{k} )^{e} \hfill \\ {\mathbf{{\varDelta} S}}_{n}^{k} &= {\mathbf{D{\varDelta} E}}_{n}^{k} \hfill \\ \end{aligned}$$

(41)

According to the linearization assumption in the incremental step, the kth iteration step allows for accumulation of generalized stress through implementation of the co-rotation method [20]

$${\mathbf{S}}_{n}^{k} = {\mathbf{S}}_{n}^{0} + {\mathbf{{\varDelta} S}}_{n}^{k}$$

(42)

According to the results of displacement and stress, assess the convergence. If not achieved, substitute Eq. (42) into Eq. (39) and continue iterative calculation using Eq. (40) until convergence is reached. Once converged, update the displacement and stress values and proceed with calculating the next incremental step.

$$\begin{gathered} {\mathbf{u}}_{n + 1} = {\mathbf{u}}_{n} + {\mathbf{{\varDelta} u}}_{n} = {\mathbf{u}}_{n} + \sum\limits_{k = 0}^{l} {{\mathbf{{\varDelta} u}}_{n}^{k} } \hfill \\ {\mathbf{S}}_{n + 1} = {\mathbf{S}}_{n} + {\mathbf{{\varDelta} S}}_{n} = {\mathbf{S}}_{n} + \sum\limits_{k = 0}^{l} {{\mathbf{{\varDelta} S}}_{n}^{k} } \hfill \\ \end{gathered}$$

(43)

where $l$ is the number of convergence steps.

In this paper, we employ the explicit central difference method to calculate and solve the dynamic crack propagation problem. We perform time discretization of Eq. (31) and obtain the total motion equation as follows:

$${\mathbf{M\ddot{u}}}_{n} = {\mathbf{P}}_{n + 1} - {\mathbf{R}}_{n} ,$$

(44)

where $n$ represents the state at time $t$, and the states at other times are depicted in Fig. 4. The physical quantities before and at time $t$ are known. To streamline the derivation process, we set the time step as ${\varDelta} t_{n - 1} = {\varDelta} t_{n} = {\varDelta} t$ and express the velocity and acceleration in the difference scheme as follows:

$$\begin{gathered} {\dot{\mathbf{u}}}_{n} = \frac{{{\dot{\mathbf{u}}}_{{n + \tfrac{1}{2}}} + {\dot{\mathbf{u}}}_{{n - \tfrac{1}{2}}} }}{2}, \hfill \\ {\mathbf{\ddot{u}}}_{n} = \frac{{{\dot{\mathbf{u}}}_{{n + \tfrac{1}{2}}} - {\dot{\mathbf{u}}}_{{n - \tfrac{1}{2}}} }}{{\varDelta} t}. \hfill \\ \end{gathered}$$

(45)

Reformulate Eq. (44) by substituting Eq. (45), enabling the solution for

$${\dot{\mathbf{u}}}_{{n + \tfrac{1}{2}}} = {\dot{\mathbf{u}}}_{{n - \tfrac{1}{2}}} + {\mathbf{M}}^{ - 1} \left( {{\mathbf{P}}_{n + 1} - {\mathbf{R}}_{n} } \right){\varDelta} t,$$

(46)

the displacement at time $t + {\varDelta} t_{n}$ can be obtained

$${\mathbf{u}}_{n + 1} = {\mathbf{u}}_{n} + {\dot{\mathbf{u}}}_{{n + \tfrac{1}{2}}}{\varDelta} t,$$

(47)

the increment in displacement is as follows:

$${\mathbf{{\varDelta} u}}_{n} = {\mathbf{u}}_{n + 1} - {\mathbf{u}}_{n} = {\dot{\mathbf{u}}}_{{n + \tfrac{1}{2}}} {\varDelta} t.$$

(48)

By substituting Eq. (48) into Eq. (41) and performing a single calculation step, the desired result can be obtained

$$\begin{aligned} {\mathbf{{\varDelta} E}}_{n}^{{}}& = ({\mathbf{B}}_{L} + {\mathbf{B}}_{N} )({\mathbf{{\varDelta} u}}_{n}^{{}} )^{e} = ({\mathbf{B}}_{L} + {\mathbf{B}}_{N} ){\mathbf{A}}^{e} {\mathbf{{\varDelta} u}}_{n} , \hfill \\ {\mathbf{{\varDelta} S}}_{n}^{{}}& = {\mathbf{D{\varDelta} E}}_{n}^{{}} . \hfill \\ \end{aligned}$$

(49)

Subsequently, Eq. (42) is utilized to derive the accumulation value as follows:

$${\mathbf{S}}_{n + 1}^{{}} = {\mathbf{S}}_{n}^{{}} + {\mathbf{{\varDelta} S}}_{n}^{{}} ,$$

(50)

by substituting ${\mathbf{S}}_{n + 1}^{{}}$ into the first equation of Eq. (39), we can obtain the total structural reaction vector ${\mathbf{R}}_{n + 1}$ at the next moment, which can then be substituted into Eq. (46) for a new iteration round.

At the initial moment, i.e., when $n$ = 0, it is typically assumed that ${\mathbf{u}}_{0} = {\dot{\mathbf{u}}}_{0} = {\mathbf{0}}$, as depicted in Eq. (45).

$${\dot{\mathbf{u}}}_{{ - \tfrac{1}{2}}} = - {\dot{\mathbf{u}}}_{{\tfrac{1}{2}}} .$$

(51)

The substitution of Eq. (51) into Eq. (46) yields.

$${\dot{\mathbf{u}}}_{{\tfrac{1}{2}}} = \frac{{\varDelta} t}{2}{\mathbf{M}}^{ - 1} {\mathbf{P}}_{0} .$$

(52)

Thus,

$${\mathbf{u}}_{1} = {\dot{\mathbf{u}}}_{{\tfrac{1}{2}}} {\varDelta} t.$$

(53)

The subsequent moment, starting from $n \ge 1$, involves repeating the iterative steps (46) and (47). During this process, it is essential to continuously update the node displacement and broken key information. In case of a broken key, it should be removed and the internal force of the node recalculated until meeting the requirements of the iterative step.

3 Numerical implementation of PD algorithm in CUDA

In the CUDA programming model, the CPU assumes the role of the ‘host,’ while the GPU is referred to as the ‘device.’ The collaborative functioning between the host and device is orchestrated in a manner where primary execution responsibility lies with the host for application code. In scenarios involving computationally intensive tasks, these tasks are delegated by the host to the device [21]. Termed as ‘kernels,’ these tasks are concurrently executed by thousands of threads. These threads are organized into thread blocks, which further form a grid structure. This hierarchical arrangement enables CUDA to efficiently manage and schedule a large number of parallel threads.

In the PD theory, nodes and elements constitute the fundamental framework of the model, serving as essential entities for calculation and analysis. Nodes typically represent discrete particles within the material, while elements connect these nodes to establish a network for transmitting forces and information. A notable characteristic of this theoretical framework lies in the independence between data associated with nodes and elements. This independence is not only evident in their respective attributes (such as position, displacement, and force) but also manifests during their calculation process. Specifically, each node or element can operate autonomously without waiting for or relying on results from other components. Such an approach significantly reduces computational complexity and dependence while enhancing computational efficiency. Moreover, it endows the model with greater flexibility and reliability when addressing complex problems.

Leveraging this attribute, the algorithm assigns each thread to an individual element or node, thereby facilitating parallel acceleration through the GPU component of the CUDA architecture. Given that each thread can independently perform computations, a significant number of threads can be concurrently scheduled for execution on the GPU, resulting in efficient GPU acceleration. The numerical solutions are illustrated in Figs. 5 and 6.

Fig. 5

Flowchart of implicit solution

Fig. 6

Flowchart of the explicit solution

3.1 Data transmission optimization

The transfer of data poses a notable bottleneck in GPU parallel computing. To optimize this process, various methods, such as asynchronous transfer (e.g., cudamecpyAsync) and CUDA stream operations [22], have been implemented. However, these techniques do not completely eradicate the intrinsic challenge of multiple data transfers, and the optimization effectiveness may diminish as the iteration count grows excessively large.

When solving PD problems, it is crucial to regularly update the data generated by calculations. The iterative computation process involved in transferring all data back to the CPU is highly time-consuming. However, it is unnecessary to transfer all data; only the final results for write operations need to be transmitted. Therefore, a highly efficient strategy entails performing computations on the GPU side and transmitting solely the final results to the CPU. This approach significantly reduces data transfer frequency and enhances parallel computation efficiency. Therefore, we opt to store and update these data directly on the GPU, necessitating careful consideration of the type of GPU memory employed. The GPU’s memory architecture encompasses various types such as global memory, registers, local memory, shared memory, constant memory and texture memory; each possesses unique roles and characteristics. Although registers offer fast access speeds, their capacity is limited and closely tied to thread lifecycles; thus they are unsuitable for long-term data storage. Local memory boasts faster access speeds than global memory but has a relatively small capacity and a lifecycle confined to thread execution periods and thread block synchronization—making it ineffective in mitigating performance losses caused by multiple data transfers. Constant memory offers certain advantages in terms of availability but suffers from limited capacity while only supporting read operations—rendering it inadequate for our specific application requirements. Texture memory excels at providing efficient access modes but entails complexity in setup and usage along with reliance on specific APIs and hardware support; simultaneously its size and access modes are also restricted—increasing complexity and limitations in use cases.

In contrast, global memory offers significant advantages by facilitating inter-thread data sharing and ensuring a consistent lifecycle aligned with the GPU device cycle, thereby enabling prolonged retention within the GPU alongside modifications. Consequently, global memory becomes an indispensable asset for mitigating performance overheads resulting from frequent transfers.

In this study, we leverage global memory for data storage, eliminating frequent data transfers between the CPU and GPU. This approach enhances computing performance, as illustrated in Fig. 7.

Fig. 7

Flow chart of data transmission

The specific implementation ideas are outlined as follows:

• 1. Import the model on the CPU side and initialize the data.

• 2. Allocate memory on the GPU side to store the data required for calculations.

• 3. Transfer node and element data to the GPU.

• 4. Conduct iterative computations on the GPU.

• 5. Modify certain node data on the CPU.

• 6. Transfer the modified data to the GPU.

• 7. Upon completion of the iteration, input the results to the host and generate the output.

The proposed method requires only one full data transmission from the host to the device, with minimal node data transmitted after each iteration. This strategy greatly improves acceleration performance compared with techniques demanding complete data transmission during each iteration.

3.2 Parallel solution

In the context of large-scale problems, the computational cost associated with generating neighborhood data for PD elements in a serial manner significantly escalates, thereby diminishing the algorithm’s computational efficiency. Notably, the process of creating neighborhood data for distinct PD elements is independent and repeatable, demonstrating high parallelism [23]. Leveraging this insight, aligning each PD element with a GPU thread enables parallel construction of neighborhood data. As depicted in Fig. 8, each element or node’s computational task can be mapped to a GPU thread using this parallelization strategy. This approach substantially reduces computation time and enhances the algorithm’s computational efficiency.

Fig. 8

Assigning threads to PD elements

The detailed invocation process of threads can be described as follows:

Initially, a unique thread index, referred to as ‘tid’, needs to be generated. The computation formula for tid is given by tid = blockIdx.x * blockDim.x + threadIdx.x. In this equation, blockIdx.x represents the index of the thread block, blockDim.x signifies the number of threads within each dimension of the thread block, and threadIdx.x denotes the index of the thread within its respective thread block. Consequently, the distinct index tid for each thread is derived from a combination of blockIdx.x, blockDim.x, and threadIdx.x.

Consequently, each thread independently computes the corresponding element data for its assigned thread ID (i.e., tid). This parallel process enables efficient and rapid processing of large datasets by allowing every thread to autonomously execute its computational task.

In the figure, δ represents the radius of the PD domain. Once the PD domain is established, each PD element within this domain is assigned a thread for calculation, thus achieving a high degree of parallelization.

3.2.1 Parallelism of implicit solutions

In the resolution of implicit PD problems, a crucial step involves aggregating single stiffness matrices into a global stiffness matrix. However, conventional parallel strategies, such as assigning a thread to each stiffness matrix, may lead to concurrent access by multiple threads to the same node during assembly, resulting in computational errors. Although generating single element stiffness matrices in parallel on the GPU and subsequently transferring them to the CPU for sequential assembly can provide acceleration benefits for small-scale problems, this approach becomes significantly limiting for large-scale problems due to the overhead associated with assembling and transmitting the global stiffness matrix.

To address this issue, this study employs an atomic operation scheme. Atomic operations in CUDA allow a thread to complete the read–write process of a specific storage element without interference from other threads. By leveraging atomic operations, this study achieves the parallel assembly of the global stiffness matrix on the GPU, eliminating the need for multiple transmissions between the CPU and GPU. Although atomic operations entail a performance loss, the resulting accelerated performance compensates for this drawback.

In the implicit solution of large PD deformation problems, after assembling the global stiffness matrix, constraints and forced displacements should be imposed on the system. Given that only a small portion of node data needs modification for imposing constraints and forced displacements, transmitting the entire node array between the CPU and GPU would lead to significant time loss. Hence, this study adopts an indexing method to identify and transmit only the required data for the modified nodes, effectively reducing data transmission overhead.

Upon applying constraints and displacements, a load vector must be generated. Considering that the forces acting on each node are independent, each node can be mapped to a thread on the GPU, enabling parallel computation of the resultant forces for each node. Once accomplished, a linear system of equations, denoted as Kd = F, emerges, where K signifies the global stiffness matrix, F represents the load vector, and d denotes the displacement vector to be solved. This system of linear equations can be resolved using the preprocessed conjugate gradient method (PCG).

The implicit solution of large deformation problems differs from other PD problems in that during the implicit solution, the displacement solution of the linear equation system obtained by each iteration step must be evaluated for convergence. If it does not converge, it must be resolved within this iteration step until the convergence condition is met, and then the current iteration step can be bypassed. This characteristic necessitates solving multiple linear equations at each iteration step when resolving large deformation problems, resulting in substantial time costs. The flow chart of the implicit solution of large deformation problems is depicted in Fig. 9.

Fig. 9

Flowchart of implicit solution for large deformation

The resolution of linear equations represents the most time-consuming phase within the overall problem-solving procedure. This is primarily attributed to the extensive numerical computations and matrix operations involved, which exhibit considerable computational complexity and volume. Therefore, solving these equations becomes notably time-intensive owing to the significant demands posed by the resolution of linear equations.

Despite the admirable performance of the CPU in processing large sets of linear equations, its computational speed and efficiency encounter limitations as the scale of the problem increases. GPU acceleration technology leverages the parallel computing capabilities of GPUs to boost computational efficiency. It achieves this by dividing the computing tasks into multiple subtasks and executing them concurrently on the GPU. When addressing the solution of linear equations, GPU acceleration technology parallelizes numerous matrix operations and numerical calculations integral to the computation, thereby significantly reducing computation time.

Owing to the limited graphics memory capacity of the GPU, storing the entire stiffness matrix in GPU memory is impractical. To address this challenge, this study employs a compression technique to transform the total stiffness matrix into a sparse matrix format and stores it using the row-first compression compressed sparse row (CSR) method [24]. To facilitate a comprehensive understanding of the CSR storage matrix, we illustrate the mapping relation between full memory and CSR sparse memory with an example, as shown in Fig. 10. The relevant parameters in the CSR, such as the Row and Col indices, are detailed in Table 1. The integration of the global stiffness matrix stored in sparse format can be conducted efficiently, considerably reducing memory consumption and solving time. This approach enables the resolution of problems with increased degrees of freedom through GPU acceleration.

Fig. 10

Example of thick matrix to CSR sparse matrix

Table 1 Relevant parameters of the CSR matrix

The cuSPARSE library in CUDA comprises a set of basic linear algebra subroutines for sparse matrices, which can notably accelerate the calculation of sparse matrices [25, 26]. The cuBLAS library implements the basic linear algebra subroutine (BLAS) in the NVIDIA^® CUDA^TM runtime, enabling users to fully utilize the computing resources of the NVIDIA^® CUDA^TM GPU [27]. Consequently, the solvers used in this study are based on the cuSPARSE and cuBLAS libraries to ensure optimal efficiency in solving linear equations.

3.2.2 Parallelism of explicit solutions

The conventional serial solving method incurs substantial time costs when calculating the links associated with PD bonds [28]. As illustrated in Fig. 11, once the size of the PD domain is established and element I is identified, any element within the same domain as element I (e.g., element J) determines the range of the PD domain. A PD bond ξ_ij is formed between node i of element I and node j of element J, thereby linking these elements. Serial computation for bond force calculation results in considerable time expenditure. However, bond force calculation exhibits high parallelism, and the independent computation of each bond facilitates GPU parallel acceleration. The computation of each bond can be delegated to an individual concurrent thread on the GPU to accomplish this task.

Fig. 11

Formation of PD bonds between PD elements

Upon completion of the bond force calculation, it must be distributed to each node. Analogous to the assembly of the global stiffness matrix, common nodes exist in the parallel distribution process. To circumvent the issue of multiple threads reading and writing the same node, atomic operations are necessary. The method employed for explicit solving is the central difference method, and the steps are as follows:

• (1) The node acceleration is obtained by calculating the derivative of the node velocity.

• (2) Multiply the node acceleration by the preset time step to obtain the node velocity.

• (3) Multiply the node velocity by the time step to obtain the current iteration step displacement.

• (4) Add the current iteration step displacement to the node displacement.

• (5) Update the node coordinates.

In the resolution of the central difference method, the data between nodes are independent, enabling solution acceleration by allocating a thread to each node for parallel computation. Prior to the next incremental step, the fracture information of the PD bonds must be updated. Given that the key state is independent, a thread can be allocated to each PD element to achieve GPU parallel acceleration and update the bond fracture state [29].

4 Numerical example

In Sect. 4.1, the accuracy of the PD algorithm is verified by comparing the results of the GPU algorithm with the traditional finite element CPU algorithm. The implicit algorithm adopts a single plate, whereas the explicit algorithm adopts a Y-shaped prefabricated crack plate. In Sect. 4.2, the efficiency of the parallel algorithm will be verified. After ensuring accuracy, the time taken to solve the PD large deformation problem using the GPU algorithm and CPU algorithm is compared, and the acceleration ratio is obtained to verify its acceleration effect. Table 2 provides the configuration information of the CPU and GPU in the calculation.

Table 2 Hardware configuration information for CPU and GPU

4.1 Precision verification of parallel solving algorithm

4.1.1 Precision verification of parallel implicit solution algorithm

The calculation example used in this section involves a single plate employed solely to test the accuracy of the parallel implicit solving algorithm. The model settings are shown in Fig. 12. The length of the plate is L = 90 mm, the width is W = 30 mm, and the thickness is h = 0.8 mm. The elastic modulus of the plate is E = 210 GPa, the Poisson’s ratio is v = 0.33, and the density is 2440 ${\text{kg/m}}^{3}$. The left end is fixed, and the uniform load acting on the right boundary of the model is P = 1 MPa. The grid size is Δx = 1 mm, and the PD domain size is set to δ = 3Δx.

Fig. 12

Model of single tie plate

The displacement results of the GPU parallel algorithm are compared with those of the CPU algorithm to verify the accuracy of the GPU parallel algorithm. The comparison of displacement results for the two algorithms is shown in Fig. 13.

Fig. 13

Comparison of displacement results between GPU parallel algorithm and CPU algorithm, a, c, e shows the displacement results in X-direction, Y-direction and Z-direction for GPU parallel algorithm, b, d, f shows the displacement results in X-direction, Y-direction, and Z-direction for CPU algorithm

By comparing the displacement results of each iteration step of the GPU parallel algorithm and CPU algorithm, we observe that the results of the two algorithms are essentially the same. This observation confirms the accuracy of the GPU parallel algorithm, demonstrating its suitability for accelerating the solution of large-scale problems.

4.1.2 Precision verification of parallel explicit solution algorithm

In this section, the example used is a Y-shaped prefabricated cracked plate, which is widely used to evaluate the accuracy of crack propagation simulation algorithms. The initial crack plate model and PD region setting are shown in Fig. 14. The length of the plate is L = 100 mm, the width is W = 40 mm, and the thickness is h = 1 mm. There is an initial prefabricated crack at L/2, with the crack length ${a}_{0}$ = 50 mm. The elastic modulus of the plate is E = 72 GPa, the Poisson’s ratio is v = 0.33, the density is 2440 ${\text{kg/m}}^{3}$, and the critical energy release rate is $G_{c}$ = 135 ${\text{J/m}}^{2}$. The uniform load acting on the upper and lower boundaries of the model is P = 12 MPa. For the crack propagation region, a grid discretization with a mesh size of Δx = 0.5 mm is used, and the PD domain size is set to δ = 3Δx.

Fig. 14

Y-shaped prefabricated cracked plate

The crack propagation paths calculated by GPU at different time steps were compared with the calculation results by CPU, as shown in Fig. 15.

Fig. 15

Crack extension paths of Y-shaped prefabricated cracked plate at different time steps, a computed results at GPU side, b computed results at CPU side

The calculation results of the GPU are basically consistent with those of the CPU, and the crack propagation path of the GPU parallel algorithm is consistent with that of the CPU algorithm. This finding verifies the accuracy of the GPU parallel explicit algorithm and can be used to accelerate the solution of large-scale problems.

4.2 Speedup verification of the parallel solution algorithm

4.2.1 Speedup verification of the parallel implicit solution algorithm

In this section, the parallel implicit algorithm is tested for its acceleration performance using a model of a uniformly pressed thin plate. The model settings are illustrated in Fig. 16. The plate has a length of L = 90 mm, a width of W = 30 mm, and a thickness of h = 0.8 mm. The elastic modulus of the plate is E = 210 GPa, the Poisson’s ratio is v = 0.33, and the density is 2440 ${\text{kg/m}}^{3}$. A fixed constraint is applied at the left end. The surface uniformly distributed load acting on the model surface is P = 1 MPa. The total number of elements is 10,800. The grid size is Δx = 0.5 mm, and the PD domain size is set to δ = 3Δx.

Fig. 16

Uniform pressure modeling of thin plates

The incremental step is set to 100 steps, and the maximum iteration times of a single incremental step are set to 100. The GPU parallel algorithm and CPU algorithm are used for solving, respectively. The displacement result of the GPU parallel algorithm is shown in Fig. 17.

Fig. 17

The displacement result of GPU parallel algorithm

By comparing the displacement results of the two algorithms, the displacement of any incremental step is basically the same in the solving process. Thus, the acceleration performance of the GPU parallel algorithm can be verified. The model with PD elements accounting for 50% of the total number of elements is selected to test the time of each link of an iteration step of the GPU parallel algorithm and the CPU algorithm, as shown in Table 3.

Table 3 Time of each session of one iteration step of the two algorithms, in (s)

Table 3 indicates that when solving large deformation implicit problems, the solving time of linear equations in the iterative step is remarkably high. Although assembling the global stiffness matrix requires some time, each incremental step only requires assembling the global stiffness matrix once. However, due to the existence of convergence conditions for displacement results, the solving of linear equations often needs to be repeated many times, and the current incremental step can only be completed when the displacement solution satisfying the displacement convergence conditions is obtained. Therefore, the solving time of the linear equations can be approximated to the total calculation time, and the acceleration ratio of the PCG parallel solution on the GPU and the UMF solution on the CPU can be calculated using the total calculation time.

The total calculation time of the GPU parallel algorithm and the CPU algorithm under different proportions of PD elements is shown in Fig. 18.

Fig. 18

Total computation time of GPU parallel algorithm and CPU algorithm with different PD element ratios

With the increase of the PD element ratio, the CPU computing time increases, whereas the GPU computing time also increases, but not significantly compared with the CPU. Therefore, the speedup ratio (CPU computing time/GPU computing time) shows an upward trend, and the acceleration effect of the GPU parallel algorithm can reach 7.4–9.8 times, demonstrating excellent acceleration performance.

To further prove that the GPU parallel algorithm has a good acceleration effect on large-scale problems, this section refines the model grid with a 50% PD element ratio and tests the acceleration effect of the GPU parallel algorithm with the same PD element ratio under different grid sizes, as shown in Table 4.

Table 4 GPU computation time vs. CPU computation time for different grid sizes at 50% PD element ratio, in (s)

Table 4 only provides statistics for the time of solving linear equations once under different grid sizes. Referring to Table 3, the time of solving linear equations can be approximately equal to the time of one iteration step t, whereas the total solving time of implicit large deformation T = n × t, where n is the total number of iterative steps. Therefore, the ratio of CPU to GPU for solving linear equations once is the acceleration ratio of the GPU parallel algorithm to the CPU algorithm.

According to Table 4, with the increase in the number of elements, the acceleration ratio also increases. When the number of elements is 270,000, the number of rows of the stiffness matrix is 27 × 4 × 6 = 6.48 million, achieving a 10 times acceleration effect when dealing with a million-order matrix. This demonstrates superior acceleration performance compared with the CPU.

4.2.2 Speedup verification of the parallel explicit solution algorithm

To validate the acceleration performance of the parallel explicit algorithm, this section investigates the progressive damage process of a square low-carbon steel plate with a preset crack under lateral load. The specific experimental process for this problem can be found in the literature [30]. As shown in Fig. 19, the length, width, and thickness of the steel plate are L = 203 mm, L = 203 mm, and h = 0.8 mm, respectively. The steel plate has an initial preset crack at X = L/2, with a crack length of a_0 = 30 mm. The elastic modulus of the low-carbon steel plate is E = 210 GPa, the Poisson’s ratio is v = 0.33, the density is 7.85 ${\text{t/m}}^{3}$, and the critical energy release rate is $G_{c}$ = 255 ${\text{kN/m}}$. The left and right ends of the steel plate are fixed and constrained, and an incremental load F is applied at both ends of the crack.

Fig. 19

Model of a square mild steel plate with preset cracks

For the crack propagation region, the grid size of Δx = 1.75 mm is initially used for grid discretization, and the PD domain size is set as δ = 3Δx, with a total of 13,456 elements in the model. The explicit central difference method is employed to calculate the crack propagation process with gradually increasing load, and the time step is set to 0.1 μs, which is sufficient to meet the stability conditions of numerical integration. After 50,000 incremental steps, the load is gradually increased to 1800 N, and the quasi-static results of the crack propagation process are obtained. The calculation results of the GPU parallel algorithm is shown in Fig. 20.

Fig. 20

Crack expansion path results for mild steel plate calculated by GPU parallel algorithm

During solving, the calculation time is statistically recorded, as shown in Fig. 21, which captures the calculation time of the GPU parallel algorithm and the CPU algorithm under different PD ratios. With the increase in the PD element ratio, CPU calculation time increases, whereas GPU calculation time also increases, but the increase is not large compared with the CPU. Therefore, the speedup ratio (CPU calculation time/GPU calculation time) shows an increasing trend, and the speedup ratio is positively correlated with the PD element ratio.

Fig. 21

GPU computation time vs. CPU computation time for different PD element ratios

At the same time, this section compares the computing time of the links that take up a large proportion of time, as shown in Fig. 22. The time-consuming links in the explicit solution of the GPU parallel algorithm and the CPU algorithm are stress and strain update and structural reaction calculation, but the GPU computing time is much lower than that of CPU computing time. With the increase in the number of PD elements, the acceleration ratio of the two links also increases, which proves that the GPU parallel algorithm has the acceleration performance that the CPU algorithm cannot reach.

Fig. 22

Comparison of computation time for the more time-consuming parts of the explicit solving process

The model grid is further refined, and the GPU computing time and CPU computing time of different grid sizes at the ratio of 100% PD elements are statistically analyzed, as shown in Table 5.

Table 5 GPU computation time vs. CPU computation time for different grid sizes at 100% PD elements, in (s)

With the gradual refinement of the grid and the increase in the number of PD elements, the calculation time of both GPU and CPU also increases. However, the GPU parallel algorithm outperforms the CPU algorithm in processing PD elements, leading to an increasing speedup ratio. As the grid of the model becomes more refined, incorporating more PD elements, the speedup ratio grows larger, highlighting the superior acceleration performance of the GPU parallel algorithm.

Scalability is a crucial performance metric for evaluating GPU algorithms, which can be classified into two main types: weak scalability and strong scalability. Weak scalability refers to the algorithm's ability to maintain efficiency as the problem scale increases, while strong scalability implies that the algorithm’s efficiency improves with increasing problem scale. From a theoretical perspective, the non-local characteristics of PD method necessitate each node to consider interactions with other nodes within a specific range during calculations. Consequently, as degrees of freedom increase, the computational workload often exhibits super linear growth trends. With an increasing number of nodes, each node will require more adjacent nodes for interactive calculations accordingly. In a two-dimensional space with uniformly distributed nodes and constant interaction range, the number of adjacent nodes needed by each node for interactive calculations is proportional to the square root of node density (this arises from considering that area in two-dimensional space is proportional to radius squared and number of nodes is proportional to area). However, since each node needs to interact with multiple other nodes, overall computational workload will approach or exceed the square of degrees of freedom. To verify GPU algorithm’s scalability effectively, we expanded data scale and computing time based on square proportionality with degrees of freedom when conducting comparative analysis under different grid sizes; subsequently comparing this expanded computing time with actual time required by smaller grids as shown in Table 6.

Table 6 The scalability analysis of GPU algorithms, in (s)

The analysis results indicate that the GPU algorithm exhibits robust scalability, with its efficiency gradually improving as the data size increases. Furthermore, optimization of data transfer and reduction in scheduling overhead effectively mitigate their impact on algorithm acceleration performance during large-scale data processing.

4.2.3 Numerical example of hexagonal prism

The model used in this section is a hexagonal prism model with a prism length of L = 304.8 mm, a bottom side length of 65.33 mm, and a thickness of h = 3.048 mm. The elastic modulus of the plate is E = 193 GPa, the Poisson’s ratio is v = 0.33, the density is 7980 ${\text{kg/m}}^{3}$, and the critical energy release rate is $G_{c}$ = 150 ${\text{kN/m}}$. The upper and lower bottom surfaces are fixedly constrained, and the uniform load acting on the model cylinder is P = 1 MPa. The schematic diagram of the model is shown in Fig. 23. The total number of elements is 19,052, and the grid size is Δx = 2.5 mm. The PD domain size is set to δ = 3Δx. The GPU calculation time is 4492 s, and the CPU calculation time is 33,102 s. The comparison result of the GPU parallel algorithm is shown in Fig. 24.

Fig. 23

Schematic diagram of hexagonal prism model

Fig. 24

The GPU algorithm calculation results

The model, with 100% PD elements, undergoes refinement by gridding. Table 7 presents the comparison of calculation time and acceleration ratio under different grid sizes. Post-gridding, the acceleration ratio increases with the growing number of elements, indicating a positive correlation between acceleration performance and the number of elements. A higher element count results in better acceleration performance for the GPU parallel algorithm.

Table 7 GPU computation time vs. CPU computation time for different grid sizes at 100% PD elements, in (s)

4.2.4 Numerical example of prefabricated cracked cylinder

The model used in this section is a cylinder with a prefabricated crack, with a height of H = 600 mm, a bottom diameter of 200 mm, and a thickness of h = 3.048 mm. The elastic modulus of the plate is E = 65 GPa, the Poisson’s ratio is v = 0.33, the density is 7850 ${\text{kg/m}}^{3}$, and the critical energy release rate is $G_{c}$ = 150 ${\text{kN/m}}$. The upper and lower bottom surfaces are fixed, the prefabricated crack is applied at H/2, and the cylindrical surface is applied with a horizontal uniform load, as shown in [31], and the schematic of the model is shown in Fig. 25. The total number of elements is 18,621, the grid size is Δx = 4.5 mm, and the PD domain size is set to δ = 3Δx. The result of the GPU parallel algorithm is shown in Fig. 26.

Fig. 25

Schematic diagram of the prefabricated cracked cylinder model

Fig. 26

The result of GPU parallel algorithm

Upon refining the model mesh, the computing time of both algorithms is statistically analyzed, and the acceleration ratio is recorded. Table 8 presents these results, showing an enhanced acceleration performance of the GPU parallel algorithm after mesh refinement. The GPU algorithm exhibits superior acceleration performance as the number of elements in the model increases, particularly in addressing large-scale PD plate shell deformation problems.

Table 8 GPU computation time vs. CPU computation time for different grid sizes at 100% PD elements, in (s)

5 Conclusion

This study introduces an innovative parallel algorithm, leveraging GPU capabilities, specifically crafted to address large deformation challenges in PD shells with notable efficiency. The algorithm exploits GPU acceleration technology to partition the computational task into numerous subtasks, allowing for concurrent execution on the GPU and resulting in a substantial improvement in computational efficiency. The accuracy and superior efficiency of this parallel algorithm are substantiated by the successful execution of six distinct examples. Although the algorithm is primarily optimized for single-GPU usage, we hypothesize that employing multi-GPU parallel computing would yield more effective results when tackling large-scale problems. In future research, our objective is to explore multi-GPU parallel algorithms to further enhance the efficiency and scalability of our proposed solution, making it capable of handling even larger-scale problems. In addition, we plan to extend the application of this algorithm to address large deformation challenges in practical engineering scenarios. This expansion aims to contribute to the development of more precise and efficient numerical simulation methodologies within the engineering domain. In conclusion, the proposed GPU-based parallel algorithm holds significant potential for addressing large deformation challenges in PD shells, demonstrating both theoretical relevance and practical applicability.