1 Introduction

In civil engineering, pile foundations are commonly employed to transmit the load of buildings to the underlying ground or rock. When piles are embedded in rock, they transfer loads to the earth either through end bearing, shaft resistance, or a mixture of the two. In scenarios where the soil overlay on top of the rock is weak and not deep, employing piles into the bedrock is perceived as one of the most fitting remedies (Carrubba 1997). The rock’s horizontal resistance can create substantial support despite minimal pile displacement in such situations. According to the results, it can be inferred that the current techniques for designing socketed piles in rock are comparably efficient (Carvalho et al. 2023; Lu et al. 2023).

Nonetheless, owing to the intricacy of the pile’s behavior, these techniques may not furnish precise forecasts (Ng et al. 2001). Consequently, it is essential to create a novel paradigm of soft computing able to accurately predict and precisely anticipate settlement of piles (SP), an essential aspect of pile design (Gutiérrez-Ch et al. 2021). Since SP can significantly affect the durability and security of structures, it should be considered a critical element in this process (Fleming 1992). Despite the various design techniques available, geotechnical engineers encounter difficulty in developing an innovative and feasible forecasting model that produces satisfactory results for SP prediction (Armaghani et al. 2020). Recent studies have demonstrated that pile performance prediction precision heavily relies on the choice of input variables. Therefore, the subsequent sentences will examine pertinent research studies to ascertain the appropriate input variables to anticipate SP (Masoumi et al. 2020).

As stated in reference (Randolph and Wroth 1978), multiple factors impact the SP. These factors include the magnitude of the load on the pile, the diameter and length of the pile, as well as the shear modulus (Le Tirant 1992). Another factor is the radial gap, where the stress from shear decreases (Nejad et al. 2009). Conversely, earlier research has suggested that the pile capacity and, consequently, the SP can be significantly influenced by the rocks’ unconfined compressive strength (UCS) in the surrounding area (Rowe and Armitage 1987). Utilizing common penetrating test data, a prediction algorithm on the basis of data mining was developed for predicting foundation settling. For training the model, about 1000 data points were employed at first from different sources. Later on, field measurements were included to enhance the model’s effectiveness further. Integrating fundamental geotechnical engineering principles is essential to underscore the applied value of models. Comprehending soil behavior, including stress–strain dynamics and shear strength, is paramount. Likewise, critical soil properties like permeability and compaction influence interactions with structures. By intertwining these principles within model elucidations, it becomes evident how models replicate authentic soil behavior and its responses to diverse forces. The incorporation of pertinent analytical methods, such as finite element analysis and analytical solutions, underscores model accuracy and relevance in predicting phenomena like pile settlement. This approach offers a holistic perspective on model alignment with established theories, augmenting their practical efficacy in geotechnical engineering (Akbarzadeh et al. 2023; Sedaghat et al. 2023).

Geotechnical engineering has become increasingly common in using artificial intelligence (AI) and machine learning (ML) in recent years. As described, an ML algorithm can generate an anticipated result once provided with experimental data (Alam et al. 2021). ML comprises several learning methods: supervised, unsupervised, semi-supervised, and reinforcement (Vapnik 1999a). Recently, researchers have integrated machine learning techniques into real-world geotechnical engineering problems. Some of the methods utilized consist of gene expression programming (GEP), artificial neural network (ANN), support vector machine (SVM), multilayer perceptron neural network (MLP), as well as the multigroup approach for data management to predict the desired output data (Vapnik et al. 1996; Smola and Schölkopf 2004).

Ge et al. (2023) used SVR coupled with two optimizer algorithms containing the Arithmetic Optimization Algorithm (AOA) and Grasshopper Optimization Algorithm (GOA). They found that the RMSE values for SVR-AOA and SVR-GOA were obtained as 0.550 and 0.592, respectively, and the MAE presented values of 0.525 and 0.561, respectively. The R-value of SVR-AOA shows a desired intensity of 0.994, which is 0.10% higher than that of SVR-GOA. Kumar and Robinson (2023) introduced the SVR combined with Henry’s Gas Solubility Optimization (HGSO) and Particle Swarm Optimization (PSO) to predict the settlement of the pile. The R2 of the model was obtained similarly at 0.99. In comparison, the RMSE of SVR-PSO appears more than double that of SVR-HGSO, 0.46 and 0.29 mm, respectively. Cesaro et al. (2023) proposed a new, simple analytical method to predict the load–deflection response at the pile tip. The reliability of the proposed method is verified against a database consisting of 50 in situ pile loading tests performed worldwide. Kumar and Samui (2020) proposed a least squares support vector machine (LSSVM), a group data processing method (GMDH), and a reliability analysis based on Gaussian process regression (GPR) of a group of piles resting on cohesive soil. The results showed that all models can be applied to analyze the settlement of a group of piles reliably.

In addition, other investigations have been studied on the effect of machine learning in geotechnical applications (Onyelowe et al. 2022; Gnananandarao et al. 2023a, b, c). Gnananandarao et al. (2020) presented the application of artificial neural networks (ANN) and multivariate regression analysis (MRA) to predict the bearing capacity and settlement of multi-sided foundations in sand. The R for multi-sided foundations ranged from 0.940 to 0.977 for the ANN model and from 0.827 to 0.934 for the regression analysis. Similarly, R for SRF prediction can be 0.913–0.985 for the ANN model and 0.739–0.932 for regression analysis. Onyelowe et al. (2021) predict erosion potential and generate a model equation using ANN learning techniques. The performance shows the model has an R2 more significant than 0.95 during training and testing between the predicted and measured values. Furthermore, the error metrics show significantly low values, indicating good performance.

This study aims to employ a supervised learning method for regression analysis to forecast SP. A regression analysis technique is implemented to ascertain the association between the independent variables or features and the dependent variable or output. Because of the capacity of AI methods to handle complex systems and process a large number of parameters, the SVR method is used to predict SP. Moreover, metaheuristic approaches are employed to enhance the accuracy, reduce errors in the model, and produce outputs similar to laboratory results. Various novel methods are going to be covered in the following part, namely the Archimedes Optimization algorithm (AOA), marine predators’ algorithm (MPA), and Augmented grey wolf optimizer (AGWO), which are among various optimizers.

The effectiveness of optimizing methods in enhancing the precision of the SVR estimating framework is highlighted through various statistical measures. The SVR model’s performance is evaluated using or not using the mentioned techniques, and the outcomes show the framework with optimizing methods outperforms the individual one. The paper generally suggests a unique strategy to forecast pile settlement by incorporating SVR and three unique optimization algorithms. The results suggest that SVR can accurately predict pile settlement, and implementing optimization algorithms improves the model’s performance. Therefore, geotechnical scientists are able to anticipate SP and optimize pile foundation planning with the help of this technology.

2 Dataset and methodology

2.1 Data gathering

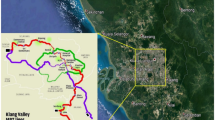
The Klang Valley Mass Rapid Transit (KVMRT) is a recent endeavor that strives to ease traffic congestion in Kuala Lumpur, Malaysia’s vibrant capital. Site analysis revealed that to prevent station failure for the KVMRT project, several bored piles would be required to be installed. Figure 1 illustrates that the project site in Malaysia includes diverse rock foundations, such as granite, sandstone, limestone, and phyllite, thus necessitating the construction of several heaps (Hatheway 2009).

Fig. 1
figure 1

Location of KVMRT project

Full size image

This research tends to look into a certain topic comprising 96 piles founded on granite rock. It was discovered that the San Trias formation is where the granite rock in the region originated. The study examined the geological characteristics of the subsurface materials at the pile locations. The study’s findings revealed that the subsoil profiles were primarily constituted of residual rocks. As per the collected data, the bedrock depth varied between 70 cm and more than 1400 m below the ground level. Further information regarding the field sampling and bore log details is discussed in the following sentences—

  • The observed rock masses ranged from moderately to extensively weathered.

  • According to the ISRM, the UCS values ranged from 25 to 68 (MPa), with the minimum and maximum values being observed.

  • The bore log data indicate that the soil is highly weathered up to 16.5 (MPa) depth, with the predominant soil composition being hard sandy mud. The minimum and the maximum N_SPT values observed were 4 and 167 blows per 300 (mm), respectively.

  • From depths of 7.5–27.0 (m), most of the subsoil materials have N_SPT values that exceed 50 blows per 300 (mm).

The initial step in developing a prediction model is to collect a dataset with robust dependent variables. Identifying and delineating the critical factors that substantially influence the model’s output is essential. Table 1 shows the statistical properties of model input and target values and the total data (96 samples) presented in Appendix 1.

Table 1 Statistical properties of model input and target values
Full size table

Figure 2 shows the correlation of input and output (Khatti and Grover 2023b, c, e). The correlation matrix observes correlations between input variables (Lp/D, Ls/Lr, N_SPT, UCS, Qu) and the output variable (SP). Lp/D and Ls/Lr exhibit strong positive correlations with SP (0.742 and 0.714, respectively), indicating increased static penetration as these ratios grow. Conversely, N_SPT and UCS demonstrate strong negative correlations with SP (− 0.727 and − 0.753, respectively), revealing reduced static penetration with higher standard penetration test blow count and unconfined compressive strength. Qu displays a moderate positive correlation with SP (0.662), suggesting elevated ultimate bearing capacity increases static penetration. Understanding these correlations aids in optimizing the given problem.

Fig. 2
figure 2

The correlation between the input and output

Full size image

2.2 Support vector regression (SVR)

SVR stands out from other models because it can improve generalization performance and achieve an optimal global solution within a shorter timeframe (Vapnik et al. 1996; Gunn 1998).

2.2.1 Linear support vector regression

Assuming a training dataset of \(\{{y}_{i}, {x}_{i}, i=1, 2, 3,\dots n\}\), where \({y}_{i}\) represents the output vector, \({x}_{i}\) represents the input vector, and n represents the dataset size. The general linear regression form of SVR can be expressed as follows:

$$f\left(x,k\right)=k\times x+b$$
(1)

In the above equation, the dot product is represented by \(\left(x,k\right)\), where k is the weight vector, x represents the normalized test pattern, and b is the bias. As shown in Eq. (2), the empirical risk is calculated using an \(\varepsilon\)-insensitive loss function denoted by \({L}_{\varepsilon }({y}_{i},f\left({x}_{i},k\right))\):

$${R}_{{\text{emp}}}\left(k,b\right)=\frac{1}{n}\sum\limits_{i=1}^{n}{L}_{\varepsilon }({y}_{i},f\left({x}_{i},k\right))$$
(2)
$${L}_{\varepsilon }\left({y}_{i},f\left({x}_{i},k\right)\right)= \left\{\begin{array}{ll}\varepsilon , & if \; \left|{y}_{i}-f\left({x}_{i},k\right)\right|\le \varepsilon \\ \left|{y}_{i}-f\left({x}_{i},k\right)\right|-\varepsilon , & otherwise\end{array}\right.$$
(3)

The \(\varepsilon\)-insensitive loss function, denoted by \({L}_{\varepsilon }\left({y}_{i},f\left({x}_{i},k\right)\right)\), represents the tolerance error between the target output \({y}_{i}\) and the estimated output values \(f\left({x}_{i},k\right)\) during the optimization process. The training pattern, \({x}_{i}\), is also defined in this context. Minimizing the squared norm of the weight vector, \({\Vert k\Vert }^{2}\), can simplify the complexity of the SVR model when using the \(\varepsilon\)-insensitive loss function for linear regression problems. The deviation of the training data outside the ε-insensitive zone can be estimated using a non-negative slack variable (\({\varphi }_{i}^{*}{\varphi }_{i})\).

$$\underset{k,b,\varphi ,{\varphi }^{*}}{{\text{Lim}}}\left[\frac{1}{2}k \cdot k+c\left(\sum_{i=1}^{n}{\varphi }_{i}^{*}+\sum_{1=1}^{n}{\varphi }_{i}\right)\right]$$
(4)
$$\text{Subjected to}, \; \left\{\begin{array}{l}{y}_{i}-k.{x}_{i}-b\le \varepsilon +{\varphi }_{i}^{*}\\ k\cdot {x}_{i}+b-{y}_{i}\le \varepsilon +{\varphi }_{i}\\ {\varphi }_{i}^{*},{\varphi }_{i}\ge 0 \end{array} i=1,...,n\right.$$

One must find the Lagrange function’s saddle point to solve the problem.

$$L(k,{\varphi }^{*},\varphi ,{\alpha }^{*},\alpha ,c,{\gamma }^{*},\gamma )=\frac{1}{2}k.k+c\left(\sum_{i=1}^{n}{\varphi }_{i}^{*}+\sum_{1=1}^{n}{\varphi }_{i}\right)-\sum_{i=1}^{n}{\alpha }_{i}\left[{y}_{i}-k\cdot {x}_{i}-b+\varepsilon +{\varphi }_{i} \right]-\sum_{i=1}^{n}{\alpha }_{i}^{*}\left[k\cdot {x}_{i}+b-{y}_{i}+\varepsilon +{\varphi }_{i}^{*} \right]-\sum\limits_{1}^{n}({\gamma }_{i}^{*}{\varphi }_{i}^{*}+{\gamma }_{i}{\varphi }_{i})$$
(5)

The KKT conditions can be applied to minimize the Lagrange function by performing partial differentiation of Eq. (5) concerning k, b, \({\varphi }_{i}^{*}\), and \({\varphi }_{i}\).

$$\frac{\updelta L}{\updelta k}=k+\sum\limits_{i=1}^{n}{\alpha }_{i}{x}_{i}-\sum\limits_{i=1}^{n}{\alpha }_{i}^{*}{x}_{i}=0, k=\sum\limits_{i=1}^{n}({\alpha }_{i}^{*}-{\alpha }_{i}){x}_{i}$$
(6)
$$\frac{\updelta L}{\updelta b}=\sum\limits_{i=1}^{n}{\alpha }_{i}-\sum\limits_{i=1}^{n}{\alpha }_{i}^{*}=0,\sum\limits_{i=1}^{n}{\alpha }_{i}=\sum\limits_{i=1}^{n}{\alpha }_{i}^{*}$$
(7)
$$\frac{\updelta L}{\updelta {\varphi }^{*}}=c-\sum\limits_{i=1}^{n}{\gamma }_{i}^{*}-\sum\limits_{i=1}^{n}{\alpha }_{i}^{*}=0,\sum\limits_{i=1}^{n}{\gamma }_{i}^{*}=c-\sum\limits_{i=1}^{n}{\alpha }_{i}^{*}$$
(8)
$$\frac{\updelta L}{\updelta \varphi }=c-\sum\limits_{i=1}^{n}{\gamma }_{i}-\sum\limits_{i=1}^{n}{\alpha }_{i}=0,\sum\limits_{i=1}^{n}{\gamma }_{i}=c-\sum\limits_{i=1}^{n}{\alpha }_{i}$$
(9)

The parameters \(k\) in Eqs. (1) and (6) are connected. The dual optimization function can be expressed as follows by substituting Eq. (6) into the Lagrange function:

$$\begin{aligned}&{{\text{max}}}_{\alpha ,{\alpha }^{*}}\left[k(\alpha ,{\alpha }^{*})\right]\\ &\quad ={{\text{max}}}_{\alpha ,{\alpha }^{*}}\left[\sum\limits_{i=1}^{n}{\gamma }_{i}\left({\alpha }_{i}^{*}-{\alpha }_{i}\right)-\varepsilon \sum\limits_{i=1}^{n}\left({\alpha }_{i}^{*}-{\alpha }_{i}\right)\right. \\ &\qquad -\left.\frac{1}{2}\sum\limits_{ij=1}^{n}\left({\alpha }_{i}^{*}-{\alpha }_{i}\right)\left({\alpha }_{i}^{*}-{\alpha }_{i}\right)({x}_{i}.{x}_{j})\right]\end{aligned}$$
$$\text{subjected to} \; \left\{\begin{array}{l}\sum\limits_{i=1}^{n}\left({\alpha }_{i}^{*}-{\alpha }_{i}\right)=0\\ 0\le {\alpha }_{i}^{*},{\alpha }_{i}\le 0\end{array}\right. i=1, \dots ,n$$
(10)

The Lagrange multipliers \({\alpha }_{i}^{*}\) and \({\alpha }_{i}\) are used to define the optimization problem (Luenberger and Ye 1984). Once Eq. (10) is solved under the constraints in Eq. (11), the ultimate linear regression function can be stated as:

$$f\left(x,{\alpha }^{*},\alpha \right)=\sum\limits_{i=1}^{n}\left({\alpha }_{i}^{*}-{\alpha }_{i}\right)\left({x}_{i},x\right)+b$$
(11)

2.2.2 Nonlinear support vector regression

Linear SVR may not be appropriate for complex real-world problems. By mapping the input data into a high-dimensional feature space where linear regression is applicable, nonlinear SVR can be obtained. A nonlinear function is used to transform the input training pattern, \({x}_{i}\), into the feature space \(\tau ({x}_{i})\). Consequently, the formulation of the nonlinear support vector regression takes shape, as shown below.

$$f\left(x,k\right)=k\times \tau (x)+b$$
(12)

The parameter vector is represented by \(k\) and \(b\), and the mapping function \(\tau (x)\) transforms input features into a feature space with higher dimensionality.

Figure 3 illustrates the diagram of nonlinear SVR with \(\varepsilon\)-insensitive loss function. The bold points have the maximum distance from the decision boundary, representing the support vectors (Saha et al. 2020).

Fig. 3
figure 3

The insensitive loss function of nonlinear SVR

Full size image

The \(\varepsilon\)-insensitive loss function that has an error tolerance \(\varepsilon\), shown on the right side of Fig. 3, and upper and lower bounds computed by the slack variable (\({\varphi }_{i}^{*},{\varphi }_{i})\). Last, nonlinear support vector regression can be communicated as:

$$\begin{aligned} & {{\text{max}}}_{\alpha ,{\alpha }^{*}}\left[k(\alpha ,{\alpha }^{*})\right]\\ & \quad ={{\text{max}}}_{\alpha ,{\alpha }^{*}}\left[\sum\limits_{i=1}^{n}{\gamma }_{i}\left({\alpha }_{i}^{*}-{\alpha }_{i}\right)-\varepsilon \sum\limits_{i=1}^{n}\left({\alpha }_{i}^{*}+{\alpha }_{i}\right)\vphantom{\sum\limits_{ij=1}^{n}}\right. \\ & \qquad -\left.\frac{1}{2}\sum\limits_{ij=1}^{n}\left({\alpha }_{i}^{*}-{\alpha }_{i}\right)\left({\alpha }_{i}^{*}-{\alpha }_{i}\right)(\tau \left({x}_{i}\right)\cdot \tau \left({x}_{j}\right))\right]\end{aligned}$$
$$\mathrm{subjected to }\left\{\begin{array}{c}\sum\limits_{i=1}^{n}\left({\alpha }_{i}^{*}-{\alpha }_{i}\right)=0\\ 0\le {\alpha }_{i}^{*},{\alpha }_{i}\le 0\end{array}\right. i=1, \dots ,n$$
(13)

The kernel function \(\tau \left({x}_{i}\right)\cdot \tau \left({x}_{j}\right)=H({x}_{i}\cdot {x}_{j})\) can be given instead of the inner product (Vapnik 1999b) because of the complexity of the inner product \(\tau \left({x}_{i}\right)\cdot \tau \left({x}_{j}\right)\)

$$\begin{aligned}&{{\text{max}}}_{\alpha ,{\alpha }^{*}}\left[k(\alpha ,{\alpha }^{*})\right]\\ &\quad ={{\text{max}}}_{\alpha ,{\alpha }^{*}}\left[\sum\limits_{i=1}^{n}{\gamma }_{i}\left({\alpha }_{i}^{*}-{\alpha }_{i}\right)-\varepsilon \sum\limits_{i=1}^{n}\left({\alpha }_{i}^{*}+{\alpha }_{i}\right)\right. \\ &\qquad -\left.\frac{1}{2}\sum\limits_{ij=1}^{n}\left({\alpha }_{i}^{*}-{\alpha }_{i}\right)\left({\alpha }_{i}^{*}-{\alpha }_{i}\right)H({x}_{i}.{x}_{j})\right]\end{aligned}$$
$$\mathrm{subjected to }\left\{\begin{array}{c}\sum\limits_{i=1}^{n}\left({\alpha }_{i}^{*}-{\alpha }_{i}\right)=0\\ 0\le {\alpha }_{i}^{*},{\alpha }_{i}\le 0\end{array}\right. i=1, \dots ,n$$
(14)

2.3 Archimedes optimization algorithm (AOA)

The suggested approach uses the AOA algorithm, in which the immersed objects represent the individuals of the population. Like other metaheuristic algorithms according to the population (Hashim et al. 2021), AOA begins the search process with an initial population of candidate solutions represented by objects with randomly assigned densities, accelerations, and volumes (Zhang et al. 2021). Once the initial population’s fitness is assessed, the AOA works through iterations until the termination condition is met, during which each object is initialized with a random position within the fluid (Houssein et al. 2021). During each iteration of the process, each object’s acceleration has additionally recalculated according to the condition of its collision with neighboring objects. Additionally, the AOA algorithm updates each object’s volume and density. The new position of an object is determined based on the updated values of its volume, acceleration, and density (Desuky et al. 2021). The steps involved in the AOA algorithm are detailed in the following mathematical expressions.

2.3.1 Algorithmic step

The mathematical formulation of the AOA algorithm is presented in this section. AOA can be regarded as a global optimization algorithm as it involves theoretical exploitation and exploration procedures. The proposed AOA algorithm’s steps are outlined mathematically in the following sections:

  1. (a)

    step one

The positions of all objects are initialized using Eq. (15):

$${R}_{i}={lb}_{i}+{\text{rand}}\times \left({ub}_{i}-{lb}_{i}\right); i=\mathrm{1,2},\dots ,N$$
(15)

The variables \({ub}_{i}\) and \({lb}_{i}\) correspond to the upper and lower boundaries of the search space, respectively, and the variable \({R}_{i}\) denotes the ith object in a population of n objects. Using Eq. (16), set the values of volume \(({vl}_{i})\) and density \(({dn}_{i})\) for every ith object during the initialization process.

$${dn}_{i}={\text{rand}}$$
$${vl}_{i}={\text{rand}}$$
(16)

Generate a D-dimensional vector called rand that randomly generates a number between 0 and 1. Next, utilize Eq. (17) to initialize the acceleration (ac) for the \(i{\text{th}}\) object.

$${{\text{ac}}}_{i}={{\text{lb}}}_{i}+{\text{rand}}\times ({ub}_{i}-{lb}_{i})$$
(17)

During this stage, evaluate the original population and select the most outstanding fitness value object. Set \({dn}_{best}\), \({x}_{best}\), \({vl}_{best}\), and \({ac}_{best}\) to the values of the selected object.

  1. (b)

    Step two

To update the densities and volumes, apply Eq. (18) to object \(i\) for iteration t + 1.

$${dn}_{i}^{t+1}={dn}_{i}^{t}+rand\times ({dn}_{best}-{dn}_{i}^{t})$$
$${vl}_{i}^{t+1}={vl}_{i}^{t}+rand\times ({vl}_{best}-{vol}_{i}^{t})$$
(18)

The variables \({dn}_{best}\) and \({vl}_{best}\) represent the density and the volume of the best object found thus far, while the rand corresponds to a random number with uniform distribution.

  1. (c)

    Step three

To start, objects will collide and eventually strive to attain a state of equilibrium. AOA utilizes the transfer operator TF to convert the search process from exploration to exploitation, as described in Eq. (19):

$${\text{TF}}={\text{exp}}(\frac{t-{t}_{{\text{max}}}}{{t}_{{\text{max}}}})$$
(19)

The TF slowly increases in value over time until it reaches 1. The variables, \({t}_{{\text{max}}}\) and t represent the maximum allowable number of iterations and the current iteration number. The density decreasing factor, d, also aids AOA’s global to-local search. It gradually decreases over time, as shown in Eq. (20):

$${d}^{t+1}={\text{exp}}\left(\frac{{t}_{{\text{max}}}-t}{{t}_{{\text{max}}}}\right)-(\frac{t}{{t}_{{\text{max}}}})$$
(20)

The variable \({d}^{t+1}\) gradually decreases over time, allowing the algorithm to focus on exploring the already identified promising region and converge toward it. It is important to handle this variable properly to achieve a balance between exploitation and exploration.

  1. (d)

    Step four

When the value of TF is less than or equal to 0.5, it displays a collision among objects. In such a scenario, the object’s acceleration for the next iteration (t + 1) is updated, and a material (mr) is chosen Eq. (21) randomly:

$${ac}_{i}^{t+1}=\frac{{dn}_{mr}+{vl}_{mr}\times {ac}_{mr}}{{dn}_{i}^{t+1}\times {vl}_{i}^{t+1}}$$
(21)

In the equation, \({vl}_{i}\), \({ac}_{i}\), and \({den}_{i}\) refer to the volume, the acceleration, and the density of object i. On the other hand, \({vl}_{mr}\), \({ac}_{mr}\), and \({dn}_{mr}\) represent the volume, the acceleration, and the density of the random material chosen. Mentioning that TF ≤ 0.5 is significant as it ensures exploration in 33% of the iterations, altering the value to anything other than 0.5 will modify the balance between exploration and exploitation.

Assuming TF is more significant than 0.5, it indicates no occurrence of object collision; thus, the object’s acceleration should be updated for iteration \(t + 1\) utilizing Eq. (22):

$${ac}_{i}^{t+1}=\frac{{dn}_{best}+{vl}_{best}\times {ac}_{best}}{{dn}_{i}^{t+1}\times {vl}_{i}^{t+1}}$$
(22)

Normalize the acceleration employing Eq. (23) to calculate the percentage of change:

$${ac}_{1-norm}^{t+1}=u\times \frac{{ac}^{t+1}-{\text{min}}(ac)}{{\text{max}}\left(ac\right)-{\text{min}}(ac)}$$
(23)

\(u\) and \(l\) define the normalization range and are set to 0.9 and 0.1. The value of \({ac}_{i,norm}^{t+1}\) is used to calculate the percentage of each agent’s steps. The acceleration value will be higher when object i is located at a considerable distance from the global optimum, denoting that the object is exploring the environment. Conversely, if object i is relatively closer to the global optimum. The acceleration value will be lower, meaning the object is in the exploitation section. This shows the transformation of the search from the exploration section to the exploitation section. It is important to note that some search agents may need additional time in the exploration section compared to the average. Therefore, AOA ensures a balance between exploration as well as exploitation. However, the acceleration factor initially has a high value and gradually decreases over time. This aids search agents in approaching the optimal global solution while moving away from local solutions.

  1. (e)

    Step five

When in the exploration section where TF is less than or equal to 0.5, the position of the ith object for the subsequent iteration t + 1 can be determined using Eq. (24):

$${x}_{i}^{t+1}={x}_{i}^{t}+{e}_{1}\times rand\times {ac}_{i-norm}^{t+1}\times d\times ({x}_{rand}-{x}_{i}^{t})$$
(24)

The constant \({e}_{1}\) is assigned a value of 2. Alternatively, during the exploitation phase where TF is higher than 0.5, the objects adjust their positions using Eq. (25):

$${x}_{i}^{t+1}={x}_{best}^{t}+F\times {e}_{2}\times rand\times {ac}_{i-norm}^{t+1}\times d\times (T\times {x}_{best}-{x}_{i}^{t})$$
(25)

The constant \({e}_{2}\) has a value of 6. The variable T increases as time passes, and its value is directly linked to the transfer operator. Precisely, T is calculated as \(T = {e}_{3} x {\text{TF}}\cdot T\), where \({e}_{3}\) is another constant. T value increases over time within the range of \({e}_{3}\)x0.3–1, and from the ideal position, takes a certain percentage. The disparity between the best and current positions will be significant when the percentage is initially low. Consequently, the magnitude of the steps taken during the random walk will be enormous. During the search, the percentage gradually narrows the gap between the top and the present positions. This outcome results in a satisfactory equilibrium between exploitation and exploration.

$$F=\left\{\begin{array}{c}+1 if p\le 0.5\\ -1 if p>0.5\end{array}\right.$$
$${\text{where}} p=2\times rand-{e}_{4}$$
(26)

Using Eq. (26), F serves as a marker for altering the direction of movement.

  1. (f)

    Step six

Use objective function f to assess every object and keep track of the most optimal solution found thus far. Set \({dn}_{best}\), \({ac}_{best}\), \({x}_{best}\), and \({vl}_{best}\) accordingly.

In addition, the flowchart of AOA is presented in Fig. 4.

Fig. 4
figure 4

Flowchart of AOA

Full size image

2.4 Marine predators’ algorithm (MPA)

The following section presents the marine predator’s algorithm formulation (Faramarzi et al. 2020). Like other metaheuristic techniques, it involves assigning random values to a group of solutions based on the search space (Soliman et al. 2020). This can be expressed as:

$$O=LB+{g}_{1}\times (UB-LB)$$
(27)

Equation (27) defines \(UB\) as the upper boundary and \(LB\) as the lower boundary of the search space. Additionally, \({g}_{1}\) is a random number between 0 and 1. This algorithm employs a strategy in which predator and prey act as search agents. This is because as the prey searches for its food, the predator also actively searches for its prey (Abdel-Basset et al. 2021). The elite will be updated at each generation’s end (i.e., the matrix containing the most exceptional predators). The details regarding the formulation of the prey and elite (O) can be found in (Faramarzi et al. 2020).

$$\begin{aligned}&Eli=\left[\begin{array}{ccc}{O}_{11}^{1}& {O}_{12}^{1}& \begin{array}{cc}\cdots & {O}_{1d}^{1}\end{array}\\ {O}_{21}^{1}& {O}_{22}^{1}& \begin{array}{cc}\cdots & {O}_{2d}^{1}\end{array} \\ \begin{array}{c}\cdots \\ {O}_{n1}^{1}\end{array}& \begin{array}{c}\cdots \\ {O}_{n2}^{1}\end{array}& \begin{array}{c}\cdots \\ \begin{array}{cc}\cdots & {O}_{nd}^{1}\end{array}\end{array}\end{array}\right] ,\\ & O=\left[\begin{array}{ccc}{O}_{11}& {O}_{12}& \begin{array}{cc}\cdots & {O}_{1d}\end{array}\\ {O}_{21}& {O}_{22}& \begin{array}{cc}\cdots & {O}_{2d}\end{array} \\ \begin{array}{c}\cdots \\ {O}_{n1}\end{array}& \begin{array}{c}\cdots \\ {O}_{n2}\end{array}& \begin{array}{c}\cdots \\ \begin{array}{cc}\cdots & {O}_{nd}\end{array}\end{array}\end{array}\right]\end{aligned}$$
(28)

The position of prey O gets updated through a three-stage process, which will be explained in detail in the following subsections. The process considers the velocity variant ratio and replicates the entire relationship between the predator and prey (Abd Elminaam et al. 2021).

2.4.1 Stage one: high-velocity ratio

During the exploration phase, which happens in the first third of the total generations (i.e., \(\frac{1}{3}{t}_{{\text{max}}}\)), the predator moves faster than O. At this stage, the following equations update the prey \({S}_{i}\).

$${S}_{i}={R}_{B}\otimes \left({Eli}_{i}-{R}_{B}\otimes {O}_{i}\right),i=\mathrm{1,2},\dots ,n$$
(29)
$${O}_{i}={O}_{i}+P\cdot R\otimes {S}_{i}$$
(30)

The vector \({R}_{B}\) describes the Brownian motion while \(\otimes\) signifies the process of multiplying each element in the vector R within the range of 0–1 with a constant value of 0.5.

2.4.2 Stage two: the ratio of the unit velocity

In this stage, the predator and prey occupy the same territory, mimicking the food search. This action also denotes the exploration to exploitation transition of the MPA’s status. Both events hold an equal probability of occurrence during this phase. As referred to (Faramarzi et al. 2020), while the prey performs exploitation, the predator’s movement is utilized during exploration. The predator is represented by Brownian motion, while the prey’s motion is represented using a Lévy flight. This is explicitly for the time range where \(\frac{1}{3}{t}_{{\text{max}}}<t<\frac{2}{3}{t}_{{\text{max}}}\) defined in Eqs. (31) and (32):

$${S}_{i}={R}_{L}\otimes \left({Eli}_{i}-{R}_{{\text{L}}}\otimes {O}_{i}\right),i=\mathrm{1,2},\dots ,n$$
(31)
$${O}_{i}={O}_{i}+P.R\otimes {S}_{i}$$
(32)

The variable represents the Lévy distribution \({R}_{{\text{L}}}\) which is a set of random numbers. The first half of the population is used to execute Eqs. (31) and (32) to indicate the exploitation stage. The latter half of the population undergoes the following modifications:

$${S}_{i}={R}_{B}\otimes \left({R}_{B}\otimes {Eli}_{i}-{O}_{i}\right),i=\mathrm{1,2},\dots ,n$$
(33)
$${O}_{i}={O}_{i}+P.CF\otimes {S}_{i}, CF={(1-\frac{t}{{t}_{{\text{max}}}})}^{2\frac{t}{{t}_{{\text{max}}}}}$$
(34)

\({t}_{{\text{max}}}\) indicates the maximum number of generations, while CF regulates the magnitude of the predator’s displacement per step.

2.4.3 Stage three: low-velocity ratio

Once the predator’s movement surpasses its prey’s, the final step in the optimization process commences. This stage is known as the exploitation phase and is identified \(by t> \frac{2}{3} {t}_{{\text{max}}}\). It signifies the culmination of the process, as represented by the following formulation:

$${S}_{i}={R}_{{\text{L}}}\otimes \left({R}_{{\text{L}}}\otimes {Eli}_{i}-{O}_{i}\right),i=\mathrm{1,2},\dots ,n$$
(35)
$${O}_{i}={O}_{i}+P\cdot {\text{CF}}\otimes {S}_{i}, {\text{CF}}={\left(1-\frac{t}{{t}_{{\text{max}}}}\right)}^{2\frac{t}{{t}_{{\text{max}}}}}$$
(36)

2.4.4 Eddy formation and FAD effect

Environmental conditions may impact the behavior of marine predators, like those attracted to fish aggregating devices (FADs). The influence of FADs on predator behavior can be described as:

$${O}_{i}=\left\{\begin{array}{l}{O}_{i}+CF\left[{O}_{{\text{min}}}+R\otimes \left({O}_{{\text{max}}}-{O}_{{\text{min}}}\right)\otimes U \right] {r}_{5}<FAD\\ {O}_{i}+\left[{\text{FAD}}\left(1-r\right)+r\right]\left({O}_{r1}-{O}_{r2}\right) {r}_{5}>FAD\end{array}\right.$$
(37)

Equation (37) utilizes FAD = 0.2 and a binary solution represented by U. The binary solution is generated randomly and converted using a threshold of 0.2. The indices identify the prey \({r}_{1}\) and \({r}_{2}\), while the random number \({r}_{2}\) is on a scale of 0–1.

The MPA’s flowchart is mentioned in Fig. 5.

Fig. 5
figure 5

Flowchart of MPA

Full size image

2.5 Augmented grey wolf optimizer (AGWO)

The nonlinear nature of specific large power system applications, such as grid-connected wind power plants, makes it challenging to determine the transfer function leading to optimal performance. As a result, online optimization is a more feasible alternative to consider while optimizing power system performance. When it comes to online optimization of power system applications using the Grey Wolf Optimizer (GWO) algorithm, the number of search agents available is a limiting factor, unlike offline optimization of benchmark functions or transfer functions optimization.

The GWO algorithm has been introduced in its simplest form to achieve global optimization and be applicable in a wide range of scenarios. This means that, like other algorithms that have been suggested (like PSO), the GWO algorithm could be enhanced and adjusted to improve both exploitation and exploration performance in various fields. M. H. Qais et al. (2018) suggested a new modification to the GWO algorithm to improve its exploration capabilities. It has been designed not to compromise the original algorithm’s global optimization, flexibility, and simplicity abilities. In the GWO algorithm, the parameter a that primarily determines exploitation and exploration is contingent on parameter a. The parameter variation shapes the algorithm’s exploitation and exploration behavior, linearly ranging from 2 to 0 in the standard GWO. The augmentation proposed in the AGWO algorithm introduces a nonlinear and random variation of parameter a, ranging from 2 to 1, as shown in Eq. (38). Accordingly, the algorithm leans toward the exploration rather than the exploitation state.

$$\overrightarrow{a}=2-{\text{cos}}(ran)\times t/Max\_it$$
(38)
$$\overrightarrow{A}=2\overrightarrow{a}\cdot {\overrightarrow{r}}_{1}-\overrightarrow{a}$$
(39)
$$\overrightarrow{H}=2\cdot {\overrightarrow{r}}_{2}$$
(40)

In the GWO algorithm, the process of decision-making and hunting is reliant on the updates made to betas (β), deltas (δ), and alphas (α). However, the AGWO algorithm, an adaptation of GWO, simplifies this process by only considering the updates made to betas and alphas (β and α) as described in Eqs. (41)–(43). This modification greatly streamlines decision-making and improves efficiency (Long et al. 2017).

$${\overrightarrow{D}}_{a}=\left|{\overrightarrow{H}}_{1}.{\overrightarrow{X}}_{ai}-{\overrightarrow{X}}_{i}\right|, {\overrightarrow{D}}_{B}=\left|{\overrightarrow{H}}_{2}.{\overrightarrow{X}}_{\beta i}-{\overrightarrow{X}}_{i}\right|$$
(41)
$${\overrightarrow{X}}_{1}={\overrightarrow{X}}_{ai}-{\overrightarrow{A}}_{i}{\overrightarrow{D}}_{a}, {\overrightarrow{X}}_{2}={\overrightarrow{X}}_{\beta i}-{\overrightarrow{A}}_{i}{\overrightarrow{D}}_{\beta }$$
(42)
$${\overrightarrow{X}}_{i+1}=\frac{{\overrightarrow{X}}_{1}+{\overrightarrow{X}}_{2}}{2}$$
(43)

Figure 6 shows the flowchart of AGWO.

Fig. 6
figure 6

Flowchart of AGWO

Full size image

2.6 Performance evaluator

This section contains indicators that enable the assessment of hybrid models by revealing their error levels and correlation. The indicators featured in this section are symmetric mean absolute percentage error (sMAPE), mean absolute percentage error (MAPE), root mean square error (RMSE), coefficient correlation (R2), and T statistic taste (Tstate). The mathematical equations for each of these indicators are provided below:

$${R}^{2}={\left(\frac{{\sum }_{i=1}^{n}\left({b}_{i}-\overline{b }\right)\left({m}_{i}-\overline{m }\right)}{\sqrt{\left[{\sum }_{i=1}^{n}{\left({b}_{i}-\overline{b }\right)}^{2}\right]\left[{\sum }_{i=1}^{n}{\left({m}_{i}-\overline{m }\right)}^{2}\right]}}\right)}^{2}$$
(44)
$${\text{RMSE}}=\sqrt{\frac{1}{n}{\sum }_{i=1}^{n}{\left({m}_{i}-{b}_{i}\right)}^{2}}$$
(45)
$${\text{MAPE}}=\frac{100}{n}\sum_{i}^{n}\frac{\left|{b}_{i}\right|}{\left|{m}_{i}\right|}$$
(46)
$${\text{sMAPE}}=\frac{100}{n}\sum_{i}^{n}\frac{2\times \left|{b}_{i}-{m}_{i}\right|}{\left|{m}_{i}\right|+\left|{b}_{i}\right|}$$
(47)
$${T}_{{\text{state}}}=\sqrt{\frac{\left(n-1\right){{\text{MBE}}}^{2}}{{{\text{RMSE}}}^{2}-{{\text{MBE}}}^{2}}}$$
(48)

Equations (44–48) utilize the following variables: \(n\) represents the number of samples, \({b}_{i}\) signifies the predicted value, \(\overline{b }\) and \(\overline{m }\) represent the average predicted and measured values, respectively. On the other hand, \({m}_{i}\) represents the measured value.

3 Results and discussion

To predict the pile settlement, multiple hybrid models have been implemented, including the SVR-archimedes optimization algorithm (SVRAO), SVR-augmented grey wolf optimizer (SVRAW), and SVR-marine predators’ algorithm (SVRMP). During this study’s training and testing phases, the measurements obtained from experimental trials were compared to the predictions produced by three models: SVRAO, SVRMP, and SVRAW. Table 2 displays that 70% of the experimental outcomes were employed in the training stage, while the remaining 30% was utilized in the testing phase. Five statistical measures (R2, RMSE, MAPE, sMAPE, and Tstate) were utilized to thoroughly assess and contrast the algorithms’ effectiveness.

Table 2 Result of developed models
Full size table

A model that has an R2 value of nearly 1 suggests excellent performance during the training and testing stages. Meanwhile, parameters like RMSE, MAPE, s MAPE, and Tstate illustrate the error present in the model, where a lower value signifies a more satisfactory error level. The effectiveness of the employed algorithms was comprehensively evaluated and compared using these metrics, whose results are compiled in Table 2.

While the statistical performance criteria values of the developed models were reasonably similar in the testing and training phases, the SVRAO hybrid model exhibited the highest level of accuracy, with an R2 value of 0.989 during the training phase and 0.997 in the testing phase. SVRAO showed the highest degree of agreement between the predicted and observed values, as evidenced by its RMSE, MAPE, and sMAPE being the lowest among all the other models. On the other hand, the SVRAW models exhibit the weakest performance with an R2 value of 0.976 and 0.968 during the training and testing phases, respectively, and the highest values of RMSE, MAPE, and sMAPE. This suggests that the SVRAW models have poor performance. However, the SVRMP has an intermediate performance among the other two models with an R2 value of 0.981.

Table 3 indicates the comparison between the best present model, as indicated in Table 2, and the published articles’ models.

Table 3 Comparing the present study’s model with the published articles’ model
Full size table

Figure 7 depicts a scatter plot that compares the performance of the hybrid models based on two parameters: R2, which indicates the level of agreement, and RMSE, which indicates the degree of dispersion. The centerline of the plot is positioned at X = Y coordinates, and the distance between the points and the centerline indicates the level of accuracy in the model’s performance. The SVRAO model exhibited a narrow range of dispersion, with the data points closely grouped around the centerline. In contrast, the SVRMP and SVRAW models indicated relatively similar levels of performance where their data points were more broadly scattered.

Fig. 7
figure 7

Training and testing phase scatter plot of the given models

Full size image

The observed variance was impacted by the deviation between the anticipated and actual values, notably diminished during the test phase, as illustrated in Fig. 8. During the training phase, the SVRAW model displayed minimal dispersion, and the difference in the line angles between the measured bold points and train triangles was more perceptible compared to the testing phase. Despite identifying disparities between the predicted and measured values for some samples during the training phase, leading to noteworthy divergences, enhancements in performance and favorable learning outcomes have somewhat mitigated this weakness.

Fig. 8
figure 8

Line series plot for comparison between the measure and predicted value of the developed model

Full size image

One additional analysis that should be carried out involves observing the percentage error for each pile, indicating the degree of difference between the predicted settlement rate and the actual rate. Figures 9 and 10 showcased how well each model type predicted pile settlement and compared their effectiveness. As per the error distribution chart, the precision of predicting pile settlement varied across SVRAW, SVRMP, and SVRAO models. SVRAO demonstrated the lowest degree of error, with most predicted values being close to the actual values. SVRMP exhibited a moderate error, with a broader range of predicted values. At the same time, SVRAW had the highest error level, with several predicted values deviating significantly from the actual values. The SVRAO model generally exhibited the most trustworthy results, while SVRAW exhibited the weakest performance, and SVRMP performance was in the middle. The distribution chart of errors offered significant insights into the relative pros and cons of each model’s predictive accuracy, aiding researchers in identifying the most efficient model for forecasting pile settlement in real-world scenarios.

Fig. 9
figure 9

Scatter box plot for error percentage of related models

Full size image
Fig. 10
figure 10

Error percentage of developed models is based on a density scatter plot

Full size image

3.1 Sensitivity analyses

3.1.1 Cosine amplitude method (CAM)

Table 4 displays the outcomes of sensitivity analyses focusing on different input parameters. Sensitivity analysis serves as a method for gaging how responsive the results of a model or study are to changes in input variables (Ardakani and Kordnaeij 2019; Khatti and Grover 2023a, d). In this context, Table 4 examines the degree of sensitivity of results to alterations in specific input parameters. Five input parameters have been selected for sensitivity evaluation: Lp/D, Ls/Lr, N_SPT, UCS, and Qu.

Table 4 Result of the sensitivity analysis
Full size table

The sensitivity measure (ST) signifies the extent to which the output changes in response to variations in the input parameter. A higher ST value implies that the output is more responsive to that specific parameter. ST_conf potentially signifies the confidence intervals associated with the sensitivity measures. Confidence intervals aid in assessing the degree of uncertainty within the results of the sensitivity analysis.

The ST fluctuates among the input parameters, indicating that the results of the model or study exhibit varying levels of sensitivity to different parameters. For instance, the parameter “N_SPT” possesses a relatively high sensitivity value of 3.7E−08, signifying that alterations in “N_SPT” exert a substantial influence on the study’s results. The “ST_conf” values, which represent confidence intervals, offer a range within which the sensitivity measures are likely to lie with a certain level of confidence.

4 Conclusion

This investigation’s principal aim is to assess the performance of 3 hybrid SVRs in estimating the rock-socketed piles settling. Three optimization algorithms, namely Archimedes Optimization algorithm (AOA), marine predators’ algorithm (MPO), and Augmented grey wolf optimizer (AGWO), are employed in constructing the SVR models. In order to achieve this goal, the investigators examined the outcomes of experiments using pile-driving analyzers as well as the features of the heaps and the soil. The investigation produced the subsequent significant findings:

  1. 1.

    The study shows the promising predictive ability of SVR models for SP, with training R2 at 0.976 and testing at 0.968. SVRAO outperformed SVRMP and SVRAW, especially for small SP values. AOA optimization demonstrated superior performance for all SP ranges.

  2. 2.

    Despite displaying weaker performance than the other SVR models across all statistical indices, SVRAW still produced acceptable results, achieving respective R2, RMSE, MAPE, sMAPE, and Tstate values of 0.968, 0.780, 5.220, 0.0018, and 1.156. On the other hand, the SVRAO model demonstrates the most optimal performance, with the highest R2, RMSE, MAPE, sMAPE, and Tstate values observed during the phases of testing and training, excluding MAPE in the training stage.

  3. 3.

    The advantages of the present study include improving predicting accuracy, robust performance, real-world data utilization, and informing decision-making.

  4. 4.

    The present study also has limitations, including limited input parameters and data variability.

  5. 5.

    The future scope for expansion can encompass diverse parameters, hybrid model integration, validation through long-term monitoring, and generalizability and scalability.