1 Introduction

The potency of soil to tolerate shear stress is referred to by the undrained shear strength (USS) of soil. It is one primary value in the computation of various geotechnical phenomena, such as settlement (Esmaeili-Falak et al. 2017, 2018). Moreover, to design foundations (deep and shallow foundations, both of them), the USS of soil is also of superior matter. Hence, circumspect appraisal of the shear strength is indispensable. Various analytical and experimental works can be performed on different types of soils to determine the properties of soils (Sarkhani Benemaran 2017; Poorjafar et al. 2021; Esmaeili-Falak 2017; Esmaeili-Falak et al. 2020). After the years, scholars had extended plenty of analytical and experiential procedures to specify the shear strength (Sarkhani Benemaran et al. 2020), for instance, bearing capacity (BCM), strain path (SPM), cavity expansion (CEM), and finite element (FEM) procedures (Huang et al. 2004). In addition, mixtures of mentioned procedures were examined as well to get an advanced commentary of shear strength, such as cavity expansion-finite element (Abu-Farsakh et al. 2003), cavity expansion-strain path (Yu and Whittle 1999), cavity expansion-bearing capacity (Salgado et al. 1997), and strain path-finite element (Teh and Houlsby 1991).

Nevertheless, many of these techniques synthesized streamlining presumptions about soil condition, margin circumstances, and failure benchmark (Esmaeili Falak et al. 2020). Hence, detecting theoretic procedures requires endorsement from in-situ and experimental soil parameters. In this regard, the unconsolidated undrained triaxial test can be very helpful. However, unfortunately, managing triaxial tests need more time as well as is costly. Furthermore, an unavoidable disorder in transport, handling, and collecting soil specimens means the test conclusions are controversial.

In-situ cone penetration tests can be effectually applied for soil recognition, appraisal of soil virtues, such as shear strength, and numbers of other geotechnical usages. In-situ CPT is trusty, quick, and economical compared to the old soil properties tests related to boring and experimental tests. The CPT test can supply persistent profile information with profundity relevant to soil stiffness and strength variables, which is good to estimate the USS of soil. Hence, some experimental procedures were extended in the last decades to approximate the USS from in-situ cone penetration test parameters (Lunne 1982; Senneset 1982). Nonetheless, many numbers of these techniques bring some presumptions and discernments in choosing suitable correlation coefficients factors like the cone tip factor, \({N}_{kt}\) among the CPT profiles information and USS that can impact the computation of shear strength. This can affect in incompatible precision of appraising the USS for various site situations.

In the recent decades, using artificial-based neural networks has enhanced and carried out with successful results in various civil (Masoumi et al. 2020) and geotechnical engineering problems, for example, shallow foundation settlement, liquefaction, the behavior of frozen soils, settlement behavior of pile foundations, swelling pressure of expansive soil and so forth (Sarkhani Benemaran et al. 2020; Das and Basudhar 2006; Ikizler et al. 2010; Neaupane and Achet 2004; Nejad and Jaksa 2017; Shahin et al. 2009; Esmaeili-Falak et al. 2019; Nassr et al. 2018). Regression is also one of the methods to determine the relationship between input and output variables such as MARS (Zhang et al. 2021; Sahraei et al. 2021; Raja and Shukla 2021).

Neural network application to estimate the USS of soil from the CPT test is anticipated to solve the deficiencies mentioned above in traditional techniques because there is no correlation hypothesis or judgment (Samui and Kurup 2012). To some extent, the neural network method tends to iterate the human brain learnings from a prior instance and is learned by specific mathematical methods. This aim can be gained from reiterative steps by regulating the weights, node numbers, and a number of layers. The difficulty of the neural network could be changed by altering the transfer function or the model form (Shahin et al. 2002). After identifying the most precise neural network model after training well, the developed algorithm could be explored for estimating the USS for other sites. An ANN is utilized to develop a model with more firm forecasting of USS from CPT records in a study (Abu-Farsakh and Mojumder 2020). First, a dataset was created of soil boring records and experimental tests from 70 sites located in Louisiana. Then, various neural network models were trained by cone tip resistance, sleeve friction, and other assessable soil characteristics. The conclusions were next compared with an experiential reference technique of specifying USS from CPT. The outputs specified that the neural network techniques outperformed the reference method, which approves this model's applicability in estimating the USS.

Another study applied data-driven extreme gradient boosting and random forest methods optimized with the Bayesian optimization method to find the relationships between the USS and soil parameters. To this aim, five variables containing the pre-consolidation stress, effective vertical stress, liquid limit, plastic limit, and natural water content are selected. It is shown that XGBoost- and RF-based models outperform others. Along with this, the XGBoost-based model provides properties significance ranks, which introduces it as an efficient tool for predicting geotechnical parameters and enhancing the model's interpretability (Zhang et al. 2021).

The prime objective of this paper is to find out the applicability of utilizing the multivariate adaptive regression splines (MARS) model for predicting the USS of soil from cone penetration test records to generate models which are to be used in practical applications. Moreover, various degrees of interactions of models are examined to have comprehensive, accurate, and reliable outputs. To gain this aim, the model had five input variables named cone tip resistance, sleeve friction, liquid limit, plastic limit, overburden weight, and USS of soil as output. To evaluate the accuracy of the proposed models, six statistical performance indices were considered.

2 Dataset and methodologies

2.1 Description of the dataset

To predict the undrained shear strength of soil from the cone penetration test, CPT data and corresponding bore log data were collected from 70 different sites in Louisiana (Fig. 1) (Mojumder 2020). Five different variables that can affect the value of the USS were considered as input variables. These variables included: cone tip resistance (CTR), sleeve friction (SF), liquid limit (LL), plastic limit (PL), and overburden weight (OBW). The statistics and histograms of the variables used for developing the model along with their normal distribution curves are given in Table 1 and Fig. 2, respectively.

Fig. 1
figure 1

Locations of cone penetration test (CPT) sites

Full size image
Table 1 The statistical values of the input and output variables
Full size table
Fig. 2
figure 2

Histograms of input (a–e) and output (f) variables and their normal distribution curves

Full size image

2.2 Multivariate adaptive regression splines (MARS)

Multivariate asymmetric regression process is defined as multivariate adaptive regression spline (MARS) (Friedman 1991; Sekulic and Kowalski 1992; Friedman and Roosen 1995). Its most important duty is the amount's forecast of a continual affiliate variable, \(y(n\times 1)\), using a series of inputs that is independent, \(X(n\times p)\). The MARS could be presented as:

$$y=f\left(x\right)+e$$
(1)

where ƒ is a sum of basis functions which is weighted that depend on \(x\), and \(e\) presented the error vector in \((n\times 1)\) dimension. The multivariate adaptive regression spline method is a generalization of classification and regression trees (Hastie et al. 2001) but prevailing the constraints of classification and regression tree (CART). This regression model does not request any preference assumption in the case of the fundamental operational connection between inputs and output variables. Apart from that, this connection is appointed from a totality of coefficients and piecewise multinomial of degree basis functions (\(q\)) fully related to the regression records \((x, y).\)

This regression method is created by coordinating the basis function to various spaces of the inputs. MARS uses bilateral shorten power operates as spline basis function (BF), shown in the below relations (Friedman and Roosen 1995):

$${[-\left(x-t\right)]}_{+}^{q}=\left\{\begin{array}{l}{\left(t-x\right)}^{q} if x<t\\ 0 otherwise\end{array}\right\}$$
(2)
$${[+\left(x-t\right)]}_{+}^{q}=\left\{\begin{array}{l}{\left(t-x\right)}^{q} if x\ge t\\ 0 otherwise\end{array}\right\}$$
(3)

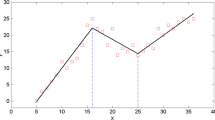
In these relations, the power to which the splines are picked up specifies the degree of the monotony of the resulting appraise all defined \(q\) (≥ 0). Notice that when \(q\) is equal to one, just simple lineal splines are appraised. For example, Fig. 3 shows a pair of splines for \(q\) equal to one at node 3.5. This figure shows a mirrored pair of hinge functions with a knot at for example 3.5.

Fig. 3
figure 3

A schematic exhibition of a spline BF. Dashed line (x < t, -(x-t)), solid line (x > t, + (x-t))

Full size image

MARS of a dependent variable \(y\) with \(M\) basis function could be represented as Eq. 4 (Xu et al. 2004; Cheng and Cao 2014; Benemaran and Esmaeili-Falak 2020):

$$\widehat{y}={\widehat{f}}_{m}\left(x\right)={c}_{0}+\sum\limits_{m=1}^{M}{c}_{m}{B}_{m}(x)$$
(4)

being ŷ the affiliate variable forecasted by the MARS, \({c}_{0}\), \({B}_{m}(x)\) and \({c}_{m}\) shows a constant, the mth basis function and the coefficient of mth basis function, respectively. Specifically, both parameters are demonstrated in the model, and the node situations for each variable have to be optimized. Moreover, this regression method utilizes generalized cross-validation (GCV) to describe the basic function contained in the model.

Indeed, the mean squared residual error apportioned by a penalty factor specifying the generalized cross-validation which pertains to the model intricacy, and it is described as Eq. 5 (Friedman 1991; Friedman and Roosen 1995):

$$GCV\left(M\right)=\frac{\frac{1}{n}\sum\limits_{i=1}^{n}{({y}_{i}-{\widehat{f}}_{M}({x}_{i}))}^{2}}{{(1-C(M)/n)}^{2}}$$
(5)

So that an intricacy penalty that increases with a number of basis function in the model is shown as \(C(M)\) (Benemaran and Esmaeili-Falak 2020):

$$C(M)=(M+1)+dM$$
(6)

where \(M\) and \(d\) value the basis function in Eq. (4) and a penalty factor for all one of BF included in the model. In addition, the must utilize the GCV make clear before with the parameters N-subsets and the residual sum of squares to achieve correct results. The MARS model was performed with the ARESLab toolbox in MATLAB (Jekabsons 2011).

2.3 Performance evaluators

Different statistical evaluators were used to appraisal the performance of developed models for predicting the USS. Coefficient of determination (\({R}^{2}\)), root mean squared error (RMSE), mean absolute percentage error (MAPE), mean absolute error (MAE), performance index (PI), and OBJ were used as precision measurements (Eqs. 7–12):

$${R}^{2}={\left(\frac{\sum\limits_{p=1}^{P}\left({t}_{P}-\overline{t }\right)\left({y}_{P}-\overline{y }\right)}{\sqrt{\left[\sum\limits_{p=1}^{P}{\left({t}_{P}-\overline{t }\right)}^{2}\right]\left[\sum\limits_{p=1}^{P}{\left({y}_{P}-\overline{y }\right)}^{2}\right]}}\right)}^{2}$$
(7)
$$RMSE=\sqrt{\frac{1}{P}\sum\limits_{p=1}^{P}{\left({y}_{p}-{t}_{p}\right)}^{2}}$$
(8)
$$MAPE=\frac{1}{P}\sum\limits_{p=1}^{P}\left|\frac{{t}_{P}-{y}_{P}}{{t}_{P}}\right|$$
(9)
$$MAE=\frac{1}{P}\sum\limits_{p=1}^{P}\left|{y}_{p}-{t}_{p}\right|$$
(10)
$$PI=\frac{1}{\left|\overline{t }\right|}\frac{RMSE}{\sqrt{{R}^{2}}+1}$$
(11)
$$OBJ=\frac{RMSE+MAE}{{R}^{2}+1}$$
(12)

where, \({y}_{P}\) represent the predicted values of the \({P}\)th pattern, \({t}_{P}\) depicts the target values of the \({P}\)th pattern, \(\overline{t }\) shows the averages of the target values, \(\overline{y }\) is the averages of the predicted values, and \(P\) is the number of dataset.

3 Result and discussion

The details of the basis functions and corresponding equations are shown in Table 2 for the degree of interactions of 2, 3, and 4 MARS equations. The explicable MARS approach different orders (from 2 to 4) formulations to estimate the USS results are created in Eqs. (13–15), respectively. Basis functions of 2, 3, and 4 order MARS models from 3 to 37 were assessed and measured. With an incremental number of basis functions, the performance indicators for data grew to the proper orientation. They gained the supreme outcomes when the number of basis functions was 17, 29, and 31 for MARS-O2, O3, and O4, respectively. By increasing the degree of interactions of equations from 2 to 4, the values of R2 raised from 0.8339 to 0.8619. on the other hand, RMSE shows a decline of about 34.8, and MAE values decreased from 296.85 to 270.84.

Table 2 Basis functions and corresponding equations of MARS approach for USS
Full size table

Order 2:

$$USS = 1213.536 +137.701\times BF1- 123.36\times BF2 + 615.968\times BF3+2791.082\times BF4 + 322.3104\times BF5 - 252.727\times BF6- 1.294\times BF7 - 2204.53\times BF8+ 1416.494\times BF9 - 774.561\times BF10 + 204.69\times BF11$$
(13)

Order 3:

$$USS = 1041.429 +108.146\times BF1-74.742\times BF 2-484.94\times BF3 +25.556\times BF4 +689.83\times BF 5-323.353\times BF 6- 826.5\times BF7 + 34.329\times BF8 + 536.98\times BF9- 32.992\times BF10+ 646.669\times BF11- 371.9\times BF12- 114.455\times BF13$$
(14)

Order 4:

$$USS= 1250.073+ 78.435\times BF1-117.763\times BF2- 456.211\times BF3 +65.9\times BF4 + 31.39\times BF5 + 274.632\times BF6- 1164.09\times BF7-1319.083\times BF8 + 1.255\times BF9 + 708.68\times BF10 +75.149\times BF11- 782.71\times BF12 + 275.08\times BF13$$
(15)

The result of developed models for predicting USS value is presented as follows. Figure 4 specifies acceptable potential in the modeling phase. Comparing the measured records from experimental efforts with those predicted by MARS-O2, O3, and O4 models are supplied in Fig. 4. It can be observed that the developed models have R2 larger than 0.834 and 0.9236. It means that the correlation between measured and predicted values from developed models is in good correlation so that it shows the highest accuracy in the regression process. Besides, to compare the productivity of the applied models, six statistical evaluators (R2, RMSE, MAE, MAPE, PI, and OBJ) were utilized. The results are shown in Table 3. MARS-O2 has the worst values regarding MARS models, which its R2 stood at 0.8339, and PI 0.1618. All indices are better by increasing the MARS interaction. For instance, RMSE declines from 393.79 to 358.99. By apprising the PI and OBJ indexes as the whole model evaluator, which considers other indexes altogether, the MARS-O4 model outperforms the other two models, with lower PI and OBJ values equal to 0.1464 and 338.27. Therefore, the 4th interaction equation of MARS for predicting USS of soil can be recognized as the proposed regression model.

Fig. 4
figure 4

The scatter plot of between observed and predicted USS

Full size image
Table 3 The results of created models
Full size table

The performance assessment results of the implemented models are portrayed in Fig. 5, showing a graphical comparison between the distribution of errors. Also, an acceptable fit between measured and predicted USS values are obtainable from the time series plots presented in Fig. 5. As can be seen, in all proposed models, the estimated USS values demonstrate acceptable agreement with experimental records, representing the workability of proposed equations for predicting the USS values with high accuracy. Comparison of three developed equations supplied that MARS-O4 has a better result than MARS-O3, followed by MARS-O2. Based on error distribution figures, the MARS-O4 model results in the lowest error percentage in the USS predicting process, providing roughly accurate predictions than those of the rest developed methods specified.

Fig. 5
figure 5

USS prediction using MARS models with distribution

Full size image

3.1 Sensitivity analysis

An evaluation of the sensitivity of the models was conducted to assess the most determinative input parameters to compute the USS. Various input data were built by removing a single input parameter simultaneously, and the test data set reported the amounts of three statistical performance criteria as \({R}^{2}\), RMSE, and MAE. The best model for the sensitivity analysis is chosen using the statistical performance criteria. In the present study, the MARS-O4 model is selected due to its remarkable performance. The results are as Table 4, which is shown that the cone tip resistance (CTR) is the most influential parameter for predicting the USS using the mentioned model, with a decline of about 0.1831 for \({R}^{2}\). From this perspective, although they are not as effective as CTR, the overburden weight (OBW) and sleeve friction (SF) parameters are in the following ranks, respectively. It is worth considering that eliminating input variables may only cause a minimal performance loss for the model, but in the present study, because the analysis was based on experimental measurements, eliminating variables could decline the model's generalizability. Considering the multicollinearity problem has not a significant impact on the fit of a model. It commonly does not impress remarkably on predictions, and the present study does not prefer deleting any variable.

Table 4 Sensitivity analysis of input variables using MARS-O4 model
Full size table

4 Conclusion

In this study, Multivariate Adaptive Regression Splines (MARS) model with different degrees of interactions were proposed for predicting the undrained shear strength of soil from cone penetration test data. To this aim, the model had five variables named cone tip resistance, sleeve friction, liquid limit, plastic limit, and overburden weight. To evaluate the accuracy of the developed model, six performance indices were considered.

MARS-O2 has the worst values regarding MARS models, which its R2 stood at 0.8339, and PI 0.1618. All indices better by increasing the MARS interaction. The MARS-O4 model outperforms the other two models by apprising the PI and OBJ indexes, with lower PI and OBJ values equal to 0.1464 and 338.27. Therefore, the 4th interaction equation of MARS for predicting USS of soil can be recognized as the proposed regression model.

In all proposed models, the estimated USS values demonstrate acceptable agreement with experimental records, representing the workability of proposed equations for predicting the USS values with high accuracy. Comparison of three developed equations supplied that MARS-O4 has a better result than MARS-O3, followed by MARS-O2. Based on error distribution figures, the MARS-O4 model results in the lowest error percentage in the USS predicting process, providing roughly accurate predictions than those of the rest developed methods specified.