Stochastic behavior of parallel system with expert repair and maintenance

Abstract

This paper examines the effect of preventive maintenance and repair done by different repairpersons on the system performance. By means of semi-Markov process and regenerative point technique, the researcher has developed a stochastic model of two unit parallel system. Both units are identical in nature. A usual repairperson visits the system to conduct preventive maintenance at the completion of maximum operation time and repair at the failure stage of the unit. At the elapse of the pre-definite time (called maximum repair time), the usual repairperson inspects the failed unit to examine the feasibility of further repair by the expert repairperson; otherwise that unit will be replaced by a new one with some replacement time. The unit may work as good as new after getting maintenance, repair and replacement as well. The switch devices are considered as perfect. Various measures of system usefulness such as MTSF, availability and profit have been derived to depict the usefulness of expert repair facility.

1 Introduction

The technological development and ever-increasing demand of society is making the designing of systems more complex. Repairing of such systems turn out to be an important issue in the reliability theory. Again, the continued function and aging of systems progressively lessen their performance, reliability and security. Thus, not only to maintain the operational power, but also to reduce the failure rate, preventive maintenance of the systems is necessary after a pre-definite phase of operation time. Many attempts from the authors, engineers and industries have been devoted to improve the repair performance of accessible machines. Numerous researchers have developed the maintenance model with different sets of assumptions such as imperfect switchover, two-phase repair, degradation of system and hard and soft failures (see (Lam 1997; Mahmoud and Mahmoud 1983; Rakesh 1986; Mokaddis et al. 1990; Niwas et al. 2013; Malik et al. 2016; Qiu et al. 2018). Furthermore, as one of the key parts of a repairable system, the repairperson (server) can affect the economic assistance of the system. Thus, the repairperson’s capability of repairing all the snags that occurred during the repairing process with in specific period of time becomes essential (Jose 2012; Barak et al. 2018; Haji and Yunus 2015). Apart from this, arrival time and vacations of repairperson are some other major issues which have been discussed in the last few years (see Chander 2005; Chander and Bhardwaj 2009; Malik and Gitanjali 2012; Tuteja and Malik 1994; Sridharan and Mohanavadivu 1998).

Thus to maintain a required level of reliability and system performance, in this paper we develop a parallel system of two identical units stochastically by incorporating the ideas of preventive maintenance and repair by an expert server. A usual repairperson visits the system to conduct preventive maintenance at the completion of maximum operation time and repair at the failure stage of the unit. At the elapse of the pre-definite time (called maximum repair time), the usual repairperson inspects the failed unit to examine the feasibility of further repair by the expert repairperson; otherwise that unit will be replaced by a new one with some replacement time. The unit may work as good as new after getting maintenance, repair and replacement as well. The switch devices are considered as perfect. By means of semi-Markov process and regenerative point technique, various measures of system usefulness such as MTSF, availability and profit have been derived to depict the usefulness of the expert repair facility.

2 System description

E :

Set of regenerative states

N ₀ :

Unit in normal and functioning mode

λ :

Constant failure rate of the unit

υ ₀ :

Constant rate of repair instance taken by the usual repairman

η ₀ :

Constant rate of operation instance of the unit

h(t)/H(t):

pdf/cdf of the inspection time of the unit

f(t)/F(t):

pdf/cdf of the replacement time of the unit

g(t)/G(t):

pdf/cdf of the repair time of the unit taken by the usual repairman

$p(t)/P(t)$ :

pdf/cdf of the preventive maintenance time of the unit

${\text{FU}}_{\text{pm}} /{\text{FU}}_{\text{PM}}$ :

Unit under preventive maintenance/under preventive maintenance continuously from the previous state

${\text{FW}}_{\text{pm}} /{\text{FW}}_{\text{PM}}$ :

Unit waiting for preventive maintenance/waiting for preventive maintenance continuously from the previous state

${\text{FW}}_{\text{r}} /{\text{FW}}_{\text{R}}$ :

Unit failed and waiting for repair/waiting for repair continuously from the previous state

${\text{FW}}_{\text{re}} /{\text{FW}}_{\text{Re}}$ :

Unit failed and waiting for repair by expert server/waiting for repair by expert server continuously from the previous state

${\text{FU}}_{\text{r}} /{\text{FU}}_{\text{R}}$ :

Unit failed and under repair/under repair continuously from the previous state

FU_re/FU_Re:

Unit failed and under repair with expert server/under repair continuously from the previous state with expert server

${\text{FU}}_{\text{Rp}} /{\text{FU}}_{\text{RP}}$ :

Unit failed and under replacement/under replacement continuously from previous state

q_ij(t)/Q_ij(t):

pdf/cdf of passage time from regenerative state i to a regenerative state j or to a failed state j without visiting any other regenerative state in (0, t]

W_i(t):

Probability that the server is busy in the state S_i up to time ‘t’ without making any transition to any other regenerative state or returning to the same state via one or more non-regenerative states

$m_{ij}$ :

Contribution to mean sojourn time in state $S_{i} \in E$ and non-regenerative state if it occurs before transition to $S_{j} \in E$. Mathematically, it can be written as $m_{ij} = \int_{0}^{\infty } {t{\text{d}}(Q_{ij} (t))} = - q_{ij}^{*\prime} (0)$

μ _i :

The mean sojourn time in state S_i which is given by $\mu_{i} = E(T) = \int_{0}^{\infty } {P(T > t)\,{\text{d}}t} = \sum\nolimits_{j} {m_{ij} } ,$ where T denotes the time to system failure

$\sim /*$ :

Symbol for Laplace–Stieltjes transform/Laplace transform

${\boxed{\varvec{S}}}/$ ©:

Symbols for Stieltjes convolution/Laplace convolution

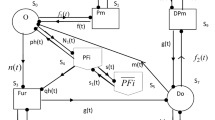
The possible transitions between states along with transition rates for the system model are shown in Fig. 1. The states S₀–S₉ are regenerative, while the other remaining states are non-regenerative.

Fig. 1

State transition diagram

2.1 Transition probabilities and mean sojourn times

The transition probability matrix (t.p.m) of the embedded Markov chain is $p = p_{ij} = Q_{ij} (\infty ) = Q(\infty )$, where the non-zero elements p_ij =  probability that the operating unit j in state S_i fails during time (t, t + dt) and unit j + 1 does not fail up to time t:

$$p_{ij} = \mathop {\lim }\limits_{t \to \infty } Q_{ij} (t) = \int \limits_{0}^{\infty } q_{ij} (t)\,{\text{d}}t.$$

Using the above relation, we have

$$p_{01} = \frac{{\eta_{0} }}{{\eta_{0} + 2\lambda }},\quad p_{05} = \frac{2\lambda }{{\eta_{0} + 2\lambda }},\quad p_{20} = p^{*} (\lambda + \eta_{0} ),$$

$$p_{23} = \frac{{\eta_{0} }}{{\lambda + \eta_{0} }}[1 - p^{*} (\lambda + \eta_{0} )],\quad p_{24} = \frac{\lambda }{{\lambda + \eta_{0} }}[1 - p^{*} (\lambda + \eta_{0} )],\quad p_{50} = g^{*} (\lambda + \eta_{0} + \alpha_{0} ),$$

$$p_{56} = \frac{{\eta_{0} }}{{\alpha_{0} + \lambda + \eta_{0} }}[1 - g^{*} (\lambda + \eta_{0} + \alpha_{0} )],\quad p_{57} = \frac{{\alpha_{0} }}{{\alpha_{0} + \lambda + \eta_{0} }}[1 - g^{*} (\lambda + \eta_{0} + \alpha_{0} )],$$

$$p_{5,10} = \frac{\lambda }{{\alpha_{0} + \lambda + \eta_{0} }}[1 - g^{*} (\lambda + \eta_{0} + \alpha_{0} )],\quad p_{6,14 } = p_{10,11 } = 1 - g^{*} (\alpha_{0} ),$$

$$p_{7,17} = \frac{\lambda }{{\lambda + \eta_{0} }}[1 - h^{*} (\lambda + \eta_{0} )],\quad p_{7,18} = \frac{{\eta_{0} }}{{\lambda + \eta_{0} }}[1 - h^{*} (\lambda + \eta_{0} )],\quad p_{79} = bh^{*} (\lambda + \eta_{0} ),$$

$$p_{9,22} = \frac{\lambda }{{\lambda + \eta_{0} }}[1 - g_{1}^{*} (\lambda + \eta_{0} )],\quad p_{25.4} = \frac{\lambda }{{\lambda + \eta_{0} }}[1 - p^{*} (\lambda + \eta_{0} )]p^{*} (0),\quad p_{90} = g_{1}^{*} (\lambda + \eta_{0} ),$$

$$p_{9,21} = \frac{{\eta_{0} }}{{\lambda + \eta_{0} }}[1 - g_{1}^{*} (\lambda + \eta_{0} )],\quad p_{11,12} = p_{14,15} = p_{17,12} = p_{18,15} = a,$$

$$p_{8,19} = \frac{{\eta_{0} }}{{\lambda + \eta_{0} }}[1 - f^{*} (\lambda + \eta_{0} )],\quad p_{11,13 } = p_{14,16} = p_{17,13} = p_{18,16} = b,$$

$$p_{22.3} = \frac{{\eta_{0} }}{{\lambda + \eta_{0} }}[1 - p^{*} (\lambda + \eta_{0} )]p^{*} (0),\quad p_{52.6} = \frac{{\eta_{0} }}{{\alpha_{0} + \lambda + \eta_{0} }}[1 - g^{*} (\lambda + \eta_{0} + \alpha_{0} )]g^{*} (\alpha_{0} ),$$

$$p_{78} = ah^{*} (\lambda + \eta_{0} ),\quad p_{52.6,14,15} = \frac{{a\eta_{0} }}{{\alpha_{0} + \lambda + \eta_{0} }}[1 - g^{*} (\lambda + \eta_{0} + \alpha_{0} )][1 - g^{*} (\alpha_{0} )]h^{*} (0)f^{*} (0),$$

$$p_{52.6,14,16} = \frac{{b\eta_{0} }}{{\alpha_{0} + \lambda + \eta_{0} }}[1 - g^{*} (\lambda + \eta_{0} + \alpha_{0} )][1 - g^{*} (\alpha_{0} )]h^{*} (0)g_{1}^{*} (0),$$

$$p_{55.10} = \frac{\lambda }{{\alpha_{0} + \lambda + \eta_{0} }}[1 - g^{*} (\lambda + \eta_{0} + \alpha_{0} )]g^{*} (\alpha_{0} ),$$

$$p_{55.10,11,12} = \frac{a\lambda }{{\alpha_{0} + \lambda + \eta_{0} }}[1 - g^{*} (\lambda + \eta_{0} + \alpha_{0} )][1 - g^{*} (\alpha_{0} )]h^{*} (0)f^{*} (0),$$

$$p_{55.10,11,13} = \frac{b\lambda }{{\alpha_{0} + \lambda + \eta_{0} }}[1 - g^{*} (\lambda + \eta_{0} + \alpha_{0} )][1 - g^{*} (\alpha_{0} )]h^{*} (0)g_{1}^{*} (0),$$

$$p_{75.17,12} = \frac{a\lambda }{{\lambda + \eta_{0} }}[1 - h(\lambda + \eta_{0} )]h^{*} (0)f^{*} (0),$$

$$p_{75.17,13} = \frac{b\lambda }{{\lambda + \eta_{0} }}[1 - h(\lambda + \eta_{0} )]h^{*} (0)g_{1}^{*} (0),$$

$$p_{72.18,15} = \frac{{a\eta_{0} }}{{\lambda + \eta_{0} }}[1 - h(\lambda + \eta_{0} )]h^{*} (0)f^{*} (0),$$

$$p_{72.18,16} = \frac{{b\eta_{0} }}{{\lambda + \eta_{0} }}[1 - h(\lambda + \eta_{0} )]h^{*} (0)g_{1}^{*} (0),\quad p_{85.20} = \frac{\lambda }{{\lambda + \eta_{0} }}[1 - f^{*} (\lambda + \eta_{0} )]f^{*} (0),$$

$$p_{82.19} = \frac{{\eta_{0} }}{{\lambda + \eta_{0} }}[1 - f^{*} (\lambda + \eta_{0} )]f^{*} \left( 0 \right),\quad p_{95.22} = \frac{\lambda }{{\lambda + \eta_{0} }}[1 - g_{1}^{*} (\lambda + \eta_{0} )]g_{1}^{*} (0),$$

$$p_{92.21} = \frac{{\eta_{0} }}{{\lambda + \eta_{0} }}[1 - g_{1}^{*} (\lambda + \eta_{0} )]g_{1}^{*} (0),$$

$$p_{12} = p_{32} = p_{45} = p^{*} (0), \quad p_{12,5} = p_{15,2} = p_{20,5} = f^{*} (0) = p_{13,5} = p_{16,2} = p_{19,2} = p_{21,2} = p_{22,5} = g_{1}^{*} (0).$$

It can easily be verified that

$$\begin{aligned} p_{01} + p_{05} & = p_{12} = p_{13} = p_{20} + p_{23} + p_{24} = p_{32} = p_{50} + p_{56} + p_{57} + p_{5,10} \\ & = p_{45} = p_{78} + p_{79} + p_{7,17} + p_{7,18} = p_{80} + p_{8,19} + p_{8,20} \\ & = p_{90} + p_{9,21} + p_{9,22} = p_{12,5} = p_{13,5} = p_{15,2} = p_{16,2} = p_{19,2} \\ & = p_{20,5} = p_{21,2} = p_{22,5} = p_{20} + p_{22.3} + p_{25.4} \\ & = p_{50} + p_{57} + p_{52.6} + p_{52.6,14,15} + p_{52.6,14,16} + p_{55.10} + p_{55.10,11,12} + p_{55.10,11,13} \\ & = p_{78} + p_{79} + p_{75.17,12} + p_{75.17,13} + p_{72.18,15} + p_{72.18,16} \\ & = p_{80} + p_{82.19} + p_{85.20} = p_{90} + p_{92.21} + p_{95.22} = 1. \\ \end{aligned}$$

(1)

The mean sojourn times μ_i in state S_i is given by

$$\mu_{0} = \int_{0}^{\infty } {P(T > t)\,{\text{d}}t} = m_{01} + m_{05} = \frac{1}{{\eta_{0} + 2\lambda }},\quad \mu_{1} = m_{12} = - p^{*\prime}(0),$$

$$\mu_{2} = m_{20} + m_{23} + m_{24} = \frac{1}{{\lambda + \eta_{0} }}(1 - p^{*} (\lambda + \eta_{0} )),$$

$$\mu_{5} = m_{50} + m_{56} + m_{57} + m_{5,10} = \frac{1}{{\alpha_{0} + \lambda + \eta_{0} }}[1 - g^{*} (\alpha_{0} + \lambda + \eta_{0} )],$$

$$\mu_{7} = m_{78} + m_{79} + m_{7,17} + m_{7,18} = \frac{1}{{\lambda + \eta_{0} }}(1 - h^{*} (\lambda + \eta_{0} )),$$

$$\mu_{8} = m_{80} + m_{8,19} + m_{8,20} = \frac{1}{{\lambda + \eta_{0} }}(1 - f^{*} (\lambda + \eta_{0} )),$$

$$\mu_{9} = m_{90} + m_{9,21} + m_{9,22} = \frac{1}{{\lambda + \eta_{0} }}(1 - g_{1}^{*} (\lambda + \eta_{0} )),$$

$$\mu_{2}^{\prime} = m_{20} + m_{22.3} + m_{25.4} = (1 - p^{*} (\lambda + \eta_{0} ))\left( {\frac{1}{{\lambda + \eta_{0} }} - p^{*\prime}(0)} \right),$$

$$\begin{aligned} \mu_{5}^{\prime} & = m_{50} + m_{52.6} + m_{52.6,14,15} + m_{52.6,14,16} + m_{57} + m_{55.10} + m_{55.10,11,12} + m_{55.10,11,13} \\ & = \frac{1}{{\alpha_{0} + \lambda + \eta_{0} }}[1 - g^{*} (\alpha_{0} + \lambda + \eta_{0} )][1 - ((\lambda + \eta_{0} )(1 - g^{*} (\alpha_{0} ))(h^{*\prime (0)} + af^{*\prime (0)} + bg_{1}^{*\prime}(0)))], \\ \end{aligned}$$

$$\begin{aligned} \mu_{7}^{\prime} & = m_{78} + m_{79} + m_{75.17,12} + m_{75.17,13} + m_{72.18,15} + m_{72.18,16} \\ & = (1 - h^{*} (\lambda + \eta_{0} ))\left( {\frac{1}{{\lambda + \eta_{0} }} - h^{*\prime}(0) - af^{*\prime}(0) - bg_{1}^{*\prime}(0)} \right), \\ \end{aligned}$$

$$\mu_{8}^{\prime} = m_{80} + m_{82.19} + m_{85.20} = (1 - f^{*} (\lambda + \eta_{0} ))\left( {\frac{1}{{\lambda + \eta_{0} }} - f^{*\prime}(0)} \right),$$

$$\mu_{9}^{\prime} = m_{90} + m_{92.21} + m_{95.22} = (1 - g_{1}^{*} (\lambda + \eta_{0} ))\left( {\frac{1}{{\lambda + \eta_{0} }} - g_{1}^{*\prime}(0)} \right).$$

(2)

3 Reliability characteristics

3.1 Mean time to system failure (MTSF)

Let $\psi_{i} (t)$ be the cdf of the first passage time from regenerative state Si to a failed state. Regarding the failed state as absorbing state, we comprise the subsequent recursive relation for $\psi_{i} (t)$:

$$\psi_{i} (t) = \sum \limits_{j} Q_{i,jj} (t){\boxed{\varvec{S}}}\psi_{j} (t) + \sum \limits_{k} Q_{i,jk} (t),$$

(3)

where S_j is an unfailed regenerative state to which the given regenerative state S_i can transit and k is a failed state to which the state S_i can transit directly.

Taking Laplace–Stieltjes transform of relation (3) and solving for $\psi_{0}^{**} (s),$ we get

$$R^{*} (s) = \frac{{1 - \psi_{0}^{**} (s)}}{s}.$$

(4)

The reliability R(t) can be obtained by taking inverse Laplace transformation of (4) and MTSF is given by

$${\text{MSTF(}}T_{0} )= \mathop {\lim }\limits_{s \to 0} R^{*} (s) = \mathop {\lim }\limits_{s \to 0} \frac{{1 - \psi_{0}^{**} (s)}}{s} = \frac{{N^{1} }}{{D^{1} }} ,$$

(5)

where $N^{1} = \mu_{0} + p_{05} (\mu_{5} + p_{57} (\mu_{7} + p_{78} \mu_{8} + p_{79} \mu_{9} ))$ and $D^{1} = 1 - p_{05} (p_{50} + p_{57} (p_{78} p_{80} + p_{79} p_{90} )).$

3.2 Availability analysis

Let $B_{i} (t)$ be the possibility that the system is in upstate at instant t given that the system entered regenerative state i at $t = 0$. The recursive relations for $B_{i} (t)$ are given as

$$B_{i} (t) = Z_{i} (t) + \mathop \sum \limits_{j} q_{i,j}^{(n)} (t)\copyright B_{j} (t),$$

(6)

where S_j is any successive regenerative state to which the regenerative state S_i can transit through n ≥ 1 (natural number) transitions and Z_i(t) is the probability that the system is up initially in regenerative state $S_{i} \in E$ at time ‘t’ without visiting any other regenerative state. Thus,

$$Z_{0} (t) = {\text{e}}^{{ - (2\lambda + \eta_{0} )t}} ,\quad Z_{2} (t) = {\text{e}}^{{ - (\lambda + \eta_{0} )t}} \bar{P}(t),\quad Z_{4} (t) = {\text{e}}^{{ - (\lambda + \eta_{0} )t}} \overline{{G_{1} }} (t),$$

$$Z_{5} (t) = {\text{e}}^{{ - (\lambda + \alpha_{0} + \eta_{0} )t}} \bar{G}(t),\quad Z_{7} (t) = {\text{e}}^{{ - (\lambda + \eta_{0} )t}} \bar{H}(t)\quad {\text{and}}\quad Z_{8} (t) = {\text{e}}^{{ - (\lambda + \eta_{0} )t}} \bar{F}(t).$$

Taking Laplace transform of relations (6) and solving for $A_{0}^{*} (s),$ we get steady-state availability as

$$B_{0} = \mathop {\lim }\limits_{s \to 0} sB_{0}^{*} (s) = \frac{{N^{2} }}{{D^{2} }},$$

(7)

where $N^{2} = (1 - p_{55.10} - p_{55.10,11,12} - p_{55.10,11,13} - p_{57} (p_{75.17,12} + p_{75.17,13} + p_{78} p_{85.20} + p_{79} p_{95.22} )((1 - p_{22.3} )\mu_{0} + p_{01} \mu_{2} )) + (p_{50} + p_{57} (p_{78} p_{80} + p_{79} p_{90} ))(p_{25.4} \mu_{0} + p_{05} \mu_{2} )) + (p_{05} (1 - p_{22.3} ) + p_{01} p_{12} p_{25.4} )(\mu_{5} + p_{57} (\mu_{7} + p_{78} \mu_{8} + p_{79} \mu_{9} )).$

$$\begin{aligned} D^{2} & = (1 - p_{57} (p_{75.17,12} + p_{75.17,13} + p_{78} p_{85.20} + p_{79} p_{95.22} )((1 - p_{22.3} )\mu_{0} + p_{12} \mu_{2}^{\prime}) \\ & \quad - p_{55.10} - p_{55.10,11,12} - p_{55.10,11,13} + (p_{50} + p_{57} (p_{78} p_{80} + p_{79} p_{90} ))(p_{25.4} \mu_{0} + p_{05} \mu_{2}^{\prime})) \\ & \quad + (p_{05} (1 - p_{22.3} ) + p_{01} p_{12} p_{25.4} )(\mu_{5}^{\prime} + p_{57} (\mu_{7}^{\prime} + p_{78} \mu_{8}^{\prime} + p_{79} \mu_{9}^{\prime})). \\ \end{aligned}$$

3.3 Busy period analysis of regular server

Let $B_{i}^{r} (t)$ be the probability that the ordinary server is busy due to preventive maintenance, repair, inspection and replacement at an instant ‘t’ given that the system entered regenerative state $S_{i}$ at $t = 0$. The recursive relations for $B_{i}^{r} (t)$ are given as

$$B_{i}^{r} (t) = H_{i} (t) + \mathop \sum \limits_{j} q_{i,j}^{(n)} (t)\copyright B_{j}^{r} (t),$$

(8)

where throughout n ≥ 1 (natural number) transitions S_j is a successive regenerative state to which state S_i transits and

$$H_{2} (t) = {\text{e}}^{{ - (\lambda + \eta_{0} )t}} \bar{P}(t) + ((\lambda {\text{e}}^{{ - (\lambda + \eta_{0} )t}} \copyright{\mathbf{1}})\bar{P}(t) + (\eta_{0} {\text{e}}^{{ - (\lambda + \eta_{0} )t}} \copyright{\mathbf{1}})\bar{P}(t)) ,$$

$$H_{5} (t) = {\text{e}}^{{ - (\lambda + \alpha_{0} + \eta_{0} )t}} \bar{G}(t) + ((\lambda {\text{e}}^{{ - (\lambda + \alpha_{0} + \eta_{0} )t}} \copyright{\mathbf{1}})\bar{G}(t) + (\eta_{0} {\text{e}}^{{ - (\lambda + \alpha_{0} + \eta_{0} )t}} \copyright{\mathbf{1}})\bar{G}(t)),$$

$$H_{7} (t) = {\text{e}}^{{ - (\lambda + \eta_{0} )t}} \bar{H}(t) + ((\lambda {\text{e}}^{{ - (\lambda + \eta_{0} )t}} \copyright{\mathbf{1}})\bar{H}(t) + (\eta_{0} {\text{e}}^{{ - (\lambda + \eta_{0} )t}} \copyright{\mathbf{1}})\bar{H}(t)),$$

$$H_{8} (t) = {\text{e}}^{{ - (\lambda + \eta_{0} )t}} \bar{F}(t) + ((\lambda {\text{e}}^{{ - (\lambda + \eta_{0} )t}} \copyright{\mathbf{1}})\bar{F}(t) + (\eta_{0} {\text{e}}^{{ - (\lambda + \eta_{0} )t}} \copyright{\mathbf{1}})\bar{F}(t)).$$

Taking Laplace transformation of relation (8) and solving for $B_{0}^{{R}^{*}} (s),$ we get in the long run the time for which the regular server is busy in steady state given by

$$B_{0}^{R} = \mathop {\lim }\limits_{s \to 0} sB_{0}^{R*} (s) = \frac{{N^{3} }}{{D^{2} }},$$

(9)

where $N^{3} = H_{2}^{*} (0)(p_{01} (1 - p_{55.10} - p_{55.10,11,12} - p_{55.10,11,13} - p_{57} (p_{75.17,12} + p_{75.17,13} + p_{78} p_{85.20} + p_{79} p_{95.22} )) + p_{05} (p_{50} + p_{57} (p_{78} p_{80} + p_{79} p_{90} ))) + (p_{05} (1 - p_{22.3} ) + p_{01} p_{12} p_{25.4} )H_{5}^{*} \left( 0 \right) + (p_{57} (p_{05} (1 - p_{22.3} ) + p_{01} p_{12} p_{25.4} ))H_{7}^{*} (0) + p_{57} p_{78} (p_{05} (1 - p_{22.3} ) + p_{01} p_{12} p_{25.4} )H_{8}^{*} (0)$ and D² is already specified.

3.4 Busy period analysis of expert server

Let $B_{i}^{e} (t)$ be the probability that the expert sever is busy in repairing the unit at an instant ‘t’ given that the system entered the regenerative state $S_{i}$ at $t = 0.$ The recursive relations for $B_{i}^{e} \left( t \right)$ are given by:

$$B_{i}^{e} (t) = H_{i} (t) + \mathop \sum \limits_{j} q_{i,j}^{(n)} (t)\copyright B_{j}^{e} (t),$$

(10)

where throughout n ≥ 1 (natural number) transitions S_j is a successive regenerative state to which state S_i transits and

$$H_{9} (t) = {\text{e}}^{{ - (\lambda + \eta_{0} )t}} \overline{{G_{1} }} (t) + ((\lambda {\text{e}}^{{ - (\lambda + \eta_{0} )t}} \copyright{\mathbf{1}})\overline{{G_{1} }} (t) + (\eta_{0} {\text{e}}^{{ - (\lambda + \eta_{0} )t}} \copyright{\mathbf{1}})\overline{{G_{1} }} (t)).$$

Taking Laplace transform of relation (10) and solving for $B_{0}^{e*} (s),$ we get the time for which the system is under repair, done by expert server as given by

$$B_{0}^{e} = \mathop {\lim }\limits_{s \to 0} sB_{0}^{{e^{*} }} (s) = \frac{{N^{4} }}{{D^{2} }} ,$$

(11)

where $N^{3} = p_{57} p_{79} (p_{05} (1 - p_{22.3} ) + p_{01} p_{12} p_{25.4} )H_{9}^{*} (0)$ and D² is already specified.

3.5 Expected number of repairs by the regular server

Let $V_{i} (t)$ be the expected number of visits by the ordinary server in $\left( {0,\left. t \right]} \right.$ given that the system entered the regenerative state $S_{i}$ at $t = 0.$ The recursive relations for $V_{i} (t)$ are given by

$$V_{i} (t) = \mathop \sum \limits_{j} Q_{i,j} (t){\boxed{\varvec{S}}} [\delta_{j} + V_{j} (t) ] ,$$

(12)

where j is any regenerative state to which the given regenerative state i transits and $\delta_{i} = 1$, if j is the regenerative state where the regular server does job afresh; otherwise $\delta_{i} = 0.$

Taking Laplace–Stieltjes transform of relation (12) and solving for $V_{0}^{**} (s),$ we get the expected number of visits by ordinary server per unit time as

$$V_{0} = \mathop {\lim }\limits_{s \to 0} s N_{0}^{**} (s) = \frac{{N^{5} }}{{D^{2} }},$$

(13)

where $N^{5} = (p_{01} p_{25.4} + p_{05} p_{22.3} )(p_{50} + p_{52.6} + p_{55.10} )$ and D² is already specified.

3.6 Expected number of visits by the expert server

Let $V_{i}^{e} (t)$ be the expected number of visits by expert server in $(0,t]$ given that the system entered the regenerative state $S_{i}$ at $t = 0.$ The recursive relations for $V_{i}^{e} (t)$ are given by:

$$V_{i}^{e} (t) = \mathop \sum \limits_{j} Q_{i,j} (t){\boxed{S}}[\delta_{j} + V_{j}^{e} (t)],$$

(14)

where j is any regenerative state to which the given regenerative state i transits and $\delta_{i} = 1$, if j is the regenerative state where the expert server does job afresh; otherwise $\delta_{i} = 0$.

Taking Laplace–Stieltjes transform of relation (14) and solving for $V_{0}^{e**} (s),$ we get the expected number of visits by expert server per unit time as

$$V_{0}^{e} = \mathop {\lim }\limits_{s \to 0} sV_{0}^{e**} (s) = \frac{{N^{6} }}{{D^{2} }},$$

(15)

where$N^{6} = (p_{01} p_{25.4} + p_{05} p_{22.3} )(p_{50} + p_{52.6} + p_{55.10} + (p_{75.17,13} + p_{79} )p_{57} )$ and D² is already specified.

3.7 Expected number of preventive maintenances by the regular server

Let $V_{i}^{\text{pm}} (t)$ be the expected number of visits by expert server $(0,t]$ given that the system entered the regenerative state $S_{i}$ at $t = 0.$ The recursive relations for $V_{i}^{\text{pm}} (t)$ are given by:

$$V_{i}^{\text{pm}} (t) = \mathop \sum \limits_{j} Q_{i,j} (t){\boxed{S}}[\delta_{j} + V_{j}^{\text{pm}} (t)],$$

(16)

where j is any regenerative state to which the given regenerative state i transits and $\delta_{i} = 1$, if j is the regenerative state where the expert server does job afresh; otherwise $\delta_{i} = 0$.

Taking Laplace–Stieltjes transform of relation (16) and solving for $V_{0}^{{\rm pm}**} (s),$ we get the expected number of visits by expert server per unit time as

$$V_{0}^{\text{pm}} = \mathop {\lim }\limits_{s \to 0} sV_{0}^{{{\text{pm}}**}} (s) = \frac{{N^{7} }}{{D^{2} }},$$

(17)

where$N^{7} = p_{01} (1 + p_{12} (1 - p_{22.3} ))(p_{5,10} - p_{57} (p_{75.17,12} + p_{75.17,13} + p_{78} p_{85.20} + p_{79} p_{95.22} )) + (p_{05} - p_{01} p_{25.4} p_{12} )(1 - p_{50} - p_{57} + p_{57} (p_{72.18,15} + p_{72.18,16} + p_{78} p_{82.19} + p_{79} p_{57} ))$ and D² is already specified.

3.8 Expected number of replacements by the regular server

Let $R_{i} (t)$ be the expected number of replacements by the unit in $(0,t]$ given that the system entered the regenerative state $S_{i}$ at $t = 0.$ The recursive relations for $R_{i} (t)$ are given by:

$$R_{i} (t) = \mathop \sum \limits_{j} Q_{i,j} (t){\boxed{S}} [ + R_{j} (t)],$$

(18)

where j is any regenerative state to which the given regenerative state i transits and $\delta_{i} = 1$, if j is the regenerative state where the failed unit is replaced by new ones; otherwise $\delta_{i} = 0$.

Taking Laplace–Stieltjes transform of relation (18) and solving for $R_{0}^{ * *} (s),$ we get the expected number of replacements per unit time as

$$R_{0} = \mathop {\lim }\limits_{s \to 0} sR_{0}^{**} (s) = \frac{{N^{8} }}{{D^{2} }},$$

(19)

where $N^{8} = (p_{57} p_{78} + p_{57} (p_{72.18,15} + p_{75.17,12} ) + (p_{50} + p_{52.6,14,15} + p_{55.10,11,12} ))(p_{25.4} + p_{05} p_{20} )$ and D² is already specified.

4 Cost–benefit analysis

Considering the various costs, profit incurred to the system model in steady state is given by:

$$P = K_{0} B_{0} - K_{1} B_{0}^{r} - K_{2} B_{0}^{e} - K_{3} V_{0} - K_{4} V_{0}^{e} - K_{5} BV_{0}^{\text{pm}} - K_{6} R_{0} ,$$

where $K_{0}$  is the revenue per unit uptime of the system, $K_{1}$ is the charge per unit time for which regular server is busy, $K_{2}$ is the charge per unit time for which expert server is busy, $K_{3}$ is the charge per unit visit for repair by the regular server, $K_{4}$ is the charge per unit visit for repair by the expert server, $K_{5}$ is the charge per unit visit for preventive maintenance, and $K_{6}$ is the charge per unit visit for replacement.

5 Case study

To observe the effect of the repair and maintenance on the system behavior and characterize the behavior of MTSF, availability and profit of the system, repair rate of ordinary and expert servers, replacement rate, inspection rate and maintenance rate of ordinary server are assumed to be negatively exponentially distributed, given by$g(t) = \theta {\text{e}}^{ - \theta t} ,\quad g_{1} (t) = \theta_{0} {\text{e}}^{{ - \theta_{0} t}} ,\quad f(t) = \beta {\text{e}}^{ - \beta t} ,\quad h(t) = \gamma {\text{e}}^{ - \gamma t} {\text{ and }}p(t) = \rho {\text{e}}^{ - \rho t} .$

By using the non-zero element $p_{ij}$, we obtain the following results:

• ${\text{MTSF(}}T_{0} )= \frac{{N^{1} }}{{D^{1} }}$, availability $(B_{0} ) = \frac{{N^{2} }}{{D^{2} }}$,

• busy period of regular server $(B_{0}^{R} ) = \frac{{N^{3} }}{{D^{2} }},$

• busy period of expert server $(B_{0}^{e} ) = \frac{{N^{4} }}{{D^{2} }},$

• expected number of repairs by regular server $(V_{0} ) = \frac{{N^{5} }}{{D^{2} }}$,

• expected number of repairs by expert server $(V_{0}^{e} ) = \frac{{N^{6} }}{{D^{2} }}$,

• expected number of preventive maintenances $(V_{0}^{\text{pm}} ) = \frac{{N^{7} }}{{D^{2} }}$,

• expected number of replacements $(R_{0} ) = \frac{{N^{8} }}{{D^{2} }},$

where $N^{1} = \frac{1}{{(2\lambda + \eta_{0} )}}\left( {1 + \frac{2\lambda }{{\theta + \lambda + \alpha_{0} + \eta_{0} }}\left( {1 + \frac{{\alpha_{0} }}{{\gamma + \lambda + \eta_{0} }}\left( {1 + \gamma \left( {\frac{a}{{\beta + \lambda + \eta_{0} }} + \frac{b}{{\theta_{0} + \lambda + \eta_{0} }}} \right)} \right)} \right)} \right),$

$$D^{1} = 1 - \frac{1}{{\theta + \lambda + \alpha_{0} + \eta_{0} }}\left( {\frac{2\lambda }{{2\lambda + \eta_{0} }}\left( {\theta + \frac{{\alpha_{0} \gamma }}{{\gamma + \lambda + \eta_{0} }}\left( {\frac{a\beta }{{\beta + \lambda + \eta_{0} }} + \frac{{b\theta_{0} }}{{\theta_{0} + \lambda + \eta_{0} }}} \right)} \right)} \right),$$

$$N^{2} = \frac{1}{{(2\lambda + \eta_{0} )(\theta + \lambda + \alpha_{0} + \eta_{0} )}}\left[ {\left( {\theta + \alpha_{0} + \eta_{0} + \frac{{\alpha_{0} }}{{\left( {\gamma + \lambda + \eta_{0} } \right)}}\left( {\lambda + \gamma \left( {\frac{a\lambda }{{\beta + \lambda + \eta_{0} }} + \frac{{b\theta_{0} }}{{\theta_{0} + \lambda + \eta_{0} }}} \right)} \right)} \right) + \left( {\frac{3\lambda }{{\rho + \lambda + \eta_{0} }}\left( {\theta + \frac{{\alpha_{0} \gamma }}{{\gamma + \lambda + \eta_{0} }}\left( {\frac{a\beta }{{\beta + \lambda + \eta_{0} }} + \frac{{b\theta_{0} }}{{\theta_{0} + \lambda + \eta_{0} }}} \right)} \right)} \right) + \left( {\frac{{\lambda \left( {\eta_{0} + 2(\rho + \lambda )} \right)}}{{\left( {\rho + \lambda + \eta_{0} } \right)}}} \right)\left( {1 + \frac{{\alpha_{0} }}{{\left( {\gamma + \lambda + \eta_{0} } \right)}}\left( {1 + \gamma \left( {\frac{a}{{\beta + \lambda + \eta_{0} }} + \frac{b}{{\theta_{0} + \lambda + \eta_{0} }}} \right)} \right)} \right)} \right],$$

$$N^{3} = \frac{1}{{\left( {2\lambda + \eta_{0} } \right)\left( {\theta + \lambda + \alpha_{0} + \eta_{0} } \right)}}\left( {\frac{{\left( {1 + \lambda + \eta_{0} } \right)}}{{\left( {\lambda + \rho + \eta_{0} } \right)}}} \right)\left[ {\left( {\theta + \frac{{\alpha_{0} \gamma }}{{\gamma + \lambda + \eta_{0} }}\left( {\frac{a\beta }{{\beta + \lambda + \eta_{0} }} + \frac{{b\theta_{0} }}{{\theta_{0} + \lambda + \eta_{0} }}} \right)} \right) + \left( {\theta + \alpha_{0} + \eta_{0} + \frac{{\alpha_{0} }}{{\left( {\gamma + \lambda + \eta_{0} } \right)}}\left( {\lambda + \gamma \left( {\frac{a\lambda }{{\beta + \lambda + \eta_{0} }} + \frac{{b\theta_{0} }}{{\theta_{0} + \lambda + \eta_{0} }}} \right)} \right)} \right) + \lambda \left( {\left( {\eta_{0} + 2\left( {\rho + \lambda } \right)} \right)\left( {1 + \frac{{\alpha_{0} }}{{\left( {\gamma + \lambda + \eta_{0} } \right)}} + \frac{{a\gamma \alpha_{0} }}{{\left( {\rho + \lambda + \eta_{0} } \right)}}} \right)} \right)} \right],$$

$$N^{4} = \frac{1}{{\left( {2\lambda + \eta_{0} } \right)\left( {\theta + \lambda + \alpha_{0} + \eta_{0} } \right)}}\left( {\frac{{\lambda \left( {1 + \lambda + \eta_{0} } \right)}}{{\left( {\theta_{0} + \lambda + \eta_{0} } \right)}}} \right)\left[ {\frac{{b\gamma \alpha_{0} }}{{\left( {\rho + \lambda + \eta_{0} } \right)}}\left( {\eta_{0} + 2(\rho + \lambda )} \right)} \right],$$

$$N^{5} = \frac{1}{{\left( {2\lambda + \eta_{0} } \right)\left( {\theta + \lambda + \alpha_{0} + \eta_{0} } \right)\left( {\rho + \lambda + \eta_{0} } \right)}}\left[ {\eta_{0} \theta \left( {1 + 2\lambda } \right)\left( {1 + \frac{{\lambda + \eta_{0} }}{{\theta + \alpha_{0} }}} \right)} \right],$$

$$N^{6} = \frac{1}{{\left( {2\lambda + \eta_{0} } \right)\left( {\theta + \lambda + \alpha_{0} + \eta_{0} } \right)\left( {\rho + \lambda + \eta_{0} } \right)}}\left[ {\left( {\eta_{0} \left( {1 + 2\lambda } \right)\left( {\theta \left( {1 + \frac{{\lambda + \eta_{0} }}{{\theta + \alpha_{0} }}} \right) + \frac{{\alpha_{0} b\left( {\gamma + \lambda } \right)}}{{\left( {\gamma + \lambda + \eta_{0} } \right)}}} \right)} \right)} \right],$$

$$N^{7} = \frac{1}{{\left( {2\lambda + \eta_{0} } \right)\left( {\theta + \lambda + \alpha_{0} + \eta_{0} } \right)\left( {\rho + \lambda + \eta_{0} } \right)}}\left[ {\lambda \left( {2(\rho + \lambda ) + \eta_{0} } \right)\left( {1 + \eta_{0} - \alpha_{0} - \theta } \right)} \right],$$

$$N^{8} = \frac{1}{{\left( {2\lambda + \eta_{0} } \right)\left( {\theta + \lambda + \alpha_{0} + \eta_{0} } \right)}}\frac{{a\lambda \left( {\lambda + \eta_{0} } \right)}}{{\left( {\rho + \lambda + \eta_{0} } \right)}}\left[ {\left( {\eta_{0} \left( {\frac{{\eta_{0} }}{{\left( {\gamma + \lambda + \eta_{0} } \right)}}} \right) + 2(\rho + \lambda )} \right) + \alpha_{0} \left( {2\lambda + \eta_{0} } \right)} \right],$$

$$D_{2} = \left[ {\left( {\theta + \alpha_{0} + \eta_{0} + \frac{{\alpha_{0} }}{{\left( {\gamma + \lambda + \eta_{0} } \right)}}\left( {\lambda + \gamma \left( {\frac{a\lambda }{{\beta + \lambda + \eta_{0} }} + \frac{{b\theta_{0} }}{{\theta_{0} + \lambda + \eta_{0} }}} \right)} \right)} \right)\left( {\frac{{\left( {\left( {\rho + \lambda } \right) + \eta_{0} \left( {1 + \left( {\frac{{\lambda + \eta_{0} }}{\rho }} \right)} \right)} \right)}}{{\rho + \lambda + \eta_{0} }}} \right) + \left( {\frac{3\lambda }{{\rho + \lambda + \eta_{0} }}\left( {3 + \frac{{2\left( {\lambda + \eta_{0} } \right)}}{\rho }} \right)} \right)\left( {\theta + \frac{{\alpha_{0} \gamma }}{{\gamma + \lambda + \eta_{0} }}\left( {\frac{a\beta }{{\beta + \lambda + \eta_{0} }} + \frac{{b\theta_{0} }}{{\theta_{0} + \lambda + \eta_{0} }}} \right)} \right) + \left( {\frac{{\lambda \left( {\eta_{0} + 2(\rho + \lambda )} \right)}}{{\left( {\rho + \lambda + \eta_{0} } \right)}}} \right)\left( {1 + \alpha_{0} \left( {\lambda + \eta_{0} } \right)\left( {\frac{1}{{\theta + \alpha_{0} }}\left( {\frac{1}{\gamma } + \frac{a}{\beta } + \frac{b}{{\theta_{0} }}} \right)} \right) + \frac{1}{{\left( {\gamma + \lambda + \eta_{0} } \right)}}\left( {\left( {\frac{1}{{\lambda + \eta_{0} }} + \frac{1}{\gamma } + \frac{a}{\beta } + \frac{b}{{\theta_{0} }}} \right) + \gamma \left( {\frac{a}{{\beta + \lambda + \eta_{0} }}\left( {\frac{1}{{\lambda + \eta_{0} }} + \frac{1}{\beta }} \right) + \frac{b}{{\theta_{0} + \lambda + \eta_{0} }}\left( {\frac{1}{{\lambda + \eta_{0} }} + \frac{1}{{\theta_{0} }}} \right)} \right)} \right)} \right)} \right]\frac{1}{{\left( {2\lambda + \eta_{0} } \right)\left( {\theta + \lambda + \alpha_{0} + \eta_{0} } \right)}} .$$

6 Numerical analysis

Using the above results for particular values, we successfully obtained the numerical results for reliability attributes function as shown in Tables 1, 2 and 3, respectively.

Table 1 MTSF vs. replacement rate

Table 2 Availability vs. replacement rate

Table 3 Profit vs. replacement rate

7 Discussion

From the numerical results depicted above in Tables 1, 2 and 3, we observe that the MTSF, availability and profit of the system increase with the increase of replacement rate (β), repair rates of ordinary server (θ) and expert server ($\theta_{0}$), while their values decrease with the increase of failure rate (λ) and maximum operation time $(\eta_{0} )$ of the unit. Also with the increase of maximum repair time ($\alpha_{0}$) and inspection rate of the unit (η) taken by the ordinary server, MTSF increases whereas profit decreases. However, there is no effect of increases of preventive maintenance (ρ) on MTSF, while availability and profit increase rapidly.

To come up with a solution, a repairable parallel system can be made more reliable and profitable to use either by increasing the repair rate of the ordinary server instead of increasing the operation time and repair time of the unit or by calling an expert server immediately after the maintenance of the unit.

8 Application

In consequence, the findings of this application will assist engineers and decision makers to avoid an incorrect reliability assessment and consequent erroneous decision making. This may also show the way to reduce unnecessary expenditures and faulty maintenance scheduling.