Performance of non-uniform cantilever based piezoelectric energy harvester

Abstract

Cantilever based piezoelectric energy harvesters (PEHs) have been optimized in terms of shape, size, material properties and damping to improve their electrical outputs. In most of the PEHs, a cantilever beam with width of rectangular, triangular and trapezoidal shapes, respectively, have been analyzed in optimizing the power output. In this paper, we investigate the influence of non-uniform beams with linearly and quartic varying widths. To analyze the model, we first modify the electromechanical formulation of uni-morph piezoelectric cantilever beam with uniform section to include the non-uniform variation of beam width. Subsequently, we obtain the voltage, current and the power output versus frequencies at different external loads for uniform and non-uniform beams with varying tapering parameters. Based on the analysis, we found that the diverging beam with tapering parameter of 0.6 can produce an enhanced power output by 3833% as compared to that of uniform beam. Since, the frequency also changes due to change in the tapering parameter of non-uniform beam, such significant changes in the output are also demonstrated for designing a wide band PEH based on an array of uniform and non-uniform beams. Finally, we also performed numerical study of PEHs of unimorph as well as coupled beams with uniform and non-uniform sections.

Introduction

There have been numerous studies related with the development of vibration based energy harvesting devices ranging from macro-scale (Sodano et al. 2004) and to micro-scale (Jeon et al. 2005) which converts mechanical to electrical energy. To carry out such conversions, different methods such as the electromagnetic, electrostatic, and the piezoelectric are used. Among all the three, the piezoelectric method offers great advantages in terms of simple structure, high output voltage, efficiency, etc. To develop piezoelectric energy harvester (PEH), the cantilever beam with uni-morph (single piezoelectric layer) (Erturk and Inman 2008a) or bi-morph (two piezoelectric layers) (Ajitsaria et al. 2007) piezoelectric materials is used under the influence of harmonic excitation (Erturk and Inman 2008a, b). To optimize the power of PEH, the rectangular, triangular, and trapezoidal shapes of cantilever beam along its length have been considered (Roundy et al. 2005; Goldschmidtboeing and Woias 2008; Benasciutti et al. 2010; Friswell and Adhikari 2010). Recently, Sriramdas and Pratap (2017) have developed scaling analysis for designing efficient MEMS piezoelectric energy harvester. In this study, we focus on analyzing the performance of non-uniform cantilever beam with linearly and quartic varying widths in a uni-morph piezoelectric energy harvester (PEH).

To optimize the performance of piezoelectric energy harvester, the coupled mechanical and electrical modeling is done either using the single degree of freedom (SDOF) model (Sirohi and Mahadik 2011) or Rayleigh–Ritz method based distributed parameter model (Erturk and Inman 2009; Erturk et al. 2009). In SDOF model, the spring-mass-damper characteristics of cantilever beam can be coupled easily with lumped electrical components of piezoelectric layer to model electro-mechanical coupling. However, this approach is limited to single mode vibration, and it is not valid for multi-modal vibration problems. Therefore, the focus has shifted towards using the Rayleigh–Ritz method based distributed parameter model in order to capture electromechanical coupling under multi-modal vibration (Erturk and Inman 2008a). The results based on both the methods for the cantilever based PEH also compared with experimental results by various researchers (Abdelkefi et al. 2013; Zhao et al. 2013). To analyze the performance of PEH, Yang et al. (2013) have studied the influence of various tip geometries on the performance characteristics of energy harvester. They found that the tip geometry with square section gives superior response. Roundy et al. (2005), Goldschmidtboeing and Woias (2008), Benasciutti et al. (2010), and Friswell and Adhikari (2010) performed theoretical and experimental analysis to improve the power output of energy harvesters by changing the shape of rectangular beam to triangular and trapezoidal. The optimization based on other factors such as stress and strain distribution have also been studied by other researchers (Benasciutti et al. 2009; Yang et al. 2009; Park et al. 2012) based on numerical modeling in ANSYS. Bayik et al. (2016) have performed numerical simulation of a piezo-patch integrated to a fully clamped thin plate and shunted to a resistive load in ANSYS. Seba et al. (2006) numerically modeled a beam structure with a piezoelectric actuator bonded to the surface of the structure and an accelerometer placed on the tip using ANSYS and Matlab. Meiling et al. (2009, 2010) have also used the finite element model to perform coupled analysis to improve the performance of PEH. Soliman et al. (2008) proposed the use of piecewise linear oscillator and Cammarano et al. (2014) optimized the non-linear response of harvester. Fan et al. (2015) have also presented a non-linear piezoelectric energy harvester to harvest energy from various mechanical motions. To improve the frequency band, Roundy et al. (2005) discussed about utilizing a system of N-spring-mass damper systems. Wen et al. (2014) incorporated PZT beam array configuration to increase the voltage output. Liu et al. performed experimental and numerical analysis for an array of cantilever beams to increase the frequency band. In short, to optimize the performance of these transducers, studies have been done to increase the output power/voltage and frequency bandwidth. The studies related with increasing the power/voltage output have been there for quite some time which involve methods to use efficient piezoelectric material, piezoelectric configuration, using different mechanical structures, optimizing power conditioning circuits, etc. The work involving the improvement of frequency bandwidth are limited to incorporating resonance tuning with uniform cantilever beam arrays, multi-modal excitation, utilizing non-linearity, etc. (Tang et al. 2010). Recently, we found that the frequency of a non-uniform cantilever beam with quartic converging width can be increased by more than 100% by changing the level of non-uniformity (Singh et al. 2015). In this paper, we systematically analyze the influence of non-uniform cantilever beam with quartic and linearly varying width on the frequency bandwidth and electrical output of vibration based piezoelectric energy harvesters.

To do the analysis, first, we briefly revisit the mathematical modeling of the piezoelectric uni-morph cantilever beam to capture the effect of non-uniform width by following the approach developed by Erturk and Inman (2008a) for uniform cantilever beam. We highlight the terms concerning varying width in the equation. Considering the Euler–Bernoulli beam equation, the cantilever beam equation is obtained under the influence of base excitation. Although, the damping related with non-uniform beams vary as compared to the uniform cantilever beams, we assume same damping ratios as that of uniform beam as we have focused on frequency band related study. The non-uniformity in the beam is modeled based on the approximation suggested by Abrate (1995) which is also described by Singh et al. (2015). The modal frequencies are validated with the results proposed by Kim and Lee (2013), and Mabie (1964). After obtaining the undamped modal frequencies and mode shapes, we perform the coupled electromechanical analysis using the first order RC-circuit equation (based on an external resistive load and internal capacitance due to piezoelectric layer on the cantilever beam) and the fourth order beam equation. Using the Galerkin approach based on three modes approximation, we solve the beam as well as electrical circuit equations simultaneously to obtain the frequency response functions of the voltage, current and the power gain as also obtained by Erturk and Inman (2008a) for uniform cantilever beam. After validating the solution technique for uniform beam, we compare the response for non-uniform cantilever beams with different tapering. To show the application of non-uniform beam in frequency tuning in an array of uniform and non-uniform beams, we have done coupled analysis using ANSYS by following the approach described by Meiling et al. (2009, 2010). We first validate the numerical modal with the analytical results for uniform beams at different resistance. Subsequently, we performed simulation to show frequency tuning for two coupled beams array and an arrays of coupled uniform beam, converging beams and diverging beams.

Electro-mechanical modelling of PEH

In this section, we present the mathematical model to capture the effect of linear and quartic varying width of uni-morph piezoelectric cantilever beam on electrical outputs of PEH. To perform the analysis, we present detail model for uni-morph PEH.

Beam equations of uni-morph cantilever based PEH

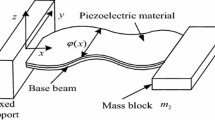
To write the governing equations of piezoelectric cantilever beam with non-uniform width, b(x), we revisit the governing equations derived by Ertuk and Inman for beam with uniform section. Let us consider an uni-morph PEH as shown in Fig. 1. It shows the vibration of a typical composite Euler–Bernoulli beam with upper layer of PZT material under the influence of transverse g(t) and rotatory h(t) excitations at the base such that the base motion $w_b(x,t)$ can be written as

$$\begin{aligned} w_b(x,t)=g(t)+xh(t). \end{aligned}$$

(1)

Consequently, the governing equation of non-uniform beam can be written same as that in Erturk and Inman (2008a)

$$\begin{aligned}&\frac{\partial ^2 {M}}{\partial x^2}+\frac{\partial ^2}{\partial x^2} \left( C_sI(x)\frac{\partial ^3 {w_{rel}(x,t)}}{\partial x^2 \partial t}\right) +C_a \frac{\partial w_{rel}(x,t)}{\partial t}+m(x)\frac{\partial ^2 {w_{rel}(x,t)}}{\partial t^2}\\ &\quad =-m(x)\frac{\partial ^2 {w_{b}(x,t)}}{\partial t^2} -C_a \frac{\partial w_b(x,t)}{\partial t} \end{aligned}$$

(2)

where, $w_{rel}(x,t)$ is the transverse deflection of the beam, M(x, t) is the internal bending moment, $C_s I(x)$ is the equivalent structural damping of the composite section, $C_a$ is the damping coefficient due to viscous air damping, and m(x) is the mass per unit length of the beam. Considering the composite beam into an equivalent beam as shown in Fig. 1c, we can write the internal bending moment as

$$\begin{aligned} M(x,t)= -\int _{h_a}^{h_b}T_{1}^{s} b(x)y dy-\int _{h_b}^{h_c}T_{1}^{p}b(x)y dy \end{aligned}$$

(3)

where, T is the stress (subscripts 1, 2 and 3 stand for x, y and z directions, respectively), b(x) is the width of the beam at a particular value of x, $h_a$ is the position of the bottom of the substructure from the neutral axis (NA), $h_b$ is the position of the bottom of the PZT layer from NA and $h_c$ is the position of the top of the PZT layer from NA. Taking $Y_s$ and $Y_p$ as the Young’s modulus of substructure and piezoelectric layers and the strain as $S_{1}=-y\frac{\partial ^2 w_{rel}}{\partial x^2}$, the constitutive relations can be written as (Erturk and Inman 2008a),

$$\begin{aligned} T_{1}^{s}=Y_s S_{1}^{s},\quad T_{1}^{p}=Y_p( S_{1}^{p}-d_{31}E_3), \end{aligned}$$

(4)

where, p and s stand for piezoelectric layer and substructure layer, respectively. Using the above equations, the internal bending moment from Eq. (3) can be written as (Erturk and Inman 2008a)

$$\begin{aligned} M(x,t)&= -\int _{h_a}^{h_b}Y_s S_{1}^{s} b(x)y dy-\int _{h_b}^{h_c}Y_p(S_{1}^{p}-d_{31}E_3)b(x)ydy \\ &= \int _{h_a}^{h_b}Y_s \frac{\partial ^2 w_{rel}}{\partial x^2} b(x)y^2 dy-\int _{h_b}^{h_c}Y_p\left( -y\frac{\partial ^2 w_{rel}}{\partial x^2}-d_{31}E_3\right) b(x)ydy \\ &= \int _{h_a}^{h_b}Y_s \frac{\partial ^2 w_{rel}}{\partial x^2} b(x)y^2 dy+\int _{h_b}^{h_c}Y_p\left( \frac{\partial ^2 w_{rel}}{\partial x^2}\right) b(x)y^2 dy -\int _{h_b}^{h_c}Y_p \frac{d_{31}}{h_p}v(t))b(x)ydy \\ &= b(x)\frac{\partial ^2 w_{rel}}{\partial x^2} \left[ Y_s\int _{h_a}^{h_b}y^2 dy+Y_p\int _{h_b}^{h_c}y^2 dy\right] -Y_p \frac{d_{31}}{h_p}v(t))b(x)\left[ \frac{h_{c}^2-h_{b}^2}{2}\right] \\ &= b(x)\frac{\partial ^2 w_{rel}}{\partial x^2} \left[ Y_s \left( \frac{h_{b}^3-h_{a}^3}{3}\right) +Y_p \left( \frac{h_{c}^3-h_{b}^3}{3}\right) \right] -Y_p \frac{d_{31}}{h_p}v(t))b(x)\left[ \frac{h_{c}^2-h_{b}^2}{2}\right] \\ &= YI(x)\frac{\partial ^2 w_{rel}}{\partial x^2}+\nu (x) v(t), \end{aligned}$$

(5)

where, $\nu$ is the electro-mechanical coupling term which is given by

$$\begin{aligned} \nu (x)=-Y_p \frac{d_{31}}{h_p}b(x)\left[\frac{h_{c}^2-h_{b}^2}{2}\right] \end{aligned}$$

(6)

and YI(x) is the flexural rigidity which is given by

$$\begin{aligned} YI(x)=b(x) \left[Y_s \left(\frac{h_{b}^3-h_{a}^3}{3}\right)+Y_p \left(\frac{h_{c}^3-h_{b}^3}{3}\right)\right]. \end{aligned}$$

(7)

Substituting M(x, t) in Eq. (2), we get the final governing equation to model the transverse motion of a non-uniform piezoelectric cantilever as

$$\begin{aligned}&\frac{\partial ^2}{\partial x^2}\left( YI(x)\frac{\partial ^2 w_{rel}}{\partial x^2}\right) +\frac{\partial ^2}{\partial x^2} \left( C_sI(x)\frac{\partial ^3 {w_{rel}(x,t)}}{\partial x^2 \partial t}\right) +C_a \frac{\partial w_{rel}(x,t)}{\partial t}\\ &\qquad +m(x)\frac{\partial ^2 {w_{rel}(x,t)}}{\partial t^2}+\nu (x)v(t)\left[ \frac{\partial \delta (x)}{\partial x}-\frac{\partial \delta (x-L)}{\partial x}\right] \\ &\quad =-m(x)\frac{\partial ^2 {w_{b}(x,t)}}{\partial t^2} -C_a \frac{\partial w_b(x,t)}{\partial t}. \end{aligned}$$

(8)

For uni-morph composite beam, YI can be found by finding equivalent beam width in terms of piezoelectric material properties (Erturk and Inman 2008a) as shown in Fig. 1b, c. If $h_{p}$ and $h_{s}$ are piezoelectric and substructure thicknesses then the neutral axis of equivalent beam of piezoelectric material from the bottom is found as $h_{sa}=\frac{h_{p}^{2}+2 h_{p} h_{s}+\mu h_{s}^{2}}{2(h_{p}+\mu h_{s})}$ and that from the top as $h_{pa}=\frac{h_{p}^{2}+2 \mu h_{p} h_{s}+\mu h_{s}^{2}}{2(h_{p}+\mu h_{s})}$, where, $\mu =Y_{p}/Y_{s}$. The distance between the neutral axis and the mid axis of top layer is $h_{pc}=\frac{ \mu h_{s}(h_{p}+ h_{s})}{2(h_{p}+\mu h_{s})}$. Consequently, the flexural rigidity can be found as

$$\begin{aligned} YI(x)= Y_p \left[\frac{\mu b(x)h_s^3}{12}+\mu b(x) h_{s} \left(h_{sa}-\frac{h_s}{2}\right)^2+\frac{b(x)h_p^3}{12}+b(x)h_ph_{pc}^2\right]. \end{aligned}$$

(9)

Alternatively, YI(x) can also be found from Eq. (7) with $h_{a}=-h_{sa}$, $h_{b}=h_{pa}-h_{p}$ and $h_{c}=h_{pa}$.

Fig. 1

a Schematic of PZT based cantilever energy harvester under base excitation. b Top view of beam with non-uniform width $b(x)=b_{0}(1\pm \alpha \frac{x}{L} )^{n}$, where, $n=1$ for linearly varying beam, $n=4$ for quartic varying beams, and $n=0$ for uniform beam, positive and negative signs represent diverging and converging beams, respectively. c Sectional view of the cross-sections of composite beam and its transformed form at any distance x, where, $\mu$ is the ratio of the Young’s modulus of substructure layer to the piezoelectric layer

Derivation of electric-circuit equation

In order to obtain electric circuit equation with mechanical coupling, we need to use piezoelectric constitutive relation as (Erturk and Inman 2008a)

$$\begin{aligned} D_3=d_{31}T_1+\epsilon _{33}^T E_3, \end{aligned}$$

(10)

where, $D_3$ is the electric displacement, $\epsilon _{33}^T$ is the permittivity at constant stress, $E_3=-v(t)/h_p$ is the electric field across the PZT, $T_1=Y_p(S_1^p-d_{31}E_3)$ is the longitudinal stress. Using the above parameters, Eq. (10) can be written as

$$\begin{aligned} D_3(x,t)=d_{31}Y_p S_{1}^{p}(x,t)-\epsilon _{33}^s \frac{v(t)}{h_p}, \end{aligned}$$

(11)

where, $\epsilon _{33}^s=\epsilon _{33}^T-d_{31}^2 Y_p$ is the permittivity at constant strain. Since, the average bending strain in the piezoelectric layer, $S_{1}^{p}(x,t)$, can be written as $S_{1}^{p}(x,t)=-h_{pc}\frac{\partial ^2 w_{rel}(x,t)}{\partial x^2}$, where $h_{pc}$ is the distance from the neutral axis of composite beam to the mid of piezoelectric layer, the above Eq. (11) can be written as,

$$\begin{aligned} D_3(x,t)= -d_{31}Y_p h_{pc}\frac{\partial ^2 w_{rel}(x,t)}{\partial x^2}-\epsilon _{33}^s \frac{v(t)}{h_p}. \end{aligned}$$

(12)

Now, computing the charge developed in PZT by integrating the electric displacement over the electrode area as

$$\begin{aligned} q(t)=\int _{A}D_3.ndA=-\int _{x=0}^{L}\left( d_{31}Y_p h_{pc}b(x)\frac{\partial ^2 w_{rel}(x,t)}{\partial x^2}dx+\epsilon _{33}^sb(x) \frac{v(t)}{h_p}\right) dx, \end{aligned}$$

(13)

and finding the current, i(t), and the voltage, v(t), generated by PZT as

$$\begin{aligned} i(t)=\frac{dq(t)}{dt}=-\int _{x=0}^{L}d_{31}Y_p h_{pc}b(x)\frac{\partial ^3 w_{rel}(x,t)}{\partial x^2\partial t}dx-\int _{x=0}^{L}\frac{\epsilon _{33}^s}{h_p}b(x) \frac{dv(t)}{dt}dx \quad \end{aligned}$$

(14)

and

$$\begin{aligned} v(t)=R_l i(t)=-R_l\left[\int _{x=0}^{L}d_{31}Y_p h_{pc}b(x)\frac{\partial ^3 w_{rel}(x,t)}{\partial x^2\partial t}dx+\int _{x=0}^{L}\frac{\epsilon _{33}^s}{h_p}b(x) \frac{dv(t)}{dt}dx\right], \end{aligned}$$

(15)

we get the final circuit equation from Eq. (15) as

$$\begin{aligned} \frac{v(t)}{R_l}+\int _{x=0}^{L}\frac{\epsilon _{33}^s}{h_p}b(x) \frac{dv(t)}{dt}dx=-\int _{x=0}^{L}d_{31}Y_p h_{pc}b(x)\frac{\partial ^3 w_{rel}(x,t)}{\partial x^2\partial t}dx. \end{aligned}$$

(16)

Reduced order model equation

To obtain the reduced order form of the beam equation given by Eq. (8), we apply Galerkin method by assuming the relative displacement $w_{rel}(x,t)$ as series of eigen functions as

$$\begin{aligned} w_{rel}(x,t)=\sum _{r=1}^\infty \phi _r(x) \eta _r(t), \end{aligned}$$

(17)

where, $\phi _r(x)$ and $\eta _r(t)$ are the mass normalized eigen function and modal co-ordinate of a cantilever beam for rth mode, respectively. By substituting Eq. (17) in Eq. (8) and using Eq. (1), we get

$$\begin{aligned}&\frac{\partial ^2}{\partial x^2}(YI(x){\eta }_r(t)\phi _r(x)'')+\frac{\partial ^2}{\partial x^2}(C_sI(x){\dot{\eta }_r(t)}\phi _r(x)'') +C_a\phi _r(x){\dot{\eta }_r(t)}\\ &\qquad +m(x)\phi _r(x){\ddot{\eta }_r(t)}+\nu (x)v(t)\left[ \frac{\partial \delta (x)}{\partial x}-\frac{\partial \delta (x-L)}{\partial x}\right] \\ &\quad =-m(x)\left( x\frac{\partial ^2 h}{\partial t^2}+\frac{\partial ^2 g}{\partial t^2}\right) -C_a\left( x\frac{\partial h}{\partial t}+\frac{\partial g}{\partial t}\right) . \end{aligned}$$

(18)

Multiplying Eq. (18) with $\phi _r(x)$ and integrating the resultant equation from $x=0$ to $x=L$, we get

$$\begin{aligned}&{\eta }_r(t)\int _{0}^{L}\phi _s(x)\frac{\partial ^2}{\partial x^2}(YI(x)\phi _r(x)'')dx +{\dot{\eta }_r(t)}\int _{0}^{L}\phi _s(x)\frac{\partial ^2}{\partial x^2}(C_sI(x)\phi _r(x)'')dx \\ &\qquad +{\dot{\eta }_r(t)}C_a\int _{0}^{L}\phi _s(x)\phi _r(x)dx+{\ddot{\eta }_r(t)}\int _{0}^{L}m(x)\phi _s(x)\phi _r(x)dx\\ &\qquad +v(t)\int _{0}^{L}\nu (x)\phi _s(x)\left[ \frac{\partial \delta (x)}{\partial x}-\frac{\partial \delta (x-L)}{\partial x}\right] dx\\ &\quad =-\int _{0}^{L}m(x)\phi _s(x)\left( x\frac{\partial ^2 h}{\partial t^2}+\frac{\partial ^2 g}{\partial t^2}\right) \\ &\qquad -C_a\int _{0}^{L}\phi _s(x)\left( x\frac{\partial h}{\partial t}+\frac{\partial g}{\partial t}\right) . \end{aligned}$$

(19)

Using the orthogonality conditions $\int _{0}^{L}m(x)\phi _s(x)\phi _r(x)dx=\delta _{rs}$ and $\int _{0}^{L}\phi _s(x)\frac{\partial ^2}{\partial x^2}(YI(x)\phi _r(x)'')dx=\omega _r^2 \delta _{rs}$, where $\delta _{rs}$ is Kronecker delta function, and the Dirac delta $\delta (x)$ with the following properties

$$\begin{aligned} \int _{-\infty }^{\infty }\frac{d^{(n)}\delta (x-x_0)}{dx^{(n)}}f(x)dx=(-1)^n\frac{df^{(n)}(x_0)}{dx^{(n)}}, \end{aligned}$$

(20)

we get the final form of Eq. (19) as

$$\begin{aligned} \frac{\partial ^2\eta _r(t)}{dt^2}+2\zeta _r \omega _r\frac{\partial \eta _r(t)}{dt}+\omega _r^2{\eta }_r(t)+\chi _r v(t)= N_r(t) \quad \end{aligned}$$

(21)

where, $2\zeta _r\omega _r=\frac{C_s\omega _{r}^{2}}{Y}+{C_a}\int _{0}^{L}\phi _r(x)\phi _r(x)dx$ is the mechanical damping ratio and $\chi _r=\frac{d}{dx}(\phi _r(x)\nu (x))|_{x=L}$ is term associate with the electromechanical coupling and the forcing term can be expressed as $N_r(t)=-\left(\gamma _r^w\frac{d^2g(t)}{dt^2}+\gamma _r^\theta \frac{d^2h(t)}{dt^2}\right)-c_a\left(\gamma _r^w\frac{dg(t)}{dt}+\gamma _r^\theta \frac{dh(t)}{dt}\right)$, $\gamma _r^w=\int _{x=0}^{L}m(x)\phi _r(x)dx$ and $\gamma _r^\theta =\int _{x=0}^{L}m(x)x\phi _r(x)dx$.

Similarly, the electrical-circuit equation from Eq. (16) can also be simplified by substituting $w_\mathrm{{rel}}$ from Eq. (17) as

$$\begin{aligned} \frac{v(t)}{R_l}+\frac{\epsilon _{33}^s}{h_p}\frac{dv(t)}{dt}\int _{0}^{L}b(x)dx= -d_{31}Y_p h_{pc}\sum _{r=1}^{\infty }\int _{0}^{L}b(x)\phi _r''(x)\dot{\eta }_r(t) dx \end{aligned}$$

(22)

Note that b(x) will be constant for uniform beam and it will be a function of x for non-uniform beams. Clubbing the terms of the above Eq. (22), we get its final form as

$$\begin{aligned} \frac{dv(t)}{dt}+\frac{v(t)}{\tau _c}= \sum _{r=1}^{\infty }{\varphi _r}{\dot{\eta }_r(t)} \end{aligned}$$

(23)

where, $\varphi _r =-\frac{d_{31}Y_ph_{pc}h_p}{\epsilon _{33}^s} \frac{\int _{0}^{L}b(x)\phi _r''(x) dx}{\int _{0}^{L}b(x)dx}$ and   $\tau _c=\frac{R_l\epsilon _{33}^s \int _{0}^{L}b(x)dx}{h_p}$ which are dependent on b(x). For uniform beam, $b(x)=b$, and for non-uniform beams $b(x)=b_0(1+\frac{\alpha x}{L})^{n}$, where $n=1$ for linearly tapered beam and $n=4$ for quartic tapered beam. Finally, we solve the coupled equations of beam (Eq. (21)) and electrical circuit (Eq. (23)) to get electromechanical frequency response of piezoelectric cantilever beam with uniform and non-uniform widths.

To obtain the coupled frequency response, we solve Eqs. (21) and (23) simultaneously by assuming the harmonic base excitation as $g(t)=Y_0e^{j\omega t}$ and $h(t)=\theta _0e^{j\omega t}$. Assuming the output modal co-ordinate as $\eta _{r}(t)=\eta _{r0} e^{j\omega t}$ and neglecting the rotational component and excitation term based on damping (Erturk and Inman 2008a), we get the voltage and current frequency response functions (FRF) as,

$$\begin{aligned} \frac{v(t)}{-\omega ^2 Y_0e^{j\omega t}}= \frac{\sum _{r=1}^{\infty }\frac{-j\omega \varphi _r \gamma _r^w}{\omega _r^2-\omega ^2+j2\zeta _r \omega \omega _r}}{\sum _{r=1}^{\infty }\frac{j\omega \chi _r \varphi _r }{\omega _r^2-\omega ^2+j2\zeta _r \omega \omega _r}+\frac{1+j\omega \tau _c}{\tau _c}} \end{aligned}$$

(24)

and

$$\begin{aligned} \frac{i(t)}{-\omega ^2 Y_0e^{j\omega t}}=\frac{v(t)}{-R_l\omega ^2 Y_0e^{j\omega t}}=\frac{\sum _{r=1}^{\infty }\frac{-j\omega \varphi _r \gamma _r^w}{\omega _r^2-\omega ^2+j2\zeta _r \omega \omega _r}}{R_l \left(\sum _{r=1}^{\infty }\frac{j\omega \chi _r \varphi _r }{\omega _r^2-\omega ^2+j2\zeta _r \omega \omega _r}+\frac{1+j\omega \tau _c}{\tau _c}\right)}. \end{aligned}$$

(25)

The power FRF is obtained from the product of voltage and current FRFs from Eqs. (24) and (25). Although, the above expressions are written in terms of infinite modes, we consider only first three transverse modes for the analysis in this paper. Therefore, we briefly describe the procedure of finding first three modal frequencies and corresponding mode shapes of uniform as well as non-uniform cantilever beams in the subsequent sections.

Mode shapes and modal frequencies of beam

• Uniform beam: To find the response of uniform cantilever beam, we take the mode shapes under undamped and free vibration conditions as (Singh et al. 2015)

  $$\begin{aligned} \phi _{r} (x)=A_1\sin \left( \lambda _{r} \frac{x}{L}\right) +A_2\cos \left( \lambda _{r} \frac{x}{L}\right) +A_3\sinh \left( \lambda _{r}\frac{x}{L}\right) +A_4\cosh \left( \lambda _{r} \frac{x}{L}\right) . \end{aligned}$$

  (26)

  Using the boundary conditions for the cantilever beam as

  $$\begin{aligned} \phi _{r}(0)= \left. \frac{\partial \phi _{r}(x)}{\partial x}\right| _{x=0}=0, \quad \left. YI\frac{\partial ^2 \phi _{r}(x)}{\partial x^2}\right| _{x=L}= \left. YI\frac{\partial }{\partial x}\left( \frac{\partial ^2 \phi _{r}(x)}{\partial x^2}\right) \right| _{x=L}=0 \end{aligned}$$

  (27)

  and the transcendental frequency equation for non-trivial solutions as

  $$\begin{aligned} (2+2\cos (\lambda _r)\cosh (\lambda _r))=0, \end{aligned}$$

  (28)

  where, $\lambda _{r}^{4}=\omega _r^{2}\frac{L^4m}{YI}$, we find the mode shapes and modal frequencies. For first three transverse modes, the frequency parameters are $\lambda _1=1.8751$, $\lambda _2=4.6949$ and $\lambda _3=7.855$. The corresponding values of mode shapes and frequencies can be found from Eq. (26) and $\omega _r=\frac{\lambda _{r}^{2}}{L^2}\sqrt{\frac{ YI}{m}}$ ( $f_{r}=\frac{\omega _{r}}{2\pi }$), where, $m=\rho _s bh_s+\rho _p bh_p$ and YI can be found from Eq. (7) with $b(x)=b$.

• Linearly tapered beam: The mode shapes and frequencies of linearly tapered non-uniform beam is found by transforming the governing equation for non-uniform beam into an equivalent equation of uniform beam as described by Abrate (1995) and Singh et al. (2015). Since, the width of linearly tapered cantilever beam varies as $b(x)=b_{0}(1+\alpha \frac{x}{L})$, the corresponding mode shapes can be written as (Singh et al. 2015),

  $$\begin{aligned} \phi _{r}(x) =\frac{A_1\sin (\lambda _{r} \frac{ x}{L})+A_2\cos (\lambda _{r} \frac{ x}{L})+A_3\sinh (\lambda _{r} \frac{ x}{L})+A_4\cosh (\lambda _{r} \frac{ x}{L})}{\sqrt{1+\frac{\alpha x}{L}}}. \end{aligned}$$

  (29)

  Using the fixed-free boundary conditions of cantilever beam as

  $$\begin{aligned} \phi _{r}(0)= \frac{\partial \phi _{r}(x)}{\partial x}\bigg |_{x=0}=0,~ YI(x)\frac{\partial ^2\phi _{r}(x)}{\partial x^2}\bigg |_{x=L}=\frac{\partial }{\partial x}\left(YI(x)\frac{\partial ^2 \phi _{r}(x)}{\partial x^2}\right)\bigg |_{x=L}=0 \end{aligned}$$

  (30)

  where, for $b(x)=b_0(1+\frac{\alpha x}{L})$, where $b_0$ is the width of the beam at the fixed end, $\alpha$ is the tapering parameter, the flexural rigidity and cross-sectional area can be written as $YI(x)=YI_0(1+\frac{\alpha x}{L})$ and $A(x)=A_0(1+\frac{\alpha x}{L})$. After substituting the mode shapes into boundary conditions, we obtain transcendental equation governing the frequency parameter $\lambda _{r}$ for non-trivial solutions as described by Singh et al. (2015). The readers can refer the above paper for the transcendental equations for converging ($\alpha < 0$) and diverging ($\alpha > 0$) beams. However, for uniform beam, we can take $\alpha =0$. The frequency parameters can be obtained by solving transcendental equation for linearly converging and diverging beams. For converging beam with tapering parameter $\alpha =-0.2$, the frequency parameters for first three transverse modes are $\lambda _1=1.9364$, $\lambda _2=4.7462$ and $\lambda _3=7.886$. For diverging beam of $\alpha =0.2$, the frequency parameters are $\lambda _1=1.8231$, $\lambda _2=4.6582$ and $\lambda _3=7.8352$. The corresponding frequencies can be found from $\omega _r=\frac{\lambda _{r}^{2}}{L^2}\sqrt{\frac{ YI_0}{m_0}}$, where $YI_0$ and $m_0=\rho _s b_{0}h_s+\rho _p b_{0}h_p$ are flexural rigidity and mass per unit length at the fixed end.

• Quartic tapered beam: Similarly, the mode shapes and frequencies of quartic tapered beam can be found by following the same procedure as described in the case of linearly tapered beam in the previous section. In this case, the beam width varies as $b(x)=b_{0}(1+\alpha \frac{x}{L})^{4}$, the corresponding mode shapes can be written as (Abrate 1995; Singh et al. 2015),

  $$\begin{aligned} \phi _{r}(x) =\frac{A_1\sin (\lambda _{r} \frac{ x}{L})+A_2\cos (\lambda _{r} \frac{ x}{L})+A_3\sinh (\lambda _{r} \frac{ x}{L})+A_4\cosh (\lambda _{r} \frac{ x}{L})}{\left( {1+\frac{\alpha x}{L}}\right) ^2}. \end{aligned}$$

  (31)

  For the given boundary conditions, the transcendental equation is obtained. For the first three modes, the frequency parameters for converging beam with $\alpha =-0.2$ are $\lambda _1=2.1419$, $\lambda _2=4.8949$ and $\lambda _3=7.9762$. For diverging beam with $\alpha =0.2$, the frequency parameters are $\lambda _1=1.6731$, $\lambda _2=4.5348$ and $\lambda _3=7.7671$. The corresponding mode shapes and frequencies are found from Eq. (31) and $\omega _r=\frac{\lambda _{r}^{2}}{L^2}\sqrt{\frac{ YI_0}{m_0}}$.

Finally, based on the mode shapes of uniform and non-uniform beams with varying widths, b(x), we obtain the voltage FRF, current FRF and the power FRF by separately computing $\quad \varphi _r =-\frac{d_{31}Y_ph_{pc}h_p}{\epsilon _{33}^s} \frac{\int _{0}^{L}b(x)\phi _r''(x) dx}{\int _{0}^{L}b(x)dx}$ and $\tau _c=\frac{R_l\epsilon _{33}^s \int _{0}^{L}b(x)dx}{h_p}$ for each type of beams.

Results and discussion

In this section, we first validate the voltage frequency response curves with that obtained by Erturk and Inman (2008a) for uniform beam at different load resistances corresponding to first modal frequency. Subsequently, for a given load resistance, we investigate the variation of these curves at different tapering parameters for linearly and quartic varying beams. Finally, we have performed numerical analysis in ANSYS to compare the voltage frequency response curves with analytical model for uniform beam. Subsequently, we have performed numerical analysis for coupled beams to enhance the electrical out and frequency bandwidth.

To do the above analysis, we take dimensions and properties of substructure layer and piezoelectric layer of cantilever beam as mentioned in Table 1 (Erturk and Inman 2008a).

Table 1 Dimensions and properties of substructure and piezoelectric layers of cantilever beam (Erturk and Inman 2008a)

For the above dimensions and properties, the mass per unit length for uni-morph beam is found as $m=0.13405$ kg/m. The flexural rigidity for uniform beam is found as $YI=0.097982$ Nm$^{2}$. For non-uniform beams with linearly varying width and quartic varying width, the flexural rigidities are given by $YI(x)=YI_0(1+\frac{\alpha x}{L})$ and $YI(x)=YI_0(1+\frac{\alpha x}{L})^{4}$, respectively, where, $YI_0=0.097982$ Nm$^{2}$ at the fixed end. The frequencies of uniform and non-uniform beams with linearly and quartic varying width at $\alpha =\pm 0.2$ are computed and mentioned in Table 2.

Table 2 First three modal frequencies of uniform and non-uniform beams with tapering parameter $\alpha =\pm 0.2$ in Hz

To find the frequency response curve corresponding to first mode, we take the same modal damping ratio $\zeta _1=0.01$ as found by Erturk and Inman (2008a) for uniform beams. Although, the damping related with non-uniform beams vary as compared to the uniform cantilever beams, we assumed the same damping ratio as that of uniform beam as we have focused our study mainly on frequency bandwidth. Therefore, $\zeta _r$ in $2\zeta _r\omega _r=\frac{C_s\omega _{r}^{2}}{Y}+{C_a}\int _{0}^{L}\phi _r(x)\phi _r(x)dx$ as mentioned in Eq. (21) for given first mode is taken as $\zeta _1=0.01$. To improve the modeling, the influence of non-uniform beam modeshape on damping can be included to accurately find the voltage output. Finally, the voltage, current and power FRFs can be obtained from Eqs. (24) and (25) for uniform as well as non-uniform beams with corresponding values of YI(x), $\nu (x)$, $\varphi _{r}$ and $\tau _{r}$.

Analysis based on analytical modeling

In this section, we study the influence of load resistance on the electromechanical coupled response of piezoelectric energy harvesters. We plot the modulus of voltage FRFs for five different resistance values of $10^2,10^3,10^4,10^5,10^6$ $\Omega$, respectively. Figure 2a shows the voltage FRFs at different load resistance for uniform beam when $\alpha =0$. The results found to be same as that obtained by Erturk and Inman (2008a) which validates the analytical model. As we can clearly see from Fig. 2a that as the resistance value ($R_l$) increases, the voltage output increases. Therefore, the maximum voltage can be obtained when the system is close to open circuit condition ($R_l=\infty$). However, we found the similar trends for the non-uniform beams, we plot the voltage frequency response curves for tapering beams corresponding to a resistance value of $10^6$ $\Omega$ for further analysis.

Linearly tapered beam

To study the influence of tapering on the voltage FRFs in uni-morph beams, we take $\alpha =\pm 0.2,$ $\pm 0.4,$ and $+0.6$ for linearly tapered beams. The curves in Fig. 2b are obtained corresponding to load resistance of $10^6~\Omega$ near the first transverse mode. It shows the variation of voltage FRF curves with tapering parameters for linearly varying converging as well as diverging beams. On analyzing the curves in Fig. 2b, for the linearly converging beam with tapering parameter of $\alpha =-0.2$, we found that the peak value of voltage output at the load resistance of $R_l=10^6$ decreases by $23.44\%$ with respect to that of the uniform beam. The corresponding frequency increases by $6.5\%$. Similarly, for the linearly diverging beam with tapering parameter $\alpha =0.2$, we found from Fig. 2a that the peak voltage output at $R_l=10^6$ increases by $22.4 \%$ w.r.t. that of the uniform beam while the natural frequency decreases by $5.1 \%$.

As the tapering parameter varies from 0.6 for diverging beam to -0.4 for converging beam, the resonance frequency reduces by $12.56\%$ for $\alpha =0.6$ and increases by $11.37\%$ for $\alpha =-0.4$ with respect to uniform beam for which $\alpha =0$. Consequently, we get increase in frequency range by $23.93\%$ when $\alpha$ varies from 0.6 to -0.4. However, we also found that the voltage output increases by $63.93\%$ w.r.t. that of uniform beam for diverging beam of $\alpha =0.6$ and is decreased by $47.49\%$ w.r.t. that of uniform beam for converging beam of $\alpha =-0.4$. Similar trends are observed in the current and power FRFs The current output is increased by $63.93\%$ for $\alpha =0.6$ and is decreased by $47.49\%$ for $\alpha =-0.4$. The power output is increased by $168.82\%$ for diverging beam with $\alpha =0.6$ and is decreased by $72.43\%$ for converging beam with $\alpha =-0.4$. Thus, the above analysis shows that the power, current and the voltage output increases but the frequency reduces for the diverging beams. Hence, gain in power is obtained with diverging beam for larger tapering ratio. However, the peak values can be further improved by including actual variation of damping ratios.

Fig. 2

a Voltage FRF (frequency response function) curves for uniform beam at different load resistance $R_{l}$, b comparison of voltage FRF curves between linearly varying and uniform beams, and c comparison of voltage FRF curves between quartic varying and uniform beams

Quartic tapered beam

Similarly, Fig. 2c shows the variation of the voltage FRFs of quartic varying beam when the tapering parameter $\alpha =\pm 0.2,$ $\pm 0.4,$ and $\pm 0.6$ for quartic diverging and converging beams. In this case, the frequency decreases by $39.03\%$ for diverging beam with $\alpha =0.6$ and increases by $75.72$ and $157.38\%$ for converging beam with $\alpha =-0.4$ and $-0.6$, respectively, with respect to that of uniform beam. On comparing the voltage response curves in Fig. 2c for tapering parameter values from 0.6 to $-0.6,$ we found that the maximum voltage output is increased by $527.08\%$ for diverging beam of $\alpha =0.6$ and for converging beams with $\alpha =-0.4$ and $\alpha =-0.6$, the voltage outputs are decreased by 93.45 and 99.5% respectively. However, we found that the current output and power output for diverging beam of $\alpha =0.6$ increases by 527.08 and 3833.21%, respectively. Similarly, for converging beams with $\alpha =-0.4$ and $\alpha =-0.6$, the voltage outputs are decreased by 93.45 and 99.5%.

Thus, the diverging quartic beam with large tapering of 0.6 can be used to improve the power out of piezoelectric cantilever beam based energy harvester. However, the frequency corresponding to diverging beam reduces and that of converging beam increases. Nevertheless, an array of converging and diverging beams can be utilized to design wide band piezoelectric energy harvesters. Therefore, we have extended our study to the numerical analysis of PEHs with single unimorph PEHs and coupled PEHs with uniform and non-uniform sections.

Analysis based on numerical modeling

To perform the numerical analysis, we used finite element software ANSYS (ANSYS Inc 2005). To model unimorph piezoelectric energy harvester, we have used SOLID5 element type (linear element with 8 nodes and each node having 6 DOFs) to model the piezoceramic layer. However, to model the substructure beam layer, SOLID45 (Linear element with 8 nodes and each node having 3 DOFs) element type is selected. To perform the electrical analysis, we have used CIRCU94 element type for the resistor and MESH200 for the electric wires. In ANSYS Inc (2005), the piezoelectric elements are poled in z-direction where as according to (Erturk and Inman 2008a) standard the properties are poled in y- direction. Therefore, the piezoelectric compliance matrix, piezoelectric stress matrix and permittivity matrix must be converted from IEEE format to required ANSYS Mechanical APDL format.

To model the unimorph piezoelectric energy harvester in ANSYS Mechanical APDL, the above mentioned three element types are selected. In preprocessor, two material models are created. The properties of the substructure layers and PZT-5A material are taken as listed in the Table 1. The material properties of the piezoelectric material poled in y- direction can be taken as follow (ANSYS Inc 2005; Meiling et al. 2009, 2010),

• (a) Elastic compliance matrix/flexibility matrix

  $$\begin{aligned} s= \left[ {\begin{array}{llllll} 15.2 & -4.55 & -5.77 & 0 & 0 & 0 \\ -4.55 & 15.2 & -5.77 & 0 & 0 & 0 \\ -5.77 & -5.77 & 1.92& 0 & 0 & 0 \\ 0 & 0 & 0& 3.97 & 0 & 0 \\ 0 & 0 & 0& 0 & 5.0 & 0 \\ 0 & 0 & 0& 0 & 0 & 5.0 \\ \end{array} } \right] 10^{-12}~\text{m}^2/\text{N} \end{aligned}$$

• (b) Piezoelectric strain matrix

  $$\begin{aligned} d= \left[ {\begin{array}{lll} 0 & -190 & 0 \\ 0 & 394 & 0 \\ 0 & -190 & 0 \\ 584 & 0 & 0 \\ 0 & 0 & 584 \\ 0 & 0 & 0 \\ \end{array} } \right] 10^{-12}~\text{m}/\text{V} \end{aligned}$$

• (c) Relative permittivity matrix

  $$\begin{aligned} \epsilon _{33}^{s}= \left[ {\begin{array}{lll} 1800 & 0 & 0 \\ 0 & 1800 & 0 \\ 0 & 0 &1800 \\ \end{array} } \right] 10^{-12}~\text{F}/\text{m} \end{aligned}$$

The solid 3D model of the substructure and the piezoceramic layers are created by using the dimensions provided in the Table 1. Figure 3a show the numerical model for the coupled piezoelectric and structural analysis of PEH. The two volumes of 3D solids are glued together. Subsequently, the whole volume can be meshed with hexagonal swept meshing or with required numbers of elements, and then the nodes and the key-points are merged with a tolerance value of $10^{-4}$. Subsequently, the elements of the substrate and piezoceramic layers are attributed to their respective element types and material models. The convergence study is also performed based on the first modal frequency of uniform beam to obtain optimized number of elements as shown in Fig. 3b.

Fig. 3

a First transverse mode shape of the cantilever based unimorph PEH, b convergence curve. Comparison between analytical and numerical voltage FRF with load resistance of c $10^2~\Omega$ and d $10^4~\Omega$

Numerical validation

To validate the numerical model, we find modal frequencies and voltage power output of uniform cantilever beam at different load resistance. Table 3 shows the comparison between frequencies obtained using analytical and numerical techniques. The percentage difference in numerical model is found in the range of 2–4%.

Table 3 First three modal frequencies of uniform beam calculated from analytical results and ANSYS Mechanical APDL in Hz

To obtain the voltage frequency response, we performed the harmonic analysis, the upper and lower layers of piezoceramic are assigned to respective coupled sets with voltage as degree of freedom. Then, the master node is selected from both the coupled sets and a resistive element is created between the two master nodes. The element type selected for the resistive element is CIRCU94. The value of the load resistance can be given as real constant for the element type. To calculate the voltage across the load resistance, the node corresponding to the bottom of the piezoceramic layer, i.e, the top of the substructure layer is grounded by nullifying the voltage at that node. As the analytical results are in terms of voltage per unit linear acceleration, a gravity load is applied at the fixed end of the cantilever. To find the response near the $1^{st}$ fundamental natural frequency, the harmonic analysis is done in a frequency range of 0–100 Hz with 2000 sub-steps. However, the mass and stiffness multipliers are taken as 4.886 and $1.2433\times 10^{-5}$, respectively (Erturk and Inman 2008a). For four different values of load resistance ($10^2~\Omega$, $10^3~\Omega$, $10^4~\Omega , 10^5~\Omega$), the electric potential across the resistive element is found in the frequency range from the active node (which is not grounded) of the resistive element. However, the voltage FRF curves for the resistance value of $10^2~\Omega$ and $10^4~\Omega$ are plotted with respect to frequency ranging from 0–100 Hz in Fig. 3c, d, respectively. Figures also show the comparison between numerical FRF obtained using ANSYS and analytical FRF obtained using Matlab. The peak values of voltage FRFs at different resistance values from numerical and analytical FRFs are tabulated in Table 4. Based on the above results, we found the percentage difference of less than $10\%$. For the resistance value of $10^4~\Omega$, the percentage error is minimum. Therefore, for further analysis of coupled beams we have considered the value of load resistance as $10^4~\Omega$.

Table 4 Values of peaks of voltage FRFs from numerical and analytical model

Numerical analysis of coupled two uniform beams

To increase the voltage output, many researchers have proposed to use arrays of cantilever beams (Soliman et al. 2008; Liu et al. 2008). In this section, we analyze the influence of two uniform beams of same dimensions as mentioned in Table 1 and are separated from each other by a constant distance 4 mm. By following the same procedure as described in the previous section for single beam and doing the analysis over the frequency range of 0–100 Hz, we analyzed the influence of coupling length $L_{c}$ along the beam length. While the length of the beam remains constant as 100 $\upmu$m from the fixed end, the coupling length which is defined as the overlapping length of two beams, i.e., $L_{c}$, as shown in Fig. 4a is varied from 0, 10, 20, 30, 40 to 50 mm (i.e., half the beam length). To perform the numerical analysis, master nodes of upper and bottom layers of piezoceramic beams are connected through a resistor of $10^4$ $\Omega$. The voltage frequency response, resonance frequency and peak voltage versus coupling length are plotted in Fig. 4a–c, respectively. Based on the comparison, it is found that the voltage amplitude in two beam arrays with $L_{c}=0$ is increased by about $48\%$ as compared to single beam. However, its value for two beam array remains nearly constant ($1\%$) as $L_{c}=0$ to 50 mm. Nevertheless, the coupling length helps in tuning the frequencies by around 5%. Now, we will utilize the influence of array of uniform and non-uniform beams.

Fig. 4

a Voltage FRF curves with different coupling lengths, b variation of natural frequency w.r.t the coupling length, and c variation of peaks of voltage FRFs w.r.t coupling length ($L_c$)

Numerical analysis of an array of uniform and non-uniform beams

Based on the theoretical analysis we found that the voltage output increases for diverging beams and decreases for converging beams, whereas, the resonance frequency increases for converging beam and decreases for diverging beam. Utilizing the above changes, we analyze a five beams array consisting of diverging beams of tapering ratio 0.1, uniform beams, and converging beams of taper ratio $-0.1.$ Taking the interbeam distance as 4 mm and coupling length as $L_{c}=10$ mm, we perform harmonic analysis over frequency range of 0–100 Hz by following the same approach as followed for single beam. All other parameters are also taken same as that of single beam analysis. To compare the results of array of uniform and non-uniform beams, we also performed simulation for array of uniform beams with same interbeam gap and coupling length.

Figure 5 shows the comparison of voltage FRF curves between two coupled beams and an array of five uniform beams and an array of combination of uniform and non-uniform beams. From Fig. 5, we found that as the number of uniform beams increases to 5, the voltage peak increases by 38%. Additionally, the frequency bandwidth in the array increases as compared to that of single beam or two beam arrays. On utilizing arrays of uniform and non-uniform beams with tapering ratio of 0.1, the frequency band over which vibration can be captured is increased to 48–54 Hz (6 Hz) as compared to arrays of uniform beams (2 Hz) as shown in Fig. 5. The maximum peak voltage is increased by 12% with respect to two beams array, and is reduced by 18% w.r.t to uniform beams array. Therefore, the use of an array of uniform and non-uniform beams can be used to increase the bandwidth of the energy harvesters. Further analysis can be done by including the variation of damping due to non-uniform beams and optimal value of load resistance for arrays.

Fig. 5

Comparison of voltage FRFs between two uniform beams array, five uniform beams array and an array of uniform and non-uniform beams

At the outset, we state that the output voltage and power of piezoelectric harvesters can be improved by incorporating different structural/geometrical changes. In this paper, we have explored the application of non-uniform sections with a single cantilever beam and an array of coupled beams to optimize the bandwidth and the electrical outputs of the energy harvesters.

Conclusion

In this paper, we have analyzed the influence of linearly and quartic varying width of a cantilever beam on the electrical output of PEH. To do the analysis, we included the effect of non-uniform beam in the existing formulation of the electromechanical coupling of piezoelectric energy harvesters based on uni-morph cantilever beam. Using the modified formulation, we found the voltage, current and power FRFs of PEH at different tapering parameters. On analyzing the curves, we obtained that the frequency increases with the degree of tapering for converging beam and decreases for the diverging beam, whereas, the electrical output increases for the diverging beam with constant external resistive load. Consequently, for the quartic diverging beam with tapering parameter of 0.6, the voltage output, current output and the power output are increased by 527, 527, and 3833, respectively, with respect to those of uniform beam when the external resistive load is $R_{l}=10^6~\Omega$. Additionally, we have found that the frequency also shifts due to non-uniform beams, an array of different non-uniform beams can be used to design a wide-band piezoelectric energy harvesters with improved electrical output. Considering such observation, we have performed numerical analysis of unimorph PEH with uniform section to validate our analytical results. Then, we extend the numerical formulation to coupled beams which helps in improving the voltage output and the bandwidth of the harvester. On analyzing the FRF curves of the coupled PEHs, we found that the peak of voltage FRF of PEH having an array of two coupled beams increases by 48% as compared to those of the unimorph PEHs. Additionally, we found that the resonance frequency of the coupled beams increases with the increase in coupling length. To study the effect of non-uniformity, an array of five uniform beams and an array of five uniform and non-uniform beams are modeled. While an array of five uniform beams gives more voltage output as compared to an array of two coupled beams, an array of uniform and non-uniform beams increases the frequency bandwidth of the energy harvester by more than 10% as compared to array of uniform beams.