1 Introduction

As typical energy harvesting structures to harvest energy from the ambient vibrations, cantilever beams are widely used and at present piezoelectric energy harvesters are particularly attractive as they possess lower resonance frequencies and relatively higher strain for a given force input. Some structure parameters play a great role in the efficiency of the electrical output of the energy harvester, for example, the width, the thickness, the length of the substructure beam and the piezoelectric layer. In addition, the shapes will also affect the responses of the structure and the electrical output. Because a normal rectangular cantilever beam has non-uniform strain distribution in the length direction, it is generally considered to have very low efficiency of energy harvesting. To overcome such a shortage, some triangular, trapezoidal or variable-shaped beam structures were presented and investigated (Mateu and Moll 2005; Roundy et al. 2005; Ayed et al. 2014). Having compared a triangular cantilever with a rectangular one with the same base and length (height) dimensions, Mateu and Moll (2005) showed that a triangular cantilever beam will have higher strain and deflection for a given load resistance. Roundy et al. (2005) convinced that the strain in trapezoidal cantilever can be made more evenly distributed throughout the beam as opposed to the non-uniform strain distribution in a rectangular beam. They showed that for the same volume of lead zirconate titanate (PZT), a trapezoidal cantilever can generate more than twice the energy of a rectangular beam. Ayed et al. (2014) concluded that a trapezoidal cantilever beam will produce more power per unit area compared to a rectangular beam as the distribution of strain is uniform. For a trapezoidal cantilever beam, there are two kinds of boundaries, one is that the large end is clamped, the other is that the small end is clamped. Benasciutti et al. (2010) performed experiments on the response of a variable-width beam and concluded that a reversed trapezoidal beam with the large end free gives more energy than the trapezoidal shape with the large end clamped and that both are better than the rectangular configuration. At the same time, other non-classical shapes are also being studied in some applications, including shell structure (Yang and Yun 2011), spiral (Hu et al. 2007), zigzag (Karami and Inman 2012) and S-shape (Shindo and Narita 2014) configurations.

Because of the complexity in theory of a non-rectangular beam, many investigations were merely made by numerical method or simulation. Based on Ritz–Rayleigh method and FEM simulation, Goldschmidtboeing and Woias (2008) found that the shape has only a little influence on the efficiency but can have an enormous effect on the maximum tolerable excitation amplitude and therefore on the maximum output power. By means of Galerkin approach, Ayed et al. (2014) studied the beam with different width functions either of linear or of quadratic form. By simulation based on MATLAB and COMSOL Multiphysics software, Muthalif and Nordin (2015) studied the effect of varying the length and shape of the beam on the generated voltage. Tabatabaei et al. (2016) made a shape optimization for piezoelectric energy harvester using artificial immune system.

It is well known that, as opposed to analytical model, by a numerical method or simulation it is difficult to give us a explicit regular relationship between the output (or responses) and the parameters of the structures. By numerical simulation, only some concrete results for a definite example with definite geometrical and physical parameters can be obtained. To understand the effect of beam shapes on the output deeply, an analytical model may be necessary.

In this paper, analytical models for vibrations and electrical output of classic cantilevered piezoelectric energy harvesters with arbitrary shape beam are presented. Experimental analysis shows a qualitative agreement with analytical models, indicating that the total output charges are independent of the width of the beam for a rectangular beam. For an arbitrary shape beam, parameters which could be sensitive for obtaining a satisfied energy harvesting are studied. Additionally, the optimal shapes obtained from Ayed et al. (2014) and Tabatabaei et al. (2016) have been proved and supported by the presented analytical model.

2 Estimation of electrical output of piezoelectric cantilever beam with arbitrary width

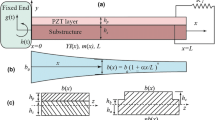
For an Euler–Bernoulli beam with rectangular section and uniform thickness but non-uniform width φ(x) shown in Fig. 1, the stress on any cross section can be expressed as:

$$ \left\{ {\begin{array}{*{20}l} {T_{s} = Y_{s} z\frac{{\partial^{2} w}}{{\partial x^{2} }}} \hfill &\quad { - (h - e) \le z < e} \hfill \\ {T_{p} = Y_{p} z\frac{{\partial^{2} w}}{{\partial x^{2} }}} \hfill \quad& {e < z \le (e + \delta )} \hfill \\ \end{array} } \right. $$
(1)

where x is the coordinate in the length direction of beam, z is the coordinate in the thickness direction, w is the deflection displacement in the opposite z direction, \( \frac{{\partial^{2} w}}{{\partial x^{2} }} \) is the bending curvature of beam, T is normal stress, Y is the Young’s modulus, the subscript s refers to the substructure (beam) while p denotes the piezoelectric layer.

Fig. 1
figure 1

The schematic diagram of a cantilever beam with arbitrary width with a tip mass

Full size image

For a composite beam made of substructure and piezoelectric layer, by making the total normal stresses (sum of the stresses) in thickness direction be zero, the neutral position of bending can be determined as

$$ e = \frac{{Y_{s} h^{2} - Y_{p} \delta^{2} }}{{2(Y_{p} \delta + Y_{s} h)}} $$
(2)

where e is the distance from the neutral surface of bending to the interface between substructure beam and piezoelectric layer shown in Fig. 2, h represents the thickness of the substructure (beam), δ represents the thickness of the piezoelectric layer.

Fig. 2
figure 2

The schema of neutral position of bending of beam

Full size image

When the mass of cantilever beam is rather smaller than the proof mass, the cantilever beam can be considered as a spring. At this time, the bending of beam can be analyzed by static method. By statically balancing between the internal normal stress and the external moment on a cross section, the static bending equation of beam can be written by:

$$ \frac{{d^{2} w}}{{dx^{2} }} = \frac{M(x)}{{K_{D} \varphi (x)}} $$
(3)

where K D is the bending rigidity of the composite beam per unit width.

Considering a cross section, the internal banding moment M I is derived by:

$$ M_{I} = \int\limits_{A} {T_{I} zdA = \int_{ - (h - e)}^{e} {bY_{s} \frac{z}{\rho }} } zdz + \int_{e}^{e + \delta } {bY_{p} \frac{z}{\rho }zdz = \frac{1}{3\rho }b[Y_{s} (h^{3} - 3h^{2} e + 3he^{2} ) + Y_{p} (\delta^{3} + 3\delta^{2} e + 3\delta e^{2} )]} $$
(4)

Substituting the geometric relation \( \frac{1}{\rho } = \frac{{\partial^{2} w}}{{\partial x^{2} }} \), Eq. (4) and M(x) = M I into (3), one may obtain:

$$ K_{D} = \frac{{[Y_{s} (h^{3} - 3h^{2} e + 3he^{2} ) + Y_{p} (\delta^{3} + 3\delta^{2} e + 3\delta e^{2} )]}}{3} $$
(5)

To balance the static moments in the length direction for a cantilever beam with a proof mass fixed at the free end, the external moment on a cross section x caused by the gravity of proof mass can be determined by

$$ M(x) = m_{2} g(L - x) + \int_{0}^{L - x} {g(\rho_{s} h + \rho_{p} \delta )\varphi (x + \xi )\xi d\xi } $$
(6)

where m 2 is the mass of the proof mass, g is the acceleration of gravity, L is the length of the beam, ρ is the density of material, also the subscript s refers to the substructure (beam) while p denotes the piezoelectric layer.

When the mass of beam is too small compared with the proof mass, that is \( \frac{1}{{m_{2} }}(\rho_{s} h + \rho_{p} \delta )\int_{0}^{L} {\varphi (x)dx} \ll 1, \) the mass of beam is negligible, then there is

$$ M(x) = m_{2} g(L - x) $$
(7)

According to the constitutive equation of piezoelectric materials and neglecting the coupling effect of electric fields, the electric displacement D 3 from the static bending forced by mass gravity can be expressed as

$$ D_{3} = d_{31} Y_{p} z\frac{{\partial^{2} w}}{{\partial x^{2} }} $$
(8)

If all over the surface is covered by the electrode, the total charge on the electrode surface can be derived as

$$ Q_{e} = \iint\limits_{S} {D_{3} dS} = d_{31} Y_{p} \left( {e + \frac{\delta }{2}} \right)\int_{0}^{L} {\frac{{\partial^{2} w}}{{\partial x^{2} }}\varphi (x)dx} = \frac{1}{{K_{D} }}d_{31} Y_{p} \left( {e + \frac{\delta }{2}} \right)\int_{0}^{L} {M(x)dx} = \frac{1}{{2K_{D} }}m_{2} gL^{2} d_{31} Y_{p} \left( {e + \frac{\delta }{2}} \right) $$
(9)

From this equation, it is clearly seen that, for a given proof mass, the total charges are independent of the width φ(x) of beam.

3 Electrical output voltage in resonant vibration

Even though in dynamic condition, when the inertia of beam is negligible compared with that of proof mass, the cantilever beam can be also considered as a spring. The basic natural frequency of such a spring-mass system can be written as \( \omega = \sqrt {\frac{k}{{m_{2} }}} \), where k is the stiffness at the tip of beam with respect to the proof mass.

For a damped vibration system, the vibration equation is expressed as:

$$ \ddot{w}(t) + 2\zeta \omega \dot{w}(t) + \omega^{2} w(t) = a(t) $$
(10)

where ζ is damping ratio.

When the exciting acceleration is a(t) = A sin ω d t, where A is amplitude and ω d is exciting frequency, the steady response can be expressed as:

$$ w(t) = \bar{w}\sin (\omega_{d} t - \varphi ) $$
(11)

where \( \bar{w} \) is the amplifier, φ is phrase whose forms are:

$$ \bar{w} = \frac{A}{{\omega^{2} \sqrt {\left[ {1 - \left( {\frac{{\omega_{d} }}{\omega }} \right)^{2} } \right]^{2} + 4\zeta^{2} \left( {\frac{{\omega_{d} }}{\omega }} \right)^{2} } }},\quad \varphi = \tan^{ - 1} \frac{{2\zeta \left( {\frac{{\omega_{d} }}{\omega }} \right)}}{{1 - \left( {\frac{{\omega_{d} }}{\omega }} \right)^{2} }} $$
(12)

If the exciting frequency is equal to the natural frequency, that is ω d  = ω, there is:

$$ \bar{w} = \frac{A}{{2\omega^{2} \zeta }} = \beta \frac{A}{{\omega^{2} }},\quad \varphi = \frac{\pi }{2} $$
(13)

where \( \beta = \frac{1}{2\zeta } \) is quality factor.

Then there is

$$ w(t) = \frac{A}{{2\omega^{2} \zeta }}\sin \left( {\omega t - \frac{\pi }{2}} \right) = - \beta \frac{A}{{\omega^{2} }}\cos \omega t $$
(14)

The mode of vibration is the same as the static bending deflection undergoing the gravity of proof mass at the free end. Thus compared with Eq. (9), the output charges on the electrode can be obtained similarly:

$$ Q_{e} = - \frac{1}{{2K_{D} }}\beta m_{2} AL^{2} d_{31} Y_{p} \left( {e + \frac{\delta }{2}} \right)\cos \omega t $$
(15)

From this equation, it is also known that, the total electric charges output are independent of the width φ(x) of beam.

According to the former reference (Erturk and Inman 2011), the capacitance of piezoelectric layer can be written by:

$$ C_{p} = \frac{{\varepsilon_{33} \int_{0}^{L} {\varphi (\xi )d\xi } }}{\delta } = \frac{{\varepsilon_{33} L\bar{\varphi }}}{\delta } $$
(16)

where \( \bar{\varphi } = \frac{{\int_{0}^{L} {\varphi (x)dx} }}{L} \) is called the average width of the beam.

Then the open circuit voltage between the two electrodes can be derived as:

$$ V = \frac{{Q_{e} }}{{C_{p} }} = \frac{{\beta m_{2} ALd_{31} Y_{p} \left( {e + \frac{\delta }{2}} \right)\delta }}{{2K_{D} \varepsilon_{33} \bar{\varphi }}}\cos \omega t $$
(17)

4 The dynamic model of piezoelectric cantilever beam energy harvester with arbitrary width

4.1 Responses of piezoelectric cantilever beam energy harvester with arbitrary width under harmonic excitation

When the inertia of beam is not small, we must take account for its mass. In this case, the dynamic equations of the beam with a proof mass can be expressed as:

$$ \left\{ {\begin{array}{*{20}l} {K_{D} \frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {\varphi (x)\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right] + (\rho_{s} h + \rho_{p} \delta )\varphi (x)\frac{{\partial^{2} w}}{{\partial t^{2} }} = q} \hfill &\quad {0 \le x < L} \hfill \\ {m_{2} \frac{{\partial^{2} w}}{{\partial t^{2} }} - K_{D} \varphi (L)\frac{{\partial^{3} w}}{{\partial x^{3} }} = f} \hfill &\quad {x = L} \hfill \\ \end{array} } \right. $$
(18)

where q is the load density of excitation applied on the beam in the opposite z direction, f is the excitation force applied on the proof mass in the opposite z direction. For an acceleration excitation a, there are q = (ρ s h + ρ p δ)a and f = m 2 a.

Equation (18) can be rearranged as:

$$ \left\{ {\begin{array}{*{20}l} {K_{D} \varphi (x)\left[ {\frac{{\partial^{4} w}}{{\partial x^{4} }} + 2\frac{{\varphi^{\prime}(x)}}{\varphi (x)}\frac{{\partial^{3} w}}{{\partial x^{3} }} + \frac{{\varphi^{\prime\prime}(x)}}{\varphi (x)}\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right] + (\rho_{s} h + \rho_{p} \delta )\varphi (x)\frac{{\partial^{2} w}}{{\partial t^{2} }} = q} \hfill & {0 \le x < L} \hfill \\ {m_{2} \frac{{\partial^{2} w}}{{\partial t^{2} }} - K_{D} \varphi (L)\frac{{\partial^{3} w}}{{\partial x^{3} }} = f} \hfill & {x = L} \hfill \\ \end{array} } \right. $$
(19)

Considering \( \frac{{\varphi^{\prime}(x)}}{\varphi (x)} \ll 1 \) and \( \frac{{\varphi^{\prime\prime}(x)}}{\varphi (x)} \ll 1 \) which can be neglected for a general slender beam, the above equations can be rewritten by

$$ \left\{ {\begin{array}{*{20}l} {K_{D} \varphi (x)\frac{{\partial^{4} w}}{{\partial x^{4} }} + (\rho_{s} h + \rho_{p} \delta )\varphi (x)\frac{{\partial^{2} w}}{{\partial t^{2} }} = q} \hfill &\quad {0 \le x < L} \hfill \\ {m_{2} \frac{{\partial^{2} w}}{{\partial t^{2} }} - K_{D} \varphi (L)\frac{{\partial^{3} w}}{{\partial x^{3} }} = f} \hfill &\quad {x = L} \hfill \\ \end{array} } \right. $$
(20)

Then using modal technique, the solution can be expressed as w = ψ(x)T(t). Substituting it into the corresponding free vibration equation, leads to

$$ \left\{ {\begin{array}{*{20}c} {\psi^{(4)} (x) - \lambda^{4} \psi (x) = 0} \\ {\ddot{T}(t) + \omega^{2} T(t) = 0} \\ \end{array} } \right. $$
(21)

where \( \lambda = \sqrt[4]{{\frac{{(\rho_{s} h + \rho_{p} \delta )}}{{K_{D} }}\omega^{2} }} \) is Eigen value.

Using the boundary conditions, ψ = 0 and ψ′ = 0 for the clamped side (x = 0), and ψ′′ = 0 and \( D\varphi (L)\psi^{\prime\prime\prime} = - m_{2} \omega^{2} \psi \) for the free side (x = L), the Eigen values and vibration modes can be derived as

$$ \left\{ {\begin{array}{*{20}l} {(\lambda L)\gamma = \frac{1 + \cosh \lambda L\cos \lambda L}{\cosh \lambda L\sin \lambda L - \sinh \lambda L\cos \lambda L}} \hfill \\ {\psi_{n} (x) = c_{1} [(\cosh \lambda_{n} x - \cos \lambda_{n} x) - \frac{{A_{n} }}{{B_{n} }}(\sinh \lambda_{n} x - \sin \lambda_{n} x)]} \hfill \\ \end{array} } \right. $$
(22)

where \( \gamma = \frac{{m_{2} }}{{(\rho_{s} h + \rho_{p} \delta )\varphi (L)L}},A_{n} = \cosh \lambda_{n} L + \cos \lambda_{n} L,B_{n} = \sinh \lambda_{n} L + \sin \lambda_{n} L. \)

By solving the Eigen value equation, a series of Eigen values λ i and corresponding natural frequencies ω i can be obtained.

From these equations, it demonstrates that, the modes and the natural frequencies are independent of the width function φ(x), while they are related to the width φ(L) at free end. For a proof mass with the same width as width φ(L) of beam at free end, \( \gamma = \frac{{\rho_{m} l_{m} h_{m} }}{{(\rho_{s} h + \rho_{p} \delta )L}} \) where ρ m , l m and h m are the density, length and height of the proof mass respectively. In this case, the natural frequencies are absolutely independent of the width function.

For a harmonic acceleration excitation a(t) = A sin ω d t where A is the amplitude of acceleration, ω d is the excitation frequency, the steady dynamic response can be given as:

$$ w(x,t) = \sum\limits_{i = 1}^{n} {\psi_{i} (x)T_{i} (t)} = \sum\limits_{i = 1}^{n} {[(\cosh \lambda_{i} x - \cos \lambda_{i} x) - \frac{{A_{i} }}{{B_{i} }}(\sinh \lambda_{i} x - \sin \lambda_{i} x)]\bar{T}_{i} \sin (\omega_{d} t - \varphi_{i} )} $$
(23)

For the resonant vibration of first mode ω d  = ω 1, there is

$$ w = - \beta_{1} \frac{{\alpha_{1} A}}{{\omega_{1}^{2} }}[(\cosh \lambda_{1} x - \cos \lambda_{1} x) - \frac{{A_{1} }}{{B_{1} }}(\sinh \lambda_{1} x - \sin \lambda_{1} x)]\cos \omega_{1} t $$
(24)
$$ \frac{\partial w}{\partial x} = - \beta_{1} \frac{{\alpha_{1} A}}{{\omega_{1}^{2} }}\lambda_{1} [(\sinh \lambda_{1} x + \sin \lambda_{1} x) - \frac{{A_{1} }}{{B_{1} }}(\cosh \lambda_{1} x - \cos \lambda_{1} x)]\cos \omega_{1} t $$
(25)
$$ w\left| {_{x = L} } \right. = - \beta_{1} \frac{{\alpha_{1} A}}{{\omega_{1}^{2} }}\psi_{1} (L)\cos \omega_{1} t $$
(26)
$$ \frac{\partial w}{\partial x}\left| {_{x = L} } \right. = - \beta_{1} \frac{{\alpha_{1} A}}{{\omega_{1}^{2} }}\psi_{1}^{\prime } (L)\cos \omega_{1} t = \frac{{\psi_{1}^{\prime } (L)}}{{\psi_{1} (L)}}w\left| {_{x = L} } \right. $$
(27)

where \( \beta_{i} = \frac{1}{{2\zeta_{i} }} \) is quality factor, \( \alpha_{i} = \frac{{\int_{0}^{L} {(\rho_{s} h + \rho_{p} \delta )\varphi (x)\psi_{i} (x)} dx + m_{2} \psi_{i} (L)}}{{\int_{0}^{L} {(\rho_{s} h + \rho_{p} \delta )\varphi (x)\psi_{i} (x)\psi_{i} (x)} dx + m_{2} \psi_{i}^{2} (L)}} \), \( \psi_{1} (L) = \frac{{A_{1}^{{\prime \prime }} B_{1} - A_{1} A_{1}^{{\prime }} }}{{B_{1} }} \), \( \psi_{1}^{{\prime }} (L) = \lambda_{1} \frac{{B_{1}^{2} - A_{1} A_{1}^{{\prime \prime }} }}{{B_{1} }} \), \( A_{1}^{{\prime \prime }} = \cosh \lambda_{1} L - \cos \lambda_{1} L \), and \( A_{1}^{\prime } = \sinh \lambda_{1} L - \sin \lambda_{1} L \).

When the mass of beam is too small compared with the proof mass to be considered, there are α 1 ψ 1(L) = 1 and \( \omega_{1} = \sqrt {\frac{k}{{m_{2} }}} \) where k is the stiffness at the tip of beam with respect to the proof mass, leads to:

$$ w\left| {_{x = L} } \right. = - \beta_{1} \frac{{m_{2} A}}{k}\cos \omega_{1} t $$
(28)

In this case, the dynamic model of piezoelectric cantilever beam degenerates into static model. The vibration mode is the same as the static bending deflection undergoing the gravity of proof mass at the free end. The total charge on the electrode is the same as in Eq. (9).

4.2 The open circuit electrical output of piezoelectric cantilever beam energy harvester with arbitrary width

When all over the surface is covered by the electrode, if neglecting the coupling effect of electric fields, the total charge on the electrode surface can be derived as

$$ Q_{e} = d_{31} Y_{p} \left( {e + \frac{\delta }{2}} \right)\int_{0}^{L} {\frac{{\partial^{2} w}}{{\partial x^{2} }}\varphi (x)dx} $$
(29)

For the first mode resonant vibration,substituting \( w(x,t) = \frac{{\psi_{1} (x)}}{{\psi_{1} (L)}}w(t)\left| {_{x = L} } \right. \) into it, leads to

$$ Q_{e} = d_{31} Y_{p} \left( {e + \frac{\delta }{2}} \right)\frac{1}{{\psi_{1} (L)}}\left[ {\int_{0}^{L} {\psi_{1}^{{\prime \prime }} (x)\varphi (x)dx} } \right]w(t)\left| {_{x = L} } \right. $$
(30)

or

$$ Q_{e} = \varTheta w(t)\left| {_{x = L} } \right. $$
(31)

where \( \varTheta = d_{31} Y_{p} \left( {e + \frac{\delta }{2}} \right)\frac{1}{{\psi_{1} (L)}}\left[ {\int_{0}^{L} {\varphi (x)\psi_{1}^{{\prime \prime }} (x)dx} } \right] \) is called coupling coefficient or mechanical–electrical converting coefficient.

Substituting \( w\left| {_{x = L} } \right. = - \beta_{1} \frac{{\alpha_{1} A}}{{\omega_{1}^{2} }}\psi_{1} (L)\cos \omega_{1} t \) into the above equation and noticing the relation \( \frac{1}{{\omega_{1}^{2} }} = - \frac{{m_{2} \psi_{1} (L)}}{{K_{D} \varphi (L)\psi_{1}^{{{\prime \prime \prime }}} (L)}} \), leads to

$$ Q_{e} = d_{31} Y_{p} \left( {e + \frac{\delta }{2}} \right)\beta_{1} \frac{{\alpha_{1} Am_{2} \psi_{1} (L)}}{{K_{D} \varphi (L)\psi_{1}^{{{\prime \prime \prime }}} (L)}}\left[ {\int_{0}^{L} {\psi_{1}^{{\prime \prime }} (x)\varphi (x)dx} } \right]\cos \omega_{1} t $$
(32)

For the uniform width, that is rectangular beam, φ′(x) = 0, there is

$$ Q_{e} = d_{31} Y_{p} \left( {e + \frac{\delta }{2}} \right)\beta_{1} \frac{{\alpha_{1} Am_{2} \psi_{1} (L)\psi_{1}^{{\prime }} (L)}}{{K_{D} \psi_{1}^{{{\prime \prime \prime }}} (L)}}\cos \omega_{1} t $$
(33)

It can be seen that, the total charges are independent of the width shape.

When φ′(x) is a constant, that is the trapezoidal beam, the output charges from the electrode is

$$ Q_{e} = d_{31} Y_{p} \left( {e + \frac{\delta }{2}} \right)\beta_{1} \frac{{\alpha_{1} Am_{2} \psi_{1} (L)}}{{K_{D} \psi_{1}^{{{\prime \prime \prime }}} (L)}}[\psi_{1}^{{\prime }} (L) - \frac{{\varphi^{{\prime }} (L)}}{\varphi (L)}\psi_{1} (L)]\cos \omega_{1} t $$
(34)

It also proves that, the total charges are independent of the width shape but associate with φ′(L) and φ(L).

The open circuit voltage between the two electrodes can be derived as

$$ V = \frac{{Q_{ave} }}{{C_{p} }} = d_{31} Y_{p} \left( {e + \frac{\delta }{2}} \right)\delta \beta_{1} \frac{{\alpha_{1} Am_{2} \psi_{1} (L)}}{{\varepsilon_{33} L\bar{\phi }K_{D} \psi_{1}^{\prime \prime \prime } (L)}}\left[ {\psi_{1}^{\prime } (L) - \frac{{\varphi^{\prime } (L)}}{\varphi (L)}\psi_{1} (L)} \right]\cos \omega_{1} t $$
(35)

Because the capacitance of the piezoelectric layer depends on the width of electrode surface, the open circuit output voltage will be affected by the shapes or in more accurate words by the area of the electrode surface.

4.3 The loop circuit electrical output of piezoelectric cantilever beam energy harvester with arbitrary width

For a loop circuit, the coupling effect of electric fields must be considered. In this case, the constitutive equations of piezoelectric materials are written as follow:

$$ \left\{ {\begin{array}{*{20}l} {T_{1} = Y_{p} \frac{z}{\rho } - e_{31} E_{3} } \hfill &\quad {e \le z \le e + \delta } \hfill \\ {T_{1} = Y_{s} \frac{z}{\rho }} \hfill & { - (h - e) \le z < e} \hfill \\ {D_{3} = e_{31} \frac{z}{\rho } + \varepsilon_{33} E_{3} } \hfill &\quad {e \le z \le e + \delta } \hfill \\ \end{array} } \right. $$
(36)

Integrating the stress multiplying distance to neutral surface in the thickness direction (z) to form a moment pro unit width on the cross section, and integrating the average electric displacement in the electrode surface, leads to:

$$ \left\{ {\begin{array}{*{20}l} {M_{unit} (x) = \frac{{K_{D} }}{\rho (x)} - e_{31} \left( {e + \frac{\delta }{2}} \right)V} \hfill \\ {Q_{e} = e_{31} \left( {e + \frac{\delta }{2}} \right)\int_{0}^{L} {\frac{{\partial^{2} w}}{{\partial x^{2} }}\varphi (x)dx} + \frac{{\varepsilon_{33} S}}{\delta }V} \hfill \\ \end{array} } \right. $$
(37)

where \( M_{unit} (x) = \frac{M(x)}{\varphi (x)} \) is moment pro unit width on a cross section.

For the first mode resonant vibration, \( w(x,t) = \frac{{\psi_{1} (x)}}{{\psi_{1} (L)}}w(t)\left| {_{x = L} } \right. \). Substituting it into the above equations and integrating the first equation in the electrode surface after multiplying \( \psi_{1}^{{\prime \prime }} (x) \), leads to

$$ \left\{ {\begin{array}{*{20}l} {\int_{0}^{L} {\varphi (x)M(x)\psi_{1}^{{\prime \prime }} (x)dx} = \frac{{K_{D} }}{{\psi_{1} (L)}}\left\{ {\int_{0}^{L} {\varphi (x)[\psi_{1}^{{\prime \prime }} (x)]^{2} dx} } \right\}w\left| {_{x = L} } \right. - e_{31} \left( {e + \frac{\delta }{2}} \right)\left[ {\int_{0}^{L} {\varphi (x)\psi_{1}^{{\prime \prime }} (x)dx} } \right]V} \hfill \\ {Q_{e} = e_{31} \left( {e + \frac{\delta }{2}} \right)\frac{1}{{\psi_{1} (L)}}\left[ {\int_{0}^{L} {\varphi (x)\psi_{1}^{{\prime \prime }} (x)dx} } \right]w\left| {_{x = L} } \right. + \frac{{\varepsilon_{33} S}}{\delta }V} \hfill \\ \end{array} } \right. $$
(38)

If the moment is caused by the transverse force f at the free end, the above equations can be written as

$$ \left\{ {\begin{array}{*{20}l} {f = \frac{{K_{D} }}{{\psi_{1}^{2} (L)}}\left\{ {\int_{0}^{L} {\varphi (x)[\psi_{1}^{{\prime \prime }} (x)]^{2} dx} } \right\}w\left| {_{x = L} } \right. - e_{31} \left( {e + \frac{\delta }{2}} \right)\frac{1}{{\psi_{1} (L)}}\left[ {\int_{0}^{L} {\varphi (x)\psi_{1}^{{\prime \prime }} (x)dx} } \right]V} \hfill \\ {Q_{e} = e_{31} \left( {e + \frac{\delta }{2}} \right)\frac{1}{{\psi_{1} (L)}}\left[ {\int_{0}^{L} {\varphi (x)\psi_{1}^{{\prime \prime }} (x)dx} } \right]w\left| {_{x = L} } \right. + \frac{{\varepsilon_{33} S}}{\delta }V} \hfill \\ \end{array} } \right. $$
(39)

In dynamic case, \( f = m_{2} a(t) - m_{2} \frac{{\partial^{2} w}}{{\partial t^{2} }}\left| {_{x = L} } \right. - c\frac{\partial w}{\partial t}\left| {_{x = L} } \right.. \) Substituting it into the above equation, gives:

$$ \left\{ {\begin{array}{*{20}l} {m_{2} \frac{{\partial^{2} w}}{{\partial t^{2} }}\left| {_{x = L} } \right. + c\frac{\partial w}{\partial t}\left| {_{x = L} } \right. + \frac{{K_{D} }}{{\psi_{1}^{2} (L)}}\left\{ {\int_{0}^{L} {\varphi (x)[\psi_{1}^{{\prime \prime }} (x)]^{2} dx} } \right\}w\left| {_{x = L} } \right. - e_{31} \left( {e + \frac{\delta }{2}} \right)\frac{1}{{\psi_{1} (L)}}\left[ {\int_{0}^{L} {\varphi (x)\psi_{1}^{{\prime \prime }} (x)dx} } \right]V = m_{2} a(t)} \hfill \\ {Q_{e} = e_{31} \left( {e + \frac{\delta }{2}} \right)\frac{1}{{\psi_{1} (L)}}\left[ {\int_{0}^{L} {\varphi (x)\psi_{1}^{{\prime \prime }} (x)dx} } \right]w\left| {_{x = L} } \right. + \frac{{\varepsilon_{33} S}}{\delta }V} \hfill \\ \end{array} } \right. $$
(40)

Differentiating the second equation with respect to time, one may obtain:

$$ \left\{ {\begin{array}{*{20}l} {m_{2} \frac{{\partial^{2} w}}{{\partial t^{2} }}\left| {_{x = L} } \right. + c\frac{\partial w}{\partial t}\left| {_{x = L} } \right. + kw\left| {_{x = L} } \right. - \varTheta V = m_{2} a(t)} \hfill \\ {I = \varTheta \dot{w}\left| {_{x = L} } \right. + C_{p} \dot{V}} \hfill \\ \end{array} } \right. $$
(41)

where \( k = \frac{{K_{D} }}{{\psi_{1}^{2} (L)}}\left\{ {\int_{0}^{L} {\varphi (x)[\psi_{1}^{{\prime \prime }} (x)]^{2} dx} } \right\} \), \( \varTheta = e_{31} \left( {e + \frac{\delta }{2}} \right)\frac{1}{{\psi_{1} (L)}}\left[ {\int_{0}^{L} {\varphi (x)\psi_{1}^{{\prime \prime }} (x)dx} } \right] \) are called stiffness and coupling coefficient respectively. As d 31 Y p  = e 31, Θ here is the same as Θ mentioned above.

Integrating it, the coupling coefficient Θ can be expressed as:

$$ \varTheta = e_{31} \left( {e + \frac{\delta }{2}} \right)\frac{1}{{\psi_{1} (L)}}\left[ {\psi_{1}^{{\prime }} (L)\varphi (L) - \varphi^{{\prime }} (L)\psi (L) + \int_{0}^{L} {\varphi^{{\prime \prime }} (x)\psi_{1} (x)dx} } \right] $$
(42)

From this equation, it can be found that, coupling coefficient Θ depends on φ(L), φ′(L) and \( \varphi^{{\prime \prime }} (x) \) respectively. In order to increase Θ, φ(L) should be increased. In addition, \( \varphi^{{\prime }} (L) \) should be negative, that is \( \varphi^{\prime }(L) < 0 \) and \( \varphi^{\prime \prime }(x) \) should be positive, that is \( \varphi^{\prime \prime }(x) > 0 \).

4.4 The influence of width function on the coupling effect of piezoelectric cantilever beam energy harvester

For a quadratic width function, \( \varphi^{\prime \prime }(x) \) is a constant. Such a quadratic width function was given in Tabatabaei et al. (2016):

$$ \varphi (x) = \varphi (0)\left[ {1 + ( - 3 - \alpha_{1} + 4\alpha_{2} )\frac{x}{L} + 2(1 + \alpha_{1} - 2\alpha_{2} )\left( {\frac{x}{L}} \right)^{2} } \right] $$
(43)

where α 2 φ(0) is the width in middle point \( \left( {x = \frac{L}{2}} \right) \) and α 1 φ(0) is the width in free end (x = L) of cantilever beam shown in Fig. 3. To insure \( \varphi^{{\prime }} (L) < 0 \) and \( \varphi^{{\prime \prime }} (x) > 0 \), the following relation have to be satisfied

$$ \frac{{1 + 3\alpha_{1} }}{4} < \alpha_{2} < \frac{{1 + \alpha_{1} }}{2} $$
(44)
Fig. 3
figure 3

An optimal width shape of a cantilever beam

Full size image

That is, an optimal width function curve φ m (x) should lie in the shaded area.

Such a shape is consistent with the optimal shape by using artificial immune system (AIS) from Tabatabaei et al. (2016) shown in Fig. 4.

Fig. 4
figure 4

The optimal width shape of a cantilever by AIS method from Tabatabaei et al. (2016)

Full size image

When \( \varphi^{{\prime }} (x) \) is a constant, the coupling coefficient can be written as

$$ \varTheta = e_{31} \left( {e + \frac{\delta }{2}} \right)\left[ {\frac{{\psi_{1}^{{\prime }} (L)}}{{\psi_{1} (L)}}\varphi (L) - \varphi^{{\prime }} (L)} \right] = e_{31} \left( {e + \frac{\delta }{2}} \right)\left[ {\lambda_{1} \frac{{B_{1}^{2} - A_{1} A_{1}^{{\prime \prime }} }}{{A_{1}^{{\prime \prime }} B_{1} - A_{1} A_{1}^{{\prime }} }}\varphi (L) - \varphi^{{\prime }} (L)} \right] $$
(45)

For a circuit with a resistor as electric load, the electric current can be written as

$$ I(t) = \frac{V(t)}{R} $$
(46)

Substituting it into the above equation, leads to

$$ \left\{ {\begin{array}{*{20}l} {m_{2} \frac{{\partial^{2} w}}{{\partial t^{2} }}\left| {_{x = L} } \right. + c\frac{\partial w}{\partial t}\left| {_{x = L} } \right. + kw\left| {_{x = L} } \right. - \varTheta V = m_{2} a(t)} \hfill \\ {\varTheta \dot{w}\left| {_{x = L} } \right. + C_{p} \dot{V} - \frac{V(t)}{R} = 0} \hfill \\ \end{array} } \right. $$
(47)

For rectangular beam, there are \( \varphi^{{\prime }} (x) = 0 \) and \( \varTheta = e_{31} \left( {e + \frac{\delta }{2}} \right)\frac{3a}{2L}. \) For trapezoidal beam with the large end clamped, there are \( \varphi^{{\prime }} (x) = - \frac{a - b}{L} \) and \( \varTheta = e_{31} \left( {e + \frac{\delta }{2}} \right)\vartheta \) where \( \vartheta = \frac{{(a - b)^{3} }}{{[(a - b)^{2} + 2b^{2} (\ln a - \ln b) + 2b(b - a)]L}} \) and a is width of the large end and b is that one of the small free end. For triangular beam, there are \( \varphi^{{\prime }} (x) = - \frac{a}{L} \) and \( \varTheta = e_{31} \left( {e + \frac{\delta }{2}} \right)\frac{a}{L} \) where a is width of the base side of beam.

5 Experiments and verifications

In order to verify the theoretical model, we designed and manufactured three kinds of structure shapes shown in Fig. 5. The first one is rectangular beam. The second one is trapezoidal beam. The third one is truncated triangular beam. The upper surface of the substructure beam is covered with a piece of polarized PZT-5H piezoelectric plate (layer). A magnet as a proof mass is fixed at the free end of the beam to adjust the resonant frequency of system. The upper and lower surfaces of the PZT-5H piezoelectric plate are covered with a layer of silver. These two layers of silver are used as the cathode and the anode respectively.

Fig. 5
figure 5

Three kinds of beam shapes a truncated triangular, b trapezoidal and c rectangular

Full size image

As shown in Fig. 6, the vibrating shaker is connected to a signal generator (providing the source vibration frequency and amplitude excitation) through a power amplifier. Lead wires from the piezoelectric cantilever beam are connected across a variable resistor to adjust the piezoelectric power output. In addition, an accelerometer (recording the vibration acceleration) and a dynamic signal analyzer (recording output voltage) are used.

Fig. 6
figure 6

Experimental setup

Full size image

The material parameters of substructure beam and the piezoelectric layer are shown in Table 1.

Table 1 Physical parameters of the designed energy harvester
Full size table

The thicknesses of beam and piezoelectric layer are h = 0.2 mm and δ = 0.2 mm respectively. The mass of proof mass is m 2 = 7.68 × 10−3 kg = 7.68 g. The damping ratio is ζ = 0.01. The amplitude of the excitation acceleration is A = 2 m/s2. The length of all these three kinds of beams is L = 22 mm. The base width of all these three kinds of beams is a = 25 mm. The widths of free end of these three beams are b = 25 mm, b = 15 mm and b = 8 mm respectively.

The open circuit output voltages versus excitation frequencies are shown in Fig. 7. The total charges on the electrode surface are shown in Fig. 8.

Fig. 7
figure 7

The open circuit voltage versus excitation

Full size image
Fig. 8
figure 8

The total charges for different shapes

Full size image

The experimental harvested power at optimal load with frequencies of loop circuit is shown in Fig. 9.

Fig. 9
figure 9

The experimental loop circuit harvested power at optimal load with frequencies

Full size image

6 Conclusion

From the above theoretical and experimental analyses, it concludes that, for a given resonant acceleration excitation and the mass of beam is considerably small with respect to the proof mass, the total charges on the electrode surface are seems to be affected hardly by the shapes in width of the beam. The shapes and widths will affect the capacitance of the piezoelectric layer directly, and then affect the open circuit output voltage. With the decreasing of the width at the free end of cantilever beam, the resonant frequency will be lower, the open circuit voltage peak will be higher and the harvested power at optimal load will increase. In addition, the optimal width shape of beam from Tabatabaei et al. (2016) or Ayed et al. (2014), which was given numerically by means of Galerkin approach or artificial immune system (AIS), has been obtained theoretically using the presented analytical model in this paper.