Introduction

Countries all over the world are coming together and making several attempts (Kyoto Protocol, Paris Agreement, etc.) to combat and reduce the effects of climate change. It is believed that climate change is majorly caused by industrial activities. Industries discharge huge amount of pollutants (wastewater, carbon dioxide, etc.) into the environment every year and consume large quantities of resources (freshwater, hydrogen, fossil fuels, etc.). Different countries are making different laws and policies to control the industrial pollution. These laws are getting stringent with each passing day and, thus, forcing industries to move towards more sustainable options for their operations. It includes minimising the discharge of untreated waste in the environment as well as minimising their resource consumption. However, cost-effectiveness of these measures is the priority concern for all the industries.

Pinch analysis, a thermodynamics based process synthesis approach, helps to minimise resource consumption and waste generation. It started as a tool for minimising utilities in heat exchanger networks (Linnhoff et al. 1982) and soon extended for minimising resources in many industrial applications as shown in Table 1. This table is basically adopted from Sahu and Bandyopadhyay (2011) and Tan et al. (2015). Table 1 also indicates equivalence of temperature and enthalpy in heat exchanger networks, for other applications. Problems listed in Table 1 minimises only one objective function. In addition to these single objective problems, Krishna Priya and Bandyopadhyay (2017) have successfully applied pinch analysis to multiple objectives problems involving power system planning. Apart from resource conservation, pinch analysis is also applied for cost optimality of various networks, for example, heat exchanger networks (Linnhoff and Ahmad 1990), water networks (Hallale and Fraser 1998), and distillation columns (Bandyopadhyay et al. 1999). Shenoy and Bandyopadhyay (2007) introduced the concept of prioritised cost to determine the cost optimal solution for problems involving multiple resources.

Table 1 A list of different industrial problems addressed by pinch analysis
Full size table

Lee et al. (2009) identified a special type of resource conservation problem, called segregated targeting problem for carbon constraint energy sector planning. This problem is later generalised by Bandyopadhyay et al. (2010b) for various resource allocation networks. A segregated targeting problem consists of multiple sets of demands called zones and a set of common internal sources. These sources are shared between all the zones. Each zone also contains a resource which is dedicated to the zone in which it is present and is not shared with other zones. Bandyopadhyay et al. (2010b) developed a decomposition algorithm using the concept of pinch analysis to determine the resource optimal solution for such problems. Chandrayan and Bandyopadhyay (2014) introduced economic aspect to the segregated targeting problems where each resource is characterised by two parameters: quality and cost. The concepts of prioritised cost, developed by Shenoy and Bandyopadhyay (2007), were applied by Chandrayan and Bandyopadhyay (2014) to determine the cost optimal solution. Jain and Bandyopadhyay (2017) noted that due to different process constraints like safety, flexibility, the proximity of different sources from different demands, etc., there is a necessity that some sources should be considered as dedicated sources for particular zones. These dedicated sources are specific to the zone in which they are present and are not shared with other zones. These types of problems are called segregated targeting problems with dedicated sources. Jain and Bandyopadhyay (2017) introduced the concept of Benefit number that helps in determining the resource optimal solution for segregated targeting problems with dedicated sources. However, apart from determining optimum resource, the minimisation of the overall cost is the major factor which dictates the economic feasibility of a problem and, hence, its acceptability by the industries.

In this paper, the economic aspect of a general segregated targeting problem with dedicated sources is discussed. It is assumed that the resource of each zone has a cost attribute attached to it. A new methodology, based on the concepts of pinch analysis, is developed for determining the cost optimal solution for segregated targeting problem with dedicated sources. The proposed methodology is based on the objective that the distribution of sources among different zones is governed by the preference of minimising the overall cost. Introduction of the proposed methodology is essential as the algorithm derived by Chandrayan and Bandyopadhyay (2014) for cost optimality of segregated problems cannot be directly applied due to the presence of dedicated sources. The proposed algorithm is generic in nature and the applicability of the proposed algorithm is demonstrated through three different examples from various domains: carbon constrained energy sector planning, water allocation network, and integrated iron and steel mill.

Problem Definition and Mathematical Formulation

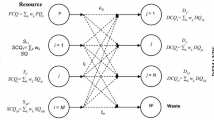
The general problem for segregated targeting problem with dedicated sources is described through a superstructure, shown in Fig. 1. It consists of a set of common sources called internal sources and multiple sets of demands called zones. Each zone has a resource associated with it and a set of dedicated internal sources. These dedicated sources are specific to the zone in which they are present and are not shared with other zones. The demands of each zone are satisfied by using the dedicated internal sources, common internal sources, and the resource. The objective of the problem is to minimise the overall cost of the resources.

Fig. 1
figure 1

Superstructure of segregated targeting problem with dedicated sources

Full size image

The problem can be mathematically stated as follows:

  • A set of N s common internal source is given. Each source i (1, 2, …, N s ) produces a flow F si at quality q si .

  • A set of N z zones is given. Each zone (k = 1, 2, …, N z ) consists of a dedicated resource, a set of demands and a set of dedicated internal sources. For a zone k, each demand (j = 1, 2, …, N dk ), requires flow F djk at a maximum allowable quality limit of q djk . Each dedicated source (l = 1, 2, …, N DSk ) produces a flow F DSlk at a given quality q DSlk . These sources are specific to the zone in which they are present and are not shared by other zones. That is, the dedicated source present in zone 1 cannot supply flow to zone 2. The resource, R k , present in zone k produces flow at quality q rk and has a cost associated with it (c rk ).

  • The resources, common internal sources, and dedicated sources are utilised to satisfy the demands present in the problem. Unutilised flow from internal sources and dedicated sources is thrown to an external demand called waste. Waste does not have any flow and quality limitations.

  • The objective of the problem is to minimise the overall cost of the resources while satisfying the flow and quality load constraints of the demands.

It should be noted that the flows are defined by non-negative real numbers and qualities are defined by real numbers. Quality follows an inverse scale, that is, the higher numerical value of quality indicates its inferiority.

Let f ijk be the flow transferred from internal source i to demand j of zone k and f iw be the flow transferred from internal source i to the waste. Let f ljk be the flow transferred from dedicated source l to demand j of zone k and f lwk be the flow transferred from dedicated source l present in zone k to waste. Let f rjk be the flow transferred from resource present in zone k to demand j present in the same zone. Equation 1 represents the flow constraint for internal sources. The flow constraint for dedicated sources is given by Eq. 2. Equations 3 and 4 express the flow and quality load constraints for the demands.

$$ \sum \limits_{k=1}^{N_z}\sum \limits_{j=1}^{N_{dk}}{f}_{ijk}+{f}_{iw}={F}_{si}\forall i\in \left\{1,2,\dots, {N}_s\right\} $$
(1)
$$ \sum \limits_{j=1}^{N_{dk}}{f}_{ljk}+{f}_{lwk}={F}_{DSlk}\forall l\in \left\{1,2,\dots, {N}_{DSk}\right\},\forall k\in \left\{1,2,\dots, {N}_z\right\} $$
(2)
$$ \sum \limits_{i=1}^{N_s}{f}_{ijk}+\sum \limits_{l=1}^{N_{DSk}}{f}_{ljk}+{f}_{rjk}={F}_{djk}\forall j\in \left\{1,2,\dots, {N}_{dk}\right\},\forall k\in \left\{1,2,\dots, {N}_z\right\} $$
(3)
$$ \sum \limits_{i=1}^{N_s}{f}_{ijk}{q}_{si}+\sum \limits_{l=1}^{N_{DSk}}{f}_{ljk}{q}_{DSlk}+{f}_{rjk}{q}_{rk}\le {F}_{djk}{q}_{djk}\forall j\in \left\{1,2,\dots, {N}_{dk}\right\},\forall k\in \left\{1,2,\dots, {N}_z\right\} $$
(4)

The objective is to minimise the overall cost of the resources being utilised in the problem.

$$ C=\sum \limits_{k=1}^{N_z}\sum \limits_{j=1}^{N_{dk}}{c}_{rk}{f}_{rjk} $$
(5)

Equations 1–5 shows that the constraints and the objective function are linear in nature, and hence, this is a linear programming problem. In next section, the cost optimal segregated targeting problem is mathematically analysed using the concepts of pinch analysis.

Mathematical Analysis

Let us assume that there are two zones with resource quality q r1 and q r2 and let the cost associated with these two zones be c r1 and c r2. Let each zone be targeted individually by using only the resource and the dedicated sources present in each zone. After this targeting is performed, three possible cases may arise.

  • Case 1: Both the zones have the pinch points.

  • Case 2: One zone has the pinch point while the other does not have the pinch point (threshold problem).

  • Case 3: None of the zones have the pinch point (both are threshold problems).

In all the three cases, the addition of flow from common internal sources to these zones may lead to a reduction in total cost of the resources being utilised in the problem. However, the optimal reduction of cost for each resource depends on the distribution of internal sources in both the zones.

Optimality Condition for Case 1

Consider case 1, where both the zones have the pinch points. Let q p1 be the pinch point for zone 1 and q p2 be the pinch point for zone 2. The resource requirement for these zones can be obtained by an expression derived by Bandyopadhyay (2015), shown in Eq. 6, and the total cost for both the zones is given by Eq. 7.

$$ {R}_k=\sum \limits_{\begin{array}{c}j=1\\ {}{q}_{djk}\le {q}_{pk}\end{array}}^{N_{dk}}{F}_{djk}\frac{\left({q}_{pk}-{q}_{djk}\right)}{\left({q}_{pk}-{q}_{rk}\right)}-\sum \limits_{\begin{array}{c}i=1\\ {}{q}_{si}\le {q}_{pk}\end{array}}^{N_s}{F}_{si}\frac{\left({q}_{pk}-{q}_{si}\right)}{\left({q}_{pk}-{q}_{rk}\right)} $$
(6)
$$ C={c}_{r1}{R}_1+{c}_{r2}{R}_2 $$
(7)

The reduction in cost (∆C) obtained by transferring δ amount of flow from mth internal source to zone 1 is shown in Eq. 8.

$$ \Delta {C}_1={c}_{r1}\delta \frac{\left({q}_{p1}-{q}_{sm}\right)}{\left({q}_{p1}-{q}_{r1}\right)} $$
(8)

Similarly, when δ is transferred from mth internal source to zone 2 instead of zone 1, the reduction in total cost is as follows:

$$ \Delta {C}_2={c}_{r2}\delta \frac{\left({q}_{p2}-{q}_{sm}\right)}{\left({q}_{p2}-{q}_{r2}\right)} $$
(9)

It is concluded from Eqs. 8 and 9 that to achieve the maximum reduction in the overall cost of the resources, δ is transferred to that zone which has the highest value of cost-benefit number (P(m, k)) as expressed in Eq. 10 and shown in Fig. 2.

$$ P\left(m,k\right)={c}_{rk}\frac{\left({q}_{pk}-{q}_{sm}\right)}{\left({q}_{pk}-{q}_{rk}\right)} $$
(10)
Fig. 2
figure 2

Comparison of reduction in overall cost to determine the correct distribution of internal sources in both the zones

Full size image

It is noted from Eq. 10 that for the cost-benefit number to be positive, quality of mth source (q sm ) from where the flow is being transferred should be less than the pinch quality (q pk ) of the zone. This mathematical analysis proves Lemma 1.

Lemma 1

Cost optimality in a segregated targeting problem with dedicated sources, involving two zones, is achieved by transferring internal source to the zone, having the highest value of the cost-benefit number.

Lemma 1 is used to generalise the cost optimality condition for k zones as follows:

Theorem

In a segregated targeting problem with dedicated sources, having k zones, the cost optimality is achieved by transferring flow from internal sources to the zone having the highest value of the cost-benefit number.

Proof

The proof is trivial for a problem involving only one zone. Well ordering principle of real numbers is used for proving the theorem for k zones. P(m, k) is a real number and according to the well ordering principle, for k ≥ 1, P(m, k) have the highest value for some k. As stated by Eqs. 8 and 9, the maximum reduction in the overall cost can be achieved by transferring flow from internal sources to kth zone as it has the maximum value of P(m, k).

It is inferred from the above theorem that the cost-benefit number plays an important role in determining the cost optimal solution for segregated targeting problem involving dedicated sources. The above theorem is a generalised optimality condition for cost optimality in various resource conservations networks. Under special cases, it reduces to specific cost optimality conditions as demonstrated through following two corollaries.

Corollary 1

In a segregated targeting problem with dedicated sources, if the pinch qualities of all the zones are the same, then the cost optimality is achieved by distributing the internal sources according to the prioritised cost.

Proof

Corollary 1 is proved for two zones and can be generalised easily for k zones. Let us assume that q p1 is the pinch point for zone 1 and q p2 is the pinch point for zone 2. Let the flow from mth internal source transferred to zone 1 and thus according to the Theorem, Eq. 11 holds true.

$$ {c}_{r1}\frac{\left({q}_{p1}-{q}_{sm}\right)}{\left({q}_{p1}-{q}_{r1}\right)}\ge {c}_{r2}\frac{\left({q}_{p2}-{q}_{sm}\right)}{\left({q}_{p2}-{q}_{r2}\right)} $$
(11)

Let us assume that the pinch point of zone 1 is equal to the pinch point of zone 2, that is q p1 = q p2. Then, Eq. 11 is reduced to Eq. 12, which is same as the prioritised cost derived by Shenoy and Bandyopadhyay (2007).

$$ \frac{c_{r1}}{\left({q}_{p2}-{q}_{r1}\right)}\ge \frac{c_{r2}}{\left({q}_{p2}-{q}_{r2}\right)} $$
(12)

Corollary 2

In a segregated targeting problem with dedicated sources, if the cost of all the resources are equal, then the overall cost optimality (equivalent to the total resource optimality) can be achieved by distributing the flow of internal sources according to the benefit number, (q pk  − q sm )/(q pk  − q rs ).

It is seen from Eq. 10 that if the costs of all the resources are identical, then the cost-benefit number is essentially reduced to benefit number derived by Jain and Bandyopadhyay (2017).

It is also seen from Eq.10 that for a particular internal source, the cost-benefit number depends on the pinch quality of a zone, the quality and per unit cost of its resource. For a zone, the quality and per unit cost of its resources remains unchanged, whereas on addition and removal of flow from a zone, its pinch quality may change. With the change in pinch quality, the cost-benefit number will change and, as a result, the distribution of internal source in different zones may also change. Therefore, it is essential to determine the minimum flow required to change the pinch point of a zone.

Condition for Pinch Jump

Jain and Bandyopadhyay (2017) have presented a detailed study about the characteristics of pinch jump. These characteristics describe the change in pinch point on addition and subtraction of flows from a network (stated in Lemmas 2–7). These lemmas are mathematically proved by Jain and Bandyopadhyay (2017).

Lemma 2

The pinch point of a zone remains unchanged when the flow is added in the above pinch region.

Lemma 3

The pinch point of the zone can jump only in the below pinch region when the flow is added in the below pinch region.

Lemma 4

The maximum amount of flow (∆) that can be added in a zone without changing the pinch point of that zone is the minimum of all ∆ i s given by Eq. 13.

$$ {\Delta }_i=\left\{\begin{array}{c}\left({R}_p-{R}_{si}\right)\frac{\left({q}_{si}-{q}_{rs}\right)\left({q}_p-{q}_{rs}\right)}{\left({q}_{sm}-{q}_{rs}\right)\left({q}_p-{q}_{si}\right)}\kern1.75em \mathrm{if}\ {q}_{sm}<{q}_{si}\\ {}\left({R}_p-{R}_{si}\right)\frac{\left({q}_p-{q}_{rs}\right)}{\left({q}_p-{q}_{sm}\right)}\kern5.5em \mathrm{if}\ {q}_{sm}\ge {q}_{si}\end{array}\right. $$
(13)

where R p is the minimum resource requirement for a zone with pinch quality q p , and R si is the resource requirement if q si is considered as the potential pinch quality.

Lemma 5

The pinch point of the zone can only jump in the above pinch region when flow is extracted from the above pinch region.

Lemma 6

The pinch point of the zone can only jump in the above pinch region when the flow is extracted from the below pinch region.

Lemma 7

The maximum amount of flow that can be extracted from a zone without changing the pinch point of that zone is the minimum of all ∆ i s given by Eq. 14.

$$ {\Delta }_i=\left\{\begin{array}{c}\left({R}_p-{R}_{si}\right)\frac{\left({q}_{si}-{q}_{rs}\right)\left({q}_p-{q}_{rs}\right)}{\left({q}_{sm}-{q}_{rs}\right)\left({q}_{si}-{q}_p\right)}\kern1.25em \mathrm{if}\ {q}_{sm}<{q}_p\\ {}\left({R}_p-{R}_{si}\right)\frac{\left({q}_{si}-{q}_{rs}\right)}{\left({q}_{si}-{q}_{sm}\right)}\kern4.5em \mathrm{if}\ {q}_{sm}\ge {q}_p\end{array}\right. $$
(14)

Optimality Condition for Other Cases

Consider case 2, where one zone does not have a pinch point, that is, it is a threshold problem for that zone and the other zone have a pinch point. In such cases, a pseudo-source is introduced in the zone, which does not have a pinch point, at a very high quality, such that the pseudo-source becomes the pinch source for that zone. It should be noted that pseudo-source does not exist in reality; they are introduced in a zone just to create pinch point in that zone. Once both the zones have the pinch points, the methodology applied for case 1 is repeated to achieve the cost optimality and the pseudo-source is entirely eliminated at the end by utilising internal sources and the resource.

Consider case 3 where both the zones do not have the pinch points, that is, both are threshold problems. Similar to the case 2, pseudo-sources are introduced in both the zones so as to create the pinch points in both the zones. Once the pinch points are created, the methodology adopted for case 2 is followed and pseudo-sources are removed at the end. Based on this mathematical analysis, an algorithm is proposed to determine the cost optimal solution for segregated targeting problem with dedicated sources.

Algorithm to Achieve Cost Optimality

An algorithm is proposed, based on the mathematical analysis and results proved in the previous section, to determine the cost optimality for segregated targeting problems with dedicated sources. Figure 3 shows the flow chart of the proposed algorithm.

  1. Step 1.

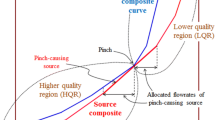
    Target each zone individually without using the common internal sources. Targeting is performed by using any of the established pinch analysis based techniques such as source composite curve and limiting composite curve.

  2. Step 2.

    Check whether all the zones have the pinch point or do not have the pinch point. If all the zones have the pinch point, go to step 4, else go to step 3.

  3. Step 3.

    Identify the zones which do not have the pinch point and introduce pseudo-sources at a very high quality in these zones. Transfer the flow from the pseudo-source to these zones such that the pseudo-source becomes the pinch point for these zones.

  4. Step 4.

    Calculate the value of cost-benefit number (Eq. 10) at all the internal sources for all the zones. Eliminate the internal sources, having negative or zero values of the cost-benefit number at all the zones. As seen from Eq. 10, negative or zero values of cost-benefit number implies that the internal source would not lead to any reduction in the overall cost.

  5. Step 5.

    Identify the maximum value of the cost-benefit number. Transfer α (Eq. 15) amount of flow from the mth internal source to the kth zone corresponding to the maximum cost-benefit number. α is the minimum of the flow available in the mth internal source and the flow (∆) needed for the pinch jump as calculated in Lemma 4.

Fig. 3
figure 3

Algorithm for cost optimality of segregated targeting problems with dedicated sources

Full size image
$$ \alpha =\min \left({F}_{sm},\Delta \right) $$
(15)

After adding α to the appropriate zone, update F sm  = F sm  − α.

If F sm  > ∆, then the pinch point changes and step 4 is repeated with the updated pinch point.

If F sm  < ∆, then step 5 is repeated with the next highest value of the cost-benefit number.

Once all the sources get exhausted, go to step 6.

  1. Step 6.

    Check whether the flow from the pseudo-source is used in the network. If it is used in the network, neglected internal sources and the resource are utilised to completely eliminate the pseudo-source. The algorithm terminates when all the pseudo-sources are eliminated. The solution obtained by following this algorithm is the cost optimal solution for segregated targeting problem with dedicated sources.

The applicability of the proposed algorithm is demonstrated through three illustrative examples from various domains: carbon constrained energy sector planning, water allocation network and integrated iron and steel mill.

Illustrative Examples

Example 1: Carbon Constrained Energy Sector Planning

Data for example 1 (Table 2) are adapted from Lee et al. (2009). In this problem, two sectors of energy consumption are considered namely transportation sector and industrial sector. Each sector has three dedicated demands. To satisfy these demands, two (oil and natural gas) common internal sources are provided and, in addition to that, one dedicated internal source (coal) is also present in industrial sector. Coal is regarded as the dedicated source for industrial sector because of its limiting use in transportation sector. The economy of transportation sector is moving more towards oil and petroleum products due to the advancement of technology in this sector. Biodiesel is considered as a resource for transportation sector. However, due to its higher cost (0.031 $/MJ) (Chandrayan and Bandyopadhyay 2014), it is not taken as a resource for industrial sector. Hydropower with a cost of 0.028 $/MJ (Chandrayan and Bandyopadhyay 2014) is considered as a resource for industrial sector. The objective is to minimise the overall cost of the problem while satisfying the energy needs and carbon emission targets for the demands.

Table 2 Flow and quality data for example 1
Full size table

The algorithm proposed in the previous section is applied to achieve the desired objective of cost optimality. According to step 1, each zone is targeted individually without using the common internal sources. It is observed that coal acts as a pinch source for industrial sector, whereas transportation sector does not have a pinch point. The total energy required is 3.32 EJ (1.84 EJ in transportation sector and 1.48 in industrial sector) and total cost obtained is $98.53 billion ($57.04 billion for transportation sector and $41.49 billion for industrial sector). Since transportation sector does not have a pinch point, by following step 3, a pseudo-source with CO2 emission factor of 200 t/TJ is introduced in this sector. Now, 0.25 EJ of energy is transferred from this pseudo-source so that it becomes the pinch source for transportation sector. The overall energy requirement after this flow addition is 3.07 EJ (1.59 EJ in transportation sector and 1.48 EJ in industrial sector), and the overall cost is $90.69 billion ($49.2 billion for transportation sector and $41.49 billion for industrial sector).

Both the sectors have the pinch points, so according to step 4, the cost-benefit number is calculated at both the internal sources for both the sectors (Table 3). As seen from Table 3, the maximum value of cost-benefit number (24,495.9 $/TJ) corresponds to transportation sector and natural gas. By following step 5, 0.8 EJ of energy (minimum of 0.8 EJ, energy available with natural gas and 1.2 EJ, the energy required for pinch jump) is transferred from natural gas to transportation sector. After this flow addition, the flow from natural gas gets exhausted and the flow utilised for pseudo-source reduces to 0.085 EJ. The resource requirement obtained is 2.44 EJ (0.96 EJ in transportation sector and 1.48 EJ in industrial sector), and the total cost is $71.09 billion ($29.6 billion for transportation sector and $41.49 billion for industrial sector). The next highest value of cost-benefit number is 21,117.2 $/TJ (Table 3), which corresponds to oil at transportation sector. According to step 5, 0.27 EJ of energy (minimum of 1 EJ, energy available with the oil and 0.27 EJ, energy required for pinch jump) is transferred from oil to transportation sector. After this flow addition, oil becomes the pinch source for transportation sector and the 0.73 EJ is the remaining energy left in the oil and the pseudo-source gets completely eliminated. The overall energy requirement is reduced to 2.25 EJ (0.77 EJ in transportation sector and 1.48 EJ in industrial sector), and the total cost is reduced to $65.44 billion ($23.95 billion for transportation sector and $41.49 billion for industrial sector).

Table 3 Cost-benefit number ($/TJ) for all the internal sources at all the zones for example 1
Full size table

Cost-benefit numbers are calculated again for both the internal sources at both the zones with the updated pinch point (Table 3). As natural gas is already exhausted, the highest value of cost-benefit number under consideration is 8000 $/TJ, which corresponds to oil at industrial sector. Energy transferred from oil to industrial sector is 0.73 EJ (minimum of 0.73 EJ, energy available with the oil and 0.95 EJ, energy required for pinch jump). After this flow addition, the oil gets exhausted and the resource requirement gets reduced to 2.04 EJ (0.77 EJ in transportation sector and 1.27 EJ in industrial sector). The overall minimum cost obtained is $59.58 billion ($23.95 billion for transportation sector and $35.63 billion for industrial sector). The algorithm stops as all the internal sources get exhausted, and the pseudo-source is completely eliminated.

The results obtained by applying the proposed algorithm are verified using the mathematical optimisation techniques. The network showing the distribution of energy from different sources to different demands is shown in Fig. 4.

Fig. 4
figure 4

Network showing the distribution of energy from different sources to different demands in example 1

Full size image

Example 2: Water Allocation Network

Data for example 1 are adopted from Bandyopadhyay et al. (2010b) and given in Table 4. In this problem, two different zones are considered. Each zone consists of four sinks ((D1, D2, D3, D4): (D5, D6, D7, D8)) which require water at specified flowrate and a maximum allowable contaminant concentration. To meet these demands, two common internal sources (S1 and S2) are provided. Due to the proximity of DS1 and DS2 from zone 1, these sources are considered as the dedicated sources for zone 1. Similarly, due to the proximity of DS3 and DS4 from zone 2, they are considered as the dedicated sources for zone 2. R1 is regarded as the resource for zone 1 with the cost of 1.5 $/t and R2 is regarded as the resource for zone 2 with the cost of 1 $/t. The objective is to minimise the total cost of the resource requirement.

Table 4 Flow and quality data for example 2
Full size table

According to step 1 of the algorithm, each zone is targeted individually without using the common internal sources. It is observed that zone 1 has a pinch point at DS1. However, zone 2 does not have a pinch point. The overall resource requirement obtained is 326.25 t/h (156.25 t/h for zone 1 and 170 t/h for zone 2), and the total cost is 404.37 $/h (234.37 $/h for zone 1 and 170 $/h for zone 2). Since zone 2 does not have a pinch point, a pseudo-source at 1000 ppm is introduced in zone 2 and 0.81 t/h of flow is added from this pseudo-source to zone 2 to create a pinch point. After this flow addition from the pseudo-source, the overall resource requirement is reduced to 325.44 t/h (156.25 t/h for zone 1 and 169.19 t/h for zone 2). The total cost of the resources is reduced to 403.57 $/h (234.37 $/h for zone 1 and 169.19 $/h for zone 2).

The cost-benefit numbers at both the internal sources (S1 and S2) for both the zones are calculated according to step 4 (see Table 5). As seen from Table 5, the highest value of cost-benefit number (1.406 $/t) corresponds to zone 1 at S1. The flow transferred from S1 to zone 1 is 50 t/h (minimum of 50 t/h, flow available in S1 and 145.33 t/h, flow required for pinch jump). After this flow addition, the overall resource requirement is reduced to 278.57 t/h (109.38 t/h for zone 1 and 169.19 t/h for zone 2) and the total cost is reduced to 333.25 $/h (164.06 $/h for zone 1 and 169.19 $/h for zone 2). The next highest value of cost-benefit number is 1.312 $/t (Table 5) which corresponds to S2 at zone 1. The flow transferred from S2 to zone 1 is 50.71 t/h (minimum of 220 t/h, flow available with S2 and 50.71 t/h, flow required for pinch jump).

Table 5 Cost-benefit number ($/t) for all the internal sources at all the zones for example 2
Full size table

The pinch point of zone 1 jumps to S2 after this flow addition, and 169.29 t/h of flow is still available in S2. The overall resource requirement is reduced to 234.19 t/h (65 t/h for zone 1 and 169.19 t/h for zone 2), and the total cost is reduced to 266.69 $/h (97.5 $/h for zone 1 and 169.19 $/h for zone 2). The cost-benefit numbers are calculated again (Table 5) with the updated pinch point.

As seen from Table 5, the highest value of cost-benefit number (0.959 $/t) corresponds to S1 at zone 2. However, S1 is already exhausted, so the algorithm proceeds with the next highest value of cost-benefit number (0.909). This value corresponds to S2 at zone 2. Flow (8.89 t/h) is added from S2 to zone 2 (minimum of 169.29 t/h, flow available in S2 and 8.89 t/h, flow required for pinch jump). The pinch points of zone 2 jump to DS4 from pseudo-source and the flow from pseudo-source gets completely eliminated after this flow addition. The resource requirement gets reduced to 226.11 t/h (65 t/h in zone 1 and 161.11 t/h in zone 2), and the total cost incurred is 258.61 $/h (97.5 $/h for zone 1 and 161.11 $/h for zone 2). The flow availability of S2 is reduced to 160.4 t/h. The values of cost-benefit number are calculated again (Table 5) with the updated pinch point.

The next highest value of cost-benefit number under consideration is 0.625 $/t (as S1 is exhausted), which corresponds to S2 at zone 2. The flow transferred from S2 to zone 2 is 66.67 t/h (minimum of 160.4 t/h, flow available with S2 and 66.67 t/h, flow required for pinch jump). The pinch point of zone 2 jumps to DS3 after this flow addition, and the availability of flow from S2 gets reduced to 93.73 t/h. The overall resource required is 184.44 t/h (65 t/h for zone 1 and 119.44 t/h for zone 2), and the total cost is 216.94 $/h (97.5 $/h for zone 1 and 119.44 $/h for zone 2). The cost-benefit numbers are calculated again with the updated pinch point (Table 5).

The next highest value of cost-benefit number under consideration is 0.357 $/t, which corresponds to S2 at zone 2. Flow (54.44 t/h) is transferred from S2 to zone 2 (minimum of 93.73 t/h, flow available in S2 and 54.44 t/h, flow required for pinch jump). The pinch point of zone 2 jumps to S2 after this flow addition. The resource requirement gets reduced to 165 t/h (65 t/h in zone 1 and 100 t/h in zone 2), and the total cost gets reduced to 197.5 $/h (97.5 $/h for zone 1 and 100 $/h for zone 2). The cost-benefit numbers are again calculated with the updated pinch point (Table 5).

As seen from Table 4, the cost-benefit numbers at S2 become zero for both the internal sources. According to step 4 of the algorithm, flow from S2 is neglected. The algorithm terminates as both the internal sources gets exhausted, and the pseudo-source is eliminated entirely. The minimum overall cost obtained is 197.5 $/h, and the results are verified by using mathematical optimisation technique. The network showing the flow distribution is depicted in Fig. 5.

Fig. 5
figure 5

Network showing the distribution of flows from different sources to different demands in example 2

Full size image

Example 3: Integrated Iron and Steel Mill

This example illustrates the application of the proposed algorithm for minimising the cost of resources in integrated iron and steel mill. The sink and source data, given in Table 6, are adopted from Chew and Foo (2009). It consists of five different processes which are segregated as five different zones. Each zone contains some demand units and a certain number of dedicated sources which satisfy those demands. In the original problem described by Chew and Foo (2009), all the sources were dedicated to the zone in which they were present. However, the sources with high flowrates may lead to significant reduction in overall cost of the resources and, hence, S1 and S2 are considered as common internal sources in this problem. The objective is to minimise the total cost of the resource requirement. The data (shown in Table 6) for the quality and the cost of the resources are adopted from Chandrayan and Bandyopadhyay (2014).

Table 6 Flow and quality data for example 3
Full size table

Initially, all the zones are targeted individually without using the common internal sources. It is observed that DS1 serves as pinch source for zone A, DS2 serves as pinch source for zone B, DS3 serves as pinch source for zone C, DS5 serves as pinch source for zone D, and zone E does not have a pinch point. The overall resource required after the targeting is performed is 1086.07 m3/year (1.67 m3/year for zone A, 6.62 m3/year for zone B, 26.88 m3/year for zone C, 582.36 m3/year for zone D, and 468.55 m3/year for zone E), and the total cost of the resource requirement is 458.35 $/year.

A pseudo-source is introduced in zone E at 500 ppm with a flow of 12.35 m3/year to create a pinch point for zone E. The total resource requirement is reduced to 1073.71 m3/year (1.67 m3/year for zone A, 6.62 m3/year for zone B, 26.88 m3/year for zone C, 582.36 m3/year for zone D, and 456.19 m3/year for zone E), and the total cost is reduced to 454.27 $/year.

The cost-benefit number is calculated for all the internal sources for all the zones (Table 6). The highest cost-benefit number is 0.484 $/m3 (corresponds to S1 at zone D). The flow transferred from S1 to zone D is 459.18 m3/year (minimum of 459.18 m3/year, flow available in S1 and 606.52 m3/year, flow required for pinch jump). After this flow addition, S1 gets exhausted and the resource requirement gets reduced to 637.72 m3/year with a total cost of 231.92 $/year.

The next highest value of cost-benefit number is 0.483 $/m3 (Table 7), which corresponds to S2 at zone D. The flow transferred from S2 to zone D is 145.18 m3/year (minimum of 558.95 m3/year, flow available in the S2 and 145.18 m3/year, flow required for pinch jump). The pinch point of this zone jumps from DS5 to DS4 after adding the flow and the flow availability in S2 is reduced to 413.76 m3/year. The overall resource requirement is reduced to 499.98 m3/year, and the total cost is reduced to 161.67 $/year. Since the pinch point of zone D jumps after this flow addition, the values of cost-benefit number are calculated again using the updated pinch point (Table 7).

Table 7 Cost-benefit number ($/m3) for all the internal sources at all the zones for example 3
Full size table

The highest value of cost-benefit number (0.321 $/m3) corresponds to S1 at zone E. As S1 is already exhausted, the next highest value of cost-benefit number under consideration is 0.32 $/m3 (corresponds to S2 at zone E). The flow transferred from S2 to zone E is 413.76 m3/year (minimum of 413.76 m3/year, flow available in S2 and 457.2 m3/year, flow required for pinch jump). After this flow is added to zone E, internal source S2 gets exhausted and the flow utilised from pseudo-source is reduced to 1.02 m3/year. The overall resource requirement is reduced to 97.54 m3/year, and the total cost is reduced to 28.86 $/year.

As all the internal sources get exhausted, the remaining pseudo-source (1.02 m3/year) utilised in zone E is eliminated using the resource of zone E. Due to this utilisation of the resource, the resource requirement of zone E gets slightly increased by 1.02 m3/year and the cost of this zone is increased by 0.34 $/year. The overall resource required is 98.57 m3/year (1.67 m3/year for zone A, 6.62 m3/year for zone B, 26.88 m3/year for zone C, 8.62 m3/year for zone D, and 54.78 m3/year for zone E), and the total cost of the resource is 29.2 $/year (0.7 $/year for zone A, 1.45 $/year for zone B, 4.57 $/year for zone C, 4.4 $/year for zone D, and 18.08 $/year for zone E). The algorithm terminates as all the internal sources get exhausted, and the pseudo-source is entirely eliminated.

The minimum cost obtained for the resource requirement in this problem is 29.2 $/year. The results obtained in this example, using the proposed algorithm, are verified by using the mathematical optimisation technique. It is to be noted that, if S1 is considered as the dedicated source for zone E and S2 is regarded as a dedicated source for zone D, then the total minimum cost obtained is 36.36 $/year. Therefore, it is concluded that there is reduction in the cost of 7.16 $/year (19.7% reduction) due to considering S1 and S2 as common internal sources. These results cannot be compared with the results obtained by Chew and Foo (2009) and Chandrayan and Bandyopadhyay (2014) as the problem presented here is not exactly same as presented in their works. The network showing the distribution of flows is depicted in Fig. 6.

Fig. 6
figure 6

Network showing the distribution of flows (million m3/year) from different sources to different demands in example 3

Full size image

Conclusions

In this paper, a pinch analysis-based methodology is developed for cost optimality of generalised segregated targeting problem with dedicated sources. Previous methodologies for resource optimization of segregated targeting problems with (Jain and Bandyopadhyay 2017) and without (Bandyopadhyay et al. 2010a) dedicated sources cannot directly be applied for cost optimality. Furthermore, the cost optimization methodology for segregated problems, proposed by Chandrayan and Bandyopadhyay (2014), also cannot be applied for problems with presence of dedicated sources. The mathematically rigorous methodology, proposed in this paper for cost optimality, identifies a quantity called cost-benefit number, which dictates the distribution of flow from different source to different zones. The concept of cost-benefit number is not just limited to segregated targeting problems with dedicated sources but can also be applied for the cost minimisation of many other resource allocation networks. The versatility and generic nature of the proposed algorithm is demonstrated through three different examples from diverse domains which includes carbon constrained energy sector planning, water allocation network and integrated iron and steel mill. The solutions obtained by applying the algorithm are verified by using mathematical optimisation techniques.