Introduction

There is a mounting interest in the use of eco-friendly fuels and raw materials to restrain emissions in energy and process industries. Due to higher costs of various green alternatives, a cost effective method is needed to integrate them with existing practices as well as to meet the environmental regulations. Process integration offers holistic system-oriented techniques that help in designing efficient systems and reduce environmental impact. Pinch analysis has evolved as a powerful algebraic tool for analysing and developing efficient processes through process integration.

Pinch technology was introduced in 1970s for maximising energy recovery in chemical processes and utility systems based on thermodynamic principles (Linnhoff et al. 1982; Smith 1995, 2005). In recent years, pinch analysis has been widely adopted for efficient resource allocation in areas such as water recovery (Hallale 2002; El-Halwagi et al. 2003; Manan et al. 2004; Prakash and Shenoy 2005; Foo et al. 2006; Bandyopadhyay et al. 2006; Shenoy and Bandyopadhyay 2007), hydrogen management (Alves and Towler 2002; Foo and Manan 2006; Bandyopadhyay 2006), energy sector planning (Tan and Foo 2007; Foo et al. 2008; Tan et al. 2009; Lee et al. 2009), etc. All these cases describe problems where resources such as energy, freshwater, hydrogen, etc. are targeted in a single source-sink allocation model. Sources are useful stream from processes that can be recycled/reused and sinks represent demands where source streams and resources are utilised. Figure 1 describes the schematic of a source-sink allocation model. Apart from minimum energy and resource targeting, pinch analysis has also been applied to achieve capital and operating cost targets in various cases such as heat exchanger networks (Ahmad and Linnhoff 1990; Ahmad 1985; Jegede and Polley 1992; Shenoy et al. 1998; Akbarnia et al. 2009), water system designs (Takama et al. 1980; Hallale and Fraser 1998; Alva-Argáez et al. 1998; Jödicke et al. 2001; Bagajewicz and Savelski 2001; Gunaratman et al. 2005; Alwi and Manan 2007), etc.

Fig. 1
figure 1

A schematic representation of the source-sink allocation model

Full size image

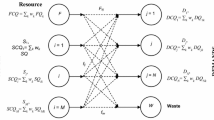
Lee et al. (2009) described a class of carbon-constrained energy planning problems, known as segregated targeting problems, where individual resource targets are needed for different demand sub-systems or zones. Figure 2 depicts the general structure of a segregated targeting problem. There is a common pool of sources that are shared across all the zones. Apart from that, each zone has a resource associated with it which can be integrated with the sources, to meet the demands of the respective zone. The objective is to minimise the total use of external resources. Bandyopadhyay et al. (2010) proved rigorously that the segregated targeting problem could be solved in a sequential manner if the goal is to minimise the total amount of external resources used. However, in practise capital and operating costs are of critical importance to maximise economic gains.

Fig. 2
figure 2

A schematic representation of the segregated targeting problem

Full size image

Cost targeting for resource allocation networks with multiple resources can be addressed by incorporating an index known as prioritised cost. The concept of prioritised cost was introduced by Shenoy and Bandyopadhyay (2007) to target multiple resources to minimise the operating cost of the overall process. Prioritised costs reflect the trade-off between cost of one resource and its potential to replace another costlier resource. Prioritised costs have been used in several pinch-based methodologies which address the problem of cost optimal design in multiple resource allocation problems. Deng and Feng (2011) have applied the concept of prioritised costs for conventional and property-based water networks with multiple water resources. Improved problem table algorithm along with the prioritised costs of fresh water sources are introduced to determine the minimum operating cost. It may be noted that the fresh water resources are utilised in increasing order of their prioritised costs (Deng and Feng 2011) as opposed to the original methodology proposed by Shenoy and Bandyopadhyay (2007). Shenoy and Shenoy (2012) have developed an algorithmic procedure for integrating sources to minimise operating cost in carbon-constrained energy planning problem with multiple carbon capture and storage (CCS) options. Prioritised costs of CCS options were used as a guide to reduce overall cost of the system. Furthermore, an MILP formulation has been proposed to optimise the total cost including the fixed cost and to study the effect of uncertainty associated with cost data. Krishnapriya and Bandyopadhyay (2012) have used the prioritised cost of power plants in Indian electricity sector to find cost optimal energy mix. The analysis considers minimisation of capital investment and annualised cost separately and shows that renewable energy sources are more favourable when the goal is to minimise annualised cost. Recently, Sahu et al. (2013) devised a methodology to minimise the operating cost of wastewater treatment network by introducing prioritised cost for treatment units. Applicability of the proposed algorithm is demonstrated to target multiple treatment units for minimising operating cost in water, hydrogen and material networks.

In this paper the concept of prioritised cost has been adopted to develop cost optimal targeting of resources for segregated problems. It may be noted that existing methodologies, summarised in the last paragraph, are not directly applicable to segregated targeting problems. External resources of the segregated targeting problem are assumed to have a cost attribute along with their quality. The objective of the problem is to minimise the cost of the external resources used while meeting constraints of demand and quality. Concepts of pinch analysis have been employed to explore the problem mathematically and to develop a decomposition algorithm by ranking resources based on their prioritised costs.

Problem statement and mathematical formulation

In this section, the general problem for cost optimal segregated targeting is stated. The problem structure can be divided into three major sets viz. set of the internal shared sources, the demand sets or zones, and set of resources associated with each zone.

  • A set of N s sources is given. Each source i (1, 2, … N s ) has a limited flow F si with a given quality index q si . It may be noted that quality index follows an inverse scale. A value of 0 indicates the highest possible quality while, larger numerical values indicate lower quality (Bandyopadhyay 2006).

  • Multiple demand sets, known as zones (N k in total), are also given. Each demand set of zone has N dk demands and each individual demand j (1, 2, … N djk ) in each zone k (1, 2, … N k ) accepts a flow F djk with a quality index limit q djk .

  • There is a set of N k external resources, each with a per unit cost of c i and quality index of q rk , and without flow limitation. Each external resource is available to only one associated zone, such that the kth external resource can only be supplied to the kth zone. It may be noted that the cardinality of the demand set and the cardinality of the external resources are identical and represented by N k .

  • Internal sources are shared by all the zones. Unused sources are discharged as waste.

The objective is to minimise the cost for external resources while integrating them with internal sources and demands. A schematic representation of the problem is shown in Fig. 2.

Let f ijk denotes the flow transferred from source i to demand j of zone k. Similarly, let f rjk and f iw represent the flow transferred from external resource r to demand j of zone k and flow transferred from source i to waste, respectively. The flow balance for every internal source and for every internal demand may be written as follows:

$$ \mathop \sum \limits_{jk = 1}^{{N_{{{\text{d}}k}} }} f_{ijk} + f_{{i{\text{w}}}} = F_{{{\text{s}}i}} \quad \forall i \in \left\{ {1, 2, \ldots N_{s} } \right\} \forall k \in \left\{ {1, 2, \ldots N_{k} } \right\} $$
(1)
$$ \mathop \sum \limits_{i = 1}^{{N_{s} }} f_{ijk} + f_{{{\text{r}}jk}} = F_{{{\text{d}}jk}} \quad \forall j \in \left\{ {1, 2, \ldots N_{{{\text{d}}k}} } \right\} \forall k \in \left\{ {1, 2, \ldots N_{k} } \right\} $$
(2)

Due to quality index constraints at every demand, the quality requirement for any internal demand may be mathematically expressed as follows:

$$ \mathop \sum \limits_{i = 1}^{{N_{s} }} f_{ijk} q_{{{\text{s}}i}} + f_{{{\text{r}}jk}} q_{{{\text{r}}k}} \le F_{{{\text{d}}jk}} q_{{{\text{d}}jk}} \quad \forall j \in \left\{ {1, 2, \ldots N_{{{\text{d}}k}} } \right\} \forall k \in \left\{ {1, 2, \ldots N_{k} } \right\} $$
(3)

The total cost of all resources used is:

$$ C = \mathop \sum \limits_{k = 1}^{{N_{k} }} \mathop \sum \limits_{jk = 1}^{{N_{{{\text{d}}k}} }} f_{{{\text{r}}jk}} c_{{{\text{r}}k}} $$
(4)

The objective is to minimise C subject to the constraints given by Eqs. 1–3. As all the constraints and the objective function are linear, this is a linear programing problem. In the next section, the segregated targeting problem is explored and analysed mathematically using techniques of pinch analysis.

Mathematical analysis and targeting algorithm

In this section it is rigorously proved that the optimisation problem, defined in the previous section, can be segregated and solved in a sequential manner. The problem is segregated based on the demand zones. After satisfying the demands of one zone, the remaining internal sources can be transferred to the next zone. Therefore, each zone now forms a different sub-problem which can be solved using any established pinch-based targeting technique.

To prove the results, two zones are analysed first. Without loss of generality, quality indices of external resources are assumed to be q r1 and q r2 with costs as c r1 and c r2, respectively. After satisfying the demands of first zone, the remaining surplus sources can be passed to the second zone. For each zone, a source with lowest quality index that is not utilised in the zone defines the pinch quality index for that zone (Pillai and Bandyopadhyay 2007). It is possible to perturb the current solution by an incremental flow of magnitude δ that may be transferred from sources from different quality regions of the first zone:

Case (1)::

δ is transferred from a source at the pinch or the higher quality region of the first zone, and

Case (2)::

δ is transferred from a source at the lower quality region

Case (1): Let δ amount of flow is transferred from source with quality index q si1 to the second zone. To meet this requirement in zone 1, two sources, one with higher quality index and other with lower quality index than q si1 are needed. Let δ 1 of flow be from a source i 2, (q si2 > q si1). Since δ is transferred from a higher quality region, no other source in this region can be used because sources in higher quality region are already used. Therefore δ 2 of the flow has to come from external resource with quality index q r1. We can thus write the following flow and mass conservation equations:

$$ \delta_{1} + \delta_{2} = \delta $$
(5)
$$ \delta_{1} q_{{{\text{s}}i2}} + \delta_{2} q_{{{\text{r}}1}} = \delta q_{{{\text{s}}i1}} $$
(6)

Solving Eqs. 6 and 7, change in flow of resource 1 can be obtained as:

$$ \delta_{{{\text{r}}1}} = \delta_{2} = \delta \frac{{q_{{{\text{s}}i2}} - q_{{{\text{s}}i1}} }}{{q_{{{\text{s}}i2}} - q_{{{\text{r}}1}} }} $$
(7)

Due to the perturbation, the following flows change in zone 2: (i) δ 1 of flow is decreased at source quality index q si2 and (ii) δ flow is increased at source quality index q si1. This changes the requirement of the external resource in zone 2 which is at quality index q r2. It should be noted that in any zone, flow changes only at the higher quality than the pinch quality of the zone affect the resource requirement. Therefore, change in external resource also depends on the relative position of q si2 and q p2. To calculate the change of resource requirement in zone 2, equation, derived by Pillai and Bandyopadhyay (2007), is used in this paper.

$$ \delta_{{{\text{r}}2}} = \left\{ {\begin{array}{*{20}c} { - \delta \frac{{q_{{{\text{p}}2}} - q_{{{\text{s}}i1}} }}{{q_{{{\text{p}}2}} - q_{{{\text{r}}2}} }} + \delta \frac{{q_{{{\text{s}}i1}} - q_{{{\text{r}}1}} }}{{q_{{{\text{s}}i2}} - q_{{{\text{r}}1}} }} \cdot \frac{{q_{{{\text{p}}2}} - q_{{{\text{s}}i2}} }}{{q_{{{\text{p}}2}} - q_{{{\text{r}}2}} }}\quad {\text{if}}\; q_{{{\text{s}}i2}} \le q_{{{\text{p}}2}} } \\ { - \delta \frac{{q_{{{\text{p}}2}} - q_{{{\text{s}}i1}} }}{{q_{{{\text{p}}2}} - q_{{{\text{r}}2}} }}\quad \quad \quad \quad \quad \quad \quad \quad \; \; {\text{otherwise}}} \\ \end{array} } \right. $$
(8)

Change in overall cost, can be determined as:

$$ \Updelta C = c_{{{\text{r}}1}} \delta_{{{\text{r}}1}} + c_{{{\text{r}}2}} \delta_{{{\text{r}}2}} $$
(9)
$$ \Updelta C = \left\{ {\begin{array}{*{20}c} {\delta \left\{ {\frac{{c_{{{\text{r}}1}} \left( {q_{{{\text{s}}i2}} - q_{{{\text{s}}i1}} } \right)}}{{\left( {q_{{{\text{s}}j}} - q_{{{\text{r}}1}} } \right)}} + \frac{{c_{{{\text{r}}2}} \left( {\left( {q_{{{\text{s}}i1}} - q_{{{\text{r}}1}} } \right) \left( {q_{{{\text{p}}2}} - q_{{{\text{s}}i2}} } \right) - \left( {q_{{{\text{p}}2}} - q_{{{\text{s}}i1}} } \right)\left( {q_{{{\text{s}}i2}} - q_{{{\text{r}}1}} } \right)} \right)}}{{\left( {q_{{{\text{s}}i2}} - q_{{{\text{r}}1}} } \right)\left( {q_{{{\text{p}}2}} - q_{{{\text{r}}2}} } \right)}}} \right\}\quad {\text{if}} \; q_{{{\text{s}}i2}} \le q_{{{\text{p}}2}} } \\ {\delta \left( {c_{{{\text{r}}1}} \frac{{q_{{{\text{s}}i2}} - q_{{{\text{s}}i1}} }}{{q_{{{\text{s}}i2}} - q_{{{\text{r}}1}} }} - c_{{{\text{r}}2}} \frac{{q_{{{\text{p}}2}} - q_{{{\text{s}}i1}} }}{{q_{{{\text{p}}2}} - q_{{{\text{r}}2}} }}} \right)\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad {\text{otherwise}}} \\ \end{array} } \right. $$
(10)

The resource allocation solution is optimum, only if the change in overall cost (ΔC) is non-negative. It can be easily proved that (not shown for brevity), \( \Updelta C \ge 0 \) implies the following relation:

$$ \frac{{c_{{{\text{r}}1}} }}{{\left( {q_{{{\text{p}}2}} - q_{{{\text{r}}1}} } \right)}} > \frac{{c_{{{\text{r}}2}} }}{{\left( {q_{{{\text{p}}2}} - q_{{{\text{r}}2}} } \right)}} $$
(11)

The quantities \( \frac{{c_{{{\text{r}}1}} }}{{\left( {q_{{{\text{p}}2}} - q_{{{\text{r}}1}} } \right)}} \) and \( \frac{{c_{{{\text{r}}2}} }}{{\left( {q_{{{\text{p}}2}} - q_{{{\text{r}}2}} } \right)}} \) may be denoted as pcr1 and pcr2, respectively and are called prioritised cost for respective resources (Shenoy and Bandyopadhyay 2007).

Case (2): Let δ be the incremental flow from source i 1 with quality index q si1 (q si1  > q p1). Now, to meet this demand, external resource r1 is not needed as resources with quality greater than pinch quality can be used. By our assumptions we know that \( q_{si2} > q_{si1} > q_{si3} \). Change in resources 2 depends on the relative position of q p2. All the changes in sources with quality index greater than pinch quality index of zone 2 do not affect the change in external resource 2 and hence are eliminated. In all other cases δ r2 > 0 and hence ΔC > 0. Similar to case 1, following expression can be derived using simple algebraic manipulations.

$$ \delta_{{{\text{r}}2}} = \left\{ {\begin{array}{*{20}c} {0 \quad \quad \quad \quad \quad \quad \; \left( {q_{{{\text{p}}2}} \ge q_{{{\text{s}}i2}} > q_{{{\text{s}}i1}} > q_{{{\text{s}}i3}} } \right)} \\ {\delta \frac{{q_{{{\text{s}}i2}} - q_{{{\text{p}}2}} }}{{q_{{{\text{s}}i3}} - q_{{{\text{s}}i2}} }} \cdot \frac{{q_{{{\text{s}}i3}} - q_{{{\text{s}}i1}} }}{{q_{{{\text{p}}2}} - q_{{{\text{r}}2}} }}\quad \left( {q_{{{\text{s}}i2}} > q_{{{\text{p}}2}} \ge q_{{{\text{s}}i1}} > q_{{{\text{s}}i3}} } \right)} \\ {\delta \frac{{q_{{{\text{s}}i1}} - q_{{{\text{s}}i2}} }}{{q_{{{\text{s}}i3}} - q_{{{\text{s}}i2}} }} \cdot \frac{{q_{{{\text{p}}2}} - q_{{{\text{s}}i3}} }}{{q_{{{\text{p}}2}} - q_{{{\text{r}}2}} }}\quad \left( {q_{{{\text{s}}i2}} > q_{{{\text{s}}i1}} > q_{{{\text{p}}2}} \ge q_{{{\text{s}}i3}} } \right)} \\ {0\quad \quad \quad \quad \quad \quad \; \left( {q_{{{\text{s}}i2}} > q_{{{\text{s}}i1}} > q_{{{\text{s}}i3}} > q_{{{\text{p}}2}} } \right)} \\ \end{array} } \right. $$
(12)

From the results of the two cases it is rigorously proved that for cost optimal allocation of resources, the zones must be targeted in definite sequence. This sequence is determined by ranking the resources using the concept of prioritised cost. Following Eq. (11), prioritised costs are defined as follows:

$$ {\text{Prioritised Cost}} \left( {{\text{r}}k} \right) = {\text{pc}}({\text{r}}k) = \frac{{c_{{{\text{r}}k}} }}{{\left( {q_{\text{p,last}} - q_{{{\text{r}}k}} } \right)}} $$
(13)

In Eq. (13), c rk is the cost of the resource and q rk is the quality index of the resource for zone k. The quality index q p,last denotes pinch quality of the last sub-problem. If there are N k zones, q p,last may be denoted by \( q_{{{\text{p}}N_{k} }} \). For resource allocation to be optimal, zones must be targeted in decreasing order of prioritised cost. From Eq. (13), it is evident that prioritised costs represent a trade-off between cost and quality of resource. Zones with resources having higher per unit cost and lower quality are targeted first. This ensures cost optimal use of internal sources. It should also be noted that the prioritised cost of resources depends on the state of the system (q p,last). These results rigorously prove the following lemma.

Lemma 1

If two independent zones are targeted in decreasing order of prioritised cost based on the pinch point of second sub-problem, the resource allocation is cost optimal.

Based on Lemma 1, the optimality condition for N k zones is generalised as follows.

Theorem 1

The minimum cost of resource requirement ( C) subject to constraints of Eqs. 1–3 is identical to the one produced by targeting the zones in decreasing order of prioritised costs, calculated based on the pinch quality index of last sub-problem.

Proof

This can be proved using the principles of mathematical induction. Theorem is trivially true for a single-zone problem (\( N_{k} = 1 \)). Lemma 1 proves that the theorem is true for two zones (\( N_{k} = 2 \)). Let us assume that the theorem is true for \( N_{k} - 1 \) zones. We can now use the principles of mathematical induction to prove that this assumption implies that the theorem is true for N k zones.

Consider the last two zones (\( N_{k} - 1{\text{th}} \) and N k th) of the N k -zone problem. By perturbing the source flows between these two zones, it can be observed that resource allocations of sub-problems 1 to \( N_{k} - 2 \) remain undisturbed. Therefore, these two zones can be considered independent and using Lemma 1, following inequality can be proved, where \( q_{{{\text{p}}N_{k} }} \) is the pinch quality index of the last sub-problem.

$$ \frac{{c_{{{\text{r}}N_{k} - 1}} }}{{q_{{{\text{p}}N_{k} }} - q_{{{\text{r}}N_{k} - 1}} }} > \frac{{c_{{{\text{r}}N_{k} }} }}{{q_{{{\text{p}}N_{k} }} - q_{{{\text{r}}N_{k} }} }} $$
(14)

Now, we eliminate the zone of \( N_{k} {\text{th}} \) sub-problem by removing the zone’s demands and the flow quantities from the respective shared sources which meet the zone’s demands. After this operation, the system contains \( N_{k} - 1 \) zones and the new pinch point of zone \( N_{k} - 1 \) will shift to the pinch quality index of zone N k i.e., \( q_{{{\text{p}}N_{k} }} \). By assumption, the theorem is true for this problem with \( N_{k} - 1 \) zones. This proves the theorem.

Based on Theorem 1 following corollary can be proved easily.□

Corollary 1

The minimum resource requirement ( R) subject to constraints of Eqs. 1–3 is identical to the one produced by targeting the zones in decreasing order of quality of their resources.

Proof

If the objective of the problem is to minimise the total resource requirement (R), it can be assumed that each of the resource has the same cost per unit. This leads to the following system of inequalities:

$$ \frac{1}{{q_{{{\text{p}}N_{k} }} - q_{{{\text{r}}1}} }} > \frac{1}{{q_{{{\text{p}}N_{k} }} - q_{{{\text{r}}2}} }} > \cdots > \frac{1}{{q_{{{\text{p}}N_{k} }} - q_{{{\text{r}}N_{k} - 1}} }} > \frac{1}{{q_{{{\text{p}}N_{k} }} - q_{{{\text{r}}N_{k} }} }} $$
(15)

Therefore, \( q_{{{\text{r}}1}} > q_{{{\text{r}}2}} > \cdots > q_{{{\text{r}}N_{k} - 1}} > q_{{{\text{r}}N_{k} }} \).

This shows that to minimise the resource requirement, zones must be targeted in decreasing order of quality. Therefore, the theorem for minimum resource segregated targeted problem, as proved by Bandyopadhyay et al. (2010), is a special case of Theorem 1.

If the prioritised cost of each zone, pc(rk), is plotted against the pinch quality index of the last sub-problem, q p,last, the hyperbolic curves of pc(rk) shall intersect to form sequence regions as shown in Fig. 3. A sequence region is defined as the range of values for q p,last for which the zones follow the same order of prioritised costs. It should also be noted that pinch point exists only at the source quality index (Pillai and Bandyopadhyay 2007). Hence, q p,last can take values only from the finite set of the quality indices of the sources. These possible pinch points are marked on the x-axis of the Fig. 3. The sequence regions (e.g. sequence region 2 in Fig. 3) which do not correspond to any feasible pinch points are therefore not optimal. This proves the following Theorem about the optimal targeting sequence.□

Fig. 3
figure 3

Formation of sequence regions due to the intersection of prioritised cost curves

Full size image

Theorem 2

The optimal targeting sequence must lie in one of the sequence regions that have at least one quality index from the shared sources.

Targeting algorithm

Based on above mathematical results, following targeting algorithm is proposed. A flowchart, depicting the proposed targeting algorithm is shown in Fig. 4.

Fig. 4
figure 4

Decomposition algorithm for the cost optimal segregated targeting problem

Full size image

  • Step 1: Arrange the zones in descending order based only on the quality index of the resources, q rk . Denote the sequence of zones obtained as S x . The sequence S x determines the order in which the zones are to be targeted.

  • Step 2: Choose the untargeted highest rank zone from S x .

  • Step 3: Determine the minimum resource requirement for this zone using any pinch-based targeting method.

  • Step 4: Determine the surplus of internal sources (shared) available for use by the remaining zones. This surplus will be used to target the remaining zones.

  • Step 5: Repeat Steps 2–4 until all the zones are targeted.

  • Step 6: Determine the pinch quality index of last sub-problem (q p,last ) and calculate prioritised cost of all the resources based on this pinch quality index.

  • Step 7: Rank the zones in decreasing order of prioritised cost (pcrk ) of their respective resources. Let this sequence of zones be S x+1.

  • Step 8: If the sequence S x is identical to sequence S x+1, the allocation of resources is cost optimal and the algorithm ends. Otherwise, update S x with sequence S x+1 and go to Step 2.

The prioritised costs of zones cannot be determined by a priori because value of q p,last is not known. Therefore the algorithm starts by generating the sequence S x , which is in decreasing order of quality index of resource. After targeting the zones by ranking, q p,last will either lead to the same sequence S x or jump to a different sequence zone, say of S x+1. If q p,last generates the same sequence S x , the solution found is optimal (Theorem 2). If q p,last generates a different sequence, algorithm targets the zones according to the new sequence (by updating S x with S x+1). The algorithm continues until q p,last converges to its own sequence region. In case there does not exist a targeting sequence which satisfies the theorem, pinch quality of the last sub-problem, q p,last will cycle between pinch points from different sequence zones. This denotes a special case where the optimum solution is obtained by perturbing the resource allocation as illustrated in example 3. Applicability of the proposed algorithm is demonstrated in the next section using different illustrative case studies.

Illustrative examples

Example 1: carbon constrained energy sector planning

Diesel, fuel oil and natural gas are common fuels for both Indian transportation and industrial sectors. In this problem, two types of demand zones viz. transportation and industrial sectors are considered. Energy from diesel and fuel oil (500,000 TJ) serves as the first internal source with a carbon emission (quality) of 72 t/TJ. Energy from natural gas (393,000 TJ) is the second internal source with a quality of 56 t/TJ. Data, for this problem, are compiled based on the IEA statistics (2009) for India and are given in Table 1.

Table 1 Diesel, fuel oil and natural gas usage in transportation and industrial sectors of India (2009)
Full size table

Energy demand for each sector can be satisfied by either of the internal sources and a low carbon external resource that is specific to that particular sector. Low carbon fuels such as biodiesel in transportation sector, while hydropower in industrial sector are assumed to be used for emissions abatement. Biodiesel is the external resource for transportation sector while hydropower is the external resource for the industrial sector. Since cost of biodiesel has high sensitivity to feedstock, process, land type and crop yield an indicative number, 0.031 $/MJ is used for its cost. Hydropower is available at 0.028 $/MJ. It has been assumed that there is no limit associated with the energy available from these low emission resources. Further it is required to reduce the emissions from each sector by a certain factor. To illustrate the methodology, a 8 % reduction of CO2 emissions in transportation sector and a 12 % reduction in industrial sector are assumed. This requires an average quality constraint of 62.76 and 54.91 t/TJ on transportation and industrial sectors, respectively (Table 2). The objective of the problem is to minimise the total cost of low carbon resources for the two sectors while satisfying the emission constraints. Unused energy is the waste for this example. Table 3 shows the internal sources, resources and demands for this example.

Table 2 Emission reduction in transportation and industrial sectors
Full size table
Table 3 Data for carbon constrained energy sector planning
Full size table

Since quality index of biodiesel (16.5 t/TJ) is higher than that of hydropower (0 t/TJ), the transportation sector is targeted before the industrial sector according to Steps 1–5 of the algorithm (S 1: zone 1 → zone 2). Calculations of the minimum biodiesel and hydropower requirements for the transportation and industrial sectors are shown in Tables 4 and 5. The methodology of source composite curve (Bandyopadhyay 2006) is used for these calculations. It may be noted that any other algebraic techniques of pinch analysis can also be used for these calculations. The minimum biodiesel and hydropower requirements for the transportation and industrial sectors are calculated to be 0 and 81,782.2 TJ, respectively. The pinch quality index of the second sub-problem is 72t/TJ. Prioritised cost, calculated based on the pinch quality index of the last sub-problem, are 0.56 $/t (transportation sector) and 0.39 $/t (industrial sector), respectively. The zones are then arranged based on Step 7 of the algorithm to give sequence S 2: zone 1 → zone 2. Since both these sequences are identical S 1  = S 2, the allocation of resources to the respective zones is cost optimal.

Table 4 Sub-problem 1: minimum biodiesel requirement for the transportation sector
Full size table
Table 5 Sub-problem 2: minimum hydropower requirement for the industrial sector
Full size table

Example 2: integrated iron and steel mill

This example illustrates the application of algorithm for targeting water resources in an integrated iron and steel plant. Sink and source data in Tables 6 and 7 are adapted from Chew and Foo (2009). The demands are process wise segregated in 5 zones; internal sources are assumed to be shared among all the zones. Table 8 lists the fresh water sources that can be used as external resources in the respective demand zones. The objective of the problem is to find the cost optimal allocation of external resources.

Table 6 Sink data for example 2
Full size table
Table 7 Internal source data for example 2
Full size table
Table 8 External freshwater (resource) data for example 2
Full size table

Iterations of the decomposition algorithm are illustrated in Table 9. In the first iteration, zones are targeted in decreasing order of concentration of their respective freshwater source (sequence S 1: CBEAD). The minimum fresh water requirement is found out to be 71.24 million m3/y with a cost of 34.436 million $/year. The pinch quality of the last sub-problem is 400 mg/L. Prioritised cost of each freshwater source is computed to be: 0.00106, 0.00056, 0.00044, 0.00128, and 0.00084. Based on the prioritised costs, a new targeting sequence is determined (sequence S 2: DAEBC). Since the sequence found by prioritised costs is not the same as sequence S 1 the solution found is sub-optimal.

Table 9 Iterations of the decomposition algorithm for example 2
Full size table

In the second iteration, zones are targeted according to the new sequence which leads to pinch point of 400 mg/L for zone A (last sub-problem). The target is optimal with the minimum cost of external resource as 18.974 million $/y. It may be noted that though the operating cost is reduced significantly, but the total fresh water requirement is increased marginally to 72.98 million m3/.

Example 3: water allocation network

In this example, solution procedure for a special case is illustrated when the zones cannot be arranged in decreasing order of prioritised cost. The situation arises when there are two pinch points around the optimum solution in the last sub-problem. However, the problem can be solved using the perturbation method which was used as a technique of proof for Lemma 1. The data for this problem are given in Tables 10,11 and 12.

Table 10 Source data for example problem 3
Full size table
Table 11 Demand data for example problem 3
Full size table
Table 12 External resource data for example problem 3
Full size table

From Table 13, it can be seen that sequence 1 leads to q p,last = 200 ppm, whereas sequence 2 leads to q p,last = 100 ppm. However, both the values of q p,last lie outside their respective sequence regions. This implies that the resource allocation is sub-optimal as the zones are not targeted in decreasing order of prioritised cost (Theorem 1) and the algorithm does not converge. It can be further observed that the overall cost of resources decreases if the allocation is perturbed by transferring flow from below pinch region of one zone to another zone in a given sequence. The overall cost will decrease until an optimum is reached and the zones are targeted in decreasing order of prioritised costs. In this example, for sequence 1 to be optimal, q p,last must jump to 100 ppm and similarly for sequence 2 to be optimal, q p,last must jump to 200 ppm. Since at the optimum, q p,last jumps to the new pinch point in respective sequences, both these pinch points must exist simultaneously. This gives us the following condition to find the perturbation flow δ:

Table 13 Iterations of the decomposition algorithm for example problem 3
Full size table
$$ \frac{{\Updelta Q_{T} - \mathop \sum \nolimits_{l = 1}^{{{\text{s}}1}} Q_{l} }}{{q_{{{\text{s}}1}} - q_{{{\text{s}}1}} }} = \frac{{\Updelta Q_{T} - \mathop \sum \nolimits_{l = 1}^{{{\text{s}}2}} Q_{l} }}{{q_{{{\text{s}}2}} - q_{{{\text{s}}2}} }} $$
(16)

where q s1 is the quality index of old pinch point and q s2 is the quality index of new pinch point.

$$ \sum\limits_{l = 1}^{k} {Q_{l} } = \sum\limits_{l = 1}^{k - 1} {F_{l} (q_{l} - q_{k} )} $$
(17)
$$ \Updelta Q_{T} = \sum\limits_{l = 1}^{n - 1} {F_{l} \left( {q_{l} - q_{k} } \right)} $$
(18)

Simplifying the above equations leads to the following condition for simultaneous existence of two pinch points:

$$ \sum\limits_{{l = {\text{s}}1}}^{{{\text{s}}2 - 1}} {F_{l} } = \sum\limits_{l = 1}^{n - 1} {F_{l} } \frac{{(q_{l} - q_{{{\text{r}}1}} )}}{{(q_{{{\text{s}}1}} - q_{{{\text{r}}1}} )}} - \sum\limits_{l = 1}^{n - 1} {F_{l} } \frac{{(q_{l} - q_{{{\text{r}}1}} )}}{{(q_{{{\text{s}}2}} - q_{{{\text{r}}1}} )}} $$
(19)

For sequence 1 in the given example, q s1 = 200 ppm and q s2 = 100 ppm. Since δ amount of flow is transferred from source at 45 ppm in zone 1 to zone 2, the flow quantity F l will change at qualities 45 ppm and 100 ppm (pinch point of zone 1).

$$ F_{{45\;{\text{ppm}}}} = 0 + \delta $$
(20)
$$ F_{{100\;{\text{ppm}}}} = 63.5 - \delta \frac{{\left( {q_{{{\text{s}}i}} - q_{{{\text{r}}1}} } \right)}}{{\left( {q_{\text{p,zone1}} - q_{{{\text{r}}1}} } \right)}} $$
(21)

where q si is the quality index at which δ is transferred (i.e. 45 ppm for this example). Substituting the given values in Eq. 21 gives δ = 5.41 t/h to achieve the optimal allocation. Similar perturbation can be performed for sequence 2, leading to the same resource allocation as shown in Table 14.

Table 14 Optimal resource allocation by perturbation method for example 3
Full size table

Conclusion

Optimal resource allocation is the key objective in many practical scenarios across a variety of industries. Resource allocation networks of linear programing nature can be solved using mathematical optimisation techniques available in various software packages. However, insight-based methodologies have been developed for few specific type of resource allocation problems. Segregated targeting is a special type of network flow optimisation problem where each demand zone has a separate external resource. In this work, cost optimal segregated targeting of resource allocation network is explored by pinch analysis. A decomposition algorithm is developed to target the zones by ranking the resources using prioritised cost. The algorithm developed is general in nature and can be used with any pinch-based optimisation technique. Concepts of pinch and linear programing have been adopted to rigorously prove the optimality theorem. The methodology is illustrated by quantitative studies in three different scenarios from carbon constrained energy planning and water allocation networks. Extension of the methodology to a special case of two pinch points is also demonstrated through example and solved using the perturbation technique.