Complement of the generalized total graph of commutative rings

Abstract

Let R be a commutative ring with identity, Z(R) its set of zero-divisors, and H a nonempty proper multiplicative prime subset of R. The generalized total graph of R is the simple undirected graph $GT_{H}(R)$ with the vertex set R and two distinct vertices x and y are adjacent if and only if $x + y \in H.$ In this paper, we investigate several graph theoretical properties of the complement $\overline{GT_{H}(R)}.$ In particular, we obtain a characterization for $\overline{GT_{P}(R)}$ to be claw-free or unicyclic or pancyclic. Also, we obtain the clique number and chromatic number of $\overline{GT_P(R)}$ and discuss the perfect, planar and outer planarity nature for $\overline{GT_{P}(R)}.$ Further, we discuss various domination parameters for $\overline{GT_{P}(R)}$ where P is a prime ideal of R.

1 Introduction

Throughout this paper R denotes a commutative ring with identity, Z(R) its set of all zero-divisors, $Z^*(R)=Z(R){\setminus }\{0\}$ and U(R) its units. Anderson and Livingston [5] introduced the zero-divisor graph of R,  denoted by $\Gamma (R),$ as the undirected simple graph with vertex set $Z^*(R)$ and two distinct vertices $x,y\in Z^*(R)$ are adjacent if and only if $xy=0.$ Subsequently, Anderson and Badawi [4] introduced the concept of total graph of commutative rings. The total graph$T_{\Gamma }(R)$ of R is the undirected graph with vertex set R and for distinct elements $x,y\in R$ are adjacent if and only if $x + y \in Z(R).$ Tamizh Chelvam and Asir [7, 15,16,17,18] have extensively studied about total graphs of commutative rings.

Recently, Anderson and Badawi [4] introduced the concept of generalized total graph of commutative rings. A nonempty proper subset H of R to be a multiplicative prime subset of R if the following two conditions hold: (1) $ab \in H$ for every $a \in H$ and $b \in R$; (2) if $ab \in H$ for $a, b \in R$, then either $a \in H$ or $b \in H$. For example, H is a multiplicative prime subset of R if H is a prime ideal of R or H is a union of prime ideals of R or $H = Z(R),$ or $H = R{\setminus } U(R).$ For a multiplicative prime subset H of R,  the generalized total graph$GT_{H}(R)$ of R is the simple undirected graph with vertex set R and two distinct vertices x and y are adjacent if and only if $x + y \in H.$ The unit graphG(R) of R is the simple undirected graph with vertex set R in which two distinct vertices x and y are adjacent if and only if $x + y\in U(R).$ Tamizh Chelvam and Balamurugan [19] studied some graph theoretical properties of the generalized total graph of finite fields and its complement.

Let $G = (V,E)$ be a graph with vertex set V and edge set E. The complement $\overline{G}$ of the graph G is the simple graph with vertex set V(G) and two distinct vertices x and y are adjacent in $\overline{G}$ if and only if they are not adjacent in G. We say that G is connected if there is a path between any two distinct vertices of G. For a vertex $v\in V(G)$, deg(v) is the degree of v. For any graph G,  $\delta (G)$ and $\Delta (G)$ denote the minimum and maximum degrees of vertices in G respectively. $K_n$ denotes the complete graph of order n and $K_{m,n}$ denotes the complete bipartite graph. For basic definitions in graph theory, we refer the reader to [10] and for the terms regarding algebra one can refer [13]. Note that if R is finite, then $\overline{GT_{Z(R)} (R)}$ is the unit graph [14].

Throughout this paper, we assume that P is a prime ideal of R with $|P|=\lambda$ and $|R/P|=\mu .$ In this paper, we study about the complement $\overline{GT_P(R)}$ of the generalized total graph $GT_P(R).$ In Sect. 2, we study the graph theoretical properties namely girth, clique number, chromatic number and Eulerian of $\overline{GT_P(R)}$. In Sect. 3, we obtain a characterization for $\overline{GT_P(R)}$ to be claw-free or unicylic or pancyclic or planar or outerplanar. In Sect. 4, we study about various domination parameters of $\overline{GT_P(R)}$ and further obtain domatic number of $\overline{GT_P(R)}.$

2 Graph theoretical properties of $\overline{GT_P(R)}$

In this section, we discuss about some graph theoretical properties of $\overline{GT_{P}(R)}.$ More specifically, we discuss about girth and Eulerian of $\overline{GT_{P}(R)}.$ Also, we obtain the independence number, clique number and chromatic number of $\overline{GT_P(R)}.$ Let us start with some basic properties of $\overline{GT_P(R)}.$

For a prime ideal P of a commutative ring R which is not an integral domain with $|P|=\lambda$ and $|R/P|=\mu ,$ we have $|P|=|a_i+P| \ge 2$ for $a_i+P \in R/P$ for $1 \le i \le \mu .$ Since R contains identity 1,  we denote $1+1$ by 2. First we recall the following structure theorem for $GT_P(R{\setminus } P).$

Theorem 1

[4, Theorem 2.2] LetPbe a prime ideal of a commutative ringR, and let$|P| = \lambda$and$|R/P| = \mu$.

• (i) If$2 \in P$, then$GT_P(R{\setminus } P)$is the union of$\mu - 1$ disjoint $K _{\lambda }$’s;

• (ii) If$2 \notin P,$then$GT_P(R{\setminus } P)$is the union of$\frac{\mu - 1}{2}$disjoint$K_{\lambda ,\lambda }$’s.

Assume that R is finite and $2 \in P.$ Since |R| is finite, $R\cong R_1 \times \cdots \times R_q$ where each $R_i$ is a local ring. Note that $P=P_1 \times \cdots \times P_q$ where $P_i \subseteq R_i$ for $1 \le i \le q.$ Since P is a prime ideal in $R,~P_i=Z(R_i)$ for exactly one $i,~1 \le i \le q$ and $P_j=R_j$ for $1 \le j \ne i \le q.$ Since $2 \in P \subseteq Z(R),~2 \in P_i \subseteq Z(R_i)$ for some $i,~1 \le i \le q.$ By [14, Corollary 2.3] $|R_i|=2^{\alpha _i}$ where $\alpha _i$ is a positive integer. This implies that $\mu$ is even. Hence we get that $\mu$ is even if $2\in P$ and $\mu$ is odd if $2\notin P.$ Throughout this paper, we consider the following partition of R into distinct cosets $a_0+P,a_1+P,\ldots , a_{\mu -1}+P$ of P with $a_0\in P.$

• (i) If $2 \in P,$ then $R= P\cup (\bigcup \nolimits _{i=1}^{\mu -1}(a_i+P));$

• (ii) If $2 \notin P,$ then $R=P\cup \bigcup \nolimits _{i=1}^{\frac{\mu -1}{2}}(a_i+P) \bigcup \nolimits _{i=1}^{\frac{\mu -1}{2}}(-a_i+P).$

Now, using Theorem 1, we obtain the degrees of vertices in $\overline{GT_P(R)}.$

Lemma 1

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inR. Assume that$|P|=\lambda$and$|R/P|=\mu .$Then the following are true in$\overline{GT_P(R)}.$

• (i) If$2\in P,$then$deg(v) = (\mu -1)\lambda$    for every$v \in R;$

• (ii) If $2 \notin P,$ then $deg(v) = \left\{ \begin{array}{ll}(\mu -1)\lambda &\,\textit{for }\,\textit{v}\in P;\\ (\mu -1)\lambda -1 & \, \textit{for }\,\textit{v} \in R{\setminus } P. \end{array}\right.$

Now, we observe some of the immediate consequences of Lemma 1.

Lemma 2

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inR. Assume that$|P|=\lambda$and$|R/P|=\mu .$Then the following hold:

• (i) $\overline{GT_P(R)}$contains no isolated vertex;

• (ii) $\overline{GT_P(R)}$ contains no vertex of degree $|R|-1;$

• (iii) $\overline{GT_{P}(R)}$is complete$\mu$-partite if and only if$2 \in P;$

• (iv) $\overline{GT_{P}(R)}$is connected bi-regular if and only if  $2 \notin P.$Moreover, $\Delta (\overline{GT_{P}(R)})= \delta (\overline{GT_{P}(R)})+1;$

• (v) $\overline{GT_P(R)}$is connected.

The following Lemma follows from Theorem 1 and is useful throughout this paper.

Lemma 3

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inR. Assume that$|P|=\lambda$and$|R/P|=\mu .$Then the following are true in$\overline{GT_{P}(R)}.$

• (i) Let$2 \in P.$Two distinct verticesxandyare adjacent in$\overline{GT_{P}(R)}$if and only ifxandyare not in the same coset ofP; 

• (ii) Let $2 \notin P.$ Two distinct vertices x and y are adjacent in $\overline{GT_{P}(R)}$ if and only if $x\in a_i+P$ and $y\in R{\setminus } (-a_i+P)$ for some $i,0 \le i \le \frac{\mu -1}{2}.$

Now we obtain the girth of $\overline{GT_{P}(R)}.$

Lemma 4

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inR. Assume that$|P|=\lambda$and$|R/P|=\mu .$Then

$$\begin{aligned} gr(\overline{GT_{P}(R)})= \left\{ \begin{array}{ll} 4 &{} if \,2\in P\, and\, \mu =2;\\ 3 &{} if\,2\in P\, and\, \mu \ge 3;\\ 3 &{} if \,2\notin P. \end{array}\right. \end{aligned}$$

Proof

Assume that $2\in P.$ If $\mu = 2,$ then by Lemma 2(iii), $\overline{GT_{P}(R)}=K_{\frac{|R|}{2},\frac{|R|}{2}}$ and so $gr(\overline{GT_{P}(R)})=4.$

If $\mu \ge 3,$ then by Lemma 2(iii), $\overline{GT_{P}(R)}=K_{\underbrace{\lambda ,\lambda ,\ldots ,\lambda }_{\mu ~times}}.$ Since $\mu \ge 3,$ choose $x \in P,~ y \in a_1+P,~ z\in a_2+P$ and $S=\{x,y,z\}.$ Then the subgraph induced by S is $C_3$ in $\overline{GT_{P}(R)}$ and so $gr(\overline{GT_{P}(R)})=3.$

Assume that $2\notin P.$ Note that, for $1 \le i \le \frac{\mu -1}{2},$$|P|=|a_i+P| =|-a_i+P|\ge 2.$ Let $S=\{x,a,b\}$ where $x\in P$ and $a,b\in a_i+P$ for some i. Then the subgraph induced by S is $C_3$ in $\overline{GT_{P}(R)}$ and so $gr(\overline{GT_{P}(R)})=3.$

Note that, a clique in a graph G is a complete subgraph of G. The order of the largest clique in a graph G is its clique number, which is denoted by $\omega (G).$ Now, we obtain the clique number of $\overline{GT_{P}(R)}.$

Lemma 5

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inR. Assume that$|P|=\lambda$and$|R/P|=\mu .$Then

$$\begin{aligned} \omega (\overline{GT_{P}(R)})= \left\{ \begin{array}{ll} \mu &{} if\,2\in P;\\ \frac{(\mu -1)}{2}\lambda +1 &{} if\, 2\notin P. \end{array}\right. \end{aligned}$$

Proof

Suppose $2\in P.$ By Lemma 2(iii), $\overline{GT_{P}(R)}$ is complete $\mu$-partite. Consider the set $S=\{x_0,x_1,\ldots ,x_{\mu -1}\}$ where $x_0\in P$ and $x_i\in a_i+P,$ for $1\le i \le \mu -1.$ Clearly $<S>=K_\mu$ is a maximum clique in $\overline{GT_{P}(R)}$ and so $\omega (\overline{GT_{P}(R)})=\mu .$

If $2\notin P,$ then $R=P \cup (\bigcup \nolimits _{i=1}^{\frac{\mu -1}{2}}((a_i+P) \cup (-a_i+P))).$ Let $S=\{a_0\}\cup \bigcup \nolimits _{i=1}^{\frac{\mu -1}{2}} (a_i+P)$ where $a_0\in P.$ By Lemma 3(ii), $<S>$ induces a complete subgraph of order $\frac{(\mu -1)}{2}\lambda +1$ in $\overline{GT_{P}(R)}.$ Note that, any two elements in P are non-adjacent in $\overline{GT_{P}(R)}.$ Also, the elements of $a_i+P$ and $-a_i+P$ are not adjacent. Thus S is a maximum clique in $\overline{GT_{P}(R)}$ and so $\omega (\overline{GT_{P}(R)})=\frac{(\mu -1)}{2}\lambda +1.$

An assignment of colors to the vertices of a graph G so that adjacent vertices are assigned different colors is called a proper coloring of G. The smallest number of colors in any proper coloring of a graph G is called the chromatic number of G and is denoted by $\chi (G).$ A set of vertices in a graph G is an independent if no two vertices in the set are adjacent. In the following lemma, we obtain the chromatic number of $\overline{GT_{P}(R)}.$

Lemma 6

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inR. Assume that$|P|=\lambda$and$|R/P|=\mu .$Then

$$\begin{aligned} \chi (\overline{GT_{P}(R)})= \left\{ \begin{array}{ll} \mu &{} if\,2\in P;\\ \left(\frac{\mu -1}{2}\right)\lambda +1 &{} if\,2\notin P. \end{array}\right. \end{aligned}$$

Proof

If $2\in P,$ then by Lemma 2(iii), $\overline{GT_{P}(R)}$ is complete $\mu$-partite and so $\chi (\overline{GT_{P}(R)})=\mu .$

If $2\notin P,$ then $R = P\cup \bigcup \nolimits _{i=1}^{\frac{\mu -1}{2}}(a_i+P) \bigcup \nolimits _{i=1}^{\frac{\mu -1}{2}}(-a_i+P).$ Note that , for $1\le i\le \frac{\mu -1}{2},~$$<a_i+P>=<-a_i+P>=K_{\mu }$ in $\overline{GT_{P}(R)}.$ By Lemma 3(ii), the elements of $a_i+P$ and $-a_i+P$ are not adjacent in $\overline{GT_{P}(R)}.$ Hence one can use $\lambda$ colours to the elements of $a_i+P$ and $-a_i+P.$ Let $S=\bigcup \nolimits _{i=1}^{\frac{\mu -1}{2}} a_i+P$ and $T=\bigcup \nolimits _{i=1}^{\frac{\mu -1}{2}} (-a_i+P).$ Then $<S>= <T>=\bigcup \nolimits _{\frac{\mu -1}{2}}K_{\lambda }$ in $\overline{GT_{P}(R)}.$ Thus we require $\frac{(\mu -1)}{2}\lambda$ colours for the union $S \cup T.$ Note that $<P>$ is an independent set and each element of P is adjacent to every element of $S \cup T$ in $\overline{GT_{P}(R)}.$ Assign a different color to all the elements of P. This implies $\chi (\overline{GT_{P}(R)})= (\frac{\mu -1}{2})\lambda +1.$

Corollary 1

([10]) A nontrivial connected graphGis Eulerian if and only if every vertex ofGhas even degree.

Using Corollary 1, we state below a characterization for $\overline{GT_{P}(R)}$ to be Eulerian.

Lemma 7

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inR. Assume that$|P|=\lambda$and$|R/P|=\mu .$Then the following are true:

• (i) If$2 \in P,$then$\overline{GT_{P}(R)}$is Eulerian if and only if$\lambda$is even;

• (ii) If$2 \notin P,$then$\overline{GT_{P}(R)}$is not Eulerian.

Proof

Proof of (i) follows from Lemma 2(iii), Lemma 2(v) and Lemma 1(i).

Proof of (ii) follows from Lemma 2(iv).

The vertex independence number (or the independence number) $\beta (G)$ of a graph G is the maximum cardinality of an independent set of vertices in G. In the following lemma, we obtain the independence number of $\overline{GT_{P}(R)}.$

Lemma 8

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inR. Assume that$|P|=\lambda$and$|R/P|=\mu .$Then the independence number$\beta (\overline{GT_{P}(R)})= \lambda .$

Proof

Suppose $2\in P.$ Then by Lemma 2(iii), $\beta (\overline{GT_{P}(R)})=\lambda.$

Suppose $2\notin P.$ Then P is an independent set in $\overline{GT_{P}(R)}$ and $|P|=\lambda \ge 2.$ Assume that $S\subseteq V(\overline{GT_{P}(R)}) {\setminus } P$ is an independent subset.

Claim : $|S| \le 2.$

Suppose $|S| \ge 3.$ Let x, y and z be three distinct vertices in S such that $x \in a_i+P,$$y \in a_j+P$ and $z \in a_k+P$ for $1 \le i,j,k \le \mu -1.$

Assume that any two of i, j and k are equal. Without loss of generality, let us take $i=j.$ Then x, y are adjacent in $\overline{GT_{P}(R)}$ and so S is not an independent in $\overline{GT_{P}(R)}.$

Assume that i, j and k are all distinct. Suppose sum of at least any two of $a_i,a_j$ and $a_k$ is 0. Without loss of generality, let us assume that $a_i+a_j=0.$ Then z is adjacent with both x and y. Hence S is not an independent set in $\overline{GT_{P}(R)}.$

Suppose sum of any two of $a_i,a_j$ and $a_k$ is not equal to 0. Then $<S>$ contains a $K_3,$ a contradiction to S is an independent set in $\overline{GT_{P}(R)}.$ Hence $|S|\le 2.$ Since each element in P is adjacent to every element in $R {\setminus } P$ in $\overline{GT_{P}(R)},~P$ is a maximal independent set in $\overline{GT_{P}(R)}$ having order $\lambda \ge 2$ and so $\beta (\overline{GT_{P}(R)})= \lambda .$

The edge independence number$\beta _1(G)$ of a graph G is the maximum cardinality of an independent set of edges. In the following lemma, we obtain the edge independence number of $\overline{GT_{P}(R)}.$

Lemma 9

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inR. Assume that$|P|=\lambda$and$|R/P|=\mu .$Then the edge independence number

$$\begin{aligned} \beta _1(\overline{GT_{P}(R)})= \left\{ \begin{array}{ll} \frac{|R|}{2} &{} ~{if}\, 2\in P;\\ \left(\frac{\mu -1}{2}\right)\lambda +\frac{\left\lfloor \lambda \right\rfloor }{2} &{}~if\, 2\notin P. \end{array}\right. \end{aligned}$$

Proof

Case 1. If $2\in P,$ then $\mu$ is even. Consider the partition $R=\bigcup \nolimits _{i=0}^{\mu -1}(a_i+P)$ where $P=a_0+P.$ Let $S=\bigcup \nolimits _{i=0}^{\frac{\mu }{2}-1}(a_i+P)$ and $T=\bigcup \nolimits _{i=\frac{\mu }{2}}^{\mu -1}(a_i+P).$ Consider $E=\{\{x_jy_j\}:~x_j \in S\, \,and\, \,y_j \in T \}$ for $1 \le j \le \frac{|R|}{2}.$ Clearly E is a maximal edge independent set in $\overline{GT_{P}(R)}$ and hence $\beta _1(\overline{GT_{P}(R)})=\frac{|R|}{2}.$

Case 2. Assume that $2 \notin P.$ Let $S_i =(a_i+P) \cup (-a_{i+1}+P)$ for $i \in \{1,\ldots ,\frac{\mu -3}{2}\}$ and $S_{\frac{\mu -1}{2}}=P \cup (-a_1+P).$ Then $K_{\lambda ,\lambda }\subseteq <S_i>$ for each i in $\overline{GT_{P}(R)}$ and so $\beta _1(<S_i>)=\lambda .$ Since $<a_\frac{\mu -1}{2}+P>=K_{\lambda },$ we have $\beta _1(<a_\frac{\mu -1}{2}+P>)=\frac{\left\lfloor \lambda \right\rfloor }{2}.$ Thus we have $\beta _1(\overline{GT_{P}(R)})=(\frac{\mu -1}{2})\lambda +\frac{\left\lfloor \lambda \right\rfloor }{2}.$

3 Some characterizations of $\overline{GT_{P}(R)}$

In this section, we characterize when $\overline{GT_{P}(R)}$ to be claw-free or unicylic or pancyclic or perfect. A graph G is said to be unicyclic if G contains exactly one cycle. A graph G is a claw-free if G does not have $K_{1,3}$(a claw) as the induced subgraph.

Theorem 2

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inRwith$|P|=\lambda$and$|R/P|=\mu .$Then the following hold:

• (i) $\overline{GT_P(R)}$ is claw-free if and only if $|P|=2;$

• (ii) $\overline{GT_P(R)}$ is unicyclic if and only if R is isomorphic to either of the rings $\mathbb {Z}_2 \times \mathbb {Z}_2,~\mathbb {Z}_4,$ $\frac{\mathbb {Z}_2[x]}{<x^2>}.$

Proof

• (i) Assume that $|P| =2$ and $S \subseteq V(\overline{GT_P(R)})$ with $|S|=4.$ Then $<S>$ contains a $C_4$ as a subgraph and so $\overline{GT_P(R)}$ is claw-free. Conversely, assume that $\overline{GT_P(R)}$ is claw-free. Suppose $|P| \ge 3.$ If $2\in P,$ then by Lemma 2(iii), $\overline{GT_P(R)}$ is $K_{\underbrace{\lambda ,\lambda ,\cdots ,\lambda }_{\mu times}}$ where $\mu \ge 2$ and so $\overline{GT_P(R)}$ contains a $K_{1,3}$ as an induced subgraph, a contradiction. Suppose $2\notin P.$ Let $S=\{u,v,w,x\}$ where $u,v,w\in P,$$x\in a_i+P$ for some $i,~1 \le i \le \frac{\mu -1}{2}.$ Then $<S>=K_{1,3}$ in $\overline{GT_P(R)},$ a contradiction.

• (ii) Assume that R is isomorphic to any one of $\mathbb {Z}_2 \times \mathbb {Z}_2$ or $\mathbb {Z}_4$ or $\frac{\mathbb {Z}_2[x]}{<x^2>}.$ Then $\overline{GT_P(R)}=C_4$ and so $\overline{GT_P(R)}$ is unicyclic. Conversely, assume that $\overline{GT_P(R)}$ is unicyclic. Since R is not an integral domain, |R| is not a prime number. Then $|R| \ge 4.$ Suppose $|R|\ge 6.$

Case 1. Let $2 \in P.$ Then R satisfies any one of the following:

(a) $\lambda =2$ and $\mu \ge 4;$ (b) $\lambda \ge 3$ and $\mu \ge 2.$

In both the situations, $\overline{GT_P(R)}$ contains $K_{3,3}$ as a subgraph, a contradiction. Hence $|R|=4$ and so R is isomorphic to either $\mathbb {Z}_2 \times \mathbb {Z}_2$ or $\mathbb {Z}_4$ or $\frac{\mathbb {Z}_2[x]}{<x^2>}.$

Case 2. Let $2 \notin P.$ Since R is not an integral domain, $|P|=|a_i+P|=\lambda \ge 2,$ for all $i,~1 \le i \le \frac{\mu -1}{2}.$ Let $x_1,x_2 \in P$ and $y_1,y_2 \in a_i+P$ for some i. Let $S_1=\{x_1,y_1,y_2\}$ and $S_2=\{x_2,y_1,y_2\}.$ Then $<S_1>=<S_2>$ are two different cycles in $\overline{GT_P(R)}$ and so $\overline{GT_P(R)}$ is not unicylic and hence no other R exists.

Note that a graph G is perfect if and only if both G and $\overline{G}$ have no induced subgraph that is an odd cycle of length at least 5 [20, 8.1.2]. Using this, now we prove that $\overline{GT_P(R)}$ is perfect.

Theorem 3

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inRwith$|P|=\lambda$and$|R/P|=\mu .$Then$\overline{GT_P(R)}$is a perfect graph.

Proof

By Theorem 1, $GT_P(R)$ does not contain an odd cycle of length $\ge 5$ as an induced subgraph. It remains to prove that $\overline{GT_P(R)}$ does not contain an odd cycle of length $\ge 5$ as an induced subgraph.

Case 1. Assume that $2\in P.$ By Lemma 2(iii), $\overline{GT_P(R)}$ is complete $\mu$-partite. If $\mu =2,$ then $\overline{GT_P(R)}$ is complete bipartite and so $\overline{GT_P(R)}$ does not contain any odd cycle.

Assume that $\mu \ge 3$ and $S \subseteq V(\overline{GT_P(R)})$ with $|S|\ge 5.$ Consider the partition of $R=\bigcup \nolimits _{i=0}^{\mu -1} (a_i+P)$ with $a_0\in P.$ If $S \subseteq a_i+P$ for some i,  then $<S>$ is totally disconnected in $\overline{GT_P(R)}.$ If S is not contained in $(a_i+P)$ for some i,  let $n=\max \{|S \cap (a_i+P)|\}$ for all i. Then $n \ge 1$ and $K_{n,|S|-n}\subseteq <S>\subseteq \overline{GT_P(R)}.$ Hence $<S>$ contains a vertex of degree at least 3. From this, any cycle of length at least 5 cannot be an induced subgraph of $\overline{GT_P(R)}.$

Case 2. Assume that $2 \notin P.$ Consider $R=P\cup \bigcup \nolimits _{i=1}^{\frac{\mu -1}{2}}(a_i+P \cup -a_i+P).$ Suppose $S \subseteq V(\overline{GT_P(R)})$ with $|S|\ge 5.$

Case 2.1. Assume that $S \cap P \ne \phi .$ If $S \subseteq P,$ then $<S>=\overline{K}_{|S|}$ in $\overline{GT_P(R)}.$ If S is not contained in P,  then the induced subgraph $<S>$ of $\overline{GT_P(R)}$ contains a $K_{n,|S \setminus P|}$ where $n=|S\cap P|.$ Hence $<S>$ contains a vertex of degree at least 3 and so any cycle of length at least 5 cannot be an induced subgraph of $\overline{GT_P(R)}.$

Case 2.2. Assume that $S \cap P = \phi .$ Then $S \subseteq \bigcup \nolimits _{i=1}^{\frac{\mu -1}{2}}(a_i+P \cup -a_i+P).$ Let $A_i=(a_i+P) \cup (-a_i+P)$ for all $i,~1 \le i \le \frac{\mu -1}{2}.$ Suppose $S \subseteq A_i$ for some i. If either $S \subseteq (a_i+P)$ or $S\subseteq (-a_i+P),$ then $<S>=K_{|S|}$ in $\overline{GT_P(R)}.$ If $S \cap (a_i+P)\ne \phi$ and $S \cap (-a_i+P)\ne \phi ,$ then either $|S \cap (a_i+P)| \ge 3$ or $|S \cap (-a_i+P)| \ge 3.$ Then $K_3$ is a subgraph of $<S>$ and in turn an induced subgraph of $\overline{GT_P(R)}.$

Assume that S is not a subset of $A_i$ for some i. Then $S \cap A_i \ne \phi$ and $S \cap A_j \ne \phi$ for some $1 \le i \ne j \le \frac{\mu -1}{2}.$ If $S\cap A_i \ne \phi$ for $1 \le i \le \frac{\mu -1}{2}$ and $|S \cap A_i|=1,$ then $<S>$ contains a $K_5$ as a subgraph in $\overline{GT_P(R)}.$ Suppose $|S \cap A_i| \ge 2$ for some i. Let $A_i=A_1,~|S \cap A_1| \ge 2,~n=|S \cap A_1|$ and $m=|S \cap \bigcup \nolimits _{i=2}^{\frac{\mu -1}{2}} A_i|.$ Since $|S|\ge 5,$ either $n \ge 3$ or $m \ge 3.$ Thus $K_{n,m}$ is a subgraph of $<S>.$ Hence, in this case also, $\overline{GT_P(R)}$ has no induced subgraph that is an odd cycle of length at least 5.

A graph G of order $m \ge 3$ is pancyclic  [8, Definition 6.3.1] if G contains cycles of all lengths from 3 to m.

Theorem 4

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inR,  where$|P|=\lambda$and$|R/P|=\mu .$Then$\overline{GT_P(R)}$is pancyclic if and only if either$2 \notin P$or$2 \in P$with$\mu >2.$

Proof

Assume that $2 \notin P.$ Consider the partition $R= P\cup \bigcup \nolimits _{i=1}^{\frac{\mu -1}{2}} (a_i+P \cup -a_i+P).$ Let $P=\{x_{01},x_{02},\ldots ,x_{0\lambda } \},~a_i+P=\{x_{i1},x_{i2},\ldots ,x_{i\lambda } \}$ and $-a_i+P=\{y_{i1},y_{i2},\ldots ,y_{i\lambda }\}$ for $1 \le i \le \frac{\mu -1}{2}.$

Note that $<P>=\overline{K}_\lambda$ and $<a_i+P>=<-a_i+P>=K_\lambda$ in $\overline{GT_P(R)}.$ Let $P_i$ and $P_i'$ be spanning paths of length $\lambda -1$ in $<a_i+P>$ and $<-a_i+P>$ respectively for $i,~1 \le i \le \frac{\mu -1}{2}.$

If $\mu =3,$ then $C:x_{01}-x_{11}-x_{02}-x_{12}-x_{03}- \cdots -x_{0(\lambda -1)}-x_{1(\lambda -1)}-x_{1\lambda }-x_{0\lambda }-P_1{'}-x_{01}$ is a spanning cycle of length |R| in $\overline{GT_P(R)}.$ By removing vertices one by one from $P_1{'} {\setminus } \{x_{11}\}, P{\setminus }\{x_{01},x_{0\lambda }\},P_1 {\setminus } \{x_{1\lambda }\},$ we get cycles of lengths $|R|-1,|R|-2,\ldots ,4$ as subgraphs in $\overline{GT_P(R)}.$ Also $x_{01}-x_{1 1}-x_{1 \lambda }-x_{01}$ is a 3-cycle in $\overline{GT_P(R)}.$ From this, we get cycles of length from 3 to |R| as subgraphs in $\overline{GT_P(R)}.$

If $\mu >3,$ then $C:x_{01}-x_{1 1}-x_{02}-x_{12}-x_{03}-\cdots -x_{0(\lambda -1)}-x_{1(\lambda -1)}-x_{0\lambda }-x_{1\lambda }-P_2-P_3- \cdots -P_{\frac{\mu -1}{2}}-P_1'-P_2'-\cdots -P_{\frac{\mu -1}{2}}'-x_{01}$ is a spanning cycle of length |R| in $\overline{GT_P(R)}.$ By removing vertices one by one from the spanning paths $P_{\frac{\mu -1}{2}}',P_{\frac{\mu -3}{2}}',\ldots ,P_1',P_{\frac{\mu -1}{2}},P_{\frac{\mu -3}{2}},\ldots ,P_2, P{\setminus }\{x_{01}\},P_1{\setminus }\{x_{11},x_{1\lambda }\},$ we get cycles of lengths $|R|-1,|R|-2,\ldots ,4,3$ as subgraphs in $\overline{GT_P(R)}.$ From this, we get cycles of length from 3 to |R| as subgraphs in $\overline{GT_P(R)}.$ Hence $\overline{GT_P(R)}$ is pancyclic.

Assume that $2 \in P$ and $\mu >2.$ Note that $R= P\cup \bigcup \nolimits _{i=1}^{\mu -1}(a_i+P)$ and $\overline{GT_P(R)}$ is complete $\mu$-partite graph. Let $P=P_0=\{x_{01},\ldots ,x_{0\lambda } \}$ and $a_i+P=\{x_{i1},\ldots ,x_{i\lambda } \}$ for $1 \le i \le \mu -1.$ Consider $C=x_{01}-x_{11}\cdots -x_{(\mu -1)1}-x_{02}-x_{12}-\cdots -x_{(\mu -1)2}-\cdots -x_{0\lambda }- \cdots -x_{(\mu -2)\lambda }-x_{(\mu -1)\lambda }-x_{01}$ in $\overline{GT_P(R)}.$ Clearly C is a spanning cycle of length |R| in $\overline{GT_P(R)}.$ By removing the vertices one by one from the sets $(a_{\mu -1}+P){\setminus } \{x_{(\mu -1)\lambda }\}, a_{\mu -2}+P,\dots ,a_2+P$ and alternatively removing the vertices one by one from the sets $(a_1+P) {\setminus } \{x_{11}\}$ and $P {\setminus} \{x_{01}\},$ we get the cycles of lengths $|R|,|R|-1,\dots ,4,3$ as subgraphs in $\overline{GT_P(R)}.$ Thus $\overline{GT_P(R)}$ is pancyclic.

Conversely, assume that $2 \in P.$ If $\mu =2,$ then $\overline{GT_P(R)}=K_{\lambda ,\lambda }$ and so $\overline{GT_P(R)}$ contains no odd cycle, which is a contradiction to our assumption.

Now, we discuss about planarity and outerplanarity of $\overline{GT_P(R)}.$ For this purpose, we recall the following results.

Theorem 5

([10, Theorem 9.7]) A graph is planar if and only if it does not contain a subdivision of$K_5$or$K_{3,3}.$

Theorem 6

([11, Theorem 11.10]) A graphGis outerplanar if and only if it does not contain a subdivision of$K_4$or$K_{2,3}.$

Using the above theorems, we determine all finite commutative rings R for which $\overline{GT_P(R)}$ to be planar or outerplanar.

Theorem 7

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inR,  where$|P|=\lambda$and$|R/P|=\mu .$Then the following hold:

• (i) If $2 \in P,$ then $\overline{GT_P(R)}$ is planar if and only if R is isomorphic to any one of $\mathbb {Z}_4,~\mathbb {Z}_2 \times \mathbb {Z}_2,~\frac{\mathbb {Z}_2[x]}{<x^2>};$

• (ii) If $2 \notin P,$ then $\overline{GT_P(R)}$ is planar if and only if $R=\mathbb {Z}_6;$

• (iii) $\overline{GT_P(R)}$ is outerplanar if and only if R is either $\mathbb {Z}_4,\mathbb {Z}_2 \times \mathbb {Z}_2 ~\textit{or}~\frac{\mathbb {Z}_2[x]}{<x^2>}.$

Proof

• (i) Assume that R is isomorphic to either $\mathbb {Z}_4$ or $\mathbb {Z}_2 \times \mathbb {Z}_2$ or $\frac{\mathbb {Z}_2[x]}{<x^2>}.$ Then $\overline{GT_P(R)}=C_4$ and so $\overline{GT_P(R)}$ is planar. Conversely assume that $\overline{GT_P(R)}$ is planar. If $|R| \ge 8,$ then any one of the following is true: (a) $|P|=2$ with $\mu \ge 4;$ (b) $|P| \ge 3.$

  • (a) Assume that $|P|=2$ with $\mu \ge 4.$ Then $\overline{GT_P(R)}=K_{2,2,\ldots ,2}$ and so $\overline{GT_P(R)}$ contains a $K_{3,3},$ as a subgraph. From this $\overline{GT_P(R)}$ is not planar.

  • (b) Assume that $|P|\ge 3.$ Note that $\mu \ge 2.$ Then once again $\overline{GT_P(R)}$ contains a $K_{3,3},$ as a subgraph and hence $\overline{GT_P(R)}$ is not planar.

  If $|R|=6,$ by assumption on R, $R\cong \mathbb {Z}_6$ and $P=<2>.$ From this one can see that the graph $\overline{GT_P(R)}$ is $K_{3,3},$ which is not planar. From the above arguments, $|R|=4$ and so R is isomorphic to either $\mathbb {Z}_4$ or $\mathbb {Z}_2 \times \mathbb {Z}_2$ or $\frac{\mathbb {Z}_2[x]}{<x^2>}.$

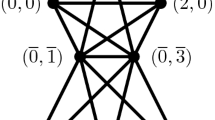
• (ii) Assume that $R\cong \mathbb {Z}_6.$ Since $2 \notin P,~P=<3>.$ The planar embedding of $\overline{GT_{P}(\mathbb {Z}_6)}$ is given in Fig. 1 and so it is planar.

Fig. 1

$\overline{GT_{\left\langle 3\right\rangle }(\mathbb {Z}_6)}$

Conversely, assume that $\overline{GT_P(R)}$ is planar and $2 \notin P.$ If $|R| \ge 9,$ then any one of the following is true:

• (a) $|P|=2$ with $\mu \ge 5;$

• (b) $|P| \ge 3.$

• (a) Assume that $|P|=2$ with $\mu \ge 5.$ Then $GT_P(R)=K_2\cup \bigcup \nolimits _{\frac{\mu -1}{2}} K_{2,2}$ and so $\overline{GT_P(R)}$ contains a $K_{3,3},$ a contradiction.

• (b) Proof is trivial.

• (iii) By above (i) and (ii), it is enough to show that $\overline{GT_P(R)}$ is not outerplanar for $R=\mathbb {Z}_6$ and $2 \notin P.$ For $R=\mathbb {Z}_6$ and $2 \notin P,$ from the Fig. 1, $\overline{GT_P(R)}$ contains a $K_{2,3}$ and so $\overline{GT_P(R)}$ is not outerplanar.

4 Domination parameters of $\overline{GT_{P}(R)}$

In this section, we discuss about various domination parameters of $\overline{GT_{P}(R)}$. More specifically, we discuss about $\gamma _t,\gamma _c,\gamma _{cl},\gamma _p,\gamma _s,\gamma _w$ and $\gamma _i$ of $\overline{GT_{P}(R)}.$ A nonempty subset S of V is called a dominating set if every vertex in $V {\setminus} S$ is adjacent to at least one vertex in S. A subset S of V is called a total dominating set if every vertex in V is adjacent to some vertex in S. A dominating set S is called a connected (or clique) dominating set if the subgraph induced by S is connected (or complete). A dominating set S is called an independent dominating set if no two vertices of S are adjacent. A dominating set S is called a perfect dominating set if every vertex in $V{\setminus }S$ is adjacent to exactly one vertex in S. A dominating set S is called a strong (or weak) dominating set, if for every vertex $u \in V{\setminus }S$ there is a vertex $v \in S$ with $deg(v) \ge deg(u)(or deg(v) \le deg(u))$ and u is adjacent to v. The domination number$\gamma$ of G is defined to be the minimum cardinality of a dominating set in G and the corresponding dominating set is called as a $\gamma$-set of G. Similar definition is applicable for the total domination number$\gamma _t,$connected domination number$\gamma _c$,clique domination number$\gamma _{cl}$, independent domination number$\gamma _i,$perfect domination number$\gamma _p$, strong domination number$\gamma _s$and the weak domination number$\gamma _w.$ For all these definitions, one can refer Haynes et al. [12]. In the following Lemma, we obtain the domination number of $\overline{GT_{P}(R)}$.

Lemma 10

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inR. Assume that$|P|=\lambda$and$|R/P|=\mu .$Then$\gamma (\overline{GT_{P}(R)})= 2.$

Proof

By Lemma 2(ii), $\gamma (\overline{GT_{P}(R)})>1.$ Let x and y be two distinct elements in R such that $x \in P$ and $y \notin P.$

If $2 \in P,$ then by Lemma 3(i), x covers all the elements in $V(\overline{GT_P(R)}){\setminus }P$ and y covers all the elements in P. Hence $\gamma (\overline{GT_{P}(R)})=2.$

Assume that $2 \notin P.$ Let $z \in V(\overline{GT_P(R)}) {\setminus }\{x,y \}.$ If $z \in P,$ then by Lemma 3(ii) z, y are adjacent in $\overline{GT_{P}(R)}.$ Suppose $z \notin P.$ Then by Lemma 3(ii) z, x are adjacent in $\overline{GT_{P}(R)}.$ Therefore $\{x,y \}$ is a dominating set in $\overline{GT_{P}(R)}.$ By Lemma 2(ii), $\{x,y \}$ is a minimal dominating set in $\overline{GT_{P}(R)}.$ From this we get that $\gamma (\overline{GT_{P}(R)})=2.$

In view of Lemma 10, we have the following characterization of $\gamma$-sets in $\overline{GT_{P}(R)}$.

Lemma 11

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inR. Then$S=\{x,y \} \subseteq V(\overline{GT_{P}(R)})$is a$\gamma$-set in$\overline{GT_{P}(R)}$if and only ifx, yare in two distinct cosets ofPinR.

Corollary 2

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inR. Assume that$|P|=\lambda$and$|R/P|=\mu .$Then$\gamma _t(\overline{GT_{P}(R)})=\gamma _c(\overline{GT_{P}(R)})=\gamma _{cl}(\overline{GT_{P}(R)})=2.$

Proof

Let $x \in P$ and $y \in V(\overline{GT_{P}(R)}) {\setminus }P.$ By Lemma 11, $S=\{x,y \}$ is a dominating set of $\overline{GT_{P}(R)}.$ By Lemma 3, x, y are adjacent in $\overline{GT_{P}(R)}.$ Therefore S is a total dominating set of $\overline{GT_{P}(R)}$ and so $\gamma _t(\overline{GT_{P}(R)})=\gamma _c(\overline{GT_{P}(R)})=\gamma _{cl}(\overline{GT_{P}(R)})=2.$

A graph G is called excellent if, for every vertex $v \in V (G),$ there is a $\gamma$-set S containing v. Using Lemma 11, we have the following result.

Corollary 3

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inR. Assume that$|P|=\lambda$and$|R/P|=\mu .$Then$\overline{GT_{P}(R)}$is excellent.

Lemma 12

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inR. Assume that$|P|=\lambda$and$|R/P|=\mu .$Then$\overline{GT_{P}(R)}$has a perfect dominating set if and only if$2\in P$and$\mu =2.$

Proof

Assume that $2\in P$ and $\mu =2.$ Then $\overline{GT_{P}(R)}$ is a complete bi-partite graph. Let $S =\{x,y\}$ where $x \in P$ and $y \in V(\overline{GT_P(R)}){\setminus }P.$ Then $S=\{x,y \}$ is a perfect dominating set of $\overline{GT_P(R)}.$

Conversely, assume that S is a perfect dominating set in $\overline{GT_{P}(R)}.$

Suppose $2\notin P.$ Since R is not an integral domain, $|P|=|a_i+P|=|-a_i+P| \ge 2, 1 \le i \le \frac{\mu -1}{2}.$ Let x, y be two distinct vertices in $V(\overline{GT_P(R)}).$ If $x,y \in P,$ then every $z \in V(\overline{GT_P(R)}){\setminus }P$ is adjacent to both x and y and hence both x and y cannot be in S.

Suppose $x \in P\cap S$ and $y \in P$ with $y \notin S$. Since P is an independent set, x and y are not adjacent in $\overline{GT_{P}(R)}.$ Since S is dominating set, $\exists ~z_1 \in S$ such that $z_1$ and y are adjacent in $\overline{GT_{P}(R)}.$ By Lemma 3(ii), $z_1 \in (a_i+P) \cup (-a_i+P)$ for some i where $1 \le i \le \frac{\mu -1}{2}.$ Without loss of generality, assume that $z_1 \in (a_1+P).$ Since $|a_1+P| \ge 2,$$\exists ~z_2\in a_1+P$ with $z_2\ne z_1.$ If $z_2 \in S,$ then, by Lemma 3(ii) and $2\notin P$, y is adjacent to $z_1,z_2$ which is a contradiction. Hence $z_2 \in V(\overline{GT_P(R)}){\setminus }S.$ By Lemma 3(ii), $x,z_2$ are adjacent and $z_1,z_2$ are also adjacent in $\overline{GT_{P}(R)}$, which is a contradiction to S is a perfect dominating set.

Suppose $x,y \in S{\setminus }P$. Since every element in P is adjacent to both x, y again a contradiction. Hence $\overline{GT_{P}(R)}$ has no perfect dominating set.

The above argument implies that $2\in P.$

Suppose $2 \in P$ and $\mu \ge 3.$ By Lemma 2(iii), $\overline{GT_{P}(R)}$ is a complete $\mu$-partite graph. Clearly $\overline{GT_{P}(R)}$ does not contain any perfect dominating set, which is a contradiction to S is a perfect dominating set. Hence $2\in P$ and $\mu =2.$

Lemma 13

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inR. Assume that$|P|=\lambda$and$|R/P|=\mu .$Then the following are true:

• (i) If $2 \in P,$ then $\gamma _s(\overline{GT_{P}(R)})=\gamma _w(\overline{GT_{P}(R)})=2;$

• (ii) If $2 \notin P,$ then $\gamma _s(\overline{GT_{P}(R)})=\lambda$ and $\gamma _w(\overline{GT_{P}(R)})=2.$

Proof

• (i) Assume that $2\in P.$ Then $\overline{GT_{P}(R)}$ is a complete $\mu$-partite graph. Let $x \in P$ and $y \in a_i+P$ for some $i, 1\le i \le \mu -1.$ Then $S =\{x,y\}$ is a dominating set of $\overline{GT_P(R)}$ and so by Lemma 1(i), $deg(v)=(\mu -1)\lambda \,\forall \,v \in \overline{GT_P(R)}.$ Therefore $\gamma _s(\overline{GT_{P}(R)})=\gamma _w(\overline{GT_{P}(R)})=2.$

• (ii) Assume that $2\notin P.$ By the definition of $\overline{GT_P(R)},$ each vertex $x \in P$ is adjacent with each vertex $y \in V(\overline{GT_P(R)}) {\setminus }P.$ By Lemma 1(ii), we have $deg~(x)=(\mu -1)\lambda \,\forall \,x \in P$ and $deg~(y)=(\mu -1)\lambda -1\, \forall \, y \in V(\overline{GT_P(R)}) {\setminus }P.$ Since P dominates $\overline{GT_{P}(R)}$ and $deg(x)> deg(y),$P is a strong dominating set in $\overline{GT_{P}(R)}.$ Then $\gamma _s(\overline{GT_{P}(R)})=\lambda .$ Let $x \in a_i+P$ and $y \in -a_i+P$ where $1 \le i \le \frac{\mu -1}{2}.$ By Lemma 11, the set $S=\{x,y \}$ is a dominating set of $\overline{GT_{P}(R)}$ and by Lemma 1(ii), $deg(x) = deg(y)=\lambda (\mu -1)=\delta (\overline{GT_{P}(R)}).$ Then $\{x,y \}$ is a weak dominating set in $\overline{GT_{P}(R)}$ and so $\gamma _w(\overline{GT_{P}(R)})=2.$

In following lemma, we obtain the independent domination number of $\overline{GT_{P}(R)}.$

Lemma 14

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inR. Assume that$|P|=\lambda$and$|R/P|=\mu .$Then

$$\begin{aligned} \gamma _i(\overline{GT_{P}(R)})= \left\{ \begin{array}{ll} \lambda \qquad &{} {if}\, 2\in P;\\ 2~\qquad &{} {if}\, 2\notin P. \end{array}\right. \end{aligned}$$

Proof

If $2\in P,$ then by Lemma 2(iii), $\overline{GT_{P}(R)}$ is $K_{\underbrace{\lambda ,\ldots ,\lambda }_{\mu ~times}}$ and so $\gamma _i(\overline{GT_{P}(R)})=\lambda .$

Suppose $2\notin P.$ Let $x \in a_i+P$ and $y \in -a_i+P$ where $1 \le i \le \frac{\mu -1}{2}.$ By Lemma 11, $\{x,y \}$ is a dominating set in $\overline{GT_{P}(R)}.$ By Lemma 3(ii), x, y are not adjacent in $\overline{GT_{P}(R)}$ and so $\gamma _i(\overline{GT_{P}(R)})=2.$

Note that, a graph G is said to be well-covered if $\beta (G)=\gamma _i(G).$ The following lemma follows from Lemmas 8 and 14.

Lemma 15

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inR. Assume that$|P|=\lambda$and$|R/P|=\mu .$Then

• (i) If$2\in P$, then$\overline{GT_{P}(R)}$is well-covered;

• (ii) If$2\notin P$, then$\overline{GT_{P}(R)}$ is well-covered if and only if$|P|=2.$

A domatic partition of G is a partition of V(G) into dominating sets of G. The maximum number of sets in a domatic partition of G is called the domatic number of G and the same is denoted by d(G).

Lemma 16

LetRbe a finite commutative ring which is not an integral domain andPbe a prime ideal inR. Assume that$|P|=\lambda$and$|R/P|=\mu .$Then

$$\begin{aligned} d(\overline{GT_{P}(R)})= \left\{ \begin{array}{ll} \frac{|R|}{2} &{}~if~2\in P;\\ \frac{|R|-\lambda }{2} + 1~&{}~if~2\notin P. \end{array}\right. \end{aligned}$$

Proof

If $2\in P,$ then $\mu$ is even. Let $S=\bigcup \nolimits _{i=1}^{\frac{\mu }{2}}(a_i+P)$ and $T=\bigcup \nolimits _{i=\frac{\mu }{2}+1}^{\mu }(a_i+P).$ Let $X_j=\{\{x_j,y_j\}:~x_j \in S\, and \,y_j \in T \}$ for $1 \le j \le \frac{|R|}{2}.$ Clearly $X_j$ is a dominating set in $\overline{GT_{P}(R)}$ and hence $d(\overline{GT_{P}(R)})=\frac{|R|}{2}.$

Suppose $2 \notin P.$ Then $\mu$ is odd and $\mu \ge 3.$ Let $S=\bigcup \nolimits _{i=1}^{\frac{\mu -1}{2}}(a_i+P)$ and $T=\bigcup \nolimits _{i=1}^{\frac{\mu -1}{2}}(-a_i+P)$ where $a_i + (-a_i)=0.$ Let $X_j=\{\{x_j,y_j\}:~x_j\in S\, and \,y_j \in T \}$ for $1 \le j \le \frac{|R|-\lambda }{2}.$ Clearly, each $X_j$ is a dominating set in $\overline{GT_{P}(R)}.$ Also, P is a dominating set in $\overline{GT_{P}(R)}.$ Hence $d(\overline{GT_{P}(R)})=\frac{|R|-\lambda }{2}+ 1.$