Subgraph of generalized co-maximal graph of commutative rings

Abstract

Let R be a commutative ring with 1. In Biswas et al. (Disc Math Algorithms Appl 11(1):1950013, 2019), we introduced a graph G(R) whose vertices are elements of R and two distinct vertices a, b are adjacent if and only if $aR+bR=eR$ for some nonzero idempotent e in R. Let $G'(R)$ be the subgraph of G(R) generated by the non-units of R. In this paper, we characterize those rings R for which the graph $G'(R)$ is connected and Eulerian. Also we characterize those rings R for which genus of the graph $G'(R)$ is $\le 2$. Finally, we show that the graph $G'(R)$ is a line graph of some graph if and only if R is either a regular ring or a local ring.

1 Introduction

The algebraic graph theory is an interesting subject for graph theorists as well as algebraists, since it relates two different areas of mathematics, involves some combinatorial approach and can be studied different levels of mathematical expertise and sophistication. One may associate rings to graphs for the benefit of studying ring structures to find some results about the graph structures and vice versa. For example, we may refer to Anderson and Naseer (1993), Anderson and Livingston (1999), Biswas et al. (2019), Biswas et al. (2020), Beck (1988), Maimani et al. (2008), Pranjali (2015), Redmond (2007), Redmond (2002) and Sharma and Bhatwadekar (1995).

The interplay between ring theoretic and graph theoretic properties was studied by several authors, and this approach has since become increasingly very popular in abstract algebraic graph theory. The area of graph theory and ring theory both benefits from the study of subgraph of the generalized co-maximal graphs. The knowledge of algebraic properties of rings can innovate new ideas for studying several properties of graphs. On the other hand after translating algebraic properties of rings into graph theoretic language, difficult problems in ring theory might be more easily solved by using techniques from graph theory. Motivated by these techniques we try to apply the above method to the class of subgraph of the generalized co-maximal graphs. As an application, a graph theoretic problem that seems rather unmanageable when restricted to methods from graph theory is solved using a straightforward ring theoretic argument.

In Biswas et al. (2019), we defined the graph G(R) on a commutative ring R with 1, having vertices as elements of R, where two distinct vertices a and b are adjacent if and only if $aR + bR = eR$ for some nonzero idempotent e in R. In Biswas et al. (2019), we proved that chromatic number $\chi (G(R))$ is the number of regular elements of R. We also characterized completeness of the graph and some other properties related to the graph.

Motivated by the papers (Maimani et al. 2008) and Wang (2008), in this paper we define the subgraph $G'(R)$ which is generated by non-units of the ring R and we study the substructure of the graph G(R). The aim of this paper is to study the notions of diameter, Eulerian property and other graph theoretic properties of $G'(R)$. We also able to determine those rings R for which $G'(R)$ is connected, those rings R for which $G'(R)$ is Eulerian. In Asir and Mano (2020), Asir and Mano (2019), Tamizh Chelvam and Selvakumar (2017), Tamizh Chelvam and Asir (2013) and Wang (2008), some authors studied the genus of graphs over rings. In this paper, we characterize the class of rings for which genus of the subgraph $G'(R)$ is less or equal to 2. Finally, we derive some results related to the line graph $L(G'(R))$.

If a surface is homeomorphic to a sphere with g handles, then the genus of this surface is g. A graph can be drawn without crossings on the surface of genus g, but not on the one of genus $g-1$, is called a graph of genus g. We write $\gamma (G)$ for the genus of a graph G. If a graph G can be embedded in a plane, we say the graph G is planar, i.e., $\gamma (G)=0$ and if a graph G can be embedded in a torus not a plane, we say the graph G is toroidal, i.e., $\gamma (G)=1$.

Throughout this paper, we assumed that the ring R is a finite commutative ring with identity, U(R) stands for the set of units of R and r(R) denotes the set of regular elements of R. The notation ${\mathbb {F}}_n$ stands for a finite field of order n and we use the notation $a\leftrightarrow b$ if a, b are adjacent in a graph G.

2 Connectedness and diameter of $G'(R)$

In this section, we determine some necessary and sufficient conditions for the connectedness of the subgraph $G'(R)$ of the graph G(R) over a finite commutative ring R with 1. Also we determine some conditions under which $diam(G'(R))$ is 1 or 2.

From Biswas et al. (2019), we get the following lemma which helps us to prove some propositions and theorems.

Lemma 2.1

(Biswas et al. 2019) Let $R=R_1\times R_2\times \cdots \times R_k$ be a finite commutative ring with identity such that each $R_i$ is local with unique maximal ideal $M_i$. Two distinct vertices $(x_1,x_2,\ldots ,x_k)$ and $(y_1,y_2,\ldots ,y_k)$ are adjacent if and only if $x_iR_i+y_iR_i$ is either $R_i$ or $\{0\}$ for $i=1,2,\ldots ,k$ (but not $\{0\}$ for at least one i).

Example 2.2

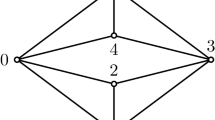
Consider the rings ${\mathbb {Z}}_3\times {\mathbb {Z}}_4$ and ${\mathbb {Z}}_4\times {\mathbb {Z}}_4$. Then the vertex set of the graph $G'({\mathbb {Z}}_3\times {\mathbb {Z}}_4)$ is ${\mathbb {Z}}_3\times {\mathbb {Z}}_4- U({\mathbb {Z}}_3\times {\mathbb {Z}}_4)=\{({\overline{0}},{\overline{0}}),({\overline{0}},{\overline{1}}),({\overline{0}},{\overline{2}}),({\overline{0}},{\overline{3}}),({\overline{1}},{\overline{0}}),({\overline{1}},{\overline{2}}),({\overline{2}},{\overline{0}}),$ $({\overline{2}},{\overline{2}})\}$ and the vertex set of $G'({\mathbb {Z}}_4\times {\mathbb {Z}}_4)$ is ${\mathbb {Z}}_4\times {\mathbb {Z}}_4- U({\mathbb {Z}}_4\times {\mathbb {Z}}_4)=\{({\overline{0}}, {\overline{0}}), ({\overline{0}},{\overline{1}}), ({\overline{0}},{\overline{2}}), ({\overline{0}},{\overline{3}}), ({\overline{1}},{\overline{0}}), ({\overline{1}},{\overline{2}}), ({\overline{2}},{\overline{0}}), ({\overline{2}},{\overline{1}}), ({\overline{2}},{\overline{2}}), ({\overline{2}},{\overline{3}}),({\overline{3}},{\overline{0}}),({\overline{3}},{\overline{2}})\}$.

Fig. 1

$G'({\mathbb {Z}}_{3}\times {\mathbb {Z}}_4)$

Fig. 2

$G'({\mathbb {Z}}_{4}\times {\mathbb {Z}}_4)$

From Fig. 1, it follows that the graph $G'({\mathbb {Z}}_3\times {\mathbb {Z}}_4)$ is connected, where ${\mathbb {Z}}_3$ is a regular ring. It follows from Fig. 2 that the graph $G'({\mathbb {Z}}_4\times {\mathbb {Z}}_4)$ is not connected as $({\bar{2}},{\bar{2}})$ is not adjacent with any other vertex in $G'({\mathbb {Z}}_4\times {\mathbb {Z}}_4)$, where ${\mathbb {Z}}_4$ is not a regular ring.

From Example 2.2, we have the following result.

Theorem 2.3

Let $R=R_1\times R_2\times \cdots \times R_k$ for some local rings $R_1,R_2,\ldots ,R_k$. Then $G'(R)$ is connected if and only if at least one of $R_i$ is regular.

Proof

We first assume that $G'(R)$ is connected. If possible, let no $R_i$ be regular for $i=1,2,\ldots ,k$. Then each $R_i$ has a unique nonzero maximal ideal $M_i$. Thus there exists $m_i\in M_i\setminus \{0\}$ for each i. Now we have a vertex $(m_1,m_2,\ldots ,m_i,\ldots ,m_k)$ of $G'(R)$. Suppose $(a_1,a_2,\ldots ,a_k)$ is an arbitrary vertex in $G'(R)$. Then at least one $a_i\in M_i$. Without loss of generality, let $a_1\in M_1$. Since $a_1R_1+m_1R_1\subseteq M_1(\ne e_1R_1)$ for any idempotent $e_1\in R_1$, $(a_1,a_2,\ldots ,a_k)\nleftrightarrow (m_1,m_2,\ldots ,m_k)$, by Lemma 2.1. Again since the vertex $(a_1,a_2,\ldots ,a_k)$ is arbitrary, it follows that $deg((m_1,m_2,\ldots ,m_k))=0$ in $G'(R)$. This contradicts the connectedness of $G'(R)$. So at least one of $R_i$ is regular.

Conversely, suppose that at least one $R_i$ is regular. Without loss of generality, let $R_1$ be regular. Since $R_1$ is local and regular, $R_1=U(R_1)\bigcup \{0\}$. Let $(x_1,x_2,\ldots ,x_k)$ be a vertex of $G'(R)$. Since $x_1\in R_1$, $x_1R_1=e_1R_1$ for some idempotent $e_1\in R_1$. Consider a regular element $(0,1,1,\ldots ,1)\in R\setminus U(R)$. Since $x_1R_1+0R_1=e_1R_1$ and $x_iR_i+1R_i=R_i$ for $i=2,3,\ldots ,k$, so we have $(x_1,x_2,\ldots ,x_k)$ is adjacent with $(0,1,1,\ldots ,1)$, by Lemma 2.1. Thus any vertex in $G'(R)$ is adjacent with $(0,1,1,\ldots ,1)\in R\setminus U(R)$. Therefore, the graph $G'(R)$ is connected. $\square$

Theorem 2.4

Let $R=R_1\times R_2\times \cdots \times R_k$, where $R_i$ is a local ring for each i. Then $diam(G'(R))=1$ if and only if R is a regular ring.

Proof

First suppose that $diam(G'(R))=1$. If possible, let R be not a regular ring. This implies that at least one of $R_i$ is not regular. Let us suppose that $R_1$ be not regular. Then $M_1\ne \{0\}$, where $M_1$ is the unique maximal ideal of $R_1$. Let $b_1\in M_1\setminus \{0\}$. Then we have two elements $(b_1,1,1,\ldots ,1,1,1,\ldots .,\!1)$ and $(0,1,1,\ldots ,1,1,1,\ldots ,\!1)$ in the vertex set of $G'(R)$. Now $b_1R_1+0R_1=b_1R_1\subseteq M_1$ and hence $b_1R_1\ne e_1R_1$ for any idempotent $e_1\in R_1$. Thus by Lemma 2.1, $(b_1,1,1,\ldots ,1,1,1,\ldots .,1)$ and $(0,1,1,\ldots ,1,1,1,\ldots ,1)$ are not adjacent. This contradicts the fact that $diam(G'(R))=1$. Hence R is a regular ring.

The converse part is trivial. $\square$

Theorem 2.5

Let $R=R_1\times R_2\times \cdots \times R_k$ for some local rings $R_1,R_2,\ldots ,R_k$. Then $diam(G'(R))=2$ if and only if at least one of $R_i$ is a regular ring but not all.

Proof

Let $diam(G'(R))=2$. Then by Theorem 2.4, it follows that R is not regular. Thus there exists at least one of $R_i$ which is not regular. Since $diam(G'(R))$ is finite, $G'(R)$ is connected. Now by Theorem 2.3, at least one of $R_i$ is regular. Thus there exists at least one $R_i$ which is regular but not all.

Conversely, suppose that at least one of $R_i$ is a regular ring but not all. Thus $diam(G'(R))>1$ $(I)$.

Without loss of generality, let $R_1$ be a regular ring. Let us take two elements $x=(a_1,a_2,\ldots ,a_i,\ldots ,a_k)$ and $y=(b_1,b_2,\ldots ,b_i,\ldots ,b_k)$ in $R\setminus U(R)$. Now we consider an element $c=(0,1,\ldots ,1,1,1,\ldots ,1)\in R\setminus U(R)$. Since $R_1$ is regular, $0R_1+a_1R_1=a_1R_1=e_1R_1$ and $0R_1+b_1R_1=b_1R_1=e_2R_1$ for some idempotents $e_1,e_2\in R_1$. Since $a_1R_1+0R_1=e_1R_1$ and $a_iR_i+1R_i=R_i$ for $i=2,3,\ldots ,k$, we have $(a_1,a_2,\ldots ,a_k)$ and $(0,1,1,\ldots ,1)$ are adjacent, by Lemma 2.1. Similarly, $(b_1,b_2,\ldots ,b_k)$ and $(0,1,1,\ldots ,1)$ are also adjacent. So we have a path $x\leftrightarrow c \leftrightarrow y$. Thus it follows that $d(x,y)\le 2$. Hence $diam(G'(R))\le 2$  $(II)$.

Now from (I) and (II), it follows that $diam(G'(R))=2$.

$\square$

From Theorems 2.4 and 2.5, we have the following characterizing result.

Theorem 2.6

Let R be a finite commutative ring with identity. Then there exists at least one direct summand of R which is regular if and only if $1\le diam(G'(R))\le 2$.

3 Degrees and Eulerianity of $G'(R)$

In this section, we determine some necessary and sufficient conditions for the Eulerianity of the subgraph $G'(R)$ of the graph G(R) over a finite commutative ring R with identity.

In Biswas et al. (2019), we proved the following result for the graph G(R) :

Theorem 3.1

(Biswas et al. 2019) Let $R_1\oplus R_2\oplus \cdots \oplus R_k$ be a finite commutative ring with identity such that each $R_i$ is a local ring with unique maximal ideal $M_i$. Let $a=(a_1,a_2,\ldots ,a_k)$ be an element of $R_1\oplus R_2\oplus \cdots \oplus R_k$. Then deg(a) in G(R) is either

(i):

$|R_{1}|\cdots |R_{q}|(|U(R_{q+1})|+1)\cdots (|U(R_k)|+1)-1$ or

(ii):

$|R_1||R_2|\cdots |R_k|-1$ or

(iii):

$(|U(R_1)|+1)(|U(R_2)|+1)\cdots (|U(R_k)|+1)-1$ or

(iv):

$|U(R_1)||U(R_2)|\cdots |U(R_m)||R_{m+1}|\cdots |R_{m+n}| (|U(R_{m+n+1})|+1)\cdots (|U(R_k)|+1)$ or

(v):

$|U(R_1)||U(R_2)|\cdots |U(R_l)|(|U(R_{l+1})|+1)\cdots (|U(R_k)|+1)$ or

(vi):

$|U(R_1)||U(R_2)|\cdots |U(R_p)||R_{p+1}|\cdots |R_{k}|$ or

(vii):

$|U(R_1)||U(R_2)|\cdots |U(R_k)|$,

where l, m, n, p, q are integers with $1\le l,m,n,p,q<k$.

Remark 3.2

For a finite commutative ring R with 1, the graph $G'(R)$ is the subgraph of the graph G(R) and vertex set of $G'(R)$ is $R\setminus U(R)$, where R is the vertex set of G(R). Then for any vertex x of $G'(R)$, $deg_{G'(R)}(x)=deg_{G(R)}(x)-|U(R)|$, where $deg_{G'(R)}(x)$ is the degree of x in $G'(R)$ and $deg_{G(R)}(x)$ is the degree of x in G(R).

Lemma 3.3

Let R be a finite commutative ring with 1 except $R= F_1\times F_2\times \cdots \times F_k$, where each $F_i$ is a field of characteristic 2. Then |U(R)| is even.

Proof

Let R be a finite commutative ring with 1. Then it follows from Bini and Flamini (2002), there exist local rings $R_1,R_2,\ldots ,\!R_k$ with unique maximal ideals $M_1,M_2,\ldots ,\!M_k$, respectively, such that $R=R_1\times R_2\times \cdots \times R_k$.

Case 1 : Assume |R| is odd. Then $|R_i|$ is odd for all i. This implies $|M_i|$ is odd for all i. Since $R_i$ is local, $|U(R_i)|=|R_i|-|M_i|$ is odd as both $|R_i|$ and $|M_i|$ are odd. So $|U(R)|=|U(R_1)||U(R_2)|\cdots |U(R_k)|$ is even as each $|U(R_i)|$ is even.

Case 2 : Suppose |R| is even.

Subcase 2a : Suppose that at least one $|R_i|$ is odd. Without loss of generality, let $|R_1|$ be odd. Then $|U(R_1)|$ is even. So $|U(R)|=|U(R_1)|\cdots |U(R_k)|$ is even as $|U(R_1)|$ is even.

Subcase 2b : Assume each $|R_i|$ is even and $R\ne F_1\times F_2\times \cdots \times F_k$, where each $F_i$ is a field of characteristic 2. Since |R| is even, each $R_i$ is a local ring of order $2^{r_i}$. Also $R\ne F_1\times F_2\times \cdots \times F_k$. This implies that there exists at least one $R_i$ which is not a field. Assume that $R_1$ is a local ring which is not a field of characteristic 2. Since $R_1$ is not field, $M\ne \{0\}$. So $|M|=2^m$ for $m\ge 1$. Now $|U(R)|=|R|-|M|=2^n-2^m$ is even. So $|U(R)|=|U(R_1)||U(R_2)|\cdots |U(R_k)|$ is even as $|U(R_1)|$ is even. $\square$

In Fig. 1, we notice that the graph $G'({\mathbb {Z}}_3\times {\mathbb {Z}}_4)$ is connected and $deg(({\bar{0}},{\bar{1}}))=7$. Thus the graph $G'({\mathbb {Z}}_3\times {\mathbb {Z}}_4)$ is not Eulerian. So the graph $G'(R)$ is not always Eulerian. Now we have the following result.

Theorem 3.4

Let $R=R_1\times R_2\times \cdots \times R_k$ be a finite commutative ring with 1, where each $R_i$ is a finite local ring, at least one $R_i$ is regular and $k\ge 2$. Then $G'(R)$ is Eulerian if and only if either |R| is odd or $R=F_1\times F_2\times \cdots \times F_k$, where each $F_i$ is a field of characteristic 2.

Proof

It is given that at least one $R_i$ is regular. This implies that $G'(R)$ is connected by Theorem 2.3.

Now we assume that |R| is odd. This implies that $|R_i|$ is odd for each i and hence $|U(R_i)|$ is even, by Lemma 3.3. Let $x\in R_1\times R_2\times \cdots \times R_k\setminus U(R_1\times R_2\times \cdots \times R_k)$. By rearranging the components of $R_1\times R_2\times \cdots \times R_k$ if necessarily x is either $(u_1,\ldots ,u_q,0,\ldots ,0)$ or $(0,0,\ldots ,0)$ or $(a_1,a_2,\ldots ,a_{m},u_{m+1},\ldots ,u_{m+n},0,\ldots ,0)$ or $(a_1,a_2,\ldots ,a_{l},0,\ldots ,0)$ or $(a_1,a_2,\ldots ,a_{p},u_{p+1},\ldots ,\!u_{k})$, where $a_i\in M_i\setminus \{0\}$ and $u_i\in U(R_i)$.

Case 1 : Assume $x=(u_1,u_2,\ldots ,u_q,0,0,\ldots ,0)$. Then by Remark 3.2 and Theorem 3.1, we have $[deg(x)]_{G'(R)}=deg_{G(R)}(x)-|U(R)|=|R_1|\cdots |R_q|(|U(R_{q+1})|+1)\cdots (|U(R_k)|+1)-|U(R_1)||U(R_2)|\cdots |U(R_k)|-1$ which is even, since $|R_i|$ and $|U(R_i)|+1$ are odd for all i.

Case 2 : Clearly, $[deg((0,0,0,\ldots ,0))]_{G'(R)}= deg_{G(R)}((0,0,\ldots ,0))-|U(R)|=(|U(R_1)|+1)(|U(R_2)|+1)\cdots (|U(R_i)|+1)\cdots (|U(R_k)|+1)-|U(R_1)||U(R_2)|\cdots |U(R_k)|-1$ is even, since $|U(R_i)|$ is even for all i.

Case 3 : Assume $x=(a_1,a_2,\ldots ,a_{m},u_{m+1},\ldots ,u_{m+n}, 0,\ldots ,0)$. Then by Remark 3.2 and Theorem 3.1, it follows that $[deg(x)]_{G'(R)}=deg_{G(R)}(x)-|U(R)|=$ $|U(R_1)|\cdots |U(R_m)||R_{m+1}|\cdots |R_{m+n}|(|U(R_{m+n+1})|+1)\cdots (|U(R_{k})| +1)-|U(R_1)||U(R_2)|\cdots |U(R_k)|$ which is even, since each $|U(R_i)|$ is even and each $|R_i|$ is odd.

Case 4 : Assume $x=(a_1,a_2,\ldots ,a_{l},0,\ldots ,0)$. Then by Remark 3.2 and Theorem 3.1, it follows that $[deg(x)]_{G'(R)}=deg_{G(R)}(x)-|U(R)|=|U(R_1)||U(R_2)|\cdots |U(R_l)| (|U(R_{l+1})|+1)\cdots (|U(R_k)|+1)-|U(R_1)||U(R_2)|\cdots |U(R_k)|$ which is even, since $|U(R_1)|$ is even.

Case 5 : Assume $x=(a_1,a_2,\ldots ,a_p,u_{p+1},\ldots ,u_k)$ be a vertex of $G'(R)$. Then $[deg(x)]_{G'(R)}=|U(R_1)||U(R_2)|\cdots |U(R_p)||R_{p+1}|\cdots |R_k|-|U(R_1)||U(R_2)|\cdots |U(R_k)|$ which is even, since $|U(R_1)|$ is even.

Since $G'(R)$ is connected and degree of any vertex is even, it follows that $G'(R)$ is Eulerian.

Again we assume that $R=F_1\times F_2\times \cdots \times F_k$, where each $F_i$ is a field of characteristic 2. Now $|U(R)|=|U(F_1)||U(F_2)|\cdots |U(F_k)|$ is odd as each $|U(F_i)|=|F_i|-1$ is odd. Let x be a vertex of $G'(R)$. Since $R=F_1\times F_2\times \cdots \times F_k$ is regular, x is adjacent with any other vertex of $G'(R)$. So $[deg(x)]_{G'(R)}=deg_{G(R)}(x)-|U(R)|=|R|-1-|U(R)|$ is even as |R| is even and |U(R)| is odd.

Since $G'(F_1\times F_2\times \cdots \times F_k)$ is connected and degree of any vertex is even, $G'(F_1\times F_2\times \cdots \times F_k)$ is Eulerian.

Conversely, suppose that $G'(R)$ is Eulerian. If possible, let |R| be even and $R\ne F_1\times F_2\times \cdots \times F_k$, where each $F_i$ is a field of characteristic 2. Then by Lemma 3.3, |U(R)| is even. Since |R| is even, there exists at least one $R_i$ whose order is $2^n$. Let $R_1$ be such a local ring of order $2^n$. Now $[deg((1,0,0,\ldots ,0))]_{G'(R)}=|R_1|(|U(R_2)|+1)\cdots (|U(R_i)|+1)|\cdots (|U(R_k)|+1)-|U(R)|-1$ is odd which is a contradiction. Hence either |R| is odd or $R=F_1\times F_2\times \cdots \times F_k$, where each $F_i$ is a field of characteristic 2. $\square$

4 Study of genus of the graph $G'(R)$

In this section, we mainly study the genus of the graph $G'(R)$ of the graph G(R). We discuss some known results from Harary (1972) which is used here.

Lemma 4.1

$\gamma (K_n)=\{\frac{1}{12}(n-3)(n-4)\}$, where $\{x\}$ is the least integer that is greater than or equal to x. In particular, $\gamma (K_n)=1$ if $n=5,6,7$.

Lemma 4.2

$\gamma (K_{m,n})=\{\frac{1}{4}(m-2)(n-2)\}$, where $\{x\}$ is the least integer that is greater than or equal to x.

The following remark is an easy observation.

Remark 4.3

$\gamma (H)\le \gamma (G)$ for all subgraphs H of G.

Lemma 4.4

Let R be a finite local ring and M be its unique maximal ideal. Then $|U(R)|\ge |M|$, where U(R) is the set of units of R and hence $|r(R)|\ge \frac{|R|}{2}+1$ if |R| is even and $|r(R)|\ge \frac{|R|-1}{2}+3$ if $|R|(>3)$ is odd.

Proof

Case 1 : Let $|R|=2n$ for some positive integer n. Let M be the unique maximal ideal of R. If $a\in M=J(R)$, then $1-a\in U(R)=R- M$. This implies $|M|\le |U(R)|$. Now $|R|=|M|+|U(R)|\le |U(R)|+|U(R)|=2|U(R)|$ implies $|U(R)|\ge \frac{|R|}{2}$. Since R is local ring, so $|r(R)|=|U(R)|+1$. Hence $|r(R)|=|U(R)|+1\ge \frac{|R|}{2}+1$.

Case 2 : Let $|R|=2n+1$ for some positive integer n. Clearly, n is not a factor of $2n+1$ but |M| is a factor of $2n+1$. Thus $|M|\ne n$ and $|M|\ngeq n+1$. So $|M|\le n-1$. Thus $|U(R)|\ge 2n+1-n+1=n+2=\frac{|R|-1}{2}+2$. Hence $|r(R)|\ge \frac{|R|-1}{2}+3$. $\square$

Lemma 4.5

$\gamma (G'(R_1\times {\mathbb {Z}}_2))\le 1$ for $R_1={\mathbb {Z}}_2,{\mathbb {Z}}_3,{\mathbb {Z}}_4, \frac{{\mathbb {Z}}_2[x]}{<x^2>}$, ${\mathbb {F}}_4$ and ${\mathbb {Z}}_5$.

Fig. 3

$G'({\mathbb {Z}}_4\times {\mathbb {Z}}_2)$

Proof

The vertex set of the graph $G'({\mathbb {Z}}_5\times {\mathbb {Z}}_2)$ is $V({\mathbb {Z}}_5\times {\mathbb {Z}}_2)={\mathbb {Z}}_5\times {\mathbb {Z}}_2- U({\mathbb {Z}}_5\times {\mathbb {Z}}_2)$. Then $|V(G'({\mathbb {Z}}_5\times {\mathbb {Z}}_2))|=6$ and all the vertices are regular elements in ${\mathbb {Z}}_5\times {\mathbb {Z}}_2$. So the graph $G'({\mathbb {Z}}_5\times {\mathbb {Z}}_2)\cong K_6$. Thus $\gamma (G'({\mathbb {Z}}_5\times {\mathbb {Z}}_2))=\gamma (K_6)=1$, by Lemma 4.1.

Similarly, we have $\gamma (G'({\mathbb {F}}_4\times {\mathbb {Z}}_2))=\gamma (K_5)=1$ as $G'({\mathbb {F}}_4\times {\mathbb {Z}}_2)\cong K_5$.

The vertex set of the graph $G'({\mathbb {Z}}_4\times {\mathbb {Z}}_2)$ is ${\mathbb {Z}}_4\times {\mathbb {Z}}_2- U({\mathbb {Z}}_4\times {\mathbb {Z}}_2)=\{({\bar{1}},{\bar{0}}),({\bar{2}},{\bar{0}}),({\bar{3}},{\bar{0}}),({\bar{0}},{\bar{0}}),({\bar{0}},{\bar{1}}),({\bar{2}},{\bar{1}})\}$.

The graph $G'({\mathbb {Z}}_4\times {\mathbb {Z}}_2)$ is shown in the Fig. 3.

From Fig. 3, it is clear that the graph $G'({\mathbb {Z}}_4\times {\mathbb {Z}}_2)$ can be drawn in the plane without crossing its edges. Thus $G'({\mathbb {Z}}_4\times {\mathbb {Z}}_2)$ is planar, i.e., $\gamma (G'({\mathbb {Z}}_4\times {\mathbb {Z}}_2))=0$.

Since $G'(\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times {\mathbb {Z}}_2)\cong G'({\mathbb {Z}}_4\times {\mathbb {Z}}_2)$, so we have $\gamma (G'(\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times {\mathbb {Z}}_2))=0$.

Again for $R_1={\mathbb {Z}}_3$, $\gamma (G'({\mathbb {Z}}_3\times {\mathbb {Z}}_2))=0$ as $G'({\mathbb {Z}}_3\times {\mathbb {Z}}_2)\cong K_4$ and for $R_1={\mathbb {Z}}_2$, $\gamma (G'({\mathbb {Z}}_2\times {\mathbb {Z}}_2))=0$ as $G'({\mathbb {Z}}_2\times {\mathbb {Z}}_2)\cong K_3$. $\square$

Lemma 4.6

Let R be a finite commutative local ring of order 8. Then $\gamma (G'(R\times {\mathbb {Z}}_2))\ge 3$.

Proof

Let $R={\mathbb {F}}_8$. Then the vertex set of $G'({\mathbb {F}}_8\times {\mathbb {Z}}_2)$ is ${\mathbb {F}}_8\times {\mathbb {Z}}_2- U({\mathbb {F}}_8\times {\mathbb {Z}}_2)$. Then $G'({\mathbb {F}}_8\times {\mathbb {Z}}_2)\cong K_{9}$. So by Lemma 4.1, $\gamma (G'({\mathbb {F}}_8\times {\mathbb {Z}}_2))= \gamma (K_{9})=3$.

Let $R(\ne {\mathbb {F}}_8)$ be a local ring of order 8 and M be the unique maximal ideal of R. Then $|M|=4$, by Lemma 4.1 in Wang (2008). Suppose $M=\{m_1,m_2,m_3,0\}$ and $U(R)=\{u_1,u_2,u_3,1\}$. The vertex set of $G'(R\times {\mathbb {Z}}_2)$ is $R\times {\mathbb {Z}}_2-$ $U(R\times {\mathbb {Z}}_2)=\{(u_1,{\bar{0}}),(u_2,{\bar{0}}),(u_3,{\bar{0}}),(1,{\bar{0}}), (0,{\bar{0}}),(0,{\bar{1}}), (m_1,{\bar{0}}),(m_2,{\bar{0}}),(m_3,{\bar{0}}),(m_1,{\bar{1}}), (m_2,{\bar{1}}),(m_3,{\bar{1}})\}$. We divide the vertex set into two subsets $\{(u_1,{\bar{0}}),(u_2,{\bar{0}}),(u_3,{\bar{0}}),(1,{\bar{0}})\}$ and$\{(m_1,{\bar{0}}),(m_2,{\bar{0}}),(m_3,{\bar{0}}),(0,{\bar{0}}),(m_1,{\bar{1}}),(m_2,{\bar{1}}), (m_3,{\bar{1}}),(0,{\bar{1}})\}$. Then $G'(R\times {\mathbb {Z}}_2)$ contains a subgraph isomorphic to $K_{4,8}$. So by Remark 4.3 and Lemma 4.2, $\gamma (G'(R\times {\mathbb {Z}}_2))\ge \gamma (K_{4,8})=\{\frac{(4-2)(8-2)}{4}\}=\{3\}=3$. $\square$

Lemma 4.7

$\gamma (G'(R_1\times {\mathbb {Z}}_3))=1$ for $R_1={\mathbb {Z}}_5, {\mathbb {F}}_4, \frac{{\mathbb {Z}}_2[x]}{<x^2>}, {\mathbb {Z}}_4$ and ${\mathbb {Z}}_3$.

Proof

The vertex set of $G'({\mathbb {Z}}_5\times {\mathbb {Z}}_3)={\mathbb {Z}}_5\times {\mathbb {Z}}_3- U({\mathbb {Z}}_5\times {\mathbb {Z}}_3)=\{({\bar{1}},{\bar{0}}),({\bar{2}},{\bar{0}}),({\bar{3}},{\bar{0}}),({\bar{4}},{\bar{0}}),({\bar{0}},{\bar{0}}),({\bar{0}},{\bar{1}}),({\bar{0}},{\bar{2}})\}$. Since all the vertices are regular elements of ${\mathbb {Z}}_5\times {\mathbb {Z}}_3$, the subgraph $G'({\mathbb {Z}}_5\times {\mathbb {Z}}_3)\cong K_7$. Thus $\gamma (G'({\mathbb {Z}}_5\times {\mathbb {Z}}_3))=\gamma (K_7)=1$, by Lemma 4.1.

Similarly, we can easily verify $\gamma (G'({\mathbb {F}}_4\times {\mathbb {Z}}_3))=\gamma (K_6)=1$ as $G'({\mathbb {F}}_4\times {\mathbb {Z}}_3)\cong K_6$.

The vertex set of $G'({\mathbb {Z}}_4\times {\mathbb {Z}}_3)={\mathbb {Z}}_4\times {\mathbb {Z}}_3- U({\mathbb {Z}}_4\times {\mathbb {Z}}_3)=\{({\bar{1}},{\bar{0}}),({\bar{2}},{\bar{0}}),({\bar{3}},{\bar{0}}),({\bar{0}},{\bar{0}}),({\bar{0}},{\bar{1}}),({\bar{0}},{\bar{2}}),({\bar{2}},{\bar{1}}),({\bar{2}},{\bar{2}})\}$. Clearly, the graph $G'({\mathbb {Z}}_4\times {\mathbb {Z}}_3)$ contains a subgraph generated by $\{({\bar{1}},{\bar{0}}),({\bar{0}},{\bar{1}}),({\bar{3}},{\bar{0}}),({\bar{0}},{\bar{2}}),({\bar{0}},{\bar{0}})\}$ which is isomorphic to $K_5$. So by Remark 4.3 and Lemma 4.1, $\gamma (G'({\mathbb {Z}}_4\times {\mathbb {Z}}_3))\ge \gamma (K_5)=1$ (I).

Now the graph $G'({\mathbb {Z}}_4\times {\mathbb {Z}}_3)$ is shown in the Fig. 4.

Fig. 4

$G({\mathbb {Z}}_4\times {\mathbb {Z}}_3)$

In Fig. 4, we note that the graph $G'({\mathbb {Z}}_4\times {\mathbb {Z}}_3)$ can be drawn on the surface of genus one without crossing its edges. So $\gamma (G'({\mathbb {Z}}_4\times {\mathbb {Z}}_3))\le 1$ (II).

Therefore, by (I) and (II), $\gamma (G'({\mathbb {Z}}_4\times {\mathbb {Z}}_3))=1$.

Similarly, $\gamma (G'(\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times {\mathbb {Z}}_3))=1$ as $G'(\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times {\mathbb {Z}}_3)\cong G'({\mathbb {Z}}_4\times {\mathbb {Z}}_3)$.

Again for $R_1={\mathbb {Z}}_3$, $\gamma (G'({\mathbb {Z}}_3\times {\mathbb {Z}}_3))=1$ as $G'({\mathbb {Z}}_3\times {\mathbb {Z}}_3)\cong K_5$. $\square$

Lemma 4.8

Let R be a finite commutative local ring of order 8. Then $\gamma (G'(R\times {\mathbb {Z}}_3))\ge 4$.

Proof

Let $R={\mathbb {F}}_8$. Then the vertex set of $G'({\mathbb {F}}_8\times {\mathbb {Z}}_3)$ is $V_{G'}={\mathbb {F}}_8\times {\mathbb {Z}}_3- U({\mathbb {F}}_8\times {\mathbb {Z}}_3)$. Here $|V_{G'}|=10$ and $G'({\mathbb {F}}_8\times {\mathbb {Z}}_3)\cong K_{10}$. So by Remark 4.3 and Lemma 4.1, $\gamma (G'({\mathbb {F}}_8\times {\mathbb {Z}}_3))\ge \gamma (K_{10})=4$.

Let $R(\ne {\mathbb {F}}_8)$ be a local ring of order 8 and M be its unique maximal ideal. Then we have $|M|=4$. Let $M=\{m_1,m_2,m_3,0\}$ and $\{u_1,u_2,u_3,1\}$ be the set of units. The vertex set of $G'(R\times {\mathbb {Z}}_3)$ is $R\times {\mathbb {Z}}_3- U(R\times {\mathbb {Z}}_3)=\{(u_1,{\bar{0}}),(u_2,{\bar{0}}),(u_3,{\bar{0}}),(1,{\bar{0}}), (0,{\bar{0}}),(0,{\bar{1}}),(0,{\bar{2}}), (m_1,{\bar{0}}),(m_2,{\bar{0}}),(m_3,{\bar{0}}),(m_1,{\bar{1}}), (m_2,{\bar{1}}),(m_3,{\bar{1}}),(m_1,{\bar{3}}), (m_2,{\bar{2}}), (m_3,{\bar{2}})\}$. Now we consider two vertex subsets $\{(u_1,{\bar{0}}),(u_2,{\bar{0}}),(u_3,{\bar{0}}),(1,{\bar{0}})\}$ and $\{(m_1,{\bar{0}}),(m_2,{\bar{0}}), (m_3,{\bar{0}}), (m_1,{\bar{1}}),(m_2,{\bar{1}}),(m_3,{\bar{1}}),(m_1,{\bar{3}}),(m_2,{\bar{2}}),(m_3,{\bar{2}})\}$ of the vertex set. Then the graph $G'(R\times {\mathbb {Z}}_3)$ contains a subgraph isomorphic to $K_{4,9}$. So by Remark 4.3 and Lemma 4.2, $\gamma (G'(R\times {\mathbb {Z}}_3))\ge \gamma (K_{4,9})=4$. $\square$

Lemma 4.9

Let $R_1,R_2$ be two commutative local rings with $|R_1|=8$ and $|R_2|=4$. Then $\gamma (G'(R_1\times R_2)\ge 2$.

Proof

Let $R_1={\mathbb {F}}_8$. Then the vertex set of $G'({\mathbb {F}}_8\times R_2)$ is $V_{G'}={\mathbb {F}}_8\times R_2- U({\mathbb {F}}_8\times R_2)$. Let $S=r({\mathbb {F}}_8\times R_2)- U({\mathbb {F}}_8\times R_2)$ be set of non-unit regular elements. Then $|S|=(|U(R_1)|+1)(|U(R_2)|+1)-|U(R_1)||U(R_2)|=|U(R_1)|+|U(R_2)|+1\ge 8$. Since S forms a clique, $G'({\mathbb {F}}_8\times R_2)$ contains a subgraph isomorphic to $K_8$. So by Remark 4.3 and Lemma 4.1, $\gamma (G'({\mathbb {F}}_8\times R_2))\ge \gamma (K_{8})=2$.

Suppose $R_1\ne {\mathbb {F}}_8$. Let $M_1,M_2$ be unique maximal ideals of $R_1,R_2$, respectively. Then we have $|M_1|=4$. Let $M_1=\{m_1,m_2,m_3,0\}$ and $\{u_1,u_2,u_3,1\}$ be the set of units. Since $|R_2|=4$, $|U(R_2)|\ge 2$, by Lemma 4.4. Let u be a non-identity unit. The vertex set of $G'(R_1\times R_2)$ is $R_1\times R_2- U(R_1\times R_2)$. Now we consider two subsets $\{(m_1,0),(m_2,0),(m_3,0),(m_1,1),(m_2,1),(m_3,1),(m_1,u),(m_2,u),(m_3,u)\}$ and $\{(u_1,0),(u_2,0),(u_3,0),(1,0)\}$ of the vertex set. Then $G'(R_1\times R_2)$ contains a subgraph isomorphic to $K_{4,9}$. So by Remark 4.3 and Lemma 4.2, $\gamma (G'(R_1\times R_2))\ge \gamma (K_{4,9})=4$. $\square$

Lemma 4.10

$\gamma (G'(R))=1$ for $R={\mathbb {Z}}_5\times {\mathbb {Z}}_4$ and ${\mathbb {Z}}_5\times \frac{{\mathbb {Z}}_2[x]}{<x^2>}$.

Fig. 5

$G({\mathbb {Z}}_5\times {\mathbb {Z}}_4)$

Proof

In ${\mathbb {Z}}_5\times {\mathbb {Z}}_4- U({\mathbb {Z}}_5\times {\mathbb {Z}}_4)$, $S=\{({\overline{0}},{\overline{0}}),({\overline{0}},{\overline{1}}),({\overline{0}},{\overline{3}}), ({\overline{1}},{\overline{0}}),({\overline{2}},{\overline{0}}),({\overline{3}},{\overline{0}}),({\overline{4}},{\overline{0}})\}$ is the set of non-unit regular elements. So the subgraph generated by S is isomorphic to $K_7$. Since $G'({\mathbb {Z}}_5\times {\mathbb {Z}}_4)$ contains a subgraph isomorphic to $K_7$, so by Remark 4.3 and Lemma 4.1, $\gamma (G'({\mathbb {Z}}_5\times {\mathbb {Z}}_4))\ge 1$ (I).

Now the graph $G'({\mathbb {Z}}_5\times {\mathbb {Z}}_4)$ is shown in the Fig. 5.

In Fig. 5, we note that the graph $G'({\mathbb {Z}}_5\times {\mathbb {Z}}_4)$ can be drawn on the surface of genus one without crossing its edges. So $\gamma (G'({\mathbb {Z}}_5\times {\mathbb {Z}}_4))\le 1$ (II).

Therefore, by (I) and (II), $\gamma (G'({\mathbb {Z}}_5\times {\mathbb {Z}}_4))=1$.

Since $G'({\mathbb {Z}}_5\times {\mathbb {Z}}_4)\cong G'({\mathbb {Z}}_5\times \frac{{\mathbb {Z}}_2[x]}{<x^2>})$, so $\gamma (G'({\mathbb {Z}}_5\times \frac{{\mathbb {Z}}_2[x]}{<x^2>}))=1$. $\square$

Lemma 4.11

$\gamma (G'(R))=1$ for $R={\mathbb {F}}_4\times {\mathbb {F}}_4,{\mathbb {Z}}_4\times {\mathbb {F}}_4,\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times {\mathbb {F}}_4,{\mathbb {Z}}_4\times {\mathbb {Z}}_4,\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times {\mathbb {Z}}_4$ and $\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times \frac{{\mathbb {Z}}_2[x]}{<x^2>}$.

Proof

In $G'({\mathbb {F}}_4\times {\mathbb {F}}_4)$, $V({\mathbb {F}}_4\times {\mathbb {F}}_4)={\mathbb {F}}_4\times {\mathbb {F}}_4- U({\mathbb {F}}_4\times {\mathbb {F}}_4)$. Then $|V({\mathbb {F}}_4\times {\mathbb {F}}_4)|=7$ and each vertex is regular in ${\mathbb {F}}_4\times {\mathbb {F}}_4$. Thus $G'({\mathbb {F}}_4\times {\mathbb {F}}_4)=K_7$. So by Lemma 4.1, $\gamma (G'({\mathbb {F}}_4\times {\mathbb {F}}_4))=\gamma (K_7)=1$.

The vertex set of the graph $G'({\mathbb {Z}}_4\times {\mathbb {Z}}_4)$ is ${\mathbb {Z}}_4\times {\mathbb {Z}}_4- U({\mathbb {Z}}_4\times {\mathbb {Z}}_4)=\{({\bar{1}},{\bar{0}}),({\bar{0}},{\bar{1}}),({\bar{3}},{\bar{0}}),({\bar{0}},{\bar{3}}),({\bar{0}},{\bar{0}}),({\bar{1}},{\bar{2}}), ({\bar{2}},{\bar{1}}), ({\bar{2}},{\bar{3}}),({\bar{3}},{\bar{2}}),({\bar{2}},{\bar{0}}),({\bar{0}},{\bar{2}}),({\bar{2}},{\bar{2}})\}$. Clearly, the graph $G'({\mathbb {Z}}_4\times {\mathbb {Z}}_4)$ contains a subgraph generated by $\{({\bar{1}},{\bar{0}}),({\bar{0}},{\bar{1}}), ({\bar{3}},{\bar{0}}),({\bar{0}},{\bar{3}}),({\bar{0}},{\bar{0}})\}$ which is isomorphic to $K_5$. So $\gamma (G'({\mathbb {Z}}_4\times {\mathbb {Z}}_4))\ge \gamma (K_5)=1$ (I).

The vertex set of the graph $G'({\mathbb {Z}}_4\times {\mathbb {F}}_4)$ is ${\mathbb {Z}}_4\times {\mathbb {F}}_4- U({\mathbb {Z}}_4\times {\mathbb {F}}_4)=\{({\bar{1}},0),({\bar{3}},0),({\bar{2}},0),({\bar{0}},0),({\bar{0}},u_1),({\bar{0}},u_2), ({\bar{0}},u_3),({\bar{2}},u_1),({\bar{2}},u_2),({\bar{2}},u_3)\}$, where ${\mathbb {F}}_4=\{u_1,u_2,u_3,0\}$. The graph $G'({\mathbb {Z}}_4\times {\mathbb {F}}_4)$ contains a subgraph generated by $\{({\bar{1}},0),({\bar{3}},0),({\bar{0}},0),({\bar{0}},u_1),({\bar{0}},u_2),({\bar{0}},u_3)\}$ which is isomorphic to $K_6$.

So by Remark 4.3 and Lemma 4.1, $\gamma (G'({\mathbb {Z}}_4\times {\mathbb {F}}_4))\ge \gamma (K_6)=1$ (II).

Now the graph $G'({\mathbb {Z}}_4\times {\mathbb {Z}}_4)$ and $G'({\mathbb {Z}}_4\times {\mathbb {F}}_4)$ are shown in the Fig. 6 and Fig. 7 respectively.

Fig. 6

$G({\mathbb {Z}}_4\times {\mathbb {Z}}_4)$

Fig. 7

$G({\mathbb {Z}}_4\times {\mathbb {F}}_4)$

In Fig. 6, we note that the graph $G'({\mathbb {Z}}_4\times {\mathbb {Z}}_4)$ can be drawn on the surface of genus one without crossing its edges. So $\gamma (G'({\mathbb {Z}}_4\times {\mathbb {Z}}_4))\le 1$ (III).

Therefore, by (I) and (III), $\gamma (G'({\mathbb {Z}}_4\times {\mathbb {Z}}_4))=1$.

Since $G'({\mathbb {Z}}_4\times {\mathbb {Z}}_4)\cong G'(\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times {\mathbb {Z}}_4)\cong G'(\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times \frac{{\mathbb {Z}}_2[x]}{<x^2>})$, $\gamma (G'(\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times {\mathbb {Z}}_4))=\gamma (G'(\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times \frac{{\mathbb {Z}}_2[x]}{<x^2>}))=1$.

In Fig. 7, we note that the graph $G'({\mathbb {Z}}_4\times {\mathbb {F}}_4)$ can be drawn on the surface of genus one without crossing its edges. So $\gamma (G'({\mathbb {Z}}_4\times {\mathbb {F}}_4))\le 1$ (IV).

Therefore, by (II) and (IV), $\gamma (G'({\mathbb {Z}}_4\times {\mathbb {F}}_4))=1$.

Since $G'({\mathbb {Z}}_4\times {\mathbb {F}}_4)\cong G'(\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times {\mathbb {F}}_4)$, $\gamma (G'(\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times {\mathbb {F}}_4))=1$. $\square$

Lemma 4.12

Let $R=R_1\times R_2\times \cdots \times R_k$ for some local rings $R_i$ with 1 such that $|R_1|\ge |R_2|\ge \cdots \ge |R_k|$, $i=1,2,3,\ldots ,k$ and $k\ge 3$. Then $\gamma (G'(R))\ge 2$ except for $R={\mathbb {Z}}_2\times {\mathbb {Z}}_2\times {\mathbb {Z}}_2$.

Proof

Case 1 : Assume $k=3$ and $|R_1|=|R_2|=|R_3|=2$. Then $R_i\cong {\mathbb {Z}}_2$, $i=1,2,3$. In this case $G'(R)\cong G'({\mathbb {Z}}_2\times {\mathbb {Z}}_2\times {\mathbb {Z}}_2)\cong K_7$. So $\gamma (G'(R))=\gamma (K_7)=1$.

Case 2 : Suppose $k=3$ and $|R_1|\ge 3$. Then $|r(R_1)|\ge 3$. Now we consider three sets $S_1=\{0,1,u_1\}\subseteq r(R_1)$, $S_2=\{0,1\}\subseteq r(R_2)$ and $S_3=\{0,1\}\subseteq r(R_3)$. Clearly, $S_1\times S_2\times S_3- \{(1,1,1),(u_1,1,1)\}\subseteq R- U(R)$. Now the elements of $S_1\times S_2\times S_3- \{(1,1,1),(u_1,1,1)\}$ forms a complete subgraph of the graph $G'(R)$ which is isomorphic to $K_{10}$. Then by Remark 4.3 and Lemma 4.1, $\gamma (G'(R))\ge \gamma (K_{10})=4$.

Case 3 : Let $k\ge 4$. Then we have a subset $S=\{0,1\}\times \{0,1\}\times \{0,1\}\times \{0,1\}\times \cdots \times \{0,1\}- \{(1,1,\ldots ,1)\}\subseteq R- U(R)$. Here $|S|\ge 2^k-1\ge 15$ as $k\ge 4$. Thus the subgraph induced by S is isomorphic to $K_{2^k-1}$ and hence $G'(R)$ has a subgraph isomorphic to $K_{15}$. Then by Remark 4.3 and Lemma 4.1, $\gamma (G'(R))\ge \gamma (K_{15})=11$.

Therefore, by Case 1, Case 2 and Case 3, $\gamma (G'(R))\ge 2$ except for $R={\mathbb {Z}}_2\times {\mathbb {Z}}_2\times {\mathbb {Z}}_2$. $\square$

Lemma 4.13

Let $R=R_1\times R_2$ for some commutative local rings $R_1,R_2$ with $|R_1|\ge |R_2|$. Then $\gamma (G'(R))\ge 2$ if one of the following holds:

• (i) $|R_2|\ge 5$.

• (ii) $|R_1|\ge 7$.

Proof

Condition (i) holds, i.e., $|R_2|\ge 5$. Then $|R_1|\ge 5$. So $|r(R_1)|=|U(R_1)|+1,|r(R_2)|=|U(R_2)|+1\ge 5$, by Lemma 4.4. If S is the set of non-unit regular elements, i.e., $S=r(R_1\times R_2)- U(R_1\times R_2)$, then $|S|=|r(R_1\times R_2)- U(R_1\times R_2)|=|r(R_1)| |r(R_2)|- |U(R_1)| |U(R_2)|=(|U(R_1)|+1) (|U(R_2)|+1)- |U(R_1)| |U(R_2)|=|U(R_1)|+|U(R_2)|+1\ge 4+4+1=9$. Thus the subgraph induced by S is isomorphic to $K_9$. Therefore, by Remark 4.3 and Lemma 4.1, $\gamma (G'(R_1\times R_2))\ge \gamma (K_9)\ge 2$.

Condition (ii) holds, i.e., $|R_1|\ge 7$.

Case I : Suppose that $|R_1|=7$. If $|R_1|=7$ and $|R_2|\ge 2$, then $|U(R_1)|=6$ and $|U(R_2)|\ge 1$. Let S be the set of non-unit regular elements of $R_1\times R_2$. Then $|S|=|r(R_1\times R_2)- U(R_1\times R_2)|=(|U(R_1)|+1) (|U(R_2)|+1)- |U(R_1)| |U(R_2)|=|U(R_1)|+|U(R_2)|+1\ge 6+1+1=8$. The subgraph induced by S is isomorphic to $K_{8}$. So by Remark 4.3 and Lemma 4.1, $\gamma (G'(R_1\times R_2))\ge \gamma (K_{8})= 2$.

Case II : Assume $|R_1|=8$. If $|R_1|=8$ and $|R_2|=2$, then by Lemma 4.6, $\gamma (G'(R_1\times R_2))\ge 2$. If $|R_1|=8$ and $|R_2|=3$, then by Lemma 4.8, $\gamma (G'(R_1\times R_2))\ge 2$. If $|R_1|=8$ and $|R_2|=4$, then by Lemma 4.9, $\gamma (G'(R_1\times R_2))\ge 2$. If $|R_1|=8$ and $|R_2|\ge 5$, then by condition (i), $\gamma (G'(R_1\times R_2))\ge 2$.

Case III : Let $|R_1|\ge 9$ and $|R_2|\ge 2$. Then $|r(R_1)|\ge 7$ and $|r(R_2)|\ge 2$ by Lemma 4.4. So the number of non-unit regular elements is $|r(R_1)||r(R_2)|-|U(R_1)||U(R_2)|=(|U(R_1)|+1) (|U(R_2)|+1)- |U(R_1)| |U(R_2)|=|U(R_1)|+|U(R_2)|+1\ge 6+1+1=8$. So the subgraph induced by non-unit regular elements is isomorphic to $K_8$. Thus $\gamma (G'(R_1\times R_2))\ge \gamma (K_8)=2$. $\square$

Theorem 4.14

Let R be a finite commutative non-local ring with 1. Then $G'(R)$ is either toroidal or planar, i.e., $\gamma (G'(R))\le 1$ if and only if R is isomorphic to one of the following rings: ${\mathbb {Z}}_2\times {\mathbb {Z}}_2\times {\mathbb {Z}}_2$, ${\mathbb {Z}}_5\times {\mathbb {Z}}_4$, ${\mathbb {Z}}_5\times \frac{{\mathbb {Z}}_2[x]}{<x^2>}$, $\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times \frac{{\mathbb {Z}}_2[x]}{<x^2>}$, ${\mathbb {Z}}_4\times {\mathbb {Z}}_4$, ${\mathbb {Z}}_4\times {\mathbb {F}}_4$, ${\mathbb {F}}_4\times {\mathbb {F}}_4$, ${\mathbb {Z}}_5\times {\mathbb {Z}}_3$, ${\mathbb {F}}_4\times {\mathbb {Z}}_3$, ${\mathbb {Z}}_4\times {\mathbb {Z}}_3$, $\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times {\mathbb {Z}}_3$, ${\mathbb {Z}}_3\times {\mathbb {Z}}_3$, ${\mathbb {Z}}_5\times {\mathbb {Z}}_2$, ${\mathbb {Z}}_4\times {\mathbb {Z}}_2$, ${\mathbb {F}}_4\times {\mathbb {Z}}_2$, $\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times {\mathbb {Z}}_2$, ${\mathbb {Z}}_3\times {\mathbb {Z}}_2$ and ${\mathbb {Z}}_2\times {\mathbb {Z}}_2$.

Proof

Assume that $\gamma (G'(R))\le 1$. Since R is a finite commutative ring with 1, $R=R_1\times R_2\times \cdots \times R_k$ for some local rings $R_1,R_2,\ldots ,R_k$. We may assume that $|R_1|\ge |R_2|\ge \cdots \ge |R_k|$. By Lemma 4.12, we may assume that $k\le 3$. However, if $k=3$, then $R={\mathbb {Z}}_2\times {\mathbb {Z}}_2\times {\mathbb {Z}}_2$, by Lemma 4.12. In this case, $\gamma (G'(R))=\gamma (K_7)=1$, as $G'({\mathbb {Z}}_2\times {\mathbb {Z}}_2\times {\mathbb {Z}}_2)\cong K_7$.

Assume that $k=2$. Then by Lemma 4.13, $|R_2|\le 4$ and $|R_1|< 7$.

Case 1 : Let $|R_2|=2$. In this case, $R_2\cong {\mathbb {Z}}_2$. Now we have $R_1$ is isomorphic to one of the following rings: ${\mathbb {Z}}_5,{\mathbb {F}}_4,{\mathbb {Z}}_4,\frac{{\mathbb {Z}}_2[x]}{<x^2>},{\mathbb {Z}}_3$, ${\mathbb {Z}}_2$. Then by Lemma 4.5, $\gamma (G'(R_1\times {\mathbb {Z}}_2))\le 1$ for $R_1={\mathbb {Z}}_5,{\mathbb {F}}_4, \frac{{\mathbb {Z}}_2[x]}{<x^2>}, {\mathbb {Z}}_4,{\mathbb {Z}}_3$ and ${\mathbb {Z}}_2$.

Case 2 : Suppose $|R_2|=3$. In this case, $R_2\cong {\mathbb {Z}}_3$. Since $3\le |R_1|<7$, so $R_1$ is isomorphic to one of the following rings: ${\mathbb {Z}}_5,{\mathbb {F}}_4,{\mathbb {Z}}_4,\frac{{\mathbb {Z}}_2[x]}{<x^2>}$ and ${\mathbb {Z}}_3$. Then by Lemma 4.7, $\gamma (G'(R_1\times {\mathbb {Z}}_3))\le 1$ for $R_1={\mathbb {Z}}_5,{\mathbb {F}}_4, \frac{{\mathbb {Z}}_2[x]}{<x^2>}, {\mathbb {Z}}_4$ and ${\mathbb {Z}}_3$.

Case 3 : Suppose $|R_2|=4$. Then $R_2\cong {\mathbb {F}}_4,{\mathbb {Z}}_4,\frac{{\mathbb {Z}}_2[x]}{<x^2>}$.

Subcase 3a : Suppose $R_2\cong {\mathbb {F}}_4$. Since $4\le |R_1|<7$, so $R_1\cong {\mathbb {Z}}_5,{\mathbb {F}}_4,{\mathbb {Z}}_4,\frac{{\mathbb {Z}}_2[x]}{<x^2>}$. The graph $G'({\mathbb {Z}}_5\times {\mathbb {F}}_4)\cong K_8$ as ${\mathbb {Z}}_5\times {\mathbb {F}}_4$ is regular ring. Thus $\gamma (G'({\mathbb {Z}}_5\times {\mathbb {F}}_4))=2$. Also for $R_1=\frac{{\mathbb {Z}}_2[x]}{<x^2>},{\mathbb {Z}}_4, {\mathbb {F}}_4$, $\gamma (G'(R_1\times {\mathbb {F}}_4))=1$, by Lemma 4.11.

Subcase 3b : Let $R_2\cong {\mathbb {Z}}_4,\frac{{\mathbb {Z}}_2[x]}{<x^2>}$. Then $|R_1|\ge 4$ and by Lemma 4.13, $|R_1|<7$. So $R_1$ is isomorphic to one of the following rings : ${\mathbb {Z}}_5,{\mathbb {F}}_4,{\mathbb {Z}}_4,\frac{{\mathbb {Z}}_2[x]}{<x^2>}$. Thus by Lemma 4.10, $\gamma (G'(R))=1$, where $R\cong {\mathbb {Z}}_5\times {\mathbb {Z}}_4, {\mathbb {Z}}_5\times \frac{{\mathbb {Z}}_2[x]}{<x^2>}$. Now by Lemma 4.11, $\gamma (G'(R))=1$, where $R\cong {\mathbb {F}}_4\times {\mathbb {Z}}_4, {\mathbb {Z}}_4\times {\mathbb {Z}}_4,\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times {\mathbb {F}}_4,\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times {\mathbb {Z}}_4$ and $\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times \frac{{\mathbb {Z}}_2[x]}{<x^2>}$.

Conversely, assume that R is isomorphic to one of the following rings : ${\mathbb {Z}}_2\times {\mathbb {Z}}_2\times {\mathbb {Z}}_2$, ${\mathbb {Z}}_5\times {\mathbb {Z}}_4$, ${\mathbb {Z}}_5\times \frac{{\mathbb {Z}}_2[x]}{<x^2>}$, $\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times \frac{{\mathbb {Z}}_2[x]}{<x^2>}$, ${\mathbb {Z}}_4\times {\mathbb {Z}}_4$, ${\mathbb {Z}}_4\times {\mathbb {F}}_4$, ${\mathbb {F}}_4\times {\mathbb {F}}_4$, ${\mathbb {Z}}_5\times {\mathbb {Z}}_3$, ${\mathbb {F}}_4\times {\mathbb {Z}}_3$, ${\mathbb {Z}}_4\times {\mathbb {Z}}_3$, $\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times {\mathbb {Z}}_3$, ${\mathbb {Z}}_3\times {\mathbb {Z}}_3$, ${\mathbb {Z}}_5\times {\mathbb {Z}}_2$, ${\mathbb {Z}}_4\times {\mathbb {Z}}_2$, ${\mathbb {F}}_4\times {\mathbb {Z}}_2$, $\frac{{\mathbb {Z}}_2[x]}{<x^2>}\times {\mathbb {Z}}_2$, ${\mathbb {Z}}_3\times {\mathbb {Z}}_2$ and ${\mathbb {Z}}_2\times {\mathbb {Z}}_2$. Then by Lemmas 4.5, 4.7, 4.10, 4.11 and 4.12, $\gamma (G'(R))\le 1$. $\square$

From Lemmas 4.5,  4.7 and Theorem 4.14, we have the following necessary and sufficient condition for the planarity of $G'(R)$.

Theorem 4.15

Let R be a finite commutative non-local ring with 1. Then $G'(R)$ is planar, i.e., $\gamma (G'(R))=0$ if and only if R is isomorphic to one of the rings : ${\mathbb {Z}}_4\times {\mathbb {Z}}_2, \frac{{\mathbb {Z}}_2[x]}{<x^2>}\times {\mathbb {Z}}_2, {\mathbb {Z}}_3\times {\mathbb {Z}}_2$ and ${\mathbb {Z}}_2\times {\mathbb {Z}}_2$.

From Lemmas 4.12,  4.13 and Theorem 4.14, we have the following theorem.

Theorem 4.16

Let $R=R_1\times R_2\times \cdots \times R_k$, where $R_i$ is a finite local ring for every i and $|R_1|\ge |R_2|\ge \cdots \ge |R_k|$. Then $\gamma (G'(R))\ge 2$ if and only if one of these five conditions holds: (i)  $k\ge 4$; (ii) $k=3$ and $|R_1|\ge 3$; (iii) $k=2$, $|R_2|\ge 5$; (iv)  $k=2$, $|R_1|\ge 7$ and (v) $k=2$, $R_1\cong {\mathbb {Z}}_5$ and $R_2\cong {\mathbb {F}}_4$.

5 Line graph of $G'(R)$

In this section, we characterize those rings for which $G'(R)$ is a line graph of some graph G. Here we also study some properties of the line graph $L(G'(R))$ of the graph $G'(R)$.

Definition 5.1

The line graph L(G) of a graph G is defined as follows : The vertices of L(G) are taken as the edges of G and two vertices are adjacent whenever the corresponding edges of G are adjacent (i.e., they share a vertex in common).

Theorem 5.2

Let R be a finite commutative ring with 1. Then $G'(R)$ is a line graph of some graph G if and only if R is either a regular ring or a local ring.

Proof

Suppose that R is either a regular ring or a local ring. First assume that R is a finite local ring. Then $G'(R)$ is a totally disconnected graph of order m, where $m=|R\setminus U(R)|$. So $G'(R)\cong L(mK_2)$. Again if R is a non-local regular ring, then $G'(R)\cong K_n$, where $n=|R\setminus U(R)|$ and hence $G'(R)\cong L(K_{1,n})$.

Conversely, assume that $G'(R)$ is a line graph of some graph G. If possible, let R be neither a regular ring nor a local ring. This implies that there exist local rings $R_1,R_2,\ldots ,R_k$ with unique maximal ideals $M_1,M_2,\ldots ,M_k$ of $R_1,R_2,\ldots , R_k$, respectively, and $k\ge 2$ such that $R=R_1\times R_2\times \cdots \times R_k$ and at least one of $R_i$ is not regular. Without loss of generality, let $R_1$ be not regular. Then $M_1\ne \{0\}$. Let $a\in M_1\setminus \{0\}$ be a non-regular element of $R_1$. Now consider the subset $A=\{(a,0,0,\ldots ,0),(a,1,1,\ldots ,1),(1,0,0,\ldots ,0) (0,0,0,\ldots ,0)\}$ of $G'(R_1\times R_2\times \cdots \times R_k)$. Then the subgraph induced by A is isomorphic to $K_{1,3}$ which is forbidden for line graph, by Theorem 1 in Soltes (1994) and hence $G'(R)$ is not a line graph. Thus R is either a regular or a local ring. $\square$

Proposition 5.3

(Sharma and Gaur 2015) Let G be a connected graph. Then L(G) is a connected graph.

Lemma 5.4

(Sharma and Gaur 2015) Let G be a simple connected graph. Then $diam(L(G))\le diam(G)+1$.

Lemma 5.5

Let $R=R_1\times R_2\times \cdots \times R_k$ for some local rings $R_1,R_2,\ldots ,R_k$ with the unique maximal ideals $M_1,M_2,\ldots ,M_k$, respectively. If the subset $I=(M_1\setminus \{0\})\times (M_2\setminus \{0\})\times \cdots \times (M_k\setminus \{0\})\ne \phi$, then the subgraph induced by $(R\setminus U(R))\setminus I$ is a connected subgraph in $G'(R)$.

Proof

Consider the set $A=\{(0,1,1,\ldots ,1),(1,0,1,\ldots ,1), (1,1,0,1,\ldots ,1),\ldots ,(1,1,\ldots ,1,0)\}$ of the elements of $(R\setminus U(R))\setminus I$. It is obvious that the subgraph induced by A forms a clique. Again we consider an arbitrary vertex v from $(R\setminus U(R))\setminus I$. Then $v=(a_1,a_2,\ldots ,a_k)$, where at least one of $a_i\in U(R_i)\cup \{0\}$ and not of all $a_i$ is unit. Assume $a_1\in U(R_1)\cup \{0\}$. Then $(a_1,a_2,\ldots ,a_k)\leftrightarrow (0,1,1,\ldots ,0)\in A$. Since v is arbitrary, any vertex of $(R\setminus U(R))\setminus I$ is adjacent to some element of A which induces a clique. Therefore, the subgraph induced by $(R\setminus U(R))\setminus I$ is a connected subgraph in $G'(R)$. $\square$

Theorem 5.6

Let R be a finite commutative non-local ring with 1 except ${\mathbb {Z}}_2\times {\mathbb {Z}}_2$. Then $L(G'(R))$ is connected with $2\le diam(L(G'(R)))\le 3$.

Proof

Suppose that R is a finite commutative non-local ring. Then $R=R_1\times R_2\times \cdots \times R_k$ for some local rings $R_1,R_2,\ldots ,R_k$ with the unique maximal ideals $M_1,M_2,\ldots , M_k$, respectively, and $k\ge 2$.

Case 1 : Suppose at least one $R_i$ is regular. Then by Theorem 2.3, $G'(R)$ is connected. So by Propositions 5.3 and 5.4, the line graph $L(G'(R))$ is connected with $diam(L(G'(R)))\le 3$. It can be easily verified that $L(G'({\mathbb {Z}}_2\times {\mathbb {Z}}_2))\cong K_3$ as $G'({\mathbb {Z}}_2\times {\mathbb {Z}}_2)\cong K_3$ but for others R, $G'(R)$ is isomorphic to neither $K_{1,n}$ nor $K_3$. So we have $L(G'(R))$ is complete only for $R={\mathbb {Z}}_2\times {\mathbb {Z}}_2$. Hence $diam(L(G'(R)))>1$. So $2\le diam(L(G'(R)))\le 3$.

Case 2 : Suppose no $R_i$ is regular. Thus $M_i\setminus \{0\}\ne \phi$ for each i. In the graph $G'(R)$, the subgraph induced by the subset $I=(M_1\setminus \{0\})\times (M_2\setminus \{0\})\times \cdots \times (M_k\setminus \{0\})$ is isomorphic to $|I|K_1$ and we denote it by $G_I$. It is easily observed that no vertex of I is adjacent to some vertices of $(R\setminus U(R))\setminus I$. The remaining vertices $(R\setminus U(R))\setminus I$ of $G'(R)$ form a connected subgraph, by Lemma 5.5 and denote it by $G_{I^c}$. Now the graph $G'(R)$ is the union of these two subgraphs, i.e., $G'(R)=G_I\cup G_{I^c}$. So $E(G'(R))=E(G_{I^c})$. This implies that $V(L(G'(R)))=E(G'(R))=E(G_{I^c})=V(L(G_{I^c}))$. Since $G_{I^c}$ is connected subgraph, the line graph $L(G_{I^c})$ is connected, by Proposition 5.3. So the line graph $L(G'(R))=L(G_{I^c})$ is connected.

Now we consider two arbitrary vertices $e_1,e_2\in V(L(G'(R)))$. This implies $e_1,e_2\in E(G_{I^c})$. Then there exists 4 vertices $(x_1,x_2,\ldots ,x_k)$, $(x_1^*,x_2^*,\ldots ,x_k^*)$, $(y_1,y_2,\ldots ,y_k)$ and $(y_1^*,y_2^*,\ldots ,y_k^*)$ in $(R\setminus U(R))\setminus I$ such that $e_1=[(x_1,x_2,\ldots ,x_k), (x_1^*,x_2^*,\ldots ,x_k^*)]$ and $e_2=[(y_1,y_2,\ldots ,y_k),(y_1^*,y_2^*,s_3^*,\ldots ,y_k^*)]$. Since $(x_1,x_2,\ldots ,x_k),(y_1,y_2,\ldots ,y_k)\in (R\setminus U(R))\setminus I$, then at least one of $x_i\in U(R_i)\cup \{0\}$ and at least one of $y_i\in U(R_i)\cup \{0\}$. Without loss of generality, suppose $x_1\in U(R_1)\cup \{0\}$ and $y_2\in U(R_2)\cup \{0\}$.

If $y_1\in U(R_1)\cup \{0\}$, then $(x_1,x_2,\ldots ,x_k)\leftrightarrow (0,1,1,\ldots ,1)$ and $(y_1,y_2,y_3,\ldots ,y_k)\leftrightarrow (0,1,1,\ldots ,1)$. Thus we have two vertices $e_3=[(x_1,x_2,\ldots ,x_k),(0,1,1,\ldots ,1)]$ and $e_4=[(0,1,1,\ldots ,1),(y_1,y_2,y_3,\ldots ,y_k)]$ such that $e_1\leftrightarrow e_3\leftrightarrow e_4\leftrightarrow e_2$. So in this case, $diam(L(G'(R)))\le 3$.

Suppose $y_1\in M_1\setminus \{0\}$. Since $(y_1,y_2,\ldots ,y_k)\leftrightarrow (y_1^*,y_2^*,y_3^*,\ldots ,y_k^*)$, so $y_1R_1+y_1^*R_1=\{0\}$ or $R_i$. This implies $y_1^*\in U(R_1)$. Then $(x_1,x_2,\ldots ,x_k)\leftrightarrow (0,1,1,\ldots ,1)$ and $(y_1^*,y_2^*,y_3^*,\ldots ,y_k^*)\leftrightarrow (0,1,1,\ldots ,1)$. Thus we have $e_3^*=[(x_1,x_2,\ldots ,x_k),(0,1,1,\ldots ,1)]$ and $e_4^*=[(0,1,1,\ldots ,1),(y_1^*,y_2^*,y_3^*,\ldots ,y_k^*)]$. Then $e_1\leftrightarrow e_3^*\leftrightarrow e_4^*\leftrightarrow e_2$. Since $e_1$ and $e_2$ are arbitrary, so $diam(L(G'(R)))\le 3$. It can be easily checked that $L(G'(R))$ is never complete. Hence $diam(L(G'(R)))>1$. Therefore, $2\le diam(L(G'(R)))\le 3$. $\square$

Theorem 5.7

Let $R=R_1\times R_2\times \cdots \times R_k$ for some local rings $R_1,R_2,\ldots ,R_k$ with unique maximal ideals $M_1,M_2,\ldots , M_k$, respectively. Suppose $p=|\{i: R_i \text{ is } \text{ non-regular } \text{ local } \text{ ring }\}|$. Then

$$\begin{aligned} diam(L(G'(R))) ~=\left\{ \begin{array}{lcl} \displaystyle 3~~~~~~~\text{ if }~ p\ge 2~ and~k\ge 3 \\ \displaystyle 2~~~~~~~otherwise.\end{array}\right. \end{aligned}$$

Proof

Let $p\ge 2$ and $k\ge 3$. Without loss of generality, we assume that $R_1,R_2$ are non-regular. Let $r_1\in M_1\setminus \{0\}$, $s_1\in M_2\setminus \{0\}$. Now we consider the edges $e_1=[(r_1,1,0,\ldots ,0),(1,s_1,0,\ldots ,0)]$ and $e_2=[(0,0,1,\ldots ,0),(0,0,0,\ldots ,0)]$. Then we can see that the subgraph induced by $\{(r_1,1,0,\ldots ,0),(1,s_1,0,\ldots ,0), (0,0,1,\ldots ,0),(0,0,0,\ldots ,0)\}$ is isomorphic to $2K_2$. So in the line graph $L(G'(R))$, there is no vertex $e_3$ such that $e_1\leftrightarrow e_3\leftrightarrow e_2$. Thus $diam(L(G'(R)))>2$. So $diam(L(G'(R)))=3$, by Theorem 5.6.

Suppose that $p=2$ and $k=2$. Let $e_1$, $e_2$ be two vertices of $L(G'(R))$. Then there exist four vertices $(x_1,x_2), (x_1^*,x_2^*),(y_1,y_2),(y_1^*,y_2^*)$ of $G'(R)$ such that $e_1=[(x_1,x_2), (x_1^*,x_2^*)]$ and $e_2=[(y_1,y_2),(y_1^*,y_2^*)]$. Then $(x_1,x_2)\leftrightarrow (x_1^*,x_2^*)$ and $(y_1,y_2)\leftrightarrow (y_1^*,y_2^*)$. This implies that $x_1R_1+x_1^*R_1=\{0\}$ or $R_1$, $x_2R_2+x_2^*R_2=\{0\}$ or $R_2$, $y_1R_1+y_1^*R_1=\{0\}$ or $R_1$ and $y_2R_2+y_2^*R_2=\{0\}$ or $R_2$. Clearly, $(x_1,x_2)$ is adjacent with either $(y_1,y_2)$ or $(y_1^*,y_2^*)$. Thus we have an edge either $e_3=[(x_1,x_2),(y_1,y_2)]$ or $e_4=[(x_1,x_2),(y_1^*,y_2^*)]$. Then $e_1\leftrightarrow e_3 \leftrightarrow e_2$ or $e_1\leftrightarrow e_4 \leftrightarrow e_2$ in $L(G'(R))$. So $diam(L(G'(R)))=2$ as $e_1$, $e_2$ are arbitrary vertices of $L(G'(R))$.

Assume that $p\le 1$.

Case 1 : Let $p=1$. Without loss of generality, suppose that $R_1$ is non-regular and $R_2,R_3,\ldots ,R_k$ are regular. Let $e_1,e_2$ be two vertices of $L(G'(R))$. Then there exist four vertices $(x_1,r_2,r_3,r_4,\ldots ,r_k)$, $(x_1^*,r_2^*,r_3^*,r_4^*,\ldots ,r_k^*)$, $(y_1,s_2,s_3,s_4,\ldots ,s_k)$ and $(y_1^*,s_2^*,s_3^*,s_4^*,\ldots ,s_k^*)$ of $G'(R)$ such that $e_1=[(x_1,r_2,r_3,r_4,\ldots ,r_k), (x_1^*,r_2^*,r_3^*,r_4^*,\ldots ,r_k^*)]$ and $e_2=[(y_1,s_2,s_3,s_4,\ldots ,s_k),(y_1^*,s_2^*,s_3^*,s_4^*,\ldots ,s_k^*)]$. Then $(x_1,r_2,r_3,r_4,\ldots ,r_k)\leftrightarrow (x_1^*,r_2^*,r_3^*,r_4^*,\ldots ,r_k^*)$ and $(y_1,s_2,s_3,s_4,\ldots ,s_k)\leftrightarrow (y_1^*,s_2^*,s_3^*,s_4^*,\ldots ,s_k^*)$. This implies that $x_1R_1+x_1^*R_1=\{0\}$ or $R_1$ and $y_1R_1+y_1^*R_1=\{0\}$ or $R_1$. This implies either $x_1=x_1^*=0$ or at least one of $x_1,x_1^*$ is unit and either $y_1=y_1^*=0$ or at least one of $y_1,y_1^*$ is unit. Clearly, $(x_1,r_2,r_3,r_4,\ldots ,r_k)$ is adjacent with either $(y_1,s_2,s_3,s_4,\ldots ,s_k)$ or $(y_1^*,s_2^*,s_3^*,s_4^*,\ldots ,s_k^*)$. Thus we have an edge either $e_3=[(x_1,r_2,r_3,r_4,\ldots ,r_k),(y_1,s_2,s_3,s_4,\ldots ,s_k)]$ or $e_4=[(x_1,r_2,r_3,r_4,\ldots ,r_k),(y_1^*,s_2^*,s_3^*,s_4^*,\ldots ,s_k^*)]$. Then $e_1\leftrightarrow e_3 \leftrightarrow e_2$ or $e_1\leftrightarrow e_4 \leftrightarrow e_2$ in $L(G'(R))$. Hence $diam(L(G'(R)))=2$.

Case 2 : Let $p=0$. Then each $R_i$ is regular and hence R is regular. Then $G'(R)$ is complete. So $diam(G'(R))=1$. Thus $diam(L(G'(R)))\le diam(G'(R))+1=2$. Since $diam(L(G'(R)))\ge 2$, it follows that $diam(L(G'(R)))=2$.

$\square$

Corollary 5.8

Let $n=p_1^{r_1}p_2^{r_2}\cdots p_k^{r_k}$, where $p_1,p_2,\ldots ,p_k$ be distinct primes and $r_1,r_2,\ldots ,r_k$ be nonnegative integers. Then

$$\begin{aligned}&diam(L(G'({\mathbb {Z}}_{n}))) \\&=\left\{ \begin{array}{lcl} \displaystyle 3~~~~~~~\text{ if }~ at~ least~ two~ r_i\ge 2~ and~k\ge 3 \\ \displaystyle 2~~~~~~~otherwise.\end{array}\right. \end{aligned}$$

Conclusion : The paper is divided into some sections. In Sects. 2 and 3 we identify those rings R for which the graph $G'(R)$ is connected and Eulerian. In Sect. 4, we characterize those rings R for which the graph $G'(R)$ will be either toroidal or planar. In Sect. 5, we prove that for any non-local ring R, $L(G'(R))$ is connected with $diam(L(G'(R)))\le 3$. We are unable to characterize those rings R for which the genus of the graph $G'(R)$ is 2. Thus it will be more interesting to find the rings R for which the genus of the graph $G'(R)$ is 2 and there shall be big opportunities for further study of the graph $G'(R)$ with topological aspects in the future.