1 Introduction

The dynamical relationship between prey and their predators has long been and will continue to be one of the dominant themes in ecology due to its universal existence and importance. The qualitative properties of prey-predator systems, such as stability, chaos, bifurcations and oscillations usually depend on the system parameters. Many researchers discussed the dynamical behaviors of prey-predator systems in population dynamics (see [1,2,3,4,5,6]). In each species, stage-structure of individuals is mainly based on characteristics of the biological sense, development, rate of survival and reproduction. The individuals in each species may belong to juvenile or adult class.

Assume that the life history of predator population has two stages: immature (or juvenile) and mature (or adult stage). Juvenile predators are not able to attack the prey species just after their birth, and it takes time for their maturity to attack the preys. Therefore, we should consider time-delays, in the model, to justify the time required for predators to be matured and attack the preys [4]. Time-lags (or time-delay) are usually incorporated into biological systems to represent the time required for maturation period, resource regeneration time, reaction time, gestation period, feeding time, etc. The logistic growth for the prey population, and mortality rate of the matured predators are important factors in the prey-predator models. Wang et al. [7] investigated the stability results of predator–prey system with stage-structure for predator. One important component of the predator–prey relationships is functional response. Functional response refers to the change in the density of prey attached per unit time per predator as the prey density changes. In theoretical ecology, there are several well-known response functions in the predator–prey interactions such as Holling type I (linear), type II (cyrtoid), type III (sigmoid), type IV, Beddington–DeAngelis-type response function, Hassel-Verley-type, etc. (see [2, 8,9,10]). In [11], Holling addressed three different types of functional response for different kinds of species to model the phenomena of predation, which make the standard Lotka–Volterra system more realistic. Xu et al. [12] studied the bifurcation analysis in a delayed Lotka–Volterra predator–prey model with two delays. However, Holling type IV response function is relatively less investigated in the literature of theoretical ecology. Xia et al. [13] discussed the effects of time-delay and harvesting on two different types of prey-predator model with Holling type II functional response. Khajanchi [14] reported the stage structure for predator–prey system with Monod–Haldane functional response and defined suitable Lyapunov function for the study of global asymptotic stability. The Beddington–DeAngelis functional response was firstly introduced by Beddington [15] and DeAngelis et al. [16] in 1975, which is similar to the Holling type functional response but contains an extra term describing mutual interference by predators. Shulin et al. [17] studied the effects of impulsive perturbations on the prey-predator model with Beddington–DeAngelis functional response and also studied global stability results.

Recently, much attention has been given to fractional-order models, due to the fact that fractional-order models are more consistent with the real phenomena than the integer-order models, and enable the description of the memory and hereditary properties of dynamical processes (see [18,19,20]). Also the fractional-order gains the model greater degree of freedom and consistency with the reality of the interactions due to its ability to provide an exact description of the nonlinear phenomena. Also, most of biological, physical, and engineering systems have long-range temporal memory and/or long-range space interactions; The presence of memory (time-lag/fractional-order) leads to a notable increase in the complexity of the observed behavior. Rihan [21] studied fractional-order modeling of HIV infection of \(CD4^{+}T\) Cells, and tumor-immune system. Nosrati et al. [8] reported the impacts of fractional-order derivative and economic profit on the dynamical analysis of singular predator–prey system. The bifurcation control analysis for incommensurate fractional-order prey-predator system with delays was addressed in [22]. Latha et al. [23] discussed the stability and bifurcation results for fractional-order model for Ebola infection and \(CD8^+ T\)-cells response. To the best of our knowledge, stability results of fractional-order stage structured predator–prey system with Beddington–DeAngelis type functional response with time-lag is an untreated topic in the existing literature and this fact is main motivation of the present work.

In this paper, we study the dynamics of fractional-order predator–prey system with Beddington–DeAngelis type functional response and time-delay. We incorporate the time-delay to justify the time required for maturation of adult predators. The authors believe that a combination of time-delay and fractional order in the model enriches the dynamics of the system. We investigate the existence of various equilibrium points, and sufficient conditions that ensure the local asymptotic stability of the steady states of such system. The positivity of the solution of such model is also derived. We discuss the theoretical analysis, using the linearization techniques and eigenvalues method. We provide some numerical simulations to show the dynamical behaviors of juvenile and adult predators with the interaction of prey species and impact the fractional-order in the system.

This paper is organized as follows. Problem formulation, definitions and lemmas are given in Sect. 2. The local asymptotic stability and bifurcation results for fractional-order predator–prey model are derived in Sect. 3. Numerical example is given, in Sect. 4, to verify the obtained theoretical results. Finally, Sect. 5 contains conclusion.

2 Problem formulation

Assume that x(t) and y(t) denote the density of prey and predator population at any time t, respectively. Assume that the prey species grow logistically in the absence of a predator spices with intrinsic growth rate \(\rho \) and the environmental carrying capacity \(\kappa \). Beddington [15] and DeAngelis et al. [16] discussed Beddington–DeAngelis type functional response of the form:

$$\begin{aligned} f(x, y)=\frac{\omega xy}{1+ \beta x+ \gamma y}, \end{aligned}$$

where \(\omega \) (\(units: time^{-1}\)) and \(\beta \) (\(units: prey^{-1}\)) are strictly positive constants, which describe the effects of capture rate and handling time respectively. \(\beta \) determines how fast the per capita feeding rate approaches its saturation value \(\omega \). \(\gamma \) (\(units: predator^{-1}\)) measures the magnitude of mutual interference between individuals of the specialist predators. The predator–prey model with Beddington–DeAngelis type functional response takes the form (see [15, 16])

$$\begin{aligned} \begin{array}{ll} \frac{dx(t)}{dt}=&{}\rho x(t)\Big (1-\frac{x(t)}{\kappa }\Big )-\frac{\omega x(t)y(t)}{1+ \beta x(t)+ \gamma y(t)},\\ \frac{dy(t)}{dt}=&{}\frac{\delta \omega x(t)y(t)}{1+ \beta x(t)+ \gamma y(t)}-\sigma y(t). \end{array} \end{aligned}$$
(1)

Assume that the predator population y(t) splits into two stages: juvenile/immature, \(y_1(t)\) and adult/mature predator, \(y_2(t)\) based on characteristics in biological sense, development, rate of survival and reproduction. The adult predators are able to attack the prey species and have reproductive capability but the immature predator are not able to attack prey species, i.e, the loss rate of the prey population. Recently, Khajanchi [24] studied the dynamical behaviors of stage structured predator–prey system with Beddington–DeAngelis type functional response of the form

$$\begin{aligned} \begin{array}{ll} \frac{dx(t)}{dt}=&{}\rho x(t)\Big (1-\frac{x(t)}{\kappa }\Big )-\frac{\omega x(t)y_2(t)}{1+\beta x(t)+ \gamma y_2(t)},\\ \frac{dy_1(t)}{dt}=&{}\frac{\delta \omega x(t)y_2(t)}{1+\beta x(t)+ \gamma y_2(t)}-(\sigma +k_{1})y_1(t),\\ \frac{dy_2(t)}{dt}=&{}\sigma y_1(t)-k_{2}y_2(t). \end{array} \end{aligned}$$
(2)

The constant \(\delta \) represents the conversion co-efficient from prey into immature predator populations and constant \(\sigma \) defines for the rate of immature predator converting to mature predators. \(k_{1}\) and \(k_{2}\) represent the natural death rate of immature and mature predator species, respectively.

Herein, we extend model (2) to include the fractional order \(0< \alpha \le 1\) and investigate the impact of combination of both fractional-order and time-delay in the response functional. The fractional order systems are more suitable than integer-order in biological modeling due to the memory effects and fractional order derivatives depends not only on local conditions but also on the past. We assume that the time-delay \(\tau \) occurs in the adult predator response term. It represents a gestation time of the adult predators. The reproduction of adult predators after predating the prey is not instantaneous but will be mediated by some discrete time lag required for gestation of the predators. Therefore, the model becomes

$$\begin{aligned} \begin{array}{ll} D^{\alpha }x(t)=&{}\rho x(t)\Big (1-\frac{x(t)}{\kappa }\Big )-\frac{\omega x(t)y_2(t-\tau )}{1+\beta x(t)+ \gamma y_2(t-\tau )},\\ D^{\alpha }y_1(t)=&{}\frac{\delta \omega x(t)y_2(t-\tau )}{1+\beta x(t)+ \gamma y_2(t-\tau )}-(\sigma +k_{1})y_1(t),\\ D^{\alpha }y_2(t)=&{}\sigma y_1(t)-k_{2}y_2(t), \end{array} \end{aligned}$$
(3)

with initial conditions

$$\begin{aligned} x(0)=x_{0}>0,\quad y_1(0)=y_{1,0}>0,\quad y_2(s)=\varphi (s)>0,\ s \in [-\tau , 0] \end{aligned}$$
(4)

where \(\varphi (s)\) is a smooth function. Here, we define fractional derivative \(D^{\alpha }\) in caputo sense, with some properties, \(0< \alpha \le 1\).

Definition 1

[19] The Caputo derivative of fractional-order \(\alpha \) for the function f(t) is defined as

$$\begin{aligned} D^{\alpha }f(t)=\frac{1}{\Gamma (n-\alpha )} \int _{0}^{t} (t- \tau )^{n-\alpha -1}f^{n}(\tau ) d\tau , \end{aligned}$$

where \(n-1<\alpha <n \in \mathbb {Z}^{+},\)\(\Gamma (\cdot )\) is the Gamma function.

Lemma 1

(see [25]) Suppose that \(f(t) \in C[a, b]\) and its derivatives\(D^{\alpha }f(t) \in C(a, b]\) for\(0< \alpha \le 1\), then we have

$$\begin{aligned} f(t)=f(a)+\frac{1}{\Gamma (\alpha )} D^{\alpha }f(\xi ) (t-a)^{\alpha }, \quad a \le \xi \le t, \forall t \in (a, b]. \end{aligned}$$

Lemma 2

(see [25, 26]) Suppose that \(f(t) \in C[a, b]\) and\(D^{\alpha }f(t) \in C(a, b]\) for\(0< \alpha \le 1.\) If\(D^{\alpha }f(t) \ge 0, \forall t \in (a, b)\), then f(t) is a nondecreasing function for each \(t \in [a, b].\) If\(D^{\alpha }f(t) \le 0, \forall t \in (a, b)\), thenf(t) is a non-increasing function for each\(t \in [a, b].\)

The nonnegative population densities of the model (3) are defined by \(\{(x, y_1, y_2) \in \mathbb {R}^3_+ : x \ge 0, \ y_1 \ge 0, \ y_2 \ge 0 \}\). We should prove the positivity of the solutions of the system.

Theorem 1

For any initial conditions satisfying (4), system (3) has a unique solution in \([0,+\infty )\). Moreover, this solution remains nonnegative.

Proof

Assume that \(\mathbb {R}^3_+=\{(x, y_1, y_2) \in \mathbb {R}^3: x \ge 0, \ y_1 \ge 0, \ y_2 \ge 0 \}\) is positively invariant. System (3) can be written in the vector form

$$\begin{aligned} D^{\alpha } X(t)=\mathcal {A}({X}(t)). \end{aligned}$$

Here \({X}(t)=(x(t), y_1(t), y_2(t))^T\), and

$$\begin{aligned} \mathcal {A}({X}(t))=\left[ \begin{array}{c} \rho x(t)\left( 1-\frac{x(t)}{\kappa }\right) -\displaystyle \frac{\omega x(t)y_2(t-\tau )}{1+\beta x(t)+ \gamma y_2(t-\tau )}\\ \displaystyle \frac{\delta \omega x(t)y_2(t-\tau )}{1+\beta x(t)+ \gamma y_2(t-\tau )}-(\sigma +k_{1})y_1(t)\\ \displaystyle \sigma y_1(t)-k_{2}y_2(t) \end{array}\right] . \end{aligned}$$

\({X}_{0}=(x(0), y_1(0), y_2(s))^T \in \mathbb {R}^3_+\). For that, we investigate the direction of the vector field \(\mathcal {A}({X}(t))\) on each coordinate space and see whether the vector field points to the interior of \(\mathbb {R}^3_+\). From (3),

$$\begin{aligned} \begin{array}{ll} D^{\alpha }x(t)|_{x=0}=&{}0,\\ D^{\alpha }y_1(t)|_{y_1=0}=&{}\frac{\delta \omega x y_2(t-\tau )}{1+\beta x+ \gamma y_2(t-\tau )} \ge 0,\\ D^{\alpha }y_2(t)|_{y_2=0}=&{}\sigma y_1 \ge 0. \end{array} \end{aligned}$$
(5)

From Lemmas 1, 2 and Eq. (5), then the vector field \(\mathcal {A}({X}(t))\) is interior of \(\mathbb {R}^3_+\). The solution of (3) with initial conditions \({X}_{0} \in \mathbb {R}^3_+,\) say \({X}(t)={X}(t, {X}_{0})\), in such a way that \({X}(t) \in \mathbb {R}^3_+.\)\(\square \)

For the boundedness of solution of system (3), we refer [27].

Lemma 3

The equilibrium point \((x^{\star }_{1}, x_{2}^{\star })\) of the following fractional-order differential equations

$$\begin{aligned} D^{\alpha }x_{1}(t)&=f_{1}(x_{1}, x_{2}), \quad D^{\alpha }x_{2}(t)=f_{2}(x_{1}, x_{2}), \quad \alpha \in (0, 1],\\ x_{1}(0)&=x_{1,0}, \qquad \qquad x_{2}(0)=x_{2,0} \end{aligned}$$

is locally asymptotically stable if all the eigenvalues of Jacobian matrix

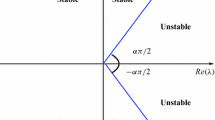
$$\begin{aligned} J= \left( {\begin{matrix} \displaystyle \partial f_{1}/ \partial x_{1} &{} \displaystyle \partial f_{1}/ \partial x_{2} \\ \displaystyle \partial f_{2}/ \partial x_{1} &{} \displaystyle \partial f_{2}/ \partial x_{2} \end{matrix}} \right) , \end{aligned}$$

calculated at \((x_{1}^{\star }, x_{2}^{\star })\) satisfies the condition \(\displaystyle |\arg (eig(J))|>\frac{\alpha \pi }{2}.\)

3 Stability and Hopf bifurcation results

In this section, we study the local asymptotic stability and bifurcation conditions for system (3). The system has three steady-stats: trivial equilibrium point \(\mathcal {E}_{0}(0, 0, 0),\) predator free equilibrium point \(\mathcal {E}_{1}(\kappa , 0, 0)\) and interior equilibrium point \(\mathcal {E}_{2}(x^{\star }, y_1^{\star }, y_2^{\star }),\) where

$$\begin{aligned} y_2^{\star }= \frac{\rho (\kappa -x^{\star })(1+\beta x^{\star })}{\kappa \omega -\gamma \rho (\kappa -x^{\star })}, y_1^{\star }= \frac{k_{2}\rho (\kappa -x^{\star })(1+\beta x^{\star })}{\sigma (\kappa \omega -\gamma \rho (\kappa -x^{\star }))}, \end{aligned}$$

and \( x^{\star }\) satisfies the quadratic equation

$$\begin{aligned}&(x^{\star })^{2}\beta (\sigma +k_{1})k_{2}\gamma \rho +x^{\star }\Big (\delta \omega \sigma -(1+\beta ) (\sigma +k_{1})k_{2}+(1-\kappa \beta )(\sigma +k_{1})k_{2}\gamma \rho \Big )\\&-(\sigma +k_{1})k_{2}(1+\kappa \gamma \rho )=0. \end{aligned}$$

In order to study the local asymptotic stability of (3), let us define the co-ordinate transformation \(\mathcal {X}(t)=x(t)-x^{\star },\ \mathcal {Y}_1(t)=y_1(t)-y_1^{\star }, \ \mathcal {Y}_2(t)=y_2(t)-y_2^{\star }.\) The corresponding linearized system of (3) at any equilibrium point \((x^{\star }, y_1^{\star }, y_2^{\star })\) is

$$\begin{aligned} \begin{array}{ll} D^{\alpha }\mathcal {X}(t)&{}=\Big (\Big(\rho -\frac{2 \rho x^{\star }}{\kappa }\Big)-\Big (\frac{(1+\beta x^{\star }+ \gamma y_2^{\star })\omega y_2^{\star }- \omega \beta x^{\star } y_2^{\star }}{(1+\beta x^{\star }+ \gamma y_2^{\star })^{2}}\Big ) \Big )\mathcal {X}(t) \\ &{} \qquad -\Big (\frac{(1+\beta x^{\star }+ \gamma y_2^{\star })\omega x^{\star }- \omega \gamma x^{\star } y_2^{\star }}{(1+\beta x^{\star }+ \gamma y_2^{\star })^{2}}\Big ) \mathcal {Y}_2(t-\tau ) , \\ D^{\alpha }\mathcal {Y}_1(t)&{}=\Big (\frac{(1+\beta x^{\star }+ \gamma y_2^{\star })\omega y_2^{\star }- \omega \beta x^{\star } y_2^{\star }}{(1+\beta x^{\star }+ \gamma y_2^{\star })^{2}}\Big ) \delta \mathcal {X}(t)-(\sigma +k_{1})\mathcal {Y}_1(t) \\ &{} \qquad +\Big (\frac{(1+\beta x^{\star }+ \gamma y_2^{\star })\omega x^{\star }- \omega \gamma x^{\star } y_2^{\star }}{(1+\beta x^{\star }+ \gamma y_2^{\star })^{2}}\Big ) \delta \mathcal {Y}_2(t-\tau ) ,\\ D^{\alpha }\mathcal {Y}_2(t)&{}= \sigma \mathcal {Y}_1(t)-k_{2}\mathcal {Y}_2(t). \end{array} \end{aligned}$$
(6)

Taking Laplace transform on both sides, yields

$$\begin{aligned} \begin{array}{ll} s^{\alpha } X(s)- s^{\alpha -1} \mathcal {X}(0)&{}= \Big ((\rho -\frac{2 \rho x^{\star }}{\kappa })-\Big (\frac{(1+\beta x^{\star }+ \gamma y_2^{\star })\omega y_2^{\star }- \omega \beta x^{\star } y_2^{\star }}{(1+\beta x^{\star }+ \gamma y_2^{\star })^{2}}\Big ) \Big ) X(s) \\ &{} \qquad - \Big (\frac{(1+\beta x^{\star }+ \gamma y_2^{\star })\omega x^{\star }- \omega \gamma x^{\star } y_2^{\star }}{(1+\beta x^{\star }+ \gamma y_2^{\star })^{2}}\Big ) e^{-s \tau } [ Y_2(s)+ \int _{-\tau }^{0} e^{-st} \varphi (t) dt],\\ s^{\alpha } Y_1(s)- s^{\alpha -1} \mathcal {Y}_1(0)&{}= \Big (\frac{(1+\beta x^{\star }+ \gamma y_2^{\star })\omega y_2^{\star }- \omega \beta x^{\star } y_2^{\star }}{(1+\beta x^{\star }+ \gamma y_2^{\star })^{2}}\Big ) \delta X(s)- (\sigma +k_{1})Y_1(s) \\ &{} \qquad + \Big (\frac{(1+\beta x^{\star }+ \gamma y_2^{\star })\omega x^{\star }- \omega \gamma x^{\star } y_2^{\star }}{(1+\beta x^{\star }+ \gamma y_2^{\star })^{2}}\Big ) \delta e^{-s \tau } [ Y_2(s)+ \int _{-\tau }^{0} e^{-st} \varphi (t) dt],\\ s^{\alpha } Y_2(s)- s^{\alpha -1} \mathcal {Y}_2(0)&{}=\sigma Y_1(s)-k_{2} Y_2(s). \end{array} \end{aligned}$$
(7)

Here, \(X(s), Y_1(s), Y_2(s)\) are the Laplace transform of \(\mathcal {X}(t), \mathcal {Y}_1(t), \mathcal {Y}_2(t)\) respectively. The above system (7) can be written as follows

$$\begin{aligned} \Delta (s) \star \left( {\begin{matrix} X(s)\\ Y_1(s)\\ Y_2(s) \end{matrix}} \right) =\left( {\begin{matrix} b_{1}(s)\\ b_{2}(s)\\ b_{3}(s) \end{matrix}} \right) \end{aligned}$$

and

$$\Delta (s) =\left( \begin{array}{lll} \displaystyle s^{\alpha}-m_1 &\displaystyle 0 & \displaystyle m_2 e^{-s\tau} \\ {\displaystyle} -m_3 &\displaystyle s^{\alpha}+m_4 & {\displaystyle} -m_5 e^{-s\tau} \\ \displaystyle 0 &{\displaystyle} -m_6 &\displaystyle s^{\alpha}+m_7 \end{array} \right).$$

where

$$\begin{aligned} b_{1}(s)=s^{\alpha -1} \mathcal {X}(0)- \Big (\frac{(1+\beta x^{\star }+ \gamma y_2^{\star })\omega x^{\star }- \omega \gamma x^{\star } y_2^{\star }}{(1+\beta x^{\star }+ \gamma y_2^{\star })^{2}}\Big ) e^{-s \tau } \int _{-\tau }^{0} e^{-st} \varphi (t) dt, \end{aligned}$$
$$\begin{aligned} b_{2}(s)=s^{\alpha -1}\mathcal {Y}_1(0)+\Big (\frac{(1+\beta x^{\star }+ \gamma y_2^{\star })\omega x^{\star }- \omega \gamma x^{\star } y_2^{\star }}{(1+\beta x^{\star }+ \gamma y_2^{\star })^{2}}\Big ) \delta e^{-s \tau } \int _{-\tau }^{0} e^{-st} \varphi (t) dt, b_{3}(s)=s^{\alpha -1} \mathcal {Y}_2(0), \end{aligned}$$
$$\begin{aligned} m_1=\Big (\Big(\rho -\frac{2 \rho x^{\star }}{\kappa }\Big)-\Big (\frac{(1+\beta x^{\star }+ \gamma y_2^{\star })\omega y_2^{\star }- \omega \beta x^{\star } y_2^{\star }}{(1+\beta x^{\star }+ \gamma y_2^{\star })^{2}}\Big ) \Big ), \end{aligned}$$
$$\begin{aligned} m_2=\Big (\frac{(1+\beta x^{\star }+ \gamma y_2^{\star })\omega x^{\star }- \omega \gamma x^{\star } y_2^{\star }}{(1+\beta x^{\star }+ \gamma y_2^{\star })^{2}}\Big ), \end{aligned}$$
$$\begin{aligned} m_3=\Big (\frac{(1+\beta x^{\star }+ \gamma y_2^{\star })\omega y_2^{\star }- \omega \beta x^{\star } y_2^{\star }}{(1+\beta x^{\star }+ \gamma y_2^{\star })^{2}}\Big ) \delta ,\quad m_4=\sigma +k_{1}, \end{aligned}$$
$$\begin{aligned} m_5=\Big (\frac{(1+\beta x^{\star }+ \gamma y_2^{\star })\omega x^{\star }- \omega \gamma x^{\star } y_2^{\star }}{(1+\beta x^{\star }+ \gamma y_2^{\star })^{2}}\Big ) \delta ,\quad m_6=\sigma ,\quad m_7=k_{2} \end{aligned}$$

Let, \(\Delta (s)\) be the characteristic matrix for system (6) at \((x^{\star }, y_1^{\star }, y_2^{\star })\). The characteristic equation of (6) is \(det(\Delta (s))=0\)

$$\begin{aligned} A_1 (s)+A_2 (s)e^{-s\tau }+A_3 e^{-s\tau } =0, \end{aligned}$$
(8)

where

$$\begin{aligned} A_1(s)=(s^\alpha )^3+p_1 (s^\alpha )^2+p_2 s^\alpha + p_3, \quad A_{2}(s)=r_1 s^\alpha , \; A_3= m_1m_5m_6+m_2m_3m_6, \end{aligned}$$
$$\begin{aligned} p_1= m_4+m_7-m_1,\quad p_2=m_4m_7-m_1(m_4+m_7),\quad p_3=-m_1m_4m_7,\quad r_1=-m_5m_6. \end{aligned}$$

Suppose \(\tau =0,\) the equilibrium point \(\mathcal {E}_{1}\) of system (3) is locally asymptotically stable when \(p_1>0, p_3+A_3>0, p_1(p_2+r_1)>p_3+A_3.\)

If \(\tau \ne 0,\) As in [28], assume \(s=iw=w (\cos \frac{\pi }{2}+ i \sin \frac{\pi }{2}), w>0,\) then s is substituted in (8), we get

$$\begin{aligned} (c_1+id_{1})+(c_2+id_2)e^{-iw \tau }+A_3 e^{-iw \tau } =0, \end{aligned}$$
(9)

where

$$\begin{aligned} c_1&=w^{3\alpha } \cos \frac{3 \alpha \pi }{2}+ p_1 w^{2 \alpha } \cos {\alpha \pi }+p_2 w^{ \alpha } \cos \frac{\alpha \pi }{2}+p_3,\\ d_1&=w^{3\alpha } \sin \frac{3 \alpha \pi }{2}+ p_1 w^{2 \alpha } \sin {\alpha \pi }+p_2 w^{ \alpha } \sin \frac{\alpha \pi }{2},\\ c_2&=w^{ \alpha }r_1 \cos \frac{\alpha \pi }{2}, d_2=w^{ \alpha }r_1 \sin \frac{\alpha \pi }{2}. \end{aligned}$$

Separating the real and imaginary parts of (9), yields

$$\begin{aligned} \begin{array}{l} (c_2+A_3) \cos w\tau +d_2 \sin w \tau +c_1 = 0,\\ d_2 \cos w \tau - (c_2+A_3) \sin w \tau +d_1 = 0. \end{array} \end{aligned}$$
(10)

From the Eq. (10), we obtain

$$\begin{aligned} \begin{array}{l} \cos w \tau = -\frac{(c_2+A_3)c_1+d_1d_2}{(c_2+A_3)^2+d_2^2},\\ \sin w \tau = \frac{(c_2+A_3)d_1-c_1d_2}{(c_2+A_3)^2+d_2^2}. \end{array} \end{aligned}$$

It is obvious that \(\cos ^2 w \tau + \sin ^2 w \tau =1,\) and

$$\begin{aligned}&w^{6\alpha }+\eta _1 w^{5\alpha }+ \eta _2w^{4\alpha }+ \eta _3w^{3\alpha }+\eta _4 w^{2\alpha }+\eta _5 w^\alpha +\eta _6=0,\nonumber \\ \text{ where }\quad&\eta _1 = p_1 \cos \frac{\alpha \pi }{2}, \eta _2= p_1^2+p_2 \cos \alpha \pi , \nonumber \\&\eta _3= p_3 \cos \frac{3\alpha \pi }{2}+ p_1 p_2 \cos \frac{\alpha \pi }{2}, \eta _4=p_2^2-r_1^2+p_1p_3 \cos \alpha \pi , \nonumber \\&\eta _5= (p_2 p_3-2 A_3r_1)\cos \frac{\alpha \pi }{2}, \eta _6= p_3^2-A_3^2. \end{aligned}$$
(11)

Label \(f(w)=w^{6\alpha }+\eta _1 w^{5\alpha }+ \eta _2w^{4\alpha }+ \eta _3w^{3\alpha }+\eta _4 w^{2\alpha }+\eta _5 w^\alpha +\eta _6\). Then, we discuss the distribution of the roots of (8).

Lemma 4

For the Eq. (8), the following results hold:

  1. (i)

    If \(\eta _1>0, \eta _2>0,\eta _3>0, \eta _4>0,\eta _5>0,\eta _6>0, p_3^2-A_3^2 \ne 0,\) the Eq. (8) has no root with zero real parts for all \(\tau \ge 0.\)

  2. (ii)

    If \(\eta _1<0, \eta _2<0,\eta _3<0, \eta _4<0,\eta _5<0,\eta _6>0,\) the Eq. (8) has a pair of purely imaginary roots \(\pm iw_+\) when\(\tau = \tau _j, j=0, 1 , 2, \ldots \) where

    $$\begin{aligned} \tau_j=\frac{1}{w_+}[arccos \Big(-\frac{(c_2+A_3)c_1+d_1d_2}{(c_2+A_3)^2+d_2^2}\Big)+2j \pi], \quad j=0,1,2,\ldots \end{aligned}$$
    (12)

    and\(w_+\) is the unique positive root of (11).

Proof

i) From \(\eta _1>0, \eta _2>0,\eta _3>0, \eta _4>0,\eta _5>0,\eta _6>0,\) we derive \(f(0)=\eta _6>0,\) and

$$\begin{aligned} f^{'}(w)=6\alpha w^{6\alpha -1}+5 \alpha \eta _1 w^{5\alpha -1}+ 4\alpha \eta _2 w^{4\alpha -1}+ 3\alpha \eta _3 w^{3\alpha -1}+2\alpha \eta _4 w^{2\alpha -1}+\alpha \eta _5 w^{\alpha -1}. \end{aligned}$$

Combining \(\alpha >0\) and \(\eta _1>0, \eta _2>0,\eta _3>0, \eta _4>0,\eta _5>0,\eta _6>0\), we claim that Eq. (11) has no real root and hence Eq. (8) has no purely imaginary root. \(p_3^2-A_3^2 \ne 0, s=0\) is not a root of (8).

ii) From \(\eta _6>0\) and \(f(0)=\eta _6>0,\) then, by \(\lim _{w \rightarrow +\infty } f(w)=+ \infty , f^{'}(w)>0\) for \(w>0,\) there exists a unique positive number \(w_+\) such that \(f(w_+)=0.\) Then \(w_+\) is a root of (11). From (10), we know that the Eq. (8) with \(\tau =\tau _j (j=0,1,2,\ldots )\) has a pair of purely imaginary roots \(\pm iw_{+}.\)\(\square \)

Lemma 5

(see [23]) Let \(s(\tau )=\zeta (\tau )+i w(\tau )\) be the root of Eq. (8) such that when \(\tau =\tau _j\) satisfying\(\zeta (\tau _j)=0\) and\(w(\tau _j)=w_+\), then the following transversality condition holds \(Re(\frac{ds}{d \tau })|_{\tau =\tau _j, w=w_+} \ne 0\).

Proof

Differentiate the Eq. (8) with respect to \(\tau \), then

$$\begin{aligned} \frac{ds}{d \tau }=\frac{e^{-s \tau }[s A_{2}(s)+ sA_3]}{A_1^{'} (s)+A_2^{'} (s)e^{-s \tau }-\tau A_2(s)e^{-s \tau }-A_3 \tau e^{-s \tau }}. \end{aligned}$$

From the above equation, consider the numerator and denominator terms described as

$$\begin{aligned} e^{-s \tau }[s A_{2}(s)+ sA_3]&=n_1 + i n_2, \\ A_1^{'} (s)+A_2^{'} (s)e^{-s \tau }-\tau A_2(s)e^{-s \tau }-A_3 \tau e^{-s \tau }&=n_3+i n_4, \end{aligned}$$
$$\begin{aligned} \text{ where } \quad n_1&=r_1 w^{\alpha +1} \Bigg [\sin w \tau \cos \frac{\alpha \pi }{2}- \cos w \tau \sin \frac{\alpha \pi }{2}\Bigg ]+ A_3 w \sin w \tau ,\\ n_2&=r_1 w^{\alpha +1} \Bigg [\cos w \tau \cos \frac{\alpha \pi }{2}+ \sin w \tau \sin \frac{\alpha \pi }{2}\Bigg ]+ A_3 w \cos w \tau ,\\ n_3&=3 \alpha w^{3 \alpha -1} \cos \frac{(3 \alpha -1)\pi }{2}+ 2 \alpha p_1 w^{2 \alpha -1} \cos \frac{(2 \alpha -1)\pi }{2}+p_2 \alpha w^{\alpha -1} \cos \frac{(\alpha -1)\pi }{2}\\&\qquad + r_1 \alpha w^{\alpha -1} \Bigg [\cos w \tau \cos \frac{(\alpha -1)\pi }{2}+ \sin w \tau \sin \frac{(\alpha -1)\pi }{2} \Bigg ]-\tau r_1 \cos w\tau ,\\ n_4&=3 \alpha w^{3 \alpha -1} \sin \frac{(3 \alpha -1)\pi }{2}+ 2 \alpha p_1 w^{2 \alpha -1} \sin \frac{(2 \alpha -1)\pi }{2}+p_2 \alpha w^{\alpha -1} \sin \frac{(\alpha -1)\pi }{2}\\&\qquad + r_1 \alpha w^{\alpha -1} \Bigg [\cos w \tau \sin \frac{(\alpha -1)\pi }{2}- \sin w \tau \cos \frac{(\alpha -1)\pi }{2} \Bigg ]+\tau r_1 \sin w\tau . \end{aligned}$$

Then,

$$\begin{aligned} Re \Bigg (\frac{ds}{d \tau }\Bigg )|_{\tau =\tau _j, w=w_+}=\frac{n_1 n_3+n_2 n_4}{n_3^2+n_4^2} \ne 0. \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \square \end{aligned}$$

Define \(\tau ^{\star }= min\{\tau _j\}\) and based on the bifurcation theorem for functional differential equations [29], we arrive the following theorem: \(\square \)

Theorem 2

Suppose the Lemmas 4 and 5 are hold;

  1. (i)

    If \(\tau \in [0, \tau _{0}),\) then the equilibrium point\(\mathcal {E}_1\) of system (3) is locally asymptotically stable.

  2. (ii)

    If \(\tau > \tau _{0},\) then the equilibrium point \(\mathcal {E}_1\) of system (3) is unstable

  3. (iii)

    System (3) can undergo a Hopf bifurcation at \(\mathcal {E}_1\), when\(\tau =\tau _j(j=0, 1, 2, \ldots ).\)

Similarly, we can prove the stability and bifurcation results for system (3) at interior equilibrium point \(\mathcal {E}_2.\)

Fig. 1
figure 1

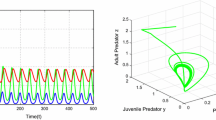
Time domain and space plane behaviors of state variables \(x(t), y_1(t)\) and \(y_2(t)\) for system (3) with fractional-order \(\alpha =0.9\) and time-delay \(\tau =\tau ^*=2.1\). We notice the oscillating behaviour

Full size image
Fig. 2
figure 2

Time domain and space plane behaviors of system (3) with fractional-order \(\alpha =0.9\) and time-delay \( \tau =1.5<\tau ^{\star }\). Stable behaviour is shown

Full size image
Fig. 3
figure 3

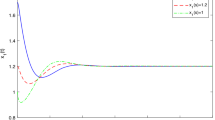
The time domain behaviors of state trajectories x(t) of system (3) with different values of fractional orders \(\alpha =0.95, 0.9, 0.85,\) conversion co-efficient \( \delta =1.5\) (left) and \(\delta =0.9\) (right). The fractional derivative damps the oscillation behaviour

Full size image
Fig. 4
figure 4

The time domain behaviors of state trajectories \(y_1(t)\) of system (3) with different values of fractional orders \(\alpha =0.95, 0.9, 0.85,\) conversion co-efficient \( \delta =1.5\) (left) and \( \delta =0.9\) (right). The fractional derivative damps the oscillation behaviour

Full size image
Fig. 5
figure 5

The time domain behaviors of state trajectories \(y_2(t)\) of system (3) with different values of fractional orders \(\alpha =0.95, 0.9, 0.85,\) conversion co-efficient \(\delta =1.5\) (left) and \( \delta =0.9\) (right). The fractional derivative damps the oscillation behaviour

Full size image

4 Numerical simulations

Since most of the fractional-order differential equations do not have exact analytic solutions, so approximation and numerical techniques must be used. Several numerical methods have been proposed to solve the fractional-order differential equations. In this section, we carry out some numerical simulations to display the qualitative behaviours of model (3), using unconditionally and stable implicit scheme, discussed in [21], with parameter values:

$$\begin{aligned} \rho =1.5, \kappa =1.6, \omega =1.4, \beta =1, \gamma =0.1, \sigma =0.09, k_{1}=0.5, k_{2}=0.05, \delta =0.9. \end{aligned}$$

The figures show impact of time-delays and fractional-order \(\alpha \) on the dynamics of the model (3). The fractional-order \(\alpha \) and time-delay are the important factors which affect the convergence speed of solutions. We deduce the critical value of time-delay which is \(\tau ^{\star } \approx 2.1.\) We also plot the diagram for system (3) with respect to the time-delay \(\tau \) as a bifurcation parameter. Figures 1, 2 display the time domain and space plane graphs of the state variables \((x, y_1, y_2)\) with initial condition \(x(s)=1.3, y_1(s)=0.5, y_2(s)=1.3\), \(\delta =0.9, \alpha =0.9\), time-delay \(\tau =\tau ^*\) and \(\tau =1.5\). Clearly, system (3) shows a sustained oscillating behaviours and stable behavior when \(\tau =1.5<\tau ^{\star }.\) The time-domain behaviors of system (3) are given in Figs. 3, 4, and 5 with different fractional orders \(\alpha =0.95, 0.9, 0.85\), \(\delta =1.5\)(left) and \(\delta =0.9\) (right). Clearly, the left graph of each figures shows an unstable behavior when \(\delta =1.5\). However, the right banner of each Figure shows a stable behavior when \(\delta =0.9.\) From the Figures, with lower values of \(\delta \), the system becomes more stable and we loose stability with higher value of \(\delta \). We notice that the convergence speed is affected by the values of the different fractional-order as well as the parameter \(\delta \).

5 Conclusion

In this work, we studied a fractional-order predator–prey system with time-delay and structured stage, by introducing Beddington–DeAngelis functional response. With the help of Laplace transform, we defined the characteristic equation of such model. Some interesting stability results have been obtained. Some new and interesting sufficient conditions that ensure the local asymptotic stability for the addressed fractional-order model have been derived. The fractional-order and time-delay in predator–prey model improves the stability results. The presence of fractional-order and time-delay enriches the dynamics of the predator–prey model with Beddington–DeAngelis functional response. The numerical simulations, shown in Figs. 1, 2, 3, 4 and 5, verified the effectiveness of the obtained theoretical results.