1 Introduction

In ecological systems, the interactions between two or more species and their dynamics are affected by each other. When the growth of one species depends on another, it is described by prey–predator system. The prey–predator dynamics is one of the principal subjects in ecology due to the worldwide importance and existence. The dynamical behaviors of prey–predator models, such as chaos, stability, bifurcations and oscillations usually depend on the system parameters. Many ecologists and mathematicians have discussed the qualitative properties of prey–predator model in population dynamics (see, e.g., [1,2,3,4]). Zhang et al. [5] reported the existence results of ratio-dependent neutral prey–predator system with Holling type II response function by using continuation theorem and coincidence degree theory. Tripathi et al. [6] derived the bifurcation and stability results of modified Leslie–Gower prey–predator model with prey refuge and Crowley–Martin response function.

In each species, stage structure of individuals is mainly based on characteristics in biological sense, development, rate of survival and reproduction. The individuals in each species may belong to juvenile or adult class. The life history of predator population have two stages, that is, juvenile or immature and adult or mature stage. Juvenile predators are not able to attack the prey species just after their birth, then it takes time for their maturity to attack the preys. The logistic growth for the prey population and mortality rate of the matured predators are important factors in the prey–predator models. Wang et al. [7] derived the stability results of prey–predator system with stage structure. The bifurcation and stability results of prey–predator system with age-based predation has been discussed by Misra et al. [8]. Chakraborty et al. [9] reported the fishery model of stage-structured prey–predator model. The authors in [10] studied the continuous and impulsive harvesting policies in the prey–predator model with stage structure for predators. Khajanchi et al. [11, 12] introduced the stage structure for prey–predator model with ratio-dependent and Monod–Haldane functional response and defined suitable Lyapunov function for the study of global asymptotic stability.

Time delays have been incorporated into biological systems to describe and take into account the time required for resource regeneration time, maturation period, reaction time, feeding time, gestation period, etc. [13,14,15]. Zhao et al. [16] investigated the dynamical behaviors of delayed SIR epidemic model; delay affects the stability results of steady states and gives limit cycle oscillations. Some complex biological phenomena arising in prey–predator model depends on the past history of model, and it have been known that time delay may have complicated impact on qualitative behaviors of such models. The authors in [17] discussed a delayed prey–predator system with stage structure and studied the global existence of multiple positive periodic solutions of such model. Liu et al. [18] derived the existence, boundedness and nonnegativity of solutions for prey–predator model with incorporating a prey refuge and also discussed the global asymptotic stability results. Lu et al. [19] introduced the delayed prey–predator Lotka–Volterra system with impulsive perturbations and stochastic effects. Some researchers focused on dynamical properties of prey–predator system with time delays and stage structure [20,21,22].

Fractional-order dynamical systems [23,24,25,26] are generally associated with systems with memory, which occur in most of biological systems. The presence of memory in the model represents the history of the process involved and carries its impact to present and future developments of the process. Accordingly, the differential equations with fractional order are more consistent with the real phenomena than those with integer order. This is due to the fact that fractional-order derivative is associated with whole time domain for a biological processes, while integer-order derivative specifies a certain attribute or variation at particular time. The authors believe that using fractional order in modeling population dynamical systems enriches the dynamics and increases the complexity of the model. Rihan et al. [27, 28] provided a class of fractional-order equations in modeling HIV infection of CD4\(^{+}\) T cells, tumor-immune model, Salmonella bacterial infection with SIRC system. The authors in [29] reported the fractional-order model of delayed HIV infection of CD4\(^{+}\)T cells. Matouk et al. [30] discussed the Hopf bifurcation, chaotic attractors and attractor crisis for fractional-order Hastings–Powell food chain system. Preethilatha et al. [31] investigated the dynamical behaviors of fractional-order delayed Ebola virus epidemic model with immune response on heterogeneous complex networks. The dynamical characteristics for fractional-order Hindmarsh–Rose neuronal model are introduced in [32].

Recently, more attentions have been given in studying fractional-order derivatives in describing the memory effects in prey–predator systems, and investigating the complexity properties of the models; See [4, 33,34,35]. Rihan et al. [4] discussed the global and local stability, Hopf bifurcation results of fractional-order prey–predator model with Holling type II response functional. Nosrati et al. [36] reported the impacts of fractional-order derivative and economic profit on the dynamical analysis of singular prey–predator system. The bifurcation control analysis for incommensurate fractional-order prey–predator system with delays was addressed in [37]. Ghaziani et al. [38] investigated the stability results for fractional-order prey–predator system with nonmonotonic functional response. Javidi et al. [39] studied the mathematical behaviors of the fractional-order prey–predator model and also discussed the local stability results.

In theoretical ecology, there are several well-known response functions in the prey-predator interactions such as Holling type I (linear), type II (cyrtoid), type III (sigmoid), type IV, Hassel–Verley-type, Beddington–DeAngelis-type response function, etc. (see [11, 22, 36]). Researchers around the world discussed and raised some open questions regarding stage structure prey–predator relationship with various kind of response functions. Holling type IV response function is relatively less investigated in the theoretical ecology. The main objective of this work is to study the dynamics of a fractional-order delayed prey–predator system with Monod–Haldane (or Holling type IV) functional response. The system describes the interaction between prey and two populations of predator species: immature/juvenile and mature/adult predator. We introduce the time delay to justify the time required for maturation of adult predators. The authors believe that a combination of time delay and fractional order in the model enriches the dynamics of the system. We provide theoretical analysis, using the eigenvalues method, linearization techniques and Lyapunov stability theory. The existence of the solution of such model is investigated. We derive the local asymptotic stability of the steady states, which gives an idea to better understand the qualitative behavior of the original system. We also construct a suitable Lyapunov functional to deduce some new sufficient conditions of global asymptotic stability results of the system.

This paper is organized as follows: In Sect. 2, we formulate the problem and provide some definitions, lemmas, and existence results related to the model. Local stability and global asymptotic stability of fractional-order prey–predator system with delays are discussed in Sect. 3. Numerical results are given in Sect. 4, to verify the importance of the theoretical results. Section 5 contains concluding remarks.

2 Problem formulation

Assume that x(t) denotes the prey population density at time t. We also assume that predator population splits two stages: immature or juvenile predator y(t) and mature or adult predator z(t). The adult predators are able to attack the prey species, i.e., the loss rate of the prey population, which have been modeled by using Monod–Haldane (or Holling type IV) functional response.Footnote 1 We consider a fractional-order prey–predator model with delays and Monod–Haldane functional response of the form

$$\begin{aligned} D^{\alpha }x(t)= & {} px(t)\Big (1-\frac{x(t)}{k}\Big )-\frac{\delta x(t)z(t-\tau )}{\varphi +\beta x^{2}(t)},\nonumber \\ D^{\alpha }y(t)= & {} \frac{c\delta x(t)z(t-\tau )}{\varphi +\beta x^{2}(t)}-(\kappa +\mu _{1})y(t),\nonumber \\ D^{\alpha }z(t)= & {} \kappa y(t)-\mu _{2}z(t), \end{aligned}$$
(1)

with initial conditions \(x(0)=x_{0}>0\), \(y(0)=y_{0}>0\), \(z(s )=\chi (s)>0\), \(s \in [-\tau , 0]\), and \(\chi (s)\) is smooth function. Here, \(D^{\alpha }\) is the Caputo fractional derivative of order \(0< \alpha \le 1\). The parameter p is the biotic potential that the prey species grow logistically without any predator species. k represents the environmental carrying capacity. \(\delta \) is maximal prey population uptake of mature predators. \(\beta \) denotes the inverse measure of inhibitory effect, and \(\varphi \) is half saturation constant. c defines the conversion coefficient (conversion of prey to juvenile predators) and \(\kappa \) represents the transition rate on the evolution of juvenile and adult predators. \(\mu _{1}\) and \(\mu _{2}\) denote the natural death rate of juvenile and adult predator populations, respectively.

Definition 1

[23] The fractional integral of order \(\alpha \in \mathbb {R}^{+}\) for a function f(t) is described as

$$\begin{aligned} I^{\alpha }f(t)= \frac{1}{\Gamma (\alpha )} \int _{0}^{t} (t- \tau )^{\alpha -1}f(\tau ) \mathrm{d}\tau . \end{aligned}$$

Definition 2

[24] The Caputo derivative of fractional-order \(\alpha \) for the function f(t) is defined as

$$\begin{aligned} D^{\alpha }f(t)=\frac{1}{\Gamma (n-\alpha )} \int _{0}^{t} (t- \tau )^{n-\alpha -1}f^{n}(\tau ) \mathrm{d}\tau , \end{aligned}$$

where \(n-1<\alpha <n \in \mathbb {Z}^{+}.\)

Theorem 1

For every \((x_{0}, y_{0}, z_{0}) \in \Omega ,\) then there exists a unique solution \(X=(x, y, z) \in \Omega \) of system (1), where \(\Omega = \{(x, y, z) \in \mathbb {R}^{3}: \max \{|x |, |y|, |z| \le \mathcal {K} \} \}\).

Proof

Define a mapping \(f(X)=\Big (f_{1}(X), f_{2}(X), f_{3}(X)\Big ),\)

$$\begin{aligned} f_{1}(X)&=px(t)\Big (1-\frac{x(t)}{k}\Big )-\frac{\delta x(t)z(t-\tau )}{\varphi +\beta x^{2}(t)},\\ f_{2}(X)&=\frac{c\delta x(t)z(t-\tau )}{\varphi +\beta x^{2}(t)}-(\kappa +\mu _{1})y(t),\\ f_{3}(X)&=\kappa y(t)-\mu _{2}z(t). \end{aligned}$$

For any \(X, \tilde{X} \in \Omega ,\)

$$\begin{aligned}&\Vert f(X)-f(\tilde{X}) \Vert \\&\quad =|p(x(t)-\tilde{x}(t))-\frac{p}{k}(x^{2}(t)-\tilde{x}^{2}(t))\\&\qquad -\,\frac{\delta x(t)z(t-\tau )}{\varphi +\beta x^{2}(t)}+\frac{\delta \tilde{x}(t)\tilde{z}(t-\tau )}{\varphi +\beta \tilde{x}^{2}(t)} |+ |\\&\qquad -\,\frac{c\delta x(t)z(t-\tau )}{\varphi +\beta x^{2}(t)}+\,\frac{c\delta \tilde{x}(t)\tilde{z}(t-\tau )}{\varphi +\beta \tilde{x}^{2}(t)}\\&\qquad -(\kappa +\mu _{1})(y(t)-\tilde{y}(t)) | \\&\qquad +\, |\kappa (y(t)-\tilde{y}(t))-\mu _{2}(z(t)-\tilde{z}(t))|,\\&\quad \le \,\Big (p+ \frac{2 \mathcal {K}p}{k}+ \frac{(1+c) \delta \mathcal {K}}{\varphi + \beta \mathcal {K}^{2}} \Big )|x-\tilde{x}|\\&\qquad +\,(2 \kappa + \mu _{1})|y-\tilde{y}|+ \Big (\frac{(1+c) \delta \mathcal {K}}{\varphi + \beta \mathcal {K}^{2}} + \mu _{2}\Big )|z-\tilde{z}|,\\&\quad \le \, \mathcal {M}\Vert X-\tilde{X} \Vert , \end{aligned}$$

where \(\mathcal {M}=\max \{\Big (p+ \frac{2 \mathcal {K}p}{k}+ \frac{(1+c) \delta \mathcal {K}}{\varphi + \beta \mathcal {K}^{2}} \Big ), (2 \kappa + \mu _{1}), \Big (\frac{(1+c) \delta \mathcal {K}}{\varphi + \beta \mathcal {K}^{2}} + \mu _{2}\Big )\}.\) Therefore, f(X) satisfies Lipschitz condition with respect to X,  from Lemma 5 in [35], the system (1) has unique solution X(t). \(\square \)

Lemma 1

The equilibrium point \((x^{\star }_{1}, x_{2}^{\star })\) of the following fractional differential equations

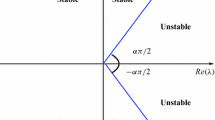
$$\begin{aligned} D^{\alpha }x_{1}(t)&=f_{1}(x_{1}, x_{2}), \quad D^{\alpha }x_{2}(t)=f_{2}(x_{1}, x_{2}), \quad \alpha \in (0, 1],\\ x_{1}(0)&=x_{1,0}, \qquad \qquad x_{2}(0)=x_{2,0} \end{aligned}$$

is locally asymptotically stable if all the eigenvalues \(\lambda _{i}, i=1,2\) of the Jacobian matrix

$$\begin{aligned} J= \Bigl ( \begin{matrix} \partial f_{1}/ \partial x_{1} &{}\quad \partial f_{1}/ \partial x_{2} \\ \partial f_{2}/ \partial x_{1} &{}\quad \partial f_{2}/ \partial x_{2} \end{matrix} \Bigr ), \end{aligned}$$

calculated at \((x_{1}^{\star }, x_{2}^{\star }),\) satisfies the condition \(|\arg (\lambda _{i})|>\frac{\alpha \pi }{2}.\)

System (1) has a trivial equilibrium point \(\mathcal {E}_{0}(0, 0, 0),\) axial equilibrium point or predator-free equilibrium point \(\mathcal {E}_{1}(k, 0, 0)\) and an interior equilibrium point \(\mathcal {E}_{2}(x^{\star }, y^{\star }, z^{\star }),\) where \(y^{\star }= \displaystyle \frac{\mu _{2}z^{\star }}{\kappa },\) and \(x^{\star }\) and \(z^\star \) satisfy the quadratic equations

$$\begin{aligned} z^{\star }= & {} \frac{p}{\delta }\Big (\varphi +\beta (x^{\star })^{2}\Big )\Big (1-\frac{x^{\star }}{k}\Big ), \quad \beta (x^{\star })^{2}\\&\quad -\,\frac{c \kappa \delta }{(\kappa +\mu _{1})\mu _{2}}x^{\star }+\varphi =0. \end{aligned}$$

The corresponding linearized system of (1) at any equilibrium point \((x^{\star }, y^{\star }, z^{\star })\) is defined as

$$\begin{aligned} D^{\alpha }x(t)&=\Big (p\Big (1- \frac{2 x^{\star }}{k}\Big )-\Big (\frac{\varphi \delta z^{\star }-\delta z^{\star }\beta (x^{\star })^{2}}{(\varphi +\beta (x^{\star })^{2})^{2}}\Big ) \Big ) x(t)\nonumber \\&\quad - \,\frac{\delta x^{\star }}{\varphi +\beta (x^{\star })^{2}}z(t- \tau ),\nonumber \\ D^{\alpha }y(t)&=\Big (\frac{c \varphi \delta z^{\star }-c\delta z^{\star }\beta (x^{\star })^{2}}{(\varphi +\beta (x^{\star })^{2})^{2}}\Big )x(t)- (\kappa +\mu _{1})y(t)\nonumber \\&\quad +\, \frac{c \delta x^{\star }}{\varphi +\beta (x^{\star })^{2}}z(t- \tau ),\nonumber \\ D^{\alpha }z(t)&=\kappa y(t)- \mu _{2} z(t). \end{aligned}$$
(2)

In order to discuss the local stability results of system (2), We take Laplace transform on both sides of (2).

$$\begin{aligned} s^{\alpha } X(s)- s^{\alpha -1} x(0)&= \Big (p\Big (1- \frac{2 x^{\star }}{k}\Big )\nonumber \\&\quad -\,\Big (\frac{\varphi \delta z^{\star }-\delta z^{\star }\beta (x^{\star })^{2}}{(\varphi +\beta (x^{\star })^{2})^{2}}\Big ) \Big ) X(s) \nonumber \\&\quad -\, \frac{\delta x^{\star }}{\varphi +\beta (x^{\star })^{2}}e^{-s \tau }\nonumber \\&\qquad [Z(s)-\int _{-\tau }^{0}e^{-st}\chi (t)\mathrm{d}t],\nonumber \\ s^{\alpha } Y(s)- s^{\alpha -1} y(0)&=\Big (\frac{c \varphi \delta z^{\star }-c\delta z^{\star }\beta (x^{\star })^{2}}{(\varphi +\beta (x^{\star })^{2})^{2}}\Big )X(s)\nonumber \\&\quad -\, (\kappa +\mu _{1})Y(s) \nonumber \\&\quad + \,\frac{c \delta x^{\star }}{\varphi +\beta (x^{\star })^{2}}e^{-s\tau }\nonumber \\&\qquad [Z(s)-\int _{-\tau }^{0}e^{-st}\chi (t)\mathrm{d}t],\nonumber \\ s^{\alpha } Z(s)- s^{\alpha -1} z(0)&=\kappa Y(s)- \mu _{2} Z(s). \end{aligned}$$
(3)

Here, X(s), Y(s), Z(s) are Laplace transform of \(x(t), y(t)\) and z(t) with \(X(s)=L(x(t)), Y(s)=L(y(t))\) and \(Z(s)=L(z(t))\). The above system (3) can be written as

$$\begin{aligned} \Delta (s) \star \Bigl ( {\begin{matrix} X(s)\\ Y(s)\\ Z(s) \end{matrix}} \Bigr ) =\left( {\begin{matrix} b_{1}(s)\\ b_{2}(s)\\ b_{3}(s) \end{matrix}} \right) \end{aligned}$$

where

$$\begin{aligned} b_{1}(s)&=s^{\alpha -1} x(0)+\frac{\delta x^{\star }}{\varphi +\beta (x^{\star })^{2}}e^{-s \tau }\int _{-\tau }^{0}e^{-st}\chi (t)\mathrm{d}t,\\ b_{2}(s)&=s^{\alpha -1} y(0)-\frac{c \delta x^{\star }}{\varphi +\beta (x^{\star })^{2}}e^{-s \tau }\int _{-\tau }^{0}e^{-st}\chi (t)\mathrm{d}t,\\ b_{3}(s)&=s^{\alpha -1} z(0), \end{aligned}$$

and

$$\begin{aligned} \Delta (s) =\left( {\begin{matrix}\displaystyle s^{\alpha }+\left( -p\Big (1- \frac{2 x^{\star }}{k}\Big )+\left( \frac{\varphi \delta z^{\star }-\delta z^{\star }\beta (x^{\star })^{2}}{(\varphi +\beta (x^{\star })^{2})^{2}}\right) \right) &{} \displaystyle 0 &{} \displaystyle \frac{\delta x^{\star }}{\varphi +\beta (x^{\star })^{2}}e^{-s \tau } \\ \displaystyle -\Big (\frac{c \varphi \delta z^{\star }-c\delta z^{\star }\beta (x^{\star })^{2}}{(\varphi +\beta (x^{\star })^{2})^{2}}\Big )&{} \displaystyle s^{\alpha }+\kappa +\mu _{1}&{}\displaystyle \quad -\frac{c \delta x^{\star }}{\varphi +\beta (x^{\star })^{2}}e^{-s \tau } \\ \displaystyle 0 &{}\displaystyle -\,\kappa &{} \displaystyle s^{\alpha }+\mu _{2} \end{matrix}} \right) . \end{aligned}$$

\(\Delta (s)\) is the characteristic matrix for the system (2) at \((x^{\star }, y^{\star }, z^{\star })\). The characteristic polynomial of (2) is \(\mathrm{det}(\Delta (s)).\) The properties of eigenvalues of characteristic equation indicate the stability of system (2).

3 Main results

Herein, we investigate the local and global asymptotic stabilities of fractional-order delayed prey–predator system (1).

Lemma 2

([35]) Let \(x(t) \in \mathbb {R}^{+}\) be a continuous and derivative function. Then, for any time \(t \ge t_{0}\)

$$\begin{aligned}&_{t_{0}}D^{\alpha }_{t}\Big [x(t)-x^{\star }-x^{\star }ln\frac{x(t)}{x^{\star }}\Big ]\\&\quad \le \Big (1-\frac{x^{\star }}{x(t)} \Big )_{t_{0}}D^{\alpha }_{t}x(t), \quad \forall \alpha \in (0, 1), x^{\star } \in \mathbb {R}^{+}. \end{aligned}$$

The characteristic matrix at trivial equilibrium point \(\mathcal {E}_{0}(0, 0, 0)\) is

$$\begin{aligned} \Delta (s)= \left( {\begin{matrix} s^{\alpha }-p &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad s^{\alpha }+\kappa +\mu _{1}&{} \quad 0 \\ 0 &{} \quad -\kappa &{}\quad s^{\alpha }+\mu _{2} \end{matrix}} \right) . \end{aligned}$$

Clearly, the eigenvalues of \(\Delta (s)\) at \(\mathcal {E}_{0}\) are: \(p>0\), \(-(\kappa +\mu _{1})<0\), and \(-\mu _{2}<0\) which confirm that the system (1) around the trivial equilibrium point \(\mathcal {E}_{0}\) is unstable.

Theorem 2

The predator-free equilibrium point \(\mathcal {E}_{1}\) is locally asymptotically stable if

$$\begin{aligned} c<\frac{\mu _{2}(\kappa + \mu _{1}) (\varphi +\beta k^{2})}{\kappa \delta k}. \end{aligned}$$

Proof

The characteristic matrix at predator-free equilibrium point \(\mathcal {E}_{1}(k, 0 ,0)\) is

$$\begin{aligned} \Delta (s)= \left( {\begin{matrix} \displaystyle s^{\alpha }+p &{}\quad \displaystyle 0 &{}\quad \displaystyle \frac{\delta k}{\varphi +\beta k^{2}}e^{-s \tau } \\ \displaystyle 0 &{}\quad \displaystyle s^{\alpha }+\kappa +\mu _{1}&{}\quad \displaystyle -\frac{c \delta k}{\varphi +\beta k^{2}}e^{-s \tau } \\ \displaystyle 0 &{}\quad \displaystyle -\kappa &{}\quad \displaystyle s^{\alpha }+\mu _{2} \end{matrix}} \right) . \end{aligned}$$

The characteristic equation at \(\mathcal {E}_{1}\) is given by

$$\begin{aligned} (s^{\alpha }+p)\Big ((s^{\alpha }+\kappa +\mu _{1})(s^{\alpha }+\mu _{2})- \frac{ \kappa c \delta k}{\varphi +\beta k^{2}}e^{-s \tau }\Big )&=0. \end{aligned}$$
(4)

  • Case (i) When \(\tau =0\).

We have

$$\begin{aligned} s^{\alpha }= & {} -p \quad and \quad (s^{\alpha })^{ 2}+ s^{\alpha }(\kappa + \mu _{1}+\mu _{2})\\&+\,\mu _{2}(\kappa + \mu _{1})-\frac{\kappa c \delta k}{\varphi +\beta k^{2}}=0. \end{aligned}$$

The Routh–Hurwitz criterion provides the sufficient and necessary conditions for all roots, \(s^\alpha _{1,2}\), of the second equation to have real negative parts. The conditions are

$$\begin{aligned}&\kappa + \mu _{1}+\mu _{2}>0, \quad \mu _{2}(\kappa + \mu _{1})-\frac{\kappa c \delta k}{\varphi +\beta k^{2}}>0.\\&\kappa + \mu _{1}+\mu _{2}>0, \quad c<\frac{\mu _{2}(\kappa + \mu _{1}) (\varphi +\beta k^{2})}{\kappa \delta k}. \end{aligned}$$

Therefore, predator-free equilibrium point is locally asymptotically stable if \(c<\frac{\mu _{2}(\kappa + \mu _{1}) (\varphi +\beta k^{2})}{\kappa \delta k}.\)

  • Case(ii) When \(\tau \ne 0\).

In this case, Eq. (4) becomes

$$\begin{aligned}&(s^{\alpha })^{ 2}+ s^{\alpha }(\kappa + \mu _{1}+\mu _{2})+ \mu _{2}(\kappa + \mu _{1})\nonumber \\&\quad -\,\frac{\kappa c \delta k}{\varphi +\beta k^{2}} e^{-s \tau }=0. \end{aligned}$$
(5)

Put \(s = iw, w>0\)

$$\begin{aligned}&((iw)^{\alpha })^{ 2}+ (iw)^{\alpha }(\kappa + \mu _{1}+\mu _{2}) + \mu _{2}(\kappa + \mu _{1})\\&\quad -\,\frac{\kappa c \delta k}{\varphi +\beta k^{2}} e^{-iw \tau }=0,\\&(w^{\alpha })^{2}(\cos \pi \alpha + i \sin \pi \alpha )\\&\quad +\,w^{\alpha }(\kappa + \mu _{1}+\mu _{2})\left( \cos \frac{\pi \alpha }{2}+ i \sin \frac{\pi \alpha }{2}\right) \\&\quad +\,\mu _{2}(\kappa + \mu _{1})\\&\quad -\frac{\kappa c \delta k}{\varphi +\beta k^{2}} \cos w \tau + i \frac{\kappa c \delta k}{\varphi +\beta k^{2}} \sin w \tau =0. \end{aligned}$$

We separate the real and imaginary parts to have

$$\begin{aligned}&(w^{\alpha })^{2} \cos \pi \alpha + w^{\alpha }(\kappa + \mu _{1}+\mu _{2})\cos \frac{\pi \alpha }{2}\\&\qquad + \mu _{2}(\kappa + \mu _{1})=\frac{\kappa c \delta k}{\varphi +\beta k^{2}} \cos w \tau ,\\&(w^{\alpha })^{2} \sin \pi \alpha + w^{\alpha }(\kappa + \mu _{1}+\mu _{2})\sin \frac{\pi \alpha }{2}\\&\quad =- \frac{\kappa c \delta k}{\varphi +\beta k^{2}} \sin w \tau . \end{aligned}$$

If we square and add both sides, we have

$$\begin{aligned}&\Big ( (w^{\alpha })^{2} \cos \pi \alpha + w^{\alpha }(\kappa + \mu _{1}+\mu _{2})\cos \frac{\pi \alpha }{2}+ \mu _{2}(\kappa + \mu _{1})\Big )^2 \nonumber \\&\qquad +\,\Big ((w^{\alpha })^{2} \sin \pi \alpha + w^{\alpha }(\kappa + \mu _{1}+\mu _{2})\sin \frac{\pi \alpha }{2}\Big )^2 \nonumber \\&\quad =\Big (\frac{\kappa c \delta k}{\varphi +\beta k^{2}}\Big )^2,\nonumber \\&(w^{\alpha })^{4}+ 2 (\kappa + \mu _{1}+\mu _{2})\cos \frac{\pi \alpha }{2} (w^{\alpha })^{3}\nonumber \\&\qquad +\, \Big ((\kappa + \mu _{1}+\mu _{2})^2+2 \mu _2(\kappa + \mu _1)\cos \pi \alpha \Big ) (w^{\alpha })^{2}\nonumber \\&\qquad +\,2 \mu _2(\kappa +\mu _1)(\kappa + \mu _{1}+\mu _{2})\cos \frac{\pi \alpha }{2} w^{\alpha }\nonumber \\&\qquad +\,\mu _{2}^{2}(\kappa + \mu _{1})^{2}- \Big (\frac{\kappa c \delta k}{\varphi +\beta k^{2}}\Big )^{2}=0. \end{aligned}$$
(6)

Obviously \(w^{\alpha }>0\), \(\cos \frac{\pi \alpha }{2}>0\) and our assumption that \(\displaystyle c<\frac{\mu _{2}(\kappa + \mu _{1}) (\varphi +\beta k^{2})}{\kappa \delta k},\) then the Eq. (6) has no real solutions. Furthermore, we can infer that Eq. (5) has no purely imaginary roots for any \(\tau >0.\) From Lemma 1 and Corollary 3 in [34], the equilibrium point \(\mathcal {E}_{1}\) is asymptotically stable for delay \(\tau \ge 0.\) \(\square \)

Here, we discuss the stability at an interior equilibrium point \(\mathcal {E}_{2}.\) The characteristic equation at \(\mathcal {E}_{2}\) is

$$\begin{aligned} \left| {\begin{matrix} \displaystyle s^{\alpha }+ a_{1} &{}\quad \displaystyle 0 &{} \quad \displaystyle a_{2}e^{-s \tau } \\ \displaystyle a_{3} &{}\quad \displaystyle s^{\alpha }+a_{4}&{}\quad \displaystyle a_{5}e^{-s \tau } \\ \displaystyle 0 &{}\quad \displaystyle a_{6} &{}\quad \displaystyle s^{\alpha }+a_{7} \end{matrix}} \right| =0. \end{aligned}$$

Therefore,

$$\begin{aligned}&s^{3 \alpha }+ s^{2 \alpha }(a_{1}+a_{4}+a_{7})+ s^{\alpha }(a_{4}a_{7}+a_{1}(a_{4}+a_{7}))\nonumber \\&\quad +\, a_{1}a_{4}a_{7} + e^{-s\tau }\Big (s^{\alpha }(-a_{5}a_{6})+(a_{2}a_{3}a_{6}-a_{1}a_{5}a_{6})\Big )=0. \end{aligned}$$
(7)

Here

$$\begin{aligned} a_{1}= & {} \frac{\varphi \delta z^{\star }-\delta \beta (x^{\star })^{2} z^{\star }}{(\varphi + \beta (x^{\star })^{2})^{2}}-p\left( 1- \frac{2 x^{\star }}{k}\right) ,\\ a_{2}= & {} \frac{\delta x^{\star }}{\varphi +\beta (x^{\star })^{2}}, a_{3}= \frac{\delta \beta c (x^{\star })^{2} z^{\star }-\varphi \delta c z^{\star }}{(\varphi + \beta (x^{\star })^{2})^{2}},\\ a_{4}= & {} \kappa +\mu _{1}, a_{5}=-\frac{c \delta x^{\star }}{\varphi +\beta (x^{\star })^{2}}, a_{6}=-\kappa , a_{7}=\mu _{2},\\ A_{1}= & {} a_{1}+a_{4}+a_{7},\ A_{2}=a_{4}a_{7}+a_{1}(a_{4}+a_{7}),\\ A_{3}= & {} a_{1}a_{4}a_{7},\ A_{4}=-a_{5}a_{6}, \ A_{5}=a_{2}a_{3}a_{6}-a_{1}a_{5}a_{6}. \end{aligned}$$

The discriminant of (7) is given by

$$\begin{aligned} D(s^{\alpha })= & {} -\left| {\begin{matrix} \displaystyle 1 &{}\quad \displaystyle \ A_{1} &{}\quad \displaystyle \ A_{2}+A_{4} &{}\quad \displaystyle \ A_{3}+A_{5}&{}\quad \displaystyle \ 0 \\ \displaystyle \ 0 &{}\quad \displaystyle \ 1 &{} \quad \displaystyle \ A_{1} &{}\quad \displaystyle \ A_{2}+A_{4} &{}\quad \displaystyle \ A_{3}+A_{5} \\ \displaystyle \ 3 &{}\quad \displaystyle \ 2 A_{1} &{}\quad \displaystyle \ A_{2}+A_{4} &{}\quad \displaystyle \ 0 &{}\quad \displaystyle \ 0 \\ \displaystyle \ 0&{}\quad \displaystyle \ 3 &{}\quad \displaystyle \ 2A_{1} &{}\quad \displaystyle \ A_{2}+A_{4} &{}\quad \displaystyle \ 0\\ \displaystyle \ 0 &{}\quad \displaystyle \ 0 &{}\quad \displaystyle \ 3 &{}\quad \displaystyle \ 2A_{1} &{} \quad \displaystyle \ A_{2}+A_{4} \end{matrix}} \right| \\= & {} 18 A_{1}(A_{2}+A_{4})(A_{3}+A_{5})\\&+\, [A_{1}(A_{2}+A_{4})]^{2}- 4 A_{1}^{3}(A_{3}+A_{5})\\&-\,4 (A_{2}+ A_{4})^{3}-27(A_{3}+A_{5})^{2} ([29]). \end{aligned}$$

Theorem 3

Let \(A_{5}^{2}-A_{3}^{2} \ge 0, A_{2}^{2}-2A_{1}A_{5}-A_{4}^{2}>0\), then the interior equilibrium point \(\mathcal {E}_{2}\) is locally asymptotically stable for \(\tau \ge 0,\) if the following conditions are satisfied

  1. (i)

    \( D(s^{\alpha })>0, A_{1}>0, (A_{3}+A_{5})>0, A_{1}(A_{2}+A_{4})-(A_{3}+A_{5})>0\)       (or)

  2. (ii)

    \( D(s^{\alpha })<0, A_{1}>0, (A_{2}+A_{4})>0, A_{1}(A_{2}+A_{4})=(A_{3}+A_{5}), \alpha \in (2/3, 1).\)

Proof

For Case (i) \(\tau =0,\) Eq. (7) takes the form

$$\begin{aligned} s^{3 \alpha }+ s^{2 \alpha }A_{1}+ s^{\alpha }(A_{2}+A_{4})+(A_{3}+A_{5})=0. \end{aligned}$$

Based on [25], the interior point \(\mathcal {E}_{2}\) is asymptotically stable if the following assumptions

  1. (i)

    \( D(s^{\alpha })>0, A_{1}>0, (A_{3}+A_{5})>0, A_{1}(A_{2}+A_{4})-(A_{3}+A_{5})>0\)       (or)

  2. (ii)

    \( D(s^{\alpha })<0, A_{1}>0, (A_{2}+A_{4})>0, A_{1}(A_{2}+A_{4})=(A_{3}+A_{5}), \alpha \in (2/3, 1).\)

hold.

For Case (ii) \(\tau \ne 0\), let us assume that the Eq. (7) has pure imaginary roots \(s=\pm iw,\) for \(\tau >0,\) then we will finally obtain that if \(A_{5}^{2}-A_{3}^{2} \ge 0,\) and \(A_{2}^{2}-2A_{1}A_{5}-A_{4}^{2}>0\) are satisfied. Similar proof of Theorem 2; hence, it is omitted. Therefore, all the roots of Eq. (7) are negative real part for all \(\tau > 0.\) \(\square \)

Now, we study the global asymptotically stability of an interior equilibrium point \(\mathcal {E}_{2}(x^{\star }, y^{\star }, z^{\star })\).

Fig. 1
figure 1

Oscillatory behavior of prey, x(t), and immature predator, y(t), and mature predator, z(t) (left) and phase portrait of the system showing a periodic orbit near (\(x^*, y^*,z^*\)) (right), with delay \(\tau =2.5\) and \(\alpha =0.9\) and parameter values given in the text

Full size image

Theorem 4

Assume that \(\displaystyle \frac{\delta z \beta (x+x^{\star })}{(\varphi +\beta x^{2})(\varphi +\beta (x^{\star })^{2})}<\frac{p}{k}\) and \(\frac{\varphi }{\beta }<xx^{\star }\), then the system (1) is globally asymptotically stable at an interior equilibrium point \(\mathcal {E}_{2}(x^{\star }, y^{\star }, z^{\star })\).

Proof

We define the positive definite function at \(\mathcal {E}_{2}(x^{\star }, y^{\star }, z^{\star })\) of system (1) as

$$\begin{aligned} V(t)= & {} \omega _{1}\Big (x(t)-x^{\star }-x^{\star }ln\frac{x(t)}{x^{\star }}\big )+ \frac{\omega _{2}}{2}(y(t)-y^{\star })^{2}\\&\quad +\,\frac{\omega _{3}}{2}(z(t)-z^{\star })^{2}, \end{aligned}$$

where \(\omega _{1}, \omega _{2}, \omega _{3}\) are nonnegative constants. Taking on fractional order derivative on both sides, using Lemma 2, we get

$$\begin{aligned}&D^{\alpha }V(t)\\&\quad \le \omega _{1}\frac{x(t)-x^{\star }}{x(t)}D^{\alpha }x(t)+\omega _{2}(y(t)-y^{\star })D^{\alpha }y(t)\\&\qquad +\,\omega _{3}(z(t)-z^{\star })D^{\alpha }z(t),\\&\quad \le \omega _{1}(x(t)-x^{\star })\Big (p\Big (1-\frac{x(t)}{k}\Big )-\frac{\delta z(t-\tau )}{\varphi +\beta x^{2}(t)}\Big )\\&\qquad +\,\omega _{2}(y(t)-y^{\star })\Big (\frac{c\delta x(t)z(t-\tau )}{\varphi +\beta x^{2}(t)}-(\kappa +\mu _{1})y(t) \Big )\\&\quad \quad + \omega _{3}(z(t)-z^{\star }) \Big (\kappa y(t)-\mu _{2}z(t) \Big ),\\&\quad \le \omega _{1}(x(t)-x^{\star })\Big (-\frac{p}{k}(x(t)-x^{\star }) +\frac{\delta z^{\star }}{\varphi +\beta (x^{\star })^{2}}\\&\qquad -\,\frac{\delta z(t-\tau )}{\varphi +\beta x^{2}(t)}\Big )+ \omega _{3}(z(t)-z^{\star })\Big (\kappa (y(t)-y^{\star })\\&\qquad -\,\mu _{2}(z(t)-z^{\star }) \Big ) +\omega _{2}(y(t)-y^{\star })\Big (\frac{c\delta x(t)z(t-\tau )}{\varphi +\beta x^{2}(t)}\\&\qquad -\, \frac{c\delta x^{\star }z^{\star }}{\varphi +\beta (x^{\star })^{2}} -(\kappa +\mu _{1})(y(t)-y^{\star }) \Big ),\\&\quad \le -\,\omega _{1}\frac{p}{k}(x(t)-x^{\star })^{2}-\omega _{2}(\kappa +\mu _{1})(y(t)-y^{\star })^{2}\\&\qquad -\,\omega _{3}\mu _{2}(z(t)-z^{\star })^{2} +\omega _{3}\kappa (y(t)-y^{\star }) (z(t)-z^{\star })\\&\qquad +\, \omega _{1}(x(t)-x^{\star })\Big (\frac{\delta z^{\star }}{\varphi +\beta (x^{\star })^{2}}-\frac{\delta z(t-\tau )}{\varphi +\beta x^{2}(t)} \Big )\\&\qquad +\, \omega _{2}(y(t)-y^{\star })\Big (\frac{c\delta x(t)z(t-\tau )}{\varphi +\beta x^{2}(t)}- \frac{c\delta x^{\star }z^{\star }}{\varphi +\beta (x^{\star })^{2}} \Big ),\\&\quad \le -\,\omega _{1}\frac{p}{k}(x-x^{\star })^{2}-\omega _{2}(\kappa +\mu _{1})(y-y^{\star })^{2}\\&\qquad -\omega _{3}\mu _{2}(z-z^{\star })^{2}+\omega _{3}\kappa (y-y^{\star })(z-z^{\star })\\&\qquad -\frac{\omega _{1}\delta (x-x^{\star })(z-z^{\star })}{(\varphi +\beta (x^{\star })^{2})}+ \frac{\omega _{1}\delta z \beta (x+x^{\star })(x-x^{\star })^{2}}{(\varphi +\beta x^{2})(\varphi +\beta (x^{\star })^{2})}\\&\qquad -\,\frac{\omega _{2}c \delta x (y-y^{\star })(z-z^{\star })}{(\varphi +\beta x^{2})}\\&\qquad +\, \frac{\omega _{2}c \delta z^{\star }(x-x^{\star })(y-y^{\star })(\varphi -\beta x x^{\star })}{(\varphi +\beta x^{2})(\varphi +\beta (x^{\star })^{2})},\\&\quad \le \omega _{1}\Big (\frac{\delta z \beta (x+x^{\star })}{(\varphi +\beta x^{2})(\varphi +\beta (x^{\star })^{2})}-\frac{p}{k}\Big )(x-x^{\star })^{2}\\&\qquad -\,\omega _{2}(\kappa +\mu _{1}) (y-y^{\star })^{2}-\omega _{3}\mu _{2}(z-z^{\star })^{2}\\&\qquad +\,\Big (\omega _{3}\kappa -\frac{\omega _{2}c \delta x}{(\varphi +\beta x^{2})} \Big ) (y-y^{\star })(z-z^{\star }) \\&\qquad +\,\frac{\omega _{2}c \delta z^{\star }(\varphi -\beta x x^{\star })}{(\varphi +\beta x^{2})(\varphi +\beta (x^{\star })^{2})}(x-x^{\star })(y-y^{\star })\\&\qquad -\,\frac{\omega _{1}\delta }{(\varphi +\beta (x^{\star })^{2})}(x-x^{\star })(z-z^{\star }). \end{aligned}$$
Fig. 2
figure 2

Prey and predator population asymptotically converge to the equilibrium state value (left). Phase portrait of the system showing that (\(x^*, y^*,z^*\)) (right) is locally asymptotically stable, when with delay \(\tau =1< \tau ^{\star }\) and \(\alpha =0.9\) parameter values given in the text

Full size image
Fig. 3
figure 3

Numerical simulations of the prey x(t) of (1) with different values of fractional orders \(\alpha =0.95, 0.9, 0.85,\) when the time delay \(\tau =1.5\) and conversion coefficient \( c=3.5\) (left) and \(c=1\)(right). Clearly, the fraction order damps the oscillatory behaviors of the model

Full size image
Fig. 4
figure 4

Numerical simulations of the juvenile predator y(t) of (1) with different values of fractional orders \(\alpha =0.95, 0.9, 0.85,\) when the time delay \(\tau =1.5\) and conversion coefficient \( c=3.5\) (left) and \(c=1\)(right). Clearly, the fractional-order damps the oscillatory behaviors of the model

Full size image
Fig. 5
figure 5

Numerical simulations of the adult predator z(t) of (1) with different values of fractional orders \(\alpha =0.95, 0.9, 0.85,\) when the time delay \(\tau =1.5\) and conversion coefficient \( c=3.5\) (left) and \(c=1\) (right). Clearly, the fraction order damps the oscillatory behaviors of the model

Full size image
Fig. 6
figure 6

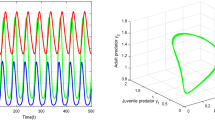
Phase plane behaviors of the model (1) with fractional order \(\alpha =0.95,\) the time delay \(\tau =1.5\) and conversion coefficient \(c=3.5\) (left) and \(c=1\)(right)

Full size image
Fig. 7
figure 7

Phase plane behaviors of the model (1) with fractional order \(\alpha =0.9,\) the time delay \(\tau =1.5\) and conversion coefficient \(c=3.5\) (left) and \(c=1\)(right)

Full size image
Fig. 8
figure 8

Phase plane behaviors of the model (1) with fractional order \(\alpha =0.85,\) the time delay \(\tau =1.5\) and conversion coefficient \(c=3.5\) (left) and \(c=1\)(right)

Full size image

Based on the assumptions that \(\frac{\delta z \beta (x+x^{\star })}{(\varphi +\beta x^{2})(\varphi +\beta (x^{\star })^{2})}<\frac{p}{k}\), \( \frac{\varphi }{\beta }<xx^{\star }\), \(\omega _{3}=\frac{c\delta x}{\varphi +\beta x^{2}}\) and \(\omega _{2}=\kappa ,\) we can get

$$\begin{aligned} D^{\alpha }V&\le \omega _{1}\Big (\frac{\delta z \beta (x+x^{\star })}{(\varphi +\beta x^{2})(\varphi +\beta (x^{\star })^{2})}-\frac{p}{k}\Big )(x-x^{\star })^{2}\\&\quad -\,\omega _{2}(\kappa +\mu _{1}) (y-y^{\star })^{2}-\omega _{3}\mu _{2}(z-z^{\star })^{2}\\&\quad +\,\frac{\omega _{2}c \delta z^{\star }(\varphi -\beta x x^{\star })}{(\varphi +\beta x^{2})(\varphi +\beta (x^{\star })^{2})}(x-x^{\star })(y-y^{\star })\\&\quad -\,\frac{\omega _{1}\delta }{(\varphi +\beta (x^{\star })^{2})}(x-x^{\star })(z-z^{\star }) \le 0. \end{aligned}$$

Hence the theorem is proved. \(\square \)

4 Numerical simulations

To check the feasibility of our theoretical findings regarding stability and bifurcation of the model system (1), we carry out extensive numerical simulations using implicit Euler’s scheme, discussed in [4] for the numerical results of fractional delay differential equations. This method is suitable for stiffFootnote 2 and non-stiff problems. The stiffness often appears due to the differences in speed between the slowest and fastest components of the solutions, and stability constraints. Given the parameter values:

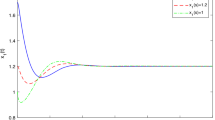
$$\begin{aligned} p= & {} 1.6,\ k=1.72, \ \varphi =0.7,\ \delta =1.4,\ \kappa =0.09,\\ \beta= & {} 0.01,\ \mu _{1}=0.5,\ \mu _{2}=0.05,\ c=1.5. \end{aligned}$$

First, we investigate the impact of time delays on prey–predator population system (1). Figure 1 shows the state trajectories and phase plane behaviors of (1) with fractional-order \(\alpha =0.9\) and time-delay \(\tau =2.5>\tau ^{\star }\), where the system displays an unstable behavior. Figure 2 shows the state trajectories of system (1) which converges to the interior equilibrium point, when time delay \(\tau =1< \tau ^{\star }\) and fractional order \(\alpha =0.9\).

We also discuss the impact of fractional-order \(\alpha \) and conversion coefficient c on the dynamics of every species of system (1). It has been shown that the fractional-order \(\alpha \) and conversion coefficient c parameter play important role on the convergence speed of solutions of model (1). We calculate the critical value of conversion coefficient, \(c_{r}\approx 1.5.\) We plot a diagram for the system (1) with respect to the conversion coefficient c as a bifurcation parameter at the critical value. Figures 3, 4 and 5 display the time domain behaviors of state trajectories (x, y, z) with initial condition \(x(s)=0.3, y(s)=1.3, z(s)=2.3\), different fractional-orders \(\alpha =0.95,\ 0.9,\ 0.85\), and conversion coefficient \(c=3.5\)(left) and \(c=1\)(right). Clearly, the left graph of each figure shows an unstable behavior when \(c=3.5>c_{r}\). However, the right banner of each figure shows a stable behavior when \(c=1<c_{r}.\) From the figures, with lower values of c, the system becomes more stable and we loose stability with higher value of c.

The numerical simulations of (1) are given in Figs. 6, 7 and 8 with different fractional orders \(\alpha =0.95,\ 0.9, \ 0.85\), and \(c=3.5\)(left), \(c=1\)(right). We notice that the convergence speed is affected by the values of the fractional order as well as the parameter c.

We arrive at the following Remarks:

Remark 1

When fractional order \(\alpha =1\) and time delay \(\tau =0\), the system (1) reduces to system given by Khajanchi in [11]. Figures 1, 2, 3, 4, 5, 6, 7 and 8 show the fractional order enlarges the stability regions compared with the corresponding integer-order differential systems. The unstable equilibrium of an integer-order model may be stable in a fractional-order model. Moreover, time delays enrich the dynamics of the model and increase its complexity.

Remark 2

It should be noted that the lower threshold value of \(c<c_{r}=1.5\) gives the system behavior is stable. If we increase the value of \(c>c_{r}\), the system exhibits an unstable behavior. When \(\tau =1< \tau ^\star \), the system demonstrates stable behavior, whereas \(\tau =2.5>\tau ^{\star }\) the system displays an unstable behavior. We choose the conversion coefficient c and time-delay \(\tau \) as bifurcation parameters, as they play an effective role in dynamics of the system.

Remark 3

The combination of a delay time and fractional order in the model can lead to a notable increase in the complexity of the observed behavior, as the solution is continuously depends on all the previous states. However, the presence of fractional-order damps the oscillatory behaviors of the model.

5 Conclusion

In this paper, we introduced a fractional-order prey–predator system with time delay in which predators are divided into juvenile and adult predators using Monod–Haldane-type response function. We also discussed the local and global stability results of all the feasible equilibrium states of the system. Some interesting and new sufficient conditions are discussed for the local asymptotic stability results of stage structured prey–predator model with fractional order. We defined a suitable Lyapunov functional, to successfully obtain the global stability at interior equilibrium point of the model. The fractional order in prey–predator system improves the stability results and sometime damps the oscillation behaviors of solutions. Time delay in the model can destabilize a stable equilibrium to become unstable and stabilize an unstable equilibrium point. A Hopf bifurcation occurs when the time delay passes through its critical value. Moreover, we studied the bifurcation diagram in terms of conversion rate c. For the low-value of conversion rate c, the system shows a stable behavior and for the upper-threshold value of c, the system becomes unstable. If we increase the value of c from prey spices to juvenile predators, the prey species x(t) goes to extinction whereas the juvenile predators y(t) become larger which lead to a catastrophe for the prey community. The high magnitude of conversion coefficient c indicates that the juvenile predators get more foods and nutrients. As a result, the juvenile predators are able to produce high biomass. The numerical simulations, shown in Figures  1, 2, 3, 4, 5, 6, 7 and 8, verified the obtained theoretical results.