Determining an optimal replenishment run time and lot size for an imperfect manufacturing system and rework under markdown policy

Abstract

This study proposes a continuous production inventory model for deteriorating items with preservation technology, rework and price-dependent demand under markdown policy. In this study, we have adopted the markdown policy to reduce inventory cost and clearance at the end of the season or to sell old or slow-moving inventory at the end of its life. Rework is another main factor to reduce production cost and environmental problem. The preservation technology is also considered during product deterioration period to control the deterioration rate of products. The shortages are not allowed. We have also considered that in one cycle, the production system can produce items in several determined replenishment cycles under markdown policy. The aim of this research is to derive the optimal production-run time, the optimal replenishment cycle length, the optimal length of time horizon and the optimal production quantity so as to minimize the total average cost. An example and sensitivity analysis is shown to illustrate the model.

1 Introduction

An economic production quantity (EPQ) model is an inventory control model that determines the amount of product to be produced on a single production setup facility so as to meet a deterministic demand over an infinite planning horizon. Decay or deterioration is defined as decay, evaporation, obsolescence, loss of quality marginal value of a commodity that results in the decreasing usefulness from the original condition. The longer the items are kept in inventory, the higher the deteriorating cost. Retailer sometime uses markdown strategy to reduce their inventory and increase their profit by assuming that demand will increase with price decreases. In this study we developed a replenishment inventory model for deteriorating items and price-dependent demand under markdown policy.

Several researchers have reviewed the inventory models for deteriorating items. Chung and Wee [4] considered short life-cycle deteriorating items with green product design. Widyadana and Wee [41] proposed an EPQ model for deteriorating items with rework and the rework is preformed after m production setups. Palanivel and Uthayakumar [16] presented an EPQ model for deteriorating items with variable production cost, time dependent holding cost and partial backlogging under inflation. Pal et al. [15] scheduled a multi-production EPQ model for deteriorating items with ramp type demand rate allowing effect of inflation when there is shortage in stock under finite time horizon. Jaggi et al. [8] investigated a replenishment policy for non-instantaneous deteriorating items in two-warehouse facilities under inflationary conditions. Sekar and Uthayakumar [19] developed an EPQ model for deteriorating items with rework where the rework is preformed after m production setups. Taleizadeh et al. [26] developed an integrated inventory model with imperfect production where stochastic machine breakdown was considered with no shortages. Recently, Mashud et al. [9] worked on non-instantaneous deteriorating items having different demand rates allowing partial backlog shortage. Pour and Ghobadi [17] presented a two echelon supply chain model for deteriorating items wherein the optimal selling price, production lot size, total cycle time, number of deliveries and delivery lot size are obtained simultaneously. A two warehouse deterministic inventory model for deteriorating items and power demand function has been analyzed by Sharmila and Uthayakumar [21].

Markdowns can play an important role in product lifecycle management. Recently, online shopping attracts the customers, such as amazon, flipkart, etc., by providing stock clearance sale [with some percentage discount on maximum retail price (MRP)] during festival time or end of the season to sell unsold items. Markdown policy is frequently used in retail business, but it can be a competitive advantage in any business where the store needs to move slow-selling merchandise off the shelves as rapidly as possible to reinvest in more-popular items. Markdown pricing can also be used to motivate bargain hunters to make a buying decision. Markdowns are often associated with margin degradation and profit loss. And some companies believe that cutting prices for their products could negatively impact their brand image. Although inevitable, retailers have historically viewed markdowns as a necessary evil, designed to help sell old or slow-moving inventory. Hence, inventory model with markdown price and stock-dependent demand is also getting attention of researchers. You and Hsieh [43] have presented an EOQ model with stock-price dependent demand to maximize profit and to obtain the order quantity and selling price. They did not consider the deteriorating items. Garg et al. [6] consider price discounting for non-instantaneous deteriorating items. Wang et al. [40] developed an optimal markdown policy model for perishable food pricing to optimize the food retailer revenue and enable a maximum aggregated consumer utility. Namin et al. [12] empirically examined the determinants of a retailer’s dynamic pricing policy and investigated consumer response to price changes (markdowns) throughout a fashion product’s selling season. The effect of inventory on demand has been analyzed in a variety of practical settings in both the operations management and marketing literature, e.g., Caro and Gallien [3], Collado [5] and Smith [22]. Srivastava and Gupta [23] presented deterioration with time and price dependent demand under markdown policy.

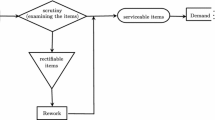
Rework is one of the major problems in reverse logistic and green supply chain management, since it can reduce production cost and environmental problem. Many researchers focus on developing rework model, but few of them developed model for deteriorating items. The earliest research that focused on reworking and remanufacturing process was done by Schrady [18]. Since then, researches on rework have attracted many researchers. Yoo et al. [42] developed an EPQ model with imperfect production quality, imperfect inspection and rework. Hsueh [7] investigated inventory control policies for manufacturing/remanufacturing system by considering different product life cycle phases. Tai [24] proposed two single-period EPQ inventory models for deteriorating/imperfect items with rework. He assumed that the imperfect quality items need to be reworked and the perfect quality items might be deteriorating. The first inventory model is a single production-rework system and the second model is a system that considers several production plants and one rework plant. Cárdenas-Barrón et al. [2] studied a vendor–buyer system with multiple deliveries and rework to derive the optimal delivery policy and replenishment batch size. In their study, the proposed problem is solved under two different scenarios; the first scenario dealt with the case that only number of shipments must take discrete values and in the second scenario both number of shipments and batch sizes are discrete values. Nobil and Taleizadeh [13] presented a single machine and multi-product inventory model for defective items in which the defective products produced are reworked or they are put on auction as they are. Benkherouf et al. [1] offered an EPQ model for deteriorating and defective items and time-varying demand over planning horizon. Recently, Taleizadeh et al. [25] dealt with an economic production quantity (EPQ) model with imperfect items and backordered demand. They assumed that the manufacturing companies decide to repair the imperfect items outside because reworking process on the imperfect items may need welding or turning machines and/or another type of machines which are not available and buying a machine is not affordable. Recently, Moshtagh and Taleizadeh [11] extended a hybrid manufacturing/remanufacturing model by considering short age, rework, and quality-dependent return rate in which quality of used items is considered as a random variable. Sekar and Uthayakumar [20] developed an imperfect production inventory model for defective items where the defective items are reworked after several production processes and there is no machine break down during the rework process. In their paper, the defective items are repaired and converted into items of perfect quality. Also some related research can be found in Taleizadeh et al. [32, 34,35,36,37,38], Mohammadi et al. [10] and Taleizadeh and Noori-daryan [33]. Table 1 shows that the difference between some existing inventory model and this inventory model.

Table 1 Summary of related literature for multi-production run, imperfect production, imperfect rework and markdown policy

In this proposed model, an EPQ model for single product subject to instantaneous deterioration under a production policy with price dependent demand under markdown policy is developed. This model is basically developed for those perishable products whose demand is low as compared to the other perishable products. To increase the profit and to reduce the storage inventory, we have adopted the markdown strategy. The main objective of the suggested model is to determine the optimum time where we can implement the markdown scheme, to minimize our total inventory cost. In addition to this, an attempt has been made to develop the mathematical expressions of replenishment cycle time, production quantity and total inventory cost. All the theoretical developments are illustrated with the help of a numerical example. The assumptions and nomenclature involved in this model are given in the Sect. 2. The Sect. 3 provides problem description of the model. The mathematical development is presented in the Sect. 4. The numerical example and the sensitivity analysis are given in the Sect. 5. Finally, the conclusion is drawn in Sect. 6.

2 Assumptions and nomenclature

The following assumptions and nomenclatures are considered to develop the proposed inventory model.

2.1 Assumptions

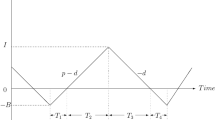
• 1. Demand increase as price is reduced. The demand (d) at time t is assumed to be $\beta \left( {as} \right)^{ - \rho }$, where $a = 1 - {\text{M}}_{\text{r}}$ ($'a'$ lies between 0 and 1 in the interval $\left[ {0, {\text{T}}_{3} } \right]$ and $a = 1$ otherwise) and $\beta$, $\rho$, ${\text{M}}_{\text{r}}$ are positive constants.

• 2. A single item is considered over a prescribed period of T units of time.

• 3. The on hand stock deteriorates at a constant rate.

• 4. Markdown price and time are known.

• 5. The rate of producing good quality items and rework must be greater than the demand rate.

• 6. No machine breakdown occurs in the production run and rework run period.

• 7. Production and rework rate are constants and demand is price-dependant.

• 8. Defective items are generated only during production run. Scrap items are occurred only during rework run.

• 9. Shortages are not allowed.

• 10. The rate of producing good quality items is greater than the sum of the demand rate and the deteriorating rate; mathematically says $\alpha p > (d + \theta (I_{1} t_{1} ))$.

2.2 Nomenclature

$p$ :

Production rate (unit/unit time)

$\delta$ :

Production percentage

$r$ :

Markdown percentage

$\gamma$ :

Percentage of deteriorated items screened out from the inventory

$\theta$ :

Percentage of items deteriorated per unit time

$\epsilon$ :

Preservation technology cost for reducing deterioration rate in order to preserve the products, $\epsilon > 0$

$\lambda$ :

Resultant deterioration rate, $\lambda = \theta - m(\epsilon )$

$\beta$ :

Constant stock dependent parameter

$\rho$ :

Increase price rate

$p_{r}$ :

Rework process rate

$\alpha$ :

Percentage of good quality items produced

$\alpha_{r}$ :

Percentage of imperfect items recovered

$s_{c}$ :

Scrap cost ($/unit)

$h_{s}$ :

Holding cost of qualified items ($/unit/unit time)

$h_{r}$ :

Holding cost of unqualified items ($/unit/unit time)

$D_{c}$ :

Deterioration cost ($/unit)

$p_{c}$ :

Penalty cost of selling deteriorated items to customers ($/unit)

$K_{s}$ :

Setup cost for a replenishment cycle ($/setup)

$K_{p}$ :

Unit production cost ($/unit)

$K_{R}$ :

Unit rework cost ($/unit)

$K_{r}$ :

Rework setup cost ($/setup)

$s$ :

Initial price of the unit ($/unit)

$T_{3}$ :

Markdown offering time

$M_{r}$ :

Markdown rate

$I_{ms}$ :

Maximum inventory level of serviceable items in a production run

$I_{mp}$ :

Inventory level of qualified items when markdown offering time started in a production run

$I_{mr}$ :

Maximum inventory level of defective items in a production run

$I_{er}$ :

Maximum inventory level of defective items at the end of $m$ replenishment cycles

$I_{sr}$ :

Maximum inventory level of serviceable items during rework run

$T$ :

Length of the time horizon

$T_{R1}$ :

Length of a replenishment cycle

$TC_{F}$ :

Total cost function per unit time

3 Problem description

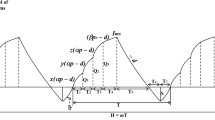
A production inventory model is considered in which production process, rework-run and inspection of deteriorating items are all imperfect. In order to provide 100% quality items to customers, during production, all the produced items are inspected. Thus, during the production run time, the imperfect items are identified and kept separately from qualified items. During production run time, the shortages do not occur. This means that the production rate is greater than the demand rate plus the production rate of imperfect items; mathematically says this is ${\text{p}} > ({\text{d}} + \left( {1 - } \right){\text{p}})$. The behavior of the inventory level of qualified and unqualified items is shown in Figs. 1 and 2. The production is performed during $T_{1}$ time period. When production is established, there are $\left( {1 - \alpha } \right)p$ products defect per unit time. $T_{2}$ is the non-production time period. The markdown policy is implemented during the time period $T_{3}$. The defective items produced in production period are reworked in $T_{4}$ time period. During the rework-run time, a portion $\left( {1 - \alpha_{r} } \right)p_{r}$ of the defective items fails in rework and they are considered as scrapped items (disposal items). $T_{5}$ is the non-rework time period. Since the inspection of deteriorated items is imperfect, only a percentage $(\gamma \theta )$ of deteriorated items are identified and the rest $(1 - \gamma )\theta$ is sold to customers, which will create penalty cost for retailers. In each replenishment cycle $({\text{T}}_{{{\text{R}}1}} )$, the similar manufacturing system is performed. T is the inventory time horizon which contains m replenishment cycles and one rework-run.

4 Mathematical formulation of the inventory model

In this section, we present the mathematical formulation for the inventory level of qualified and unqualified items.

4.1 Deteriorative inventory level of qualified items

The behavior of the inventory level of serviceable items with three production runs including markdown policy and one rework run is illustrated in Fig. 1. The inventory levels of serviceable items at time ‘t’ over the five periods in a replenishment cycle are determined by the following differential equations:

Fig. 1

Serviceable inventory level of 3 production runs and one rework run

The inventory level of qualified items in a production run period $\left[ {0, T_{1} } \right]$ can be presented as:

$$ \frac{{dI_{1} (t_{1} )}}{{dt_{1} }} + \gamma \lambda I_{1} \left( {t_{1} } \right) = \alpha p - d\quad 0 \le t_{1} \le T_{1} $$

(1)

The inventory level of qualified items in a non-production run period $\left[ {0, T_{2} } \right]$ can be presented as:

$$ \frac{{dI_{2} (t_{2} )}}{{dt_{2} }} + \gamma \lambda I_{2} \left( {t_{2} } \right) = - d\quad 0 \le t_{2} \le T_{2} $$

(2)

The inventory level of qualified items in a non-production run time during markdown policy period $\left[ {0, T_{3} } \right]$ is represented by:

$$ \frac{{dI_{3} (t_{3} )}}{{dt_{3} }} + \gamma \lambda I_{3} \left( {t_{3} } \right) = - d\quad 0 \le t_{3} \le T_{3} $$

(3)

The inventory level of qualified items during rework run period $\left[ {0, T_{4} } \right]$ is given by

$$ \frac{{dI_{4} (t_{4} )}}{{dt_{4} }} + \gamma \lambda I_{4} \left( {t_{4} } \right) = \alpha_{r} p_{r} - d{\kern 1pt} \quad 0 \le t_{4} \le T_{4} $$

(4)

The inventory level of qualified items during non-rework run period $\left[ {0, T_{5} } \right]$ is given by

$$ \frac{{dI_{5} (t_{5} )}}{{dt_{5} }} + \gamma \lambda I_{5} \left( {t_{5} } \right) = - d\quad 0 \le t_{5} \le T_{5} $$

(5)

When $t_{1} = 0$, $I_{1} \left( {t_{1} } \right) = 0$, the inventory level of qualified items in a production run time is given by:

$$ I_{1} \left( {t_{1} } \right) = \frac{{\alpha p - \beta \left( s \right)^{ - \rho } }}{\gamma \lambda }\left( {1 - e^{{ - \gamma \lambda t_{1} }} } \right)\quad 0 \le t_{1} \le T_{1} $$

(6)

When $t_{2} = 0$, $I_{2} \left( {t_{2} } \right) = I_{ms}$, the inventory level of qualified items in a non-production run time is:

$$ I_{2} \left( {t_{2} } \right) = \frac{{ - \beta \left( s \right)^{ - \rho } }}{\gamma \lambda } + \left( {I_{ms} + \frac{{\beta \left( s \right)^{ - \rho } }}{\gamma \lambda }} \right)e^{{ - \gamma \lambda t_{2} }} \quad 0 \le t_{2} \le T_{2} $$

(7)

Since $I_{3} \left( {t_{3} } \right) = 0$ when $t_{3} = T_{3}$, the inventory level of qualified items during markdown period is:

$$ I_{3} \left( {t_{3} } \right) = \frac{{\beta \left( {as} \right)^{ - \rho } }}{\gamma \lambda }\left( {e^{{\left( {T_{3} - t_{3} } \right)\gamma \lambda }} - 1} \right)\quad 0 \le t_{3} \le T_{3} $$

(8)

Using $I_{4} \left( 0 \right) = 0$ in Eq. (4), we obtain the inventory level of qualified items during rework run period as:

$$ I_{4} \left( {t_{4} } \right) = \frac{{\alpha_{r} p_{r} - \beta \left( s \right)^{ - \rho } }}{\gamma \lambda }\left( {1 - e^{{ - \gamma \lambda t_{4} }} } \right)\quad 0 \le t_{4} \le T_{4} $$

(9)

and using the boundary condition $I_{5} \left( {T_{5} } \right) = 0$ in Eq. (5), we get the inventory level of qualified items during non-rework run time:

$$ I_{5} \left( {t_{5} } \right) = \frac{{\beta \left( s \right)^{ - \rho } }}{\gamma \lambda }\left( {e^{{\left( {T_{5} - t_{5} } \right)\gamma \lambda }} - 1} \right)\quad 0 \le t_{5} \le T_{5} $$

(10)

When $t_{1} = T_{1}$, it can be deduced from Eq. (1) that the maximum inventory level of qualified items:

$$ I_{ms} = \frac{{\alpha p - \beta \left( s \right)^{ - \rho } }}{\gamma \lambda }\left( {1 - e^{{ - \gamma \lambda T_{1} }} } \right) $$

Since $\left( {\gamma \lambda } \right)T_{1}$ is very small, we adopt the Taylor series approximation as $e^{x} \approx 1 + x + \frac{{x^{2} }}{2}.$

Hence, the $I_{ms}$ can be simplified as

$$ I_{ms} = \left( {\alpha p - \beta \left( s \right)^{ - \rho } } \right)\left( {T_{1} - \left( {\frac{\gamma \lambda }{2}} \right)T_{1}^{2} } \right) $$

(11)

Since $I_{3} \left( 0 \right) = I_{mp}$, the inventory level of qualified items during the period of markdown policy is derived as:

$$ I_{mp} = \beta \left( {as} \right)^{ - \rho } \left( {T_{3} + \left( {\frac{\gamma \lambda }{2}} \right)T_{3}^{2} } \right) $$

(12)

Similarly, the maximum inventory level of qualified items at the end of rework run is obtained from Eq. (9). That is, when $t_{4} = T_{4}$, $I_{4} \left( {t_{4} } \right) = I_{sr}$. The $I_{sr}$ is given by

$$ I_{sr} = \left( {\alpha_{r} p_{r} - \beta \left( s \right)^{ - \rho } } \right)\left( {T_{4} - \left( {\frac{\gamma \lambda }{2}} \right)T_{4}^{2} } \right) $$

(13)

4.2 Deteriorative inventory level of unqualified items

The behavior of the inventory level of unqualified items with three production runs and one rework run is illustrated in Fig. 2. The inventory levels of unqualified items during production and non-production run at t time over an inventory cycle are determined by the following differential equations:

Fig. 2

Unqualified items inventory level of 3 production runs and one rework runs

The inventory level of unqualified items in a production-run period $\left[ {0, T_{1} } \right]$ can be modeled as:

$$ \frac{{dI_{r1} (t_{r1} )}}{{dt_{r1} }} + \gamma \lambda I_{r1} \left( {t_{r1} } \right) = (1 - \alpha )p\quad 0 \le t_{r1} \le T_{1} $$

(14)

The inventory level of unqualified items in a non-production-run period $\left[ {0, T_{2} } \right]$ can be represented as:

$$ \frac{{dI_{r23} (t_{r23} )}}{{dt_{r23} }} + \gamma \lambda I_{r23} \left( {t_{r23} } \right) = 0\quad 0 \le t_{r23} \le \left( {m - 1} \right)T_{1} + m\left( {T_{2} + T_{3} } \right) $$

(15)

The inventory level of unqualified items in a rework run period $\left[ {0, T_{4} } \right]$ can be derived as:

$$ \frac{{dI_{r4} (t_{r4} )}}{{dt_{r4} }} + \gamma \lambda I_{r4} \left( {t_{r4} } \right) = - p_{r} \quad 0 \le t_{r4} \le T_{4} $$

(16)

The inventory level of unqualified items during $\left[ {0, T_{1} } \right]$ is obtained by solving the Eq. (14) with the help of the boundary condition ${\text{I}}_{{{\text{r}}1}} \left( 0 \right) = 0$.

$$ I_{r1} \left( {t_{r1} } \right) = \frac{{\left( {1 - \alpha } \right)p}}{\gamma \lambda }\left( {1 - e^{{ - \gamma \lambda t_{r1} }} } \right)\quad {\kern 1pt} 0 \le t_{r1} \le T_{1} $$

(17)

Solving the Eq. (15) by using the boundary condition $I_{r23} \left( 0 \right) = I_{mr}$, we obtain the inventory level of unqualified items during the non-production period.

$$ I_{r23} \left( {t_{r23} } \right) = I_{mr} e^{{ - \gamma \lambda t_{r23} }} \quad 0 \le t_{r23} \le \left( {m - 1} \right)T_{1} + m\left( {T_{2} + T_{3} } \right) $$

(18)

It is evident from Eq. (16) that the on hand inventory level of unqualified items during the rework run time $\left[ {0, T_{4} } \right]$ is given by:

$$ I_{r4} \left( {t_{r4} } \right) = \frac{{p_{r} }}{\gamma \lambda }\left( {e^{{\gamma \lambda \left( {T_{4} - t_{r4} } \right)}} - 1} \right)\quad 0 \le t_{r4} \le T_{4} $$

(19)

Since $I_{r1} \left( {t_{r1} } \right) = I_{mr}$ when $t_{r1} = T_{1}$, the inventory level of unqualified items in each production can be modeled as:

$$ I_{mr} = \frac{{\left( {1 - \alpha } \right)p}}{\gamma \lambda }\left( {1 - e^{{ - \gamma \lambda T_{1} }} } \right) $$

Using the Taylor series approximation, the $I_{ms}$ can be simplified under the assumption that $\left( {\gamma \lambda } \right)T_{1}$ is very small.

$$ I_{mr} = \left( {1 - \alpha } \right)p\left( {T_{1} - \left( {\frac{\gamma \lambda }{2}} \right)T_{1}^{2} } \right) $$

(20)

The total inventory level of unqualified items in the end of m replenishment cycle $\left( {I_{er} } \right)$ is equal to the maximum inventory level of unqualified items in a production-run reduced by number of deteriorating items (screened out in m replenishment cycles) during the production and the non-production run time. That is,

$$ I_{er} = \mathop \sum \limits_{k = 1}^{m} I_{mr} e^{{ - \left( {\gamma \lambda } \right)(\left( {k - 1} \right)T_{1} + k\left( {T_{2} + T_{3} } \right))}} $$

This can be reformulated using Taylor series expansion as:

$$ I_{er} = \left( {1 - \alpha } \right)p\left( {T_{1} - \left( {\frac{\gamma \lambda }{2}} \right)T_{1}^{2} } \right)\mathop \sum \limits_{k = 1}^{m} \left( {1 - \left( {\gamma \lambda } \right)\left( {\left( {k - 1} \right)T_{1} + k\left( {T_{2} + T_{3} } \right)} \right) + \frac{{\left( {\left( {\gamma \lambda } \right)(\left( {k - 1} \right)T_{1} + k\left( {T_{2} + T_{3} } \right))} \right)^{2} }}{2}} \right) $$

(21)

Next we perform the cost analysis to calculate the total cost function of the proposed model. The total replenishment time consists of the production up time and production down time. The total time horizon consists of m replenishment cycles and one rework run.

(i) Production cost (PRC)

In a replenishment cycle, the production run is carried out during the period $\left[ {0, T_{1} } \right]$. The production cost for one replenishment cycle is calculated by

$$ PRC = \frac{{k_{p} }}{T}\left( {pT_{1} } \right) $$

Since there are m replenishment cycles in a time horizon, the production cost of one inventory cycle is:

$$ PRC = \mathop \sum \limits_{i = 1}^{m} \frac{{k_{p} }}{T}\left( {pT_{1} } \right) = m\left( {\frac{{pk_{p} T_{1} }}{T}} \right) $$

(22)

(ii) Rework cost (RC)

During the time interval $\left[ {0, T_{3} } \right]$, the rework run is processed. Since there is one rework-run in an inventory cycle, the rework cost of an inventory cycle is:

$$ RC = \frac{{k_{R} }}{T}\left( {p_{r} T_{4} } \right) $$

(23)

(iii) Setup cost ($SC_{1}$)

In a replenishment cycle, the production-run setup cost occurs when ${\text{t}}_{1} = 0$ in $\left[ {0, {\text{T}}_{1} } \right]$ for every production-run. Therefore, the setup cost is: SC₁ = setup cost of production-run for m replenishment cycle + setup cost of rework-run

$$ SC_{1} = \frac{1}{T}\left( {mk_{s} + k_{r} } \right) $$

(24)

(iv) Deterioration cost (DC)

Total deteriorating items from the inventory of qualified items over $\left[ {0, T} \right]$ is calculated as follows: The number of deteriorating units is equal to the number of total units produced minus the number of total demand and scrap units.

DC =  $\frac{{D_{c} }}{T}$ {Total qualified items produced in production-run period $\left[ {0, T_{1} } \right]$  + Total qualified items produced in rework-run period $\left[ {0, {\text{T}}_{4} } \right]$  − demand over $\left[ {0, {\text{T}}_{1} } \right]$, $\left[ {0, {\text{T}}_{2} } \right]$, $\left[ {0, {\text{T}}_{3} } \right]$, $\left[ {0, {\text{T}}_{4} } \right]$ and $\left[ {0, {\text{T}}_{5} } \right]$  − scrap items produced in $\left[ {0, {\text{T}}_{4} } \right]$  − No. of items deteriorated during waiting for rework}.

Hence, the total deteriorating items of m replenishment cycles is

$$ \begin{aligned} DC &= \frac{{D_{c} }}{T}\left\{ {\left( {m\alpha pT_{1} + \alpha_{r} p_{r} T_{4} } \right) - d\left( {m(T_{1} + T_{2} + T_{3} } \right) + T_{4} + T_{5} ) - \left( {1 - \alpha_{r} } \right)p_{r} T_{4} + (m\left( {1 - \alpha } \right)pT_{1} - I_{er} )} \right\} \hfill \\ DC &= \frac{{D_{c} }}{T}\left\{ {mpT_{1} + \left( {2\alpha_{r} - 1} \right)p_{r} T_{4} - \beta \left( s \right)^{ - \rho } \left( {m\left( {T_{1} + T_{2} } \right) + T_{4} + T_{5} } \right) - m\beta \left( {as} \right)^{ - \rho } T_{3} - I_{er} } \right\} \hfill \\ \end{aligned} $$

(25)

(v) Penalty cost (PC)

Penalty cost for selling the deteriorated items to customers occurs during the intervals $\left[ {0, T_{1} } \right]$, $\left[ {0, T_{2} } \right]$ and $\left[ {0, T_{3} } \right]$ in a replenishment cycle and $\left[ {0, T_{4} } \right]$ and $\left[ {0, T_{5} } \right]$ in a rework-run time. The penalty cost for m replenishment cycles with one rework-run is obtained as:

$$ PC = \frac{{(1 - \gamma )p_{c} }}{\gamma T}\left\{ {mpT_{1} + \left( {2\alpha_{r} - 1} \right)p_{r} T_{4} - \beta \left( s \right)^{ - \rho } \left( {m\left( {T_{1} + T_{2} } \right) + T_{4} + T_{5} } \right) - m\beta \left( {as} \right)^{ - \rho } T_{3} - I_{er} } \right\} $$

(26)

(vi) Scrap cost ($SC_{2}$)

Scrap items are generated during rework-run period $\left[ {0, T_{4} } \right]$ only. The cost of the disposable items is:

$$ SC_{2} = \frac{{s_{c} }}{T}\left( {1 - \alpha_{r} } \right)p_{r} T_{4} $$

(27)

(vii) Holding cost of qualified items $(HC_{q} )$

As we have to keep the items in stock during the inventory time horizon $\left[ {0, T} \right]$, we calculate the holding cost of the qualified items in the inventory time horizon.

$$ \begin{aligned} HC_{q} &= \frac{{h_{s} }}{T}\left\{ {m\mathop \smallint \limits_{0}^{{T_{1} }} I_{1} \left( {t_{1} } \right)dt_{1} + m\mathop \smallint \limits_{0}^{{T_{2} }} I_{2} \left( {t_{2} } \right)dt_{2} + m\mathop \smallint \limits_{0}^{{T_{3} }} I_{3} \left( {t_{3} } \right)dt_{3} + \mathop \smallint \limits_{0}^{{T_{4} }} I_{4} \left( {t_{4} } \right)dt_{4} + \mathop \smallint \limits_{0}^{{T_{5} }} I_{5} \left( {t_{5} } \right)dt_{5} } \right\} \hfill \\ HC_{q} &= \frac{{h_{s} }}{T}\left\{ {\frac{{m(\alpha p - \beta \left( s \right)^{ - \rho } )}}{2}T_{1}^{2} + mI_{ms} T_{2} - \frac{{m\left( {\gamma \lambda I_{ms} + d} \right)}}{2}T_{2}^{2} + \frac{{\alpha_{r} p_{r} - \beta \left( s \right)^{ - \rho } }}{2}T_{4}^{2} + \frac{{\beta \left( s \right)^{ - \rho } }}{2}\left( {m\left( a \right)^{ - \rho } T_{3}^{2} + T_{5}^{2} } \right)} \right\} \hfill \\ \end{aligned} $$

(28)

(viii) Holding cost of unqualified items $\left( {HC_{uq} } \right)$

The unqualified items produced in m replenishment cycles are reworked immediately after mth replenishment cycle. Since the unqualified items produced in 1, 2, …, m replenishment cycles are waiting until rework-run started, they may deteriorate during the waiting time. Hence, the holding cost of unqualified items is written as:

$$ \begin{aligned} HC_{uq} &= \frac{{h_{r} }}{T}\left\{ {m\mathop \smallint \limits_{0}^{{T_{1} }} I_{r1} \left( {t_{r1} } \right)dt_{r1} + \mathop \sum \limits_{k = 1}^{m} \mathop \smallint \limits_{0}^{{(k - 1)T_{1} + k(T_{2} + T_{3} )}} I_{r23} \left( {t_{r23} } \right)dt_{r23} + \mathop \smallint \limits_{0}^{{T_{4} }} I_{r4} \left( {t_{r4} } \right)dt_{r4} } \right\} \hfill \\ HC_{uq} &= \frac{{h_{r} }}{T}\left\{ {\frac{{m\left( {1 - \alpha } \right)p}}{2}T_{1}^{2} + \frac{{I_{mr} }}{2}\mathop \sum \limits_{k = 1}^{m} \left( {k\left( {T_{1} + T_{2} + T_{3} } \right) - T_{1} } \right)\left( {2 - \gamma \lambda \left( {k\left( {T_{1} + T_{2} + T_{3} } \right)} \right)} \right) + \frac{{p_{r} }}{2}T_{4}^{2} } \right\} \hfill \\ \end{aligned} $$

(29)

Now the total inventory cost for m replenishment cycle is consists of production cost, rework cost, setup cost, deterioration cost, penalty cost of selling the deteriorated items to customers, scrap cost, holding cost of qualified items and unqualified items.

That is, $TC_{F} = \frac{{\left( {PRC + RC + SC_{1} + DC + PC + SC_{2} + HC_{q} + HC_{uq} } \right)}}{{m\left( {T_{1} + T_{2} + T_{3} } \right) + T_{4} + T_{5} }}$

$$ TC_{F} = \frac{1}{T}\left[ {\begin{array}{*{20}l} {m\left( {pk_{p} T_{1} } \right) + k_{R} \left( {p_{r} T_{4} } \right) + mk_{s} + k_{r} + s_{c} \left( {1 - \alpha _{r} } \right)p_{r} T_{4} } \hfill \\ { + D_{c} \left\{ {mpT_{1} + \left( {2\alpha _{r} - 1} \right)p_{r} T_{4} - \beta \left( s \right)^{{ - \rho }} \left( {m\left( {T_{1} + T_{2} } \right) + T_{4} + T_{5} } \right) - m\beta \left( {as} \right)^{{ - \rho }} T_{3} - I_{{er}} } \right\}} \hfill \\ { + \frac{{(1 - \gamma )p_{c} }}{\gamma }\left\{ {mpT_{1} + \left( {2\alpha _{r} - 1} \right)p_{r} T_{4} - \beta \left( s \right)^{{ - \rho }} \left( {m\left( {T_{1} + T_{2} } \right) + T_{4} + T_{5} } \right) - m\beta \left( {as} \right)^{{ - \rho }} T_{3} - I_{{er}} } \right\}} \hfill \\ { + ~h_{s} \left\{ {\frac{{m(\alpha p - \beta \left( s \right)^{{ - \rho }} )}}{2}T_{1}^{2} + mI_{{ms}} T_{2} - \frac{{m\left( {\delta \gamma I_{{ms}} + d} \right)}}{2}T_{2}^{2} + \frac{{\alpha _{r} p_{r} - \beta \left( s \right)^{{ - \rho }} }}{2}T_{4}^{2} + \frac{{\beta \left( s \right)^{{ - \rho }} }}{2}\left( {m\left( a \right)^{{ - \rho }} T_{3}^{2} + T_{5}^{2} } \right)} \right\}} \hfill \\ { + ~h_{r} \left\{ {\frac{{m\left( {1 - \alpha } \right)p}}{2}T_{1}^{2} + \frac{{I_{{mr}} }}{2}\mathop \sum \limits_{{k = 1}}^{m} \left( {k\left( {T_{1} + T_{2} + T_{3} } \right) - T_{1} } \right)\left( {2 - \gamma \lambda \left( {k\left( {T_{1} + T_{2} + T_{3} } \right)} \right)} \right) + \frac{{p_{r} }}{2}T_{4}^{2} } \right\}} \hfill \\ \end{array} } \right] $$

(30)

In order to simplify the total cost function, the relations between $T_{i} (i = 1,2,3,4,5)$, $T_{R1}$ and $T$ are required. First we note down the replenishment time $T_{1}$, $T_{2}$ and $T_{3}$ in terms of $T_{R1}$ as given below:

$$ T_{1} = \delta T_{R1} $$

(31)

$$ T_{2} = r\left( {T_{R1} - T_{1} } \right) = r(1 - \delta )T_{R1} $$

(32)

$$ T_{3} = T_{R1} - \left( {T_{1} + T_{2} } \right) = T_{R1} \left( {1 - \delta } \right)\left( {1 - r} \right) $$

(33)

When $t_{r4} = 0$, the inventory level of unqualified items is equal to $I_{er}$.

$$ \frac{{p_{r} }}{\gamma \lambda }\left( {e^{{\gamma \lambda T_{3} }} - 1} \right) = I_{er} $$

Since $\gamma \lambda T_{3} < < 1$ and using Taylor series expansion results in:

$$ T_{4} = \frac{{I_{er} }}{{p_{r} }} $$

(34)

$$ T_{4} = \frac{{\left( {1 - \alpha } \right)p\left( {T_{1} - \left( {\frac{\gamma \lambda }{2}} \right)T_{1}^{2} } \right)}}{{p_{r} }}\mathop \sum \limits_{k = 1}^{m} \left( {1 - \left( {\gamma \lambda } \right)\left( {\left( {k - 1} \right)T_{1} + k\left( {T_{2} + T_{3} } \right)} \right) + \frac{{\left( {\left( {\gamma \lambda } \right)(\left( {k - 1} \right)T_{1} + k\left( {T_{2} + T_{3} } \right))} \right)^{2} }}{2}} \right) $$

Since $I_{4} \left( {T_{4} } \right) = I_{5} \left( 0 \right)$, we have

$$ \frac{{\alpha_{r} p_{r} - \beta \left( s \right)^{ - \rho } }}{\gamma \lambda }\left( {1 - e^{{ - \gamma \lambda T_{4} }} } \right) = \frac{{\beta \left( s \right)^{ - \rho } }}{\gamma \lambda }\left( {e^{{\gamma \lambda T_{5} }} - 1} \right) $$

Simplifying the above equation by using Taylor series expansion we get the non-rework-run time:

$$ T_{5} = \frac{{\left( {\alpha_{r} p_{r} - \beta \left( s \right)^{ - \rho } } \right)\left( {2T_{4} - \gamma \lambda T_{4}^{2} } \right)}}{{2\beta \left( s \right)^{ - \rho } }} $$

(35)

Finally, the inventory time horizon $T$ is defined as

$$ T = \mathop \sum \limits_{i = 1}^{3} (mT_{{R_{i} }} ) + T_{4} + T_{5} \quad {\text{where}}\quad T_{Ri} = T_{1} + T_{2} + T_{3} $$

Now the total inventory cost $TC_{F}$ is a function of $m$ and $T_{R1}$ where both $m$ and $T_{R1}$ are decision variables. Now we can optimize i.e., minimize the total inventory cost $TC_{F} (m,T_{R1} )$ by obtaining the time taken $T_{R1}^{*}$ of our model by using the necessary condition

$$ \frac{{\partial TC_{F} (m,T_{R1} )}}{{\partial T_{R1} }} = 0 $$

for different value of m where the optimum value $m^{*}$ is obtained from those values of m for which the total cost is minimum. To ensure that the objective function is convex, the derived value of $TC_{F} (m^{*} ,T_{R1}^{*} )$ must satisfy the sufficient condition:

$$ TC_{F} \left( {m^{*} - 1,T_{R1} } \right) \ge TC_{F} \left( {m^{*} ,T_{R1} } \right) \le TC_{F} \left( {m^{*} + 1,T_{R1} } \right) $$

Since the total inventory cost function (Eq. 30) is a nonlinear equation and finding $\frac{{\partial TC_{F}^{2} (m,T_{R1} )}}{{\partial T_{R1}^{2} }}$ is extremely complicated, closed form solution cannot be derived. This means that the optimal solution cannot be guaranteed. However, by means of empirical experiments, one can indicate that Eq. (30) is convex for a small value of $T_{R1}$. The optimal value of $T_{R1}$ can be obtained by using iterative method. The mathematical software MATLAB 2013 is used to validate the empirical experiment results.

5 Numerical illustration and sensitivity analysis

In this section, a numerical example is given to demonstrate the proposed inventory model. Sensitivity analysis is also provided in order to present the managerial insights of the proposed model.

5.1 Numerical example

5.1.1 Example problem

In this section, the present study provides the following numerical example to illustrate the theoretical results as reported in Sect. 4 with the parameter values of the inventory system: Assume that a manufacturing system has a production rate 7700 units per cycle with the demand given by $\beta \left( {as} \right)^{ - \rho }$ where the selling price is $40 per unit and the rate of increase is 0.3. The retailer has to invest $1 for production setup per replenishment cycle, $15 for rework setup per cycle, $3 for producing one unit and $2 to rework one unit of items. The rate of deterioration is 0.04 per unit per cycle and the rate of deterioration is reduced by the function $\theta (1 - exp( - 0.1\epsilon )$ by using preservation technology investment. The retailer has to keep the qualified and unqualified items in the store which cost him $1.3 and 25 respectively per unit item per replenishment cycle. Let the percentage of producing good quality items is 0.75 and the remaining portion is defective. Among the unqualified quality items, a portion 0.4 is considered to be scrap and the rest can be reworked. Since the inspection of deteriorating items is not perfect, a fraction 0.3 of deteriorating items cannot be removed from the inventory so that which are sold in the market. The rework-run starts when production ends, at a rate 3000 units per cycle. The additional parameters are summarized as follows: $\beta = 5000$, $\gamma = 0.7$, $\epsilon = 3.25$, $\delta = 0.6$, $M_{r} = 0.5$, $a = 0.5$, $r = 0.6$, $k_{p} = 3$, $k_{R} = 2$, $D_{c} = 6$, $p_{c} = 2$ and $s_{c} = 11$ (Fig. 3).

Fig. 3

Total cost per unit time in varies of m and $T_{R1}$

5.1.2 Solution

We observe from Fig. 4 that the total cost is minimum for $m^{*} = 3$ and $T_{R1}^{*} = 0.33208$ and the minimum total cost is $55,253.45.

Fig. 4

Total cost per unit time in varies of $T_{R1}$

From the Eqs. (31)–(35) we find the value of $T_{1}^{*}$, $T_{2}^{*}$, $T_{3}^{*}$, $T_{4}^{*}$ and $T_{5}^{*}$ and they are given below: $T_{1}^{*} = 0.2258$, $T_{2}^{*} = 0.0638$, $T_{3}^{*} = 0.0425$, $T_{4}^{*} = 0.1432$ and $T_{5}^{*} = 0.012$.

The optimal length of a replenishment cycle and the optimal length of the time horizon are respectively given by:$T_{R1}^{*} = 0.33208$ years and $T^{*} = 1.15144$ years.

The economic production quantity is obtained by

$$ Q^{*} = pT_{1} \approx 1739\;{\text{units}} . $$

That is, in order to minimize the total cost, the retailer has to produce 1739 units of items per replenishment cycle in 0.2258 year.

From Eq. (11), we obtain the maximum serviceable inventory during production run time:

$$ I_{ms} \approx 929\;{\text{units}} $$

i.e., at the end of replenishment cycle, the retailer has 929 units of serviceable items on hand which are used to sell in the market during non-replenishment-run time.

From Eq. (12), we get the no. of units which is to be sold under markdown price:

$$ I_{mp} \approx 87\;{\text{units}} $$

The retailer can be sold 87 units of products during the period of markdown policy.

From Eq. (20), we find the maximum inventory level of defective items during production run time:

$$ I_{mr} \approx 434\;{\text{units}} $$

At the starting of rework-run time, the retailer has 434 units of defective items on hand per replenishment cycle in which 174 units are scrap units.

From Eq. (13), we gain maximum serviceable inventory during rework run time:

$$ I_{sr} \approx 21\;{\text{units}} $$

i.e., at the end of rework-run, the retailer has 21 units of serviceable items on hand which are used to sell in the market during non-rework-run time.

5.2 Sensitivity analysis

In this section, we conduct a sensitivity analysis based on the numerical example. The sensitivity is conducted by changing one of the value of $p$, $p_{r}$, $a$, $s$, $\delta$, $r$, $M_{r}$, $h_{s}$ and $h_{r}$ at a time and keeping the others unchanged. We notice the changes by changing the parameters and operating costs by − 40, − 20, + 20 and + 40% and the results are shown in Tables 2 and 3.

Table 2 Sensitivity analysis of $Q$ and $T_{R1}$

Table 3 Sensitivity analysis of the total cost function $(TC_{F} )$ per unit time ($)

Table 2 shows that the optimal replenishment cycle time $(T_{R1}^{*} )$ decreases with the increasing $\delta$ and $h_{r}$ values and with the decreasing $p_{r}$ and $h_{s}$ values, it increases when the value of $h_{s}$ increases and the value of $p$, $\delta$ and $h_{r}$ decreases. The economic production quantity $(Q^{*} )$ increases when the value of $\delta$ and $h_{s}$ increases and the value of $h_{r}$ decreases, and it decreases with the increasing $p$, $\delta$, $h_{s}$ values and the decreasing $p$ and $h_{s}$ values. We also observe from Figs. 5 and 6 that the optimal replenishment cycle and economic production quantity are highly sensitive to the holding cost of the serviceable and defective items. When holing cost of the qualified items increases, $T_{R1}^{*}$ increases that means $Q^{*}$ also increases and if holding cost of unqualified items increases, then $T_{R1}^{*}$ decreases that means $Q^{*}$ also decreases. It means if we increase production quantity, the $T_{R1}^{*}$ increases and hence holding cost of the inventory increases. The optimal replenishment cycle and economic production quantity is insensitive to changes in the markdown rate and markdown price.

Fig. 5

$Q$ sensitivity analysis

Fig. 6

$T_{R1}$ sensitivity analysis

The optimal total cost per unit time for varying parameters is show in Table 3. We can see that the total cost per unit time tends to increase when the value of parameters increases. We observe that the model is highly sensitive to changes in the holding cost. As the holding cost increases the total cost also increases so we must keep low holding cost to get lesser value of total cost. It means if we hold any item for longer time with high value of holding cost, then obviously the total cost will increase whereas our aim is to reduce the total cost. We can also observe from Fig. 7 that the optimal total cost $\left( {TC_{F}^{*} } \right)$ is highly sensitive to changes in production rate (p) and production percentage ($\delta$) and less sensitive to the changes in the rework rate ($p_{r}$), markdown price (a), selling price (s), markdown percentage (r) and markdown rate ($M_{r}$). If markdown price increases obviously the optimal total cost increases and vice versa. So the retailer has to reduce markdown price to get less total cost. Since the variance of optimal total cost is superior when markdown is applied earlier, the retailer should apply at the optimum time period $T_{3}^{*}$. If the markdown price is different at a given markdown time, the variance of the replenishment cycle and production quantity is negligible but give totally different optimal total cost.

Fig. 7

Total cost per unit time sensitivity analysis

Managerial insights

This model is presented for a number of practical issues focused by the production oriented organizations like deterioration, defective, rework and screening. This model is an addition to this line of research. The approach implemented here provides the industry managers with more functional alternative because it prevents the defective products through the screening process and gives more accurately the economic replenishment lot size, replenishment-run time, number of units of defective and scrap items. This model emphasized that the inspection part in the model is suitable for industry managers who have an automated screening system to prevent the defective and deteriorating items. This model helps the company managers to produce high quality products by eliminating defective items through 100% screening process so that high quality items can be sold in marketplaces and consumers, which will create a positive impact on corporate image.

6 Conclusion

This paper deals with an EPQ model for deteriorating items with price dependent demand under markdown policy where the demand increases when price decreases. In practical, a retailer in supermarket has to deal with the problem of highly perishable seasonal product where the effect of deterioration is considerable. In this study, the preservation technology is taken into account to reduce the deterioration rate during the deterioration period of instantaneous deteriorating items. This model is appropriate for those perishable items, whose demand in market is low as compared to other items and they deteriorate continuously with time. This model gives optimal replenishment cycle time, economic production quantity and optimal total inventory cost accurately. The results exhibit that markdown offering time and markdown rate give significant contribution to optimize the total cost per unit time and a policy maker must be exceptionally watchful to set markdown offering time and markdown rate, because optimum policy is diverse for various cases. The model can also be extended to consider stochastic demand dependent rate instead of deterministic rate and Weibull deterioration rate instead of constant deterioration rate.

A few proposals for future research are:

• Imperfect inspection of ensuring quality (i.e., an inspector may classify a serviceable items to be defective (Type I error) and he may also classify an imperfect item to be serviceable (Type II error)) would be taken into account.

• Shortage can occur in a combination of backorders and lost-sales.

• Multiproduct multi-constraint problems can be developed and solved.