The impact of system deterioration and product warranty on optimal lot sizing with maintenance and shortages backordered

Abstract

The imperfect production system with continuous-time Markovian process for maintenance and warranty issues has been investigated in the existing literature. For practical purposes, we apply a discrete-time Markov chain to model this imperfect system with backordering in which the items produced are sold with free post-sale service warranty based on the failure occurrence for given items sold following a non-homogeneous Poisson process. In this paper, we take into account the effects of service warranty, system reliability, and maintenance on the optimal lot size policies in the production system in order to reflect the practical situation. These policies involve how much lot size per production run and maximum backordering quantity should be to achieve the minimum total expected cost under various warranty periods. By applying mathematical analytic solution procedures, we investigate the properties and bounds to obtain the optimal lot size. Moreover, we provide an algorithm for efficiently solving the problems described herein. An illustrative example is presented to verify our proposal model and through parameter sensitivity analysis to provide some managerial implications. The results of this study are a useful reference for operations/quality managers and researchers who are interested in determining levels of suitable production lot size and deploy a strategic plan that includes process maintenance and products warranty decisions with backordering to ensure that all items sold meet customer quality expectations.

1 Introduction

The traditional economic production quantity (EPQ) model is especially suitable for the production-inventory environment with a perfectly reliable production process. All items are produced with perfect quality. It is useful when production and consumption simultaneously occur in the production run length. Once the economic production quantity is known, we can obtain the optimal production time and achieve minimum cost or maximum profit to establish the optimal lot sizing policy for manufacturers. It should be emphasized that the above observations in the production environment are unrealistic. For example, the manufacturing process will not be degraded, many items are produced with 100% perfect quality when the production system is controlled, all items produced can meet the customers’ specifications required, but also with no involved post-sale warranty, machine capability is adequate, and so forth (see, for example, Sarkar et al. [33], Sinha et al. [40], and Taleizadeh et al. [43]). However, deterioration of manufacturing systems may reduce its availability and affect the overall production capacity in a real-production environment. Therefore, the production process may shift to an uncontrolled state from the controlled state after a period of time. In this situation, a proportion of the items produced might be nonconforming. Of course, it may not be practicable to meet customers’ demand. Obviously, these nonconforming products will incur subsequent reworking or replacement costs. Then some costs of service warranty, reverse logistics or loss of goodwill will be incurred if they pass them on to the customers. In one realistic situation, the manufacturer’s production-inventory and service warranty decisions have been given considerate attention for a deteriorating production system. In this scenario, Murthy [21] developed a structure required for product reliability with effective management to assist the manager in choosing appropriate warranty policies in the product’s marketing and sales. Wu et al. [47] also emphasized that the service warranty plays an important role in marketing. Wang and Sheu [46] developed a production lot size model in which the items produced are sold with free post-sale service offered by the manufacturer based on the production process following a general shift distribution. Sana [28] addressed an imperfect production system with allowable shortages to determine preventive maintenance and optimal buffer level for products sold with free minimal repair warranty. Chen et al. [3] considered the product’s selling price decision in post-sale service warranty under the assumption that the selling price depends on the warranty period offered by the manufacturer. Shang et al. [38] determined the optimal warranty policies by considering a condition-based renewable replacement and hybrid preventative maintenance effects. Recently, Tang et al. [45] investigated the decisions of pricing and warranty about products sold in a closed-loop supply chain. For promotion, Mitra [20] considered the situation in which the service warranty strategy can be expressed as a marketing tool in which a satisfactorily-extended policy with the warranty time and usage is determined to enhance consumers’ willingness to purchase products with warranty. Clearly, the product’s warranty is a very key factor in sales services as the manufacturer expects to gain customers’ trust in product quality. It is indeed a popular issue in this research field.

In an earlier study of imperfect production systems, Rosenball and Lee [25] assumed that certain percentage of defects in a production lot when the production process becomes out-of-control. Porteus [24] assumed that the manufactured products are defective with a 100% rate when the production process becomes out of control. However, due to production uncertainty, in both controlled and uncontrolled states, there is a fraction of the nonconforming items as shown by Djamaludin et al. [10]. Chung and Hou [4] extended the work of Rosenball and Lee [25] by considering shortages backordered for a deteriorating production system. Sana [29] considered that there are a certain fraction of defective items in an uncontrolled state in which the defective rate depends on the production run-length and the production rate. Sana and Chaudhuri [30] further considered the impact of system deterioration, machine breakdown and repair time with safety stocks on the optimal production decision. Recently, Hou et al. [11] extended the work of Porteus [24] in order to determine the optimal production lot size by considering rework and maintenance effects in which there is a proportion of the defective items in a production lot when the system becomes out of control. More recently, Khan et al. [13] developed two different inventory models for perishable items with advanced payment and linearly time-dependent increasing holding cost. In their model, the demand of the product is dependent on the selling price and advertisement as well. Khan et al. [14] investigated an inventory model to study the effects of advance payment with discount facility on supply decisions of deteriorating products where the demand function is considered to be price and stock dependent. Shaikh and Cárdenas-Barrón [35] discussed an EOQ inventory model for non-instantaneous deteriorating products with advertisement and price sensitive demand by considering trade credit is dependent on order quantity. Mishra et al. [18] and Shaikh et al. [36, 37] discussed their excellent models in this direction. Yang et al. [48] considered a two-phase maintenance framework in which imperfect inspection, preventive maintenance, and imperfect repair are incorporated to measure the expected net revenue for a single-component system with random defect time and delay time. Khakzad and Gholamian [12] considered the effect of inspection times on average deterioration rate so as to minimize the cost function by establishing the optimal number of inspections. Other related studies can be found in the works of Bhunia et al. [2], Roy and Sana [9], Pal and Mahapatra [22], and Panda et al. [23]. Researchers, who are interested in this topic, should pay attention to the above references.

It should be noted that, in all of the above-mentioned models, it was assumed that shortages backordered are not allowed. However, shortages may sometimes occur due to uncertainty of the product’s quality, lead time or labour problems. Thus, clearly, shortages are often permitted and are completely backordered practically. For example, retailers or suppliers may use planned shortages when sales revenue cannot make up for the shortages; Or the customers are usually willing to wait when they decide to buy a new brand product even if the product is out of stock or there are not enough stocks to meet their needs. On the issue of shortage cases, Roy et al. [26] presented an economic production lot-size model for defective items with stochastic demand, backlogging and rework. Shaikh et al. [34] studied a fuzzy inventory model for a deteriorating item with variable demand and permissible delay in payments. In this work, it is considered that the shortage follows the inventory policy. Recently, Roy and Sana [27] further developed an inter-dependent reduction strategy of lead time and ordering cost in a two-stage single vendor and single buyer supply chain model with a variable backorder and price-sensitive stochastic demand. In addition, a few works have examined sustainability issues in production-inventory models. Taleizadeh et al. [44] incorporated environmental issues to establish the optimal policies for the sustainable economic production quantity (EPQ) model by taking account of different shortage situations. Mishra et al. [19] considered the case when the carbon emission rate can be controlled by investing in green technology for a sustainable production quantity model with shortages. Bhattacharyya and Sana [1] developed a lot-sizing model by considering green technology and capital invested for setup on eco-friendly manufacturing system under probabilistic demand. Based upon the above arguments, the shortages cannot be ignored and are worth being discussed in this study.

The purpose of this study is two-fold. Firstly, we extend the work of Hou et al. [11] in order to develop a Markovian EPQ model with shortages backordered and for products sold with a free service warranty under a non-homogeneous Poisson process with increasing intensity function. Besides, we present Theorem 1 in which we prove that there is a unique optimal solution. Our Theorem 2, on the other hand, provides the bounds for solving the optimal solution. Secondly, we present an algorithm to efficiently determine the optimal solution and assess its performance by an illustrative example. The rest of the paper is designed as follows. First, the basic assumptions and notations are provided in Sect. 2. Then, in Sect. 3, we formulate the proposed problem as a cost minimization model. By following the mathematical models, we provide some properties to indicate that the unique optimal lot size is bounded in a finite interval and we also present an algorithm to efficiently determine the optimal lot size. In Sect. 4, a numerical example and sensitivity analysis are presented in order to illustrate the model and to provide managerial insights. Finally, in Sect. 5, conclusions and directions for future researches of this and other related models are given.

2 Notation and assumptions

2.1 Notations

In order to develop an imperfect EPQ model with shortages backordered, the following notations are needed.

d:

Demand per unit time

p:

Production per unit time, $p > d$

C:

Production cost per unit

$C_k$:

Setup cost per production cycle

$C_h$:

Holding cost per unit per unit time

$C_m$:

Adjustment cost for restoring the system into an operational (in-control) state from an out-of-control state by maintenance actions

$C_r$:

Repair cost incurred at an item sold with service warranty

$C_b$:

Stock-out cost per unit per unit time

$a_{ij}$:

The probability of a transition from state i to state j during the production period of a product, and state set $i,j\in \{0,1\}$ where 0 and 1 represent in-control state and out-of-control state, respectively

$\theta _0$:

The percentage of a nonconforming item being finished when the system is in-control during the production period for the item

$\theta _1$:

The percentage of a nonconforming item being finished when the system is out-of-control during the production period for the item, where $\theta _0 < \theta _1$

W:

Warranty period

$V_1$:

The mean number of free service repairs per unit item for conforming items sold within the warranty period

$V_2$:

The mean number of free service repairs per unit item for nonconforming items sold within the warranty period, where $V_1 < V_2$

I:

Maximum inventory level

N:

The number of nonconforming items produced for each production run

T:

Production cycle length

$T_1$:

Production time when backorder is replenished

$T_2$:

Production time when inventory builds up

$T_3$:

Time period when there is no production and inventory depletes

$T_4$:

Time period when there is no production and shortages occurs

B:

Maximum amount of backlogged demand per lot (decision variable)

y:

Production quantity per lot (decision variable)

2.2 Assumptions

The following assumptions are used in our model.

• 1. The system deteriorating behavior can be described by a two-state Markov chain with transition matrix A given by A=$\left\{ a_{ij}\right\}$, where the state set $i,j \in$ {in-control, out-of-control}. We note that the state j = “out-of-control” state is an absorbing state, that is, $a_{jj}$ = 1 and no other state is accessible from it. In other words, the system will remain in the out-of-control state until the end of a production run when the system shifts to the out-of-control state.

• 2. Due to the uncertain nature of the manufacturing process, all items sold may be either conforming or nonconforming which depend on whether its specifications can achieve desired quality. It is reasonable to assume that a nonconforming item is more likely to fail than a conforming item.

• 3. The failure of components associated with conforming (or nonconforming) items is a non-homogeneous Poisson process with an increasing intensity function $v_1(t)$ (or $v_2(t)$).

• 4. Shortages are completely backordered.

• 5. The demand rate is known and constant.

Fig. 1

The inventory level for imperfect EPQ model with shortages backordered

3 Mathematical formulation of the model

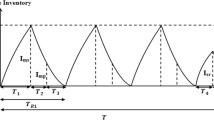
Figure 1 represents an imperfect production system with allowable backorders. The production cycle is divided into four major inventory stages in which time for stage i is indicated by $T_i$. We note that the production cycle length is equal to $T = y/d$ and T= $T_1 + T_2 + T_3 + T_4$. Based on the four stages shown in Fig. 1, the total expected cost incurred in a production cycle discussed in this paper include the production cost, inventory holding cost, backorder cost, restoration cost, and the post-sale warranty cost which are derived as follows:

The production cost  The production cost per cycle, $\mathrm{PC}$, is given by

$$\begin{aligned} \text {The production cost }\mathrm{PC}=C_k+Cy. \end{aligned}$$

(1)

The holding cost  The inventory holding cost will occur during $T_2$ and $T_3$. We note that $T_2 = I/(p-d)$ and $T_3 = I/d$, where $I=y(1-d/p)-B$ represents the maximum inventory level. Hence, we can easily derive the holding cost per cycle, HC, as shown below:

$$\begin{aligned} HC=\dfrac{C_h\left[ y\left( 1-d/p\right) -B\right] ^2}{2d\left( 1-d/p\right) }. \end{aligned}$$

(2)

The backordering cost  The backordering cost will occur during $T_1$ and $T_4$, in which $T_1=B/(p-d)$ and $T_4=B/d$. So, the backordering cost per cycle, SC, is given by

$$\begin{aligned} SC=\dfrac{C_bB^2}{2d\left( 1-d/p\right) }. \end{aligned}$$

(3)

The restoration cost  We note that the restoration cost is only incurred when the production process is out-of-control at the end of a production run for a lot size y. Hence, the expected restoration cost per cycle, RC, is given by

$$\begin{aligned} RC=C_m\left[ 1-\left( a_{00}\right) ^y\right] . \end{aligned}$$

(4)

The warranty cost  Before deriving the expected post-sale service warranty cost, we need the following Lemma.

Lemma

The expected mean number E[N] of nonconforming items N sold in a lot size y is given by

$$\begin{aligned} E[N]=\theta _1y-\left( \theta _1-\theta _0\right) \sum \limits _{l=1}^y\left( a_{00}\right) ^l. \end{aligned}$$

(5)

Proof

In a lot of size y, we note that the probability distribution of number of items produced in the in-control state, L, is given as follows:

$$\begin{aligned} P_r\{L=l\} = \left\{ \begin{array}{ll} (a_{00})^l[1-a_{00}], &{}\quad \hbox { if ~~}\ 0\leqq l<y \\ \text{( }a_{00})^y, &{}\quad \hbox { if ~~}\ l=y. \\ \end{array} \right. \end{aligned}$$

Then, clearly, the expected value of L is given by

$$\begin{aligned} E[L]=(1-a_{00})\sum _{l=1}^{y-1}l(a_{00})^l+y(a_{00})^y =\sum _{l=1}^{y}(a_{00})^l. \end{aligned}$$

(6)

Moreover, the number of nonconforming items in a lot size y becomes

$$\begin{aligned} N=\theta _0L+\theta _1(y-L). \end{aligned}$$

Hence, the expected value E[N] of N is derived as follows:

$$\begin{aligned} E[N]=\theta _1y-(\theta _1-\theta _0)\sum _{l=1}^{y} (a_{00})^l. \end{aligned}$$

The proof of the Lemma is thus completed. $\square$

We note that the failure of the components associated with conforming (or nonconforming) items is non-homogeneous Poisson process with an increasing intensity function $v_1$(t) (or $v_2$(t)). Therefore, for a given item sold under free service warranty, we have

$$\begin{aligned} V_1=\int _0^Wv_1(t)~dt ~~\text {or}~~ V_2=\int _0^Wv_2(t)~dt, \end{aligned}$$

where $V_1$ (or $V_2$) represents the mean number of free service repairs per unit item for conforming (or nonconforming) items sold in the interval (0, W), where $V_1 < V_2$.

Based on the above Lemma, we know that the mean number of failures under warranty with free service repairs for the sold items, denoted by ER, is given by

$$\begin{aligned} ER=\left( y-E[N]\right) V_1+E[N]V_2. \end{aligned}$$

(7)

Hence, we have the expected warranty cost for the sold items per cycle as follows:

$$\begin{aligned} C_W=C_r\left\{ yV_1+\left( V_2-V_1\right) \left[ \theta _1y-\left( \theta _1-\theta _0\right) \sum _{l=1}^y\left( a_{00}\right) ^l\right] \right\} . \end{aligned}$$

(8)

Consequently, the total expected cost per cycle, $\mathrm{TCPC}(y,B)$, is given by

$$\begin{aligned} \mathrm{TCPC}(y, B)= & {} C_k+Cy+\dfrac{C_h\left[ y\left( 1-d/p\right) -B\right] ^2}{2d\left( 1-d/p\right) }+\dfrac{C_bB^2}{2d\left( 1-d/p\right) }\nonumber \\&+C_m\left[ 1-\left( a_{00}\right) ^y\right] +C_ryV_1+C_r\left( V_2-V_1\right) \left[ \theta _1y-\left( \theta _1-\theta _0\right) \sum _{l=1}^y\left( a_{00}\right) ^l\right] .\nonumber \\ \end{aligned}$$

(9)

When the lot size is y, the total expected cost per cycle divided by the lot size is the total expected cost per item as shown below:

$$\begin{aligned} \mathrm{TCPI}(y, B)= & {} \dfrac{C_k}{y}+C+\frac{C_h\left[ y\left( 1-d/p\right) -B\right] ^2}{2yd\left( 1-d/p\right) }+\frac{C_bB^2}{2yd\left( 1-d/p\right) }\nonumber \\&+\dfrac{C_m\left[ 1-\left( a_{00}\right) ^y\right] }{y}+C_rV_1+\dfrac{C_r\left( V_2-V_1\right) }{y} \left[ \theta _1y-\left( \theta _1-\theta _0\right) \sum _{l=1}^y\left( a_{00}\right) ^l\right] .\nonumber \\ \end{aligned}$$

(10)

The main purpose in this study is to seek the optimal lot size and backordering quantity which minimize the $\mathrm{TCPI}(y,B)$ given in the Eq. (10). First, we show that the optimal backordering quantity, $B^*$, exists for given y. Next, we can get a unique $y^*$ that minimizes the total expected cost per item as shown in the Eq.  (12) below.

4 Optimal solution and algorithm

We know that the $\mathrm{TCPI}(y,B)$ is convex in B for given y because

$$\begin{aligned} \dfrac{\partial ^2\mathrm{TCPI}(y, B)}{\partial B^2}>0. \end{aligned}$$

Thus, upon setting

$$\begin{aligned} \dfrac{\partial \mathrm{TCPI}(y,B)}{\partial B}=0, \end{aligned}$$

we have

$$\begin{aligned} B^*=\dfrac{C_hy\left( 1-d/p\right) }{C_h+C_b}. \end{aligned}$$

(11)

which minimizes the $\mathrm{TCPI}(y,B)$ in the Eq. (10) for a given y. Substituting from the Eq.  (11) into the Eq. (10), the total expected cost per item, $\mathrm{TCPI}(y)$, can be expressed as the function of a single decision variable y as the following equation:

$$\begin{aligned} \mathrm{TCPI}(y)= & {} \dfrac{C_k}{y}+C+\dfrac{C_h\left( p-d\right) y}{2pd}\left( \dfrac{C_b}{C_h+C_b}\right) \nonumber \\&+\dfrac{C_m\left[ 1-\left( a_{00}\right) ^y\right] }{y}+C_rV_1+\dfrac{C_r\left( V_2-V_1\right) }{y}\left[ \theta _1y-\left( \theta _1-\theta _0\right) \sum _{l=1}^y\left( a_{00}\right) ^l\right] .\nonumber \\ \end{aligned}$$

(12)

Next, in order to obtain the optimal lot size $y^*$ which minimizes the $\mathrm{TCPI}(y)$ given in the Eq. (12), by taking the first derivative of the Eq. (12) with respect to y, we have that

$$\begin{aligned} \mathrm{TCPI}'(y)= & {} \dfrac{-C_k}{y^2}+\dfrac{C_h\left( p-d\right) }{2pd}\left( \dfrac{C_b}{C_h+C_b}\right) \nonumber \\&-\dfrac{1}{y^2}\left( C_m-\delta \right) \left[ 1-\left( a_{00}\right) ^y+y\left( a_{00}\right) ^y\ln \left( a_{00}\right) \right] ~~ (0<a_{00} <1), \end{aligned}$$

(13)

where

$$\begin{aligned} \delta = \dfrac{C_r\left( \theta _1-\theta _0\right) \left( V_2-V_1 \right) a_{00}}{1-a_{00}}, V_1=\int _0^Wv_1(t)~dt \end{aligned}$$

and

$$\begin{aligned} V_2=\int _0^Wv_2(t)~dt. \end{aligned}$$

At this point, we note that, for $y = y^*$ to be optimal, the necessary condition is that

$$\begin{aligned} \dfrac{d}{dy}\left\{ \mathrm{TCPI}(y)\right\} =0. \end{aligned}$$

Hence, the following theorems verify that there exists a unique $y^*$ satisfying the following condition:

$$\begin{aligned} \dfrac{d}{dy}\left\{ \mathrm{TCPI}(y)\right\} =0. \end{aligned}$$

and also that the optimal lot size $y^*$ is bounded in a finite interval.

Theorem 1

There exists a unique optimal lot size $y*$ which minimizes $\mathrm{TCPI}(y)$ given in the Eq. (12).

Proof

In view of the Eq. (13), let

$$\begin{aligned} \mathrm{TC}(y)=y^2\mathrm{TCPI}'(y). \end{aligned}$$

Then, for $0<a_{00}<1$, we have

$$\begin{aligned} \mathrm{TC}(y)=-C_k+\dfrac{C_h\left( p-d\right) }{2pd}\left( \dfrac{C_b}{C_h+C_b}\right) y^2-\left( C_m-\delta \right) \left[ 1-\left( a_{00}\right) ^y+y\left( a_{00}\right) ^y\ln \left( a_{00}\right) \right] \nonumber \\ \end{aligned}$$

(14)

Since $\mathrm{TC}(y)$ is a continuous function with

$$\begin{aligned} \lim \limits _{~y\rightarrow 0^+}\mathrm{TC}(y)= -k < 0~~\hbox { and}~~ \lim \limits _{~y\rightarrow \infty }\mathrm{TC}(y)=\infty > 0, \end{aligned}$$

there is at least a sign change of $\mathrm{TC}(y)$ from negative to positive as y increases. Additionally, the first derivative of $\mathrm{TC}(y)$ with respect to y, $\mathrm{TC}'(y)$, is given by

$$\begin{aligned} \mathrm{TC}'(y)=y\left[ \dfrac{c_h(p-d)}{pd}\left( \dfrac{C_b}{C_h+C_b} \right) -\left( C_m-\delta \right) \Big [ \ln \left( a_{00}\right) \Big ] ^2 \left( a_{00}\right) ^y \right] . \end{aligned}$$

(15)

Obviously, if $C_m\leqq \delta$, then $\mathrm{TC}'(y) > 0$ for all $y > 0.$ In this case, $\mathrm{TC}(y)$ is strictly increasing on $y > 0$. It shows that there exists a unique $y^*$ which satisfies the following condition:

$$\begin{aligned} \mathrm{TC}(y^*) = 0, \end{aligned}$$

that is, that $y^*$ is the optimal solution minimizing $\mathrm{TCPI} (y)$ given in the Eq. (12).

Alternatively, if $C_m > \delta$, we have

$$\begin{aligned} \mathrm{TC}'(y) \leqq 0~~~ (y\leqq y_g) \end{aligned}$$

and

$$\begin{aligned} \mathrm{TC}'(y)> 0 ~~ (y>y_g), \end{aligned}$$

where

$$\begin{aligned} y_g=\dfrac{1}{\ln \left( a_{00}\right) } \ln \left[ \dfrac{C_h\left( 1-d/p\right) \left( C_b/\left( C_h+C_b\right) \right) }{d\left( C_m-\delta \right) \Big ( \ln \left( a_{00} \right) \Big ) ^2}\right] \end{aligned}$$

and $y_g$ satisfies the following condition:

$$\begin{aligned} \mathrm{TC}'(y_g)=0. \end{aligned}$$

It implies that $\mathrm{TC}(y)$ is strictly decreasing on $(0, y_g)$ and, therefore, it strictly increasing on $(y_g, \infty )$ as y increases. As a result, $\mathrm{TC}(y)$ has the changes of signs just one time, so does $\mathrm{TCPI}'(y)$. Thus, clearly, $\mathrm{\mathrm{TC}}(y)$ is a convex function with respect to $y > y_g$. Therefore, there exists a unique $y^*$ satisfying the following condition:

$$\begin{aligned} \mathrm{TC}(y^*) = 0, \end{aligned}$$

that is, $y^*$ is the optimal solution which minimizes $\mathrm{TCPI}(y)$ in the Eq. (12).

By combining above results, Theorem 1 is proved. $\square$

Remark 1

The implication of Theorem 1 indicates the optimal lot size $y^*$ exists and is unique. For the case when $0<a_{00}<1,$ there is no explicit formula for writing the exact solution $y^*$, which can be found by using both bisection method and Newton’s method. However, we can verify that there exists an explicit formula to solve for $y^*$ in the cases of $a_{00}=0$ and $a_{00}=1$. Later on in this paper, both of them will be discussed to provide the bounds to obtain the optimal lot size $y^*$.

Remark 2

When $a_{00}=0,$ that is, the transition probability $a_{00}$ equals zero, the production process will transfer to an uncontrolled state (that is, $a_{01}=1$) at the start of the production run. From the Eq. (12), the total expected cost per item for $a_{00}=0$ becomes

$$\begin{aligned} \mathrm{TCPI}_0(y)=\dfrac{C_k+C_m}{y}+C+\dfrac{C_h\left( p-d\right) y}{2pd}\left( \dfrac{C_b}{C_h+C_b} \right) +C_r\theta _1V_2+C_r\left( 1-\theta _1\right) V_1.\nonumber \\ \end{aligned}$$

(16)

From the Eq. (16), there is an explicit expression for the optimal lot size $y_0^*$ is given by

$$\begin{aligned} y_0^*=\sqrt{\dfrac{2d\left( C_k+C_m\right) }{C_h\left( 1-d/p\right) }\left( \dfrac{C_h+C_b}{C_b}\right) }. \end{aligned}$$

(17)

Remark 3

It should be note that $y_0^*$ is the traditional EPQ model developed in [25] with a fixed setup cost $C_k$ and machine maintenance/restoration cost $C_m$, and a service repair cost incurred for a nonconforming (or a conforming) item which failed within the warranty period W with the rate $\theta _1V_2$(or $(1-\theta _1)V_1)$.

When $a_{00}=1$, that is, when the production process does not deteriorate and remains in the in-control mode to keep better operating condition with the fraction of nonconforming item $\theta _0.$ From the Eq. (12), the total expected cost per item for $a_{00}=1$ becomes

$$\begin{aligned} \mathrm{TPCI}_1(y)=\dfrac{C_k}{y}+C+\dfrac{C_h\left( p-d\right) y}{2pd}\left( \dfrac{C_b}{C_h+C_b}\right) +C_r\theta _0V_2+C_r\left( 1-\theta _0\right) V_1. \end{aligned}$$

(18)

From the Eq. (18), there is an explicit expression for the optimal lot size $y_1^*$ is given by

$$\begin{aligned} y_1^*=\sqrt{\dfrac{2dC_k}{C_h(1-d/p)}\left( \dfrac{C_h+C_b}{C_b}\right) }. \end{aligned}$$

(19)

It is also noticed that $y_1^*$ is the traditional EPQ model with a fixed setup cost $C_k$ and a service repair cost incurred for a nonconforming (or a conforming) item which failed within the warranty period W with rate $\theta _0V_2$(or $(1-\theta _0)V_1)$. In other words, the classical EPQ model with backordering quantity, given in the Eq. (19) is a special case in our proposed model when the system deterioration and a free-repair warranty policy are not considered.

As mentioned above, although there is no closed-form expression for $y^*$, the bounds of $y^*$ can be obtained by comparing it to the optimal solutions $y_0^*$ and $y_1^*$ given in the Eqs. (17) and (19), respectively. Hence, we have the following result.

Theorem 2

If $C_m \leqq \delta ,$ then $0<y^* \leqq y_1^* \leqq y_0^*$. Otherwise $y_1^*<y^*<y_0^*,$ where

$$\begin{aligned} y_0^*=\sqrt{\dfrac{2d\left( C_k+C_m\right) }{C_h\left( 1-d/p\right) }\left( \dfrac{C_h+C_b}{C_b}\right) } \end{aligned}$$

and

$$\begin{aligned} y_1^*=\sqrt{\dfrac{2dC_k}{C_h\left( 1-d/p\right) }\left( \dfrac{C_h+C_b}{C_b}\right) }. \end{aligned}$$

Proof

When $0<a_{00}<1$, by setting

$$\begin{aligned} u(y)=1-(a_{00})^y+y(a_{00})^y\ln (a_{00}), \end{aligned}$$

we can easily verify u(y) is a strictly increasing function of y and $0<u(y)<1$ for $y > 0$. In view of Theorem 1, we know that $\mathrm{TCPI}'(y)$ changes its sign exactly once from negative to positive as y increases. Hence, from the Eqs. (13) and (17), we have

$$\begin{aligned} \mathrm{TCPI}'(y_0^*)=\dfrac{C_m}{(y_0^*)^2}\left[ 1-u(y_0^*) \right] +\dfrac{\delta }{(y_0^*)^2}u(y_0^*). \end{aligned}$$

(20)

From the Eq. (20), we know that

$$\begin{aligned} \mathrm{TCPI}'(y_0^*)\geqq 0 = \mathrm{TCPI}'(y^*), \end{aligned}$$

which implies that $y^*\leqq y_0^*$. Furthermore, from the Eqs. (13) and (19), we have

$$\begin{aligned} \mathrm{TCPI}'(y_1^*)=-\dfrac{1}{(y_1^*)^2}\left( C_m-\delta \right) u(y_1^*). \end{aligned}$$

(21)

Therefore, from the Eq. (21), we see that

$$\begin{aligned} \mathrm{TCPI}'(y_1^*)\geqq 0 = \mathrm{TCPI}'(y^*)~~( C_m\leqq \delta ), \end{aligned}$$

which implies that $y^*\leqq y_1^*$. Similarly, for $C_m > \delta$, we have

$$\begin{aligned} \mathrm{TCPI}'(y_1^*)< 0 = \mathrm{TCPI}'(y^*), \end{aligned}$$

which implies that $y^*>y_1^*$.

Upon combining the above results, our demonstration of Theorem 2 is completed. $\square$

Remark 4

We know that the optimal lot size $(y^*)$ shown in Theorem 2 is less than the traditional EPQ $(y_1^*)$ as the restoration cost is relatively low compared to the warranty cost. However, the optimal lot size $(y^*)$ becomes more than the traditional EPQ $(y_1^*)$ as the restoration cost is higher than the warranty cost which incurred by nonconforming items. Using the bounds as shown in Theorem 2, a simplified and efficient search procedure. which is based on the bisection method, is provided for solving the optimal lot size $y^*$ as follows.

Algorithm

• Step 1: Let $\varepsilon = 0.001> 0$ and compute $y_0^*$ and $y_1^*$ using the Eqs. (17) and (19) , respectively.

• Step 2: If $C_m>\delta$, set $y_L=y_1^*$ , $y_U=y_0^*$ . Otherwise, set $y_L=0$ and $y_U=y_1^*$.

• Step 3: Set $y_{opt}=\dfrac{y_L+y_U}{2}$ .

• Step 4: If $\vert \mathrm{TC}(y_{opt})\vert$ $\leqq \varepsilon$ , go to Step 6. Otherwise, go to Step 5.

• Step 5: If $\mathrm{TC}(y_{opt})<0$ , set $y_L=y_{opt}$ ; however, if $\mathrm{TC}(y_{opt})>0$ and $y_U=y_{opt},$ then go to Step 3.

• Step 6: Set $y^*=y_{opt}$ and compute $B^*(y^*)$ and $\mathrm{TCPI}(y^*)$ by using the Eqs. (11) and (12), respectively.

5 An illustrative numerical example and sensitivity analysis

In this section we use a numerical example to illustrate the algorithm above and through parameter sensitivity analysis to summarise some managerial implications.

5.1 Numerical example

For numerical study, the following parameters values for a deteriorating system are considered:

$C_k = 100$ ($/setup), p = 2000 (items/year), d = 1000 (items/year), $C_h = 1$ ($/item/year), $C_b= 2$ ($/item/year), C = 10 ($/item), $C_r = 2$ ($/item), $C_m = 100$ ($/item), W = 2 (year), $\theta _0=0.1$, and $\theta _1=0.6$. Furthermore, suppose the failures of components associated with both the conforming and nonconforming items are non-homogeneous Poisson process with increasing intensity functions $v_1(t)$ = 0.2t and $v_2(t) = t$, respectively. Then, we have

$$\begin{aligned} V_1=\int _0^2 0.2t~dt=0.4~~~ and ~~~ V_2=\int _0^2t~dt=2. \end{aligned}$$

In this example, we solve the cases for reliable system with $a_{00} = 0.999$ and for unreliable system with $a_{00} = 0.75$, respectively.

5.2 Model solution and sensitivity analysis

By applying the Algorithm,The optimal lot size $(y^*)$, optimal backordering quantity $(B^*)$, and corresponding the total expected cost per item $(\mathrm{TCPI}^*)$ are obtained and summarized in Table 1. As shown in Theorem 2, we have the optimal lot size $y^*~(y^*=333.84)$ is less than the traditional $y_1^*~(y_1^*=774.60)$ for reliable system $(a_{00} = 0.999)$ since

$$\begin{aligned} C_m-\delta = -1818.1 < 0. \end{aligned}$$

However, we have the optimal lot size $y^* ~(y^* = 1079.56)$ is greater than the traditional $y_1^* ~(y_1^* = 774.60)$ for unreliable system $(a_{00} = 0.75)$ since

$$\begin{aligned} C_m-\delta = 94.2 > 0. \end{aligned}$$

Next, we present a sensitivity analysis to investigate the effects of transition probability $a_{00}$, warranty period W and restoration cost $C_m$ on decisions. For this, we experiment for different values of $a_{00}$, W and $C_m$. Table 2 and Figs. 2, 3, 4, 5 and 6 present the following numerical results:

• 1. Figure 2 presents the effects of the transition probability $a_{00}$ on the optimal lot size $y^*$. It is shown that the $y^*$ is very sensitive to $a_{00}$ when $a_{00}$ is close to 1.

• 2. We solve various warranty periods for $a_{00}$ = 0.999, 0.95, 0.75 cases and presented in Table 2. From Table 2, we can see that when the transition probability $a_{00}$ increases, both the optimal lot size and the expected cost per item decrease. It is shown that the impacts of the $a_{00}$ on the optimal lot size $y^*$ is more significant. On the other hand, we find out that $y^*$ decreases and $\mathrm{TCPI}^*$ increases as W increases, since a longer warranty period results in a higher warranty cost.

• 3. It should be noted that the expected proportion of nonconforming items can be reduced by process improvement, so as to decrease the failure occurrence of items sold within the warranty period and avoid a higher warranty cost. From Fig. 3, it is clear that the optimal lot size $y^*$ decreases as W increases.

• 4. Figure 3 shows that the optimal lot size $y^*$ is more sensitive to warranty period W for $a_{00}$ = 0.999 (that is, reliable system case). Similarly, Fig. 4 indicate that the expected cost $\mathrm{TCPI}^*$ is also more sensitive to warranty period W for $a_{00}$= 0.999 case.

• 5. From Fig. 5, we know that $y^*$ increases as $C_m$ increases. This result is reasonable since $y^*$ is an increasing function of $C_m$. We note that if W = 0 (taht is, without a product warranty), then $C_m>\delta$ (where $\delta =0$) and hence $y^* > y_1^*$ (where $y_1^*$ = 774.60) from Theorem 2. For W> 0, (that is, with a product warranty) when $C_m$ increase from 0, $y^*$ first is less than $y_1^*$ and then increases to be greater than $y_1^*$.

• 6. From Fig. 6, it is clear that if restoration cost $C_m$ increases, then the total expected cost per item $\mathrm{TCPI}^*$ increases under various periods W. In particular, the longer warranty period results in a higher total expected cost.

Table 1 Lot sizes and corresponding expected cost with reliable/unreliable production systems

Table 2 Lot sizes and corresponding expected cost under various warranty periods for the production systems

6 Managerial implications

We derive out some important managerial implications obtained from the results as mentioned above.

• 1. The expected proportion of nonconforming items can be reduced by process improvement, so as to decrease the failure occurrence of items sold within the warranty period and avoid a higher warranty cost. Therefore, the optimal lot size $y^*$ can be reduced as W increases and as illustrated in Fig. 3.

• 2. We note that the case for $a_{00}$ = 0.999 (for reliable system) can perform a lower cost performance under various warranty periods as shown in Fig. 4. This is, because the higher the $a_{00}$, the higher the process quality level obtained through correct maintenance activities, which will produce fewer lot sizes with good-quality items compared to unreliable case as shown in Table 2. It reveals that when the system or equipment status of in-of-control increases, this can reduce the total production cost and maintenance cost so the total expected cost decreases.

• 3. From Fig. 5, we find that under the normal one-year post-sale warranty, it is possible to obtain larger lot sizes than those of traditional EOQ/EPQ model when the restoration cost is relatively higher than the warranty cost as shown in Theorem 2. In this way, if the warranty period is extended, the expected total cost will increase. Therefore, it is important to perform appropriate warranty and maintenance actions as found in this study.

• 4. Another important managerial insight of our research is considering shortage possibility resulting from uncertainty of the product’s quality and system deterioration for a Markovian EPQ model. The model can be useful for operations/quality managers who are interested in determining levels of suitable production lot size and deploy a strategic plan that includes process maintenance and products warranty decisions with backordering to ensure that all items meet customer quality expectations.

Fig. 2

The effect of $a_{00}$ on $y^*$

Fig. 3

The effect of W on $y^*$

Fig. 4

The effect of W on $\mathrm{TCPI}^*$

Fig. 5

The effect of $C_m$ on $y^*$

Fig. 6

The effect of $C_m$ on $\mathrm{TCPI}^*$

7 Concluding remarks and observations

In this paper, we have successfully employed a two-state discrete-time Markov chain to model an imperfect production system with shortages backordered for products sold with a free-repair warranty under non-homogeneous Poisson process. We have minimized the total expected cost of the production system through the determination of the optimal lot size and backordering quantity. Since there is no closed-form expression for the optimal lot size, bounds are derived for the solution procedure. It is shown that the optimal lot sizing policy using our proposed model can perform significantly better than the traditional EPQ policy. This policy is supported by a numerical example, so from the practical point of view, this policy is valid and useful to the competitive business. Moreover, the effects of the model parameters on the optimal solution are carried out by using sensitivity analysis.

For future researches emerging from our present investigation, there are several ways to extend this study. For example, a possible research topic is to explore the effects of various warranty policies and marketing factors such as different pricing strategies. With a view to motivating interested readers, we have chosen to cite a number of other related recent works on the subject-matter of this investigation such as those by Chung et al. [5,6,7,8], Liao et al. [15,16,17], Srivastava et al. [41, 42], and by other authors. Other environment performance considering sustainability issues such as green production, green technology, and corporate social responsible can also be taken into account (see, for example, Sana [31, 32]).